基于扩展卡尔曼滤波的TDOA与AOA定位方法
AOA混合定位算法及其性能分析

文章编号1005-0388(2002)06-0633-04一种TDOA /AOA 混合定位算法及其性能分析!邓平李莉范平志(西南交通大学移动通信研究所,四川成都610031)摘要在蜂窝移动通信系统中,智能天线阵列的应用使得服务基站(BS )能提供较准确的移动台(MS )电波到达角(AOA )测量值,从而可以用于对移动台的定位估计。
文中对文献[1]的电波到达时间差(TDOA )定位算法进行了改进,提出了一种既能继承原算法的优良性能,又可充分利用AOA 测量值信息提高定位性能的TDOA /AOA 混合定位算法,该算法还具有解析表达式解。
仿真结果表明,只要AOA 测量值达到一定精度,该算法就能取得比文献[1]的单纯TDOA 定位算法更好的性能。
关键词到达时间差,到达角,移动台,加权最小二乘算法中图分类号TN929.53文献标识码AA hybrid TDOA /AOA location algorithm andits performance analysisDENG PingLI LiFAN Ping-zhi(Institute of Mobile Communication ,Southwest Jiaotong Uniuersity ,Chengdu Sichuan 610031,China )Abstract In ceiiuiar mobiie communication systems ,due to the appiication of smart array an-tenna ,it is possibie for serving base station (BS )to deiiver accurate angie of arrivai (AOA )measurement of mobiie station (MS )radio wave.In this paper ,a time difference of arrivai (TDOA )iocation aigorithm in reference [1]is extended to a TDOA /AOA hybrid iocation aigo-rithm which can not oniy inherit the good performance of the originai aigorithm ,but aiso im-prove the iocation accuracy by making fuii use of the AOA measurement.The new aigorithm ai-so has a ciosed-form soiution which has been derived in this paper.Simuiation shows that ,if a reasonabie precision of the AOA measurement is achieved ,much better iocation performance can be obtained ,compared with the singie TDOA iocation aigorithm in reference [1].Key wordsTDOA ,AOA ,MS ,WLS aigorithm1引言在蜂窝网络中提供对移动台(MS )的定位服务即将成为各种蜂窝网络必须具备的基本功能[2]。
基于TDOA的定位技术性能分析

基于TDOA的定位技术性能分析作者:杨雪峰吴琼来源:《卷宗》2011年第08期摘要:本文提出了一种能应用在无线传感器网络中,基于扩展卡尔曼滤波的TDOA定位方案:先利用测得的TDOA值进行定位,再将算法得出的目标节点估计值作为扩展卡尔曼的观测值进行滤波估计,以四个锚节点为例,进行了仿真分析。
该定位方案不需要节点间全局同步,能有效减小节点设计的额外硬件开销,降低了节点功耗和成本。
关键词:无线传感器网络;TDOA算法;扩展卡尔曼滤波的TDOA算法1 概述无线传感器网络(无线传感器网络,Wireless Sensor Network)是微机电系统(MEMS Micro-Electro-Mechanism-System)、片上系统(SOC,Syetem-On-Chip)和无线通信技术高度集成而孕育出的一种新型信息获取和处理模式。
在传感器网络的许多应用中,用户关心的一个重要问题是在什么位置或区域发生了特定事件。
节点定位问题是传感器网络诸多应用的前提,实现传感器节点的定位对各种应用有着及其重要的作用,也是传感器网络研究中的基础性问题和热点问题之一。
TDOA(Time Difference of Arrival)定位技术是目前在WSN定位系统中最具发展潜力的目标定位技术。
为了提高定位精度,本文提出一种基于时间测量值的无线传感器网络定位算法,该方法基本思想:采用改进的泰勒序列展开算法对目标节点进行初始位置估计,并用扩展卡尔曼滤波器在后台PC上对算法估计值进行集中滤波处理。
2 网络模型与参数获取本文将简要介绍适合于定位算法应用的户外传感器网络简单模型。
本文所讨论的传感器网络由许多未知位置且随机分布的SN (sensor node)传感器节点和几个已知位置的锚节点(beacon node)组成,如下图所示,所有节点都处于静止状态。
TDOA估计值的获取方法简述如下:锚节点周期性地向它射程内的待测目标SN节点及其他锚节点发射射频信标信号,若目标SN节点不在锚节点的射程内,我们可以通过将待监测的区域划分成几个小的子区域并增加锚节点的方法来处理。
三维TDOAAOA定位的扩展卡尔曼滤波仿真主程序
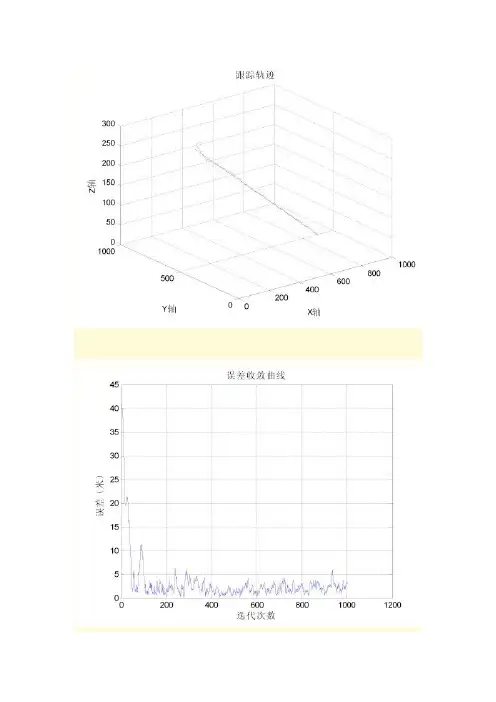
%% 三维TDOA/AOA定位的扩展卡尔曼滤波仿真主程序clcclearclose all%% 设置观测站分布N=4;%观测站个数%主站位于坐标原点x1=0;y1=0;z1=0;x2=1000;y2=0;z2=0;x3=0;y3=1000;z3=0;x4=1000;y4=1000;z4=0;XI=[x1,x2,x3,x4];YI=[y1,y2,y3,y4];ZI=[z1,z2,z3,z4];%% 产生观测数据%假设被定位对象匀速地从A点(100,300,300)运动到B点(900,700,0),单位:米Px=[100:0.8:900]';Py=[300:0.4:700]';Pz=[300:-0.3:0]';%假设采样时间间隔为1sT=1;%根据观测误差水平,产生各个观测站的观测量M=length(Px);%离散点数Alpha=zeros(M,N);Beta=zeros(M,N);Distance=zeros(M,N);Sigma_Alpha_Theta=1;%以角度形式表示的角度噪声标准差Sigma_Alpha=((Sigma_Alpha_Theta)/180)*pi;%转化为弧度表示的角度噪声方差Sigma_Beta_Theta=1.5;%以角度形式表示的角度噪声标准差Sigma_Beta=((Sigma_Beta_Theta)/180)*pi;%转化为弧度表示的角度噪声方差Sigma_Distance=2;%距离测量的标准差for n=1:NAlpha(:,n)=atan2(Py-YI(n),Px-XI(n))+Sigma_Alpha*randn(M,1);Beta(:,n)=atan2(Pz-ZI(n),sqrt((Px-XI(n)).^2+(Py-YI(n)).^2))+Sigma_Beta*randn(M, 1);Distance(:,n)=sqrt((Px-XI(n)).^2+(Py-YI(n)).^2+(Pz-ZI(n)).^2)+Sigma_Distance*ra ndn(M,1);endRho=Distance(:,2:end)-Distance(:,1)*ones(1,N-1);%% 使用扩展卡尔曼滤波进行定位SigmaU=0.005;%驱动噪声S0=[120,270,320,0.5,0.1,-0.4]';%初始状态向量P0=0.01*ones(6,6);%预测误差矩阵的初始值[MX,MY,MZ]=EKF_TDOA_AOA_3D(Alpha,Beta,Rho,XI,YI,ZI,SigmaU,Sigma_Alpha,Sigma_Bet a,Sigma_Distance,T,S0,P0);%% 绘图figureplot3(Px,Py,Pz,'b');xlabel('X轴');ylabel('Y轴');zlabel('Z轴');grid onaxis([0 1000 0 1000 0 300]);hold onplot3(MX,MY,MZ,'r');title('跟踪轨迹');%figureplot(MX-Px);xlabel('迭代次数');ylabel('误差(米)');title('X轴收敛曲线');grid on%figureplot(MY-Py);xlabel('迭代次数');ylabel('误差(米)');title('Y轴收敛曲线');grid on%figureplot(MZ-Pz);xlabel('迭代次数');ylabel('误差(米)');title('Z轴收敛曲线');grid on%figureERR=sqrt((MX-Px).^2+(MY-Py).^2+(MZ-Pz).^2);plot(ERR);xlabel('迭代次数');ylabel('误差(米)');title('误差收敛曲线');grid onfunction [X,AllX,Alldxy]=TDOA_AOA_3D(X0,Theta,Phi,Tau,xb,yb,Delta,K)% GreenSim团队原创作品,转载请注明% Email:greensim@% GreenSim团队主页:/greensim% [color=red]欢迎访问GreenSim——算法仿真团队→[url=http://blog.s /greensim]/greensim[/url][ /color]N=length(Theta);H=zeros(3*N-1,2*N+2);Rho=zeros(3*N-1,1);AllX=zeros(K,2*N+2);Alldxy=zeros(K,1);dxy=Inf;X=X0;counter=1;while dxy>Deltaxm=X(2*N+1);ym=X(2*N+2);x1=X(1);y1=X(2);for i=1:Nxi=X(2*i-1);yi=X(2*i);if xi==xmxi=xm+0.000001;endif yi==ymyi=ym+0.000001;endif xi==xbxi=xb+0.000001;endif yi==ybyi=yb+0.000001;endH(i,2*i-1)=-(yi-ym)/(xi-xm)^2/(1+(yi-ym)^2/(xi-xm)^2);H(i,2*i)=1/(xi-xm)/(1+(yi-ym)^2/(xi-xm)^2);H(i,2*N+1)=(yi-ym)/(xi-xm)^2/(1+(yi-ym)^2/(xi-xm)^2);H(i,2*N+2)=-1/(xi-xm)/(1+(yi-ym)^2/(xi-xm)^2);Rho(i,1)=atan((yi-ym)/(xi-xm));H(N+i,2*i-1)=-(yi-yb)/(xi-xb)^2/(1+(yi-yb)^2/(xi-xb)^2);H(N+i,2*i)=1/(xi-xb)/(1+(yi-yb)^2/(xi-xb)^2);Rho(N+i,1)=atan((yi-yb)/(xi-xb));if i>=2H(2*N+i-1,1)=-1/2/(x1^2-2*x1*xm+xm^2+y1^2-2*y1*ym+ym^2)^(1/2)*(2*x1-2*xm)-1/2/( x1^2-2*x1*xb+xb^2+y1^2-2*y1*yb+yb^2)^(1/2)*(2*x1-2*xb);H(2*N+i-1,2)=-1/2/(x1^2-2*x1*xm+xm^2+y1^2-2*y1*ym+ym^2)^(1/2)*(2*y1-2*ym)-1/2/( x1^2-2*x1*xb+xb^2+y1^2-2*y1*yb+yb^2)^(1/2)*(2*y1-2*yb);H(2*N+i-1,2*i-1)=1/2/(xi^2-2*xi*xm+xm^2+yi^2-2*yi*ym+ym^2)^(1/2)*(2*xi-2*xm)+1/ 2/(xi^2-2*xi*xb+xb^2+yi^2-2*yi*yb+yb^2)^(1/2)*(2*xi-2*xb);H(2*N+i-1,2*i)=1/2/(xi^2-2*xi*xm+xm^2+yi^2-2*yi*ym+ym^2)^(1/2)*(2*yi-2*ym)+1/2/ (xi^2-2*xi*xb+xb^2+yi^2-2*yi*yb+yb^2)^(1/2)*(2*yi-2*yb);H(2*N+i-1,2*N+1)=1/2/(xi^2-2*xi*xm+xm^2+yi^2-2*yi*ym+ym^2)^(1/2)*(-2*xi+2*xm)-1 /2/(x1^2-2*x1*xm+xm^2+y1^2-2*y1*ym+ym^2)^(1/2)*(-2*x1+2*xm);H(2*N+i-1,2*N+2)=1/2/(xi^2-2*xi*xm+xm^2+yi^2-2*yi*ym+ym^2)^(1/2)*(-2*yi+2*ym)-1 /2/(x1^2-2*x1*xm+xm^2+y1^2-2*y1*ym+ym^2)^(1/2)*(-2*y1+2*ym);Rho(2*N+i-1,1)=sqrt((xi-xm)^2+(yi-ym)^2)+sqrt((xi-xb)^2+(yi-yb)^2)-sqrt((x1-xm) ^2+(y1-ym)^2)-sqrt((x1-xb)^2+(y1-yb)^2);endendY=[Theta;Phi;Tau]-Rho;X=X+DX;AllX(counter,:)=X';Alldxy(counter,1)=dxy;counter=counter+1;if counter>KreturnendendAllX=AllX(1:counter-1,:);Alldxy=Alldxy(1:counter-1,1);。
基于扩展卡尔曼滤波的TDOA与AOA定位方法
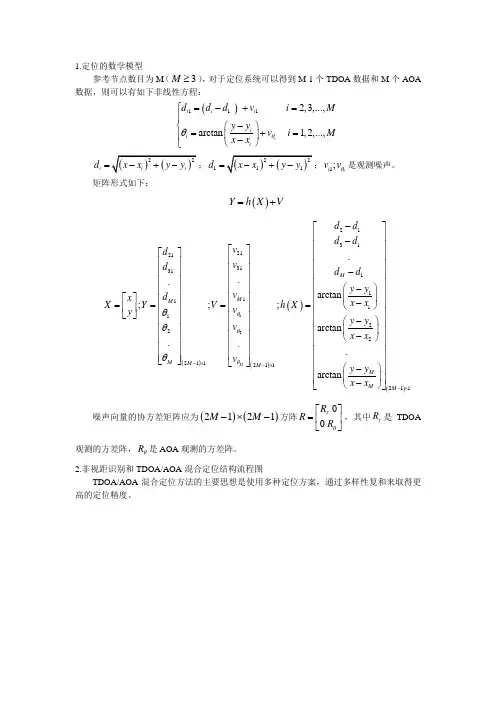
1.定位的数学模型参考节点数目为M (3M ≥),对于定位系统可以得到M-1个TDOA 数据和M 个AOA 数据,则可以有如下非线性方程:()1112,3,...,arctan 1,2,...,i i i i i ii d d d v i M y y v i Mx x θθ=-+=⎧⎪⎛⎫⎨-=+= ⎪⎪-⎝⎭⎩()()22i i i d x x y y =-+-;()()22111d x x y y =-+-;1;i i v v θ是观测噪声。
矩阵形式如下:()Y h X V =+()()()12213121213131111111222211211...arctan ;;;arctan ...arctan M M M M M M M M M d d d d v d v d d d y y v d x x x X Y V h X v y y y v x x v y y x x θθθθθθ-⨯-⨯-⎡-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎛⎫⎢⎥-⎢⎥ ⎪⎢⎥⎡⎤⎢⎥-====⎝⎭⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎛⎫-⎢⎥⎢⎥ ⎪-⎢⎥⎝⎭⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎛⎫- ⎪-⎝⎭⎣()211M -⨯⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎦ 噪声向量的协方差矩阵应为()()2121M M -⨯-方阵00R R R τθ⎡⎤=⎢⎥⎣⎦,其中R τ是TDOA观测的方差阵,R θ是AOA 观测的方差阵。
2.非视距识别和TDOA/AOA 混合定位结构流程图TDOA/AOA 混合定位方法的主要思想是使用多种定位方案,通过多样性复和来取得更高的定位精度。
NLOS 识别和TDOA/AOA 混合定位结构图3.NLOS 识别假设参与定位的目标节点数目为M ,目标节点向参考节点发送信号的传播时间为i τ,则距离为:i i r c τ=。
取K 个观察时刻,则第i 个参考节点和目标节点在k t 时刻的距离()i k r t 角度()i k t θ分别如下:()()()()()()()(),,,,,,1,2,...,0,1,....,1i k Los i k rang i k NLos i k i k Los i k bearing i k NLos i k r t r t n t r t i M k K t t n t t θθθ=++⎧⎪==-⎨=++⎪⎩;()(),,,Los i k Los i k r t t θ分别是真实距离与真实角度;()(),,,rang i k bearing i k n t n t 分别是距离的观测噪声和角度的观测噪声;均为零均值的高斯白噪声,方差分别为22,r θσσ()(),,,NLos i k NLos i k r t t θ分别是由NLOS 引起的距离误差(服从指数分布)和角度误差(服从均匀分布);由NLOS 引起的误差与观测误差的分布不同,且有NLOS 引起的误差对TOA 测量值的影响很大,所以通过卡尔曼滤波器对数据进行处理,使TOA 估计更精确的逼近真实TOA ,以消除有NLOS 引起的误差。
基于TDOA和TOA的定位技术研究

本人签名:
导师签名:
日 期:
日 期:
摘要
摘要
无论是在民用系统还是在军用系统中,对目标的精确定位,都有着非常重要 的作用。有源定位、无源定位以及自定位是目前常见的三种目标定位问题。其中, 无源定位是在对目标不发射电磁波的条件下,通过测量辐射源诸如通信发射机、 雷达等的电磁波,来确定目标的位置信息。其定位方式决定了无源定位具有隐蔽 性强、不易被察觉的优点,因而使其成为现代一体化防空系统、远程预警系统以 及机载对敌等方面的重要组成部分,在电子对抗领域发挥着与日俱增的关键作用。 目前,在对目标的定位问题中,常用的定位参数主要有到达时差(TDOA)、到达时 间(TOA)、到达角(AOA)以及它们的混合参数等。
一 方 面 , 本 文 分 别 研 究 并 分 析 了 基 于 TDOA 信 息 的 静 止 目 标 和 基 于 TDOA/FDOA 信息的运动目标的定位算法。对于静止目标,主要介绍了几种经典 的 TDOA 无源定位算法,并分析了各自的定位性能;对于运动目标,主要研究了 几种常用的基于 TDOA 测量值和 FDOA 测量值的联合定位算法。
(2)第二章首先介绍了 TDOA 定位算法的基本原理以及估计 TDOA 值的主 要方法,然后重点介绍了 3 种典型的 TDOA 定位算法,包括加权最小二乘(WLS) 算法、泰勒级数法以及 Chan 算法,并分别分析比较了各算法的优缺点及其定位性 能。
(3)第三章首先介绍了一种近些年提出的多维尺度分析(MDS)算法以及它 在 TOA 定位问题中的应用,随后在此基础上对该算法进行改进,针对多运动基站 的 TOA 定位模型,提出了一种新的利用多个时刻 TOA 测量值的 MDS 定位算法, 该算法考虑了二阶误差项的影响,在传统 MDS 算法的基础上利用了多个时刻的基 站位置信息和 TOA 测量信息,进一步提高了定位精度。
CDMA 网络中TSOA AOA 定位跟踪技术

置进行多点测量,以实现等效的多台定位设备协同定位。
Sk +1 = Φ Sk + Wk
Tபைடு நூலகம்
(9)
其中, Sk=[xk yk vxk vyk] 是 tk 时刻的状态向量, (xk, yk)是目标 的位置坐标,(vxk, vyk)代表目标在 x 轴和 y 轴的速度;状态转 移矩阵为 Φ;噪声向量 Wk 的协方差矩阵为 Q,它们的定义 如下:
⎡1 ⎢0 Φ =⎢ ⎢0 ⎢ ⎣0 0 1 0 0 T 0⎤ ⎡0 ⎢ 0 T⎥ ⎥ , Q = ⎢0 ⎢0 1 0⎥ ⎢ ⎥ 0 1⎦ ⎣0 0 0 0⎤ 0 0 0⎥ ⎥ 2 0 σu 0 ⎥ 2⎥ 0 0 σu ⎦
Z k = h( S k ) + Vk
(11)
其中,Zk 是观测数据向量;h(Sk)是非线性变换;Vk 是观测噪 声, Vk 的协方差矩阵为
⎡σ 2 I R = ⎢ L M ×M ⎣ 0
0 ⎤ ⎥ σ θ I M ×M ⎦ 2 M ×2 M
2
2
数学模型
假设参与定位的定位设备个数为 M(M ≥ 1) 个,令 (x0,y0 ) 表示基站位置坐标, (xi,yi)表示第 i(i=1,2,… ,M)个定位设备的 位置坐标, (x,y)表示目标的位置坐标。 M 个定位设备利用基 站可以获得 M 个距离之和的观测数据:
T
式 (13)展开可得
(4)
T M (2 M ) T (2 M )
TDOA,AOA定位的扩展卡尔曼滤波定位算法Matlab源码
TDOA,AOA定位的扩展卡尔曼滤波定位算法Matlab源码TDOA/AOA定位的扩展卡尔曼滤波定位算法Matlab源码(2007-08-24 01:48:23) 标签:知识/探索function[MX,MY,SS]=ExtendedKalmanFilter(D1,D2,D3,A1,A2,A3,Flag1,FLAG2,S0,P0, SigmaR,SigmaAOA)%% TDOA/AOA定位的扩展卡尔曼滤波定位算法%% 输入参数列表% D1 基站1和移动台之间的距离% D2 基站2和移动台之间的距离% D3 基站3和移动台之间的距离% A1 基站1测得的角度值% A2 基站2测得的角度值% A3 基站3测得的角度值1×1矩阵,取值1,2,3,表明是以哪一个基站作为基准站计算TDOA数据的 % Falg1% FLAG2 N×3矩阵,取值0和1,每一行表示该时刻各基站的AOA是否可选择, % 1表示选择AOA数据,FLAG2并非人为给定,而是由LOS/NLOS检测模块确定% S0 初始状态向量,4×1矩阵% P0 预测误差矩阵的初始值,4×4的矩阵% SigmaR 无偏/有偏卡尔曼输出距离值的方差,由事先统计得到 % SigmaAOA 选择AOA数据的方差,生成AOA数据的规律已知,因此可以确定 %% 输出参数列表% MXM% Y%% 第一步:计算TDOA数据if Flag1==1TDOA1=D2-D1;TDOA2=D3-D1;elseif Flag1==2TDOA1=D1-D2;TDOA2=D3-D2;elseif Flag1==3TDOA1=D1-D3;TDOA2=D2-D3;elseerror('Flag1输入有误,它只能取1,2,3');end%% 第二步:构造两个固定的矩阵%构造状态转移矩阵ΦPhi=[1, 0,0.025, 0;0, 1, 0,0.025;0, 0, 1, 0;0, 0, 0, 1]; %构造W的协方差矩阵QSigmaU=0.00001;%噪声方差取很小的值Q=[0, 0, 0, 0;0, 0, 0, 0;0, 0,SigmaU, 0;0, 0, 0,SigmaU]; %% 第三步:输出数据初始化N=length(D1);MX=zeros(1,N);MY=zeros(1,N);MX(1)=S0(1);MY(1)=S0(2);SS=zeros(4,N);SS(:,1)=S0;%% 第四步:以下是迭代过程for i=2:NFlag2=FLAG2(i,:);%当前各信道环境的LOS/NLOS判据R=FunR(SigmaR,SigmaAOA,Flag2);%调用产生R矩阵的子函数S1=Phi*S0;%由状态方程得到的预测值H=FunH(S1,Flag1,Flag2);%调用产生H矩阵的子函数P1=Phi*P0*(Phi')+Q;%计算上述预测值的协方差矩阵K=P1*(H')*inv(H*P1*(H')+R);%计算滤波增益(加权系数)Z=FunZ(TDOA1,TDOA2,A1,A2,A3,SigmaR,SigmaAOA,Flag2,i);%调用构造观察向量的子函数hS1=FunhS1(S1,Flag1,Flag2);%调用构造观测值的估计值向量的子函数S2=S1+K*(Z-hS1);%加权得到滤波输出值%更新S0和P0P2=P1-K*H*P1;S0=S2;P0=P2;%记录滤波输出值MX(i)=S2(1);MY(i)=S2(2);SS(:,i)=S2;endfunction Z=FunZ(TDOA1,TDOA2,A1,A2,A3,SigmaR,SigmaAOA,Flag2,i) %调用构造观察向量的子函数m=sum(Flag2);Z=zeros(2+m,1);Z(1)=TDOA1(i);Z(2)=TDOA2(i);if Flag2(1)==0&&Flag2(2)==0&&Flag2(3)==0%空语句elseif Flag2(1)==1&&Flag2(2)==0&&Flag2(3)==0Z(3)=A1(i);elseif Flag2(1)==0&&Flag2(2)==1&&Flag2(3)==0Z(3)=A2(i);elseif Flag2(1)==0&&Flag2(2)==0&&Flag2(3)==1Z(3)=A3(i);elseif Flag2(1)==1&&Flag2(2)==1&&Flag2(3)==0Z(3)=A1(i);Z(4)=A2(i);elseif Flag2(1)==1&&Flag2(2)==0&&Flag2(3)==1Z(3)=A1(i);Z(4)=A3(i);elseif Flag2(1)==0&&Flag2(2)==1&&Flag2(3)==1Z(3)=A2(i);Z(4)=A3(i);elseif Flag2(1)==1&&Flag2(2)==1&&Flag2(3)==1Z(3)=A1(i);Z(4)=A2(i);Z(5)=A3(i);elseerror('Flag2格式不正确,它的元素只能取0或者1'); endfunction R=FunR(SigmaR,SigmaAOA,Flag2)%% 产生R矩阵的子函数m=sum(Flag2);B=[-1,1,0;-1,0,1];R11=B*[SigmaR,0,0;0,SigmaR,0;0,0,SigmaR]*(B');R12=zeros(2,m);R21=zeros(m,2);if m==0R22=[];elseif m==1R22=SigmaAOA;elseif m==2R22=[SigmaAOA, 0;0,SigmaAOA]; elseif m==3R22=[SigmaAOA, 0, 0;0,SigmaAOA, 0;0, 0,SigmaAOA];elseerror('Flag2格式不正确,它的元素只能取0或者1'); end R=[R11,R12;R21,R22];function hS1=FunhS1(S1,Flag1,Flag2)%% 构造观测值的估计值向量的子函数%提取估计的移动台坐标x=S1(1);y=S1(2);%三个基站的横纵坐标x1=0;y1=0;x2=5;y2=8.66;x3=10;y3=0;%计算移动台到三个基站的距离(估计值)d1=((x-x1)^2+(y-y1)^2)^0.5;d2=((x-x2)^2+(y-y2)^2)^0.5;d3=((x-x3)^2+(y-y3)^2)^0.5;M=2+sum(Flag2);hS1=zeros(M,1);if Flag1==1%以第一个基站为基准计算TDOA数据hS1(1)=d2-d1;hS1(2)=d3-d1;elseif Flag1==2%以第二个基站为基准计算TDOA数据hS1(1)=d1-d2;hS1(2)=d3-d2;elseif Flag1==3%以第三个基站为基准计算TDOA数据hS1(1)=d1-d3;hS1(2)=d2-d3;elseerror('Flag1格式不正确,它只能取1,2,3');endh1=atan2(y-y1,x-x1);h2=atan2(y-y2,x-x2);h3=atan2(y-y3,x-x3);if Flag2(1)==0&&Flag2(2)==0&&Flag2(3)==0%空语句elseif Flag2(1)==1&&Flag2(2)==0&&Flag2(3)==0hS1(3)=h1;elseif Flag2(1)==0&&Flag2(2)==1&&Flag2(3)==0hS1(3)=h2;elseif Flag2(1)==0&&Flag2(2)==0&&Flag2(3)==1hS1(3)=h3;elseif Flag2(1)==1&&Flag2(2)==1&&Flag2(3)==0hS1(3:4)=[h1;h2];elseif Flag2(1)==1&&Flag2(2)==0&&Flag2(3)==1hS1(3:4)=[h1;h3];elseif Flag2(1)==0&&Flag2(2)==1&&Flag2(3)==1hS1(3:4)=[h2;h3];elseif Flag2(1)==1&&Flag2(2)==1&&Flag2(3)==1hS1(3:5)=[h1;h2;h3];elseerror('Flag2格式不正确,它的元素只能取0或者1'); end。
03TDOA_AOA定位的扩展卡尔曼滤波算法MATLAB源代码
TDOA/AOA定位的扩展卡尔曼滤波算法MATLAB源代码TDOA/AOA是无线定位领域里使用得比较多的一种定位体制,扩展卡尔曼滤波器是最经典的非线性滤波算法,可用于目标的定位和动态轨迹跟踪。
function[MX,MY,SS]=ExtendedKalmanFilter(D1,D2,D3,A1,A2,A3,Flag1,FLAG2,S0,P0,SigmaR,SigmaA OA)%% TDOA/AOA定位的扩展卡尔曼滤波定位算法% GreenSim团队——专业级算法设计&代写程序% 欢迎访问GreenSim团队主页→/greensim%% 输入参数列表% D1 基站1和移动台之间的距离% D2 基站2和移动台之间的距离% D3 基站3和移动台之间的距离% A1 基站1测得的角度值% A2 基站2测得的角度值% A3 基站3测得的角度值% Falg1 1×1矩阵,取值1,2,3,表明是以哪一个基站作为基准站计算TDOA数据的% FLAG2 N×3矩阵,取值0和1,每一行表示该时刻各基站的AOA是否可选择,% 1表示选择AOA数据,FLAG2并非人为给定,而是由LOS/NLOS检测模块确定% S0 初始状态向量,4×1矩阵% P0 预测误差矩阵的初始值,4×4的矩阵% SigmaR 无偏/有偏卡尔曼输出距离值的方差,由事先统计得到% SigmaAOA 选择AOA数据的方差,生成AOA数据的规律已知,因此可以确定%% 输出参数列表% MX% MY%% 第一步:计算TDOA数据if Flag1==1TDOA1=D2-D1;TDOA2=D3-D1;elseif Flag1==2TDOA1=D1-D2;TDOA2=D3-D2;elseif Flag1==3TDOA1=D1-D3;TDOA2=D2-D3;elseerror('Flag1输入有误,它只能取1,2,3');end%% 第二步:构造两个固定的矩阵%构造状态转移矩阵ΦPhi=[1, 0,0.025, 0;0, 1, 0,0.025;0, 0, 1, 0;0, 0, 0, 1];%构造W的协方差矩阵QSigmaU=0.00001;%噪声方差取很小的值Q=[0, 0, 0, 0;0, 0, 0, 0;0, 0,SigmaU, 0;0, 0, 0,SigmaU];%% 第三步:输出数据初始化N=length(D1);MX=zeros(1,N);MY=zeros(1,N);MX(1)=S0(1);MY(1)=S0(2);SS=zeros(4,N);SS(:,1)=S0;%% 第四步:以下是迭代过程for i=2:NFlag2=FLAG2(i,:);%当前各信道环境的LOS/NLOS判据R=FunR(SigmaR,SigmaAOA,Flag2);%调用产生R矩阵的子函数S1=Phi*S0;%由状态方程得到的预测值H=FunH(S1,Flag1,Flag2);%调用产生H矩阵的子函数P1=Phi*P0*(Phi')+Q;%计算上述预测值的协方差矩阵K=P1*(H')*inv(H*P1*(H')+R);%计算滤波增益(加权系数)Z=FunZ(TDOA1,TDOA2,A1,A2,A3,SigmaR,SigmaAOA,Flag2,i);%调用构造观察向量的子函数hS1=FunhS1(S1,Flag1,Flag2);%调用构造观测值的估计值向量的子函数S2=S1+K*(Z-hS1);%加权得到滤波输出值%更新S0和P0P2=P1-K*H*P1;S0=S2;P0=P2;%记录滤波输出值MX(i)=S2(1);MY(i)=S2(2);SS(:,i)=S2;endfunction Z=FunZ(TDOA1,TDOA2,A1,A2,A3,SigmaR,SigmaAOA,Flag2,i)%调用构造观察向量的子函数m=sum(Flag2);Z=zeros(2+m,1);Z(1)=TDOA1(i);Z(2)=TDOA2(i);if Flag2(1)==0&&Flag2(2)==0&&Flag2(3)==0%空语句elseif Flag2(1)==1&&Flag2(2)==0&&Flag2(3)==0 Z(3)=A1(i);elseif Flag2(1)==0&&Flag2(2)==1&&Flag2(3)==0 Z(3)=A2(i);elseif Flag2(1)==0&&Flag2(2)==0&&Flag2(3)==1 Z(3)=A3(i);elseif Flag2(1)==1&&Flag2(2)==1&&Flag2(3)==0 Z(3)=A1(i);Z(4)=A2(i);elseif Flag2(1)==1&&Flag2(2)==0&&Flag2(3)==1 Z(3)=A1(i);Z(4)=A3(i);elseif Flag2(1)==0&&Flag2(2)==1&&Flag2(3)==1 Z(3)=A2(i);Z(4)=A3(i);elseif Flag2(1)==1&&Flag2(2)==1&&Flag2(3)==1 Z(3)=A1(i);Z(4)=A2(i);Z(5)=A3(i);elseerror('Flag2格式不正确,它的元素只能取0或者1'); endfunction R=FunR(SigmaR,SigmaAOA,Flag2)%% 产生R矩阵的子函数m=sum(Flag2);B=[-1,1,0;-1,0,1];R11=B*[SigmaR,0,0;0,SigmaR,0;0,0,SigmaR]*(B');R12=zeros(2,m);R21=zeros(m,2);if m==0R22=[];elseif m==1R22=SigmaAOA;elseif m==2R22=[SigmaAOA, 0;0,SigmaAOA];elseif m==3R22=[SigmaAOA, 0, 0;0,SigmaAOA, 0;0, 0,SigmaAOA];elseerror('Flag2格式不正确,它的元素只能取0或者1'); endR=[R11,R12;R21,R22];function hS1=FunhS1(S1,Flag1,Flag2)%% 构造观测值的估计值向量的子函数%提取估计的移动台坐标x=S1(1);y=S1(2);%三个基站的横纵坐标x1=0;y1=0;x2=5;y2=8.66;x3=10;y3=0;%计算移动台到三个基站的距离(估计值)d1=((x-x1)^2+(y-y1)^2)^0.5;d2=((x-x2)^2+(y-y2)^2)^0.5;d3=((x-x3)^2+(y-y3)^2)^0.5;M=2+sum(Flag2);hS1=zeros(M,1);if Flag1==1%以第一个基站为基准计算TDOA数据hS1(1)=d2-d1;hS1(2)=d3-d1;elseif Flag1==2%以第二个基站为基准计算TDOA数据hS1(1)=d1-d2;hS1(2)=d3-d2;elseif Flag1==3%以第三个基站为基准计算TDOA数据hS1(1)=d1-d3;hS1(2)=d2-d3;elseerror('Flag1格式不正确,它只能取1,2,3');endh1=atan2(y-y1,x-x1);h2=atan2(y-y2,x-x2);h3=atan2(y-y3,x-x3);if Flag2(1)==0&&Flag2(2)==0&&Flag2(3)==0%空语句elseif Flag2(1)==1&&Flag2(2)==0&&Flag2(3)==0 hS1(3)=h1;elseif Flag2(1)==0&&Flag2(2)==1&&Flag2(3)==0hS1(3)=h2;elseif Flag2(1)==0&&Flag2(2)==0&&Flag2(3)==1 hS1(3)=h3;elseif Flag2(1)==1&&Flag2(2)==1&&Flag2(3)==0 hS1(3:4)=[h1;h2];elseif Flag2(1)==1&&Flag2(2)==0&&Flag2(3)==1 hS1(3:4)=[h1;h3];elseif Flag2(1)==0&&Flag2(2)==1&&Flag2(3)==1 hS1(3:4)=[h2;h3];elseif Flag2(1)==1&&Flag2(2)==1&&Flag2(3)==1 hS1(3:5)=[h1;h2;h3];elseerror('Flag2格式不正确,它的元素只能取0或者1'); end。
基于TDOA和Kalman滤波的声音定位系统的设计
基于TDOA和Kalman滤波的声音定位系统的设计作者:王雷郝建新陈蔚蔚来源:《现代电子技术》2018年第19期摘要:使用单片机STM32F103ZET6为控制核心,通过以LM324芯片、LM567鉴频芯片为主组成的固定声音识别电路设计声音定位系统。
针对在固定音频信号采集过程中,由元器件本身以及周围环境等影响而产生的噪声误差,采用TDOA算法和Kalman滤波相结合的方式,对于TDOA算法的计算结果进行优化处理,得出音源位置的最优估计值。
经过运行调试,使用Kalman滤波之后,使得系统的定位精度得到较大的提高,实现对目标的快速稳定跟踪。
关键词:声音识别;声音定位; TDOA; Kalman滤波; STM32F103; Arduino中图分类号: TN710⁃34; TP273 文献标识码: A 文章编号: 1004⁃373X(2018)19⁃0161⁃04Abstract: A sound location system is designed by taking microcontroller STM32F103ZET6 as the control core, LM324 chip and LM567 frequency discrimination chip as the major components of fixed voice recognition circuit. In the acquisition process of fixed audio signal, the method combining TDOA algorithm and Kalman filtering is used to eliminate the noise error generated by components themselves and surrounding environment. The calculation result of the TDOA algorithm is optimized to get the optimal estimation value of voice source location. The debugging and running results show that the location accuracy of the system has been greatly improved by means of Kalman filtering, and the system can realize rapid and stable target tracking.Keywords: voice recognition; sound positioning; TDOA; Kalman filtering;STM32F103; Arduino聲音定位是一种应用广泛的技术[1],利用声学传感器以及与其相连的电子设备(MCU)和相关电路,处理接收到的声波信号,确定声源的位置[2]。
一种双站TDOA-AOA两步法无源定位方法[发明专利]
(19)中华人民共和国国家知识产权局(12)发明专利申请(10)申请公布号 (43)申请公布日 (21)申请号 201810641932.2(22)申请日 2018.06.21(71)申请人 电子科技大学地址 611731 四川省成都市高新区(西区)西源大道2006号(72)发明人 殷吉昊 梁婷欢 狄路杰 庄杰 万群 (74)专利代理机构 电子科技大学专利中心51203代理人 邹裕蓉(51)Int.Cl.G01S 5/06(2006.01)(54)发明名称一种双站TDOA-AOA两步法无源定位方法(57)摘要本发明公开了一种双站TDOA-AOA两步法无源定位方法,属于电子信息技术领域。
本发明所述方法包括如下步骤:矩阵化处理观测数据、求解辐射源位置的初始闭式解、求解位置向量的最终估计。
本发明将无源定位问题描述为一个带两个约束的优化问题,随后将该约束优化问题等价地化简为两个简单的、均存在最优闭式解的凸优化子问题,序贯接力地求解这两个凸优化子问题得到最终的最优解,给出辐射源的三维位置估计,实现辐射源的无源定位。
权利要求书1页 说明书4页 附图1页CN 108717177 A 2018.10.30C N 108717177A1.一种双站TDOA -AOA两步法无源定位方法,其特征在于,包括以下步骤:步骤1.矩阵化处理观测数据:利用两个观测站的观测测量值写出矩阵和向量其中,以提供二维到达角估计的观测站为右手直角坐标系的坐标原点,a为另一观测站的位置向量,为辐射源到两个观测站间距离差的测量值,I 3为3×3阶的单位矩阵,为测量方位角,为测量仰角,上标T表示转置,|| ||表示求向量2-范数;步骤2.求解辐射源位置的初始闭式解:利用凸优化强对偶理论和KKT最优解条件,求解下述凸优化问题的最小二乘解:s.t.2f T x≤0其中,x为待求解的位置变量,f=[0,0,0,-0.5]T ;求解得到x的初始闭式解其中为初始闭式解中的目标空间位置向量,为初始闭式解的第四个元素,表示辐射源到坐标原点的距离;步骤3.求解位置向量u的最终估计:基于广义不变量准则和泰勒级数展开技术处理下述优化问题:s.t.x T Bx=0得到位置向量u的最终估计其中,泰勒级数展开一阶导数矩阵泰勒级数展开误差向量03×1为3×1的零矩阵。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.定位的数学模型参考节点数目为M (3M ≥),对于定位系统可以得到M-1个TDOA 数据和M 个AOA 数据,则可以有如下非线性方程:()1112,3,...,arctan 1,2,...,i i i i i ii d d d v i M y y v i Mx x θθ=-+=⎧⎪⎛⎫⎨-=+= ⎪⎪-⎝⎭⎩()()22i i i d x x y y =-+-;()()22111d x x y y =-+-;1;i i v v θ是观测噪声。
矩阵形式如下:()Y h X V =+()()()12213121213131111111222211211...arctan ;;;arctan ...arctan M M M M M M M M M d d d d v d v d d d y y v d x x x X Y V h X v y y y v x x v y y x x θθθθθθ-⨯-⨯-⎡-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎛⎫⎢⎥-⎢⎥ ⎪⎢⎥⎡⎤⎢⎥-====⎝⎭⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎛⎫-⎢⎥⎢⎥ ⎪-⎢⎥⎝⎭⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎛⎫- ⎪-⎝⎭⎣()211M -⨯⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎦ 噪声向量的协方差矩阵应为()()2121M M -⨯-方阵00R R R τθ⎡⎤=⎢⎥⎣⎦,其中R τ是TDOA观测的方差阵,R θ是AOA 观测的方差阵。
2.非视距识别和TDOA/AOA 混合定位结构流程图TDOA/AOA 混合定位方法的主要思想是使用多种定位方案,通过多样性复和来取得更高的定位精度。
NLOS 识别和TDOA/AOA 混合定位结构图3.NLOS 识别假设参与定位的目标节点数目为M ,目标节点向参考节点发送信号的传播时间为i τ,则距离为:i i r c τ=。
取K 个观察时刻,则第i 个参考节点和目标节点在k t 时刻的距离()i k r t 角度()i k t θ分别如下:()()()()()()()(),,,,,,1,2,...,0,1,....,1i k Los i k rang i k NLos i k i k Los i k bearing i k NLos i k r t r t n t r t i M k K t t n t t θθθ=++⎧⎪==-⎨=++⎪⎩;()(),,,Los i k Los i k r t t θ分别是真实距离与真实角度;()(),,,rang i k bearing i k n t n t 分别是距离的观测噪声和角度的观测噪声;均为零均值的高斯白噪声,方差分别为22,r θσσ()(),,,NLos i k NLos i k r t t θ分别是由NLOS 引起的距离误差(服从指数分布)和角度误差(服从均匀分布);由NLOS 引起的误差与观测误差的分布不同,且有NLOS 引起的误差对TOA 测量值的影响很大,所以通过卡尔曼滤波器对数据进行处理,使TOA 估计更精确的逼近真实TOA ,以消除有NLOS 引起的误差。
卡尔曼滤波器是一种通过迭代算法实现的估计器,它可以对状态向量做出线性、无偏及最小方差的估计。
用卡尔曼滤波器进行参数估计,关键是找到合适的状态向量及状态向量与观测向量之间的关系。
卡尔曼滤波器的状态方程:11k k k X X W --=Φ+Γ其中:'Tk k k X r r ⎡⎤=⎣⎦是在k t 时刻的状态向量,'k r 表示k r 的径向速度。
1k W -是输入噪声向量,其协方差矩阵为2u Q I σ=Φ是状态转移矩阵,101T ⎡⎤Φ=⎢⎥⎣⎦;Γ是噪声输入矩阵,0T ⎡⎤Γ=⎢⎥⎣⎦;T 为采样间隔。
测量方程为:k k k Y HX V =+其中:k Y 是观测数据向量;[]10H =;k V 为观测噪声序列,其协方差矩阵为2x R I σ=;卡尔曼滤波函数有两个递归步骤组成: 一、时间更新:,11,1k k k k k X X ---=Φ(1),1,1,1,11,11k k k k T Tk k k k k k k k P P Q -------=ΦΦ+ΓΓ(2) ()1,1,1k k k kT T k k k k k K P H H P H R ---=+(3)二、测量更新:(),1,1k k k k k k k k X X K Y H X --=+-(4)(),1k k k k k P I K H P -=-(5)其中,k K 是卡尔曼滤波增益; k P 是k X 的协方差矩阵;由于无法事先确定待测目标与参与定位的M 个参考节点之间的环境是LOS 还是NLOS ,可以利用历史距离测量值和无偏卡尔曼滤波处理结果周期性的检测待测节点与参考节点之间的LOS/NLOS 传播环境,其中检测周期和误差计算样本值test N 有实验确定。
对于每一个参考节点,通过收集一组test N 个TOA 原始数据周期性的完成LOS/NLOS 的假设测试。
设()i k X t 是第i 个参考节点在k t 时刻经卡尔曼滤波平滑后的距离值,测量距离数据的标准差计算公式如下:()()()211testN i i k i k k testr t X t N σ==-∑(6)在视距环境下,样本标准差将近似等于LOS 环境下的观测噪声方差r σ; 在非视距环境中,此样本将远远大于LOS 环境下的观测噪声方差r σ。
对于超宽带系统,LOS/NLOS 假设测试的判断规则如下:01::i r i rH LOS H NLOS σγσσγσ<>环境环境(7)式中1γ>,值有实验确定,用来消除因误差的随机性而引起的LOS/NLOS 传播判断错误。
4.非视距环境下TOA 误差消除和AOA 信息选择NLOS 误差消除由两部分组成:NLOS 传播环境下的TOA 数据误差消除和AOA 信息的选择。
如果是在LOS 传播环境下,可以采用无偏卡尔曼滤波器对TOA 数据进行平滑;如果是在NLOS 传播环境下,TOA 测量值会发生很大偏差,且由于NLOS 传播引起误差的标准差远远大于观测噪声误差的标准差,此时,将采用有偏卡尔曼滤波消除由NLOS 传播产生的TOA 误差,此外可以通过指定噪声协方差矩阵的对角线元素,来减少TOA 测量值中由非视距传播造成的正向偏差的影响。
噪声协方差对角线元素定义如下:1,1,0,k k x r k r if Y H X and NLOSσασσ++=->=否则其中α的值是由试验确定的。
从所有参考节点得到的TOA 数据均被用于计算TDOA ,TDOA 数据可以用于计算待测节点的位置和对待测节点进行跟踪。
超宽带环境中,有NLOS 引起的距离误差(),NLos i k r t 服从指数分布,设有NLOS 引起的误差使观测噪声k V 的均值[]k E V C =,由11k k k X X W --=Φ+Γ可知k W 是均值为零的白噪声,可以用,11k k k X X --=Φ作为k X 的预测估计,考虑到[]k E V C =,所以对于k 时刻的观测值k Y 的预测估计为:,1,1k k k k Y H X C --=+在k 时刻获得的观测值k Y 与其预测估计值,1k k Y -之间存在误差:,1,1k k k k k k Y Y Y H X C ε--=-=--为了得到k 时刻k X 的滤波值,可以利用预测误差ε来修正原来的状态预测估计,1k k X -,于是有(),1,1k k k k k k k k X X K Y H X C --=+--,其中k K 是卡尔曼滤波增益。
有偏卡尔曼滤波的方程为: 一、时间更新:,11,1k k k k k X X ---=Φ(8),1,1,1,11,11k k k k T Tk k k k k k k k P P Q -------=ΦΦ+ΓΓ(9) ()1,1,1k k k kT T k k k k k K P H H P H R ---=+(10)二、测量更新:(),1,1k k k k k k k k X X K Y H X C --=+--(11)(),1k k k k k P I K H P -=-(12)其中,k K 是卡尔曼滤波增益; k P 是k X 的协方差矩阵;为了避免引入大的NLOS 角度误差,来自所有参考节点的AOA 信息都要通过AOA 信息选择。
只有那些来自LOS 基站的AOA 数据用于参考节点位置估计,即那些来自NLOS 基站的AOA 数据将被抛弃而不用于待测目标的位置估计。
非视距识别和NLOS 误差消除的仿真步骤:1、令0k =,给定初值:00P X 、; 2、当test k N <时,根据式(1)~(5)重复递推计算,即采用无偏卡尔曼滤波消除噪声,否则直接进行步骤3;3、当test k N >时,根据式(6)计算历史距离测量数据的标准差;4、根据式(7)判断传播环境是LOS 还是NLOS ;5、如果是LOS 则采用第二步中的无偏卡尔曼滤波消除观测噪声,如果是NLOS 则采用式(8)~(12)采用有偏卡尔曼滤波消除观测噪声,并把此时的AOA 观测值抛弃;6、令1k k =+返回第二步,重复递推计算;。
