5.1.2曲线运动(小船过河、速度关联)
合集下载
人教版高一物理必修第二册专题:5.2小船过河和关联速度

10
2.绳末端速度分解的分析: 如右图所示,取船与绳的连 结点 A 为研究对象(此点既 是船上的点,又是绳子上的 点).因为船上 A 点的速度即船的实际运动速度 v, 绳子 A 点既有沿绳方向的收缩(或伸长)速度 v1(沿 绳方向的直线运动),又有沿垂直绳方向的转动速 度 v2(以绳轮间支点为中心的圆周运动),所以 v 是 v1 和 v2 的合速度.
提示:将船的 运动分解成沿 绳方向的运动 和垂直绳方向 的运动。
V1
V V2
V=V1/cos600=8m/s
8
※6、一人骑自行车向西行驶,当车速为4m/s
时,他感觉到风从正南方向吹来,当车速增加到
7m/s时,他感觉到风从东南(东偏南45°)方
向吹来,则风对地的速度大小为( )
A、4m/s
B、5m/s
C、6m/s
D、7m/s
v合
v合 v2
v2
v1
v1
45
v1 3m / s
9
二、绳拉船模型分析 1.模型展示:船在靠岸的过程中,通过一条跨过定滑轮的绳拉 船.研究拉船的绳端速度与船速的关系.在绳跟滑轮间的支撑点 看绳拉船头部位,该部位的实际运动是受水面约束的直线运动, 这也是合运动.它实际上是同时参与了两个分运动:一是沿绳方 向的直线运动,二是具有沿垂直绳方向线速度的圆周运动.此类 问题在建筑工地的塔吊工作中也很常见.
7.两个典型模型的分析 一、小船渡河模型分析
1.模型展示:小船在渡河时,同时参与了两个运
动:一是随水沿水流方向的运动,二是船本身相
对水的运动.小船实际发生的运动是合运动,而
这两个运动是分运动.模型主要讨论船渡河时间
最短和位移最短这两个问题.设一条河宽 d,船
2.绳末端速度分解的分析: 如右图所示,取船与绳的连 结点 A 为研究对象(此点既 是船上的点,又是绳子上的 点).因为船上 A 点的速度即船的实际运动速度 v, 绳子 A 点既有沿绳方向的收缩(或伸长)速度 v1(沿 绳方向的直线运动),又有沿垂直绳方向的转动速 度 v2(以绳轮间支点为中心的圆周运动),所以 v 是 v1 和 v2 的合速度.
提示:将船的 运动分解成沿 绳方向的运动 和垂直绳方向 的运动。
V1
V V2
V=V1/cos600=8m/s
8
※6、一人骑自行车向西行驶,当车速为4m/s
时,他感觉到风从正南方向吹来,当车速增加到
7m/s时,他感觉到风从东南(东偏南45°)方
向吹来,则风对地的速度大小为( )
A、4m/s
B、5m/s
C、6m/s
D、7m/s
v合
v合 v2
v2
v1
v1
45
v1 3m / s
9
二、绳拉船模型分析 1.模型展示:船在靠岸的过程中,通过一条跨过定滑轮的绳拉 船.研究拉船的绳端速度与船速的关系.在绳跟滑轮间的支撑点 看绳拉船头部位,该部位的实际运动是受水面约束的直线运动, 这也是合运动.它实际上是同时参与了两个分运动:一是沿绳方 向的直线运动,二是具有沿垂直绳方向线速度的圆周运动.此类 问题在建筑工地的塔吊工作中也很常见.
7.两个典型模型的分析 一、小船渡河模型分析
1.模型展示:小船在渡河时,同时参与了两个运
动:一是随水沿水流方向的运动,二是船本身相
对水的运动.小船实际发生的运动是合运动,而
这两个运动是分运动.模型主要讨论船渡河时间
最短和位移最短这两个问题.设一条河宽 d,船
5.1.2 曲线运动(小船过河、速度关联)ppt课件
例题:
1、关于曲线运动,下列说法正确的是:( AB)
A.曲线运动一定是变速运动 B.曲线运动速度的方向不断的变化,但速度 的大小可以不变 C.曲线运动的速度方向可能不变 D.曲线运动的速度大小和方向一定同时改变
3
2、如图所示的质点运动轨迹中,可能的是( D )
A
B
C
D
4
3、如图是演示小蜡块在玻璃管中运动规律的装置。 现让玻璃管沿水平方向做初速度为零的匀加速直线 运动,同时小蜡块从O点开始沿竖直玻璃管向上做 匀速直线运动,那么下图中能够大致反映小蜡块运
13
练习:A、B两物体通过一根跨过定滑轮的轻 绳相连放在水平面上,现物体A以v1的速度向 右匀速运动,当绳被拉成与水平面夹角分别是
α、β时。物体B的运动速度vB为:D
总结:处理速度关联问题的关键: 1、确定好合运动和分运动 2、画出合速度和分速度的矢量图,抓住沿
绳或杆的方向的速度大小是相等的。
14
8
一、小船过河问题:
1、最短时间问题:V要使Fra bibliotek船渡河时间最短,
则小船船头应垂直河岸
d
渡河,渡河的时间最短:
9
一、小船过河问题:
2、渡河航程最短
①船速v2大于水流速度 V2
v1时,即v2>v1时,合速 度v与河岸垂直时,最短
d
航程就是河宽d
V1
小船在200m宽的河中渡河,水流的速度是3m/s, 小船在静水中的速度是5m/s,求:
1、要使小船渡河耗时最少,应该如何航行?最短时 间为多少?
2、要使小船航程最短,应该如何航行?最短航程为 多少?
10
②船速v2小于水流速度vl
时,即v2<v1时,合速度v
51曲线运动小船渡河和牵连速度课件

cosθ=vv21=34,θ=arccos34,故船头斜向 上游河对岸,且与河岸所成的夹角为
arccos
3 4
,
所
用
的
时
间
为
t
=
d v1sinθ
=
4
100 m m/s×
7=1007 4
7
s.
(3)当水流速度v2=5 m/s大于船在静水中的 速度v1=4 m/s时,不论v1方向如何,其合速 度方向总是偏向下游,故不能垂直河岸渡
一、小船渡河的两类典型问题
例1 已知某船在静水中的速度为v1=4 m/s,现让 船渡过某条河,假设这条河的两岸是理想的平 行线,河宽为d=100 m,水流速度为v2=3 m/s, 方向与河岸平行,
(1)欲使船以最短时间渡河,航向怎样?最短时间是多少? 船发生的位移有多大?
(2)欲使船以最小位移渡河,航向又怎样?渡河所用时间 是多少?
摩托艇救人,假设江岸是平直的,洪水
沿江向下游流去,水流速度为 v1,摩托 艇在静水中的航速为 v2,战士救人的地 点 A 离岸边最近处 O 的距离为 d,如战
士在最短时间内将人送上岸,则摩托艇
登陆的地点离 O 点的距离为( )
dv2 A. v22-v21
B.0
C.dvv21
D.dvv12
解析:选 C.战士要在最短时间内将人送上岸,必须驾 驶摩托艇正对着岸行驶,由于洪水沿江向下以速度 v1 运动,所以摩托艇相对岸参与两个运动,根据运动的 合成知识,摩托艇实际上沿着 v 合方向做匀速直线运动, 如图所示.假设摩托艇登陆地离 O 点的距离为 s,由 几何图形可求得 tanθ=vv12=ds,得 s=vv12·d.故选 C.
【自主解答】将小船的速度v′正交分解沿: 绳的分速度v′1,垂直绳的分速度v′2,拉绳的 速度大小等于v′1,
小船渡河和关联速度问题课件

当船头斜向下游渡河时,船的航行方向与河岸有一定的夹角,此 时需要考虑水流速度对船的影响。
渡河时间与水流速度的关系
随着水流速度的增加,渡河时间会逐渐减少。当水流速度达到一 定值时,渡河时间达到最短。
船的行程变化
由于船头斜向下游,船的行程会随着水流速度的增加而逐渐减小 。
船头斜向上游渡河
船的航行方向
01
小船过河时,船头方向与水流方向不一致,导致 船的速度与水流速度关联。
分解速度
将小船的速度分解为沿河岸方向和垂直于河岸方 向的两个分量。
结论
通过分解速度和考虑小船的运动轨迹,可以解决 关联速度问题并得到最优解决方案。
07
练习题与解答
小船渡河问题练习题
总结词
小船渡河问题是对经典力学和运动学理论的综合性考查,需要掌握速度、位移、时间等基本物理量之 间的关系。
。
在非直线渡河的情况下,需要 对船只的航线进行规划,以确 保船只在安全的情况下到达目
的地。
在非直线渡河的情况下,需要 考虑船只的转向半径和船头方 向的变化,以避免船只在渡河
过程中发生危险。
多船渡河的情况
当多艘船同时渡河时,需要考虑每艘船的速度和航向,以及它们之间的相互影响 。
在多船渡河的情况下,需要制定合理的调度计划,以确保所有船只都能够安全到 达目的地。
实际应用
在现实生活中,小船渡河的问题并不常见,因为小船的速度通常比河水的流速小得多。但是,在某些特定的情 况下,如急流或者狭窄的河流中,小船渡河的问题仍然可能出现。在这些情况下,关联速度的计算方法仍然适 用。
05
问题建模的扩展
非直线渡河的情况
船在非直线渡河时,会受到水 流的影响,需要考虑到水流的 速度和方向对船只渡河的影响
渡河时间与水流速度的关系
随着水流速度的增加,渡河时间会逐渐减少。当水流速度达到一 定值时,渡河时间达到最短。
船的行程变化
由于船头斜向下游,船的行程会随着水流速度的增加而逐渐减小 。
船头斜向上游渡河
船的航行方向
01
小船过河时,船头方向与水流方向不一致,导致 船的速度与水流速度关联。
分解速度
将小船的速度分解为沿河岸方向和垂直于河岸方 向的两个分量。
结论
通过分解速度和考虑小船的运动轨迹,可以解决 关联速度问题并得到最优解决方案。
07
练习题与解答
小船渡河问题练习题
总结词
小船渡河问题是对经典力学和运动学理论的综合性考查,需要掌握速度、位移、时间等基本物理量之 间的关系。
。
在非直线渡河的情况下,需要 对船只的航线进行规划,以确 保船只在安全的情况下到达目
的地。
在非直线渡河的情况下,需要 考虑船只的转向半径和船头方 向的变化,以避免船只在渡河
过程中发生危险。
多船渡河的情况
当多艘船同时渡河时,需要考虑每艘船的速度和航向,以及它们之间的相互影响 。
在多船渡河的情况下,需要制定合理的调度计划,以确保所有船只都能够安全到 达目的地。
实际应用
在现实生活中,小船渡河的问题并不常见,因为小船的速度通常比河水的流速小得多。但是,在某些特定的情 况下,如急流或者狭窄的河流中,小船渡河的问题仍然可能出现。在这些情况下,关联速度的计算方法仍然适 用。
05
问题建模的扩展
非直线渡河的情况
船在非直线渡河时,会受到水 流的影响,需要考虑到水流的 速度和方向对船只渡河的影响
高一物理人教版必修二:5.1曲线运动-小船过河

度的关系正确的是( C )
A.水流速度越大,则路程越长,所用时 间也越长;
B.水流速度越大,则路程越短,所用时 间也越短;
C.水流速度越大,路程越长,但所用时 间不变;
D.水流速度增大,路程和时间均不变。
一、小船渡河时间最短
结论:当船头垂直河岸时,渡河时间最短,其与水流
速度无关,其值为
t mi n
d v2
二、小船过河最短路程
v v 1.当有 1 2 时,小船能够垂直过河,其所用时间为
td d v v22 v12
v v 如果
,小船渡河时向下游漂流的距离是多少呢?
12
分析:当 v1 v2时,小船不能垂直过河,
xmin
v12 v22 d v2
针对练习:
一小船在静水中的速度是,一条河
宽,河水的速度为。下列说法正确
的是( )
C
A.小船在这条河中运动的最大速度
是;
B.小船在这条河中运动的最小速度
是;
C.小船渡过这条河的最短时间是;
D.小船渡过这条河的最小距离是。
针对练习:
已知船速大于水速,欲横渡宽为的河流:
①船头垂直河岸正对彼岸航行时,横 渡时间最短;
②船头垂直河岸正对彼岸航行时,实 际航程最短;
③船头朝上游转过一定角度,使实际 航线垂直河岸,此时航程最短;
④船头朝上游转过一定角度,使实际 航速增大,此时横渡时间最短;
以上说法正确的是( C )
A.①② B.③ C.①③ D.②④
针对练习:
一轮船以一定的速度,船头垂直河岸向 对岸行驶,河水匀速流动(河道使直的)。 轮船渡河通过的路径和所用时间与水流速
v v1 x
A.水流速度越大,则路程越长,所用时 间也越长;
B.水流速度越大,则路程越短,所用时 间也越短;
C.水流速度越大,路程越长,但所用时 间不变;
D.水流速度增大,路程和时间均不变。
一、小船渡河时间最短
结论:当船头垂直河岸时,渡河时间最短,其与水流
速度无关,其值为
t mi n
d v2
二、小船过河最短路程
v v 1.当有 1 2 时,小船能够垂直过河,其所用时间为
td d v v22 v12
v v 如果
,小船渡河时向下游漂流的距离是多少呢?
12
分析:当 v1 v2时,小船不能垂直过河,
xmin
v12 v22 d v2
针对练习:
一小船在静水中的速度是,一条河
宽,河水的速度为。下列说法正确
的是( )
C
A.小船在这条河中运动的最大速度
是;
B.小船在这条河中运动的最小速度
是;
C.小船渡过这条河的最短时间是;
D.小船渡过这条河的最小距离是。
针对练习:
已知船速大于水速,欲横渡宽为的河流:
①船头垂直河岸正对彼岸航行时,横 渡时间最短;
②船头垂直河岸正对彼岸航行时,实 际航程最短;
③船头朝上游转过一定角度,使实际 航线垂直河岸,此时航程最短;
④船头朝上游转过一定角度,使实际 航速增大,此时横渡时间最短;
以上说法正确的是( C )
A.①② B.③ C.①③ D.②④
针对练习:
一轮船以一定的速度,船头垂直河岸向 对岸行驶,河水匀速流动(河道使直的)。 轮船渡河通过的路径和所用时间与水流速
v v1 x
人教版高一物理必修二第五章 5.1曲线运动之小船过河(22张ppt) 课件

vB大小不变,θ变小,cosθ增大,所以
v2增大,即物体A向上做加速运动,由牛顿第二定律 得:FT-mg=ma,可知:FT=mg+ma>mg,故A正确. 答案 A 方法提炼
在进行速度分解时,首先要分清合速度与分速度. 合速度就是物体实际运动的速度,由物体的实际运 动确定,分速度由合速度的效果利用平行四边形定 则确定.
第一章 抛体运动
1.2 运动的合成与分解
小船过河 绳杆末端速度分解问题
典型问题1、小船过河
例1:一艘小船在100m宽的河中横渡 到对岸,已知水流速度是3m/s,小 船在静水中的速度是4m/s,求: (1)欲使船渡河时间最短,船应 该怎样渡河?最短时间是多少?船 经过的位移多大?
v静
v
d
v水
分析:欲使船渡河时间最短,船头的方向
A.大于mg B.总等于mg C.一定小于mg D.以上三项都不正确
绳拉物体或物体拉绳问题的主要思路: (1)物体的实际运动为合运动; (2)沿绳的运动为一个分运动; (3)垂直于绳的运动为另一个分运动。
解析 物体B向左的速度vB是合速度, 根据其效果,分解为如右图所示的两 个速度v1和v2,其中v2=vA,又因v2= vBcosθ,当物体B向左匀速运动时,
v静 v
d
θ
v水
结论:当v静>v水时,最短航程等于河宽d。
设船头指向与上游河岸成θ:
cos
v水 v静
解:1.当船头指向斜上游,与岸夹角为 Ѳ时,合运动垂直河岸,航程最短,数值 等于河宽100m.
则 cos v1 3
v2 4
合速度:v v22 v12 42 32 m s 7 m s
过河时间:t d 100 s 100 7 s
v2增大,即物体A向上做加速运动,由牛顿第二定律 得:FT-mg=ma,可知:FT=mg+ma>mg,故A正确. 答案 A 方法提炼
在进行速度分解时,首先要分清合速度与分速度. 合速度就是物体实际运动的速度,由物体的实际运 动确定,分速度由合速度的效果利用平行四边形定 则确定.
第一章 抛体运动
1.2 运动的合成与分解
小船过河 绳杆末端速度分解问题
典型问题1、小船过河
例1:一艘小船在100m宽的河中横渡 到对岸,已知水流速度是3m/s,小 船在静水中的速度是4m/s,求: (1)欲使船渡河时间最短,船应 该怎样渡河?最短时间是多少?船 经过的位移多大?
v静
v
d
v水
分析:欲使船渡河时间最短,船头的方向
A.大于mg B.总等于mg C.一定小于mg D.以上三项都不正确
绳拉物体或物体拉绳问题的主要思路: (1)物体的实际运动为合运动; (2)沿绳的运动为一个分运动; (3)垂直于绳的运动为另一个分运动。
解析 物体B向左的速度vB是合速度, 根据其效果,分解为如右图所示的两 个速度v1和v2,其中v2=vA,又因v2= vBcosθ,当物体B向左匀速运动时,
v静 v
d
θ
v水
结论:当v静>v水时,最短航程等于河宽d。
设船头指向与上游河岸成θ:
cos
v水 v静
解:1.当船头指向斜上游,与岸夹角为 Ѳ时,合运动垂直河岸,航程最短,数值 等于河宽100m.
则 cos v1 3
v2 4
合速度:v v22 v12 42 32 m s 7 m s
过河时间:t d 100 s 100 7 s
高一下学期物理人教版必修第二册5.2 课时2 小船过河与绳——杆关联速度问题 课件(共20张PPT)

一分运动的速度大小不变, 研究其速度方向
不同时对合运动的影响,这样的运动系统可看
做小船渡
视
频
2.模型分析
(1)船的实际运动是水流的运动和船相对静水的运动的合运动。
(2)三种速度:v1(船在静水中的速度)、v2(水流速度)、v(船的实际速度)。
(3)两个极值
d
①过河时间最短:v1⊥v2,tmin=—(d为河宽).
速度v⊥=v船sin
α,故小船渡河时间为t=
,当α
船sin
=90°,即船头与河岸垂直时,渡河时间最短,最短
时间为tmin=50 s.
【练一练】小船要渡过200 m宽的河,水流速度为2 m/s,船在静水中的速度为4 m/s,求:
(4)若水流速度是5 m/s,船在静水中的速度是3 m/s,则怎样渡河才能使船驶向下游的距
离最小?最小距离是多少?(结果取整数)
(4)因为v′船<v′水,船不可能垂直河岸横渡.如图所示,设船头(v′
船)与上游河岸成β角,合速度v′与下游河岸成γ角,可以看出γ角
越大,船驶向下游的距离x′越小.以v′水矢量的末端为圆心,以v′
船的大小为半径画圆,当合速度v′与圆相切时,γ角最大.cos
′船
水平方向向右做匀速直线运动的过程中( BCD )
A.物体 A 也做匀速直线运动
B.绳子的拉力始终大于物体 A 所受的重力
C.物体 A 的速度小于物体 B 的速度
D.地面对物体 B 的支持力逐渐增大
小船过河
运动的合成与分解的应用
绳——杆关联速度
且v2>v1,下面用小箭头表示小船及船头的指向,则能正确反映小
船在最短时间内渡河、最短位移渡河的情景图示依次是
不同时对合运动的影响,这样的运动系统可看
做小船渡
视
频
2.模型分析
(1)船的实际运动是水流的运动和船相对静水的运动的合运动。
(2)三种速度:v1(船在静水中的速度)、v2(水流速度)、v(船的实际速度)。
(3)两个极值
d
①过河时间最短:v1⊥v2,tmin=—(d为河宽).
速度v⊥=v船sin
α,故小船渡河时间为t=
,当α
船sin
=90°,即船头与河岸垂直时,渡河时间最短,最短
时间为tmin=50 s.
【练一练】小船要渡过200 m宽的河,水流速度为2 m/s,船在静水中的速度为4 m/s,求:
(4)若水流速度是5 m/s,船在静水中的速度是3 m/s,则怎样渡河才能使船驶向下游的距
离最小?最小距离是多少?(结果取整数)
(4)因为v′船<v′水,船不可能垂直河岸横渡.如图所示,设船头(v′
船)与上游河岸成β角,合速度v′与下游河岸成γ角,可以看出γ角
越大,船驶向下游的距离x′越小.以v′水矢量的末端为圆心,以v′
船的大小为半径画圆,当合速度v′与圆相切时,γ角最大.cos
′船
水平方向向右做匀速直线运动的过程中( BCD )
A.物体 A 也做匀速直线运动
B.绳子的拉力始终大于物体 A 所受的重力
C.物体 A 的速度小于物体 B 的速度
D.地面对物体 B 的支持力逐渐增大
小船过河
运动的合成与分解的应用
绳——杆关联速度
且v2>v1,下面用小箭头表示小船及船头的指向,则能正确反映小
船在最短时间内渡河、最短位移渡河的情景图示依次是
人教版高一物理必修2课件 5.1曲线运动——小船渡河问题

小船渡河模型
运动的合成与分解
小船渡河模型 1.小船参与的两个分运动 (1)船随水漂流的运动,它的方向与河岸平行。
V水
小船渡河模型 1.小船参与的两个分运动 (1)船随水漂流的运动,它的方向与河岸平行。 (2)船相对水的运动(即船在静水中的运动),它的方向 与船头的指向相同
V船
V水
小船渡河模型
小船渡河模型
S1
S2
小船渡河模型:如何渡河时间最短
No Image
v船=10m/s 河宽D=15m 3s内过河, 求θ范围
θ
小船渡河模型:如何渡河时间最短 No ≤3s
Image
No Image
v船=10m/s
河宽D=15m
3s内过河,
θ
求θ范围
小船渡河模型:如何渡河时间最短 No Image
No ≤3s
V船
v
V水
小船渡河模型:如何渡河距离最短 当最短的距离为河宽D
V船
v
V水
小船渡河模型:如何渡河距离最短 当最短的距离为河宽D
V船
v
V船
V水
小船渡河模型:如何渡河距离最短 V船>v水 最短的距离为河宽D
V船
v
V船
V水
小船渡河模型:如何渡河距离最短
V船>v水 最短的距离为河宽D 此时渡河时间?
V船
Image
No Image
v船=10m/s 河宽D=15m
No Image
3s内过河,
θ
求θ范围
小船渡河模型:如何渡河时间最短 No Image
No ≤3s
Image
No Image
v船=10m/s 河宽D=15m
No Image
运动的合成与分解
小船渡河模型 1.小船参与的两个分运动 (1)船随水漂流的运动,它的方向与河岸平行。
V水
小船渡河模型 1.小船参与的两个分运动 (1)船随水漂流的运动,它的方向与河岸平行。 (2)船相对水的运动(即船在静水中的运动),它的方向 与船头的指向相同
V船
V水
小船渡河模型
小船渡河模型
S1
S2
小船渡河模型:如何渡河时间最短
No Image
v船=10m/s 河宽D=15m 3s内过河, 求θ范围
θ
小船渡河模型:如何渡河时间最短 No ≤3s
Image
No Image
v船=10m/s
河宽D=15m
3s内过河,
θ
求θ范围
小船渡河模型:如何渡河时间最短 No Image
No ≤3s
V船
v
V水
小船渡河模型:如何渡河距离最短 当最短的距离为河宽D
V船
v
V水
小船渡河模型:如何渡河距离最短 当最短的距离为河宽D
V船
v
V船
V水
小船渡河模型:如何渡河距离最短 V船>v水 最短的距离为河宽D
V船
v
V船
V水
小船渡河模型:如何渡河距离最短
V船>v水 最短的距离为河宽D 此时渡河时间?
V船
Image
No Image
v船=10m/s 河宽D=15m
No Image
3s内过河,
θ
求θ范围
小船渡河模型:如何渡河时间最短 No Image
No ≤3s
Image
No Image
v船=10m/s 河宽D=15m
No Image
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
α、β时。物体B的运动速度vB为:D
总结:处理速度关联问题的关键: 1、确定好合运动和分运动 2、画出合速度和分速度的矢量图,抓住沿
绳或杆的方向的速度大小是相等的。
不可能与河岸垂直,只有
d
当合速度v方向越接近垂
直河岸方向,航程越短。
二、关联物体的速度分解:
例题:如图所示,在河岸上利用定滑轮拉绳索 使小船靠岸,拉绳的速度为v,当拉船头的绳 索与水平面的夹角为α时,船的速度是多少?
二、关联物体的速度分解:
绳、杆等连接的两个物体在运动过程中,其速 度通常是不相等的,但两者之间是有联系的: 两个物体沿绳或杆的方向的速度大小是相等的。
如图,一根长直轻杆AB在墙角沿竖直墙和水 平地面滑动,当AB杆和墙的夹角为θ时,杆 的A端沿墙下滑的速度大小为v1,B端沿地面
的速度大小为v2。则v1、v2的关系是C( )
练习:A、B两物体通过一根跨过定滑轮的轻 绳相连放在水平面上,现物体A以v1的速度向 右匀速运动,当绳被拉成与水平面夹角分别是
动轨迹的是( B )
A
B
C
D
5、飞机空投物资时,由于降落伞的作用,使物体在空中 匀速下落,若降落伞和物体下降的速度为10m/s,飞机 在500m高空以108km/h的速度水平飞行时,求:
• 1、物体在空中的运动时间t
• 2、物体在下降的过程中水平移动的距离s
例题:
小船在200m宽的河中渡河,水流的速度是2m/s,小船 在静水中的速度是4m/s,求:
1、若小船船头垂直河岸渡河,小船的合速度是多少?小 船到达对岸后距出发点多远?
2、若使小船的航线垂直于河岸,小船该如何行驶,渡河 的实际速度是多少?
一、小船过河问题:
1、最短时间问题:
V
要Hale Waihona Puke 小船渡河时间最短,则小船船头应垂直河岸
d
渡河,渡河的时间最短:
一、小船过河问题:
2、渡河航程最短
①船速v2大于水流速度 V2
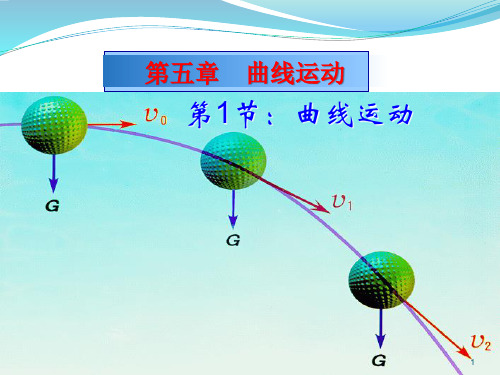
第五章 曲线运动
第1节:曲线运动
复习:
1、什么是曲线运动?曲线运动的速度方 向如何确定? 2、曲线运动的条件是什么?曲线运动的 轨迹、速度、受力有什么特点? 3、如何研究曲线运动? 4、运动的合成与分解的本质是什么?遵 循什么法则? 5、如何判断合运动和分运动? 6、合运动和分运动有什么性质?
例题:
v1时,即v2>v1时,合速 度v与河岸垂直时,最短
d
航程就是河宽d
V1
小船在200m宽的河中渡河,水流的速度是3m/s, 小船在静水中的速度是5m/s,求:
1、要使小船渡河耗时最少,应该如何航行?最短时 间为多少?
2、要使小船航程最短,应该如何航行?最短航程为 多少?
②船速v2小于水流速度vl
时,即v2<v1时,合速度v
1、关于曲线运动,下列说法正确的是:( AB)
A.曲线运动一定是变速运动 B.曲线运动速度的方向不断的变化,但速度 的大小可以不变 C.曲线运动的速度方向可能不变 D.曲线运动的速度大小和方向一定同时改变
2、如图所示的质点运动轨迹中,可能的是( D )
A
B
C
D
3、如图是演示小蜡块在玻璃管中运动规律的装置。 现让玻璃管沿水平方向做初速度为零的匀加速直线 运动,同时小蜡块从O点开始沿竖直玻璃管向上做 匀速直线运动,那么下图中能够大致反映小蜡块运
总结:处理速度关联问题的关键: 1、确定好合运动和分运动 2、画出合速度和分速度的矢量图,抓住沿
绳或杆的方向的速度大小是相等的。
不可能与河岸垂直,只有
d
当合速度v方向越接近垂
直河岸方向,航程越短。
二、关联物体的速度分解:
例题:如图所示,在河岸上利用定滑轮拉绳索 使小船靠岸,拉绳的速度为v,当拉船头的绳 索与水平面的夹角为α时,船的速度是多少?
二、关联物体的速度分解:
绳、杆等连接的两个物体在运动过程中,其速 度通常是不相等的,但两者之间是有联系的: 两个物体沿绳或杆的方向的速度大小是相等的。
如图,一根长直轻杆AB在墙角沿竖直墙和水 平地面滑动,当AB杆和墙的夹角为θ时,杆 的A端沿墙下滑的速度大小为v1,B端沿地面
的速度大小为v2。则v1、v2的关系是C( )
练习:A、B两物体通过一根跨过定滑轮的轻 绳相连放在水平面上,现物体A以v1的速度向 右匀速运动,当绳被拉成与水平面夹角分别是
动轨迹的是( B )
A
B
C
D
5、飞机空投物资时,由于降落伞的作用,使物体在空中 匀速下落,若降落伞和物体下降的速度为10m/s,飞机 在500m高空以108km/h的速度水平飞行时,求:
• 1、物体在空中的运动时间t
• 2、物体在下降的过程中水平移动的距离s
例题:
小船在200m宽的河中渡河,水流的速度是2m/s,小船 在静水中的速度是4m/s,求:
1、若小船船头垂直河岸渡河,小船的合速度是多少?小 船到达对岸后距出发点多远?
2、若使小船的航线垂直于河岸,小船该如何行驶,渡河 的实际速度是多少?
一、小船过河问题:
1、最短时间问题:
V
要Hale Waihona Puke 小船渡河时间最短,则小船船头应垂直河岸
d
渡河,渡河的时间最短:
一、小船过河问题:
2、渡河航程最短
①船速v2大于水流速度 V2
第五章 曲线运动
第1节:曲线运动
复习:
1、什么是曲线运动?曲线运动的速度方 向如何确定? 2、曲线运动的条件是什么?曲线运动的 轨迹、速度、受力有什么特点? 3、如何研究曲线运动? 4、运动的合成与分解的本质是什么?遵 循什么法则? 5、如何判断合运动和分运动? 6、合运动和分运动有什么性质?
例题:
v1时,即v2>v1时,合速 度v与河岸垂直时,最短
d
航程就是河宽d
V1
小船在200m宽的河中渡河,水流的速度是3m/s, 小船在静水中的速度是5m/s,求:
1、要使小船渡河耗时最少,应该如何航行?最短时 间为多少?
2、要使小船航程最短,应该如何航行?最短航程为 多少?
②船速v2小于水流速度vl
时,即v2<v1时,合速度v
1、关于曲线运动,下列说法正确的是:( AB)
A.曲线运动一定是变速运动 B.曲线运动速度的方向不断的变化,但速度 的大小可以不变 C.曲线运动的速度方向可能不变 D.曲线运动的速度大小和方向一定同时改变
2、如图所示的质点运动轨迹中,可能的是( D )
A
B
C
D
3、如图是演示小蜡块在玻璃管中运动规律的装置。 现让玻璃管沿水平方向做初速度为零的匀加速直线 运动,同时小蜡块从O点开始沿竖直玻璃管向上做 匀速直线运动,那么下图中能够大致反映小蜡块运
