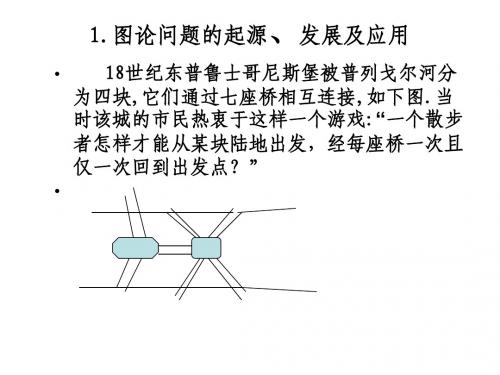
图论问题起源
合集下载
图论

Dijkstra(迪克斯特拉算法)
算法思想: 是从一个顶点到其余各顶点的最短路径算法,解决的是有向 图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为 中心向外层扩展,直到扩展到终点为止,算法求最短路径的 步骤如下: G={V,E} 1. 初始时令 S={V0},T=V-S={其余顶点},T中顶点对应的距 离值 若存在<V0,Vi>,d(V0,Vi)为<V0,Vi>弧上的权值 若不存在<V0,Vi>,d(V0,Vi)为∞ 2. 从T中选取一个与S中顶点有关联边且权值最小的顶点W, 加入到S中 3. 对其余T中顶点的距离值进行修改:若加进W作中间顶点, 从V0到Vi的距离值缩短,则修改此距离值 重复上述步骤2、3,直到S中包含所有顶点,即W=Vi为止。
解决图论的算法
Dijkstra(迪克斯特拉算法)——标号法,求一个顶 点(单源点)到其余各顶点的最短路径算法
Floyd(弗洛伊德算法) ——插点法,求任意一对 顶点(多源点)之间最短路径的方法
Prim(普里姆)算法——构造最小生成树的算法(与 点有关) Kruskal(克鲁斯卡尔)--构造最小生成树的算 法算法(只与边有关)
C (cij ) nn {0,1 } (i, j ) E, 1, cij (i, j ) E. 0,
也就是说,如果两顶点之间有边相连,则邻接矩阵 中对应的元素为1;否则为0。
n n
v v A= v v
1
0 1 2 3 1 4 1
v v vv
1
2 3
(1 )
d (v) 2E
v V
(2) 任意一个图的奇顶点的个数是偶数。
奇/偶顶点:顶点的度数为奇数的顶点为奇顶点,度数为偶 数的顶点为偶顶点。 加权图:对图的边赋相应的权值(数值),权值可以代表 距离,费用,代价等一些实际的意义。 权值为 7
图论发展史

6
问题三:Ramsey 问题
几个事实:
1. 任意的6个人中,总有3个人互相认识或有3个人互不认 识。
2. 任意的9个人中,总有3个人互相认识或有4个人互不认 识。
3. 问题:
4.
对任意的自然数k和t,是否存在一个最小的正整
数r(k,t),使得每个至少有r(k,t)个人的团体,总有k个
人互相认识或有t个人互不认识。
1
返回 结束
七桥问题
C
A
D
B
转化
Euler 1736年
包含两个要素:对象(陆 地)及对象间的二元关系 (是否有桥连接)
C
A
D
B 图论中讨论的图
问题:是否能从四块陆地中 的任一块开始,通过每座桥 恰好一次再回到起点?
转化 是否能从任意一个顶点开 始,通过每条边恰好一次 再回到起点?
2
返回 结束
问题一:四色问题
9
部分资料从网络收集整 理而来,供大家参考,
感谢您的关注!
3
1872年,英国当时最著名的数学家凯利正式向伦敦数学 学会提出了这个问题,于是四色猜想成了世界数学界关注的 问题。
1878~1880年两年间,著名的律师兼数学家肯普和泰勒 两人分别提交了证明四色猜想的论文,宣布证明了四色定理, 大家都认为四色猜想从此也就解决了。
1890年,在牛津大学就读的年仅29岁的赫伍德以自己的 精确计算指出了肯普在证明上的漏洞。不久,泰勒的证明也 被人们否定了。后来,人们开始认识到,这个貌似容易的题 目,其实是一个可与费马猜想相媲美的难题。
4
进入20世纪以来,科学家们对四色猜想的证明
基本上是按照肯普的想法在进行。后来美国数学家
富兰克林于1939年证明了22国以下的地图都可以用
问题三:Ramsey 问题
几个事实:
1. 任意的6个人中,总有3个人互相认识或有3个人互不认 识。
2. 任意的9个人中,总有3个人互相认识或有4个人互不认 识。
3. 问题:
4.
对任意的自然数k和t,是否存在一个最小的正整
数r(k,t),使得每个至少有r(k,t)个人的团体,总有k个
人互相认识或有t个人互不认识。
1
返回 结束
七桥问题
C
A
D
B
转化
Euler 1736年
包含两个要素:对象(陆 地)及对象间的二元关系 (是否有桥连接)
C
A
D
B 图论中讨论的图
问题:是否能从四块陆地中 的任一块开始,通过每座桥 恰好一次再回到起点?
转化 是否能从任意一个顶点开 始,通过每条边恰好一次 再回到起点?
2
返回 结束
问题一:四色问题
9
部分资料从网络收集整 理而来,供大家参考,
感谢您的关注!
3
1872年,英国当时最著名的数学家凯利正式向伦敦数学 学会提出了这个问题,于是四色猜想成了世界数学界关注的 问题。
1878~1880年两年间,著名的律师兼数学家肯普和泰勒 两人分别提交了证明四色猜想的论文,宣布证明了四色定理, 大家都认为四色猜想从此也就解决了。
1890年,在牛津大学就读的年仅29岁的赫伍德以自己的 精确计算指出了肯普在证明上的漏洞。不久,泰勒的证明也 被人们否定了。后来,人们开始认识到,这个貌似容易的题 目,其实是一个可与费马猜想相媲美的难题。
4
进入20世纪以来,科学家们对四色猜想的证明
基本上是按照肯普的想法在进行。后来美国数学家
富兰克林于1939年证明了22国以下的地图都可以用
第1章图论简介
6.基本的网络优化问题
基本的网络优化问题有:最短路径问题、最小生成树问 题、最大流问题和最小费用问题.图论作为数学的一个 分支,已经有有效的算法来解决这些问题.当然这当中 的有些问题也可以建立线性规划的模型,但有时若变量 特别多,约束也特别多,用线性规划的方法求解效率不 高甚至不能在可忍受的时间内解决.而根据这些问题的 特点,采用网络分析的方法去求解可能会非常有效.例 如,在1978年,美国财政部的税务分析部门在对卡特尔 税制改革做评估的过程中,就有一个100,000个约束以 上,25,000,000个变量的问题,若用普通的线性规划求 解,预计要花7个月的时间.他们利用网络分析的方法, 将其分解成6个子问题,利用特殊的网络计算机程序,花 了大约7个小时问题就得到了解决.
其他一些常见关系:
LA={<x,y>∣x,y Ax≤y},此处AR. DB={<x,y>∣x,y Ax整除y},此处BZ*.
R= {<x,y>∣x,y Fxy},此处F是集合簇.
例1.8.设A={1,2,3,4},下面定义的R都是A上的关系,试用列举法 表示R.(1)R={<x,y>∣x是y的倍数};(2)R={<x,y>∣(x-y)2A}; 1.3.二元关系的表示方法:给出一个关系的方法有三种:集合表达 式,关系矩阵和关系图.例1.5就是用集合表达式. 1. 关 系 矩 阵 表 示 法 : 设给定集合 A={a1 , a2 , … , an} ,集合 B={b1 , b2 , … , bm} , R 为从 A 到 B 的一个二元关系,构造一个 n×m矩阵。用集合A的元素标注矩阵的行,用集合B的元素标注 矩阵的列,对于a∈A和b∈B,若 <a ,b>∈R,则在行 a 和列 b 交 叉处标1,否则标0。这样得到的矩阵称为R的关系矩阵。
数模竞赛中的图论问题大专

实际应用Байду номын сангаас景
数模竞赛中的图论问题通常与实际应用紧密相关 ,要求选手具备将实际问题转化为数学模型的能 力,以及利用图论知识进行实际问题的优化和解 决的能力。
图论问题的发展趋势与展望
算法优化与数据结构创新
随着大规模数据的不断涌现,图论问题的解决需 要更加高效的算法和更加优化的数据结构。未来 研究将更加注重算法的时间和空间复杂度优化, 以及新型数据结构的开发和应用。
详细描述
最小生成树问题在数模竞赛中常以实际应用问题形式出现,如网 络设计、电路设计等。解决该问题通常采用Kruskal算法或Prim算 法,通过逐步添加边来构建最小生成树。
最短路径问题
总结词
最短路径问题是图论中的另一个基本问题,旨在找到连接两个顶点的最短路径。
详细描述
最短路径问题在数模竞赛中常见于诸如最佳路线规划、物流配送等问题。常用 的算法有Dijkstra算法和Bellman-Ford算法,它们能够处理带权重的图,并找 到最短路径。
总结词
旅行商问题是一个经典的组合优化问题,目标是在给定一系列城市和每对城市之间的距离的情况下, 找到一条旅行路线使得每个城市恰好经过一次并回到原点,且总距离最短。
详细描述
旅行商问题是数模竞赛中经常出现的图论问题之一。解决这类问题的方法包括暴力枚举、回溯算法、 遗传算法等。该问题在物流配送、路线规划等领域有广泛应用。
历史
图论起源于18世纪欧拉的研究, 后来在19-20世纪得到快速发展 ,成为组合数学的一个重要组成 部分。
图论的基本概念
01
02
03
04
05
节点(顶点):图中的点 边:连接两个节点的线段 连通性:图中的节点或边 路径:一系列连续的边和
数模竞赛中的图论问题通常与实际应用紧密相关 ,要求选手具备将实际问题转化为数学模型的能 力,以及利用图论知识进行实际问题的优化和解 决的能力。
图论问题的发展趋势与展望
算法优化与数据结构创新
随着大规模数据的不断涌现,图论问题的解决需 要更加高效的算法和更加优化的数据结构。未来 研究将更加注重算法的时间和空间复杂度优化, 以及新型数据结构的开发和应用。
详细描述
最小生成树问题在数模竞赛中常以实际应用问题形式出现,如网 络设计、电路设计等。解决该问题通常采用Kruskal算法或Prim算 法,通过逐步添加边来构建最小生成树。
最短路径问题
总结词
最短路径问题是图论中的另一个基本问题,旨在找到连接两个顶点的最短路径。
详细描述
最短路径问题在数模竞赛中常见于诸如最佳路线规划、物流配送等问题。常用 的算法有Dijkstra算法和Bellman-Ford算法,它们能够处理带权重的图,并找 到最短路径。
总结词
旅行商问题是一个经典的组合优化问题,目标是在给定一系列城市和每对城市之间的距离的情况下, 找到一条旅行路线使得每个城市恰好经过一次并回到原点,且总距离最短。
详细描述
旅行商问题是数模竞赛中经常出现的图论问题之一。解决这类问题的方法包括暴力枚举、回溯算法、 遗传算法等。该问题在物流配送、路线规划等领域有广泛应用。
历史
图论起源于18世纪欧拉的研究, 后来在19-20世纪得到快速发展 ,成为组合数学的一个重要组成 部分。
图论的基本概念
01
02
03
04
05
节点(顶点):图中的点 边:连接两个节点的线段 连通性:图中的节点或边 路径:一系列连续的边和
图论的起源

莱昂哈德· 欧拉
如何才能在所有桥都恰巧只走一遍的前提下,回到原出发点?
桥所连接的地区 视为点 A A
C
C D B B
D
每一座桥视为一 条线
求从图中任一点出发,通过每条边一次,最后回到起点。
如果通奇数座桥的地方不止两个,那麽 满足要求的路线便不存在了。
如果只有两个地方通奇数座桥,则可从 其中一地出发可找到经过所有桥的路线。 若没有一个地方通奇数座桥,则从任何 一地出发,所求的isberg七桥问题(Euler问题)
柯尼斯堡七桥问题是图论中的著名问题。 这个问题是基于一个现实生活中的事例: 位于当时东普鲁士柯尼斯堡(今日俄罗斯加里 宁格勒)有一条河,河中心有两个小岛。小岛 与河的两岸有七条桥连接。如何才能在所有 桥都恰巧只走一遍的前提下,回到原出发点?
如何才能在所有桥都恰巧只走一遍的前提下,回到原出发点?
图论的起源
图论诞生和孕育于民间游戏。 创生:1736年 瑞士数学家欧拉——图论之父; 进展:1936年,匈牙利数学家寇尼希(Konig)发 表名著 《有限图和无限图理论》 1930年,波兰数学家库拉托父斯基 (Kulatowsky)证明了平面图可以画在平面上。 其后,图论在现代数学、计算机科学、工程 技术、优化管理等领域有大用而得以大力发 展
不少数学家都尝试去解析这个事例。而 这些解析,最后发展成为了数学中的图论。 莱昂哈德· 欧拉(Leonhard Euler)在1736 年圆满地解决了这一问题,证明这种方法并 不存在。他在圣彼得堡科学院发表了图论史 上第一篇重要文献。欧拉把实际的抽象问题 简化为平面上的点与线组合,每一座桥视为 一条线,桥所连接的地区视为点。这样若从 某点出发后最后再回到这点,则这一点的线 数必须是偶数。
图论—基本概念

2) 在无向图中,两个结点间(包括结点自身间)若有几条 边,则这几条边称为平行边;
3) 两结点vi,vj间相互平行的边的条数称为边(vi,vj) 或<vi,vj>的重数;
4) 含有平行边的图称为多重图; 5) 非多重图称为线图; 6) 无自回路的线图称为简单图。
2020年3月14日
计算机科学与技术学院
G3=<V3,E3>=<{1,2,3,4,5},{<1,2>,(1,4),<4,3>,
<3,5>,<4,5>}>
2020年3月14日
计算机科学与技术学院
第9页
几个基本概念
1) 在一个图中,关联结点vi和vj的边e,无论是有向的 还是无向的,均称边e与结点vI和vj相关联,而vi和 vj称为邻接点,否则称为不邻接的;
设V={v1, v2,…,vn}为图G的结点集,称 (deg(v1),deg(v2),…,deg(vn))为G的度数序列。
上图的度数序列为(3,3,5,1,0)。
2020年3月14日
计算机科学与技术学院
第18页
例
1) (3,3,2,3),(5,2,3,1,4)能成为图的度数序列吗? 为什么?
2) 已知图G中有10条边,4个度数为3的结点,其余结点 的度数均小于等于2,问G中至少有多少个结点?为什 么?
对任意e∈E,都有e与<u,v>∈VV或者
(u,v)∈V&V相对应。
2020年3月14日
计算机科学与技术学院
第6页
图的分类(按边的方向)
1) 若边e与无序结点对(u,v)相对应,则称边e为无向边, 记为e=(u,v),这时称u,v是边e的两个端点;
3) 两结点vi,vj间相互平行的边的条数称为边(vi,vj) 或<vi,vj>的重数;
4) 含有平行边的图称为多重图; 5) 非多重图称为线图; 6) 无自回路的线图称为简单图。
2020年3月14日
计算机科学与技术学院
G3=<V3,E3>=<{1,2,3,4,5},{<1,2>,(1,4),<4,3>,
<3,5>,<4,5>}>
2020年3月14日
计算机科学与技术学院
第9页
几个基本概念
1) 在一个图中,关联结点vi和vj的边e,无论是有向的 还是无向的,均称边e与结点vI和vj相关联,而vi和 vj称为邻接点,否则称为不邻接的;
设V={v1, v2,…,vn}为图G的结点集,称 (deg(v1),deg(v2),…,deg(vn))为G的度数序列。
上图的度数序列为(3,3,5,1,0)。
2020年3月14日
计算机科学与技术学院
第18页
例
1) (3,3,2,3),(5,2,3,1,4)能成为图的度数序列吗? 为什么?
2) 已知图G中有10条边,4个度数为3的结点,其余结点 的度数均小于等于2,问G中至少有多少个结点?为什 么?
对任意e∈E,都有e与<u,v>∈VV或者
(u,v)∈V&V相对应。
2020年3月14日
计算机科学与技术学院
第6页
图的分类(按边的方向)
1) 若边e与无序结点对(u,v)相对应,则称边e为无向边, 记为e=(u,v),这时称u,v是边e的两个端点;
图的基本概念

为弧的始结点(Initial Vertex), 称为弧的终结点(Terminal Vertex), 统称为的端点
(Endpoint)。
5
无向图 & 有向图
• 【定义】在图G中,
①如果每条边都是有向边, 该图G称为有向图(Directed Graph)
②若每条边都是无向边, 该图G称为无向图(Undirected Graph)
(Edge);
③称为关联函数, 是从E到V中的有序对或无序对的映射。
•
若边∈E与无序结点对(, )相联系, 则()=(, ), 这时边称为无向边, 有时简称为边;
•
若边∈E与有序结点对<, >相联系, 则()=<, >, 此时边称为有向边或弧(Arc), 称
③如果有些边是有向边, 另一些边是无向边, 图G称为混合图(Mixed Graph)
• 【定义】一个有向图中, 如果将每条有向边都改为无向边, 便得到该有向图的
底图(Underlying Undirected Graph)或基础图。
6
图的表示
• 一个图可以用几何图形表示,方法与二元关系的表示法相同。
多重图(Multiple Graph): 含有平行边的图;
•Leabharlann 线 图: 非多重图称为线图;•
简单图(Simple Graph): 不含平行边和自回环的图。
简单图是一
个非常重要
的概念
13
图的分类(续)
• 3.按G的边有序, 无序分为有向图, 无向图和混合图。
• 有向图(Directed Graph): 每条边都是有向边的图称为有向图
图的基本概念
图论的前世今生
• 1736年,欧拉(L.Eular)发表了第一篇关于图论的论文,解决了哥尼斯
图论2011

定义7.2.1 无向图G是一个二元组<V,E>
V
: vertex set 顶点集
常写作V(G),也称点(point),结点(node),接点(junction) 非空有限集 它的元素,习惯上用数字或小写英文字母a,b,c,u,v,w,x,y,z等(或加 足标)表示
E : edge set 边集合
例
G'=<V',E'>=<{a,b,c,d,e,f},{<a,b>,<b,a>,<b,c >,<c,c>,<a,d>,<e,e>}>
简单图
只讨论V是有限集的情况
若#V(G)=p,#E(G)=q,则称G是一个(p.q)图
p称为图G的阶 (1,0)图——孤立点或平凡图
(p,0)图(p≥2)——空图或零图
uG
d (u) 2q
个数有什么特点? 2. 是否存在奇数阶奇数 度正则图?
证明 图中顶点度之和是指图中与各个顶点相关联的边数 之和,每条边(包括自环线和平行线)都将恰好被计数两次, 所以定理成立。
推论1 在图中,次数为奇数的结点必为偶数个 推论2 不存在奇数阶奇数度正则图
思考题
p阶简单图中顶点的最大度数是多少? 证明:在任何p(p≥2)阶简单图中,至少有两 个顶点具有相同的度 设G是一个有19条边的图,且图中顶点的度 至少是3,那么G的阶最大是多少? 说明下面的序列中哪些不可能是图的度序 列,哪些不可能是简单图的度序列
结点数相等 边数相等 度数相同的结点数相等 注意:不是充分条件
G
G’
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图论问题起源
吴雪芬 刘姝
小问题
一笔画
世界数学难题——哥尼斯堡七桥问题
• 18世纪时,欧洲有一个风景秀丽的小城哥尼斯堡(今俄罗 斯加里宁格勒),那里的普莱格尔河上有七座桥。将河中 的两个岛和河岸连结,城中的居民经常沿河过桥散步,于 是提出了一个问题:一个人怎样才能一次走遍七座桥,每 座桥只走过一次,最后回到出发点?大家都试图找出问题 的答案,但是谁也解决不了这个问题…………
• 这就是哥尼斯堡七桥问题,一个著名的图走法是不可能的。他的论 点是这样的,除了起点以外,每一次当一个人由一座桥进 入一块陆地(或点)时,他(或她)同时也由另一座桥离 开此点。所以每行经一点时,计算两座桥(或线),从起 点离开的线与最後回到始点的线亦计算两座桥,因此每一 个陆地与其他陆地连接的桥数必为偶数。
答案
• 七桥所成之图形中,没有一点含有偶数条数,因此上述的 任务无法完成
• 欧拉的这个考虑非常重要,也非常巧妙,它正表明了数学 家处理实际问题的独特之处——把一个实际问题抽象成合 适的“数学模型”。这种研究方法就是“数学模型方法”。 这并不需要运用多么深奥的理论,但想到这一点,却是解 决难题的关键。
• 1736年,欧拉在交给彼得堡科学院的《哥尼斯堡7座桥》 的论文报告中,阐述了他的解题方法。他的巧解,为后来 的数学新分支——拓扑学的建立奠定了基础。
一笔画: ⒈凡是由偶点组成的连通图,一定可以一笔画成。画时可以 把任一偶点为起点,最后一定能以这个点为终点画完此图。 ⒉凡是只有两个奇点的连通图(其余都为偶点),一定可以一 笔画成。画时必须把一个奇点为起点,另一个奇点终点。 ⒊其他情况的图都不能一笔画出。(奇点数除以二便可算出此 图需几笔画成。)
• 七桥问题和欧拉定理。欧拉通过对七桥问题的研究,不仅 圆满地回答了哥尼斯堡居民提出的问题,而且得到并证明 了更为广泛的有关一笔画的三条结论,人们通常称之为 欧拉定理。对于一个连通图,通常把从某结点出发一笔画 成所经过的路线叫做欧拉路。人们又通常把一笔画成回到 出发点的欧拉路叫做欧拉回路。具有欧拉回路的图叫做欧 拉图。
吴雪芬 刘姝
小问题
一笔画
世界数学难题——哥尼斯堡七桥问题
• 18世纪时,欧洲有一个风景秀丽的小城哥尼斯堡(今俄罗 斯加里宁格勒),那里的普莱格尔河上有七座桥。将河中 的两个岛和河岸连结,城中的居民经常沿河过桥散步,于 是提出了一个问题:一个人怎样才能一次走遍七座桥,每 座桥只走过一次,最后回到出发点?大家都试图找出问题 的答案,但是谁也解决不了这个问题…………
• 这就是哥尼斯堡七桥问题,一个著名的图走法是不可能的。他的论 点是这样的,除了起点以外,每一次当一个人由一座桥进 入一块陆地(或点)时,他(或她)同时也由另一座桥离 开此点。所以每行经一点时,计算两座桥(或线),从起 点离开的线与最後回到始点的线亦计算两座桥,因此每一 个陆地与其他陆地连接的桥数必为偶数。
答案
• 七桥所成之图形中,没有一点含有偶数条数,因此上述的 任务无法完成
• 欧拉的这个考虑非常重要,也非常巧妙,它正表明了数学 家处理实际问题的独特之处——把一个实际问题抽象成合 适的“数学模型”。这种研究方法就是“数学模型方法”。 这并不需要运用多么深奥的理论,但想到这一点,却是解 决难题的关键。
• 1736年,欧拉在交给彼得堡科学院的《哥尼斯堡7座桥》 的论文报告中,阐述了他的解题方法。他的巧解,为后来 的数学新分支——拓扑学的建立奠定了基础。
一笔画: ⒈凡是由偶点组成的连通图,一定可以一笔画成。画时可以 把任一偶点为起点,最后一定能以这个点为终点画完此图。 ⒉凡是只有两个奇点的连通图(其余都为偶点),一定可以一 笔画成。画时必须把一个奇点为起点,另一个奇点终点。 ⒊其他情况的图都不能一笔画出。(奇点数除以二便可算出此 图需几笔画成。)
• 七桥问题和欧拉定理。欧拉通过对七桥问题的研究,不仅 圆满地回答了哥尼斯堡居民提出的问题,而且得到并证明 了更为广泛的有关一笔画的三条结论,人们通常称之为 欧拉定理。对于一个连通图,通常把从某结点出发一笔画 成所经过的路线叫做欧拉路。人们又通常把一笔画成回到 出发点的欧拉路叫做欧拉回路。具有欧拉回路的图叫做欧 拉图。
