第三讲 线性规划的灵敏度分析与最优解的解释
线性规划-灵敏度分析
若进一步问： 1）当原材料涨价或产品价格发生变化时，原最优生产计划变否？ 2）若在生产中采用了新的工艺，产品对原材料的消耗发生了变化，原最优生产 计划变否？ 3）为适应市场需要，管理者可能会生产新的产品或停止生 产某种产品，原最优 生产计划变否？
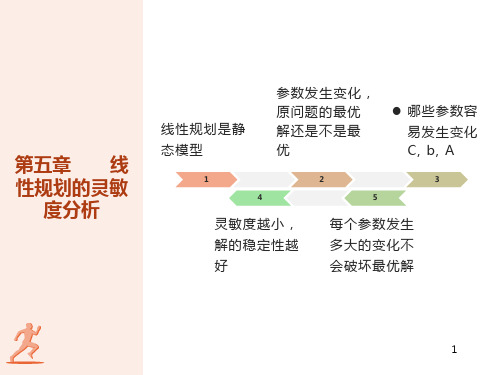
二、灵敏度分析的定义 研究数学模型某些系数的变化对最优解的影响及其影响程度的分析称为灵 敏度分析（Sensitivity Analysis）或优化后分析。
1 1
B 1b 故：原最优基不变，但最优解变为： X 5 1 0 0 0 T 0 1 b 2） 设： b b 1 3 3
要使原最优基不变，就要有： B-1b≥ 0 ，
4 1 b1 B b 1 1 3 0
5）是否有更好的增加资源的方案，实际上是问：①应增加哪种资源？②花多大代价增 加这种资源? ③最佳增量是多少？ ① 资源甲的影子价格 y1 = 5 > 1 ＝ y2 资源乙的影子价格，故应首先考虑增加资源甲。 ② 单位资源增量所支付的费用应< 资源的影子价格，即：单位费用< 5 才合算。 ③ 最佳增量应满足：
三、灵敏度分析的内容
1 当线性规划模型系数中的一个或几个发生变化时，已经求得的最优解是否会 发生变化？ 2 线性规划模型的系数在什么范围内变动时，原来的最优解不变？
3 当线性规划模型系数的变化时，已经引起原最优解的变化时，如何才能尽快
求出新的最优解？
四、灵敏度分析的理论依据及方法
记最优基矩阵为B，最优解： 最优值： X = B－1b z = CB B－1b 与b无关 与b、C无关 与C无关
4 1 1 / 3 1 0 即： N ' 1 0 0 c 1 ' 3 1 1 7 / 3 0 1 0时，原最优解不变 N ' c1 '5 4c1 '3 c1 '3 0
论述：线性规划的灵敏度分析
论述：线性规划的灵敏度分析论述：线性规划的灵敏度分析。
分析的基本步骤，各参数变化带来的影响以及最优基发⽣改变后相应的处理⽅法。
线性规划的灵敏度分析研究的问题是：研究线性规划模型中aij、bi、cj等参数中的⼀个或⼏个发⽣变化时，问题最优解会发⽣什么变化；研究这些参数在⼀个多⼤范围内变化时，问题的最优解不变。
研究的前提条件:1、原线性规划问题已取得了最优解；2、每次只讨论⼀种参数的变化，⽽参数之间的变化互不关联。
分析的基本步骤：1、将参数的改变通过计算反映到最终单纯形表上来2、检查原问题是否仍为可⾏解3、检查对偶问题是否仍为可⾏解4、按照单纯形表所列情况得出结论活决定继续计算的步骤。
各参数变化带来的影响：1、⾮基变量cj发⽣变化当⽬标函数中cj发⽣变化，将影响最终单纯形表中⾮基变量的检验数。
如果是⾮基变量的价值系数发⽣变化，只影响该⾮基变量的检验数。
如果是基变量的价值系数发⽣变化，将影响所有⾮基变量的检验数。
如果变化后所有的检验数仍然⼩于等于0，则最优解不变；否则，使⽤单纯形法求变化后的新最优解。
2、右端常数项bi发⽣变化当右端常数项发⽣变化时，将影响最优单纯形表中基变量的值。
如果基变量的值仍然都⼤于等于0，则线性规划问题的最优解不变，但是基变量的值将发⽣变化；如果有基变量的值⼩于0，则⽤对偶单纯形法对原最优单纯形表继续求解。
3、增加⼀个变量增加⼀个变量也就是多⽣产⼀种产品。
只需考虑该产品（变量）的检验数是否⼤于0，如果⼤于0则表⽰应该⽣产，⽤单纯形表进⾏求解；如果⼩于等于0则该产品不⽤⽣产，最优解也不发⽣变化。
4、增加⼀个约束条件增加⼀个约束条件，可能影响的只是该约束条件的松弛变量的值。
如果该松弛变量的值⼤于等于0，则线性规划最优解不变；如果该松弛变量的值⼩于0，则⽤对偶单纯形法进⾏计算。
5、aij发⽣变化改变aij只会影响检验数，如果改变后所有的检验数均⼩于等于0，则最优解不变；如果存在检验数⼤于0，则⽤单纯形法进⾏求解。
线性规划的灵敏度分析与最优解的解释
3.3 灵敏度分析：计算机求解
为了使用管理科学家软件，我们使用小数代替分数。Par 公司的问题用小数形式的系数表示如下：
现在，模型的最优解540个标准袋和252个高级袋。每个目 标函数系数都有一个最优范围，即目标函数系数在什么范围 内变化，模型的最优解保持不变。
3.2 图解法灵敏度分析
3.2.1 目标函数系数 认真观察图发现，只要
目标函数直线的斜率处于 直线A（和切割与印染约 束线重合）的斜率与直线 B（与成型约束线重合） 的斜率之间，极点3 （S=540，D=252）就是最 优解的点。
则直线A和直线B的斜率都已经计算出来了，我们来看 保持极点3仍然为最优解点，应满足条件：
-3/2≤目标函数的斜率≤-7/10
3.2 图解法灵敏度分析
现在让我们考虑目标直线斜率的一般形式。用CS表示标
准袋的利润，CD表示高级袋的利润，P表示目标函数值。 使用这些标识，目标函数直线可以写成：
P=CSS+CDD 把上面方程写成斜截式，得到
第三章 线性规划的灵敏度分析与最优解 的解释
引言
灵敏度分析是研究当一个线性规划问题中的系 数发生变化时，其对函数最优解的影响程度。运 用灵敏度分析，我们可以回答以下问题： 1.如果目标函数的系数发生了变化，对最优解会产 生什么影响？ 2.如果改变约束条件的右端值，对最优解会产生什 么影响？
首先我们将介绍如何使用图解法进行双变量 线性规划问题的灵敏度分析，然后介绍如何使用 管理科学家软件得到灵敏度分析报告。
顺时针转动目标函数直线，使其斜率变成一个绝对值更 大的负数，从而斜率变小了。直到与B重合，我们又获得了 多重最优解——极点3和极点2之间都是最优点。因此B的斜 率是目标函数直线斜率的下限。
第3章 线性规划灵敏度分析与最优解的解释
使用Excel Excel进行灵敏度分析 3.4 使用Excel进行灵敏度分析 LINGO的灵敏度分析报告 3.5 LINGO的灵敏度分析报告
�
x2
5 4 Q4 3 2 5x1+2x2=20 (1.5, 3.25) 4x2=13 Q3 (2,3) Q2(3,2.5) x1+2x2=8 Q1 1 2 3 4 5
1.5 X = 3.25
*
ቤተ መጻሕፍቲ ባይዱz = 19.25
*
1 0
x1
对偶价格: 对偶价格:约束条件右端项每增加一个单位引起的最优 值的改进量称为对偶价格. 值的改进量称为对偶价格.
max
z = 2 x1 + 5 x2 x1 + 2 x2 ≤ 8 5 x + 2 x ≤ 20 1 2 4 x2 ≤ 12 x1 , x2 ≥ 0
x2
5 4 3 2 1 0 Q1 1 2 3 4 5 Q4 5x1+2x2=20 Q3 (2,3) 4x2=12 Q2 (3,2.5) x1+2x2=8
线性规划的灵敏度分析与最优解的解释31灵敏度分析简介32图解法与灵敏度分析321目标函数系数322约束条件右端值204x32523直线q204x3252315325对偶价格
第3章 线性规划的灵敏度分析 与最优解的解释 3.1 灵敏度分析简介 3.2 图解法与灵敏度分析 3.2.1 目标函数系数 3.2.2 约束条件右端值
灵敏度分析: 3.3 灵敏度分析:计算机求解 Scientist) (Management Scientist)
目标函数系数的100%法则: 法则: 目标函数系数的 法则 对所有变化的目标函数系数, 对所有变化的目标函数系数,计算其占允许增加量和 允许减少量的百分比之和.如果和没有达到100%,最优 允许减少量的百分比之和.如果和没有达到 , 解就不会改变. 解就不会改变. 约束条件右端值的100%法则: 法则: 约束条件右端值的 法则 对所有变化的右端值, 对所有变化的右端值,计算其占允许增加量和允许减 少量的百分比之和.如果和没有达到100%,对偶价格就 少量的百分比之和.如果和没有达到 , 不会改变. 不会改变.
线性规划模型-灵敏度分析
0.8千克B1
获利44元/千克
至多100公斤A1
制订生产计划，使每天净利润最大
• 30元可增加1桶牛奶，3元可增加1小时时间，应否投 资？现投资150元，可赚回多少？ • B1，B2的获利经常有10%的波动，对计划有无影响？
钢管下料
原料下料问题 生产中通过切割、剪裁、冲压等 手段，将原材料加工成所需大小 按照工艺要求，确定下料方案， 使所用材料最省，或利润最大
整数非线性规划模型
钢管下料问题2
增加约束，缩小可行域，便于求解
每根原料钢管长19米
需求：4米50根，5米10 根，6米20根，8米15根
4 50 5 10 6 20 8 15 26 原料钢管总根数下界： 19
引 言
由于战争的需要, 美国的经济学家T. C. Koopmans (库普曼斯) 重新独立的研究运输问 题, 并很快看到了线性规划在经济学中应用的 意义. 在这之后, 线性规划也被人们广泛地用 于军事、经济等各方面。 由于Kantorovich 和 Koopmans在这方面 的突出贡献,他们一起得到1975年诺贝尔经济 学奖。 为更好地理解线性规划所描述的问题， 我们先看一个例子。
原料最多增加10 时间最多增加53
• 35元可买到1桶牛奶，每天最多买多少？ 最多买10桶!
例2 奶制品的生产销售计划 在例1基础上深加工
1桶 牛奶 或 3千克A1 12小时 1千克 获利24元/千克
2小时,3元 获利16元/千克 8小时 4千克A2 1千克 获利32元/千克 0.75千克B2 50桶牛奶, 480小时 2小时,3元
35 <48, 应该买！
• 聘用临时工人付出的工资最多每小时几元？ 2元！
线性规划的灵敏度分析
资源有剩余，在 最优解中就有对 应松弛变量存在， 且其影子价为 0
影子价为 0， 资源并不一定有 剩余
4
5.2 价值系数 cj 的灵敏度分析
• cj 变动可能由于市场价格的波动，或生产成本的变动 • cj 的灵敏度分析是在保证最优解的基变量不变的情况下，分
析cj 允许的变动范围cj • cj 的变化会引起检验数的变化，有两种情况:
1300 4.25 5 5.75 4 0 0.25 1
zj-cj 3.25 0 2.75 0 0 0.25 1
c c j k
由于基变m量对应的价值系数 cj 在CB中出现，
2 基变量 zj zj (cjk c因jki )此ai它j 会影c响jk a所ij 有非cj基k a变kj (量z的j 检验zj数) 。
5.4 （技术系 数 aij 的灵敏 度分析）暂不 讲授(转5.5）
技术系数aij变化的影响比较复杂
对应基变量的 aij ，且资源bi已全部用完 对应基变量的 aij ，但资源bi未用完 对应非基变量的 aij ，且资源bi全用完或未用完
1、对应基变量的 aij ，且资源bi已全部用完 aij=0 2、对应基变量的 aij ，但资源bi未用完 aijxn+i /xj
3
z8c8 qiai8c8(5040.2 531)9 i1
50
结论：生产x8有利。 将B–1P8加入最优单纯型表中，以x8为入基变量进行迭代。 （过程学生完成）
17
5.6 新增约束 条件的分析
1、将最优解代入新的约束条件，若满足，则最优解不变 2、若不满足，则当前最优解要发生变化；将新增约束条件
(x)
b
i
i1
(C
B
第二章 线性规划的图解法(简)
第二节 图解法
在线性规划中，对一个约束条件中没使用的资源或能力的大小称 之为松弛量。记为Si。
第二节 图解法
像这样把所有的约束条件都写成等式 ，称为线性规划模型的标准化，所得结果 称为线性规划的标准形式。
第二节 图解法
同样对于≥约束条件中，可以增加一些代表
最低限约束的超过量，称之为剩余变量，把≥约
第二章 线性规划的图解法
主要内容：
§1 问题的提出 （什么是线性规划） §2 图解法 §3 图解法的灵敏度分析
重点和难点
重点： （1）线性规划问题的主要概念 （2）线性规划问题的数学模型 （3）线性规划图解法的过程 （4）阴影价格的定义和灵敏度分析 难点： 灵敏度分析
第一节 问题的提出
约束条件对偶价格小于零时，约束条件
右边常数增加一个单位，就使得最优目
标函数值减少一个其对偶价格。
第三节 图解法的灵敏度分析
对目标函数值求最小值的情况下， 当对偶价格大于零时，约束条件右边常数增加 一个单位就使其最优目标函数值减少一个其对 偶价格； 当对偶价格等于零时，约束条件右边常数增加 一个单位，并不影响其最优目标函数值； 当对偶价格小于零时，约束条件右边常数增加 一个单位，就使得其最忧目标函数值增加一个 其对偶价格。
具有上述3个特征的问题为线性规划问题。
第一节 问题的提出
我们的仸务就是要选择一组或多组方案，使目
标函数值最大或最小。从选择方案的角度说，
这是规划问题。从使目标函数值最大或最小的
角度说，就是优化问题。
线性规划数学模型的一般表示方式
max(min) f ( x) c1 x1 c2 x2 cn xn a11 x1 a12 x2 a1n xn a x a x a x 21 1 22 2 2n n s.t. a x a x a x m2 2 mn n m1 1 x1 , x2 , , xn n : 变量个数 ; m : 约束行数 ; n m : 线性规划问题的规模 c j : 价值系数 ; b j : 右端项; aij : 技术系数 (, )b1 (, )b2 (, )bm 0
运筹学：第1章 线性规划 第3节 对偶问题与灵敏度分析
s.t.
4x1 3x1
5x2 200 10x2 300
x1, x2 0
9x1 4x2 360
s.t.
34xx11
5x2 10 x
200 2 300
3x1 10x2 300
x1, x2 0
则D为
min z 360y1 200y2 300y3 300y4
9 y1 4 y2 3y3 3y4 7 s.t.4 y1 5y2 10 y3 10 y4 12
amn xn bm ym xn 0
机会成本 a1 j y1 a2 j y2 aij yi amj ym
表示减少一件产品所节省的可以增加的利润
（3）对偶松弛变量的经济解释——产品的差额成本
机会成本
利润
min w b1 y1 b2 y2 bm ym
a11 y1
st
a12
y1
a1n y1
max z CX
（P）
AX b
s
.t
.
X
0
（D）
min w Yb
s.t.
YA C Y 0
• （2）然后按照（D）、（P）式写出其对偶
例：写出下面线性规划的对偶规划模型：
max z 2x1 3x2
min w 3 y1 5y2 1y3
x1 2x2 3 y1 0
s.t.
2xx11
例如，在前面的练习中已知
max z 2.5x1 x2 的终表为
3x1 5x2 15 s.t.5x1 2x2 10
x1, x2 0
0 x3 9 2.5 x1 2
0 19 1 - 3
5
5
1
2
0
1
5
第三章 线性规划的灵敏度分析和最优解的解释
3.1 灵敏度分析简介
灵敏度分析是研究线性规划的参数(非可控输入)发生 变化对最优解的影响程度
线性规划的参数包括：
• 目标函数系数 • 约束条件右侧值 • 约束条件系数矩阵
最优解中包含的信息：
• 目标函数值 • 决策变量值 • 递减成本(reduced cost) • 松弛/剩余变量
4
3.1 灵敏度分析简介
利用Lingo 软件做灵敏度分析
16
17
利用Excel做灵敏度分析
Microsoft Excel 16.0 敏感性报告 工作表: [数据模型与决策第3章例题.xlsx]第三章例题1 报告的建立: 2021/5/29 10:48:56
可变单元格
单元格 $B$15 $C$15
名称 决策变量值 x1 决策变量值 x2
作者
John Loucks
St. Edward’s University
1
第三章 线性规划的灵敏度分析和最优解的解释
3.1 灵敏度分析简介 3.2 目标函数系数变化的分析 3.3 约束条件右端值变化的分析 3.4 传统灵敏度分析的局限性
2
第三章 线性规划的灵敏度分析和最优解的解释
3.1 灵敏度分析简介 3.2 目标函数系数变化的分析 3.3 约束条件右端值变化的分析 3.4 传统灵敏度分析的局限性
6
x1 < 6
2x1 + 3x2 < 19 x1 + x2 < 8
x1, x2 > 0
固定x2的系数7，改变x1 的系数
5
最优解:
Max 14/3x1 + 7x2
4
x1 = 5, x2 = 3
3
Max 7x1 + 7x2
线性规划的灵敏度分析
,
b3
33
5
1
,
5 1
,
15
1
5,5,15
故有 15 b3 5,b3 在[0，20]上变化时最优基不变。
若线性规划模型是一个生产计划模型，当求出cj或bi 的最大允许变化范围时，就可随时根据市场的变化来掌握 生产计划的调整。
灵敏度分析方法还可以分析工艺系数aij的变化对最优解 的影响，对增加约束、变量或减少约束、变量等情形的分 析，下面以一个例子来说明这些分析方法。
（8）增加新约束 5x1 x2 2x3 10
§2.4 灵敏度分析
Ch2 Dual Problem
Sensitivity Analysis
2023年2月1日星期三 Page 19 of 34
【解】加入松弛变量x4、x5、x6，用单纯形法计算，最优表如2－7所 示。
表2－7
Cj
2 -1
4
0
0
0
b
CB XB x1
x2
x3
x4
x5
x6
4 x3 0 5/7
1
1/7 3/7
0
2
2 x1 1 2/7
0 －1/7 4/7
0
1
0 x6 0 －2
0
0
－1
1
1
λj
0 －31/7 0 －2/7 －20/7 0
§2.4 灵敏度分析 Sensitivity Analysis
Ch2 Dual Problem
2023年2月1日星期三 Page 20 of 34
§2.4 灵敏度分析 Sensitivity Analysis
cj
－2 1
－4
0
线性规划灵敏度分析
淮北师范大学2011届学士学位论文线性规划灵敏度分析学院、专业数学科学学院数学与应用数学研究方向运筹学学生姓名陈红学号20071101008指导教师姓名张发明指导教师职称副教授2011年4月10日线性规划的灵敏度分析陈 红（淮北师范大学数学科学学院，淮北，235000）摘 要本文主要从价值系数j c 的变化，技术系数ij a 的变化，右端常数i b 的变化以及增加新的约束条件和增加一个新变量的灵敏度这几个方面来进行研究；资源条件是线性规划灵敏度分析中的主要应用内容,而对于资源条件b 的一个重要应用是：“影子价格问题”的实际应用，最后简述了线性规划在经济及管理问题上的典型应用和从求解例题的图解法揭示了最优解的一些重要特征。
关键词 单纯形法，灵敏度分析,最优解，资源条件，价值系数Sensitivity Analysis of Linear ProgrammingChen Hong(School of Mathematical Science,Huaibei Normal University ，Huaibei,235000)AbstractThis thesis is mainly from the variety of the cost coefficient ‘j c ’, the variety of technology coefficient ‘ij a ’， the var iety of the resources condition‘i b ’and increase the new restraint and new variable to analytical linear programming of sensitivity analysis 。
This thesis is mainly based on the simplex method and dual simplex method of linear programming to system analytical the influence of the variety upon the optical solution of the coefficient of the simplex table 。
浅谈线性规划问题的灵敏度分析
浅谈线性规划问题的灵敏度分析符龙飞2016年5月15日摘要线性规划是运筹学的一个重要的分支，本文主要讨论有关线性规划问题的灵敏度分析，灵敏度分析顾名思义就是指对事物或者使整个系统因为其自身周围环境条件变化而表现出来的敏感程度的分析，在线性规划问题中，我们都假定技术数据、资源数据和价值数据向量或者矩阵中元素为已知常数，但是在实际的问题工作中这些数据往往只是一些预测的数据和估计值，在处理实际问题的建立线性规划模型时，这些数据并不是不会变化的，不是很精确,有可能进行了修改.因此本文讨论在实际问题中当技术系数、资源系数、价值系数以及增加一个变量和增加一个约束条件时，原问题最优解的变化，对原线性规划问题进行灵敏度分析.关键词：线性规划；灵敏度；最优解AbstractLinear programming is an important branch of operational research, this paper mainly discusses the sensitivity analysis of linear programming, sensitivity analysis of the definition refers to the analysis of the sensitivity of its own because of changes in ambient conditions and displayed on things or to make the whole system of linear programming problems, we assume that the technology of data resources the data value and data vector or matrix elements in the known constant, but in the actual problems in these data are just some forecast data and estimates, the establishment of a linear programming model to deal with practical problems, will not change the data, is not very accurate, may be modified in this paper.When discussing technical factors, in the actual problem of resource factor, value factor and add a variable and add a constraint condition, the original problem of optimal solution Sensitivity analysis of the original linear programming problem.Keywords: Linear programming; sensitivity; optimal solution目录第一章前言 (1)1.1 线性规划问题及线性规划发展史 (1)1.2 灵敏度分析的概念 (1)1.3线性规划模型 (1)1.4灵敏度分析的方法及步骤 (2)1.5 符号说明 (2)第二章技术系数a的变化分析 (3)ij2.1 非基变量系数列向量发生变化 (3)2.2 基变量系数列向量发生变化 (4)第三章资源系数b的变化分析 (7)ic的变化分析 (10)第四章价值系数i4.1 非基变量价值系数变化 (10)4.2基变量价值系数变化 (11)第五章增加新的变量的变化分析 (13)第六章增加新约束条件的变化分析 (16)总结 (18)[参考文献] (19)第一章前言1.1 线性规划问题及线性规划发展史线性规划是我们研究运筹学最基本的也是最重要的问题之一，是运筹学中相对比较成熟的一个重要分支.线性规划是近几十年发展起来的一种数学规划的方法，它主要研究在给定的线性不等式或者线性方程约束条件下，对所求的目标函数在一定意义下的极值问题，使其线性指标最优.它广泛应用于工、商、农、军事、交通运输、经济管理以及计划等各个领域.具有应用广泛、适应性强、计算技术比较简单等特点，线性规划在理论上已经也来越成熟，其应用也越来越广泛和深入[1].线性规划的发展是运筹学史上几代人智慧的结晶.1939年，原苏联数学家康托洛维奇发表了《生产组织与计划中的数学方法》学术报告，首次提出了线性规划问题，但是他没有找到一个统一的求解这类问题的方法，1941年美国学者希奇柯克独立的提出了运输问题这样一类特殊的线性规划问题，1947年，美国学者丹捷格提出求解线性规划的单纯形法和许多相关的理论，为线性规划奠定了理论基础，推动了线性规划的发展.自此以后线性规划在计算上趋向成熟，应用也更加广泛深入[2].1.2 灵敏度分析的概念灵敏度分析顾名思义就是指对事物或者使整个系统因为其自身周围环境条件变化而表现出来的敏感程度的分析.在线性规划问题中，我们都假定技术数据、资源数据和价值数据向量或者矩阵中元素为已知常数，但是在实际的问题工作中这些数据往往只是一些预测的数据和估计值，在处理实际问题的建立线性规划模型时，这些数据并不是不会变化的，不是很精确,有可能进行了修改.如果市场条件发生了变动，价值系数的值就会发生变化，技术系数会随着工艺技术条件的变化而变化，同样，在资源投入量发生变化时，资源系数也会随之发生变化，它的值会根据资源投入后能产出多大经济效果来决定的一种决策选择.因此，当这些数据发生变化时，线性规划的最优目标值或者最优解会发生怎样的变化？或者是不是这些参数在一定的范围内其线性规划问题的最优解不会发生变化？这就是本文我们研究线性规划问题的灵敏度分析所要解决的问题.1.3线性规划模型线性规划模型的标准形式如下：max z CX(0)0AX b b X =≥⎧⎨≥⎩我们在求解线性规划问题时首先就应该把数学模型转化成标准形式.1.4灵敏度分析的方法及步骤要进行灵敏度分析，首先要弄明白的就是上述问题：①当系数发生变化时，最优解或者最优目标值发生变化，我们如何简便地求出新的最优目标值和最优解；②当系数在什么一定范围内，线性规划的最优解是不变的.我们可以将灵敏度度分析归纳为：（1）将参数的改变计算反映到最终单纯形表上来，具体的计算方法是按下列公式计算出由技术参数、资源参数和价值参数的变化引起的最终单纯形表上有关数字的变化，即*1b B b -∆=∆*1j j P B P -∆=∆()()*1mj j j j ij i i c z c z a y =∆-=∆--∑（2）检查原问题是否仍为可行解； （3）检查对偶问题是否仍为可行解.（4）我们可以按照下表1-1所列出的情况得出结论或者得出继续计算的步骤[3].表1-1原问题 对偶问题 结论或者继续计算的步骤 可行解 可行解 表中的解仍为最优解 可行解 非可行解 用单纯法继续迭代求最优解 非可行解 可行解 用对偶单纯形法继续迭代求最优解 非可行解非可行解引入人工变量，编制新的的单纯形表，求最优解1.5 符号说明①ij a 技术数据； ②i b 资源数据； ③j c 价值数据； ④B 最优基； ⑤s .t . 约束条件.第二章 技术系数ij a 的变化分析2.1 非基变量系数列向量发生变化如果我们用最优基B 来说，当非基变量j x 的系数列向量j A 改变为'j j jA A A =+∆就会有变化后的检验数为()'1j j B j j j j c C B A A Y A σσ-=-++∆=+∆ ()1,2,,j n =[4]在这里，对偶可行解为1B Y C B -=，我们要使原来的线性规划最优基B 仍然保持不变的话，必须有'0j σ≥，即j j Y A σ∆≥- ()1,2,,j n =而当()0,,,,0Tj ij P a ∆=∆时，则由上式可得()10,,0im i ij j ij y y y y a a σ⎡⎤⎢⎥⎢⎥⎢⎥=∆≥-∆⎢⎥⎢⎥⎢⎥⎣⎦我们可以导出 当0i y >时，有jij ja y σ∆≥-；当0i y <时，有jij ja y σ∆≤-.例1已知线性规划问题12345max 2300Z x x x x x =---++s .t .()12341234347901,2,3,4,5j x x x x x x x x x j ⎧+++=⎪⎪+++=⎨⎪≥=⎪⎩ 23a 怎样变化时最优解保持不变？解：最终单纯形表如下表2-1j c2- 3- 1-0 0bB C B X 1x2x3x 4x5x2-1x 1 0 1-43 13- 1 3-2x0 1 2 13- 13 2j σ353138Z =-由此表可得[]133323234113312,311331233B cC B p a a σ-⎡⎤-⎢⎥⎡⎤=-=----⎢⎥⎢⎥⎣⎦⎢⎥-⎢⎥⎣⎦=+ 32323120233a a σ=+≥⇒≥-所以[232,)a ∈-+∞原最优解保持不变.2.2 基变量系数列向量发生变化仍然对于最优基B 来说，当基变量j x 的系数列向量j A 发生变化的时候，对于基向量B 和它的逆矩阵1B -都会有一定的影响，则线性规划的解的可行性、最优性以及它的最优目标值都会随之发生变化.我们要求出一个一般公式是很难的，因此，我们会用单纯形法重新求解变化后的线性规划问题.对于重新的求解可以在原来的单纯形终表上变换数据后进行迭代[5].例2已知线性规划问题1234max 534Z x x x x =+++s .t .()123412341234232800543412003453100001,2,3,4jx x x x x x x x x x x x x j +++≤⎧⎪+++≤⎪⎨+++≤⎪⎪≥=⎩如果非基变量3x 的系数由135⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦变为141⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，那么原线性规划的最优解是否还是最优？如果不是求出最优.解:由3110431154A ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥∆=-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦则330115110,,114444Y A σ⎡⎤⎛⎫⎢⎥∆==-<-=- ⎪⎢⎥⎝⎭⎢⎥-⎣⎦因此不满足j j Y A σ∆≥-，那么原线性规划的最优解就不再是最优解了，根据灵敏度分析的步骤，求新的最优解我们应该先求出新的检验数'1'3330130,,111044B c C B A σ-⎡⎤⎛⎫⎢⎥=-+=-+=-< ⎪⎢⎥⎝⎭⎢⎥-⎣⎦所以可以取3x 为进基变量，然后计算1'311111401143312014B A -⎡⎤-⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦-⎢⎥⎣⎦用它去替换原线性规划最优单纯形表表2-1的第3列，从而得到表2-2，继续迭代可以得到表2-3，如下表2-1 原线性规划最优单纯形表15341x2x3x4x5x6x7x5x 100 140 134- 0 1 141- 4x20022-111-2x100 34-1 114 0 0 34-1 1300134114141表2-2 改变后的单纯形表15341x2x3x4x5x6x7x5x 100 140 1 0 1 141- 4x 200 20 31 0 11-2x100 34-1 2- 0 0 34-1 13001341-141表2-3 迭代后的单形表15341x2x3x4x5x6x7x5x 1003 512- 0 0 13- 1 112-23- 4x 2003 23 0 1 13 0 13 13- 2x7003 712 1 0 23 0 112- 13 41003471213712 23我们由上表就可以看得出来，求得的最优解*7002001000,,,0,,0,0333X ⎛⎫= ⎪⎝⎭以及改变后的最优值*41003z =.第三章 资源系数i b 的变化分析我们知道，资源系数发生变化的问题关键就是怎样把i b 的变化直接的反映到原来线性规划问题的最终单纯形表，对于单纯形法的迭代过程，其实就是矩阵的初等变换过程，用所学的知识我们知道，对于分块矩阵[]BI我们进行初等变换时，把矩阵B 变成单位矩阵I ,会有单位矩阵I 变成矩阵1B -，即1IB -⎡⎤⎣⎦因此我们可以知道，若在已知的最终单纯形表中基可行解所对应的基“B ”（最终单纯形表中的基变量在初始单纯形表中的列向量所构成的矩阵），即可在最终单纯形表中找到“1B -”（初始单纯形表中的单位矩阵I 在最终单纯形表中所对应的矩阵），我们可以有'1b B b -=[6].例3对于线性规划问题12max 2z x x =+s .t .212121251562245,0x x x x x x x ≤⎧⎪+≤⎪⎨+≤⎪⎪≥⎩ 如果把第二个约束条件的右端项增大到32，那么分析一下最优解如何让变化.解：由最终单纯形表表3-1表3-1 最终单纯形表1x2x3x4x5x3x 152 0 0 1 54 152- 1x 72 1 0 0 14 12- 2x32114- 32i i z c -0 0 014 12因为003224880b ⎡⎤⎡⎤⎢⎥⎢⎥∆=-=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦，由*1b B b -∆=∆，得*51514201011082420213042b ⎡⎤-⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥∆=-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦⎣⎦⎢⎥-⎢⎥⎣⎦将其加到表3-1一列数字上的最终单纯形表的基变量解，得表3-2.表3-21x2x3x4x5x3x 352 0 0 1 54 152- 1x 112 1 0 0 14 12- 2x12- 0 1 0 14- 32 i i z c -1412又因为上表中原问题是非可行解，因此我们需继续计算，采用对偶单纯形法可以得到表3-3表3-31x2x3x4x5x3x 15 0 5 1 0 0 1x 5 1 10 0 12x20 4-0 1 6-i i z c -12从表中我们可以看出新的最优解15x =，*2510z =⨯=.第四章 价值系数i c 的变化分析4.1 非基变量价值系数变化假设()12n A p p p =.若j j j c c c =+∆，j N ∈,则1T j j B j j j c c B p c σσ-=-=+∆如果使最优基不变，则必须有0j σ≤，因此非基变量价值系数j c ，j N ∈的变动范围应该满足j j c σ∆≤-例4已知线性规划问题123max 234Z x x x =---s .t .123412341234523234,,,,0x x x x x x x x x x x x x ---+=-⎧⎪-+-+=-⎨⎪≥⎩求解价值系数在什么范围变化时，最优解不变.解：表4-1是最终单纯形表表4-1j c →2-3- 4- 0 0b cB X b1x2x3x4x5x3-2x 25 0 0 15- 25- 15 2-1x1151 0 75 15- 25- j σ95- 85- 15- 由单纯形法计算可得表4-2表4-2j c →2-3-34c -+∆0 0b cb x b1x2x3x4x5x3-2x 25 0 0 15- 25- 15 2-1x115175 15- 25- j σ0 0395c -+∆85- 15- 从表4-2中我们可以看出当395c ∆≤时，最优解不变. 4.2基变量价值系数变化如果B B B c c c =+∆,则对于j N ∀∈,11TT B j j j j B j c c B p c B p σσ--=-=-∆这时，若保持最优基不变，一定要使得0j σ≥，j N ∀∈.所以基变量价值系数Bc 满足不等式组的取值范围为1T B j jc B p j N σ-∆≤∀∈例5已知线性规划问题123max 2z x x x =-++s .t .1231241234624,,,0x x x x x x x x x x ++=⎧⎪-+=⎨⎪≥⎩当1c 变为4时，求新问题的最优解.解：这个线性规划模型的最终单纯形表为表4-3 .表4-31x2x3x4x2x 6 1 1 1 0 4x1030 11 i i 1c 是非基变量的系数，则()1133,132c c ∆≤--=≤-+=所以，1c 在12c ≤的范围内变化时，最优解不变.当1c 变为4时，超出范围，则重新计算()()1'1241144,42,003TB j c B p c c p σ-⎛⎫=-=-=-> ⎪⎝⎭把表4-3中13σ=-变为2，选择1x 为入基变量，4x 为出基变量，进行迭代，得到的最终单纯形表，表4-4表4-41x2x3x 4x2x83 0123 13- 4x 1031 013 13 i i c z - 0 053- 23- 新的最优解为：1234108,,033x x x x ====；最优值：*563z =.第五章 增加新的变量的变化分析增加一个新的变量实际上就是在单纯形表中增加一列，假如增加一个新的变量1n x +，1n c +是它所对应的价值系数，()111211,,,Tn n n mn A a a a ++++=是它在约束矩阵中的对应系数列向量，则增加一列'11'''2111'1n n n n mn a a A B A a +++++⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦其检验数1111n n B n c C B A σ-+++=-+那么就得到了新问题的单纯形表，如果10n σ+≥，则原线性规划问题的最优解不变.我们通过具体例题来讨论增加新的约束条件.例6某生产加工厂计划用两种不同的原料生产四种商品，四种商品的收益和消耗的原料数以及消耗的原料定量如表5-1表5-1产品（万件）/原料（kg ）甲 乙 丙 丁 提供量 第一种原料3 2 104 18 第二种原料 0 0 2 1/2 3 求：如果增加第一种原料，增加多少原最优基不变？解：设生产甲、乙、丙、丁四种产品各1x ，2x ，3x ，4x 万件，则线性规划模型为1234max 985019Z x x x x =+++s .t .()1234343210418123201,2,3,4j x x x x x x x j ⎧+++≤⎪⎪+≤⎨⎪⎪≥=⎩增加第一种原料时，1b 就会发生变化，设1118b b =+∆，1(18,3)b b =+∆，则1111210221833314311636b b B b b -⎡⎤⎡⎤-+∆⎢⎥⎢⎥+∆⎡⎤==⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥--∆⎢⎥⎢⎥⎣⎦⎣⎦则需满足12203b +∆≥，11106b -∆≥原最优基不变，得136b -≤∆≤，即11524b ≤≤.函数1112(0,0,1,2)63t X b b =-∆+∆，113883Z b =+∆是1b ∆最优值和最优解，当16b ∆>，13b ∆<-时，原来的最优基就会改变，原问题的最优基如下表表5-2.表5-2j c9 8 50 19 0 0bB cB x 1x2x3x4x5x6x19 4x 243 0 1 23 103-2 503x12- 13- 1 0 16- 43 1j σ4- 23- 0133- 103- 88Z =当16b ∆>时，情形如下，常数项用111223116b B b b -⎡⎤+∆⎢⎥=⎢⎥⎢⎥-∆⎢⎥⎣⎦代替，用对偶单纯法得表5-3.表5-3j c9 8 50 19 0 0bB cB x 1x2x3x4x5x6x19 4x 243 0 1 23 103-1223b +∆503x12- 13- 116- 43 1116b -∆j σ4-23- 0 0133- 103-113883Z b =+∆用对偶单纯形法求解，第二行需乘以3-,第一行加上第二行乘以43-,可以得到单纯形表表5-4.表5-4j c9 8 50 19 0 0bB cB x 1x2x3x4x5x6x19 4x 00 41 02683x321 3-0 124-1132b ∆- j σ3- 02- 04-6-1904Z b =+∆当11302b ∆-≥，即16b ∆>，新的最优基42(,)B P P =,最优解为11(0,3,0,6)2b ∆-，最大收益为1904b +∆万元.第六章 增加新约束条件的变化分析我们在处理实际问题时，往往会遇到在其问题的基础上增加新的约束条件，如果新添加的约束条件能够使原来的最优解得到满足，那么它的最优解一定不变，反之，则需对问题继续进行分析.例7对于线性规划问题 12max 2z x x =+s .t .212121251562245,0x x x x x x x ≤⎧⎪+≤⎪⎨+≤⎪⎪≥⎩增加一个新的约束条件123212x x +≤，分析最优解的变化.解：把原来线性规划问题最优解带入新的约束条件中，因为 73273212222⨯+⨯=> 则约束条件可以写成1263212x x x ++=，6x 为基变量，反映到表3-1中得表6-1.表6-11x2x 3x 4x5x6x 0 3x 152 0 0 1 54 152- 0 2 1x 72 1 0 0 14 12- 0 1 2x 320 1 0 14- 320 06x12 3 2 0 01 i i c z -14121将1x ，2x 列系数变为单位向量，用对偶单纯法进行迭代，得最终单纯形表，表6-2.表6-21x2x 3x 4x5x 6x0 3x 15 0 0 1 52 0 5-2 1x 4 1 0 0 13 0 13-1 2x 0 0 1 0 12- 0 16x13 2 0 16 1 23- i i c z -16- 013-则新的最优解为*124,0,8x x z ===.总结从本文中讨论我们可以看出，在线性规划问题中，一些数据发生变化时，特别是当数据变化的幅度较小时，用灵敏度分析新的问题要比从头求解新问题简便的多，因此我们要学会掌握线性规划问题的灵敏度分析并加以推广.[参考文献][1] 李小光.线性规划中的灵敏度分析[J].2000,20(3),15-20.[2] 张伯声．运筹学[M]．北京：科学出版社，2008，65-75．[3] 党耀国，李邦义．运筹学[M]．北京：科学出版社，2009，61-73．[4] 施泉生.运筹学[M].北京：中国电力出版社，2004，44-50.[5] 孙麟平.运筹学[M].北京：科学出版社，2005，32-38.[6] 吕蓬，潘志.运筹学数学规划篇[M].北京：清华大学出版社，2011，32-40.。
运筹与决策PPT：线性规划的灵敏度分析
G
Hours Available
4 12 18
Total Profit $4,000
门的单位利润PD=$300升到 PD=$500，而最优解保持不变！
案例1：Wyndor 玻璃制品公司产品组合问题
改变目标系数（利润）会怎样？
B
C
D
3
Doors
Windows
4
Unit Profit
$1,000
$500
一般说来，不同的问题参数会求出不同 的最优解。但由于实际环境中，要精确估计 各种参数几乎是不可能的。
在无法精确估计参数的情况下，最优解 是否还有意义？参数的波动对最优解的影响 到底有多大？
灵敏度分析就是解决以上问题的强有力的工具！
3.1 灵敏度分析的基本概念
▪ 数学模型只是实际问题的一个粗略的抽象； ▪ 最优解一般只是针对某一特定的问题环境的； ▪ 管理者要对未来可能发生的事件做各种假设，
门的单位利润PD=$300升到 PD=$1000时，最优解发生变化！
案例1：Wyndor 玻璃制品公司产品组合问题 目标系数（单位利润）变化对最优解的影响
案例1：Wyndor 玻璃制品公司产品组合问题
利用Excel Solver进行灵敏度分析
Unit Profit
Doors $300
Windows $500
以上信息对于有效指导管理者作出最终的决 策是至关重要的
3.2 目标函数系数的灵敏度分析
▪ 单个系数发生变化 ▪ 多个系数同时发生变化
目标系数代表对未来收益 情况（不可控环境因素）的预期， 相应的灵敏度分析是考察环境的 不确定性或变化对最优解有什么 影响。
案例1：Wyndor 玻璃制品公司产品组合问题
线性规划模型的应用与灵敏度分析(DOC)
摘要线性规划是解决稀缺资源最优分配的有效方法，使付出的费用最少或获得的利益最大。
它的研究对象是有一定的人力、财力、资源条件下，如何合理安排使用，效益最高；某项任务确定后，如何安排人、财、物，使之最省。
它要解决的问题的目标可以用数值指标反映，对于要实现的目标有多种方案可以选择，有影响决策的若干约束条件。
本文主要介绍了线性规划模型在实际生活中的应用，其中包括解线性方程组的各种方法，如图解法、单纯形法、以及对偶单纯形法等等，以及简单介绍了有关灵敏度分析的方法。
由于许多问题仅仅利用线性规划的方法还不足以解决，因此用到了对偶理论，也因此引出了对偶单纯形法。
对偶规划是线性规划问题从另一个角度进行研究，是线性规划理论的进一步深化，也是线性规划理论整体的一个不可分割的组成部分。
灵敏度分析是对线性规划结果的再发掘，是对线性规划理论的充要应用，本文以实例验证灵敏度分析的实际应用。
关键词：线性规划；单纯形法；对偶单纯形法ABSTRCTLinear programming is an effective method to solve the optimal allocation of scarce resources, make the cost of pay or receive at least the interests of the largest. Its object of study is the human and financial resources, resource conditions, how to reasonably arrange to use, benefit is supreme; A task is determined, how to arrange people, goods, and make it the most provinces. It to the target can be used to solve the problem of the numerical indicators, to achieve a variety of solutions to choose from, have an impact on the decision of some constraint conditions. Through the subject design, can deepen the operations research, optimization method, linear programming, nonlinear programming, to improve the integrated use of knowledge, improve the ability of using the sensitivity analysis to solve various practical problems. This article mainly introduces the application of linear programming model in real life, including the various methods of solving linear equations, as shown in figure method, simplex method and dual simplex method, etc., and simply introduces the method of sensitivity analysis. Due to many problems just by using the method of linear programming is not enough to solve, so use the duality theory, thus raises the dual simplex method. The dual programming is linear programming problem from another Angle, is the further deepening of linear programming theory, linear planning theory as a whole is also an integral part of. Sensitivity analysis is to discover, the result of the linear programming is the charge to application of linear programming theory. Keywords: linear programming；Simplex method；The dual simplex method目录前言线性规划模型的应用与灵敏度分析 (1)第一章线性规划问题 (1)1. 线性规划及灵敏度分析简介 (1)2. 线性规划模型应用的发展 (1)3. 线性规划模型研究的问题 (2)4. 线性规划模型的应用 (2)4.1问题 (2)4.2线性规划方法的特点及局限性 (2)4.3线性规划模型的基本结构 (3)4.4线性规划模型的一般形式 (3)4.4线性规划的性质…………………………………………………………………………………5第二章求解线性规划的方法 (6)1. 图解法 (6)2. 单纯行法 (7)2.1 单纯行法的基本思路 (7)2.2 单纯形法的求解步骤 (11)2.3 单纯形法的求解过程小结 (12)2.3.1人造基、初始基本可行解 (12)2.3.2最优解判别定理： (14)2.3.3单纯行过程的两种方法 (14)3. 单纯行法 (14)3.1对偶问题的提出 (14)3.2线性规划的对偶理论 (15)3.3对偶单纯形法的步骤 (15)4. 单纯行表......................................................................................................错误!未定义书签。
灵敏度分析(第三章线性规划)
为了回答这些问题，可以在变化了的条件下重新求解
线性规划问题。但是这样做太麻烦，也不必要。本节的目
的是讲，如何在已经得到的最优解的基础上，进行适当的
修改计算，即可回答上面的问题。这就是灵敏度分析的基
本内容。
精选2021版课件2二、灵敏度分析的定义灵敏度分析就是研究cj、bi、aij等参数在 什么范围内变化时最优解不变，若最优 解发生变化，如何用简便的方法求出新 的最优解。
8 x2 0 1 1 1 1 8
f 0 0 C3-28 2 3 84
由上表可知：当C3-8≤ 0 ，即 0≤ C3≤8时，最优解不变。
精选2021版课件
9
1.2基变量对应价值系数变化
(1)基变量对应的价值系数C1的变化 C51 8 6 0 0
x1 x2 x3 x4 x5
bi
C51 x1 1 0 0 2 1
bi
5 x1 1 0 0 2 1 4
C82 x2 0 1 1 1 1
8
f 0 0 6-C22 C2-210 5-C32 -(2804+8C2)
由上表可知：当 6-C2 ≤ 0 ， C2-10 ≤ 0，同时 5-C2 ≤ 0 ，
即 6≤ C2≤10时，最优解不精变选。2021版课件
11
价值系数cj变化的分析总结
17
结论
当b1=22,b2=20时， 最优基改变，最优解变为： x1=20，x4=2
精选2021版课件
18
保持b2=20,分析b1在什么范围内
变化时，最优基不变?
B 1b' 2 1 1 1 2 b 1 0 2b b 1 1 2 2 0 0 0
解之得：10≤b1≤20
•b的变化量b可能导致原最优解变为非基可行解 设b’=b+ b
第三讲 线性规划的灵敏度分析与最优解的解释
主要内容
灵敏度分析简介 图解法灵敏度分析 灵敏度分析：计算机求解 多于两个决策变量的情况
7 S 1D 630 10
1 S 5 D 600
2
6
1S 2 D 708 3
1 S 1 D 135
10
4
S，D≥0
切割与印染 缝合 成型 检查与包装
Par公司管理决策上的改变
假设管理层希望生产一种轻便的、可以被球手随身携带 的球袋模型。设计部门计算得出，每个轻型袋需要0.8小 时进行切割印染，1小时缝合，1小时成型，0.25小时检 验和包装。因为这种设计是独一无二的，管理层认为在 当前销售期内每个轻便袋的利润可达12.85美元。
目标函数系数S的上限是13.499 D的下限是6.6667，允许减少量：
93，允许增加量：上限-目前值 目前值-下限=9-6.6667
=13.49993-10=3.49993。标 =2.33330。高档袋的利润减少
准袋的利润增加到11.50美元， 了0.75（从9美元到8.25美元）
增加了（从10美元到11.50美元） 美元，占允许减少量的
这些系数的变化会对模型的最优解产生什么样的影响呢问题如果我们要用lp模型去解决实际问题模型中的系63011017d52s60062sds708135311d4110sd0ds切割与印染缝合成型检查与包装max10s9dst85灵敏度分析简介2问题模型中的系数哪个更能左右最优解max10s9dst63011017d52s60062sds708135311d4110sd0ds切割与印染缝合成型检查与包装667142989925灵敏度分析简介3问题右端值变化对最优解有什么影响max10s9dst63011017d52s60062sds708135311d4110sd0ds切割与印染缝合成型检查与包装利润图解法灵敏度分析目标函数系数变化多系数同时改变右端项改变目标函数系数问题目标函数系数变化会对par公司的最优产量产生什么样的影响
灵敏度分析
２、基变量的目标系数 c j 的灵敏度分析
例2.1
已知线性规划问题
max η = 30x 1 + 25x 2 + 35x 3 x 1 + 2x 2 + x 3 ≤ 800 x + x + 2x ≤ 1000 1 2 3 s.t. 2x 1 + x 2 + x 3 ≤ 2000 x 1, x 2 , x 3 ≥ 0
25 X2 3 -1 -4 1 3 -1 -4 -6
35 X3 0 1 0 2 0 1 0 0
0 X4 2 -1 -3 0 2 -1 -3 -4
0 X5 -1 1 1 0 -1 1 1 3
0 0 0 1 0 0 0 0 1 0 0
0 0 0 0 1 0 0 0 0 1 0 600 200 600 -600 600 200 600 1600
课堂练习
1 已知线性规划问题：
P153(4)
max Z = 3x 1 + 2x 2 x 1 + 2x 2 ≤ 40 s.t. 2x 1 + x 2 ≤ 50 x , x ≥ 0 1 2
求（1）为使最优解不发生变化时目标函数系数 c j 允许 变化的范围。 （2）每个约束条件的影子价格
X6 X7 b
-30 0
-25 -5
-30 0
-25 -5
30 25 30 X1 35 X3 0 0 X6 X7 1 0 0 0 0 30 X1 35 X3 0 0 X6 X7 1 0 0 0 0 3 -1 -4 -6 0 0 0 1 0
35 0 0 1 0 0 0 1 0 0 0 2 -1 -3 -4 -25 0
XB
-1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
课外练习
表3-1牧草农场饲料的营养值和成本值
饲料成分
普通饲料 高营养燕麦 饲料添加剂
A B C 每磅成本(美元)
50
0.0 3.0 2.0 3.00
案例报告
一、选择的问题
为了环保不需要封面，不需要原问题的全部内容，只需 也务必标明选择案例的名字。
4
S，D，L≥0
多重最优解的情况
假设我们使D的系数正好增加1.15003美元。
增加新的约束条件
假设管理者在审核了上述的解决方案后发现，他们会放 弃所有不生产高级袋的方案，并要求高级袋的产量至少 要达到标准袋产量的30%。
D≥0.3S 或者 -0.3S+D ≥0
课外练习
牧草农场位于肯塔基州列克星敦。农场正在实验一种新 的赛马食品。赛马食品有以下三种，由普通饲料，富含 维生素的燕麦饲料和一种新的含维生素和矿物质的食品 添加剂饲料。这些高营养食品的各组成要素的成本如表 3-1所示。我们可以看到，每磅普通饲料中含0.8单位A， 1单位B和0.1单位C，一匹马一天的最少进食3单位A， 6单位B，4单位C。为了保持马的体型，总摄入量不可 以超过6磅。农场希望找到一种饲料组合，可以满足马 一天的营养需要，又可以使总成本最低。
物流管理系 薛伟霞
Par问题的数学描述
max 10S+9D
S.t.
7 S 1D 630 10
1 S 5 D 600 26
1S 2 D 708 3
1 S 1 D 135 10 4
切割与印染 缝合 成型 检查与包装
S，D≥0
灵敏度分析
研究当一个线性规划问题中的系数发生变化时， 其对目标函数最优解的影响程度。
总产量约束 时间约束
关于对偶价格的解释
小于等于型约束条件的对偶价格总是大于或等于0的，因为 增加其右端值不会使目标函数变得更坏。
大于等于型约束条件的对偶价格总是小于或等于0的，因为 增加其右端值不会对最优解有所改进。
当约束条件的右端值表示某种资源的可利用量时（沉没成 本），对偶价格通常可以解释为公司对额外支付一单位这种 资源所愿意提供的金额。
会增加，反而会减少。在最小化问题中，目标函数结果变得 更坏意味着总成本的增加。 影子价格——每增加一个单位的约束条件右端值最优解的变 化量。一般来说，对于最大化问题，影子价格和对偶价格相 同；对于最小化问题，影子价格是对偶价格的相反数。
主要内容
灵敏度分析简介 图解法灵敏度分析 灵敏度分析：计算机求解 多于两个决策变量的情况
2
CD
10
6.3 CS 13.5
6.67 CD 14.29
另一例——目标函数继续旋转
CS 3
CD
2
多系数同时改变
3 CS 7 2 CD 10
假设标准袋的利润增加到13美元，高档袋的利润减少到8美元。
6.3 CS 13.5
新的目标函数的斜率：
例：假设切割与印染部门能够获得额外的20小时时间， 同时成型部门能够获得额外的100小时时间。对偶价格 是否适用？
计算机输出的解释——
M&D公司的最小化问题
min 2A+3B s.t.
1A ≥125 产品A的需求量 1A + 1B ≥350 总产量 2A + 1B ≤600 生产时间 A，B ≥0
max S.t.
10S+9D
8.5 7 S 1D 630
10
1 S 5 D 600
2
6
1S 2 D 708 3
1 S 1 D 135
10
4
S，D≥0
切割与印染 缝合 成型 检查与包装
灵敏度分析简介（2）
问题——模型中的系数哪个更能左右最优解？
max 10S+9D
(6.67-14.29) (8.9-9.25)
S.t.
7 S 1D 630 10
1 S 5 D 600
2
6
1S 2 D 708 3
1 S 1 D 135
10
4
切割与印染 缝合 成型 检查与包装
S，D≥0
灵敏度分析简介（3）
问题——右端值变化对最优解有什么影响？
max S.t.
CS 13 1.625
CD
8
6.67 CD 14.29
右端项
假设Par公司的切割印染部门又多出了10个小时的可 工作时间。
新的约束条件： 7 S 1D 640 10
运用图解法
新的最优解
S=527.5， D=270.75。
新的目标函数值 10×527.5+9×270.7 5=7711.75美元，
7 S 1D 630 10
1 S 5 D 600
2
6
1S 2 D 708 3
1 S 1 D 135
10
4
S，D≥0
切割与印染 缝合 成型 检查与包装
Par公司管理决策上的改变
假设管理层希望生产一种轻便的、可以被球手随身携带 的球袋模型。设计部门计算得出，每个轻型袋需要0.8小 时进行切割印染，1小时缝合，1小时成型，0.25小时检 验和包装。因为这种设计是独一无二的，管理层认为在 当前销售期内每个轻便袋的利润可达12.85美元。
1．如果目标函数的系数发生变化，对最优解会 产生什么影响？
2．如果改变约束条件右边的值，对最优解会产 生什么影响？
主要内容
灵敏度分析简介 图解法灵敏度分析 灵敏度分析：计算机求解 多于两个决策变量的情况
灵敏度分析简介（1）
问题——如果我们要用LP模型去解决实际问题，模型中 的系数就不可能是一成不变的。这些系数的变化会对模 型的最优解产生什么样的影响呢？
利润增量7711.757668.00=43.75美元。
利润增加率 43.75/10=4.375美 元。
对偶价格
约束条件右端值每增加一个单位引起的最优解的增加量。 对偶价格可以用来求出当某个约束条件右端值变化一个单位
时目标函数值将会有什么变化。 对偶价格只适用于约束条件的右侧值变化比较小的情况。 任何非束缚性约束条件的对偶价格都是0。 负的对偶价格告诉我们，如果使右端值增加，目标函数值不
二、模型 三、软件求解结果 四、求解结果的最优解解释及灵敏度分析
目标函数系数S的上限是13.499 D的下限是6.6667，允许减少量：
93，允许增加量：上限-目前值 目前值-下限=9-6.6667
=13.49993-10=3.49993。标 =2.33330。高档袋的利润减少
准袋的利润增加到11.50美元， 了0.75（从9美元到8.25美元）
增加了（从10美元到11.50美元） 美元，占允许减少量的
10S+9D
7 S 1D 630 10
1 S 5 D 600
2
6
1S 2 D 708 3
1 S 1 D 135
10
4
S，D≥0
利润
切割与印染 缝合 成型 检查与包装
图解法灵敏度分析
目标函数系数变化——多系数同时改变 右端项改变
目标函数系数
问题——目标函数系数变化会对Par公司的最优 产量产生什么样的影响。
目标函数的最优范围——目标函数系数在什么范 围内变化时，模型的最优解保持不变。
目标函数系数
目标函数系数
第一步：目标函数直线斜率的范围 直线B斜率≤目标函数的斜率≤直线A的斜率
3 目标函数的斜率 7
2
10
第二步：目标函数系数的范围
P=CSS+CDD
3 CS 7
令L为轻便袋的产量
修正的Par公司问题
max 10S+9D+12.85L
S.t.
7 S 1D 0.8L 630 切割与印染
10
1 S 5 D 1L 600 缝合
2
6
1S 2 D 1L 708 成型 3
1 S 1 D 0.25L 135 检查与包装
10
灵敏度分析：计算机求解
使用管理科学家软件求解Par公司的线性规划问 题。
最优解 松弛/剩余变量
目标函数最优解
对偶价格
减少的成本—目 标函数的每个系数 应提高多少，目标 函数的变量值才能
是正数
目标系数范围
右端值范围——对偶价格适用范围的限制条件
多系数同时变化——100%法则
假设，Par公司的会计部门发现原来高档袋和标准袋的利 润计算——分别为10美元和9美元有误，正确的利润分别 应该是11.50美元和8.25美元。
允许增加量——对于目标函数的系数，在不超过最优范 围的情况下，系数可能增加的最大量；
允许减少量——在不低于最优范围下限的情况下，系数 可能减少的最大量。
目标函数系数的100%法则
对所有变化的目标函数系数，计算其占允许增加量和允许减少量 的百分比之和。如果和没有达到100%，最优解就不会改变。
管理者经常会遇到是否有必要引进新技术的问题，而一般新 技术的开发或购买都是为了节约资源。在这种情况下，对偶 价格可能对问题的解决有所帮助，它可以帮助我们了解节约 这些资源会为我们带来多大的利益，进而决定这项新技术的 价值。
多于两个决策变量的情况
Par公司原来问题的模型
max S.t.
10S+9D
1.50美元。占总允许增加量的 （0.75/2.333 30）
（1.50/3.499 93）
×100%=32.14%。
×100%=42.86%。