人教版九年级数学上册圆周角
人教版数学九年级上册24.1.4:圆周角的概念和圆周角的定理(教案)

2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
3.培养学生的数学抽象能力:让学生从具体的圆周角实例中抽象出一般性规律,理解圆周角与圆心角、弧和弦之间的关系,提升数学抽象思维。
4.培养学生的数学建模能力:通过解决与圆周角相关的问题,使学生能够建立数学模型,运用所学知识解决实际问题,提高数学应用能力。
三、教学难点与重点
1.教学重点
-圆周角的概念:强调圆周角定义中“顶点在圆上,两边分别与圆相交”的特点,以及与圆心角的关系。
a.圆周角定理:圆周角等于其所对的圆心角的一半。
b.圆周角推论:在同圆或等圆中,相等的圆周角所对的弧相等,所对的弦也相等。
二、核心素养目标
1.培养学生的几何直观能力:通过观察圆周角与圆心角的关系,使学生能够直观理解圆周角的概念及定理,提高空间想象力和几何直观感知。
2.发展学生的逻辑推理能力:在学习圆周角定理及其推论的过程中,引导学生运用严密的逻辑推理,掌握证明方法,增强解决问题的能力。
-掌握圆周角定理的证明:学生需要掌握如何运用严密的逻辑推理证明圆周角定理,并能够灵活运用。
-圆周角推论的应用:学生需学会将圆周角推论应用于解决实际问题,如求弧长、弦长等。
举例1:针对圆周角定义的难点,教师可通过以下步骤帮助学生理解:
a.展示不同类型的角,让学生辨别哪些是圆周角,哪些是圆心角。
b.通过动态演示,让学生观察圆周角与圆心角的变化关系,加深理解。
人教版数学九年级上册圆周角的概念和圆周角的定理课件(第一课时18张)

1
= 2∠AOD,∠CBD
= 1∠COD,
2
∴ ∠ABC = 1∠AOC.
2
A C
●O B
一条弧所对的圆周角等于它所对的圆心角的一
半.
活动三:学以致用
1. 如图1,在圆O中, ∠BOC=50°,则∠BAC = 25°;
2.变式1:如图2,已知∠BCD=120°,则∠AOB= 120; °
3.变式2:如图3,已知圆心角∠AOB=100°,则
⌒ BC所对圆周角是∠ BAC , 圆心角
是∠BOC,
则∠
BAC=
1 2
∠BOC
O
A
C
B
例1.如图:OA、OB、OC都是⊙ O的半径
∠AOB=2∠BOC. ∠ACB=40°,求∠BAC的度数.
证明:∵
∠ACB=
1 2
∠AOB=40
°
∴ ∠AOB= 80 °
∵ ∠AOB=2∠BOC
O
∴ ∠BOC=40 °
特征:① 角的顶点在圆上.
② 角的两边都和圆相交 (即两边是圆的两条弦)
判别下列各图形中的角是不是圆周角。
×
√
×
√
×
×
×
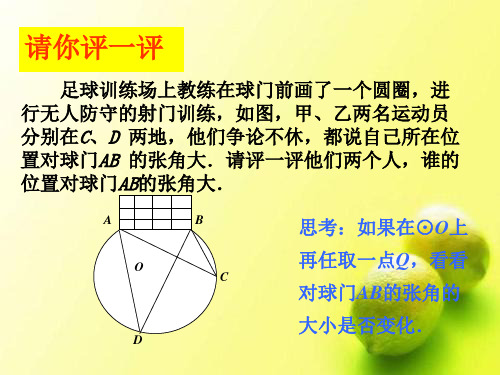
当球员在B,D,E处射门时, 他所处的位置对球门AC 分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角 的大小有什么关系?.
A C
●O
B
E
D
圆周角: ∠ABC,
∠ADC, ∠AEC.
新人教版九年级上册数学
24.1.4圆周角(第1课时)
问题:请同学们想一想,球员射中球门的难易 与什么有关?
总结:如图所示,球员射中球门的难易与他所在的位置B对球门
人教版九年级上册数学圆周角课件

1 ∴∠AOB=90°,∴∠ADB=2 ∠AOB=45°, ∴∠AEB=180°﹣∠ADB=135°。
∴此弦所对的圆周角等于45°或135°。
例题讲授
例5.已知弦AB、CD相交于E,AC 的度数为90°,BD 的度数为30°,则∠AEC=_6__0_°___。
例题讲授
解:如图,∵∠AOC=160°, ∴∠ABC= 12∠AOC= 12×160°=80°, ∵∠ABC+∠AB′C=180°, ∴∠AB′C=180°﹣∠ABC=180°﹣80°=100°。 ∴∠ABC的度数是:80°或100°。 故选D。
练一练
1.如图,将⊙O沿弦AB折叠,圆弧恰好经过圆心 O,点P是优弧 AMB 上一点,则∠APB的度数为( )。 A.45° B.30° C.75° D.60°
1
1
证明:∠A=2 ∠BOC,∠D= 2(360°-∠BOC)
1
1
∴∠A+∠D=2 ∠BOC+ 2(360°-∠BOC)
1
=2 ×360°=180°
∴∠A与∠D互补。
结论:在同圆或等圆中,等弦所对圆周角相等或互补。
探究新知
探究二: 圆的内接多边形
引入概念
探究新知
探究二: 圆的内接多边形
探索圆的内接四边形四个角之间的关系。
解:连接BC, ∵ AC 的度数为90°,BD 的度数为30°, ∴∠ABC=45°,∠BCD=15°, ∴∠AEC=∠ABC+∠BCD=60°。
练一练
等腰△ABC的顶角∠A=120°,腰AB=AC=10, △ABC的外接圆半径等于___1_0___。
24.1.4 圆周角 课件-2024-2025学年人教版九年级数学上册

与
应
用
[概括新知]
推论:(1)同弧或等弧所对的圆周角 相等
(2)半圆(或直径)所对的圆周角是
对的弦是
直径
.
直角
.
,90°的圆周角所
探
究
与
应
用
[理解应用]
例2 (教材典题)如图24-1-24,☉O的直径AB为10 cm,弦AC为
6 cm,∠ACB的平分线交☉O于点D,求BC,AD,BD的长.
解:如图,连接OD.
得AB=12 cm,BC=5 cm,则圆形镜面的半径为
图24-1-32
13
2
cm .
谢 谢 观 看!
D.100°
图24-1-27
课
堂
小
结
与
检
测
[本课时认知逻辑]
圆心角
圆周角
的定义
类比
圆周角
圆周角与直
径的关系
圆周角定理
圆周角定理
的推论
课
堂
小
结
与
检
测
[检测]
1.如图24-1-28,△ABC是☉O的内接三角形.若∠ABC=70°,则
∠AOC的度数为
A.140°
B.130°
C.120°
D.110°
( A )
图24-1-28
课
堂
小
结
与
检
测
2.如图24-1-29,BD是☉O的直径,点A,C在圆上,∠A=50°,则
∠DBC的度数是
A.50°
B.45°
C.40°
D.35°
( C )
图24-1-29
课
堂
小
结
人教版初中数学九年级上册圆周角课件

。
4.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的是( D )
A.50°
B.60°
C .80°
D.100°
5.如图,在⊙O中,OC⊥AB,∠ADC=32°,则∠OBA的度数是( D )
A.64°
B.58°
C.32°
D.26°
6.已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对
几何语言:
=
,
∵
∴ ∠ =பைடு நூலகம்
1
∠.
2
结论
同弧或等弧所对的圆周角相等,
都等于该弧所对的圆心角的一半.
例题分析
(
已知:在⊙O中,AB 所对的圆周角是 ∠C,圆心
角是 ∠AOB. 求证: ∠C =
1
2
∠AOB.
证明: ∵ OA=OC
∴∠A=∠C
又 ∠AOB=∠A+∠C
∴∠AOB= 2∠C
图来证明刚才我们发现的同弧所对的圆周角与圆心角的大小
关系吗?
你能发现几杆类似的“红旗”图案?
这些对该情况下命题的证明有哪些启示?
证一证
A
A
O
O
C D
D
B
作辅助线
分离右旗
分离左旗
∴∠A=∠C.
∵∠BOC是△AOC的外角,
C ∴∠BOC=∠A+∠C.
(“红旗”图案)
撤消辅助线
还原右旗
闪动角
还原左旗
证明∵OA=OC
∴∠BOC=2∠A.
1
即 ∠BAC = 2∠BOC.
学生完成证明过程,思考交流后一种情况的证明思路,在展
示台上展示学生的证明过程,教师做思路和规范性点评)
人教版数学九年级上册圆周角的概念和圆周角定理课件
(2)∠BOC=____7_0°,理由是
__同__弧__所__对__的__圆__周__角__等__于__该__弧__所__对_ __的__圆__心__角__的__一__半__.___________.
DAC 1 DOC . 2
∴ DAC DAB 1 (DOC BOD) , 2
即BAC 1 BOC. 2
议一议
一条弧所对的圆周角等于它所 对的圆心角的一半. 同弧或等弧所对的圆周角相等。
思考
C
A
O
B
如图,AB是直径,则∠ACB=_9_0_°。 半圆(或直径)所对的圆周角是直角, 90度的圆周角所对的弦是直径。
∵ ∠BAC=∠BFC (同弧
B
所对的圆周角相等).
A
D
F
E O
C
请你说一说 这节课你有哪些收获和困惑? 圆周角定义及定理。
课后作业 课本P89第3题,P90第14题; 练习册P7∠BAC的内部或外部时, BAC 1 BOC 的关系还成立吗?
2
思考与探索
证明:作直径AD.
∵BAD 1 BOD ,
2
DAC 1 DOC. 2
∴ BAD DAC 1 (BOD DOC ) , 2
即BAC 1 BOC .
2
思考与探索
证明:作直径AD.
∵BAD 1 BOD , 2
思考与探索
3.当圆心O在∠BAC的一边上时,圆周角 ∠BAC与圆心角∠BOC之间有怎样的数量关系? 你能证明你的发现吗?
思考与探索
4.BAC 1 BOC .
证明:
2
24.1.4 圆周角 人教版数学九年级上册教案

24.1.4 圆周角一、【教材分析】知识技能1、理解圆周角的概念,掌握圆周角的两个特征、定理的内容及简单应用;2、掌握圆周角定理的三个推论,并会熟练运用这些知识进行有关的计算和证明.过程方法1、培养学生观察、分析、想象、归纳和逻辑推理的能力;2、渗透由“特殊到一般”,由“一般到特殊”,体验分类讨论的数学思想方法.教学目标情感态度敢于面对数学活动中的困难,并能有意识地运用已有知识解决新问题.教学重点圆周角定理及定理的三个推论的应用.教学难点圆周角定理的证明,三个推论的灵活应用.二、【教学流程】教学环节问题设计师生活动二次备课情景创设观察与思考:(教师边演示自制教具边介绍,其中底面圆片上标注好有关的字母、线条)假设这是一个圆柱形的房子,同学们可以站在房中通过圆弧形玻璃窗AB向外观看外面的风景,同学甲站在圆心O的位置,同学乙站在正创设问题情境,开展学习活动,引起学生学习的兴趣图图c图画出来.3、利用第2题的图形,分别证明图a、图b、图c中的∠B OC=2∠B AC.4、用自己的语言说出圆周角定理的内容是什么?(1)在同圆或等圆中,同弧或等弧所对的圆周角相等;动,归纳出:⑴在圆周角的一条边上(如图a);⑵在圆周角的内部(如图b);⑶在圆周角的外部(如图c).学生自己独立完成图a的证明.对于图b、图c两种情况的证明,我们可以先尝试让学生小组交流,寻找证题方法,教师可以参与小组讨论,及时给予引导、点拨,然后板书展示证明过程,最后全班进行点评,引导学生体会“转换化归”在解决从特殊到一般问题时的应用思路和方法.以小组为单位讨论、探索,教师参与其中,指导帮助学生完成问题的解答.最后归纳通过制作演示折纸,培养学生动手操作的能力,促进学生参与教学的意识的形成.学会分类讨论、转换化归是教学突破的关键通过观察、交流、归纳,锻炼学生的逻辑思维能力,体验分类讨论的数学思想方法C三、【板书设计】四、【教后反思】本节课首先设计了一个问题情境,展示了圆心角与圆周角的位置关系,引出圆周角的概念.然后通过测量、猜想,得出同弧所对的圆周角等于圆心角的一半的结论.接着通过让学生折纸,观察与思考,利用分类讨论的思想方法,分三种情况给出系统的证明及思维过程.至此我们利用迁移、转化的思想方法化未知为已知,将圆周角的问题转化为圆心角来求解.其后为进一步探索圆周角的其他性质,我们又以设置的问题为导线,将学生带入到教学活动中,同时再次通过交流、讨论、合作、归纳出圆周角定理的三个推论,并运用它们进行解题,实现从认识到应用的转化.。
初中数学人教九年级上册第二十四章 圆 圆周角定理PPT

(2)∵BA=BC,∴∠A=∠C. 由圆周角定理得∠A=∠E, ∴∠C=∠E,∴DC=DE.
27
28
知识点三:圆周角定理的推论
合作探究
先独立完成导学案互动探究1、3, 再同桌相互交流,最后小组交流;
1.如图,在⊙O中,弦AB=3cm,点C在 ⊙O上,∠ACB=30°.求⊙O直径. 2.如图,AB是⊙O的直径,BD是⊙O的弦 ,延长BD到点C,使AC=AB,BD与CD的 大小有什么关系?为什么?
B A
O A
O B
知识点三:圆周角定理的推论
学以致用
1、如图,AB是半圆的直径,点D是AC的中
点,∠ABC=50°,则∠DAB等于( ) C
A.55°B.60°C.65°D.70°
B
A
O
2.如图,⊙O的半径为1,AB是⊙O的一条
弦,且AB= 3,则弦AB所对的圆周角的度 A
数为( )D A.30º B.60º C.30º或150 º D.60º或120º
如果AB=CD,那么∠E和∠F是什么关系? O1 D
反过来呢?
C
A
F
结合⑴、⑵你能得到什么结论?
O2
B
21
知识点三:圆周角定理的推论
归纳总结
圆周角定理推理1
同弧或等弧所对的圆周角相等; 在同圆或等圆中,相等的圆周角所对的弧相等.
∵ AB=CD ∴∠E=∠F
在⊙O中∵∠E=∠F ∴AB=CD
E
A
F
O D
对的弧也相等;②两条弦相等,弦所对的弧也相等;③弦
心距弦心距所对的弦相等;④两个圆周角相等,圆周角所
对的弧相等;⑤弧相等弧所对的弦相等;
C
⑥弧相等弧所对的圆周角也相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
又在Rt△ABD中,AD2+BD2=AB2,
D
AD BD 2 AB 2 10 5 2(cm)
2
2
8/5/2020
练习
3.求证:如果三角形一边上的中线等于这边的一半,那
么这个三角形是直角三角形.(提示:作出以这条边为
直径的圆.)
已知:△ABC 中,CO为AB边上的中线,且CO= 1 AB
2
分别量一下图中 AB所对的两个
C
圆周角的度数,比较一下,再
变动点C在圆周上的位置,圆 D
周角的度数有没有变化?你能
·O
发现什么规律吗?
再分别量出图中 AB所对的圆周 A
B
角和圆心角的度数,比较一下,
你什么发现?
同弧所对的圆周角的度数没有变化,并且它的度数
恰好等于这条弧所对的圆心角的度数的一半.
练习
A
O·
B
C
∵OA=OC, ∴∠A=∠C. 又∠BOC=∠A+∠C
∴∠BOC=2∠A 即 A 1 BOC
2
(2)在圆周角的内部.
圆心O在∠BAC的内部,作直径AD,利用(1)的
结果,有
BAD 1 BOD
A
2
DAC 1 DOC
O·
2
1
B
C
BAD DAC (BOD DOC)
D
2
BAC 1 BOC 2
七、例题解析
例 如图,⊙O直径AB为10cm,弦AC 为6cm,∠ACB的平分线交⊙O于D,
求BC、AD、BD的长.
C
A
O
B
D
解:∵AB是直径, ∴ ∠ACB= ∠ADB=90°.
在Rt△ABC中,
C
BC AB2 AC2 102 62 8
∵CD平分∠ACB,
ACD BCD.
A
O
B
∴AD=BD.
8/5/2020
作业
1. 习题24.1
求证: △ABC 为直角三角形.
C
A
·
B
O
证明:以AB为直径作⊙O, ∵AO=BO,CO= 1 AB, 2 ∴AO=BO=CO
.∴点C在⊙O上.
又∵AB为直径,
A
∴∠ACB= 1 ×180°= 90°.
2
∴ △ABC 为直角三角形.
C
·
B
O
8/5/2020
课堂小结
1、圆周角的定义; 2、圆周角定理及证明; 3、圆周角定理的运用。
(3)在圆周角的外部.
圆心O在∠BAC的外部,作直径AD,利用(1)的
结果,有
BAD 1 BOD 2
DAC 1 DOC 2
DAC DAB 1 (DOC DOB) 2
A
O·
D
C
B
BAC 1 BOC 2
五、定理
定理
在同圆或等圆中,同弧或等弧所对的圆周角 相等,都等于这条弧所对的圆心角的一半.
C2 C1
推论 C3 半圆(或直径)所对的圆周角
A
·O
是直角;
B
90°的圆周角所对的弦是直径.
练习
2.如图,你能设法确定一个圆形纸片的圆心吗?你有多 少种方法?与同学交流一下.
方法一
A
B
C
O
方法二
D
A
Hale Waihona Puke ·B方法三
O
方法四
O
六、
在同圆或等圆中,如果两个圆周角相等, 它们所对弧一定相等吗?为什么?
在同圆或等圆中,如果两个圆周角相等,它 们所对的弧一定相等.
他们的视角(∠AOB 和∠ACB) 丁E
B
有什么关系?如果同学丙、丁
分别站在他靠墙的位置D和E,
他们的视角( ∠ADB 和
∠AEB )和同学乙的视角相同
吗?
思考
D
AOB是AB所对的圆心角
A
C
ACB是AB所对的圆周角
O
ADB是AB所对的圆周角
E
B
AEB是AB所对的圆周角
它们之间有什么关系呢?
三、探究
24.1.4 圆周角
一、概念
什么叫做圆周角?
顶点在圆上,并且两边都和圆相交的角.
D
A
试找出图中的圆周角 C
O·
E
B
二、观察
如图是一个圆柱形的海洋馆的
丙D
横截面的示意图,人们可以通
过其中的圆弧形玻璃AB 观看
A
窗内的海洋动物,同学甲站在 乙C
甲O
圆心的O 位置,同学乙站在
正对着玻璃窗的靠墙的位置C,
1.如图,点A、B、C、D在同一个圆上,四边形 ABCD的对角线把4个内角分成8个角,这些角中
哪些是相等的角?
∠1 = ∠4 ∠5 = ∠8 ∠2 = ∠7 ∠3 = ∠6
A1
2
C
8 7
3
4
B
6 5
D
四、同弧所对的圆周角和圆心角的关系
为了进一步探究上面的发现,如图在⊙O任取一个 圆周角∠BAC,将圆对折,使折痕经过圆心O和 ∠BAC的顶点A.由于点A的位置的取法可能不同, 这时折痕可能会:(1)在圆周角的一条边上;
