线段等分法
(八年级数学教案)平行线等分线段定理

平行线等分线段定理八年级数学教案教学建议1.平行线等分线段定理定理:如果一组平行线在一条直线上截得的线段相等,那么在其他需直线上截得的线段也相等.注意事项:定理中的平行线组是指每相邻的两条距离都相等的特殊的平行线组;它是由三条或三条以上的平行线组成.定理的作用:可以用来证明同一直线上的线段相等;可以等分线段.2.平行线等分线段定理的推论推论1:经过梯形一腰的中点与底平行的直线,必平分另一腰.推论2:经过三角形一边的中点与另一边平行的直线,必平分第三边。
记忆方法:“中点”+“平行”得“中点”.推论的用途:(1)平分已知线段;(2)证明线段的倍分.重难点分析本节的重点是平行线等分线段定理.因为它不仅是推证三角形、梯形中位线定理的基础,而且是第五章中“平行线分线段成比例定理”的基础.本节的难点也是平行线等分线段定理.由于学生初次接触到平行线等分线段定理,在认识和理解上有一定的难度,在加上平行线等分线段定理的两个推论以及各种变式,学生难免会有应接不暇的感觉,往往会有感觉新鲜有趣但掌握不深的情况发生,教师在教学中要加以注意.教法建议平行线等分线段定理的引入生活中有许多平行线等分线段定理的例子,并不陌生,平行线等分线段定理的引入可从下面几个角度考虑:①从生活实例引入,如刻度尺、作业本、栅栏、等等;②可用问题式引入,开始时设计一系列与平行线等分线段定理概念相关的问题由学生进行思考、研究,然后给出平行线等分线段定理和推论.教学设计示例一、教学目标1. 使学生掌握平行线等分线段定理及推论.2. 能够利用平行线等分线段定理任意等分一条已知线段,进一步培养学生的作图能力.3. 通过定理的变式图形,进一步提高学生分析问题和解决问题的能力.4. 通过本节学习,体会图形语言和符号语言的和谐美●二、教法设计学生观察发现、讨论研究,教师引导分析●三、重点、难点1.教学重点:平行线等分线段定理2.教学难点:平行线等分线段定理●四、课时安排l课时●五、教具学具计算机、投影仪、胶片、常用画图工具●六、师生互动活动设计教师复习引入,学生画图探索;师生共同归纳结论;教师示范作图,学生板演练习七、教学步骤【复习提问】1.什么叫平行线?平行线有什么性质.2.什么叫平行四边形?平行四边形有什么性质?【引入新课】由学生动手做一实验:每个同学拿一张横格纸,首先观察横线之间有什么关系?(横线是互相平等的,并且它们之间的距离是相等的),然后在横格纸上画一条垂直于横线的直线,看看这条直线被相邻横线截成的各线段有什么关系?(相等,为什么?)这时在横格纸上再任画一条与横线相交的直线,测量它被相邻横线截得的线段是否也相等?(引导学生把做实验的条件和得到的结论写成一个命题,教师总结,由此得到平行线等分线段定理)平行线等分线段定理:如果一组平行线在一条直线上挂得的线段相等,那么在其他直线上截得的线段也相等.注意:定理中的“一组平行线”指的是一组具有特殊条件的平行线,即每相邻两条平行线间的距离都相等的特殊平行线组,这一点必须使学生明确.下面我们以三条平行线为例来证明这个定理(由学生口述已知,求证).已知:如图,直线,.求证:.分析1:如图把已知相等的线段平移,与要求证的两条线段组成三角形(也可应用平行线间的平行线段相等得),通过全等三角形性质,即可得到要证的结论.(引导学生找出另一种证法)分析2:要证的两条线段分别是梯形的腰,我们借助于前面常用的辅助线,把梯形转化为平行四边形和三角形,然后再利用这些熟悉的知识即可证得.证明:过点作分别交、于点、,得和,如图.∴∵,∴又∵,,∴∴为使学生对定理加深理解和掌握,把知识学活,可让学生认识几种定理的变式图形,如图(用计算机动态演示).引导学生观察下图,在梯形中,,,则可得到,由此得出推论1.推论1:经过梯形一腰的中点与底平行的直线,必平分另一腰.再引导学生观察下图,在中,,,则可得到,由此得出推论2.推论2:经过三角形一边的中点与另一边平行的直线必平分第三边.注意:推论1和推论2也都是很重要的定理,在今后的论证和计算中经常用到,因此,要求学生必须掌握好.接下来讲如何利用平行线等分线段定理来任意等分一条线段.例已知:如图,线段.求作:线段的五等分点.作法:①作射线.②在射线上以任意长顺次截取.③连结.④过点.、分别作的平行线、、、,分别交于点、、、.、、就是所求的五等分点.(说明略,由学生口述即可)【总结、扩展】小结:(l)平行线等分线段定理及推论.(2)定理的证明只取三条平行线,是在较简单的情况下证明的,对于多于三条的平行线的情况,也可用同样方法证明.(3)定理中的“平行线组”,是指每相邻两条平行线间的距离都相等的特殊平行线组.(4)应用定理任意等分一条线段.●八、布置作业教材P188中A组2、9●九、板书设计●十、随堂练习教材P182中1、2。
平行线等分线段定理

A
B
B1
C
C1
推论2:
A
B
B1
C
C1
推论2:
A A1
l1
B
B1
l2
C
C1
l3
推论2:
A
B
B1
C
C1
推论2:
A B1
B
C
C1
推论2:
A B C
B1 C1
推论2: 经过三角形一边的中点与另一边平行的直线
必平分第三边.
A
在△ACC1中, AB=BC, BB1∥CC1,
∴AB1=B1C.
B C
B1 C1
求证:AG=2GD. 分析:需要证明GH=2GD=2DH.
证明:
∵AD、BE是中线,
∴AE=EC,BD=DC,
∵CH∥EB, B
∴AG=GH,
GD=DH,
∴AG=2GD.
本题说明三角形的两中线的交点把中线分成2:1的两部分. 这个结论叫做重心定理.(现行课本已把它略去.)
A
E G
D
C
H
6、已知:梯形ABCD中,AD∥BC,
这里给出动画显示,证明的语句略去。 证法1:
. . D B
A .
. H
C E
F
7、已知:△ABC中,AB=AC, D在AB上,F在AC的延长线上, 且BD=CF,DF交BC于E,
求证:DE=EF. 证法2:
(以下略去。)
A
D B H
C E
F
8、已知:AC⊥AB,DB⊥AB, 求证:OA=OB. 分析:需证明点O在AB的垂直平分线上.
M为AD的中点,
直线CM交AB于点P,
定距等分操作方法

定距等分操作方法
定距等分操作是指将一个线段或一段长度的区域等分为若干个相等长度的小段。
以下是一种基本的定距等分操作方法:
1.确定需要等分的线段或区域的起点和终点位置。
2.确定需要的等分段数,即将线段或区域分成的小段数量。
3.计算每个小段的长度,即将线段或区域的总长度除以等分段数。
4.从起点开始,按照每个小段的长度逐步移动,将小段的起点和终点位置确定下来,形成等分后的线段或区域。
例如,我们要将一个长度为10的线段等分为5个小段,操作步骤如下:
1.起点位置为A,终点位置为B。
2.需要等分成5个小段。
3.每个小段的长度为10/5=2。
4.从起点A开始,按照每个小段长度2逐步移动,确定每个小段的起点和终点位置,得到等分后的线段为AB、BC、CD、DE、EF。
需要注意的是,定距等分操作适用于直线段和区域等分,对于曲线等分或复杂形状的区域等分,可能需要进行其他专门的操作方法。
线段等分法
课时教案
课题第二节基本作图- 线段等分法课型新授课
教学
目标
知识目标线段等分法的作图方法。
水平目标学习使用绘图工具
德育目标遵守国家标准
重点线段等分法
难点线段等分法
教学
方法
讲授法、演示法
教学
媒体
计算机,课件
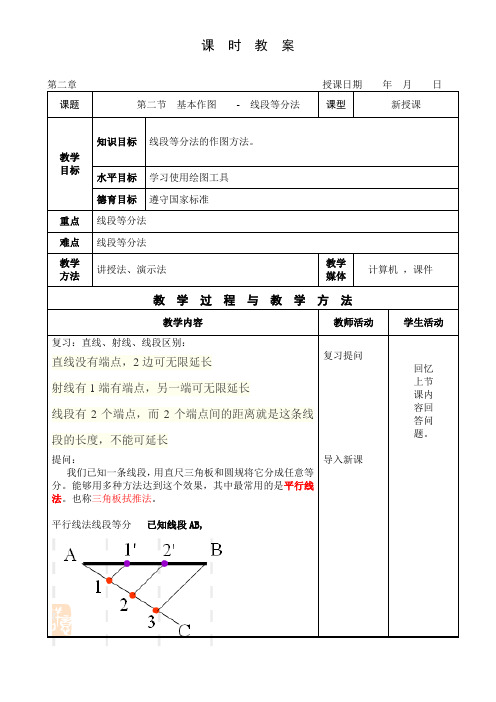
教学过程与教学方法
教学内容教师活动学生活动复习:直线、射线、线段区别:
直线没有端点,2边可无限延长
射线有1端有端点,另一端可无限延长
线段有2个端点,而2个端点间的距离就是这条线
段的长度,不能可延长
提问:
我们已知一条线段,用直尺三角板和圆规将它分成任意等
分。
能够用多种方法达到这个效果,其中最常用的是平行线
法。
也称三角板拭推法。
平行线法线段等分已知线段AB,
复习提问
导入新课
回忆
上节
课内
容回
答问
题。
教学过程与教学方法
教学内容教师活动学生活动
⑴过A点作射
线AC,与已
知线段AB成
任意锐角。
⑵用分规在
AC上上,以
任意长度截得
跟随
教师
作图教学过程与教学方法
教学内容教师活动学生活动
课堂练习
用平行线将已知线段AB分为5段。
检查学生掌握
情况。
掌握
作平
行线
技巧
小
结
线段等分法
作业将50mm线段平均分为6分
板书
设计
一、线段等分法
作图步骤:
1、
2、
3、。
数学教案-平行线等分线段定理_平行线等分线段成比例定理

1.教学重点:平行线等分线段定理
在横格纸上画一条垂直于横线的直线 ,看看这条直线被相邻横线截成的
2.教学难点:平行线等分线段定理
各线段有什么关系?〔相等,为什么?〕这时在横格纸上再任画一条与横
四、课时支配
线相交的直线 ,测量它被相邻横线截得的线段是否也相等?
l 课时
〔引导学生把做试验的条件和得到的结论写成一个命题,教师总结,
五、教具学具
由此得到平行线等分线段定理〕
计算机、投影仪、胶片、常用画图工具
平行线等分线段定理:假如一组平行线在一条直线上挂得的线段相等,
六、师生互动活动设计
那么在其他直线上截得的线段也相等.
教师复习引入,学生画图探究;师生共同归纳结论;教师示范作图,
留意:定理中的“一组平行线〞指的是一组具有特殊条件的平行线,
助线,把梯形转化为平行四边形和三角形,然后再利用这些熟识的学问即
推论 1:经过梯形一腰的中点与底平行的直线,必平分另一腰.
可证得 .
再引导学生观看下列图,在 中, , ,则可得到 ,由此得出推论 2.
证明:过 点作 分别交 、 于点 、 ,得 和 ,如图.
推论 2:经过三角形一边的中点与另一边平行的直线必平分第三边.
求作:线段 的五等分点.
八、布置作业
作法:①作射线 .
教材 P188 中 A 组 2、9
②在射线 上以任意长顺次截取 .
九、板书设计
③连结 .
④过点 . 、 、 分别作 的平行线 、 、 、 ,分别交 于点 、 、 、 .
、 、 、 就是所求的五等分点.
〔说明略,由学生口述即可〕
【总结、扩展】 小结: 〔l〕平行线等分线段定理及推论. 〔2〕定理的证明只取三条平行线,是在较简洁的状况下证明的,对 于多于三条的平行线的状况,也可用同样方法证明. 〔3〕定理中的“平行线组〞,是指每相邻两条平行线间的距离都相
《超级画板》对线段进行任意等分的作法

《超级画板》对线段进行任意等分的作法摘要:如何对任意线段进行等分?利用《超级画板》的功能,本文列举了几种方法。
关键词:线段;等分;作法作者简介:尚强,任职于深圳市教育科学研究院;许苏华,任教于深圳教苑中学。
怎样把一条任意线段三等分? 如果把引题进行推广:对任意线段进行n等分,又如何作图呢?利用《超级画板》几何作图及编程功能,给出8种他人的作法以及3种笔者的作法。
一、尺规作图等分线段只利用尺规,怎样把任意一条线段三等分?如图1所示,操作步骤如下:1. 先画出要等分的线段,并作射线;2. 以点为圆心,以任意长度为半径画圆,交射线于点;3. 再以点为圆心,作同样半径的圆,交射线于点,同法作出点;4. 连接,作,则点、把线段分成三等分。
对于线段的n等分,同法。
二、单尺作图等分线段只利用直尺,怎样把任意一条线段三等分?如图2所示,操作步骤如下:1. 先画出要等分的线段,并任作其平行线,在直线的另一侧任取一点;2. 连接和,交直线于点、,再连接和相交于点,连接,并延长交于点,则点平分线段;3. 再连接,交于点,连接并延长交于点,则点是三等分点。
对于线段的四等分,最简单的办法就是平分线段后再平分线段,也可以利用上面的方法,在三等分点的基础上再作四等分点,依次可作五等分点、六等分点、直到n等分点。
三、大卫-丹尼尔等分线段早在1996年,美国康涅狄格州的两名中学生,15岁的大卫·戈登汉姆和16岁的丹尼尔·李奇菲尔德,借助几何画板成功地用另一种方法,证明了线段可以任意等分的这一古老定理,我们简称为大卫-丹尼尔等分线段法.如图3所示,把任意一条线段三等分的操作步骤如下:1. 先画出要等分的线段,以为边作正方形;2. 连接,作的中点,连接,交于点;3. 过点作的垂线,点即为线段的三等分点。
对于n等分点,都是可以通过二等分点和三等分点迭代作。
四、秦世锐等分线段1998年秦世锐提出了一种新方法,如图4所示,把任意一条线段三等分的操作步骤如下:1. 先画出要等分的线段,并作射线;2. 在上任取一点,再取点使得;3. 连接,并延长到点使得;4. 连接交于点,点即是线段的三等分点。
线段等分的方法

线段等分的方法
以下是 7 条关于线段等分的方法:
1. 折叠法呀,这可是个超简单的办法呢!就像折纸一样,你把线段对折,那对折处不就把线段等分啦!比如说,你有一根绳子,对折一下,是不是就完美地把它分成两段一样长的啦,多神奇呀!
2. 还可以用测量法哟!拿个尺子量一量线段的长度,然后除以你想要等分的份数,不就知道每份多长啦,再标记出来就等分成功呀!好比说你要把一条长木板等分成 5 份,量好长度除以 5 后做标记,这不就搞定啦!
3. 借助工具也很棒呀!像圆规就很有用呢!以线段的一端为圆心,画弧,再以另一端为圆心画弧,两条弧的交点连线不就可以等分线段啦!这就好像是给线段来了个特别的“魔法改造”,很有趣吧!
4. 比例法也别错过呀!根据一定的比例关系去确定等分点呢!比如说,知道一条线段的长度和想要按 3:2 的比例去等分,那就能算出等分的位置呢,这是不是超级厉害呀!
5. 平行线法也很有意思噢!先画一条与线段平行的线,然后通过一些巧妙的步骤就可以等分线段啦!这就如同给线段找到了一个“好伙伴”一起完成等分这件事呀!
6. 切割法也可以试试呀!把线段想象成一块蛋糕,你慢慢切割,确保切得均匀,这不就相当于等分它啦!哎呀,就像分生日蛋糕一样呢,很形象吧!
7. 用角度去等分也不错呢!通过特定角度的绘制来实现等分,多么有创意呀!就好像我们在通过角度给线段编造一个独特的故事一样,真的很奇妙呢!
我觉得呀,这些线段等分的方法都各有千秋,都能帮助我们很好地完成线段等分这件事呢,大家可以根据实际情况选择最喜欢最适合自己的方法哟!。
平行线等分线段定理及推论中位线定理(一)

第七讲 平行线等分线段定理及推论三角形和梯形的中位线定理一、知识点和方法概述1、平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等. 根据被截的两条直线的位置关系,可以分五种图形情况(如图1-图5):推论1:经过梯形一腰的中点与底平行的直线,必平分另一腰.已知:在梯形ACFD 中,CFAD //,AB=BC求证:DE=EF推论2:经过三角形一边的中点与另一边平行的直线必平分第三边.已知:在△ACF 中,CF BE //,AB=BC求证:AE=EF2、三角形的中位线定理三角形的中位线:连结三角形两边中点的线段叫做三角形的中位线。
三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半。
已知:如图,D 、E 分别为AB 、AC 的中点求证:BC DE //,BC DE 21= 3、梯形的中位线定理梯形的中位线:连结梯形两腰中点的线段叫做梯形的中位线。
梯形的中位线定理:梯形的中位线平行于底边,并且等于两底和的一半。
已知:梯形ABCD 中,BC AD //,E 、F 分别是AB 、CD 的中点求证:BC AD EF ////,)(21BC AD EF +=. 4、和梯形中点有关的辅助线的作法:二、例题例1 如图,在直角梯形ABCD 中,E AB BC AD BC AD C ,,//,90=+︒=∠是CD 的中点,且AD=2,BC=8,求BE 的长度.法1:提示:过E 作BC EF //,交AB 于F ,过B 作CD BG //,交EF 延长线于G. ∴四边形GBCE 是平行四边形 ∵在直角梯形ABCD 中,BC AD C //,90︒=∠,AD=2,BC=8 ∴四边形GBCE 是矩形 ∴ EG=BC=8 ∵E 是CD 的中点 ∴DE=EC ∴AF=FB ∴5)(21,//=+=BC AD EF BC EF ∴GF=EG-EF=3 ∵AB BC AD =+ ∴AB=10,521==AB BF ∵在BGF Rt ∆中,︒=∠90G ∴ BG=4 ∴在BGE Rt ∆中,54842222=+=+=GE BG BE .(法2) (法3) (法4)例2 如图,梯形ABCD 中,M DC AB ,//是腰BC 的中点,AD MN ⊥于N 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
1
1' 2
2'
3'
4'
5'
用圆规依次截取相等的五段
C
连接B5’端
3
4
B
注意:
用两把三角尺推平行线,下方的三角尺 不能动,否则做不出标准图形。
过1’,2’,3’,4’点做B5’的平行线
1,2,3,4点即为线段的等分点
已知一线段长25cm,用平 行线法将其4等分,保留作 图痕迹。
A
.
N
P
B
讨论:如果将已知线段2、4、8……..等分 呢? 结论:可采用垂直平分,将任意线段线的画法:
一副三角板配合使用,可画任意已知直 线的垂直线或平行线。
一副三角板配合画线
将已知线段5等分。
A
B
步骤
将已知线段5等分。
4
细心+标准化 =专业
已知一线段长30cm,用垂直平 分法和平行线法将其四等分, 保留作图痕迹。
迁西职教中心
用一副三角板可以作出一 些什么样的角呢?
30 ° 45 ° 60 ° 15 ° 75 ° 105 ° 135 ° 150 ° 165 ° 90 ° 120 °
这些角(大于0度小于180度) 是怎么组合出来的呢?
这些角都是15 °的倍角,共有11个。
一次做出: 30° 45 ° 60° 90° 辅助做出: 15°=45°-30°
75° =30°+45° 105°=60°+45° 120°=60°+60° 135°=90°+45° 150°=90°+60° 165°=90°+45°+30°
实例:如果你有一个刻度模糊的直尺和 一个圆规,你能将一条直线2等分吗?
A
B
求作:将已知线 段2等分。
步骤:
M
1.以点A为圆心,以大于线段AB一半 的长为半径,在AB两侧画圆弧; 2.以点B为圆心,以同样的长为半 径,在AB两侧画圆弧,交点分别为 M、N。 3.连接点M、N,直线MN与线段AB的 交点为P。点P就是直线的2等分点。
提示:
步骤如下: (1)过已知直线段AB的一个端点A任作一射线AC, 由端点A起在射线上以任意长度截取4等份; (2)将射线上的等份终点与已知直线段的另一端 点B连线,并过射线上各等份点作此连线的平行 线与已知直线段相交,交点即为所求。
垂直平分法等分线段
1
2
垂直线和平行线画法 平行线法等分线段 3 研究方法,交流收获
