2016届高三物理一轮复习 第9章 第3讲 电磁感应的综合问题练习
2016届高三物理一轮复习 第9章 第3讲 电磁感应的综合问题课件

2. 答案 C 线圈刚进入B1磁场,由楞次定律可以判断线圈内产生的感应
电流方向为逆时针方向,选项B、D错误。当整个线圈都进入B1磁场时,线 圈内无感应电流。当线圈右侧进入B2匀强磁场,左侧仍在B1匀强磁场中时,
由于B1=2B2,所以磁通量减小,由楞次定律知线圈内产生顺时针方向的感应
电流,选项A错误、C正确。
(2)由给定的有关图像分析④ 电磁感应 过程,求解相应的物理量
左手定则、安培定则、右手定则、⑤ 楞次定律 、⑥ 法拉第电
应用知识
磁感应定律 、欧姆定律、牛顿运动定律、函数图像知识等
三、电磁感应中的动力学问题 1.通电导体在磁场中受到① 安培力 作用,电磁感应问题往往和力学 问题联系在一起。解决的基本方法如下: (1)用法拉第电磁感应定律和楞次定律求感应电动势的大小和方向; (2)求回路中的电流; (3)分析导体受力情况(包含安培力在内的全面受力分析); (4)根据平衡条件或② 牛顿第二定律 列方程。
BLv 动,A正确;最后合力为零,加速度为零,做匀速运动,由F-mg=0得,B L=mg, mgR v= ,D正确;导体棒克服安培力做功,减少的机械能转化为电能,由于电 R
流的热效应,电能又转化为内能,B正确C错误。
B 2 L2
2.一个矩形线圈匀速地从无磁场的空间先进入磁感应强度为B1的匀强磁 场,然后再进入磁感应强度为B2的匀强磁场,最后进入没有磁场的右边空间, 如图所示。若B1=2B2,方向均始终和线圈平面垂直,则在下列所示图中能定 性表示线圈中感应电流i随时间t变化关系的是(电流以逆时针方向为正) ( )
电阻R两端的电压UR。 (2)若磁感应强度的大小与时间成正比(B=kt),在外力作用下金属棒ab保持 静止,且当t=2 s时外力恰好为零。则金属棒ab的热功率P为多大?
高考物理一轮复习成套课时练习 第九章第三单元电磁感应规律的综合应用课时作业 选修32
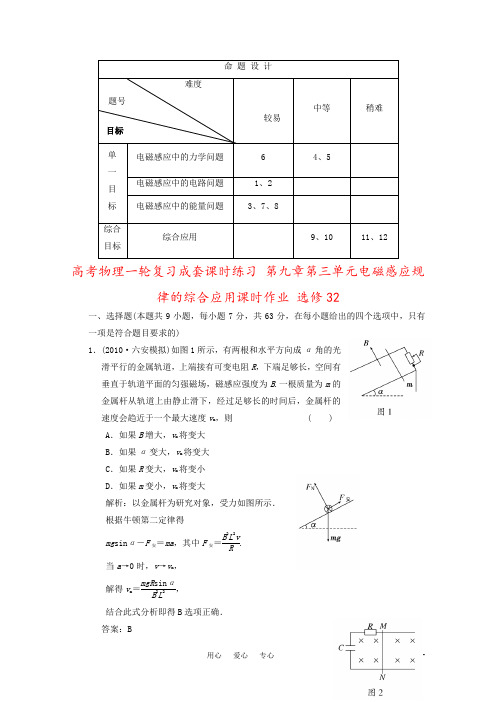
命 题 设 计难度题号 较易中等稍难单 一 目 标 电磁感应中的力学问题64、5电磁感应中的电路问题 1、2 电磁感应中的能量问题3、7、8综合 目标综合应用 9、10 11、12高考物理一轮复习成套课时练习 第九章第三单元电磁感应规律的综合应用课时作业 选修32一、选择题(本题共9小题,每小题7分,共63分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(2010·六安模拟)如图1所示,有两根和水平方向成α角的光滑平行的金属轨道,上端接有可变电阻R ,下端足够长,空间有垂直于轨道平面的匀强磁场,磁感应强度为B .一根质量为m 的金属杆从轨道上由静止滑下,经过足够长的时间后,金属杆的速度会趋近于一个最大速度v m ,则 ( ) A .如果B 增大,v m 将变大 B .如果α变大,v m 将变大 C .如果R 变大,v m 将变小 D .如果m 变小,v m 将变大解析:以金属杆为研究对象,受力如图所示. 根据牛顿第二定律得mg sin α-F 安=ma ,其中F 安=B 2L 2vR.当a →0时,v →v m , 解得v m =mgR sin αB 2L 2, 结合此式分析即得B 选项正确. 答案:B目标2.如图2所示,两光滑平行金属导轨间距为L ,直导线MN 垂直跨在导轨上,且与导轨接触良好,整个装置处于垂直纸面向里的匀强磁场中,磁感应强度为B .电容器的电容为C ,除电阻R 外,导轨和导线的电阻均不计.现给导线MN 一初速度,使导线MN 向右运动,当电路稳定后,MN 以速度v 向右做匀速运动,则 ( ) A .电容器两端的电压为零 B .电阻两端的电压为BLv C .电容器所带电荷量为CBLvD .为保持MN 匀速运动,需对其施加的拉力大小为B 2L 2v R解析:当导线MN 匀速向右运动时,导线MN 产生的感应电动势恒定,稳定后,电容器既不充电也不放电,无电流产生,故电阻两端无电压,电容器两极板间电压U =E =BLv ,所带电荷量Q =CU =CBLv ,故A 、B 错,C 对;MN 匀速运动时,因无电流而不受安培力,故拉力为零,D 错. 答案:C3.如图3所示的电路中,两根光滑金属导轨平行放置在倾角为θ的 斜面上,导轨下端接有电阻R ,导轨电阻不计,斜面处在竖直向上 的磁感应强度为B 的匀强磁场中,电阻可略去不计的金属棒ab 质 量为m ,受到沿斜面向上且与金属棒垂直的恒力F 的作用,金属 棒沿导轨匀速下滑,则它在下滑h 高度的过程中,以下说法正确的 是 ( ) A .作用在金属棒上各力的合力做功为零 B .重力做功将机械能转化为电能C .重力与恒力F 做功的代数和等于电阻R 上产生的焦耳热与金属棒的动能之和D .金属棒克服安培力做功等于重力与恒力F 做的总功与电阻R 上产生的焦耳热 之和解析:由于金属棒匀速下滑,故作用在棒上的各个力的合力做功为零,故A 对;克服安培力做功将机械能转化为电能,故B 错误;列出动能定理方程W G -W F -W 安=0,变形可得W G -W F =W 安,可知C 、D 错误. 答案:A4.如图4所示,竖直平面内有一金属环,半径为a ,总电阻为R (指拉直时两端的电阻),磁感应强度为B 的匀强磁场垂直穿过环平面,在环的最高点A 用铰链连接长度为2a 、电阻为R2的导体棒AB ,AB 由水平位置紧贴环面摆下,当摆到竖直位置 时,B 点的线速度为v ,则这时AB 两端的电压大小为( ) A.Bav3B.Bav6C.2Bav3D .Bav 解析:摆到竖直位置时,AB 切割磁感线的瞬时感应电动势E =B ·2a ·(12v )=Bav .由闭合电路欧姆定律,U AB =E R 2+R 4·R 4=13Bav ,故选A.答案:A5.如图5所示,光滑的“∏”形金属导体框竖直放置,质量为m 的金属棒MN 与框架接触良好.磁感应强度分别为B 1、B 2的有界匀强磁场方向相反,但均垂直于框架平面,分别处在abcd 和cdef 区域.现从图示位置由静止释放金属棒MN ,当金属棒进入磁场B 1区域后,恰好做匀速运动.以下说法中正确的有 ( ) A .若B 2=B 1,金属棒进入B 2区域后将加速下滑 B .若B 2=B 1,金属棒进入B 2区域后仍将保持匀速下滑 C .若B 2<B 1,金属棒进入B 2区域后可能先加速后减速下滑 D .若B 2>B 1,金属棒进入B 2区域后可能先减速后加速下滑解析:若B 2=B 1,金属棒进入B 2区域后,磁场反向,回路电流反向,由左手定则知:安培力并没有反向,大小也没有变,故金属棒进入B 2区域后,mg -B 12L 2vR=0,仍将保持匀速下滑,B 对;若B 2<B 1,金属棒进入B 2区域后,安培力没有反向但大小变小,由F =BIL =B BLv R L =B 2L 2v R 知,mg -B 22L 2vR >0,金属棒进入B 2区域后可能先加速后匀速下滑,故C 错;同理,若B 2>B 1,金属棒进入B 2区域后mg -B 22L 2vR<0,可能先减速后匀速下滑,故D 错. 答案:B6.如图6所示,用粗细相同的铜丝做成边长分别为L 和2L 的两只闭合线框a 和b ,以相同的速度从磁感应强度为B 的匀强磁场区域中匀速地拉到磁场外,不考虑线框的动能,若外力对环做的功分别为W a 、W b ,则W a ∶W b 为 ( ) A .1∶4 B .1∶2 C .1∶1 D .不能确定解析:根据能量守恒可知,外力做的功等于产生的电能,而产生的电能又全部转化为焦耳热W a =Q a =(BLv )2R a ·L v W b =Q b =(B ·2Lv )2R b ·2L v由电阻定律知R b =2R a ,故W a ∶W b =1∶4.A 项正确. 答案:A7.如图7所示,有一用铝板制成的U 型框, 将一质量为m 的带电小球用绝缘细线悬 挂在框中,使整体在匀强磁场中沿垂直 于磁场方向向左以速度v 匀速运动,悬挂拉 力为F T ,则 ( ) A .悬线竖直,F T =mg B .悬线竖直,F T >mg C .悬线竖直,F T <mg D .无法确定F T 的大小和方向解析:设两板间的距离为L ,由于向左运动的过程中竖直板切割磁感线,产生动生电动势,由右手定则判断下板电势高于上板,动生电动势大小E =BLv ,即带电小球处于电势差为BLv 的电场中,所受电场力F 电=qE 电=q EL =q BLvL=qvB . 设小球带正电,则所受电场力方向向上.同时小球所受洛伦兹力F 洛=qvB ,方向由左手定则判断竖直向下,即F 电=F 洛,所以F T =mg .同理分析可知当小球带负电时,F T =mg .故无论小球带什么电,F T =mg .选项A正确. 答案:A8.(2010·芜湖模拟)如图8甲所示,光滑导轨水平放置在与水平方向夹角为60°的斜向下的匀强磁场中,匀强磁场的磁感应强度B 随时间t 的变化规律如图8乙所示(规定斜向下为正方向),导体棒ab 垂直导轨放置,除电阻R 的阻值外,其余电阻不计,导体棒ab 在水平外力F 作用下始终处于静止状态.规定a →b 的方向为电流的正方向,水平向右的方向为外力F 的正方向,则在0~t 1时间内,图9中能正确反映流过导体棒ab的电流i和导体棒ab所受水平外力F随时间t变化的图象是( )解析:由楞次定律可判定回路中的电流方向始终为b→a,由法拉第电磁感应定律可判定回路中电流大小恒定,故A、B错;由F安=BIL可得F安随B的变化而变化,在0~t0时间内,F安方向向右,故外力F与F安等值反向,方向向左为负值;在t0~t1时间内,F安方向改变,故外力F方向也改变为正值,故C错误,D正确.答案:D9.(2010·黄山模拟)如图10所示,固定放置在同一水平面内的两根平行长直金属导轨的间距为d,其右端接有阻值为R的电阻,整个装置处在竖直向上的磁感应强度大小为B的匀强磁场中.一质量为m(质量分布均匀)的导体杆ab垂直于导轨放置,且与两导轨保持良好接触,杆与导轨之间的动摩擦因数为μ.当杆在水平向左、垂直于杆的恒力F作用下从静止开始沿导轨运动距离l时,速度恰好达到最大(运动过程中杆始终与导轨保持垂直).设杆接入电路的电阻为r,导轨电阻不计,重力加速度大小为g.则此过程 ( )A .杆的速度最大值为(F -μmg )RB 2d2B .流过电阻R 的电荷量为Bdl2(R +r )C .恒力F 做的功与摩擦力做的功之和等于杆动能的变化量D .恒力F 做的功与安培力做的功之和大于杆动能的变化量解析:当杆的速度达到最大时,安培力F 安=B 2d 2vR +r ,杆受力平衡,故F -μmg -F 安=0,所以v =(F -μmg )(R +r )B 2d 2,A 错;流过电阻R 的电荷量为q =ΔΦR +r =B ΔSR +r=BdlR +r,B 错;根据动能定理,恒力F 、安培力、摩擦力做功的代数和等于杆动能的变化量,由于摩擦力做负功,所以恒力F 、安培力做功的代数和大于杆动能的变化量,C 错,D 对. 答案:D二、计算题(本题共3小题,共37分,解答时应写出必要的文字说明、方程式和演算 步骤,有数值计算的要注明单位)10.(11分)如图11甲所示,用粗细均匀的导线制成的一只圆形金属圈,现被一根绝缘丝线悬挂在竖直平面内处于静止状态,已知金属圈的质量为m ,半径为r ,导线的电阻率为ρ,截面积为S .金属圈的上半部分处在一方向垂直圈面向里的有界匀强磁场中,磁感应强度B 随时间t 的变化满足B =kt (k 为常量),如图11乙所示.金属圈下半部分在磁场外.若丝线所能承受的最大拉力F Tm =2mg ,求:从t =0时刻起,经过多长时间丝线会被拉断?解析:设金属圈受重力mg 、拉力F T 和安培力F 的作用处于静止状态,则F T =mg +F ,又F =2BIr ,金属圈中的感应电流I =ER, 由法拉第电磁感应定律得E =ΔΦΔt ,ΔΦΔt =ΔB Δt ·πr 22,金属圈的电阻R =ρ2πr S,又B =kt ,F Tm =2mg 由以上各式求得t =2mgρk 2Sr2.答案:2mgρk 2Sr211.(12分)(2010·淮南模拟)如图12所示,两平行长直金属导轨置于竖直平面内,间距为L ,导轨上端有阻值为R 的电阻,质 量为m 的导体棒垂直跨放在导轨上,并搁在支架上,导轨和 导体棒电阻不计,接触良好,且无摩擦.在导轨平面内有一 矩形区域的匀强磁场,方向垂直于纸面向里,磁感应强度为B .开始时导体棒静止,当磁场以速度v 匀速向上运动时,导体棒也随之开始运动,并很快达到恒定的速度,此时导体棒 仍处在磁场区域内,试求: (1)导体棒的恒定速度;(2)导体棒以恒定速度运动时,电路中消耗的电功率. 解析:(1)设棒速为v ′,有E =BL (v -v ′) ①F 安=BIL =BLE R =B 2L 2(v -v ′)R②棒受力平衡有:mg =F 安 ③ 联立得:v ′=v -mgRB 2L 2④ 方向向上(2)P =E 2R ⑤联立①④⑤得:P =m 2g 2RB 2L 2.答案:(1)v -mgR B 2L 2 向上 (2)m 2g 2RB 2L212.(14分)(2010·亳州模拟)在拆装某种大型电磁设备的过程中,需将设备内部的处于强磁场中的线圈先闭合,然后再提升直至离开磁场,操作时通过手摇轮轴A 和定滑轮O 来提升线圈.假设该线圈可简化为水平长为L 、上下宽度为d 的矩形线圈,其匝数为n ,总质量为M ,总电阻为R .磁场的磁感应强度为B ,如图13所示.开始时线圈的上边缘与有界磁场的上边缘平齐,若转动手摇轮轴A ,在时间t 内把线圈从图示位置匀速向上拉出磁场.求此过程中: (1)流过线圈中每匝导线横截面的电荷量是多少 ? (2)在转动轮轴时,人至少需做多少功?(不考虑摩擦影响)解析:(1)在匀速提升的过程中线圈运动速度v =d t① 线圈中感应电动势E =nBLv ② 产生的感应电流I =E R③ 流过导线横截面的电荷量q =It ④ 联立①②③④得q =nBLdR. (2)匀速提升的过程中,要克服重力和安培力做功,即W =W G +W 安 ⑤又W G =Mgd ⑥W 安=nBILd ⑦联立①②③④⑤⑥⑦得W =Mgd +n 2B 2L 2d 2Rt.答案:(1)nBLd R (2)Mgd +n 2B 2L 2d 2Rt。
高三物理一轮复习必考部分第9章电磁感应专题突破练

电磁感应(限时:40分钟)对点强化1等效法在电磁感应中的应用1. (多选)用一根横截而积为S 、电阻率为Q 的硬质导线做成一个半径为r 的圆环,ab 为圆环的一条直径.如图1所示,在必的左侧存在一个匀强磁场,磁场方向垂直圆环所在 平而,方向如图,磁感应强度大小随时间的变化率—=A (K0)・则( )【导学号:96622419]A. 圆环中产生逆时针方向的感应电流B. 圆环具有扩张的趋势D.图中a 、b 两点间的电势差/BD 根据楞次左律和安培泄则,圆环中将产生顺时针方向的感应电流,且具有扩张的趋势.A 错误、B 正确:根据法拉第电磁感应左律,圆环中产生的感应电动势大小为E=o JT •• F lcvS 由电阻怎律知斤=门二7二,所以感应电流的大小为/=”= 了亍,c 错误:根据闭合电路欧姆泄律可得a 、b 两点间的电势差, D 正确.2. 半径为&的圆形区域内有匀强磁场,磁感应强度为5=0. 2 T,磁场方向垂直纸面向 里.半径为b 的金属圆环与磁场同心放置,磁场与环面垂直,英中<2=0. 4 m, b=0.6m, 金属环上分别接有灯L :、L=,两灯的电阻均为凡=2 Q, —金属棒IfV 与金属环接触良好, 棒与环的电阻均忽略不计.图2⑴若金属棒.0以vb=5 m/s 的速率在环上向右匀速滑动,求金属棒滑过圆环直径 00’的瞬间(如图2所示),金属棒JfV 中的电动势和流过灯L’的电流;(2)撤去中间的金属棒恵\;将右而的半圆环久以加'为轴向上翻转90° ,若此后A B 4磁场的磁感应强度随时间均匀变化,其变化率为—=—T/s,求此时匚的功率・【解析】 ⑴金属棒妙滑过圆环宜径加’的瞬间,金属棒血•切割磁感线的有效长度 为2a,产生的感应电动势E 、=B ・ 2a%=0・ 2X2X0. 4X5 V=0. 8 V由欧姆怎律得,流过灯L,的电流C. 圆环中感应电流的大小为迄0.8Ti=~=o A=0. 4 A.屉z(2)设此时产生的感应电动势为E,由法拉第电磁感应泄律得△ G 1 . △万 1 . 4*卞7飞心• ^7=2X N XO-4'X T V=0-32 VLi、L:串联,每个灯上分得的电压* 怂=0. 16 V从I亠“& 0・16’一L,的功率为R=~=—z-W=l. 28X10 • W.【答案】(1)0.8 V 0.4 A (2)1.28X10's W对点强化2电磁感应中的“杆+导轨”模型3.(多选)如图3所示,abed是由粗细均匀的电阻丝制成的长方形线框,导体棒MV有电阻,可在ad边与加边上无摩擦滑动,且接触良好,线框处于垂直纸而向里的匀强磁场中.当棒由靠ab边处向c/边匀速移动的过程中,下列说法中正确的是()【导学号:96622420]图3A.血•棒中电流先减小后增大B.血•棒两端电压先增大后减小C.JA•棒上拉力的功率先增大后减小D.矩形线框中消耗的电功率先减小后增大AB设导体棒JfV的速度为儿长为电阻为r,导体棒血'两边的电阻并联,则导体棒妬由"向cd 运动的过程中,导体棒在ad中点时,回路的总电阻最大,导体棒产生的感应电动势E=Blv,恒左不变,切割磁感线的导体棒相当于电源,可见在导体棒移动Rl v过程中,电路的总电阻先变大后减小:由闭合电路欧姆左律知,MV棒中电流先减小后增大,选项A正确;由U=Blv~Ir可知,血「棒两端电压先增大后减小,选项B正确:根据功率的泄义可得P=Fv=BIlv,血•棒上拉力的功率先减小后增大,选项C错误:由于导体棒的电阻和线框电阻的大小关系不确宦,无法确怎矩形线框中消耗的电功率的变化,选项D错误.4.间距为£=2m的足够长的金属直角导轨如图4甲所示放置,它们各有一边在同一水平面内,另一边垂直于水平而.质量均为z^=0. 1 kg的金属细杆ab、c/与导轨垂宜放置形成闭合回路.细杆与导轨之间的动摩擦因数均为“=0.5,导轨的电阻不计,细杆ab. cd 的电阻分别为丘= 0.6 Q,用=0.4 Q.整个装巻处于磁感应强度大小为5=0. 50 T.方向竖直向上的匀强磁场中(图中未画出)•当ab在平行于水平导轨的拉力尸作用下从静I匕开始沿导轨匀加速运动时,杆也同时从静止开始沿导轨向下运动.测得拉力尸与时间r 的关系 如图乙所示.g 取10 m/sl甲乙图4(1) 求站杆的加速度a ;(2) 求当cd 杆达到最大速度时ab 杆的速度大小:(3) 若从开始到cd 杆达到最大速度的过程中拉力尸做了 5. 2 J 的功,通过cd 杆横截面 的电荷量为2 C,求该过程中訪杆所产生的焦耳热.【解析】 ⑴由题图乙可知,在上=0时,5=1.5 N对ab 杆进行受力分析,由牛顿第二泄律得F- Pmg=ma 代入数据解得10 m/s -.⑵从〃向c 看,对加杆进行受力分析如图所示,当cd 杆速度最大时,有 综合以上各式,解得v=2 m/s.2" (3)整个过程中,a&杆发生的位移*=后=拧p m=0.2 m对ab 杆应用动能泄理,有W r — “碑Y —他=£/代入数据解得严安=4.9 J根据功能关系Q 总=0很所以必杆上产生的热量如=斤¥評总=2.94 J.【答案】(1)10 m/s' (2)2 m/s (3)2.94 J对点强化3与电磁感应有关的图象问题5. 一边长为厶的正方形线框位于一个方向垂直线框平而向里的磁场中,如图5甲所示, 磁感应强度万随时间F 的变化规律如图乙所示.以尸表示线框ab 边所受到的安培力,以安 培力向上为正.则下列产r 图象中正确的是()【导学号:96622421]图5B 0〜1 s 内磁感应强度均匀增大,由楞次泄律知在线框内产生恒左逆时针方向的感应 电流,由左手泄则判得必边受到向下的安培力,由尸 =万〃可知其大小线性增大;1〜2 s 内磁感应强度不变,在线框内不产生感应电流,ab 边不受安培力的作用:2〜3 s 内磁感应 强度均匀减小,由楞次定律知在线框内产生恒泄顺时针方向的感应电流,由左手立则判得 ab 边受到向上的安培力,由Q 刃•厶可知其大小线性减小.故选项B 正确,选项A 、C 、D 错 误.6. 在边长为Z 的等边三角形区域自氐内存在着垂直纸面向外的匀强磁场,一个边长也 为L 的等边三角形导线框尿/•在纸面上以某一速度向右匀速运动,底边ef 始终与磁场的底 边界加在Ft=mg=卩民尺=尸匚,F 心=BIL 、1= BLv同一直线上,如图6所示.取沿顺时针的电流为正,在线框通过磁场的过程中,其感应电流随时间变化的图象是()图6B线框通过磁场的过程中,通过线框的磁通量先增大后减小,故感应电流方向一泄发生变化,A、C项错:线框通过磁场过程中,切割磁感线的有效长度匸=后,由片甩'P 和闭合电路欧姆定律』=乡可知,感应电流随时间均匀变化,B项正确,D项错.7.如图7所示,一半径为斤,圆心角为240。
高三物理一轮总复习 第9章《电磁感应》3.2 电磁感应规律的综合应用(二)(动力学和能量)课时作业

电磁感应规律的综合应用(二)(动力学和能量)一、选择题 1.(多选)如图所示,电阻不计的平行金属导轨固定在一绝缘斜面上,两相同的金属导体棒a 、b 垂直于导轨静止放置,且与导轨接触良好,匀强磁场垂直穿过导轨平面.现用一平行于导轨的恒力F 作用在a 的中点,使其向上运动.若b 始终保持静止,则它所受摩擦力可能( )A .变为0B .先减小后增大C .等于FD .先增大再减小【解析】 a 导轨在恒力F 作用下加速运动,闭合回路中产生感应电流,导体棒b 受到安培力方向应沿斜面向上,且逐渐增大.由力平衡可知,b 导体棒受到的摩擦力先沿斜面向上逐渐减小到零,然后沿斜面向下逐渐增大,所以选项A 、B 正确,C 、D 错误.【答案】 AB 2.如图所示,边长为L 的正方形导线框质量为m ,由距磁场H 高处自由下落,其下边ab 进入匀强磁场后,线圈开始做减速运动,直到其上边cd 刚刚穿出磁场时,速度减为ab 边进入磁场时的一半,磁场的宽度也为L ,则线框穿越匀强磁场过程中产生的焦耳热为( )A .2mgLB .2mgL +mgHC .2mgL +34mgHD .2mgL +14mgH【解析】 设ab 刚进入磁场时的速度为v 1,cd 刚穿出磁场时的速度v 2=v 12,线框自开始进入磁场到完全穿出磁场共下落高度为2L ,由题意得,12mv 21=mgH ,12mv 21+mg·2L=12mv 22+Q ,解得,Q =2mgL +34mgH ,C 项正确.【答案】 C 3.如图所示,间距为L 、电阻不计的足够长平行光滑金属导轨水平放置,导轨左端用一阻值为R 的电阻连接,导轨上横跨一根质量为m 、电阻也为R 的金属棒,金属棒与导轨接触良好.整个装置处于竖直向上、磁感应强度为B 的匀强磁场中.现使金属棒以初速度v 0沿导轨向右运动,若金属棒在整个运动过程中通过的电荷量为q 下列说法正确的是( )A .金属棒在导轨上做匀减速运动B .整个过程中电阻R 上产生的焦耳热为mv 202C .整个过程中金属棒在导轨上发生的位移为qR BLD .整个过程中金属棒克服安培力做功为mv 22【解析】 由牛顿第二定律可得B 2L 2vR=ma, 金属棒做a 减小的减速运动,A 错.由能量守恒定律可知,克服安培力做功等于电阻R 和金属棒上产生的焦耳热之和,W 安=12mv 2=Q ,因此B 错,D 正确.整个过程中通过金属棒的电量q =ΔΦ2R =BLx 2R ,得金属棒位移x =2qRBL,C错.【答案】 D 4.竖直平面内有一形状为抛物线的光滑曲面轨道,如图所示,轨道下半部分处在两个水平向里的匀强磁场中,磁场的边界分别是y =a 、y =b 、y =c 的直线(图中虚线所示).一个小金属环从抛物线上y =d 处由静止释放,金属环沿抛物线下滑后环面总保持与磁场垂直,那么产生的焦耳热总量是( )A .mgdB .mg(d -a)C .mg(d -b)D .mg(d -c) 【解析】 小金属环进入和穿出磁场的过程都要切割磁感线,因此小金属环的机械能不断地转化为电能,电能又转化为内能;最后小金属环在y =c 的直线与x 轴之间的磁场内往复运动,整个过程中机械能的减小量为ΔE =mg(d -c),由能的转化与守恒定律可知,产生的焦耳热总量为Q =ΔE =mg(d -c),所以D 项正确.【答案】 D5.(多选)如图所示,虚线矩形abcd 为匀强磁场区域,磁场方向竖直向下,圆形闭合金属线框以一定的速度沿光滑绝缘水平面向磁场区域运动.如图所示给出的是圆形闭合金属线框的四个可能到达的位置,则圆形闭合金属线框的速度可能为零的位置是( )【解析】 因为线框在进、出磁场时,线框中的磁通量发生变化,产生感应电流,安培力阻碍线框运动,使线框的速度可能减为零,故A 、D 正确.【答案】 AD 6.如图所示,光滑斜面的倾角为θ,斜面上放置一矩形导体线框abcd ,ab 边的边长为l 1,bc 边的边长为l 2,线框的质量为m ,电阻为R ,线框通过绝缘细线绕过光滑的滑轮与重物相连,重物质量为M ,斜面上ef 线(ef 平行底边)的右方有垂直斜面向上的匀强磁场,磁感应强度为B ,如果线框从静止开始运动,进入磁场的最初一段时间是做匀速运动的,且线框的ab 边始终平行底边,则下列说法正确的是( )A .线框进入磁场前运动的加速度为Mg -mg sin θmB .线框进入磁场时匀速运动的速度为Mg -mg sin θRBl 1C .线框做匀速运动的总时间为B 2l 21Mg -mg sin θRD .该匀速运动过程产生的焦耳热为(Mg -mg sin θ)l 2【解析】 对重物和线框系统受力分析,由牛顿第二定律得,Mg -mg sin θ=(M +m)a ,解得,a =Mg -mg sin θm +M,A 项错误;对线框受力分析,由平衡条件得,Mg -mg sin θ-F 安=0,又F 安=BIl 1,I =E/R ,E =Bl 1v ,联立解得,v =Mg -mg sin θRB 2l 21,B 项错误;线框做匀速运动的总时间为t =l 2v =B 2l 21l 2Mg -mg sin θR,C 项错误;由能量守恒定律得,该匀速运动过程产生的焦耳热等于系统重力势能的减小,Q =(Mg -mg sin θ)l 2,D 项正确.【答案】 D 7.如图所示的甲、乙、丙图中,MN 、PQ 是固定在同一水平面内足够长的平行金属导轨.导体棒ab 垂直放在导轨上,导轨都处于垂直水平面向下的匀强磁场中.导体棒和导轨间接触良好且摩擦不计,导体棒、导轨和直流电源的电阻均可忽略,甲图中的电容器C 原来不带电.今给导体棒ab 一个向右的初速度v 0,在甲、乙、丙图中导体棒ab 在磁场中的最终运动状态是( )A .甲、丙中,棒ab 最终将以相同速度做匀速运动;乙中ab 棒最终静止B .甲、丙中,棒ab 最终将以不同速度做匀速运动;乙中ab 棒最终静止C .甲、乙、丙中,棒ab 最终均做匀速运动D .甲、乙、丙中,棒ab 最终都静止【解析】 甲图中ab 棒产生的感应电动势对电容器C 充电,C 两极板间电势差与感应电动势相同时,电路中没有电流,ab 棒做向右的匀速直线运动;乙图中导体棒在初速度作用下,切割磁感线,产生电动势,出现安培力,阻碍其向前运动,其动能转化为热能,最终会静止;而丙图虽在初速度作用下向右运动,但却受到向左的安培力,则杆向右减速运动,然后还要向左运动.当金属杆切割磁感线产生电动势与电源的电动势相等时,电路中没有电流,所以金属杆最终处于向左的匀速直线运动.由此得选项B 正确,A 、C 、D 错误.【答案】 B 8.两根足够长的光滑导轨竖直放置,间距为L ,底端接阻值为R 的电阻.将质量为m 的金属棒悬挂在一个固定的轻弹簧下端,金属棒和导轨接触良好,导轨所在平面与磁感应强度为B 的匀强磁场垂直,如图所示.除电阻R 外其余电阻均不计.现将金属棒从弹簧原长位置由静止释放.则( )A .金属棒将做往复运动,动能、弹性势能与重力势能的总和保持不变B .金属棒最后将静止,静止时弹簧的伸长量为mg/kC .金属棒最后将静止,电阻R 上产生的总热量为mg·mg kD .当金属棒第一次达到最大速度时,弹簧的伸长量为mg/k 【解析】 金属棒在往复运动的过程中不断克服安培力做功产生电能,进而转化成焦耳热,机械能不断减少,最终静止,静止时弹力等于金属棒的重力,故A 错误,B 正确;由能量守恒定律可得mg·mgk=Q +E 弹,故C 错误;当金属棒第一次达到最大速度时,加速度为零,则mg =kx +F 安,故D 错误.【答案】 B 9.如图所示,水平地面上方矩形区域内存在垂直纸面向里的匀强磁场,两个边长相等的单匝闭合正方形线圈Ⅰ和Ⅱ,分别用相同材料、不同粗细的导线绕制(Ⅰ为细导线).两线圈在距磁场上界面h 高处由静止开始自由下落,再进入磁场,最后落到地面.运动过程中,线圈平面始终保持在竖直平面内且下边缘平行于磁场上边界.设线圈Ⅰ、Ⅱ落地时的速度大小分别为v 1、v 2,在磁场中运动时产生的热量分别为Q 1、Q 2.不计空气阻力,则( )A .v 1<v 2,Q 1<Q 2B .v 1=v 2,Q 1=Q 2C .v 1<v 2,Q 1>Q 2D .v 1=v 2,Q 1<Q 2【解析】 线圈进入磁场前机械能守恒,进入磁场时速度均为v =2gh ,设线圈材料的密度为ρ1,电阻率为ρ2,线圈边长为L ,导线横截面积为S ,则线圈的质量m =ρ14LS ,电阻R =ρ24L S ,由牛顿第二定律得mg -B 2L 2v R =ma ,解得a =g -B 2v16ρ1ρ2,可见两线圈在磁场中运动的加速度相同,两线圈落地时速度相同,即v 1=v 2,故A 、C 选项错误;线圈在磁场中运动时产生的热量等于克服安培力做的功,Q =W 安,而F 安=B 2L 2v R =B 2Lv4ρ2S ,线圈Ⅱ横截面积S 大,F 安大,故Q 2>Q 1,故选项D 正确,B 错误.【答案】 D 二、非选择题 10.如图所示,电动机牵引一根原来静止的、长为1 m 、质量为0.1 kg 的导体棒MN ,其电阻R 为1 Ω,导体棒架在处于磁感应强度B =1 T ,竖直放置的框架上,当导体棒上升h =3.8 m 时获得稳定的速度,导体产生的热量为2 J ,电动机牵引导体棒时,电压表、电流表计数分别为7 V 、1 A ,电动机的内阻r =1 Ω,不计框架电阻及一切摩擦;若电动机的输出功率不变,g 取10 m /s 2,求:(1)导体棒能达到的稳定速度为多少?(2)导体棒从静止达到稳定所需的时间为多少?【解析】 (1)电动机的输出功率为P =U A I A -I 2A r =6 WF 安=BIL =B 2L 2vR当导体棒的速度稳定时,由平衡条件得,P v =mg +B 2L 2v R解得,v =2 m /s .(2)由能量守恒定律得,Pt -Q -mgh =12mv 2解得,t =1 s .【答案】 (1)2 m /s (2)1 s11.如图所示,相距L =1 m 、电阻不计的平行光滑长金属导轨固定在绝缘水平面上,两导轨左端间接有阻值R =2 Ω的电阻,导轨所在区域内加上与导轨所在平面垂直、方向相反的匀强磁场,磁场宽度d 均为0.6 m ,磁感应强度大小B 1=25T 、B 2=0.8 T .现有电阻r =1 Ω的导体棒ab 垂直导轨放置且接触良好,当导体棒ab 从边界MN 进入磁场后始终以速度v =5 m /s 做匀速运动,求:(1)棒ab 在磁场B 1中运动时克服安培力做功的功率;(2)棒ab 经过任意一个磁场B 2区域过程中通过电阻R 的电荷量. 【解析】 (1)在磁场B 1中,棒ab 切割磁感线产生的电动势E 1=B 1Lv感应电流I 1=E 1r +R安培力F =B 1I 1L克服安培力做功的功率P =Fv =B 1Lv2r +R=0.67 W(2)在磁场B 2中,棒ab 切割磁感线产生的电动势E 2=B 2Lv感应电流I 2=E 2r +R棒ab 经过任意一个磁场B 2区域过程中通过电阻R 的电荷量q =I 2Δt 2=B 2Lv Δt 2r +R =B 2Ldr +R=0.16 C .【答案】 (1)0.67 W (2)0.16 C 12.(2015·四川卷)如图所示,金属导轨MNC 和PQD ,MN 与PQ 平行且间距为L ,所在平面与水平面夹角为α,N 、Q 连线与MN 垂直,M 、P 间接有阻值为R 的电阻;光滑直导轨NC 和QD 在同一水平面内,与NQ 的夹角都为锐角θ.均匀金属棒ab 和ef 质量均为m ,长均为L ,ab 棒初始位置在水平导轨上与NQ 重合;ef 棒垂直放在倾斜导轨上,与导轨间的动摩擦因数为μ(μ较小),由导轨上的小立柱1和2阻挡而静止.空间有方向竖直的匀强磁场(图中未画出).两金属棒与导轨保持良好接触.不计所有导轨和ab 棒的电阻,ef 棒的阻值为R ,最大静摩擦力与滑动摩擦力大小相等,忽略感应电流产生的磁场,重力加速度为g.(1)若磁感应强度大小为B ,给ab 棒一个垂直于NQ 、水平向右的速度v 1,在水平导轨上沿运动方向滑行一段距离后停止,ef 棒始终静止,求此过程导体上产生的热量;(2)在(1)问过程中,ab 棒滑行距离为d ,求通过ab 棒某横截面的电量;(3)若ab 棒以垂直于NQ 的速度v 2在水平导轨上向右匀速运动,并在NQ 位置时取走小立柱1和2,且运动过程中ef 棒始终静止.求此状态下最强磁场的磁感应强度及此磁场下ab 棒运动的最大距离.【解析】 (1)设ab 棒的初动能为E k ,ef 棒和电阻R 在此过程产生的热量分别为W 和W 1,有W +W 1=E k ①且W =W 1②由题有E k =12mv 21③得W =14mv 21④(2)设在题设过程中,ab 棒滑行时间为Δt ,扫过的导轨间的面积为ΔS ,通过ΔS 的磁通量为ΔΦ,ab 棒产生的电动势平均值为E ,ab 棒中的电流为I ,通过ab 棒某横截面的电荷量为q ,则E =ΔΦΔt⑤ 且ΔΦ=B ΔS⑥I =qΔt⑦又有I =2ER⑧由图1所示ΔS =d(L -d cot θ)⑨联立⑤~⑨,解得q =2Bd L -d cot θR○10 (3)ab 棒滑行距离为x 时,ab 棒在导轨间的棒长 L x =L -2x cot θ⑪此时,ab 棒产生的电动势 E x =Bv 2L x ⑫流过ef 棒的电流I x =E xR⑬ef 棒所受安培力F x =BI x L ⑭联立⑪~⑭,解得F x =B 2v 2LR(L -2x cot θ)⑮由⑮式可得,F x 在x =0和B 为最大值B m 时有最大值F 1.由题知,ab 棒所受安培力方向必水平向左,ef 棒所受安培力方向必水平向右,使F 1为最大值的受力分析如图2所示,图中f m 为最大静摩擦力,有F 1cos α=mg sin α+μ(mg cos α+F 1sin α)⑯联立⑮⑯,得B m =1L mg sin α+μcos αRcos α-μsin αv 2⑰⑰式就是题目所求最强磁场的磁感应强度大小,该磁场方向可竖直向上,也可竖直向下.由⑮式可知,B 为B m 时,F x 随x 增大而减小,x 为最大x m 时,F x 为最小值F 2,由图3可知F 2cos α+μ(mg cos α+F 2sin α)=mg sin α⑱ 联立⑮⑰⑱,得x m =μL tan θ1+μ2sin αcos α+μ⑲ 【答案】 (1)14mv 21 (2)2Bd L -d cot θR(3)1L mg sin α+μcos αRcos α-μsin αv 2,磁场方向可竖直向上,也可竖直向下;μL tan θ1+μ2sin αcos α+μ 13.(2015·天津卷)如图所示,“凸”字形硬质金属线框质量为m ,相邻各边互相垂直,且处于同一竖直平面内,ab 边长为l ,cd 边长为2l ,ab 与cd 平行,间距为2l.匀强磁场区域的上下边界均水平,磁场方向垂直于线框所在平面.开始时,cd 边到磁场上边界的距离为2l ,线框由静止释放,从cd 边进入磁场直到ef 、pq 边进入磁场前,线框做匀速运动.在ef 、pq 边离开磁场后,ab 边离开磁场之前,线框又做匀速运动.线框完全穿过磁场过程中产生的热量为Q.线框在下落过程中始终处于原竖直平面内,且ab 、cd 边保持水平,重力加速度为g.求:(1)线框ab 边将离开磁场时做匀速运动的速度大小是cd 边刚进入磁场时的几倍; (2)磁场上下边界间的距离H.【解析】 (1)设磁场的磁感应强度大小为B ,cd 边刚进入磁场时,线框做匀速运动的速度为v 1,cd 边上的感应电动势为E 1,由法拉第电磁感应定律,有E 1=2Blv 1①设线框总电阻为R ,此时线框中电流为I 1,由闭合电路欧姆定律,有I 1=E 1R②设此时线框所受安培力为F 1,有F 1=2I 1lB ③ 由于线框做匀速运动,其受力平衡,有mg =F 1④由①②③④式得v 1=mgR4B 2l2⑤设ab 边离开磁场之前,线框做匀速运动的速度为v 2,同理可得。
2016届高三物理一轮复习 第9章 电磁感应 3 电磁感应定律的综合应用课件

线框由(5)位置运动到(6)位置过程中,导体有效切割长度 变小,直到为零.
综上所述,可知B正确.
解法2:在电磁感应现象中,流过线框某一横截面的电量 与磁通量的变化量成正比,当线框穿入和穿出磁场之后,线框 内的磁通量变化量为零,流过线框某一横截面的电量也必将为 零.而在电流—时间图像中,图线与坐标轴围成的面积就是电 量,所以电流图像在时间轴上下围成的面积必然相等.观察四 个选项,符合条件的只有B和D.利用楞次定律判断t=0时刻后 一段时间的电流方向可知B正确.
A.E1>E2 C.E1<E2
B.E1=E2 D.无法判定 E1、E2 大小
【解析】 设 PQ 棒的质量为 m,匀速运动的速度为 v, 导轨宽 l,则由平衡条件,得 BIl=mg,则 I=ER,E=Blv,所 以 v=RBm2l2g,可见 PQ 棒匀速运动的速度与何时闭合开关无关, 即 PQ 棒两种情况下落地速度相同,由能的转化和守恒定律得: 机械能的损失完全转化为电能,故两次产生的电能相等.
【答案】 见解析
考向二 电磁感应中的图像问题 1.图像类型
2.分析方法
典例2 如图所示,EOF和E′O′F′为空间一匀强磁场 的 边 界 , 其 中 EO∥E′O′ , FO∥F′O′ , 且 EO⊥OF ; OO′为∠EOF的角平分线,OO′间的距离为l;磁场方向垂直 于纸面向里.一边长为l的正方形导线框沿O′O方向匀速通过 磁场,t=0时刻恰好位于图示位置.规定导线框中感应电流沿 逆时针方向时为正,则感应电流i与时间t的关系图线可能正确 的是( )
2 C.3E
1 B.3E D.E
【解析】 a、b 间的电势差等于路端电压,而小环电阻占
2016届高三物理一轮复习学案:电磁感应

2016届高三物理一轮复习学案:电磁感应一、知识梳理(一)电磁感应现象1、磁通量(1)定义:设在磁感应强度为 B 的匀强磁场中,有一个与磁场方向垂直的平面,面积为 S,我们把 B 与 S 的乘积叫做穿过这个面积的磁通量,简称磁通。
用字母Φ 表示。
(2)公式:Φ = BS(条件:B⊥S)。
(3)单位:韦伯(Wb),1 Wb = 1 T·m²。
(4)磁通量是标量,但有正负之分。
2、电磁感应现象(1)定义:当穿过闭合导体回路的磁通量发生变化时,闭合导体回路中就产生感应电流,这种利用磁场产生电流的现象叫做电磁感应。
(2)产生感应电流的条件:穿过闭合回路的磁通量发生变化。
(二)感应电流方向的判定1、楞次定律(1)内容:感应电流具有这样的方向,即感应电流的磁场总要阻碍引起感应电流的磁通量的变化。
(2)应用楞次定律判断感应电流方向的步骤:①确定原磁场的方向;②确定穿过闭合回路的磁通量是增加还是减少;③根据楞次定律,确定感应电流的磁场方向;④利用安培定则,确定感应电流的方向。
2、右手定则(1)内容:伸开右手,使拇指与其余四个手指垂直,并且都与手掌在同一平面内;让磁感线从掌心进入,并使拇指指向导线运动的方向,这时四指所指的方向就是感应电流的方向。
(2)适用情况:导体切割磁感线产生感应电流。
(三)法拉第电磁感应定律1、感应电动势(1)定义:在电磁感应现象中产生的电动势叫做感应电动势。
(2)产生条件:无论回路是否闭合,只要穿过回路的磁通量发生变化,回路中就会产生感应电动势。
2、法拉第电磁感应定律(1)内容:电路中感应电动势的大小,跟穿过这一电路的磁通量的变化率成正比。
(2)公式:E =nΔΦ/Δt(n 为线圈的匝数)。
(四)导体切割磁感线时的感应电动势1、导体垂直切割磁感线(1)公式:E = BLv(B、L、v 两两垂直)。
(2)当 v 是瞬时速度时,E 为瞬时感应电动势;当 v 是平均速度时,E 为平均感应电动势。
高考物理一轮复习 第9单元电磁感应第3讲 电磁感应定律的综合应用课件 新人教版

培力与阻力平衡时,金属框的速度最大.由E=2BL(v-vm),I=
E R
,2BIL=f,
解得vm=
4B2L2v 4B2 L2
fR
,C项正确.
【答案】C
知识建构
技能建构
3.(2011年江苏南通模拟)如图所示,在磁感强度为B的匀强磁场中,有 半径为r的光滑半圆形导体框架,OC为一能绕O在框架上滑动的导体 棒,OC之间连一个电阻R,导体框架与导体棒的电阻均不计,若要使 OC能以角速度ω匀速转动,则外力做功的功率是 ( )
知识建构
技能建构
(2)负电荷受到重力和电场力而静止, mg=Eq
E=
U MN d
mgd
所以UMN= q =0.1 V
R3两端电压与电容器两端电压相等,由欧姆定律得通过R3的电流
I=
U MN R3
=0.05
A
ab棒两端的电压为
Uab=UMN+I
R1R2 =0.4
R1 R2
V.
知识建构
技能建构
(3)由法拉第电磁感应定律得感应电动势为
平衡条件,即合外力为 零
加速度不为零的运动
牛顿第二定律或结合功 能关系
知识建构
技能建构
3.电磁感应中的动力学临界问题
(1)感应电流在磁场中受到安培力的作用,解决这类问题需要综合应 用电磁感应规律(法拉第电磁感应定律)及力学中的有关规律(牛顿 运动定律等)寻找运动过程中的临界状态,分析时要特别注意a=0、 速度v达最大值的特点.
知识建构
技能建构
1.解决这类问题的基本步骤是:
(1)用法拉第电磁感应定律和楞次定律确定电动势的大小和方向;
(2)画出等效电路,求出回路中电阻消耗电功率的表达式; (3)分析导体机械能的变化,用能量守恒关系得到机械功率的改变与 回路中电功率的改变所满足的方程.
高考物理一轮复习第九章电磁感应第3讲电磁感应规律的综合应用模拟试题新人教版选修3-2

第3讲电磁感应规律的综合应用高考·模拟·创新图9-3-131.(2015年高考·福建卷)如图9-3-13,由某种粗细均匀的总电阻为3R 的金属条制成的矩形线框abcd ,固定在水平面内且处于方向竖直向下的匀强磁场B 中.一接入电路电阻为R 的导体棒PQ ,在水平拉力作用下沿ab 、dc 以速度v 匀速滑动,滑动过程PQ 始终与ab 垂直,且与线框接触良好,不计摩擦.在PQ 从靠近ad 处向bc 滑动的过程中()A .PQ 中电流先增大后减小B .PQ 两端电压先减小后增大C .PQ 上拉力的功率先减小后增大D .线框消耗的电功率先减小后增大解析:PQ 棒垂直切割磁感线匀速运动,它相当于恒定电源.PQ 棒移动过程中,abcd 线棒移到PQ ,R13R -R13R+R =总R ,所以1R 左边线路电阻为PQ 框的等效电阻是变化的,设中间时,abcd 框的等效电阻最大,此刻PQ 棒电流最小,故PQ 中电流先减小后增大,A 项错误;PQ 两端电压U =E -IR ,因为电流先减小后增大,所以电压先增大后减小,B 项错误;PQ 棒到中间时,安培力最小,据P =Fv ,拉力的瞬时功率最小,C 项正确;当外电阻为R 时,故线圈消耗功率先大再小、再大再小,R 再减小到小于R 32增至R 功率最大,外电阻由小于D 错.答案:C为定值电阻,两金属圆环固定在同一0R 甲,14-3-9如图)山东卷·年高考(2015.2的电流0R 的正弦交流电源上,经二极管整流后,通过0T 绝缘平面内.左端连接在一周期为i 始终向左,其大小按图乙所示规律变化.规定内圆环a 端电势高于b 端时,a 、b 间的电压)(图象可能正确的是t —ab u 为正,下列ab u 图9-3-14时间内,通过大圆环的电流为顺时针逐渐增加,由楞次定律可00.25T 在第一个解析:判断内环内a 端电势高于b 端,因电流的变化率逐渐减小故内环的电动势逐渐减小;同理在时间内,通过大圆环的电流为顺时针逐渐减小,由楞次定律可判断内环内00.5T ~00.25T 第a 端电势低于b 端,因电流的变化率逐渐变大,故内环的电动势逐渐变大;故选项C 正确.答案:C3.(2015年高考·北京卷)如图9-3-15所示,足够长的平行光滑金属导轨水平放置,宽度L =0.4 m ,一端连接R =1 Ω的电阻.导轨所在空间存在竖直向下的匀强磁场,磁感应强度B =1 T .导体棒MN 放在导轨上,其长度恰好等于导轨间距,与导轨接触良好.导轨和导体棒的电阻均可忽略不计.在平行于导轨的拉力F 作用下,导体棒沿导轨向右匀速运动,速度v =5 m /s .求:图9-3-15(1)感应电动势E 和感应电流I ;的大小;F I 时间内,拉力的冲量s 0.1 在(2)(3)若将MN 换为电阻r =1 Ω的导体棒,其他条件不变,求导体棒两端的电压U.解析:(1)根据法拉第电磁感应定律可得,感应电动势E =BLv =1 T ×0.4 m ×5 m /s =2 V.A 2 =2 V 1 Ω=E R =I 感应电流,N 8 0.=BIL =安F 导体棒所受安培力大小(2)N0.8 =安F =F 导体棒在匀速运动过程中,拉力大小等于安培力,所以导体棒所受拉力.s ·N 0.08 =s ×0.1 N 0.8 =Ft =F I 拉力的冲量(3)由闭合电路欧姆定律可得,电路中电流,A 1 =E R +r =I ′由欧姆定律可得,导体棒两端电压U =I ′R =1 V .答案:(1)2 V 2 A (2)0.08 N ·s (3)1 V。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016届高三物理一轮复习第9章第3讲电磁感应的综合问题练习1.(2013浙江理综,15,6分)磁卡的磁条中有用于存储信息的磁极方向不同的磁化区,刷卡器中有检测线圈。
当以速度v0刷卡时,在线圈中产生感应电动势,其E-t关系如图所示。
如果只将刷卡速度改为,线圈中的E-t 关系图可能是( )2.(2013山东理综,18,5分)将一段导线绕成图甲所示的闭合回路,并固定在水平面(纸面)内。
回路的ab边置于垂直纸面向里的匀强磁场Ⅰ中。
回路的圆环区域内有垂直纸面的磁场Ⅱ,以向里为磁场Ⅱ的正方向,其磁感应强度B随时间t变化的图像如图乙所示。
用F表示ab边受到的安培力,以水平向右为F的正方向,能正确反映F随时间t变化的图像是( )3.(2013安徽理综,16,6分)如图所示,足够长平行金属导轨倾斜放置,倾角为37°,宽度为0.5 m,电阻忽略不计,其上端接一小灯泡,电阻为1 Ω。
一导体棒MN垂直于导轨放置,质量为0.2 kg,接入电路的电阻为1 Ω,两端与导轨接触良好,与导轨间的动摩擦因数为0.5。
在导轨间存在着垂直于导轨平面的匀强磁场,磁感应强度为0.8 T。
将导体棒MN由静止释放,运动一段时间后,小灯泡稳定发光,此后导体棒MN的运动速度以及小灯泡消耗的电功率分别为(重力加速度g取10 m/s2,sin 37°=0.6)()A.2.5 m/s 1 WB.5 m/s 1 WC.7.5 m/s 9 WD.15 m/s 9 W4.(2013天津理综,3,6分)如图所示,纸面内有一矩形导体闭合线框abcd,ab边长大于bc边长,置于垂直纸面向里、边界为MN的匀强磁场外,线框两次匀速地完全进入磁场,两次速度大小相同,方向均垂直于MN。
第一次ab边平行MN进入磁场,线框上产生的热量为Q1,通过线框导体横截面的电荷量为q1;第二次bc边平行MN进入磁场,线框上产生的热量为Q2,通过线框导体横截面的电荷量为q2,则( )A.Q1>Q2,q1=q2B.Q1>Q2,q1>q2C.Q1=Q2,q1=q2D.Q1=Q2,q1>q25.(2013课标Ⅰ,17,6分)如图,在水平面(纸面)内有三根相同的均匀金属棒ab、ac和MN,其中ab、ac在a 点接触,构成“V”字形导轨。
空间存在垂直于纸面的均匀磁场。
用力使MN向右匀速运动,从图示位置开始计时,运动中MN始终与∠bac的平分线垂直且和导轨保持良好接触。
下列关于回路中电流i与时间t的关系图线,可能正确的是( )6.(2012福建理综,18,6分)如图甲,一圆形闭合铜环由高处从静止开始下落,穿过一根竖直悬挂的条形磁铁,铜环的中心轴线与条形磁铁的中轴线始终保持重合。
若取磁铁中心O为坐标原点,建立竖直向下为正方向的x轴,则图乙中最能正确反映环中感应电流i随环心位置坐标x变化的关系图像是( )7.(2014安徽理综,23,16分)如图1所示,匀强磁场的磁感应强度B为0.5 T,其方向垂直于倾角θ为30°的斜面向上。
绝缘斜面上固定有“”形状的光滑金属导轨MPN(电阻忽略不计),MP和NP长度均为2.5 m,MN 连线水平,长为3 m。
以MN中点O为原点、OP为x轴建立一维坐标系Ox。
一根粗细均匀的金属杆CD,长度d 为3 m、质量m为1 kg、电阻R为0.3 Ω,在拉力F的作用下,从MN处以恒定速度v=1 m/s在导轨上沿x轴正向运动(金属杆与导轨接触良好)。
g取10 m/s2。
(1)求金属杆CD运动过程中产生的感应电动势E及运动到x=0.8 m处电势差U CD;(2)推导金属杆CD从MN处运动到P点过程中拉力F与位置坐标x的关系式,并在图2中画出F-x关系图像;(3)求金属杆CD从MN处运动到P点的全过程产生的焦耳热。
8.(2014天津理综,11,18分)如图所示,两根足够长的平行金属导轨固定在倾角θ=30°的斜面上,导轨电阻不计,间距L=0.4 m。
导轨所在空间被分成区域Ⅰ和Ⅱ,两区域的边界与斜面的交线为MN,Ⅰ中的匀强磁场方向垂直斜面向下,Ⅱ中的匀强磁场方向垂直斜面向上,两磁场的磁感应强度大小均为B=0.5 T。
在区域Ⅰ中,将质量m1=0.1 kg,电阻R1=0.1 Ω的金属条ab放在导轨上,ab刚好不下滑。
然后,在区域Ⅱ中将质量m2=0.4 kg,电阻R2=0.1 Ω的光滑导体棒cd置于导轨上,由静止开始下滑。
cd在滑动过程中始终处于区域Ⅱ的磁场中,ab、cd始终与导轨垂直且两端与导轨保持良好接触,取g=10 m/s2。
问(1)cd下滑的过程中,ab中的电流方向;(2)ab刚要向上滑动时,cd的速度v多大;(3)从cd开始下滑到ab刚要向上滑动的过程中,cd滑动的距离x=3.8 m,此过程中ab上产生的热量Q是多少。
9.(2014福建理综,22,20分)如图,某一新型发电装置的发电管是横截面为矩形的水平管道,管道的长为L、宽为d、高为h,上下两面是绝缘板,前后两侧面M、N是电阻可忽略的导体板,两导体板与开关S和定值电阻R相连。
整个管道置于磁感应强度大小为B,方向沿z轴正方向的匀强磁场中。
管道内始终充满电阻率为ρ的导电液体(有大量的正、负离子),且开关闭合前后,液体在管道进、出口两端压强差的作用下,均以恒定速率v0沿x轴正向流动,液体所受的摩擦阻力不变。
(1)求开关闭合前,M、N两板间的电势差大小U0;(2)求开关闭合前后,管道两端压强差的变化Δp;(3)调整矩形管道的宽和高,但保持其他量和矩形管道的横截面积S=dh不变,求电阻R可获得的最大功率P m及相应的宽高比d/h的值。
10.(2012浙江理综,25,22分)为了提高自行车夜间行驶的安全性,小明同学设计了一种“闪烁”装置。
如图所示,自行车后轮由半径r1=5.0×10-2 m的金属内圈、半径r2=0.40 m的金属外圈和绝缘辐条构成。
后轮的内、外圈之间等间隔地接有4根金属条,每根金属条的中间均串联有一电阻值为R的小灯泡。
在支架上装有磁铁,形成了磁感应强度B=0.10 T、方向垂直纸面向外的“扇形”匀强磁场,其内半径为r1、外半径为r2、张角θ=。
后轮以角速度ω=2π rad/s相对于转轴转动。
若不计其他电阻,忽略磁场的边缘效应。
(1)当金属条ab进入“扇形”磁场时,求感应电动势E,并指出ab上的电流方向;(2)当金属条ab进入“扇形”磁场时,画出“闪烁”装置的电路图;(3)从金属条ab进入“扇形”磁场时开始,经计算画出轮子转一圈过程中,内圈与外圈之间电势差U ab随时间t变化的U ab-t图像;(4)若选择的是“1.5 V、0.3 A”的小灯泡,该“闪烁”装置能否正常工作?有同学提出,通过改变磁感应强度B、后轮外圈半径r2、角速度ω和张角θ等物理量的大小,优化前同学的设计方案,请给出你的评价。
1.D 刷卡速度改为原来一半时,磁卡通过检测线圈的时间即有感应电动势产生的时间变为原来的2倍,可知A、B错误;由E=BLv知当只减小v时,磁卡与检测线圈在相同的相对位置处产生的感应电动势也减小,故C错误、D正确。
2.B 由图乙知,0~内,=-k(常量),~T内,=k(常量),由法拉第电磁感应定律及楞次定律知,回路中产生的电流为方波形交流电。
0~内电流由b到a,由F=BIL和左手定则,知安培力F恒定且水平向左,为负方向;同理~T 内,F恒定且水平向右,为正方向,故B正确,A、C、D错误。
3.B 小灯泡稳定发光说明棒做匀速直线运动。
此时:F安=对棒满足:mg sin θ-μmg cos θ-=0因为R灯=R棒,则:P灯=P棒再依据功能关系:mg sin θ·v-μmg cos θ·v=P灯+P棒联立解得v=5 m/s,P灯=1 W,所以B项正确。
4.A 设线框边长分别为l1、l2,线框中产生的热量Q=I2Rt=()2·R·==l1,由于l ab>l bc,所以Q1>Q2。
通过线框导体横截面的电荷量q=·Δt=·Δt==,故q1=q2,A选项正确。
5.A 设金属棒MN匀速运动的速度为v,t时刻导轨内切割磁感线的有效长度L=2vt tan θ设导轨单位长度的电阻为R0,则组成闭合回路的总电阻R=2(+vt tan θ)R0=2vtR0(+tan θ)电动势E=BLv=2Bv2t tan θi==为恒量故A正确,B、C、D错误。
6.B 条形磁铁的磁感线分布示意图如图所示。
铜环由静止开始下落过程中磁通量的变化率是非均匀变化的,故环中产生的感应电动势、环中的感应电流也是非均匀变化的,A错误。
在关于O点对称的位置上磁场分布对称,但环的速率是增大的,则环在O点下方的电流最大值大于在O点上方电流的最大值,故C错误。
由于磁通量在O点上方是向上增大而在O点下方是向上减小的,故环经过O点时电流方向发生改变,D错误。
可知B 选项正确。
7.答案见解析解析(1)金属杆CD在匀速运动中产生的感应电动势E=Blv(l=d),解得E=1.5 V (D点电势高)当x=0.8 m时,金属杆在导轨间的电势差为零。
设此时杆在导轨外的长度为l外,则l外=d-d、OP=,得l外=1.2 m由楞次定律判断D点电势高,故CD两端电势差U CD=-Bl外v,即U CD=-0.6 V(2)杆在导轨间的长度l与位置x关系是l=d=3-x对应的电阻R l为R l=R,电流I=杆受的安培力F安=BIl=7.5-3.75x根据平衡条件得F=F安+mg sin θF=12.5-3.75x(0≤x≤2 m)画出的F-x图像如图所示。
(3)外力F所做的功W F等于F-x图线下所围的面积,即W F=×2 J=17.5 J而杆的重力势能增加量ΔE p=mg sin θ故全过程产生的焦耳热Q=W F-ΔE p=7.5 J8.答案(1)由a流向b (2)5 m/s (3)1.3 J解析(1)由a流向b。
(2)开始放置ab刚好不下滑时,ab所受摩擦力为最大静摩擦力,设其为F max,有F max=m1g sin θ①设ab刚好要上滑时,cd棒的感应电动势为E,由法拉第电磁感应定律有E=BLv②设电路中的感应电流为I,由闭合电路欧姆定律有I=③设ab所受安培力为F安,有F安=ILB④此时ab受到的最大静摩擦力方向沿斜面向下,由平衡条件有F安=m1g sin θ+F max⑤综合①②③④⑤式,代入数据解得v=5 m/s⑥(3)设cd棒的运动过程中电路中产生的总热量为Q总,由能量守恒有m2gx sin θ=Q总+m2v2⑦又Q=Q总⑧解得Q=1.3 J⑨9.答案(1)Bdv 0(2) (3)解析(1)设带电离子所带的电量为q,当其所受的洛伦兹力与电场力平衡时,U0保持恒定,有qv0B=q①得U0=Bdv0②(2)设开关闭合前后,管道两端压强差分别为p1、p2,液体所受的摩擦阻力均为f,开关闭合后管道内液体受到安培力为F安,有p1hd=f③p2hd=f+F安④F安=BId⑤根据欧姆定律,有I=⑥两导体板间液体的电阻r=ρ⑦由②③④⑤⑥⑦式得Δp=⑧(3)电阻R获得的功率为P=I2R⑨P=R⑩当=时电阻R获得的最大功率P m=10.答案见解析解析(1)金属条ab在磁场中切割磁感线时,所构成的回路的磁通量变化。
