上海初中数学一模冲刺讲义(二)教师版

合集下载

中考数学模拟冲刺卷2 华东师大版

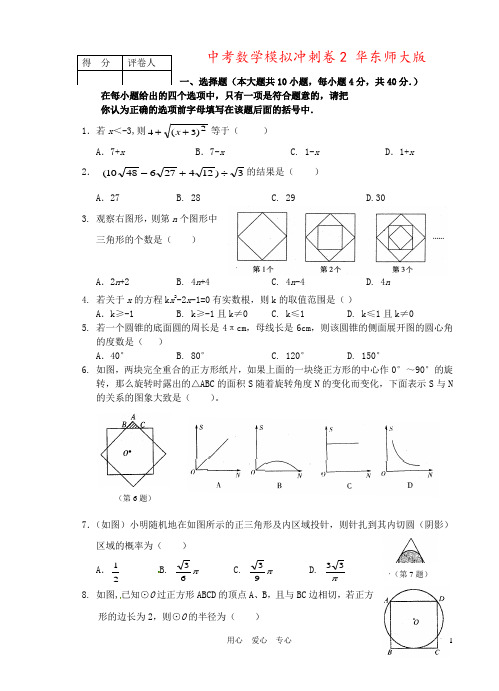
中考数学模拟冲刺卷2 华东师大版一、选择题（本大题共10小题，每小题4分，共40分．）在每小题给出的四个选项中，只有一项是符合题意的，请把你认为正确的选项前字母填写在该题后面的括号中．1．若x＜-3,则2)3(4++x等于（）A．7+x B．7-x C. 1-x D．1+x2．3)1242764810(÷+-的结果是（）A．27 B. 28 C. 29 D.303. 观察右图形，则第n个图形中三角形的个数是（）A．2n+2 B. 4n+4 C. 4n-4 D. 4n4. 若关于x的方程k x2-2x-1=0有实数根，则k的取值范围是（）A．k≥-1 B. k≥-1且k≠0 C. k≤1 D. k≤1且k≠05. 若一个圆锥的底面圆的周长是4πcm，母线长是6cm，则该圆锥的侧面展开图的圆心角的度数是（）A．40° B. 80° C. 120° D. 150°6. 如图，两块完全重合的正方形纸片，如果上面的一块绕正方形的中心作0°～90°的旋转，那么旋转时露出的△ABC的面积S随着旋转角度N的变化而变化，下面表示S与N 的关系的图象大致是（）。

7．（如图）小明随机地在如图所示的正三角形及内区域投针，则针扎到其内切圆（阴影）区域的概率为（）A．21 B.π63 C.π93 D.π338. 如图,已知⊙O过正方形ABCD的顶点A、B，且与BC边相切，若正方形的边长为2，则⊙O的半径为（）得分评卷人（第7题）（第6题）A ．34B. 45C.35 D. 1 9. 下列命题中是真命题的有（）①两个端点能够重合的弧是等弧 ②圆的任意一条弦把圆分成优弧和劣弧两部分 ③长度相等的弧是等弧 ④半径相等的圆是等圆 ⑤直径是最大的弦 ⑥半圆所对的弦是直径 A ．3个B. 4个C. 5个D. 6个10. 如图⊙M 与x 轴相切于原点，平行于Y 轴的直线交圆于P 、Q 两点，P点在Q 点的下方，若P 点的坐标是（2，1），则圆心M 的坐标是（） A ．（0，3） B. (0, 25) C. （0，2）D.（0，23）二、填空题（本大题共6小题，每小题5分，共30分）11．函数212-+=x x y 有意义，则x 范围是_________.12．1999)2010)(2008(=--a a ，则=-+-2)2010(2)2008(a a __________. 13. ⊙O 的半径为7cm ，⊙O 内有一点P ，OP=5cm ，则经过P 点所有弦中，弦长为整数的有______条。

(上海)2020年中考数学学科一模冲刺精品课

考知
经典题型回顾
填空压轴题（第 18 题）题型一：翻折问题；
性质：翻折前后两个图形全等：边相等，角相等折痕垂直平分对应点的连线学会找等腰
画图：已知折痕：过对应点做折痕的垂线并延长已知对应点：做对应点连线的垂直平分线
经典题型回顾
答案： 39
5
经典题型回顾
填空压轴题（第 18 题）题型二：旋转问题
如果△MBF 与△AOM 相似，求所有符合条件的抛物线 C2 的表达式．
经典题型回顾
几何压轴题常考题型
动点直角三角形存在性讨论
动点等腰三角形存在性讨论动点相似三角形存在性讨论动点面积问题及其他类型
经典题型回顾
（2019 年黄浦 25 题）
在 ABC 中，ACB 90 ，BC 3 ，AC 4 ，点 O 是 AB 的中点，点 D 是边 AC 上一点，DE BD ，交 BC 的延长线于点 E ，OD DF ，交 BC 边于点 F ，过点 E 作 EG AB ，垂足为点 G ，EG 分别交 BD 、 DF 、 DC 于点 M 、 N 、 H .
一模重要性
【三】一模常见问题解答
一模还有一个多月，应该如何准备？
最后时刻还是需要根据版块来查缺补漏，特别是二次函数和相似三角形。通过有目标、有针对的复习与巩固，才能在有限定的时间内更好的提高自己。最简单的复习方式是将历年一模试卷提前做一遍，看一下自己哪一块错误最多，进行专项复习。这样才能更加具有针对性。
（1）求证： DE NE ； DB OB
（2）设 CD x ， NE y ，求 y 关于 x 的函数关系式及其定义域；
（3）当 DEF 是以 DE 为腰的等腰三角形时，求线段 CD 的长.

(完整版)初中数学辅导讲义沪教版初二C专题(一次函数的图像与性质1星)

$、主题-------- 一次函数的图像与性质（★）1. 能够理解一次函数的概念及一次函数与正比例函数的关系；2. 会判断一次函数经过的象限和图像的增减；3. 能够求出平移后的函数图像；4. 会求一次函数与坐标轴的交点及两个一次函数的交点坐标；5. 理解一次函数与一次不等式之间的关系。

知识结构函数图象性质经过象限变化规律y=kx+b（k、b为常数，且k工0）k > 0b > 0b=0b v 0 k v 0b > 0b=0b v 01. 本部分建议时长5分钟.2. 请学生先试着自行补全上图，发现学生有遗忘时教师帮助学生完成1. 本部分建议时长20分钟.2. 进行例题讲解时，教师宜先请学生试着自行解答.若学生能正确解答，则不必做过多的讲解；若学生不能正确解答，教师应对相关概念、公式进行进一步辨析后再讲解例题3. 在每一道例题之后设置了变式训练题，应在例题讲解后鼓励学生独立完成，以判断学生是否真正掌握了相关考点和题型.4. 教师应正确处理好例题与变式训练题之间的关系，宜采用讲练结合的方式，切不可将所有例题都讲完后再让学生做变式训练题•(★) (1)已知y2(m 3)x m 2m 2是正比例函数，则m= .(★) (2)当m=时，函数：y (m 3)x2m 1 4x 5(x 0)是一个一次函数答案：-1，,0“典例精讲”这一部分的教学，可采用下面的策略: 次函数的概念(1) 一次函数：形如y kx b(k,b为常数,且k 0)的函数叫做一次函数;(2) 正比例函数：形如y kx(k 0,k为常数)的函数叫做正比例函数；(3) 正比例函数与一次函数的关系：正比例函数是一次函数的特殊情形我来试一试2(★) (1)若函数y=( a+ 1) x a a1为正比例函数,则a的值为A. -1B.OC.1D.-1(★) (2)在一次函数y (m 3)x m 1 x 3,若x 0,则m的取值为解答：1.B; 2.m=2例题2(★) ( 1).函数y=-x-1的图像不经过( )象限.A.第一 B .第二 C .第三 D .第四2(★) ( 2)、正比例函数y= -—x中，y随着x的增大而。

2023年上海市15区中考一模数学试题知识点汇编相似图形的相关概念含详解

2023年上海市15区中考数学一模汇编专题03相似图形的相关概念（60题）一．选择题（共24小题）1．（2022秋•徐汇区校级期末）如图，已知a∥b∥c，直线m分别交直线a、b、c于点A、B、C，直线n分别交直线a、b、c于点D、E、F，若＝，则的值是（）A．B．C．D．12．（2022秋•徐汇区期末）如果把Rt△ABC的三边长度都扩大2倍，那么锐角A的四个三角比的值（）A．都扩大到原来的2倍B．都缩小到原来的C．都没有变化D．都不能确定3．（2022秋•闵行区期末）如图，已知在Rt△ABC中，∠ACB＝90°，∠B＝β，CD⊥AB，垂足为点D，那么下列线段的比值不一定等于sinβ的是（）A．B．C．D．4．（2022秋•嘉定区校级期末）如果点H、G分别在△DEF中的边DE和DF上，那么不能判定HG∥EF的比例式是（）A．DH：EH＝DG：GF B．HG：EF＝DH：DEC．EH：DE＝GF：DF D．DE：DF＝DH：DG5．（2022秋•浦东新区校级期末）如果两个相似三角形的面积比是1：4，那么它们的周长比是（）A．1：16B．1：4C．1：6D．1：26．（2022秋•浦东新区校级期末）如图，在△ABC中，点D、E分别在边AB、AC上，如果DE∥BC，且∠DCE＝∠B，那么下列说法中，错误的是（）A．△ADE∽△ABC B．△ADE∽△ACD C．△ADE∽△DCB D．△DEC∽△CDB7．（2022秋•徐汇区期末）如图，在△ABC中，DE∥FG∥BC，AD：AF：AB＝1：2：5，则S△ADE：S四边形DEGF：S＝（）四边形FGCBA．1：2：5B．1：4：25C．1：3：25D．1：3：218．（2022秋•青浦区校级期末）如图，DE∥AB，如果CE：AE＝1：2，DE＝3，那么AB等于（）A．6B．9C．12D．139．（2022秋•青浦区校级期末）如图，在△ABC中，点D在边BC上，点G在线段AD上，GE∥BD，且交AB于点E，GF∥AC，且交CD于点F，则下列结论一定正确的是（）A．＝B．＝C．＝D．＝10．（2022秋•黄浦区期末）如图，梯形ABCD中，AD∥BC，点E、F分别在腰AB、CD上，且EF∥BC，下列比例成立的是（）A．＝B．＝C．＝D．＝11．（2022秋•徐汇区校级期末）如图，已知在Rt△ABC中，∠ACB＝90°，CD⊥AB于D，则下列结论错误的是（）A．CD•AB＝AC•BC B．AC2＝AD•ABC．BC2＝BD•AB D．AC•CD＝AB•BC12．（2022秋•杨浦区校级期末）如图，已知AB∥CD∥EF，AD：AF＝3：5，BE＝24，那么BC的长等于（）A．4B．C．D．813．（2022秋•青浦区校级期末）在梯形ABCD中，AD∥BC，对角线AC与BD相交于点O，下列说法中，错误的是（）A．S△AOB＝S△DOC B．＝C．＝D．＝14．（2022秋•青浦区校级期末）如图，已知在Rt△ABC中，∠C＝90°，点G是△ABC的重心，GE⊥AC，垂足为E，如果CB＝10，则线段GE的长为（）A．B．C．D．15．（2022秋•浦东新区期末）如图，DF∥AC，DE∥BC，下列各式中正确的是（）A．B．C．D．16．（2022秋•青浦区校级期末）下列图形中，一定相似的是（）A．两个正方形B．两个菱形C．两个直角三角形D．两个等腰三角形17．（2022秋•徐汇区期末）已知点P、点Q是线段AB的两个黄金分割点，且AB＝10，那么PQ的长为（）A．5（3﹣）B．10（﹣2）C．5（﹣1）D．5（+1）18．（2022秋•徐汇区期末）如图，正方形ABCD与△EFG在方格纸中，正方形和三角形的顶点都在格点上，那么与△EFG相似的是（）A．以点E、F、A为顶点的三角形B．以点E、F、B为顶点的三角形C．以点E、F、C为顶点的三角形D．以点E、F、D为顶点的三角形19．（2022秋•闵行区期末）如图，某零件的外径为10cm，用一个交叉卡钳（两条尺长AC和BD相等）可测量零件的内孔直径AB．如果＝＝3，且量得CD＝4cm，则零件的厚度x为（）A．2cm B．1.5cm C．0.5cm D．1cm20．（2022秋•徐汇区期末）在△ABC中，点D、E分别在边BA、CA的延长线上，下列比例式中能判定DE∥BC 的为（）A．＝B．＝C．＝D．＝21．（2022秋•杨浦区期末）如图，在△ABC中，点D、E分别在AB和AC边上且DE∥BC，点M为BC边上一点（不与点B、C重合），联结AM交DE于点N，下列比例式一定成立的是（）A．＝B．＝C．＝D．＝22．（2022秋•静安区期末）如图，已知△ABC与△DEF，下列条件一定能推得它们相似的是（）A．∠A＝∠D，∠B＝∠E B．∠A＝∠D且C．∠A＝∠B，∠D＝∠E D．∠A＝∠E且23．（2022秋•静安区期末）如图，在△ABC中，中线AD与中线BE相交于点G，联结DE．下列结论成立的是（）A．B．C．D．24．（2022秋•黄浦区校级期末）下列说法中，正确的是（）A．两个矩形必相似B．两个含45°角的等腰三角形必相似C．两个菱形必相似D．两个含45°角的直角三角形必相似二．填空题（共36小题）25．（2022秋•徐汇区期末）在△ABC中，点D、E分别在边AB和BC上，AD＝2，DB＝3，BC＝10，要使DE∥AC，那么BE必须等于．26．（2022秋•青浦区校级期末）已知线段MN的长是10cm，点P是线段MN的黄金分割点，则较长线段MP的长是cm．27．（2022秋•浦东新区期末）如图，已知AD∥BE∥CF．如果AB＝4.8，DE＝3.6，EF＝1.2，那么AC的长是．28．（2022秋•徐汇区期末）如图，已知AD∥EB∥FC，AB＝4，EF＝2，则BC⋅DE＝．29．（2022秋•青浦区校级期末）已知线段AB＝2，P是AB的黄金分割点，且AP＞BP，那么AP＝．30．（2022秋•杨浦区期末）已知线段AB＝8cm，点C在线段AB上，且AC2＝BC•AB，那么线段AC的长cm．31．（2022秋•静安区期末）已知△ABC∽△A1B1C1∽△A2B2C2，△ABC与△A1B1C1的相似比为，△ABC与△A2B2C2的相似比为，那么△A1B1C1与△A2B2C2的相似比为．32．（2022秋•黄浦区校级期末）Rt△ABC两直角边之比为3：4，若△DEF与△ABC相似，△DEF最长边为20，则△DEF面积为．33．（2022秋•嘉定区校级期末）已知点P是线段AB的一个黄金分割点，且AB＝4cm，AP＞BP，那么AP＝cm．34．（2022秋•嘉定区校级期末）如果△ABC∽△DEF，且△ABC的三边长分别为3、4、5，△DEF的最短边长为6，那么△DEF的周长等于．35．（2022秋•徐汇区校级期末）若P是线段AB的黄金分割点，且AP＞BP，AP＝﹣1，则AB＝．36．（2022秋•浦东新区期末）在△ABC中，∠A＝2∠B，如果AC＝4，AB＝5，那么BC的长是．37．（2022秋•金山区校级期末）如果两个相似三角形对应高的比为3：4，那么这两个三角形的面积比为．38．（2022秋•闵行区期末）如果两个相似三角形的相似比为2：3，那么这两个相似三角形的面积比为．39．（2022秋•闵行区期末）若点P是线段AB的黄金分割点，且AP＞BP，AB＝2，则AP＝．（保留根号）40．（2022秋•闵行区期末）已知D、E分别是△ABC的边AB、AC上的点，若要使△ABC与△ADE相似，则只需添加一个条件：即可（只需填写一个）．41．（2022秋•徐汇区期末）已知线段AB＝10，P是线段AB的黄金分割点（AP＞PB），则AP＝．42．（2022秋•青浦区校级期末）如果两个相似三角形的相似比为1：3，那么它们的周长比为．43．（2022秋•黄浦区校级期末）已知线段MN的长为4，点P是线段MN的黄金分割点，那么较长线段MP的长是．44．（2022秋•黄浦区校级期末）如图，AB∥CD∥EF，如果AC＝2，CE＝3，BD＝1.5，那么BF的长是．45．（2022秋•黄浦区校级期末）如果两个相似三角形对应边上的中线之比为4：9，那么这两个三角形的周长之比为．46．（2022秋•黄浦区校级期末）如图，已知△ABC是边长为2的等边三角形，正方形DEFG的顶点D、E分别在边AC、AB上，点F、G在边BC上，那么AD的长是．47．（2022秋•徐汇区校级期末）如图所示，△ABC中，DE∥BC，AB＝9，DB＝3，则△ADE与四边形DBCE的面积比是．48．（2022秋•杨浦区校级期末）已知点P是线段AB的黄金分割点（AP＞BP），如果，那么AB＝．49．（2022秋•杨浦区校级期末）如图，G是△ABC的重心，延长BG交AC于点D，延长CG交AB于点E，P、Q 分别是△BCE和△BCD的重心，BC长为6，则PQ的长为．50．（2022秋•青浦区校级期末）如图，已知直线l1、l2、l3分别交直线l4于点A、B、C，交直线l5于点D、E、F，且l1∥l2∥l3，AB＝6，BC＝3，DF＝12，则DE＝．51．（2022秋•青浦区校级期末）如图，在△ABC中，D是AB上一点，如果∠B＝∠ACD，AB＝6cm，AC＝4cm，＝45cm2，则△ACD的面积是cm2．若S△ABC52．（2022秋•浦东新区期末）已知点P是线段MN的黄金分割点，MP＞PN，如果MN＝8，那么PM的长是．53．（2022秋•浦东新区期末）两个相似三角形的对应边的中线之比是2：3，周长之和是20，那么这两个三角形中较小三角形的周长是．54．（2022秋•金山区校级期末）已知点P是线段AB上的黄金分割点，且AB＝2，AP＞BP，那么AP＝．55．（2022秋•徐汇区期末）如图，在△ABC中，∠ACB＝90°，E为BC上一点，过点E作DE⊥AB，垂足为点D，并交AC的延长线于点F，联结AE，如果AE＝6，CE＝2，的值为．56．（2022秋•浦东新区校级期末）如图，直线AD∥BE∥CF，，DE＝6，那么EF的值是．57．（2022秋•浦东新区校级期末）如图，已知DE∥BC，且DE经过△ABC的重心G，若BC＝6cm，那么DE等于cm．58．（2022秋•浦东新区期末）如果两个相似三角形的面积比是4：9，那么它们对应高的比是．59．（2022秋•浦东新区期末）在Rt△ABC中，∠A＝90°，已知AB＝1，AC＝2，AD是∠BAC的平分线，那么AD 的长是．60．（2022秋•青浦区校级期末）已知点G是△ABC的重心，AB＝AC＝5，BC＝8，那么AG＝．2023年上海市15区中考数学一模汇编专题03相似图形的相关概念（60题）一．选择题（共24小题）1．（2022秋•徐汇区校级期末）如图，已知a∥b∥c，直线m分别交直线a、b、c于点A、B、C，直线n分别交直线a、b、c于点D、E、F，若＝，则的值是（）A．B．C．D．1【分析】根据平行线分线段成比例定理即可得到结论．【解答】解：∵＝，∴＝，∵a∥b∥c，∴＝＝，故选：B．【点评】本题考查了平行线分线段成比例定理，熟练掌握此定理是解题的关键．2．（2022秋•徐汇区期末）如果把Rt△ABC的三边长度都扩大2倍，那么锐角A的四个三角比的值（）A．都扩大到原来的2倍B．都缩小到原来的C．都没有变化D．都不能确定【分析】根据三角形三边扩大相同的倍数，可得边的比不变，根据锐角三角函数的定义，可得答案．【解答】解：如果把Rt△ABC的三边长度都扩大2倍，锐角A不变，锐角三角函数值不变，故选：C．【点评】本题考查了锐角三角函数，注意锐角不变，锐角三角函数值不变．3．（2022秋•闵行区期末）如图，已知在Rt△ABC中，∠ACB＝90°，∠B＝β，CD⊥AB，垂足为点D，那么下列线段的比值不一定等于sinβ的是（）A．B．C．D．【分析】由锐角的正弦定义，即可判断．【解答】解：A、不一定等于sinβ，故A符合题意；B、△ABC是直角三角形，sinβ＝，正确，故B不符合题意；C、CD⊥AB，∠ACD+∠A＝∠B+∠A＝90°，∠ACD＝∠B，sinβ＝，正确，故C不符合题意；D、△BCD是直角三角形，sinβ＝，正确，故D不符合题意．故选：A．【点评】本题考查解直角三角形，关键是掌握锐角的正弦定义．4．（2022秋•嘉定区校级期末）如果点H、G分别在△DEF中的边DE和DF上，那么不能判定HG∥EF的比例式是（）A．DH：EH＝DG：GF B．HG：EF＝DH：DEC．EH：DE＝GF：DF D．DE：DF＝DH：DG【分析】根据平行线分线段成比例定理判断即可．【解答】解：A、当DH：EH＝DG：GF，即＝时，HG∥EF，本选项不符合题意；B、当HG：EF＝DH：DE，不能判定HG∥EF，本选项符合题意；C、当EH：DE＝GF：DF，即＝时，HG∥EF，本选项不符合题意；D、当DE：DF＝DH：DG，即＝时，HG∥EF，本选项不符合题意；故选：B．【点评】本题考查的是平行线分线段成比例定理成比例定理，灵活运用定理、找准对应关系是解题的关键．5．（2022秋•浦东新区校级期末）如果两个相似三角形的面积比是1：4，那么它们的周长比是（）A．1：16B．1：4C．1：6D．1：2【分析】根据相似三角形周长的比等于相似比，相似三角形面积的比等于相似比的平方解答即可．【解答】解：∵两个相似三角形的面积比是1：4，∴两个相似三角形的相似比是1：2，∴两个相似三角形的周长比是1：2，故选：D．【点评】本题考查的是相似三角形的性质，掌握相似三角形周长的比等于相似比，相似三角形面积的比等于相似比的平方是解题的关键．6．（2022秋•浦东新区校级期末）如图，在△ABC中，点D、E分别在边AB、AC上，如果DE∥BC，且∠DCE＝∠B，那么下列说法中，错误的是（）A．△ADE∽△ABC B．△ADE∽△ACD C．△ADE∽△DCB D．△DEC∽△CDB【分析】由相似三角形的判定方法得出A、B、D正确，C不正确；即可得出结论．【解答】解：∵DE∥BC，∴△ADE∽△ABC，∠BCD＝∠CDE，∠ADE＝∠B，∠AED＝∠ACB，∵∠DCE＝∠B，∴∠ADE＝∠DCE，又∵∠A＝∠A，∴△ADE∽△ACD；∵∠BCD＝∠CDE，∠DCE＝∠B，∴△DEC∽△CDB；∵∠B＝∠ADE，但是∠BCD＜∠AED，且∠BCD≠∠A，∴△ADE与△DCB不相似；正确的判断是A、B、D，错误的判断是C；故选：C．【点评】本题考查了相似三角形的判定方法；熟练掌握相似三角形的判定方法，由两角相等得出三角形相似是解决问题的关键．7．（2022秋•徐汇区期末）如图，在△ABC中，DE∥FG∥BC，AD：AF：AB＝1：2：5，则S△ADE：S四边形DEGF：S ＝（）四边形FGCBA．1：2：5B．1：4：25C．1：3：25D．1：3：21【分析】由DE∥FG∥BC，可得△ADE∽△AFG∽△ABC，又由AD：AF：AB＝1：2：5，利用相似三角形的面：S△AFG：S△ABC＝1：4：25，然后设△ADE的面积是a，则△AFG和△积比等于相似比的平方，即可求得S△ADEABC的面积分别是3a，21a，即可求两个梯形的面积，继而求得答案．【解答】解：∵DE∥FG∥BC，∴△ADE∽△AFG∽△ABC，∴AD：AF：AB＝1：2：5，：S△AFG：S△ABC＝1：4：25，∴S△ADE设△ADE的面积是a，则△AFG和△ABC的面积分别是4a，25a，＝S△AFG﹣S△ADE＝3a，S四边形FBCG＝S△ABC﹣S△AFG＝21a，则S四边形DFGE：S四边形DFGE：S四边形FBCG＝1：3：21．∴S△ADE故选：D．【点评】此题考查了相似三角形的判定与性质．此题难度适中，解题的关键是掌握相似三角形面积的比等于相似比的平方．8．（2022秋•青浦区校级期末）如图，DE∥AB，如果CE：AE＝1：2，DE＝3，那么AB等于（）A．6B．9C．12D．13【分析】证明△CED∽△CAB，根据相似三角形的性质列式计算即可．【解答】解：∵DE∥AB，∴△CED∽△CAB，∴＝，即＝，解得，AB＝9，故选：B．【点评】本题考查的是相似三角形的判定和性质，掌握相似三角形的判定定理和性质定理是解题的关键．9．（2022秋•青浦区校级期末）如图，在△ABC中，点D在边BC上，点G在线段AD上，GE∥BD，且交AB于点E，GF∥AC，且交CD于点F，则下列结论一定正确的是（）A．＝B．＝C．＝D．＝【分析】利用相似三角形的性质和平行线分线段成比例依次判断可求解．【解答】解：∵GE∥BD，∴，△AEG∽△ABD，∴，∵GF∥AC，∴，，△DGF∽△DAC，∴，∴，，，＝1，∴只有选项A符合题意，故选：A．【点评】本题考查了相似三角形的判定和性质，灵活运用相似三角形的性质是本题的关键．10．（2022秋•黄浦区期末）如图，梯形ABCD中，AD∥BC，点E、F分别在腰AB、CD上，且EF∥BC，下列比例成立的是（）A．＝B．＝C．＝D．＝【分析】由平行线分线段成比例的性质可直接求解．【解答】解：∵AB∥CB，EF∥BC，∴AB∥EF∥BC，∴，故选：D．【点评】本题考查了梯形的性质，平行线分线段成比例，掌握平行线分线段成比例的性质可求解．11．（2022秋•徐汇区校级期末）如图，已知在Rt△ABC中，∠ACB＝90°，CD⊥AB于D，则下列结论错误的是（）A．CD•AB＝AC•BC B．AC2＝AD•ABC．BC2＝BD•AB D．AC•CD＝AB•BC【分析】根据三角形的面积公式判断A、D，根据射影定理判断B、C．【解答】解：由三角形的面积公式可知，CD•AB＝AC•BC，A正确，不符合题意，D不正确，符合题意；∵Rt△ABC中，∠ACB＝90°，CD⊥AB，∴AC2＝AD•AB，BC2＝BD•AB，B、C正确，不符合题意；故选：D．【点评】本题考查的是射影定理、三角形的面积计算，掌握射影定理、三角形的面积公式是解题的关键．12．（2022秋•杨浦区校级期末）如图，已知AB∥CD∥EF，AD：AF＝3：5，BE＝24，那么BC的长等于（）A．4B．C．D．8【分析】根据平行线分线段成比例得到，即可求出BC．【解答】解：∵AB∥CD∥EF，∴，∵BE＝24，∴，解得：．故选：C．【点评】本题考查了平行线分线段成比例；熟练掌握三条平行线截两条直线，所得的对应线段成比例是本题的关键．13．（2022秋•青浦区校级期末）在梯形ABCD中，AD∥BC，对角线AC与BD相交于点O，下列说法中，错误的是（）A．S△AOB＝S△DOC B．＝C．＝D．＝＝S△DCB，则S△AOB＝S△DOC，于是可对A选项进行判断；根据平【分析】如图，利用三角形面积公式得到S△ABC行线分线段成比例定理得到＝，再利用三角形面积公式得到＝，于是可对B选项进行判断；证明△AOD∽△COB，利用相似三角形的性质可对C选项进行判断；利用两平行线的距离的定义得到点B到AD 的距离等于点A到BC的距离，然后根据三角形面积公式可对D选项进行判断．【解答】解：如图，∵AD∥BC，＝S△DCB，∴S△ABC+S△OBC＝S△OBC+S△DOC，即S△AOBS△AOB＝S△DOC，所以A选项的结论正确；∵AD∥BC，∴＝，∵＝，∴＝；所以B选项的结论正确；∵AD∥BC，∴△AOD∽△COB，∴＝（）2，所以C选项的结论错误；∵AD∥BC，∴点B到AD的距离等于点A到BC的距离，∴＝，所以D选项的结论正确；故选：C．【点评】本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形；可利用相似三角形的性质得到对应角相等，通过相似比进行几何计算．也考查了梯形和三角形面积公式．14．（2022秋•青浦区校级期末）如图，已知在Rt△ABC中，∠C＝90°，点G是△ABC的重心，GE⊥AC，垂足为E，如果CB＝10，则线段GE的长为（）A．B．C．D．【分析】因为点G是△ABC的重心，根据三角形的重心是三角形三条中线的交点以及重心的性质：重心到顶点的距离与重心到对边中点的距离之比是2：1，可知点D为BC的中点，，根据GE⊥AC，可得∠AEG＝90°，进而证得△AEG∽△ACD，从而得到，代入数值即可求解．【解答】解：如图，连接AG并延长交BC于点D．∵点G是△ABC的重心，∴点D为BC的中点，，∵CB＝10，∴，∵GE⊥AC，∴∠AEG＝90°，∵∠C＝90°，∴∠AEG＝∠C＝90°，∵∠EAG＝∠CAD（公共角），∴△AEG∽△ACD，∴，∵，∴，∴，∴．故选：D．【点评】本题考查了相似三角形的判定和性质，三角形的重心的定义及其性质，熟练运用三角形重心的性质是解题的关键．15．（2022秋•浦东新区期末）如图，DF∥AC，DE∥BC，下列各式中正确的是（）A．B．C．D．【分析】根据平行线分线段成比例定理逐个判定即可．【解答】解：A．∵DE∥BC，∴＝，∴＝，故本选项符合题意；B．∵DF∥AC，∴＝，故本选项不符合题意；C．∵DE∥BC，∴＝，∴＝，即＝，故本选项不符合题意；D．∵DE∥BC，DF∥AC，∴，，∴＝，故本选项不符合题意；故选：A．【点评】本题考查了平行线分线段成比例定理和比例的性质，能根据平行线分线段成比例定理得出正确的比例式是解此题的关键．16．（2022秋•青浦区校级期末）下列图形中，一定相似的是（）A．两个正方形B．两个菱形C．两个直角三角形D．两个等腰三角形【分析】根据相似形的对应边成比例，对应角相等，结合正方形，菱形，直角三角形，等腰三角形的性质与特点对各选项分析判断后利用排除法．【解答】解：A、两个正方形角都是直角一定相等，四条边都相等一定成比例，所以一定相似，故本选项正确；B、两个菱形的对应边成比例，角不一定相等，所以不一定相似，故本选项错误；C、两个直角三角形的边不一定成比例，角不一定相等，所以不一定相似，故本选项错误；D、两个等腰三角形的边不一定成比例，角不一定相等，所以不一定相似，故本选项错误．故选：A．【点评】本题主要考查了相似图形的定义，比较简单，要从边与角两方面考虑．17．（2022秋•徐汇区期末）已知点P、点Q是线段AB的两个黄金分割点，且AB＝10，那么PQ的长为（）A．5（3﹣）B．10（﹣2）C．5（﹣1）D．5（+1）【分析】先由黄金分割的比值求出BP＝AQ＝5（﹣1），再由PQ＝AQ+BP﹣AB进行计算即可．【解答】解：如图，∵点P、Q是线段AB的黄金分割点，AB＝10，∴BP＝AQ＝AB＝5（﹣1），∴PQ＝AQ+BP﹣AB＝10（﹣1）﹣10＝10（﹣2），故选：B．【点评】本题考查了黄金分割：把线段AB分成两条线段AC和BC（AC＞BC），且使AC是AB和BC的比例中项（即AB：AC＝AC：BC），叫做把线段AB黄金分割，点C叫做线段AB的黄金分割点，熟记黄金比是解题的关键．18．（2022秋•徐汇区期末）如图，正方形ABCD与△EFG在方格纸中，正方形和三角形的顶点都在格点上，那么与△EFG相似的是（）A．以点E、F、A为顶点的三角形B．以点E、F、B为顶点的三角形C．以点E、F、C为顶点的三角形D．以点E、F、D为顶点的三角形【分析】△EFG中∠EGF＝135°，利用两组对应边的比相等且夹角对应相等的两个三角形相似判断A、B、D；根据三组对应边的比相等的两个三角形相似判断C．【解答】解：由题意可得，△EFG中∠EGF＝135°，EG＝2，GF＝，EF＝．A、△EFA中，∠AEF＞135°，则△EFA与△EFG不相似，故本选项不符合题意；B、△EFB中，∠BEF＞135°，则△EFB与△EFG不相似，故本选项不符合题意；C、△EFC中，EF＝，CE＝，CF＝5，∵＝＝＝，∴△EFG∽△FCE，即△EFC与△EFG相似，故本选项符合题意；D、△EFD中，90°＜∠DEF＜135°，则△EFD与△EFG不相似，故本选项不符合题意；故选：C．【点评】本题考查了相似三角形的判定，掌握判定两个三角形相似的方法是解题的关键．19．（2022秋•闵行区期末）如图，某零件的外径为10cm，用一个交叉卡钳（两条尺长AC和BD相等）可测量零件的内孔直径AB．如果＝＝3，且量得CD＝4cm，则零件的厚度x为（）A．2cm B．1.5cm C．0.5cm D．1cm【分析】根据相似三角形的判定和性质，可以求得AB的长，再根据某零件的外径为10cm，即可求得x的值．【解答】解：∵＝＝3，∠COD＝∠AOB，∴△COD∽△AOB，∴AB：CD＝2，∵CD＝4cm．∴AB＝8cm．∵某零件的外径为10cm，∴零件的厚度x为：（10﹣8）÷2＝1（cm），故选：D．【点评】本题考查相似三角形的应用，解答本题的关键是求出AB的值．20．（2022秋•徐汇区期末）在△ABC中，点D、E分别在边BA、CA的延长线上，下列比例式中能判定DE∥BC 的为（）A．＝B．＝C．＝D．＝【分析】根据平行线分线段成比例定理、平行线的判定定理判断即可．【解答】解：如图：A、当时，不能判定DE∥BC，不符合题意；B、当时，不能判定DE∥BC，不符合题意；C、当，能判定DE∥BC，符合题意；D、当时，能判定DE∥BC，而当时，不能判定DE∥BC，不符合题意；故选：C．【点评】本题考查的是平行线分线段成比例定理、平行线的判定定理，掌握相关的判定定理是解题的关键．21．（2022秋•杨浦区期末）如图，在△ABC中，点D、E分别在AB和AC边上且DE∥BC，点M为BC边上一点（不与点B、C重合），联结AM交DE于点N，下列比例式一定成立的是（）A．＝B．＝C．＝D．＝【分析】根据相似三角形的判定和性质分析即可．【解答】解：∵DE∥BC，∴△ADN∽△ABM，△ANE∽△AMC，∴，，∴，即，故选：B．【点评】此题考查了相似三角形的判定和性质，牢记定理是解决此题的关键．22．（2022秋•静安区期末）如图，已知△ABC与△DEF，下列条件一定能推得它们相似的是（）A．∠A＝∠D，∠B＝∠E B．∠A＝∠D且C．∠A＝∠B，∠D＝∠E D．∠A＝∠E且【分析】根据相似三角形的判定方法一一判断即可．【解答】解：A、由∠A＝∠D，∠B＝∠E，可以判断两个三角形相似，本选项符合题意；B、由∠A＝∠D且，无法判断个三角形相似，本选项不符合题意；C、由∠A＝∠B，∠D＝∠E，无法判断个三角形相似，本选项不符合题意；D、由∠A＝∠E且＝，无法判断个三角形相似，本选项不符合题意；故选：A．【点评】本题考查相似三角形的判定，解题的关键是掌握相似三角形的判定方法，属于中考常考题型．23．（2022秋•静安区期末）如图，在△ABC中，中线AD与中线BE相交于点G，联结DE．下列结论成立的是（）A．B．C．D．【分析】由AD，BE是△ABC的中线，得到DE是△ABC的中位线，推出△DEG∽△ABG，△CDE∽△CBA，由相似三角形的性质即可解决问题．【解答】解：AD，BE是△ABC的中线，∴DE是△ABC的中位线，∴DE∥AB，DE＝AB，∴△DEG∽△ABG，∴DG：AG＝DE：AB＝1：2，BG：EG＝AB：DE，＝＝，∴DG＝AG，∵BG：EG＝AB：DE＝2：1，∴GB：BE＝2：3，：S△AEB＝2：3，∴S△AGB∵AE＝EC，＝S△ABC，∴S△AEB＝S△ABC，∴S△AGB∵△CDE∽△CBA，∴＝＝，＝S△ABC，∴S△CDE∴＝，结论成立的是＝，故选：C．【点评】本题考查相似三角形的判定和性质，关键是掌握相似三角形的性质．24．（2022秋•黄浦区校级期末）下列说法中，正确的是（）A．两个矩形必相似B．两个含45°角的等腰三角形必相似C．两个菱形必相似D．两个含45°角的直角三角形必相似【分析】直接利用相似图形的判定方法得出答案．【解答】解：A、两个矩形对应边不一定成比例，故此选项不符合题意；B、两个含45°角的等腰三角形，45°不一定是对应角，故不一定相似，故此选项不符合题意；C、两个菱形的对应角不一定相等，不一定相似，故此选项不符合题意；D、两个含45°角的直角三角形必相似，故此选项符合题意．故选：D．【点评】此题主要考查了相似图形，正确掌握相似图形的判定方法是解题关键．二．填空题（共36小题）25．（2022秋•徐汇区期末）在△ABC中，点D、E分别在边AB和BC上，AD＝2，DB＝3，BC＝10，要使DE∥AC，那么BE必须等于6．【分析】此题主要考查了平行线分线段成比例定理的逆定理，根据题意得出要使DE∥AC，必须即可得出BE的长．【解答】解：∵在△ABC中，点D、E分别在边AB和BC上，AD＝2，DB＝3，BC＝10，∴要使DE∥AC，∴，∴，解得：BE＝6．故答案为：6．【点评】此题主要考查了平行线分线段成比例定理的逆定理，根据题意得出要使DE∥AC，必须是解决问题的关键．26．（2022秋•青浦区校级期末）已知线段MN的长是10cm，点P是线段MN的黄金分割点，则较长线段MP的长是（）cm．【分析】根据黄金分割点的定义即可进行解答．【解答】解：∵点P是线段MN的黄金分割点，线段MN的长是10cm，线段MP为较长线段，∴MP＝10×＝（5﹣5）cm，故答案为：（5﹣5）．【点评】本题考查的是黄金比例，解题的关键清楚黄金比例概念以及黄金分割比为．27．（2022秋•浦东新区期末）如图，已知AD∥BE∥CF．如果AB＝4.8，DE＝3.6，EF＝1.2，那么AC的长是 6.4．【分析】根据三条平行线截两条直线，所得的对应线段成比例列出比例式解答即可．【解答】解：∵AD∥BE∥CF，∴，∵AB＝4.8，DE＝3.6，EF＝1.2，∴，解得BC＝1.6，∴AC＝AB+BC＝4.8+1.6＝6.4．故答案为：6.4．【点评】本题考查了平行线分线段成比例定理，解题的关键是掌握定理并灵活运用列出正确的比例式．28．（2022秋•徐汇区期末）如图，已知AD∥EB∥FC，AB＝4，EF＝2，则BC⋅DE＝8．【分析】根据三条平行线截两条直线，所得的对应线段成比例解答即可．【解答】解：∵AD∥EB∥FC，∴，∵AB＝4，EF＝2，∴BC•DE＝AB•EF＝4×2＝8．故答案为：8．【点评】本题考查了平行线分线段成比例，熟练掌握平行线分线段成比例定理是解题的关键．29．（2022秋•青浦区校级期末）已知线段AB＝2，P是AB的黄金分割点，且AP＞BP，那么AP＝﹣1．【分析】根据黄金分割的概念、黄金比值为计算．【解答】解：∵P是AB的黄金分割点，AP＞BP，∴AP＝AB＝﹣1，故答案为：．【点评】本题考查了黄金分割的概念，熟记黄金比值为是解题的关键．30．（2022秋•杨浦区期末）已知线段AB＝8cm，点C在线段AB上，且AC2＝BC•AB，那么线段AC的长4﹣4cm．【分析】根据黄金分割的定义得到点C是线段AB的黄金分割点，根据黄金比值计算得到答案．【解答】解：∵AC2＝BC•AB，∴点C是线段AB的黄金分割点，AC＞BC，∴AC＝AB＝×8＝（4﹣4）cm，故答案为：4﹣4．【点评】本题考查的是黄金分割的概念和性质，掌握黄金比值为是解题的关键．31．（2022秋•静安区期末）已知△ABC∽△A1B1C1∽△A2B2C2，△ABC与△A1B1C1的相似比为，△ABC与△A2B2C2的相似比为，那么△A1B1C1与△A2B2C2的相似比为．【分析】根据相似三角形的相似比写出对应边的比，计算出A1B1与A2B2的比值，也就是两三角形的相似比．【解答】解：∵△ABC与△A1B1C1的相似比为，△ABC与△A2B2C2的相似比为，∴AB：A1B1＝1：5，AB：A2B2＝2：3，设AB＝2x，则A1B1＝10x，A2B2＝3x，∴A1B1：A2B2＝10：3，∴△A1B1C1与△A2B2C2的相似比为．故答案为：．【点评】根据相似三角形的相似比写出对应边的比，计算出A1B1与A2B2的比值，也就是两三角形的相似比．32．（2022秋•黄浦区校级期末）Rt△ABC两直角边之比为3：4，若△DEF与△ABC相似，△DEF最长边为20，则△DEF面积为96．【分析】根据相似三角形的性质得到△DEF是直角三角形，且两直角边之比为3：4，根据勾股定理计算，得到答案．【解答】解：∵Rt△ABC的两直角边之比为3：4，△DEF与△ABC相似，∴△DEF是直角三角形，且两直角边之比为3：4，设一条直角边为3x，则另一条直角边为4x，由勾股定理得：（3x）2+（4x）2＝202，解得：x1＝4，x2＝﹣4（舍去），∴△DEF的一条直角边为12，则另一条直角边为16，＝×12×16＝96．∴S△DEF故答案为：96．【点评】本题考查的是相似三角形的性质、勾股定理，掌握相似三角形的对应边成比例是解题的关键．33．（2022秋•嘉定区校级期末）已知点P是线段AB的一个黄金分割点，且AB＝4cm，AP＞BP，那么AP＝（2﹣2）cm．【分析】根据黄金分割的定义，把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分割叫做黄金分割，他们的比值（）叫做黄金比．【解答】解：∵点P是线段AB上的一个黄金分割点，且AB＝4cm，AP＞BP，。

沪教版九年级一模冲刺复习讲义第3讲几何计算与证明(学生版)

考点分析年份 200820092010201120122013201420152016题型解答21 解答21 解答21 解答21 解答21 解答22 解答22 解答22 解答21 分值1010 101010 10101010内容圆背景下求线段梯形背景下求余弦值及线段长度圆背景下求三角比圆背景下求弦长锐角三角比、解直角三角形锐角三角比的应用解直角三角形解直角三角形的应用相似三角形的性质考点一：与锐角三角比相关的计算：（1）熟练的掌握三个特殊角的四个特殊值；（2）将锐角放在直角三角形中，通过作垂线构造．【例1】如图，在梯形ABCD 中，AD ∥BC ，AC ⊥AB ，AD =CD ，cosB =513，BC =26．求（1）cos ∠DAC 的值；（2）线段AD 的长．CBA图4D几何计算与证明模块一：几何计算【巩固】如图，在梯形ABCD 中，81260AD BC AB DC BC B ===∠=，，，∥°，联结AC ．（1）求tan ACB ∠的值；（2）若M N 、分别是AB DC 、的中点，联结MN ，求线段MN 的长．【例2】如图所示，在Rt ABC ，90ACB ∠=︒，D 是边AB 的中点，BE CD ⊥，垂足为E ，已知315cos 5AC A ==，，. （1）求线段CD 的长；（2）求sin DBE ∠的值．【巩固】如图，已知Rt △ABC 中，∠ACB ＝90°，CD 是斜边AB 上的中线，过点A 作 AE ⊥CD ，AE 分别与CD 、CB 相交于点H 、E ，AH ＝2CH ．（1）求sin B 的值；（2）如果CD ＝5，求BE 的值．ADCBED BC A A BCDEH AABQDPMN考点二：锐角三角比的应用将实际问题转化到直角三角形中，建立合适的直角三角形．【例3】某地下车库出口处“两段式栏杆”如图7-1所示，点A 是栏杆转动的支点，点E 是栏杆两段的连接点．当车辆经过时，栏杆AEF 升起后的位置如图7-2所示，其示意图如图7-3所示，其中AB ⊥BC ，EF ∥BC ，0143EAB ∠=， 1.2AB AE ==米，求当车辆经过时，栏杆EF 段距离地面的高度（即直线EF 上任意一点到直线BC 的距离）．（结果精确到0.1米，栏杆宽度忽略不计参考数据：sin 37° ≈ 0.60，cos 37° ≈ 0.80， tan 37° ≈ 0.75．）【巩固】如图，MN 表示一段笔直的高架道路，线段AB 表示高架道路旁的一排居民楼．已知点A 到MN 的距离为15米，BA 的延长线与MN 相交于点D ，且∠BDN ＝30°，假设汽车在高速道路上行驶时，周围39米以内会受到噪音的影响．（1）过点A 作MN 的垂线，垂足为点H ．如果汽车沿着从M 到N 的方向在MN 上行驶，当汽车到达点P 处时，噪音开始影响这一排的居民楼，那么此时汽车与点H 的距离为多少米?（2）降低噪音的一种方法是在高架道路旁安装隔音板．当汽车行驶到点Q 时，它与这一排居民楼的距离QC 为39米，那么对于这一排居民楼，高架道路旁安装的隔音板至少需要多少米长?(精确到1米) (参考数据：3≈1.7)．图7-1图7-2图7-3AEFAE FAE FBC考点三：圆内相关的计算圆内常做的两种辅助线：1、连半径，构造等腰或直角三角形；2、做垂线，根据垂径定理解直角三角形．【例4】如图，点C、D分别在扇形AOB的半径OA、OB的延长线上，且OA＝3，AC＝2，CD平行于AB，并与弧AB相交于点M、N．（1）求线段OD的长；（2）若1tan2C∠=，求弦MN 的长．【例5】机器人“海宝”在某圆形区域表演“按指令行走”，如图5所示，“海宝”从圆心O出发，先沿北偏西67.4°方向行走13米至点A处，再沿正南方向行走14米至点B处，最后沿正东方向行走至点C处，点B、C都在圆O上.（1）求弦BC的长；（2）求圆O的半径长．（本题参考数据：sin 67.4°=1213，cos 67.4° = 513，tan 67.4° =125）AB COSN67.4°北南COABDM N图5【巩固】已知：如图，在ABC∆中，3tan ,14445ABCA AB∠=︒==，；（1）求：ABC∆的面积；（2）若以C为圆心的圆C与直线AB相切，以A为圆心的圆A与圆C相切，试求圆A的半径．年份200820092010201120122013201420152016题型解答23解答23解答23解答23解答23解答23解答23解答23解答23分值121212121212121212内容判定特殊的四边形开放性求边相等（四边形）菱形背景证明位置关系梯形背景下特殊的四边形菱形背景下判定特殊的四边形平行四边形的判定及性质四边形相似三角形四边形相似三角形圆、平行四边形的判定模块二：几何证明考点四：三角形背景下相关证明两种证明方向：1、通过证明全等，寻找边与角的关系；2、通过相似，证明边、角之间的关系．【例6】在△ABC 中，点D 在边AC 上，DB =BC ，点E 是CD 的中点，点F 是AB 的中点．（1）求证：EF =12AB ；（2）过点A 作AG ∥EF ，交BE 的延长线于点G ，求证：△ABE ≌△AGE ．【例7】如图，在△ABC 中，90ACB ∠=， B A ∠>∠，点D 为边AB 的中点，DE BC ∥交AC 于点E ，CF AB ∥交DE 的延长线于点F ．（1）求证：DE EF =；（2）联结CD ，过点D 作DC 的垂线交CF 的延长线于点G ，求证：B A DGC ∠=∠+∠．ABFEDC图6FEDABC【巩固】已知：如图，在梯形ABCD 中，AD ∥BC ，BC =DC ，CF 平分 ∠BCD ，DF ∥AB ，BF 的延长线交DC 于点E ．求证：（1）△BFC ≌△DFC ；（2）AD =DE ．考点五：四边形背景下相关证明1、熟练的掌握特殊的平行四边形的性质；2、利用特殊的平行四边形的性质得出相应的边之间的关系．其中特殊的平行四边形的判定定理也是常考的一个知识点．【例8】如图，在梯形ABCD 中，AD //BC ，AB ＝DC ，过点D 作DE ⊥BC ，垂足为E ，并延长DE 至F ，使EF ＝DE ．联结BF 、CD 、AC ．（1）求证：四边形ABFC 是平行四边形；（2）如果DE 2＝BE ·CE ，求证四边形ABFC 是矩形．ABDFCE ABCD EF【例9】已知梯形ABCD中，AD//BC，AB=AD（如图所示），∠BAD的平分线AE交BC于点E，连结DE.（1）在图中，用尺规作∠BAD的平分线AE（保留作图痕迹，不写作法），并证明四边形ABED是菱形；（2）∠ABC＝60°，EC=2BE，求证：ED⊥DC．【巩固】如图，已知平行四边形ABCD中，对角线AC、BD交于点O，E是BD延长线上的点，且△ACE是等边三角形．（1）求证：四边形ABCD是菱形；（2）若∠AED=2∠EAD，求证：四边形ABCD是正方形．【例10】如图所示，在菱形ABCD中，点E、F分别在BC、CD上，BAF DAE∠=∠，AE 与BD相交于点G.（1）求证：BE DF=；（2）当DF ADFC DF=时，求证：四边形BEFG是平行四边形．EDCBAFGAB CDEOAB CDE FO【例11】已知：如图，梯形ABCD 中，AD ∥BC ，AB ＝DC ，对角线AC 、BD 相交于点F ，点E 是边BC 延长线上一点，且∠CDE ＝∠ABD ．（1）求证：四边形ACED 是平行四边形；（2）联结AE ，交BD 于点G ，求证：DG DFGB DB．【巩固】已知：如图，平行四边形ABCD 的对角线相交于点O ，点E 在边BC 的延长线上，且OE ＝OB ，联结DE ．（1）求证：DE ⊥BE ；（2）如果OE ⊥CD ，求证：BD ·CE ＝CD ·DE ．F BCEDAOEDCBA【回家作业】1、如图，在Rt ABC ∆中，90ACB ∠=︒，3AC BC ==，点D 在边AC 上，且2AD CD =， DE AB ⊥，垂足为点E ，联结CE ，求：（1）线段BE 的长；（2）ECB ∠的余切值；2. 如图，已知梯形ABCD 中，AD //BC ，AC 、BD 相交于点O ，AB ⊥AC ，AD =CD ，AB =3， BC =5．求：（1）tan ACD ∠的值；（2）梯形ABCD 的面积．ABCDOABCD E3、小明与班级数学兴趣小组的同学在学校操场上测得旗杆BC 在地面上的影长AB 为12米，同一时刻，测得小明在地面的影长为2.4米，小明的身高为1.6米. （1）求旗杆BC 的高度；（2）兴趣小组活动一段时间后，小明站在A B 、两点之间的D 处（A D B 、、三点在一条直线上），测得旗杆BC 的顶端C 的仰角为α，且tan 0.8α=，求此时小明与旗杆之间的距离．4、已知，如图，⊙O 是ABC ∆的外接圆，AB AC =，点D 在边BC 上，AE ∥BC ， AE BD =；（1）求证：AD CE =；（2）如果点G 在线段DC 上（不与点D 重合），且AG AD =，求证：四边形AGCE 是平行四边形．ABCDE ODABCD EFMN（第7题图）5、如图9-1，在Rt △ABC 中，90ACB ∠=︒，点D 是边AB 的中点，点E 在边BC 上，AE =BE ，点M 是AE 的中点，联结CM ，点G 在线段CM 上，作∠GDN =∠AEB 交边BC 于N . （1）如图9-2，当点G 和点M 重合时，求证：四边形DMEN 是菱形；（2）如图9-1，当点G 和点M 、C 不重合时，求证：DG =DN ．6、已知：如图，在正方形ABCD 中，点E 、F 分别在BC 和CD 上，AE ＝AF ．（1）求证：BE ＝DF ；（2）连接AC 交EF 于点O ，延长OC 至点G ，使OG ＝OA ，连接EG 、FG ．判断四边形AE GF 是什么特殊四边形，并证明你的结论．7、如图，在梯形ABCD 中，AD ∥BC ，点E 、F 分别是边BC 、CD 的中点，直线EF 交边 AD 的延长线于点M ，交边AB 的延长线于点N ，联结BD ．（1）求证：四边形DBEM 是平行四边形；（2）联结CM ，当四边形ABCM 为平行四边形时，求证：MN =2DB ．ABCD EN G M图9-2 ABC D ENM G图9-2ABCD EF GO8、已知：如图，四边形ABCD 中，DB BC ⊥，DB 平分ADC ∠，点E 为边CD 的中点，AB BE ⊥．（1）求证：2BD AD DC =⋅；（2）联结AE ，当BD BC =时，求证：ABCE 为平行四边形．9. 已知：如图8，在平行四边形ABCD 中，AC 为对角线，E 是边AD 上一点，BE ⊥AC 交 AC 于点F ，BE 、CD 的延长线交于点G ．（1）求证：四边形ABCD 是矩形；（2）如果AE=EG ，求证：2AC BC BG =⋅．ABCD EFG。

上海初三数学一模考知识点

比例的基本性质 1、比例的基本性质：=←⎯→=b d ad bc a c。

2、反比性质：=←⎯→=b d a c a c b d 。

3、更比性质：=←⎯→=bd c dac a b 。

4、比例问题中关于k 的使用（设k 法）：（1）对比例问题，常用的处理方法是将“一份”看成k （当=b a 21，设=a k ，=b k 2）；（2）对于比例连等式，常用处理方法是设“公比”为k （当=b d a c ，设公比==b dk a c）。

5、合比性质：(1)=←⎯→=++b d b d a c a b c d（合比性质）； (2) =←⎯→=−−b d b da c abcd （分比性质）。

6、等比性质：如果===b d n a c m ...+++≠b d n (...0)，那么+++=+++b d n ba c m a ......。

注意点：使用等比性质的前提是各式各分母的和不等于零．．．．．．．．．．．（+++≠b d n ...0）。

黄金分割在线段AB 上取一点C ，把线段AB 分成两条线段AC 和BC （AC ＞BC ），且使AC 是AB 和BC 的比例中项，这样的分割方法叫做把线段AB 黄金分割。

点C 就叫做线段AB 的黄金分割点。

在线段AB 倍得到点C ，则点C 就是AB 的黄金分割点。

注意点：一条线段上的黄金分割点有两个。

注意点：黄金分割是一种特殊的比例中项问题，必须同时满足：=b ca b与=+c a b （稍短:稍长=稍长:总长）。

黄金比例0.618:1 = 1:1.618 = 0.382:0.618 ） ⎝⎭⎪⎪=⎫22132；⎝⎭⎪ ⎪=⎛⎫2213。

三角形重心性质重心落在三角形每条中线上；重心落在每条中线的三等分点处。

✧ 技巧当题目中出现重心时，通常需要做出中线。

≈0.618≈0.618==平行线分线段成比例定理三条平行线截两条直线，所得的对应线段成比例（平行线等分线段定理是平行线分线段成比例定理的特殊情况）。

上海中考数学考前冲刺课讲义

2016年中考冲刺一、基本模型CD双高模型“山顶洞”模型“风筝”型或“钻石”型平行线+角平分线角平分线+垂直，延长相交证全等垂径定理勾股定理“中点”的畅想二、记忆部分1外离：外切：相交：内切：内含：2、n边形的内角和；外角和；从一个顶点出发可以引条对角线，共条对角线3、你学过的中心对称图形有4AB=5、圆的周长公式；面积公式；弧长公式；扇形面积公式6、写出二次函数的对称轴7求根公式89、特殊角锐角三角比：10= …11、基本的尺规作图三、题目扫描1、下列各运算中，正确的运算是（）【答案】B2则下列判断中正确的是（）A ．抛物线开口向上； BC 3； D【答案】C3、下列命题正确的是（）【答案】C4、如图，四边形ABCD 中，AC 与BD 相交于点O ，根据下列条件，一定能判断AD//BC 的是（）【答案】DBC5、下列函数关系中，是二次函数的是( )A.在弹性限度内，弹簧的长度y与所挂物体质量x之间的关系B.当距离一定时，火车行驶的时间t与速度v之间的关系C.等边三角形的周长C与边长a之间的关系D.圆心角为120°的扇形面积S与半径R之间的关系【答案】D6、在1、2、3三个数中随机抽取一个数，其中确定事件是（）A.抽取的数是素数；B.抽取的数是合数；C.抽取的数是奇数；D.抽取的数是偶数．【答案】B7=8【答案】-2或19= ．【答案】110的解是．11【答案】212、关于xk 的取值范围是13、在平面直角坐标系中，点A y 轴的交点，点B 是这条抛物线上的另一点，且AB ∥x 轴，则以AB 为边的等边三角形的周长为______ __ 【答案】1814【答案】-115、已知在Rt△ABC 中，∠A = BC = a ，点D 在边BC上，将这个三角形沿直线AD 折叠，点C 恰好落在边AB 上，那么BD = （用a 的代数式表示）．16、如图，在△ABC 中，∠C=90°，点D 为AB 的中点，BC=3DBC 沿着CD 翻折后, 点B 落到点E ，那么AE 的长为．【答案】717、在Rt△ABC C旋转后得到Rt△A'B'C，其中点B' 正好落在AB上，A'B'与AC相交于点D18【答案】619、已知△ABC中，AB=AC，BD是AC边上的中线，若AB=13，BC=10，试求tan∠DBC的值．【答案】4520、已知：如图，正方形ABCD ，BM 、DN 分别是正方形的两个外角平分线，45MAN ∠=，将MAN ∠绕着正方形的顶点A 旋转，边AM 、AN 分别交两条角平分线于点M 、N ，联结MN ；（1）求证：ABM ∆∽ADN ∆；（2）联结BD ，当BAM ∠的度数为多少时，四边形BMND 为矩形，并加以证明；【答案】（1）证明：∵四边形ABCD 是正方形，∴∠ABC=∠ADC=∠BAD=90°，∵BM 、DN 分别是正方形的两个外角平分线，∴∠ABM=∠ADN=135°，∵∠MAN=45°，∴∠BAM=∠AND=45°﹣∠DAN ，∴△ABM ∽△NDA ；（2）解：∵四边形BMND 为矩形，∴BM=DN ，∵△ABM ∽△NDA ，∴=，∴BM 2=AB 2，NMD C BA∴BM=AB ，∴∠BAM=∠BMA==22.5°．21、已知：如图，在△ABC 中，AB AC =，DE ∥BC ，点F 在边AC 上，DF 与BE 相交于点G ，且∠EDF =∠ABE ．求证：（1）△DEF ∽△BDE ；（2）DG DF DB EF ⋅=⋅．【答案】证明：（1）∵AB=AC ，∴∠ABC=∠ACB ．…………………………………………（1分）∵DE ∥BC ，∴∠ABC+∠BDE=180°，∠ACB+∠CED=180°．……………（1分）∴∠BDE=∠CED ．………………………………………………………………（1分） ∵∠EDF=∠ABE，∴△DEF∽△BDE．………………………………………（2分）（2）由△DEF∽△BDE，得EFDE DE DB =．………………………………………（1分） ∴EF DB DE ⋅=2．………………………………………………………………（1分）由△DEF∽△BDE，得∠BED=∠DFE ．………………………………………（1分）∵∠GDE=∠EDF ，∴△GDE ∽△EDF ．………………………………………（1分） ∴DFDE DE DG =．……………………………………………………………………（1分） ∴DF DG DE ⋅=2．………………………………………………………………（1分） ∴EF DB DF DG ⋅=⋅．…………………………………………………………（1分）22、解决三角形面积问题的方法及由此推出的相似三角形面积之比及同高（等高）、同底（等底）时如何思考；或通过中间量进行转化★如图，已知梯形ABCD ，AD ∥BC ，AB ＝AD ＝5，3tan 4DBC ∠=．E 为射线BD 上一动点，过点E 作EF ∥DC 交射线BC 于点F ．联结EC ，设BE= x ，ECFBDC S y S ∆∆=．（1）求BD 的长；（2）当点E 在线段BD 上时，求y 关于x 的函数关系式，并写出自变量x 的取值范围；（3）联结DF ，若△BDF 与△BDA 相似，试求BF 的长．【答案】解：（1）过点A作A H⊥B D于点H,∵AD∥BC，AB＝AD=5∴∠ABD=∠ADB=∠D BC, BH＝HD………………………（1分）在Rt△ABH(1分) ∴BH=DH=4，…………………………………………（1分）∴BD=8 …………………………………………………（1分）（2）∵EF∥DC∵△EFC与△EFB2分）由EF∥DC可得：△FEB∽△CDB1分）（2分，1分）（3）∵AD∥BC ∴∠ADB=∠D BC,∵△BDF与△BDA相似①∠BFD=∠A，可证四边形ABFD是平行四边形∴BF=AD=5．………………………………………………（2分）②∠BFD=∠ABD，∴ DB=DF．可求得：BF=645．………………………………………（2分）综上所述，当△BDF与△BDA相似时，BF的长为5或645．★已知在正△ABC中，AB=4，点M是射线AB上的任意一点（点M与点A、B不重合），点N在边BC的延长线上，且AM=CN．连接MN，交直线AC于点D．设AM=x，CD=y．（1）如图，当点M在边AB上时，求y关于x的函数解析式，并写出自变量x的取值范围．（2）当点M在边AB上，且四边形BCDM的面积等于△DCN面积的4倍时，求x的值．（3）过点M作ME⊥AC，垂足为点E．当点M在射线AB上移动时，线段DE的长是否会改变？请证明你的结论．23、已知平面直角坐标系xOy （如图7），抛物线c bx x y ++=221经过点)0,3(-A 、)23,0(-C . （1）求该抛物线顶点P 的坐标；（2）求CAP ∠tan 的值；（3）设Q 是（1）中所求出的抛物线的一个动点，点Q 的横坐标为t ，当点Q 在第四象限时，用含t的代数式表示△QAC的面积.【答案】解：（1）将A（﹣3，0）、C（0，﹣）．代入得解得所以抛物线的表达式为y=x2+x﹣．其顶点P的坐标为（﹣1，﹣2）．…（1分）（2）延长AP交y轴于G，过C作CH⊥AG，垂足是H．设直线AP的表达式为y=kx+b，将A（﹣3，0）、P（1，﹣2）代入，得，解得．∴y=﹣x﹣3．进而可得G（0，﹣3）．∴OG=OA，∠G=∠OAG=45°，在Rt△CHG中，HG=CH=CG•sin45°=．在Rt△AOG中，AG==3，∴AH=AG﹣HG=∴tan∠CAP==．（3）设Q（t，t2+t﹣），由Q在第四象限，得|t|=t，|t2+t﹣|=﹣t2﹣t+）．联结OQ，易得S△QAC=S△AOC+S△QOC﹣S△AOQ．∵S△AOC=×|﹣3|×|﹣|=，S△QOC=×|﹣|×t=t，S△AOQ=×|﹣3|×|t2+t﹣|=﹣t2﹣t+，∴S△QAC=+t﹣（﹣t2﹣t+）=t2+t．24（1）求抛物线的表达式；（2标；（3）在（2）的条件下，.【答案】（1（2（325、如图，在平面直角坐标系中，O为坐标原点，开口向上的抛物线与x轴交于点A（﹣1，0）和点B（3，0），D为抛物线的顶点，直线AC与抛物线交C（5，6）．（1）求抛物线的解析式；（2）点E在x轴上，且△AEC和△AED相似，求点E的坐标；（3）若直角坐标平面中的点F和点A、C、D构成直角梯形，且面积为16，试求点F的坐标．【答案】解：（1）设抛物线的解析式为y=ax2+bx+c，把A（﹣1，0），B（3，0），C（5，6）代入解析式得：，解得：，∴抛物线的解析式为：．（2）如图1，过点D作ND⊥x轴于点N，过点C作CM⊥x轴于点M，顶点坐标为D（1，﹣2）．∵A（﹣1，0），B（3，0），C（5，6），D（1，﹣2）．∴AN=2，ND=2，CM=6，AM=1+5=6，∴AN=ND，CM=AM，AD=，AC=，∴∠NAD=∠ADN=45°，∠CAM=∠ACM=45°，∴∠CAE=∠DAE=45°，当△CAE∽△DAE时，，不合题意，舍去；当△CAE∽△EAD时，，即，AE=，当点E在点A的右边时，点E为（﹣1，0）；当点E在点A的左边时，点E为（﹣﹣1，0）；∴E（﹣1，0）或（﹣﹣1，0）．（3）如图2，当FC ⊥AC 时，（FC+AD ）•AC=16，即，解得：FC=，则；当FD ⊥AD 时，（FD+AC ）•AD=16，即，解得：FD=，∴AF=，∴OF=AF ﹣AO=4﹣1=3 则F 2（3，0）．26、已知：如图，在梯形ABCD 中，BC AD //，5==CD AB ，6=AD ，12=BC ．点E 在AD 边上，2:1:=ED AE ，连结CE ．点P 是AB 边上的一个动点，过点P 作PQ CE ∥，交BC 于点Q ．设x BP =，y CQ =．(1) 求B cos 的值；(2) 求y 与x 的函数解析式，并写出函数的定义域；（3）联结EQ ，试探索△EQC 有无可能是直角三角形，若有可能，试求出x 的值；若不能，请简要说明理由。

沪教版九年级一模冲刺复习讲义第2讲代数运算及函数(解析版)

考点分析年份 2008 2009 201020112012 2013 2014 2015 2016 题型解答19解答19解答19 解答19解答19解答19解答19解答19解答19分值10 10 10 10 10 10 10 10 10内容实数的运算代数式计算实数的运算实数的运算实数的运算实数的运算实数的运算分式化简与求值实数的运算题型解答20 解答20 解答20 解答20 解答20 解答20 解答20 解答20解答20分值10 10 10 10 10 10 10 10 10内容解分式方程解二元二次方程组解分式方程解二元二次方程组解分式方程解二元二次方程组解分式方程解不等式组解分式方程考点一：实数的运算：注意一般的运算顺序及符号．【例1】计算：（1）01(3)271232--+-++；（2）1122112(31)32221-⎛⎫⨯-++- ⎪ ⎪-⎝⎭．【答案】（1）23-；（2）3．代数运算及函数模块一：代数运算注：1．01(0)a a =≠；2.n m n ma a =；3.1(0)a a≠．【解析】（1）0(3)1-11=-=-（2）112211)32-⨯+-⎝⎭1(31132=+-=．【例2】先化简，再求值：2222211()a ab ba b a b-+÷--，其中11a b==，．【答案】．【解析】解：原式＝2()()()a b b aa b a b ab--÷+-aba b=-+，当11a b==，时，原式＝4=．【巩固】（10111()2π--+；（21382+；（3）先化简，再求值：221(1)211a aa a a+÷+++-，其中2sin451a=︒-．【答案】（1）2；（3）1-【解析】（10111()2π--+112=-+=（2138222+=-+-=（3）2211(1)2111a a aa a a a+-÷+=++-+，将02sin4511 a=-=-代入，得221(1)1211a aa a a+÷+==++-．210-30-2-2考点二：不等式组的运算不等式组的取值法则是：“同大取大，同小取小，大小取中间”．【例3】（1）不等式240x +≤的解集在数轴上表示正确的是（）A ．B ．C ．D ．（2）求不等式组1023x x x ->⎧⎨+>⎩的解集是____________．【答案】（1）C ；（2）x>1．【解析】（1）不等式的解集为2x ≤-，在数轴上表示为C ；（2）由x -1>0，得x >1，由2x +3>x ，得x >32-，得原不等式组的解集为x >1．【总结】考察不等式的解法和数轴的表示，注意有等号需要用实心点及不等式组解集的求法．【例4】解不等式组：4261139x x x x >-⎧⎪-+⎨≤⎪⎩，并把解集在数轴上表示出来．【答案】-3<2x ≤．【解析】4261139x x x x >-⎧⎪⎨-+≤⎪⎩①②由①得：x >-3，由②得：2x ≤，综上得：-3<2x ≤，在数轴上画出解集，如下图所示：【巩固】1.不等式组1228x x ->⎧⎨<⎩①②的解集是________________；2. 解不等式组：()2131 5 5 2x x x x ->-⎧⎪⎨-<+⎪⎩①②，并写出它的所有非负整数解．【答案】1．3<x <4； 2．0和1．【解析】（1）由①得：x>3，由②得：x<4，故原不等式组的解集是3<x<4；（2）由①可得：2x<；由②可得：53 x>-，∴不等式组的解集为523x-<<，∴它的所有非负整数为0，1．【总结】考察不等式组的解法，注意非负整数解的确定．考点三：方程的运算分式方程及二元二次方程组是中考中常涉及的内容，注意在求分式方程的解后，要检验是不是方程的增根．【例5】解方程：1512x xx x-+=-．【答案】12x=，21x=-．【解析】[方法一]设1xyx-=，则原方程化为152yy+=，整理得：22520y y-+=，∴11 2y=，22y=；当12y=时，112xx-=，得2x=；当2y=时，12xx-=，得1x=-，经检验：12x=，21x=-是原方程的根；∴原方程的解为：12x=，21x=-；[方法二]去分母，得：222(1)25(1)x x x x-+=-，整理得：220x x--=，解得：12x=，21x=-，经检验：12x=，21x=-是原方程的根，∴原方程的解为：12x=，21x=-．【总结】本题考察了分式方程的解法，注意检验方程的根的情况．【例6】解方程：2121111x x x x +-=--+．【答案】01(x x ==-；舍）．【解析】通分后，原方程可化为：2201x x x +=-，解得：1201x x ==-，，经检验，当x =-1时原方程分母为零，x =-1为原方程的增根，所以原方程的根为x =0．【总结】注意分式方程的时候一定要检验是否是增根的情况【巩固】1．解方程：22101x x x x---=-； 2．解方程：261393x x x x +=+--．【答案】1．12122x x ==，； 2．x =1 ．【解析】1．去分母，得：()()()221110x x x x x x ⋅----⋅⋅-=，即()()222110x x x x ----=，化简得：22520x x -+=，解得：12122x x ==，，经检验：12122x x ==，均是原方程的根，所以原方程的解为：12122x x ==，；2．去分母，得：(3)63x x x -+=+，化简得： 2430x x -+=，解得：1213x x ==，，经检验：x =3是方程的增根，所以原方程的根为x =1．【总结】解分式方程的方法通常为去分母法，注意解完之后一定要验根．【例7】解方程组： 22220x y x xy y -=-⎧⎨--=⎩．【答案】12124121x x y y ⎧=-=-⎧⎪⎨⎨=-=⎪⎩⎩，．【解析】22220x y x xy y -=-⎧⎨--=⎩①② 由②得x =2y 或x =-y 和①将原方程组转换为以下的方程组 222x y x y x y x y ⎧-=--=-⎧⎪⎨⎨==-⎪⎩⎩和，解得原方程组的解为：12124121x x y y ⎧=-=-⎧⎪⎨⎨=-=⎪⎩⎩，．【总结】本题考察了二元二次方程组的问题，常用直接代入法或降次消元法解决．【巩固】解方程组：21220y x x xy -=⎧⎪⎨--=⎪⎩①②【答案】12122130x x y y ⎧==-⎧⎪⎨⎨==⎪⎩⎩，．【解析】由方程①得y = x +1，③将③代入②，得：22(1)20x x x -+-=，整理，得220x x --= 解得：1221x x ==-，分别将1221x x ==-，代入③，得1230y y ==，，所以原方程组的解为：12122130x x y y ⎧==-⎧⎪⎨⎨==⎪⎩⎩，．【总结】本题考察了二元二次方程组的解法．考点四、方程的简单应用本小结主要针对中考中常出现的一元二次方程和分式方程的应用进行简单的梳理，这类题型主要出现在填空题中，难度系数较低，主要是寻找到等量关系，列出方程即可．【例8】（1）某商品的原价为100元，如果经过两次降价，且每次降价的百分率都是m ，那么该商品现在的价格是元（结果用含m 的代数式表示）；（2）某工厂七月份的产量是100万元，计划第三季度的总产值要达到364万．如果每月产量的增长率相同，求这个增长率．【答案】（1）2100(1)m -；（2）20%．【解析】（1）原价是100元的商品第一次降价后的价格是100（1-m ），第二次降价后的价格是2100(1)m -；（2）设每个月的增长率是x ，则七月份产量是100万，八月份的产量是100（1+x ），九月份的产量是2100(1)x +，第三季度的总产量为100+100（1+x ）+2100(1)x +=364，解得：10.2x =，2 3.2x =-（舍），即八九月份的增长率是20%．【总结】本题考察了一元二次方程的应用类问题，直接套用增长率和降低率的公式即可，注意第（2）小题是季度产量．【例9】某市为了美化环境，计划在一定的时间内完成绿化面积200万亩的任务，后来市政府调整了原定计划，不但绿化面积在原计划上要增加20%，而且要提前1年完成任务，经测算，要完成新计划，平均每年的绿化面积必须比原计划多20万亩，求原计划平均每年的绿化面积．【答案】40万亩．【解析】设原计划平均每年完成的绿化面积为x 万亩，根据题意，可列出方程200200(120%)120x x +-=+，解得：1240100x x ==-，，经检验，1240100x x ==-，均是原方程的根，但2100x =-不符合题意，故舍去，即计划平均每年完成绿化面积40万亩．【总结】本题考察了分式方程的应用，注意解完要检验．【巩固】（1）一辆汽车，新车的购买价是20万元，第一年使用后折旧20%，以后该车的年折旧率有所变化，但它在第二、三年的年折旧率相同，已知在第三年末，这辆车折旧后价值11.56万元，求这辆第二、第三年的折旧率．（2）某中学八年级学生到离校15千米的青少年营地举行庆祝十四岁生日活动，先遣队与大部队同时出发．已知先遣队的行进速度是大部队的行进速度的1.2倍，预计比大部队早半个小时到达目的地，求先遣队与大部队的行进速度．【答案】（１）15%；（2）先遣队的速度是6千米/小时，大部队的速度是5千米/小时．【答案】（1）设这辆车第二、三年的年折旧率是x，根据题意可得220(120%)(1)11.56x--=，整理解得：x1=0.15，x2=1.85（舍），即这辆车第二、三年中的折旧率为15%；（2）设大部队的行进速度是x千米/小时，则先遣队的行进速度为1.2x千米/小时，根据题意，可列出方程151511.22x x=-，解得：x=5，经检验，x=5是原方程的根，且符合题意．当x=5时，1.2x=6，即大部队的行进速度是5千米/小时，先遣队的行进速度是6千米/小时．【总结】本题主要考查方程在实际问题中的运用，注意分式方程要检验．考点分析年份20122013201420152016题型解答22解答21解答21解答21解答22分值1010101010内容一次函数的应用一次函数、反比例函数一次函数的应用反比例、一次函数的应用一次函数的应用模块二：一次函数考点九：一次函数的应用---实际问题类【例10】 1、一辆汽车在行驶过程中，路程 y （千米）与时间 x （小时）之间的函数关系如图3所示当时0≤x ≤1，y 关于x 的函数解析式为 y = 60 x ，那么当 1≤x ≤2时，y 关于x 的函数解析式为_____________.2、一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x (h )，两车之间的距离为y (km )，图中的折线表示 y 与x 之间的函数关系．根据图像进行以下探究：（1）甲、乙两地之间的距离为_____________km ．（2）求慢车和快车的速度；（3）求线段BC 所表示的y 与x 之间的函数关系式，并写出自变量x 的取值范围．【答案】1、y =100x -40；2、（1）900；（2）慢车75 km /h ，快车150km /h ；（3）()22590046y x x =-≤≤．【解析】1、设y 关于x 的函数解析式为y =kx +b ，由当0≤x ≤1时，y 关于x 的函数解析式为 y = 60 x ，得y =kx +b 过（1，60）和（2，160）两点，即602160k b k b +=⎧⎨+=⎩，解得：10040k b =⎧⎨=-⎩，∴函数解析式为y =100x -40；2、（1）由题意得：甲、乙两地之间的距离为900km ；（2）由图像可得，慢车速度为900÷12=75 （km /h ），快车速度为（900÷4）-75=150（km /h ）；（3）由题意得：900÷150=6小时，即快车行驶到乙地用时6小时，此时，慢车距离乙地的距离为6×75=450即点C 坐标为()6450，，因为()40B ，，所以利用待定系数法可得线段BC 的解析式为：()22590046y x x =-≤≤．【总结】本题考察了函数在实际生活中的应用，注意认真观察图形．12160 图3A BC Dx/hy/km9004 12 注意：解题的过程中注意画好行程图，与一次函数的图像相结合【例11】为发展电信事业，方便用户，电信公司对移动电话采用不同的收费方式，所使用的便民卡和如意卡在我市范围内每月(30天)的通话时间x (分钟)与通话费y (元)的关系如图所示，分别求出通话费y 1、y 2与通话时间x 之间的函数关系式，如果小方3月份通话时间为170分钟，他选择哪种卡比较合适．【答案】选便民卡．【解析】11295y x =+；212y x =．当x =170时，163y =，265y =，12y y <．所以选便民卡．【总结】考查一次函数在实际问题中的应用．【例12】研究中心观测一场沙尘暴从发生到结束全过程，开始时风暴平均每小时增加2千米/时，4小时后，沙尘暴经过开阔荒漠地，风速变为平均每小时增加4千米/时，一段时间，风暴保持不变，当沙尘暴遇到绿色植被区时，其风速平均每小时减小1千米/时，最终停止．结合风速与时间的图像，回答下列问题：（1）在y 轴括号内填入相应的数值；（2）沙尘暴从发生到结束，共经过多少小时?（3）求出当x ≥25时，风速y (千米/时)与时间x (小时)之间的函数关系式．（4）若风速达到或超过20千米/时，称为强沙尘暴，则强沙尘暴持续多长时间? 【答案】（1）8，32；（2）57小时；（3）57y x =-+；（4）30小时．【解析】（1）2×4=8，则8+4×（10-4）=32；（2）32÷1+25=57小时；（3）根据图象，CD 经过点（25，32）、（57，0），利用待定系数法可求得：57(2557)y x x =-+≤≤；（4）（57-20）-（20-8）÷4-4=30， ∴强沙尘暴持续30小时．【总结】考查一次函数在实际问题中的应用，注意认真理解图像．30201030201035302010102030A （0,29） B （30,35） xy xy(30,15)25104x (小时)y (千米/时) AB C（）（）【巩固】1．某工厂生产一种产品，当生产数量至少为10吨，但不超过50吨时，每吨的成本y万元与生产数量x 吨的函数关系式如图所示． ①求y 与x 的函数关系式，并写出其定义域；②当生产这种产品的总成本为280万元时，求该产品的生产数量．（注：总成本=每吨的成本×生产数量）【答案】 ① y =－x +11（10x 50）； ② 40．【解析】（1）直接（10，10）、（50，6）代入 y =kx +b（2）由题意，可得：1(11)28010x x -+=，解得：140x =或270x =，由于1050x ≤≤，故40x =，即该产品的生产数量为40吨．【总结】本题考察了一次函数的应用类问题，注意认真观察图像．2．已知水银体温计的读数y (℃)与水银柱的长度x (cm )之间是一次函数关系．现有一支水银体温计，其部分刻度线不清晰，表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度．水银柱的长度x (cm ) 4.2 … 8.2 9.8 体温计的读数y (℃)35.0…40.042.0（1）求y 关于x 的函数关系式(不需要写出函数的定义域)；（2）用该体温计测体温时，水银柱的长度为6.2㎝，求此时体温计的读数．【答案】（1）511944y x =+；（2）37.5．【解析】（1）设函数解析式为y =kx +b ，由题意知，函数图像过点（4.2，35）、（8.2，40），即 4.2358.240k b k b +=⎧⎨+=⎩，解此方程组得函数解析式为511944y x =+；（2）将x =6.2代入函数解析式中即可得到y =37.5，故此时体温计的读数为37.5℃．【总结】本题考察了一次函数的应用类问题，注意认真观察表格．101≤≤10 5010 xO y63．某物流公司引进A 、B 两种机器人用来搬运某种货物，这两种机器人充满电后可以连续搬运5小时，A 种机器人于某日0时开始搬运，过了1小时，B 种机器人也开始搬运，如图，线段OG 表示A 种机器人的搬运量A y （千克）与时间x （时）的函数图像，线段EF 表示B 种机器人的搬运量B y （千克）与时间x （时）的函数图像，根据图像提供的信息，解答下列问题：（1）求B y 关于x 的函数解析式；（2）如果A 、B 两种机器人各连续搬运5个小时，那么B 种机器人比A 种机器人多搬运了多少千克？【答案】（1）9090B y x =- （16x ≤≤）；（2）150千克．【解析】（1）设B y 关于x 的函数解析式为1B y k x b =+（10k ≠），由线段EF 过点(1,0)E 和点(3,180)P ，得1103180k b k b +=⎧⎨+=⎩，解得19090k b =⎧⎨=-⎩，所以B y 关于x 的函数解析式为9090B y x =-（16x ≤≤）；（2）设A y 关于x 的函数解析式为2A y k x =（20k ≠），由题意，得21803k =，即260k =， ∴60A y x =；当5x =时，560300A y =⨯=（千克），当6x =时，90690450B y =⨯-=（千克）， 450300150-=（千克）；即如果A 、B 两种机器人各连续搬运5小时，那么B 种机器人比A 种机器人多搬运了150 千克．【总结】本题考察了一次函数的应用类问题，注意认真观察图像．FG PO E 1 3 51806y (千克)x （小时）考点十：一次函数的应用2—几何类【例13】已知平面直角坐标系xoy（如图6），直线12y x b=+经过第一、二、三象限，与y轴交于点B ，点A（2，t）在这条直线上，联结AO，△AOB的面积等于1．（1）求b的值；（2）如果反比例函数kyx=（k是常量，0k≠）的图像经过点A，求这个反比例函数的解析式．【答案】（1）b=1；（2）4yx =．【解析】（1）过A作AC⊥y轴，连接OA，∵A（2，t），∴AC=2，对于直线12y x b =+令x=0，得到y=b，即OB=b，∵112AOBS OB AC OB=⋅==，∴b=1．（2）由b=1，得到直线112y x=+，将A（2，t）待入函数解析式得：t=1+1=2，即A（2，2），把A（2，2）代入反比例函数解析式kyx=，得：k=4，则反比例函数的解析式为4yx =．【总结】本题考察了初步的数形结合，由点求函数解析式．【例14】如图所示，直线l1的解析表达式为y=－3x+3，且l1与x轴交于点D，直线l2经过点A、B，直线l1、l2交于点C（1）求点D的坐标；（2）求直线l2的解析表达式；（3）求△ADC的面积（4）在直线l2上存在异于点C的另一点P，使得△ADP与△ADC的面积相等，请直接写出点P的坐标．【答案】（1）（1，0）；（2）362y x=-；（3）92；（4）P（6，3）．【解析】（1）令y=－3x+3=0，解得：1x=，所以D（1，0）；（2）因为直线l2经过点A（4，0）、B（3，32 -），故利用待定系数可求得直线l2的解析式为：362y x=-；Ox1y图6ABC（3）联立33362y x y x =-+⎧⎪⎨=-⎪⎩，解得：23x y =⎧⎨=-⎩， ∴C （2，-3），∴193322ADC S =⨯⨯=；（4）令362y x =-=3，解得：6x =，所以P （6，3）．【总结】考查一次函数在几何图形中的简单运用，注意面积的准确求解．【巩固】1．已知一次函数y =2x +b 与两坐标轴围成的三角形面积为24，求b 的值．【答案】±【解析】因为一次函数图像与x 轴的交点坐标为（2b-，0），与y 轴的交点坐标为（0，b ），所以三角形的面积12422bS b =⋅⋅=，解得：b =± 【总结】考查一次函数在几何图形中的简单运用，注意考虑全面，不要漏解．2. 已知：一个正比例函数和一个一次函数的图像交于点P （-2、2）且一次函数的图像与y 轴的交点Q 的纵坐标为4．（1）求这两个函数的解析式；（2）求△PQO 的面积．【答案】（1）y x =-，4y x =+；（2）4．【解析】（1）过点（0，0）、（-2，2），利用待定系数法可求得解析式为：y x =-，过点（-2，2）、（0，4），利用待定系数法可求得解析式为：4y x =+；（2）14242S =⨯⨯=．【总结】考查一次函数在几何图形中的简单运用，注意考虑全面，不要漏解．考点十一：一次函数应用3-文字类【例15】某人用充值50元的IC 卡从A 地向B 地打长途电话，按通话时间收费，3分钟内收费2.4元，以后每超过1分钟加收1元，若此人第一次通话t 分钟（3≤t ≤45），则IC 卡上所余的费用y （元）与t （分）之间的关系式是____________．【答案】50.6y t =-．【解析】由题意得：50 2.41(3)50.6y t t =--⨯-=-【总结】本题考查了根据实际问题列一次函数关系式，解题的关键是根据题意，找出等量关系，注意题中y 表示卡上剩余费用，以免造成错误．【例16】某工厂有甲、乙两条生产线先后投产，在乙生产线投产以前，甲生产线已生产了200t成品；从乙生产线投产开始，甲、乙两条生产线每天分别生产20t 和30t 成品．（1）分别求出甲、乙两条生产线投产后，总产量y (t )与从乙开始投产以来所用时间x (天)之间的函数关系式，并求出第几天结束时，甲、乙两条生产线的总产量相同；（2）分别求出第15天和第25天结束时，甲、乙两条生产线的产量是多少，并比较哪条生产线的总产量高．【答案】（1）y 甲=20x +200，y 乙=30x ，20天后甲、乙两条生产线的总产量相同．（2）第15天时，甲的生产量是500t ，乙的生产量是450t ，甲的总产量高；第25天时，甲的生产量是700t ，乙的生产量是750t ，乙的总产量高．【解析】（1）y 甲=20x +200，y 甲=30x ，令20x +200=30x ，解得:x =20；（2）当x =15时，y 甲=300+200=500，y 乙=30×15=450，y 甲＞y 乙；当x =25时，y 甲=500+200=700，y 乙=30×25=750，y 乙＞y 甲．【总结】考查一次函数图像在实际问题中的应用．【巩固】某中学预计用1500元购买甲商品个，乙商品个，不料甲商品单价上涨1.5元，乙商品单价上涨1元，尽管购买甲商品的个数比预定减少10个，总金额还是多了29元．又若甲、乙商品单价上涨1元，并且购买甲商品的数量只比预定数少5个，那么买甲、乙两商品支付的总金额是1563.5元．（1）求、的关系式；（2）若预计购买甲商品的个数的2倍与预计购买乙商品的个数的和大于205，但小于210，求、的值．【答案】（1）2186x y +=；（2）x =76，y =55．【解析】（1）设预计购买甲、乙商品的单价分别是a 元和b 元，可得：1500( 1.5)(10)(1)1529(1)(5)(1)1563.5ax by a x b y a x b y +=⎧⎪+-++=⎨⎪+-++=⎩，化简可得：2186x y +=；（2）依题意，有20522102186x y x y <+<⎧⎨+=⎩，解得：254553y <<，由于y 是整数，所以y =55，从而x =76．【总结】本题是方程组、函数和一元一次不等式的综合题，解决本题的关键是读懂题意，找到合适的关系式，当必需的量没有时，应设出未知数，解题过程中消去无关的量．【回家作业】一轮1、当x =22266(3)443x x x x x x x-+-÷+⋅-+-的值．【答案】4+【解析】222662(3)44432x x x x x x x x -+-÷+⋅===+-+--．x y x y x y2、求不等式组2620x x -<⎧⎨-<⎩的整数解【答案】-2，-1，0，1．【解析】2620x x -<⎧⎨-<⎩①②，由①得：x >-3，由②得：x <2，综上原不等式组的解集是-3<x <2，故整数解为：-2，-1，0，1．【总结】本题考查了解不等式组的一般方法，注意看清题目的要求．3、解方程：1x x -─22x x-─ 1 = 0 【答案】12122x x ==，．【解析】去分母，得：222(1)(1)0x x x x ----=，化简，得：22520x x -+=，解此方程得12122x x ==，，经检验，原分式方程的解为12122x x ==，．【总结】分式方程需要检验增根的情况．4、解方程组：22220x y x xy y -=⎧⎨--=⎩．【答案】12124121x x y y ⎧==⎧⎪⎨⎨==-⎪⎩⎩，．【解析】22220x y x xy y -=⎧⎨--=⎩①②，由②得（x -2y ）（x +y ）=0，所以x =2y 或x =-y ，则原方程组可以转化成两个方程组222x y x y x y x y -=-=⎧⎧⎨⎨==-⎩⎩或，解得原方程组的解为：12124121x x y y ⎧==⎧⎪⎨⎨==-⎪⎩⎩，．【总结】本题主要考查二元二次方程组的解法．5、（本题满分10分，第（1）题满分3分，第（2）题满分5分，第（3）题满分2分）近五十年来，我国土地荒漠化扩展的面积及沙尘暴发生的次数情况如表1、表2所示．表1：土地荒漠化扩展的面积情况年代50、60年代的20年70、80年代的20年90年代的10年平均每年土地荒漠化扩展的面积（km 2）156021002460表2：沙尘暴发生的次数情况年代 50年代的10年 60年代的10年 70年代的10年 80年代的10年 90年代的10年每十年沙尘暴发生次数58131423（1）求出五十年来平均每年土地荒漠化扩展的面积；（2）在图5中画出不同年代沙尘暴发生的次数的折线图；（3）观察表2或（2）所得的折线图，你认为沙尘暴发生次数呈（选择“增加”、“稳定”或“减少”）趋势．【答案】（1）1956km 2；（2）见图；（3）增加．【解析】（1）平均每年土地荒漠化扩展的面积为：156020210020246010202010⨯+⨯+⨯++1956=（km 2），答：所求平均每年土地荒漠化扩展的面积为1956 km 2；（2）右图；（3）增加．【总结】本题主要考查一次函数的实际应用，注意对图像的观察与理解．50年代 60年代 70年代 80年代 90年代252015 105次数年代图550年代 60年代 70年代 80年代 90年代252015 105次数年代二轮小练习1、先化简，再求值：2214422x x x x x x x -÷-++++，其中1x =．1．【解析】221114422222x x x x x x x x x x x x --÷-=-=+++++++，将1x =代入，得原式=2214422x x x x x x x -÷-++++1．2、解方程：214124x x -=--；【答案】x =-1．【解析】去分母，得2244x x +-=-；移项、整理得220x x --=；经检验：12x =是增根，舍去；21x =-是原方程的根；所以原方程的根是1x =-．3、解方程组：223024x y x xy y -=⎧⎨-+=⎩【答案】1131x y =-⎧⎨=-⎩，2231x y =⎧⎨=⎩．【解析】223024x y x xy y -=⎧⎨-+=⎩①②由②x -y =2或x -y =-2，与①相结合得到方程组302x y x y -=⎧⎨-=-⎩或302x y x y -=⎧⎨-=⎩解此方程组得原方程组的解为1131x y =-⎧⎨=-⎩，2231x y =⎧⎨=⎩．4．已知：如图，在平面直角坐标系xOy 中，正比例函数y ＝43x 的图像经过点A ，点A 的纵坐标为4，反比例函数y ＝mx的图像也经过点A ，第一象限内的点B 在这个反比例函数的图像上，过点B 作BC ∥x 轴，交y 轴于点C ，且AC ＝AB ．求：（1）这个反比例函数的解析式；（2）直线AB 的表达式．【答案】（1）12y x ＝；（2）y =-23x +6．【解析】（1）∵正比例函数y =43x 的图象经过点A ，点A 的纵坐标为4，∴点A 的坐标为（3，4），∵反比例函数y =mx的图象经过点A ， ∴m =12，∴反比例函数的解析式为：12y x＝；（2）如图，连接AC 、AB ，作AD ⊥BC 于D ，∵AC =AB ，AD ⊥BC ， ∴BC =2CD =6，∴点B 的坐标为：（6，2），由题意得，3k +b ＝4，6k +b=2，解得，k ＝-23，b ＝6，∴直线AB 的表达式为：y =-23x +6．【总结】（1）根据正比例函数y = 4 3x 的图象经过点A ，点A 的纵坐标为4，求出点A 三角形的性质求出点B 的坐标，运用待定系数法求出直线AB 的表达式．DyxAOCB1 2 3 4 5（小时）200 150 100 50 0y(千米)小轿车中巴车x5、鞋子的“鞋码”和鞋长（cm ）存在一种换算关系，下表是几组“鞋码”与鞋长换算的对应鞋长（cm ） 16 19 21 24 鞋码（号）22283238（1）设鞋长为x ，“鞋码”为y ，试判断点（x ，y ）在你学过的哪种函数的图象上? （2）求x 、y 之间的函数关系式；（3）如果某人穿44号“鞋码”的鞋，那么他的鞋长是多少? 【答案】（1）一次函数；（2）210y x =-；（3）27cm ．【解析】（1）鞋长每增加1cm ，鞋码增加2号，符合一次函数；（2）设(0)y kx b k =+≠，代入（16，22）和（19，28）得：16221928k b k b +=⎧⎨+=⎩，解得：210k b =⎧⎨=-⎩，∴210y x =-；（3）当44y =时，27x =．【总结】本题考察了一次函数的实际应用．6、 “五一”期间，上海市先后有两批游客分别乘中巴车和小轿车沿相同路线从上海市赶往奉贤区海湾度假村旅游，如图表示其行驶过程中路程随时间的变化图象．（1）根据图象，请分别直接写出中巴车和小轿车行驶过程中路程与时间之间的函数关系式（不要求写自变量的取值范围）；（2）直接写出中巴车和小轿车行驶速度各是多少? （3）试求小轿车出发后多长时间赶上中巴车? 【答案】（1）100200y x =-小轿车，40y x =中巴车；（2）小轿车：100千米/时，中巴车：40千米/时；（3）43小时；【解析】（1）由图像及待定系数法，可得： 100200y x =-小轿车，40y x =中巴车；（2）由图像可知：小轿车的速度为：100千米/时，中巴车的速度为：40千米/时；（3）由40100200x x =-，得：103x =，所以104233-=，故小轿车出发43小时后追上了中巴车．【总结】本题主要考察了对函数的图像的理解，要看清楚问的究竟是哪部车子的行驶时间．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

DCBAABCD FE G S 3 S 2S 1 一模冲刺（二）1．关于二次函数()21y a x =+的图像，下列说法中，正确的是（）A ．是一条开口向上的抛物线；B ．顶点坐标为()1,0；C ．可以由二次函数2y ax =的图像向上平移一个单位得到；D ．可以由二次函数2y ax =的图像向左平移一个单位得到．答案：D2．已知△ABC 与△DEF 相似，且A D ∠=∠,那么下列结论中，一定成立的是（）A ．B E ∠=∠； B ．AB AC DE DF =； C ．相似比为AB DE ；D ．相似比为BCEF．答案：D3. 如图，甲、乙两船同时从港口O 出发，其中甲船沿北偏西30︒方向航行，乙船沿南偏西70︒方向航行，已知两船的航行速度相同，如果1小时后甲、乙两船分别到达点A 、B 处，那么点B 位于点A 的（）A ．南偏西40︒；B ．南偏西30︒；C . 南偏西20︒；D .南偏西10︒．答案：C .4. 如图，D 、E 、F 、G 是△ABC 边上的点，且DE ∥FG ∥BC ，DE ，FG 将△ABC 分成三个部分，它们的面积比为123::1:2:3S S S =，那么::DE FG BC = .答案：1；5．如图1，已知抛物线2y x =，把该抛物线向上平移，使平移后的抛物线经过点()1,3A ,那么平移后的抛物线的表达式是．答案：22+=x y6．已知一个二次函数的图像具有以下特征：（1）经过原点；（2）在直线1x =左侧的部分，图像下降，在直线1x =右侧的部分，图像上升，试写出一个符合要求的二次函数解析式．答案：（-3，2） 7．已知A 、B 是抛物线221y x x =+-上的两点（A 在B 的左侧），且AB 与x 轴平行，4AB =，则点A 的坐标为．答案：x x y 22-=(答案不唯一)．8．如图，D 是△ABC 内一点，且∠ADC =∠BDA =∠BDC ,如果2AD =，3BD =，∠ABC =60︒，那么CD = .答案：92； 9.已知函数()2230y ax ax a =-+>图像上点()2,n 与()3,m ，则n m . （填“>,<或无法确定”）答案：<；10．已知抛物线x x y 62+=，点()2,A m 与点(),4B n 关于该抛物线的对称轴对称，那么m n +的值等于．答案：-411．如图3，已知△ABC 中，90ACB ∠=︒，D 是边AB 的中点，CE AB ⊥，垂足为点E ，3sin 5DCE ∠=，则cot A = ．CAD EB答案：212．如图4，平面直角坐标系中，已知矩形OABC ，O 为原点，点A 、C 分别在x 轴、y 轴上，点B 的坐标为()1,2，联结OB ，将△ABC 沿直线OB 翻折，点A 落在点D 的位置，则点D 的坐标为．答案：)54,53(-13．如图，河流两岸a ，b 互相平行，C ，D 是河岸a 上间隔50米的两个电线杆．小英在河岸b 上的A 处测得 ∠DAB =30°，然后沿河岸走了100米到达B 处，测得∠CBM =60°，求河流的宽度．B D Ca bA 第22题图M14．已知：如图，在△ABC 中，AB AC =，DE ∥BC ，点F 在边AC 上，DF 与BE 相交于点G ，且∠EDF =∠ABE ．求证：（1）△DEF ∽△BDE ；（2）DG DF DB EF ⋅=⋅．答案：证明：（1）∵AB =AC ，∴∠ABC =∠ACB ．…………………………………………（1分）∵DE ∥BC ，∴∠ABC +∠BDE =180°，∠ACB +∠CED =180°．……………（1分） ∴∠BDE =∠CED ．………………………………………………………………（1分） ∵∠EDF =∠ABE ，∴△DEF ∽△BDE ．………………………………………（2分）（2）由△DEF ∽△BDE ，得EFDEDE DB =．………………………………………（1分） ∴EF DB DE ⋅=2．………………………………………………………………（1分）由△DEF ∽△BDE ，得∠BED =∠DFE ．………………………………………（1分） ∵∠GDE =∠EDF ，∴△GDE ∽△EDF ．………………………………………（1分） ∴DFDEDE DG =．……………………………………………………………………（1分） ∴DF DG DE ⋅=2．………………………………………………………………（1分） ∴EF DB DF DG ⋅=⋅．…………………………………………………………（1分）15．已知在平面直角坐标系xOy 中，二次函数)0(2>+-=b c bx x y 的图像经过点()1,A b -，与y 轴相交于点B ，且∠ABO 的余切值为3．（1）求点B 的坐标；（2）求这个函数的解析式；（3）如果这个函数图像的顶点为C ，求证：∠ACB =∠ABO ．解：（1）根据题意，得b =1+b +c ．……………………………………………………（1分）∴c = -1．…………………………………………………………………………（1分） ∴B （0，-1）．……………………………………………………………………（1分）（2）过点A 作AH ⊥y 轴，垂足为点H ．∵∠ABO 的余切值为3，∴3cot ==∠AHBHABO ．……………………………（1分）而AH =1，∴BH =3．∵BO =1，∴HO =2．………………………………………………………………（1分）BC（第23题图）∴b =2．……………………………………………………………………………（1分） ∴所求函数的解析式为122--=x x y ．………………………………………（1分）（3）由2)1(1222--=--=x x x y ，得顶点C 的坐标为（1，-2）．…………（1分） ∴52=AC ，10=AB ，2=BC ，5=AO ，BO =1．…………………（1分）∴2===BOBCAO AB AB AC ．………………………………………………………（1分） ∴△ABC ∽△AOB ．………………………………………………………………（1分） ∴∠ACB =∠ABO ． ………………………………………………………………（1分）16. 已知二次函数()2230y ax ax a a =-->.（1）求此二次函数图像与x 轴交点A 、B （A 在B 的左边）的坐标；（2）若此二次函数图像与y 轴交于点C ，且△AOC ∽△COB （字母依次对应）. ①求a 的值；②求此时函数图像上关于原点中心对称的两个点的坐标.解：（1）令2230ax ax a --=----------------------------------（1分）解得11x =-，23x =----------------------------------（2分）所以A （1-，0），B （3,0）. ----------------------------（1分）（2）①易知()0,3C a -，由△AOC ∽△COB ，------------------（1分）则OA OC OC OB =，即1333aa =，------------------------------（2分）解得a =. ----------------------------------（1分）②此时函数解析式为2y x x =--设函数图像上两点2(t -，2())t t t ---， ----------------------------------------------------------（1分）由两点关于原点中心对称，得：233-2()()33t t ----------------（1分）解得t =------------------------------------------（1分）∴这两个点的坐标为)2-与()2.------------------（1分）17．如图，已知抛物线2y x bx c =-++过点()2,0A ，对称轴为y 轴，顶点为P ．（1）求该抛物线的表达式，写出其顶点P 的坐标，并画出其大致图像；（2）把该抛物线先向右平移m 个单位，再向下平移m 个单位（0m >），记新抛物线的顶点为B ，与y 轴的交点为C ．①试用m 的代数式表示点B 、点C 的坐标；②若45OBC ∠=︒，试求m 的值．解：(1)∵抛物线c bx x y ++-=2过点A(2，0)，对称轴为y 轴∴ b=0，c=4 ∴42+-=x y P(O ，4) 大致图像如图。

(2)①∵抛物线先向右平移m 个单位，再向下平移m 个单位(m>0)∴B(m ．4-m) m m x y -+--=4)(2所以C(0，42+--m m )②由已知，∠OPB=45°，又∠OBC= 45° ∴△OCB 与△OBP 相似。

i ）当点C 在y 轴正半轴，即42+--m m >0时OP OC BO ∙=2 ∵168222+-=m m BO 42+--=m m OC OP=4 解得01=m (舍去)322=m ii)当点C 在y 轴负半轴，点42+--m m <0时CP OC BC ∙=2∵ m m CP m m OC m m BC +=-+=+=22422,4,解得01=m （舍去） 313,2±=m （负根舍去）∴ 31+=m18．如图，在梯形ACDB 中，AB ∥CD ，∠A =90︒，3AB =，6CD =，BE CB ⊥交直线AD 于点E .（1）当点E 与D 恰好重合时，求AD 的长；（2）当点E 在边AD 上时（E 不与A 、D 重合），设AD x =，ED y =试求y 关B CD E A于x 的函数关系式，并写出定义域；（3）问：是否可能使△ABE 、△CDE 与△BCE 都相似？若能，请求出此时AD 的长；若不能，请说明理由.解：（1）当点E 与D 重合时，由∠ABD =∠BDC ，∠DBC =∠A ，得△ABD ∽△BDC ，则AB BD BD DC=，∴BD =3AD ==. （2）作BH ⊥DC ，H 为垂足，则∠ABE +∠EBH =90︒, ∠EBH +∠HBC =90︒，∴∠HBC =∠ABE ，又∠BHC =∠A =90︒， ∴△ABE ∽△HBC ，又AB ‖CD ，得HB =AD =x ，HC =633CD DH -=-=，∴AE HC AB HB =，即33x y x -=，解得9y x x=-，定义域为()3x >.（3）假设能使△ABE 、△CDE 与△BCE 都相似，当点E 在边AD 上时，（如图1）易知∠EBC =∠A =∠D =90︒，考虑∠1的对应角，容易得到∠1ABE ≠∠,∠1DCE ≠∠, 所以必有∠1=∠2=∠3=60︒，于是在△ABE 、△CDE中，易得AE =DE =∴AD =,此时，BE =CE = BC =6, 即能使△ABE 、△CDE 与△BCE 都相似；当点E 在边AD 的延长线上时，（如图2）类似分析可得∠1=∠2=∠3=30︒，可求得AD =同样能使△ABE 、△CDE 与△BCE 都相似.是MON ∠内一19．如图，已知点，PC OM ⊥，垂足为点C ，2PC =，6OC =，A 是OC ON 交于点B ．（1）当点P 恰好是线段AB 的中点时，试判断△AOB 的形状，并说明理由；（2）当CA 为长度为多少时，△AOB 是等腰三角形；（3）设APk AB=，是否存在适当的k ，使得APC OBPC S k S ∆=四边形，若存在，试求出k 的值；若不存在，试说明理由．N BOCPAMN BOCPAM解：(1)过点B 作BE ⊥0M,垂足为点E ∵PC ⊥0M ∴BE//PC∵点P 恰好是线段AB 的中点 PC=2∴ BE=4 1分又∵ 2tan =∠MON∴OE=2 1分 ∵OC=6 ∴EC=CA=4可得OB=AP=52，AB=54 1分 ∴222AB OB OA += ∴ △AOB 是直角三角形． (2)设OE=a ,则BE=2a由AEACBE PC =设CA=x ，则a x xa -+=622 ∴16++=x x ai)如果OA =OB ，即a x 56=+解得15-=x 2分ii)如果AO=AB ，即22)6(46a x a x -++=+解得23=x 2分iii)如果OB=AB 时，OE=EA∴ )6(21+=x a 解得x=1 2分综上，当CA 的值为15-、23、1时,△AOB 是等腰三角形（3）同（2）设CA=x ,OE=a∵x x S APC =∙∙=∆221ONBPM ACON EBPMACa x a x S ABO )6(2)6(21+=∙+=∆ 1分若,k S S CBPCAPC =∆四边形由k ABAP =，得a k 1=，则ax a x x 1)6(=-+ 1分∴ 4,921-==x x （舍去） 1分 ∴ 32611=++==x x a k 1分ONEBPMAC。