第四章 晶体的微观对称性
晶体结构 知识点总结

简 单 立 方
体 心 立 方
面 心 立 方
简 单 四 方
体 心 四 方
四方底心, 四方底心,四方面心
(2)晶胞的二个基本要素 ) ①晶胞参数 晶胞形状
a, b, c, α , β , γ
α=bΛc β =aΛc γ =aΛb
晶轴
②晶胞内各原子的位置
分数坐标
例1:某种金属,立方体心晶胞 :某种金属, 含原子数为8*1/8 + 1 = 2 含原子数为 (顶点1,体心 ) 顶点 ,体心1) (0,0,0), (1/2,1/2,1/2) , , , , )
第四章 晶体结构 Chapt 4 Crystal Structure
固态物质按其原子(或分子、离子) 固态物质按其原子(或分子、离子)在空 间排列是否长程有序分成晶态和无定形两类。 间排列是否长程有序分成晶态和无定形两类。 晶体 例:聚乙烯 微粒在空间按周期性排列 微粒在空间按周期性排列 在空间按周期性
晶轴的夹角 90°60°… ° ° Notes: (1)优先考虑对称性 优先考虑对称性; 优先考虑对称性
(2)对称性相同时,优先选择素晶胞 对称性相同时,优先选择素 对称性相同时
晶胞 (平行六面体 平行六面体) 平行六面体 (1)晶胞 晶胞
并置堆积
实际晶体
素晶胞:含结构基元(点阵点 个 素晶胞:含结构基元(点阵点)1个 复晶胞:含结构基元(点阵点) ≥2个 复晶胞:含结构基元(点阵点 个
六方最密堆积 (A3)
正当晶胞含原子数目 = 8*1/8+1 = 2 顶点 体心
a=b=2r, c=1.633a (最密堆积 最密堆积) 最密堆积
Notes: ① 晶胞参数 a=b=2r, c=1.663a 晶胞中含原子数=2 ② 晶胞中含原子数
晶体结构的对称性

滑移面—滑移反映操作:由反应与平移组成的复 合对称操作。根据滑移方向的不同分为3类。第 一类轴线滑移面a(或b,c):如图虚线所示,对应的 操作为反映后,再沿a(或b,c)轴方向平移a/2(或 b/2,c/2);第二类对角 5 线滑移面n:如图B所 示。实点和虚点分别 4 a 3 是位于纸面的上方和 下方,且距离相等处。 对应的操作使反映后 a 2 沿a轴方向移动a/2,再 沿b轴方向移动b/2,即 1' 1 b 反映后又平移a/2+b/2
分子对称性与警惕宏观对称性对照表
分子对称性 晶体宏观对称性
对称操作及 其符号 旋转L(a) 反映M 倒反I 对称元素及其 对称操作及其 对称元素及 符号 符号 其符号 旋转 对称轴C 旋转轴n 对称面s
n
反映 反演 旋转反映
反映面或镜 面m 对称中心i 反轴
对称中心i 象转轴Sn
旋转倒反 L(a)I
1.2 晶体结构的对称性
1.2.1 晶体的对称元素和对称操作
晶体结构最基本的特征是具有空间点阵结构。 晶体的点阵结构使晶体的对称性和分子的对称性 有差别。分子结构的对称性是点对称性,只有4种 类型的对称元素和对称操作。 (1)旋转轴—旋转操作; (2)镜面—反映操作; (3)对称中心—反演操作; (4)反轴—旋转反映操作。 晶体的点阵结构,包括平移的对称操作。一方面 使晶体结构的对称性在上述点对称性的基础上还 增加下列3种类型的对称元素和对称操作。
对同一晶体,在划分平行六面体时,由于选择 向量的大小和方向不同,有许多划分方法,也就 能找到多种不同形状的晶胞。这些晶胞基本分为 二类:素晶胞和复晶胞。素晶胞包含的内容实质 上就是结构基元。若不考虑其他因素,任何晶体 均可划分为素晶胞。如图: 晶胞的基本要素:一个是晶胞的大小和形状, 可用晶胞参数(a,b,c,a,b,g)表示;另一个是晶 胞中原子的位置,通常用分数坐标(x,y,z)表示。 晶胞参数的定义与空间点阵的参数完全相同。 根据a,b,c,选择晶体的坐标轴X,Y,Z,使它们分别 和向量a,b,c平行。因此将a,b,c表示的方向也叫 晶轴。
1-3 晶体对称性
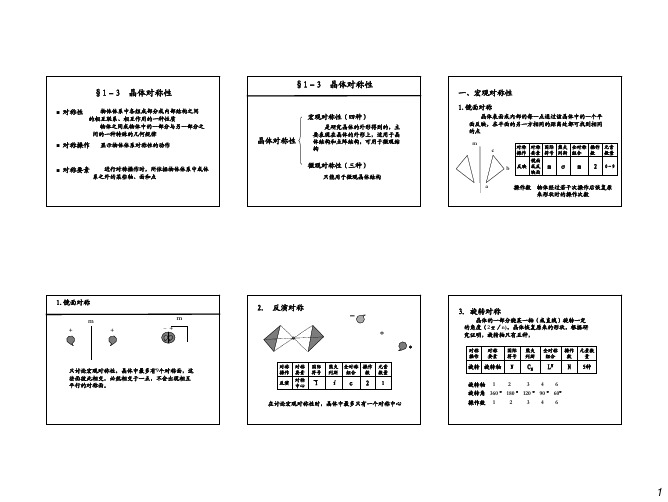
2
1 2 3 4 6 2 2 6 4 6
示
平行 斜插纸 纸面 面
二、宏观对称性的组合关系
1. 如果晶体中有两个或两个以上的镜面相交,则每两 个镜面的交线必定是一个对称轴,而对称轴的转角比 定时镜面夹角的二倍。
镜面夹角 180° 90° 60° 45° 30°
旋转轴转 角
360°
180°
120°
90°
Th
Td
O
Oh
晶类(点群)符号 国际符号(全) 国际符号(缩)
1 I(1)
1 I(1)
m
m
2
2
2/m
2/m
3
3
3
3
3m
3m
32
32
32/m
3m
2mm
mm
222
222
2/m2/m2/m
mmm
23
23
2/m3
m3
43m
43m
432
43
4/m32/m
m3m
全对称要素组合
I m(2)
2 2mI
3 3(3I) 33m 332 3323m(3323mI) 23m
三、平移群、布拉菲点阵 例:四方晶系
C→P
F→I
4
晶系 三斜 单斜
菱形
正交
立方
最低对称要素 无
一根二次旋转轴2 或旋转-反演轴2
一根三次旋转轴3 或旋转-反演轴3
三根相互垂直的旋 转轴32或旋转-反 演轴32
四根三次旋转轴43
熊夫列斯符号
C1 Ci(S2) Cs(C1h)
C2 C2h C3 C3i(S6) C3V D3 D3d C2V D2(V) D2h(Vh) T
07-2.3晶体的对称性

定义:点群是指一个晶体中所有点对称元素的集合。 点对称操作的集合称为点群。
晶体可能存在的对称类型可通过宏观对称元素在一点 上组合运用而得出。
点群在宏观上表现为晶体外形的对称。利用组合定律 可导出晶体外形中只能有32种对称点群。
点群可以用对称元素相结合而导出,在不破坏原有对称的
前提下,结合方式有n/m (表示m⊥n,镜面垂直于n次旋转轴), nm (表示m∥n,镜面包含n次旋转轴), n/mm或n/m m(第
晶体绕某一轴回转能复原n次,就称之为n次对称轴。 晶体中实际可能存在的对称轴有五种,并用符号1,
2,3,4,和6来表示。
旋转角 n名称 符号
360 180 120 90 60 度
1
2 3 4 6 次轴
1
2 356
2. 对称面
立方晶系{100} {110}
晶体通过某一平面作 镜像反映而能复原, 则该平面称为对称面 或镜面,用符号m表示。 对称面通常是晶棱或 晶面的垂直平分面或 者为多面角平分面, 且必定通过晶体几何
晶体基本的对称操作有点对称操作和平移对称操作。
在对称操作过程中保持空间至少有一个不动点的操作 称为点对称操作。在一般的对称操作过程中,空间有许多 点在动,但操作前后状态一样。 如旋转,反演,平面反映 均为点对称操作。
用点对称操作ห้องสมุดไป่ตู้组合可以描述有规则几何外形的单晶 体所具有的点对称性,但许多金属单晶体虽然不一定具备 规则的几何外形,但它们相应的点对称性却仍然存在。
180º与P3点重合,再经O点反 演而与P’重合,则称BB‘为2
次旋转—反演轴。
旋转—反演轴有1,2,3,4
和6次五种,分别以国际符号
_ ____
固体物理学-晶体对称性

轴为n度旋转—反演轴,又称为n度象转轴。只有1,2,3,4,6。
(2)符号表示
1,2,3,4,6
2.n度象转轴简析
n度象转轴实际上并不都是独立的,通过下面的分析,可以
得到象旋转轴只有 4 是独立的。
Solid State Physics
(1) 1 象转轴—实际上就是对称心i
z ( u轴 )
A
A 点 绕 旋 转 轴 (z 轴 ) 旋
于不同的群。由旋转、中心反演、镜象和旋转--反演点对称操作构成的群,
称作点群。
理论证明,所有晶体只有32种点群,即只有32种不同的点对称操作类型。
这种对称性在宏观上表现为晶体外形的对称及物理性质在不同方向上的对称性。
所以又称宏观对称性。
**在数学分析中需要考虑晶体结构周期性重复的制约。当晶体具有一个以上
如图所示,A和A'等同,如同镜子一样。
2.表示方式
(1)熊夫利符号表示— ;
(2)国际符号表示—m。
z
A
A
y
O
x
x , y, z
A
A
x , y, z
O-xy 相当于镜面。
Solid State Physics
镜面操作的数学描述
如以x3=0面作为对称面,镜象是将图形的任何一点
0 0
0
0
1
|A|=1 or -1
单位矩阵
Solid State Physics
基本对称操作
平移(Translation)
中心反演(Inversion)—具有对称中心
转动(Rotation)—具有对称轴
镜面(Reflection)—具有对称面
平移是一切晶体的内部结构都具有的对称性
晶体的对称性和分类

2
4
2 4
晶体中独立的宏观对称操作 (或对称元素)只有8种,
即:1、2、3、4、6、i、4m、 。其中数字n(1、2、
3、4、6)表示纯转动对称操作(或转动轴);i表示中心
反演(或对称中心);m表示镜面反映(或对称镜
面这)。种表示方法属于国际符号(International not
ation)标记法,是海尔曼(Hermann)和毛衮(Ma
晶体结构可以用布拉维格子或布拉维点阵来描 述,这样以来,晶体变为无限大的空间点阵.从而, 晶体具有了平移对称性,借助于点阵平移矢量,晶 格能够完全复位.我们把考虑平移后的对称性称 为晶体的微观对称性.
由于晶体的宏观对称操作不包含平移,所以宏 观对称操作时,晶体至少保持有一个点不动,相应 的对称操作又称为点对称操作.
a23
y
z z a31 a32 a33 z
其中: r
x y
z
x
r
y
z
a11
A
a21
a31
a12 a22 a32
a13
a23
a33
x x a11 a12 a13 x
y
y
a21
a22
a23
y
z z a31 a32 a33 z
x x
y
y
cos
z
sin
z
y
sin
z
cos
x 1 0
0 x
y
0
cos
sin
y
z 0 sin cos z
所以,绕x轴旋转的变换矩阵为:
1 0
0
Ax
0
cos
sin
高中化学竞赛【晶体的对称性】

晶面3
c
晶面2
晶面1
b a
晶面指标示例
例题: 1. 某一立方晶系晶体,晶胞的顶点位置全为
A占据,棱心为B占据, 体心为C占据。①写
出此晶体的化学组成; ②写出A、B、C的
(4)十四种空间点阵形式 立方晶系有立方简单点阵P (立方P ) 、立方
体心点阵I (立方I ) 、立方面心点阵F (立方F );四 方晶系只有四方简单点阵P (四方P ) 、四方体心 点阵I (四方I ); 正交晶系有正交P 、正交I 、正交 F 、正交C (或侧心A和B); 单斜晶系有单斜P 、 单斜C ; 三方、六方、三斜都只有素格子。可见, 晶体只有14种空间点阵型式。见下图。
晶体的对称性
1.晶体的宏观对称性 晶体的宏观对称性就是晶体外型的对称性。
也就是有限物体的对称性。
方铅矿
金绿宝石
(1)晶体的宏观对称元素: 由于习惯原因, 晶体宏观对称元素与分
子对称性中的对称元素名称、符号都不完全 相同。
对称元素 旋转轴n 反映面或镜面m 对称中心i
反轴 n
对应对称操作 旋转L(α) 反映M 倒反I 旋转倒反L(α) I
3.晶面和晶面指标 晶面:晶体中平面点阵所在的平面。 晶面指标: 晶面在三个晶轴上的倒易
截数的互质整数之比。记为: (h*k*l*) 晶面与晶面的交线称为晶棱, 晶棱与
直线点阵对应。
例如, 右图中晶面 1在3个晶轴上的截数 分别:1/2,∞,∞, 因此倒 易截数:2,0,0, 划成互质 整数比后成为: 1:0:0, 因此晶面1的晶面指标 是: (100)。
晶体的对称性

点群的Schönflies符号:
主轴:Cn、Dn、Sn、T和O Cn:n次旋转轴; Sn : n次旋转-反映轴; Dn:n次旋转轴加上一个与之垂直的二次轴 T: 四面体群; O: 八面体群。
脚标:h、v、d h:垂直于n次轴(主轴)的水平面为对称面; v:含n次轴(主轴)在内的竖直对称面; d:垂直于主轴的两个二次轴的平分面为对称面。
用的几何变换(旋转和反射)都是正交变换——保持
两点距离不变的变换: ⎛ x ' ⎞ ⎛ a11 a12 a13 ⎞ ⎛ x ⎞
数学上可以写作:
⎜ ⎜⎜⎝
y z
' '
⎟ ⎟⎟⎠
=
⎜ ⎜⎜⎝
a21 a31
a22 a32
a23 a33
⎟⎟⎟⎠i⎜⎜⎜⎝
y z
⎟ ⎟⎟⎠
其中 Aij 为正交矩阵
从解析几何知道,符合正交 变换的是:绕固定轴的转动 (Rotation about an axis)
准晶态结构特点:具有长程取向序,没有长程平移对 称性。
其实准晶可以看作是具有平移对称性的六维超空间在三维真实 空间的投影
黄昆书 47-48 陈长乐书 20-22
1974年Penrose提出的数学游戏
五次对称的黄金分割无理数
边长有两种取值:1, 1+ 5 = 1.618
2
二十面体AlPdMn表面的STM图像
D2、C2V、D2h
C3、S6、D3 C3V、D3d
C4、S4、C4h、D4 C4V、D2d、D4h C6、C3h、C6h、 D6、C6V、D3h、
D6h T、Th、Td
O、Oh
P、C P、C、I、
F R P、I
H
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章晶体的微观对称性第一节十四种空间格子第二节晶体的微观对称元素第三节微观对称元素组合原理第四节空间群第五节等效点系第一节十四种空间格子•点阵的对称类型三斜格子:C单斜格子:L2 PC正交格子:3L23PC四方格子:L4 4L25PC三方格子:L3 3L2 3PC六方格子:L6 6L2 7PC立方格子:3L4 4L3 6L2 9PC•空间格子的选取方式•布拉威法则:1、划分出来的平行六面体单位必须充分地反映晶体的固有对称性。
2、在不违背晶体固有对称性的条件下,平行六面体单位的棱间直角数尽量多。
3、在满足条件1和2的前提下,平行六面体单位的体积应为最小。
D6h D2h•十四种空间格子1)三斜晶系:P三斜I = 三斜P三斜C = 三斜P三斜F = 三斜P2)单斜晶系:P,C单斜B = 单斜P,单斜I = 单斜C,单斜F =单斜C 3)正交晶系:P,C,I,F4)四方晶系:P,I四方C = 四方P,四方F = 四方IA或B面加心会破坏四次轴对称性。
5)立方晶系:P,I,F单独在某一面上加心会破坏四个三次轴对称性。
在平行六面体体心或底心位置加阵点会破坏六次轴对称性。
在平行六面体面心位置加阵点会破坏六次轴对称性。
绿色点在c/2置,蓝色点在0或位置。
位置。
黄色点在c/3位置。
六方格子与三方格子的关系六方平面点阵沿垂直于ab 面的c方向平移得到六方晶系的空间点阵。
六方平面点阵平移矢量为:t2a/3 + b/3 + c/3, 得到的空间点阵只有三次轴,为三方晶系的空间点阵。
心复杂格子,它是一个六方三重复格子。
宏观微观第二节晶体的微观对称元素晶体的宏观对称性是晶体结构微观对称性的反映。
晶体的宏观对称元素在微观对称中也同样存在。
晶体结构是由其结构单位(晶胞)在三维空间上的无限排列,晶体的微观对称性还具有宏观对称不能出现的对称元素—平移,平移和旋转或反映的复合对称操作,又产生新的对称元素,螺旋轴和滑移面。
它们是在微观的无限空间中所特有的,称为微观对称元素。
微观对称性和宏观对称性的主要区别:1、宏观对称性对称元素必须相交一点,微观对称性中对称元素不须交于一点,可以在三维空间无限分布。
2、宏观对称性中对称元素只考虑方向,微观对称性中需要考虑对称元素的相互位置关系。
等同点:晶体结构中具有相同的物质环境和几何环境的质点。
等效(质)点:晶体结构中由对称元素联系起来的一组质点,表现为具有相同的物质环境和化学环境的质点。
同一晶体结构中的同一组等效质点可以属于不同的等同点,但同一组等同点必属于同一组等效质点。
同一组等同点的任意两点不存在对映体,但同一组等效质点的某两个质点可以互为对映体。
晶体结构中的等同点的排列规律性,反映了晶体结构的平移周期性。
晶体中的等效质点的排列规律性,形成了晶体的微观对称性。
点阵(平移轴):对应的对称操作为平移。
点阵反映了晶体结构的周期性,这种周期性也就是点阵的平移复原的特性。
对于点阵,连接任意两个阵点的位置矢量:R= m a+ n b+ p c,进行平移可以使点阵复原,表现在晶体结构上就是使在三维空间无限伸展的相同部分得以重复。
R可以定义为晶体微观结构平移的方向矢量。
十四种空间格子反映了晶体结构中平移对称的组合规律。
任何一种点阵格子,都具有基本平移矢量a, b, c以及a + b, a + c, b + c, a + b + c等。
对于复格子,则增加附加平移矢量:C格子:(a + b)/2, B格子:(a + c)/2, A格子:(b + c)/2I格子:(a + b + c)/2F格子:(a + b)/2, (a + c)/2, (b + c)/2滑移面(glide plane):晶体结构沿着某一平面进行反映,再平行于该平面平移一定距离,结构中的每个质点均与相同的质点重复。
相应的对称操作为反映和平移的复合操作。
NaCl 结构沿[001]方向的投影m •b =m在晶体的微观对称性中,反映操作等同于反映与点阵某个平移矢量的复合操作。
对于晶体结构中的反映和平移复合操作,如平移分量为点阵平移矢量的分数值,则进行反映操作所依据的平面就是滑移面。
m •b/2 = bCO2分子晶体对于滑移面,为使滑移面的平移分量不与点阵矛盾,经过两次滑移操作,其平移分量和应属于点阵的平移矢量。
点阵格子的平移矢量都有a, b, c及a+b, a+c, b+c, a+b+c,对应的滑移面平移分量可以为:1、a/2, b/2, c/2 –a、b、c滑移面,统称为轴向滑移面。
2、(a+b)/2, (a+c)/2, (b+c)/2, (a+b+c)/2 –n滑移面,对角线滑移面。
复格子产生附加平移矢量:(a+b)/2, (a+c)/2, (b+c)/2, (a+b+c)/2,对应滑移面的平移分量可以为:3、(a+b)/4, (a+c)/4, (b+c)/4, (a+b+c)/4 –d滑移面,金刚石滑移面金刚石结构沿[001]方向的投影螺旋轴(screw axe):晶体结构围绕一条直线旋转一定角度后,再沿着该直线方向平移一定距离,结构中的每个质点均与相同质点重复。
相应的对称操作为旋转和平移的复合操作。
4 •c =4在晶体的微观对称性中,旋转操作等同于旋转与点阵平移矢量的复合操作。
对于晶体结构中的旋转和平移复合操作,如平移分量为点阵平移矢量的分数值。
则进行旋转操作所依据的直线即为螺旋轴。
2 •c/2 = 21与旋转轴的轴次类似,螺旋轴的轴次n只能为1,2,3,4,6。
为使螺旋轴作用结果与点阵一致,螺旋轴经过n次作用后的平移分量和应为点阵平移矢量的整数倍,即:n t= m T或t = m T/n其中:n为螺旋轴轴次,t为螺旋轴平移分量,T 为晶体结构的点阵平移矢量,m为小于n的正整数。
对于取定的n,m取小于n的不同整数,可以得到不同的类型的螺旋轴,记为nm,表示平移分量为m T/n的n次螺旋轴。
晶体结构中允许存在的螺旋轴类型为:21, 31, 32, 41, 42,43, 61, 62, 63, 64, 65。
c/23c/4金刚石结构沿[001]方向的投影第三节微观对称元素组合原理•平行反映面(滑移面)的组合•平移与正交反映面(滑移面)的组合•平移与斜交反映面(滑移面)的组合•旋转轴(螺旋轴)与垂直平移的组合•旋转轴(螺旋轴)与斜交平移的组合定理一:两个互相平行反映面的连续操作相当于一个平移操作,其平移距离为反映面间距的二倍。
m1 •m2 = Ta1 •a2 = m1 •a/2 •m2 •a/2 = m1 •m2 •a= t•a= T推论:两个平行滑移面的连续操作相当于一个平移操作,并且该平移操作垂直于滑移面的分量也是一个平移操作。
定理二:平移t 及垂直于平移的反映面的连续操作相当于与该反映面相距t /2处的一个反映面的反映操作。
m •t = m •m1 •m2 = I •m2 = m2推论:平移t 及垂直于平移的滑移面的连续操作相当于与该反映面相距t /2处的一个滑移面的反映平移复合操作。
a •t = m •a /2 •t = m2 •a /2 = a2d •a = m •(b+c)/4 •a •= m a/2•(b+c)/4 = d a/2定理三:平移T 与反映面m 斜交,如T 在垂直于反映面的平移分量为t ,平行于反映面的平移分量为g ,则存在一平行于m 的滑移面G ,它与反映面相距t /2,滑移操作的平移分量为g 。
m •T = m •t •g = m1•g = Gm •(a+b)/2 = m •a/2 •b/2 = m a/4•b/2 = b a/4 NaCl结构沿[001]方向的投影推论:平移T与滑移面G斜交,如滑移面的平移分量为g1, T在垂直于滑移面的平移分量为t,平行于滑移面G 的平移分量为g2,则存在一平行于G的滑移面G’,它与滑移面G’相距t/2,滑移操作的平移分量为g1 + g2。
G •T= m •g1 •t•g2 = m1 •g1 •g2 = G’b •(a+b) = m •b/2 •a•b= m •a•b•b/2 = m a/2•b•b/2= m a/2•b/2 = b a/2NaCl结构沿[001]方向的投影推论:基转角为α的螺旋轴A与垂直于它的平移T连续动作相当于与A平行的螺旋轴B,其基转角也为α,旋转方向和平移分量与A相同,且B位置取决于α和T。
定理五:基转角为α的旋转轴A与平移T斜交,如T垂直于A的平移分量为t,平行于A的平移分量为r,则存在一平行于A的螺旋轴B,它的基转角也为α,旋转方向与A相同,平移分量为r,且B位置取决于α和t。
A •T= A •t •r= B’•r= B推论:基转角为α的螺旋轴A与平移T斜交,如A的平移分量为r1,T垂直于A的平移分量为t,平行于A的平移分量为r2,则存在一平行于A的螺旋轴B,它的基转角也为α,旋转方向与A相同,平移分量为r1+r2,且B位置取决于α和t。
A •T= A’•r1 •t•r2 = A’•t•(r1 •r2) = B’•(r1 •r2) = B第四节空间群•晶体的微观对称元素有以下七类:1、旋转轴:1,2,3,4,62、反映面:m3、对称中心:14、反轴:45、螺旋轴:21,31,32,41,42,43,61,62,63,64,656、滑移面:a,b,c,n,d7、平移这七类对称元素的在空间的组合所表现出的对称性的集合即为空间群,它反映了晶体微观结构的全部对称性。
