2.3直线平面垂直的判定及其性质练习题
2.3.1直线与平面垂直的判定(经典)

如图,点Q是_点_P_在_平_面_内_的_射_影_ _线_段_PQ_是点P到平面 的垂线段
(2)斜线
一条直线和一个平面相交,但不和
这个平面垂直,这条直线叫做这个平面
的斜线.
P
斜线和平面的交点
叫做斜足。
从平面外一点向平 面引斜线,这点与斜
R
足间的线段叫做这点
到这个平面的斜线段
思考:平面外一点到一个平面的垂线段有 几条?斜线段有几条?
A
B
O
D
α
C
这条直线垂直于梯形所在的平面。(√ )
(4)若一条直线与一个平面不垂直,则这个平面内
没有与这条直线垂直的直线。(× )
定理应用
四:典型例题
例1 如图,已知 a//b,a,求证 b.
证明:在平面 内作两条相交
直线m,n.
a
b
m n
巩固练习
例2 如图,在三棱锥V—ABC中,VA=VC, AB=BC,求证:VB⊥AC。
如图,长方体ABCD—A1B1C1D1中,棱
AA1,BB1,CC1,DD1 所在直线与底面ABCD的 位置关系如何?它们彼此之间具有什么
位置关系? C1
D1
B1
A1
C
D
B
A
一、线面垂直的性质定理
垂直于同一个平面的两条直线平行
已知:a⊥α, b⊥α, 求证:a // b
证明:
假设 a与b不平行.
记直线b和α的交点为o,
A
A
B
D
CB
C D
过 ABC 的顶点A翻折纸片,得到折痕AD,将翻
折后的纸片竖起放置在桌面上(BD,DC于桌面接
触).
(1)折痕AD与桌面垂直吗?
2.3直线_平面垂直的判定及其性质

【典型例题】 例.如图9-10, 在正三棱柱ABC-A1B1C1中,A1A=AB, D是CC1的中 点,F是A1B的中点.求证: (1) DF平面ABC; (2) AFBD
直线和平面所成的角
1.射影
p O
自一点向平面引垂线,垂足叫做 这点在这个平面上的射影;
这个点与垂足间的线段叫做这点 到这个平面的垂线段。
2、斜线
一条直线和一个平面 A 相交,但不和这个平面垂 直,这条直线叫做这个平 面的斜线,斜线和平面的 B C 交点叫做斜足。 斜线上任意一点在 斜线上一点与斜足间 平面上的射影,一定在 的线段叫做这点到这个平 斜线的射影上。 面的斜线段。 过斜线上斜足以外的一点向平面引垂线,过垂 足和斜足的直线叫做斜线在这个平面上的射影;
思想: 直线与平面垂直
直线与直线垂直
典型例题
例2 如图,已知 a // b, a ,求证 b .
证明:在平面 内作 两条相交直线m,n. 根据直线与平面垂直的定义知 因为直线 a ,
a m, a n.
a
b
m
n
又因为 b // a 所以 b m, b n. 又 m , n , m, n 是两条相交直线, 所以 b .
例 如图,已知A、B是120的二面角 —l—棱l上的两点,线段AC,BD分别 在面,内,且AC⊥l,BD⊥l ,AC=2, BD=1,AB=3,求线段CD的长。 ∠OAC =120
2 2
B C
l
D
A O
AO=BD=1, AC=2
2
CO AC AO 2 AO AC COS120 7
2.3.1直线与平面垂直的判定
直线平面垂直的判定及其性质

定义:如果直线l与平面 α 内的任意一条直线都 垂直,则称直线l和平面 α 互相垂直。
记 作 : l α
l
A
直线l叫做平面 α的垂 线,平面 α 叫做直线l 的垂面,惟一的公共 点A叫做垂足
直线与平面垂直的判定:
l m l n 1 l α m n A m α , α n a//b 2 b α a α
练习7
如图所示,已知ΔADB和ΔADC都是以D为直角顶点 的直角三角形,且AD = BD = CD,∠BAC = 600. (1)求证 : BD⊥平面ADC (2)若H为ΔABC的垂心,求证 : H是D在平面ABC内的射影
D
A B
H
C E
(1 )若 P A P B P C ,则 O是 ΔAB C 的
由(1)知,MN⊥CD,PC∩CD=C, ∴MN⊥平面PCD.
知能迁移1
Rt△ABC所在平面外一点S,且SA=SB=SC,
D为斜边AC中点.(1)求证:SD⊥面ABC;
(2)若AB=BC,求证:BD⊥面SAC.
证明
(1)如图所示,取AB中点E, 连结SE,DE,在Rt△ABC中,
D、E分别为AC、AB的中点, 故DE∥BC, 且DE⊥AB,∵SA=SB,
B C
D
性质定理:两个平面垂直,则一个平面内垂直于交
线的直线 与另一个平面垂直
AB a AB β a
α
α
β
A
a B
练习3.(2009·广东理,5)给定下列四个命题:
①若一个平面内的两条直线与另一个平面都 平行,那么这两个平面相互平行; ②若一个平面经过另一个平面的垂线,那么这 两个平面相互垂直;
直线、平面垂直的判定及其性质(基础训练)

直线、平面垂直的判定及其性质〔根底训练〕〕A.a⊥α⇔b是α内任一直线且a⊥ba⊥α,那么a可与α内的某条直线不垂直a⊥α,那么a可与α没有公共点a和平面α内的某条直线垂直,那么a与α垂直答案:Aa垂直于α内的一条直线,那么a⊥αB.假设a垂直于α内的两条直线,那么a⊥αa垂直于α内的三条直线,那么a⊥αa垂直于α内的两条相交直线,那么a⊥α答案:D不正确的选项是.......〔〕A.假设两条平行线中的一条垂直于某个平面,那么另一条也垂直于这个平面平行线中的一条不垂直于某个平面,那么另一条也不垂直于这个平面三条平行线中的一条垂直于某个平面,那么这三条直线都垂直于这个平面D.假设三条平行线中的一条不垂直于某个平面,那么另两条中可以有一条和这个平面垂直答案:Dl⊥平面α,直线m⊂α,那么有〔〕A.l和m异面B.l和m相交C.l∥mD.l不平行于m答案:D解析:直线l⊥平面α,那么l和平面α有且只有一个交点即垂足P,平面α内任一直线m经过P时,l和m相交,直线m不经过P时,由异面直线的判定定理知,l和m异面,故l和m不会平行.l和平面α内无数条直线垂直,那么〔〕A.l和α相互平行B.l和α相互垂直C.l在α答案:D解析:直线l和平面α内无数条直线垂直,可能关系是l∥α,l⊂α,或l和α相交〔也可能垂直〕,即l和α的位置关系不确定.l和平面α垂直是指〔〕A.l和α内的无数条直线垂直B.l和α内的两条直线垂直C.l和α内的所有直线垂直D.l和α内的某些直线垂直答案:C°的二面角内一点分别向二面角的两个面引垂线,两垂线所成的角与二面角的平面角的关系是〔〕答案:Bα—l—β的大小为ϕ,直线a⊂α,a与β所成的角为θ,那么〔〕A. ϕ≥θB. ϕ≤θϕ>90°时,ϕ>θ;当ϕ≤90°时,ϕ≤θD. ϕ与θ的大小关系不确定 αβl PO CB a答案:A 解析:当ϕ≥90°时,由θ≤90°知ϕ≥θ.当ϕ<90°时,假设a ⊥l ,那么ϕ=θ;假设a 和l 不垂直,设a ∩l =B ,过a 上的点P 作PO ⊥β于O ,作OC ⊥l 于C ,连结PC , 那么∠PBO =θ,∠PCO =ϕ.∵sin θ=PB PO ,sin ϕ=PCPO . 在Rt △PBC 中,PC <PB ,∴sin ϕ>sin θ,∴ϕ>θ. 综上所述,选A.。
(同步)人教新课标A版必修2数学2.3 直线、平面垂直的判定及其性质A卷

人教新课标 A 版必修 2 数学 2.3 直线、平面垂直的判定及其性质 A 卷姓名:________班级:________成绩:________一、 选择题 (共 15 题;共 30 分)1. (2 分) 设 m,n 是两条不同的直线, 是三个不同的平 面,则下列为假命题的是 ( )A.若,则B.若,则C.若,则D.若,则2. (2 分) (2019 高二下·丽水期末) 设 确的是( )为两条不同的直线,为两个不同的平面,下列命题中正A.若,,,则B.若,,,则C.若,,,则D.若,,,则3. (2 分) (2020·晋城模拟) 已知是两条不同的直线,是两个不同的平面,且,,则下列命题中为真命题的是( )A.若 B.若,则 ,则C.若,则D.若,则第 1 页 共 25 页4. (2 分)为正方体,下列结论错误的是( )A.平面B.C.平面D.5. (2 分) (2020 高一下·通州期末) 已知直线“,且”的( )平面 ,直线A . 充分而不必要条件B . 必要而不充分条件C . 充分必要条件D . 既不充分也不必要条件平面 ,则“直线”是6. (2 分) 如图所示,平面四边形折成四面体,使平面中, 平面, ,则下列说法中不正确的是(,将其沿对角线 )A.B.C.D.7. (2 分) (2018 高二上·吕梁月考) 点 P 为 ΔABC 所在平面外一点,PO⊥平面 ABC,垂足为 O,若 PA=PB=PC,则点 O 是 ΔABC 的( )第 2 页 共 25 页A . 内心B . 外心C . 重心D . 垂心8. (2 分) (2020 高一下·石家庄期中) 如图,四棱锥的底面为正方形,,则下列结论中不正确的是( )A. B. C . 平面 D.平面9. (2 分) 已知 是两个平面,直线 l 不在平面 内,l 也不在平面 内,设① 以其中两个作为条件,另一个作为结论,则正确命题的个数为( );② ;③A.0B.1C.2D.3.若第 3 页 共 25 页10. (2 分) (2019 高一上·河南月考) 设 , 表示两个不同平面,m 表示一条直线,下列命题正确的是 ()A.若,,则.B.若,,则.C.若,,则.D.若,,则.11. (2 分) (2019·黄冈模拟) 如图, 的平面, 为圆周上不与点 、 重合的点,为圆 的直径, 于,, 垂直于圆 所在 于 ,则下列不正确的是( )A . 平面平面B . 平面平面C . 平面平面D . 平面平面12. (2 分) (2019 高一上·西安月考) 设 中正确的是( )A.若,则是两条不同的直线,B.若,则C.若,则第 4 页 共 25 页是两个不同的平面,则下列命题D.若,则13. (2 分) (2020 高二上·慈溪期末) 如图,四面体中的面在平面 内,平面,,且平面,已知内,则两点所经过的路程之和等于( ),若将四面体以 为轴转动,使点 落到A. B.C. D. 14. (2 分) 如图,在三棱锥 P-ABC 中,不能证明 AP⊥BC 的条件是( )A . AP⊥PB , AP⊥PCB . AP⊥PB , BC⊥PBC . 平面 BCP⊥平面 PAC , BC⊥PCD . AP⊥平面 PBC15. (2 分) (2020 高一下·成都期末) 在矩形 ABCD 中,AB=2BC=2,点 P 在 CD 边上运动(如图甲),现以 AP为折痕将折起,使得点 D 在平面 ABCP 内的射影 恰好落在 AB 边上(如图乙).设二面角 D-AP-B 的余弦值为 ,则函数的图象大致是( )第 5 页 共 25 页A. B. C.第 6 页 共 25 页D.二、 填空题 (共 7 题;共 7 分)16.(1 分)在三棱锥 P﹣ABC 中,PA⊥PB,PA⊥PC,PC⊥PB,则定点 P 在底面的投影是底面△ABC 的________ 心. 17. (1 分) (2017 高二上·苏州月考) 设 m,n 是两条不同的直线,α、β 是两个不同的平面,则下列命题 不正确的是________. ①若 m⊥n,m⊥α,n α,则 n∥α ②若 m⊥β,α⊥β,则 m∥α 或 m α ③若 m⊥n,m⊥α,n⊥β,则 α⊥β ④若 ∥α,α⊥β,则 ⊥β 18. (1 分) (2018 高二上·吕梁月考) 如图,以等腰直角三角形 ABC 的斜边 BC 上的高 AD 为折痕,把△ABD 和△ACD 折成互相垂直的两个平面后,某学生得出下列四个结论:①BD⊥AC;②△BAC 是等边三角形;③三棱锥 D-ABC 是正三棱锥;④平面 ADC⊥平面 ABC。
直线、平面垂直的判定及其性质(一)(习题)
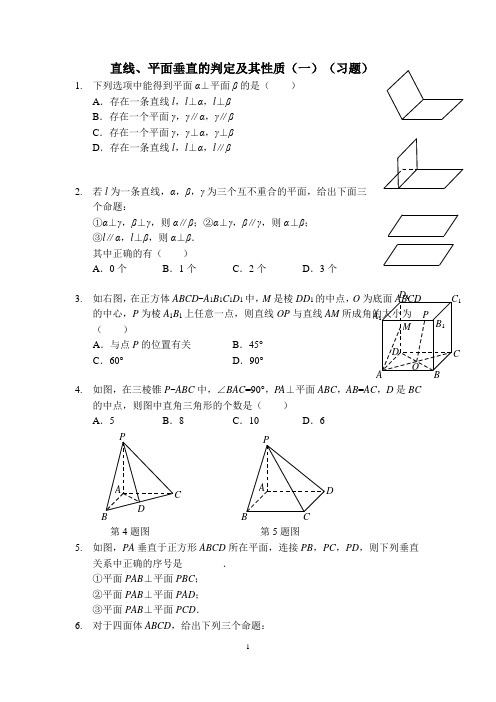
直线、平面垂直的判定及其性质(一)(习题)1. 下列选项中能得到平面α⊥平面β的是( )A .存在一条直线l ,l ⊥α,l ⊥βB .存在一个平面γ,γ∥α,γ∥βC .存在一个平面γ,γ⊥α,γ⊥βD .存在一条直线l ,l ⊥α,l ∥β2. 若l 为一条直线,α,β,γ为三个互不重合的平面,给出下面三个命题:①α⊥γ,β⊥γ,则α∥β;②α⊥γ,β∥γ,则α⊥β; ③l ∥α,l ⊥β,则α⊥β. 其中正确的有( )A .0个B .1个C .2个D .3个3. 如右图,在正方体ABCD -A 1B 1C 1D 1中,M 是棱DD 1的中点,O为底面ABCD的中心,P 为棱A 1B 1上任意一点,则直线OP 与直线AM 所成角的大小为( )A .与点P 的位置有关B .45°C .60°D .90°4. 如图,在三棱锥P -ABC 中,∠BAC =90°,P A ⊥平面ABC ,AB =AC ,D 是BC的中点,则图中直角三角形的个数是( ) 关系中正确的序号是________. ①平面PAB ⊥平面PBC ; ②平面PAB ⊥平面PAD ; ③平面PAB ⊥平面PCD .6. 对于四面体ABCD ,给出下列三个命题:A BC DA 1B 1C 1D 1M P O①若AB=AC,BD=CD,则BC⊥AD;②若AB=CD,AC=BD,则BC⊥AD;③若AB⊥AC,BD⊥CD,则BC⊥AD.其中真命题的序号是________.ADCB7.如图,已知正三棱柱ABC-A1B1C1的侧棱长与底面边长相等,则AB1与侧面ACC1A1所成角的正弦值为________.AB CA1B1C18.如图1,在正三角形ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,如图2,BC=12AB,这时二面角B-AD-C的大小是___________.图1 图2DBAB CD9.如图,在三棱锥A-BCD中,AB=AD,CB=CD,E为BD的中点.求证:BD⊥平面ACE.DCB AE10. 如图,在三棱锥D -ABC 中,BD ⊥底面ABC ,AC =BC ,N 是棱AB 的中点.求证:CN ⊥AD .A BCDN【参考答案】1. D2. C3. D4. B5.①②6.①7.48.60°9.略10.略。
直线与平面垂直性质定理练习题
2.3.3 直线与平面垂直的性质一、选择题1.下列说法正确的是( )A .若l 上有无数个点不在平面α内,则l ∥αB .若直线l 与平面α垂直,则l 与α内的任一直线垂直C .若E 、F 分别为△ABC 中AB 、BC 边上的中点,则EF 与经过AC 边的所有平面平行D .两条垂直的直线中有一条和一个平面平行,则另一条和这个平面垂直2.若M 、n 表示直线,α表示平面,则下列命题中,正确命题的个数为( )① ⎭⎪⎬⎪⎫m ∥n m ⊥α⇒n ⊥α; ②⎭⎪⎬⎪⎫m ⊥αn ⊥α⇒M ∥n ;③⎭⎪⎬⎪⎫m ⊥αn ∥α⇒M ⊥n; ④⎭⎪⎬⎪⎫m ∥αm ⊥n⇒n ⊥α. A .1 B .2 C .3 D .43.已知直线PG ⊥平面α于G ,直线EF ⊂α,且PF ⊥EF 于F ,那么线段PE ,PF ,PG 的大小关系是( )A .PE >PG >PFB .PG >PF >PEC .PE >PF >PGD .PF >PE >PG4.PA 垂直于以AB 为直径的圆所在平面,C 为圆上异于A ,B 的任一点,则下列关系不正确的是( )A .PA ⊥BCB .BC ⊥平面PAC C .AC ⊥PBD .PC ⊥BC 5.下列命题:①垂直于同一直线的两条直线平行; ②垂直于同一直线的两个平面平行; ③垂直于同一平面的两条直线平行; ④垂直于同一平面的两平面平行. 其中正确的个数是( ) A .1 B .2 C .3 D .46.在△ABC 所在的平面α外有一点P ,且PA =PB =PC ,则P 在α内的射影是△ABC 的( )A.垂心 B.内心 C.外心 D.重心二、填空题7.线段AB在平面α的同侧,A、B到α的距离分别为3和5,则AB的中点到α的距离为________.8.直线a和b在正方体ABCD-A1B1C1D1的两个不同平面内,使a ∥b成立的条件是________.(只填序号)①a和b垂直于正方体的同一个面;②a和b在正方体两个相对的面内,且共面;③a和b平行于同一条棱;④a和b在正方体的两个面内,且与正方体的同一条棱垂直.9.如图所示,平面ABC⊥平面ABD,∠ACB=90°,CA=CB,△ABD 是正三角形,O为AB中点,则图中直角三角形的个数为________.三、解答题10.如图所示,在正方体ABCD—A1B1C1D1中,M是AB上一点,N是A1C的中点,MN⊥平面A1DC.求证:(1)MN∥AD1;11.如图所示,设三角形ABC的三个顶点在平面α的同侧,AA′⊥α于A′,BB′⊥α于B′,CC′⊥α于C′,G、G′分别是△ABC 和△A′B′C′的重心,求证:GG′⊥α.2.3.4 平面与平面垂直的性质1.平面与平面垂直的性质定理:两个平面垂直,则一个平面内________于________的直线与另一个平面垂直.用符号表示为:α⊥β,α∩β=l,a⊂α,a⊥l⇒________.2.两个重要结论:(1)如果两个平面互相垂直,那么经过第一个平面内的一点垂直于第二个平面的直线在________________________.图形表示为:符号表示为:α⊥β,A∈α,A∈a,a⊥β⇒________.(2)已知平面α⊥平面β,a⊄α,a⊥β,那么________(a与α的位置关系).一、选择题1.平面α⊥平面β,直线a∥α,则( )A.a⊥βB.a∥βC.a与β相交 D.以上都有可能2.平面α∩平面β=l,平面γ⊥α,γ⊥β,则( )A.l∥γB.l⊂γC.l与γ斜交 D.l⊥γ3.若平面α与平面β不垂直,那么平面α内能与平面β垂直的直线有( )A.0条 B.1条 C.2条 D.无数条4.设α-l-β是直二面角,直线a⊂α,直线b⊂β,a,b与l都不垂直,那么( )A.a与b可能垂直,但不可能平行B.a与b可能垂直,也可能平行C.a与b不可能垂直,但可能平行D.a与b不可能垂直,也不可能平行5.已知两个平面互相垂直,那么下列说法中正确的个数是( ) ①一个平面内的直线必垂直于另一个平面内的无数条直线②一个平面内垂直于这两个平面交线的直线必垂直于另一个平面内的任意一条直线③过一个平面内一点垂直于另一个平面的直线,垂足必落在交线上④过一个平面内的任意一点作交线的垂线,则此直线必垂直于另一个平面A .4B .3C .2D .16.如图所示,平面α⊥平面β,A ∈α,B ∈β,AB 与两平面α、β所成的角分别为π4和π6.过A 、B 分别作两平面交线的垂线,垂足分别为A ′、B ′,则AB ∶A ′B ′等于( )A .2∶1B .3∶1C .3∶2D .4∶3 二、填空题7.若α⊥β,α∩β=l ,点P ∈α,PD /∈l ,则下列命题中正确的为________.(只填序号)①过P 垂直于l 的平面垂直于β; ②过P 垂直于l 的直线垂直于β; ③过P 垂直于α的直线平行于β; ④过P 垂直于β的直线在α内. 三、解答题8.如图,在三棱锥P -ABC 中,PA ⊥平面ABC ,平面PAB ⊥平面PBC .求证:BC ⊥AB .9.如图所示,P 是四边形ABCD 所在平面外的一点,四边形ABCD 是∠DAB =60°且边长为a 的菱形.侧面PAD 为正三角形,其所在平面垂直于底面ABCD.(1)若G为AD边的中点,求证:BG⊥平面PAD;(2)求证:AD⊥PB.10.如图所示,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点,求证:(1)DE=DA;(2)平面BDM⊥平面ECA;(3)平面DEA⊥平面ECA.。
直线、平面垂直的判定及其性质练习题(基础、经典、好用)
直线、平面垂直的判定及其性质一、选择题1.α、β、γ为不同的平面,m,n,l为不同的直线,则m⊥β的一个充分条件是() A.n⊥α,n⊥β,m⊥α B.α∩γ=m,α⊥γ,β⊥γC.α⊥γ,β⊥γ,m⊥α D.α⊥β,α∩β=l,m⊥l2.(2013·深圳模拟)设a,b是两条不同的直线,α、β是两个不同的平面,则下列四个命题中正确命题的个数是()①若a⊥b,a⊥α,b⊄α,则b∥α;②若a∥α,a⊥β,则α⊥β;③若a⊥β,α⊥β,则a∥α或a⊂α;④若a⊥b,a⊥α,b⊥β,则α⊥β.A.1 B.2 C.3 D.4图7-5-123.如图7-5-12,PA⊥正方形ABCD,下列结论中不正确的是()A.PB⊥BC B.PD⊥CDC.PD⊥BD D.PA⊥BD图7-5-134.如图7-5-13正方体ABCD—A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=12,则下列结论中错误的是()A.AC⊥BEB.EF∥平面ABCDC.三棱锥A—BEF的体积为定值D.△AEF的面积与△BEF的面积相等5.如图7-5-14所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°.将△ADB沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A—BCD.则在三棱锥A—BCD中,下列命题正确的是()图7-5-14A.AD⊥平面BCDB.AB⊥平面BCDC.平面BCD⊥平面ABCD.平面ADC⊥平面ABC二、填空题6.(2012·江苏高考)如图7-5-15,在长方体ABCD-A1B1C1D1中,AB=AD=3 cm,AA1=2 cm,则四棱锥A-BB1D1D的体积为________cm3.图7-5-15图7-5-167.如图7-5-16所示,在四棱锥P—ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足________时,平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可).图7-5-178.如图7-5-17所示,PA⊥圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E、F分别是点A在PB、PC上的正投影,给出下列结论:①AF⊥PB;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC.其中正确结论的序号是________.三、解答题9.(2012·江苏高考)如图7-5-18,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E 分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.图7-5-18求证:(1)平面ADE⊥平面BCC1B1;(2)直线A1F∥平面ADE.图7-5-1910.(2013·揭阳模拟)如图7-5-19,在四棱锥S—ABCD中,平面SAD⊥平面ABCD.四边形ABCD为正方形,且P为AD的中点,Q为SB的中点.(1)求证:CD⊥平面SAD;(2)求证:PQ∥平面SCD;(3)若SA=SD,M为BC的中点,在棱SC上是否存在点N,使得平面DMN⊥平面ABCD,并证明你的结论.图7-5-2011.(2012·浙江高考)如图7-5-20,在侧棱垂直底面的四棱柱ABCD-A1B1C1D1中,AD∥BC,AD⊥AB,AB=2,AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E 与直线AA1的交点.(1)证明:①EF∥A1D1;②BA1⊥平面B1C1EF.(2)求BC1与平面B1C1EF所成的角的正弦值.解析及答案一、选择题1.【解析】由n⊥α,n⊥β知α∥β,又m⊥α,∴m⊥β,但当m⊥β时,n⊥α,n⊥β不一定成立,故选A.【答案】A2.【解析】由空间线面位置关系容易判断①②③④均正确.【答案】D3.【解析】由CB⊥BA,CB⊥PA,PA∩BA=A,知CB⊥平面PAB,故CB⊥PB,即A正确;同理B正确;由条件易知D正确,故选C.【答案】C4.【解析】连接BD,则AC⊥平面BB1D1D,BD∥B1D1,从而A、B、C正确.因为点A、B到直线B1D1的距离不相等,所以△AEF与△BEF的面积不相等.【答案】D5.【解析】在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,∴BD⊥CD,又平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD,∴CD⊥平面ABD,∴CD⊥AB,又AD⊥AB,故AB⊥平面ADC,从而平面ABC⊥平面ADC.【答案】D二、填空题6.【解析】关键是求出四棱锥A-BB1D1D的高.连接AC交BD于O,在长方体中,∵AB=AD=3,∴BD=32且AC⊥BD.又∵BB1⊥底面ABCD,∴BB1⊥AC.又DB∩BB1=B,∴AC⊥平面BB1D1D,∴AO为四棱锥A-BB1D1D的高且AO=12BD=322.∵S矩形BB1D1D=BD×BB1=32×2=62,∴V A-BB1D1D=13S矩形BB1D1D·AO=13×62×322=6(cm3).【答案】 67.【解析】由定理可知,BD⊥PC.∴当DM⊥PC时,即有PC⊥平面MBD,而PC⊂平面PCD.∴平面MBD⊥平面PCD.【答案】DM⊥PC(答案不唯一)8.【解析】由题意知PA⊥平面ABC,∴PA⊥BC,又AC⊥BC,PA∩AC=A,∴BC⊥平面PAC.∴BC⊥AF.∵AF⊥PC,BC∩PC=C,∴AF⊥平面PBC,∴AF⊥PB,AF⊥BC.又AE⊥PB,AE∩AF=A,∴PB⊥平面AEF.∴PB⊥EF.故①②③正确.【答案】①②③三、解答题9.【证明】(1)因为ABC-A1B1C1是直三棱柱,所以CC1⊥平面ABC.又AD⊂平面ABC,所以CC1⊥AD.又因为AD⊥DE,CC1,DE⊂平面BCC1B1,CC1∩DE=E,所以AD⊥平面BCC1B1.又AD⊂平面ADE,所以平面ADE⊥平面BCC1B1.(2)因为A1B1=A1C1,F为B1C1的中点,所以A1F⊥B1C1.因为CC1⊥平面A1B1C1,且A1F⊂平面A1B1C1,所以CC1⊥A1F.又因为CC1,B1C1⊂平面BCC1B1,CC1∩B1C1=C1,所以A1F⊥平面BCC1B1.由(1)知AD⊥平面BCC1B1,所以A1F∥AD.又AD⊂平面ADE,A1F⊄平面ADE,所以A1F∥平面ADE.10.【证明】(1)因为四边形ABCD为正方形,所以CD⊥AD.又平面SAD⊥平面ABCD,且平面SAD∩平面ABCD=AD,所以CD⊥平面SAD.(2)取SC的中点R,连接QR,DR.由题意知:PD∥BC且PD=12BC.在△SBC中,Q为SB的中点,R为SC的中点,所以QR∥BC且QR=12BC.所以QR∥PD且QR=PD,则四边形PDRQ为平行四边形,所以PQ∥DR.又PQ⊄平面SCD,DR⊂平面SCD,所以PQ∥平面SCD.(3)存在点N为SC的中点,使得平面DMN⊥平面ABCD.连接PC、DM交于点O,连接PM、SP、NM、ND、NO,因为PD∥CM,且PD=CM,所以四边形PMCD为平行四边形,所以PO=CO.又因为N为SC的中点,所以NO∥SP.易知SP⊥AD,因为平面SAD⊥平面ABCD,平面SAD∩平面ABCD=AD,并且SP⊥AD,所以SP⊥平面ABCD,所以NO⊥平面ABCD.又因为NO⊂平面DMN,所以平面DMN⊥平面ABCD.11.【证明】(1)①因为C1B1∥A1D1,C1B1⊄平面ADD1A1,所以C1B1∥平面A1D1DA.又因为平面B1C1EF∩平面A1D1DA=EF,所以C1B1∥EF,所以A1D1∥EF.②因为BB1⊥平面A1B1C1D1,所以BB1⊥B1C1.又因为B1C1⊥B1A1,所以B1C1⊥平面ABB1A1,所以B1C1⊥BA1.在矩形ABB1A1中,F是AA1的中点,tan∠A1B1F=tan∠AA1B=22,即∠A1B1F=∠AA1B,故BA1⊥B1F.所以BA1⊥平面B1C1EF.(2)设BA1与B1F交点为H,连接C1H.由(1)知BA1⊥平面B1C1EF,所以∠BC1H是BC1与平面B1C1EF所成的角.在矩形AA1B1B中,AB=2,AA1=2,得BH=4 6 .在Rt△BHC1中,BC1=25,BH=46,得sin∠BC1H=BHBC1=3015.所以BC1与平面B1C1EF所成角的正弦值是30 15.。
直线、平面垂直的判定及其性质经典例题
直线、平面垂直的判定及其性质经典例题经典例题透析类型一、直线和平面垂直的定义1.下列命题中正确的个数是( )①如果直线与平面内的无数条直线垂直,则;②如果直线与平面内的一条直线垂直,则;③如果直线不垂直于,则内没有与垂直的直线;④如果直线不垂直于,则内也可以有无数条直线与垂直.A.0B.1 C.2 D.3答案:B解析:当内的无数条直线平行时,与不一定垂直,故①不对;当与内的一条直线垂直时,不能保证与垂直,故②不对;当与不垂直时,可能与内的无数条直线垂直,故③不对;④正确.故选B.总结升华:注意直线和平面垂直定义中的关键词语.举一反三:【变式1】(2010 山东)在空间,下列命题正确的是A.平行直线的平行投影重合B.平行于同一直线的两个平面平行C.垂直于同一平面的两个平面平行D.垂直于同一平面的两条直线平行答案:D解析:A项,平行直线的平行投影也可以是两条平行线;B项,平行于同一直线的两个平面可平行、可相交;C项,垂直于同一平面的两个平面可平行、可相交;D项,正确.总结升华:本题主要考察对基础知识的掌握.类型二、直线和直线、平面垂直的判定2.(2011 广东理18)如图,在椎体P-ABCD中,ABCD是边长为1的菱形,且∠DAB=60,,PB=2, E,F分别是BC,PC的中点.(1)证明:AD 平面DEF;(2)求二面角P-AD-B的余弦值.解析:(1)证明:取AD中点G,连接PG,BG,BD.∵PA=PD,∴,在中,,∴为等边三角形,∴,∴AD⊥平面PBG,∴又PB//EF,得,又∵DE//GB,得AD⊥DE,又,∴AD⊥平面DEF.(2)为二面角P—AD—B的平面角,在,在中,总结升华:要判定一条已知直线和一个平面是否垂直,取决于在这个平面内能否找出两条相交直线和这条直线垂直,至于这两条相交直线是否和已知直线有公共点,则无关紧要.举一反三:【变式1】如图所示,直三棱柱中,∠ACB=90°,AC=1,,侧棱,侧面的两条对角线交点为D,的中点为M.求证:平面CBD ⊥平面BDM.证明:如下图,连接、、,则.∵,∴为等腰三角形.又知D为其底边的中点,∴.∵,,∴.又,∴.∵为直角三角形,D为的中点,∴,.又,,∴..即CD⊥DM.∵、为平面BDM内两条相交直线,∴CD⊥平面BDM.又∵,∴平面CBD⊥平面BDM.总结升华:处理面面垂直问题转化为处理线面垂直问题,进一步转化为处理线线垂直问题.所以证明平面与平面垂直,只要在一个平面内找到两条相交直线和另一个平面内的一条直线垂直即可.类型三、直线和平面所成的角3.如图所示,已知∠BOC在平面内,OA是平面的斜线,且∠AOB=∠AOC=60°,OA=OB=OC=,BC=,求OA和平面所成的角.解析:∵,∠AOB=∠AOC=60°,∴△AOB、△AOC为正三角形,∴.∵,∴,∴△ABC为直角三角形.同理△BOC也为直角三角形.过A作AH垂直平面于H,连接OH,∵AO=AB=AC,∴OH=BH=CH,H为△BOC的外心.∴H在BC上,且H为BC的中点.∵Rt△AOH中,,∴,∴∠AOH=45°.即AO和平面所成角为45°.总结升华:(1)确定点在平面内的射影的位置,是解题的关键,因为只有确定了射影的位置,才能找到直线与平面所成的角,才能将空间的问题转化为平面的问题来解.(2)求斜线与平面所成的角的程序:①寻找过直线上一点与平面垂直的直线;②连接垂足和斜足得出射影,确定出所求解;③把该角放入三角形计算.(3)直线和平面所成的角,也应考虑到直线和平面垂直、直线和平面平行或在平面内诸情况,也就是直线和平面成90°角和0°角的情况,所以求线面所成角时,应想到以上两种情况.举一反三:【变式1】(2011 全国大纲19)如图,四棱锥中,,,侧面为等边三角形,.(Ⅰ)证明:;(Ⅱ)求与平面所成角的大小.解析:(I)取AB中点E,连结DE、SE,∴四边形BCDE为矩形,DE=CB=2,∵侧面为等边三角形∴又∵SD=1,,∴为直角.又∵,∴AB⊥平面SDE,∴.又SD与两条相交直线AB、SE都垂直.∴SD⊥平面SAB.(II)作垂足为F,FG⊥BC,垂足为G,连结SG∵AB⊥平面SDE,∴平面ABCD⊥平面SED.∴SF⊥平面ABCD,∵∴,又∵FG⊥BC,∴BC⊥平面SFG,∵∴平面SBC⊥平面SFG.作,H为垂足,则FH⊥平面SBC.又∵在中,,在中,∴,即F到平面SBC的距离为.∵ED//BC,∴ED//平面SBC,∴E到平面SBC的距离d也是.设AB与平面SBC所成的角为α,则.∴与平面所成的角为.【变式2】如图所示,在正三棱柱中,侧棱长为,底面三角形的边长为1,则与侧面所成的角是________.答案:解析:如下图.由题取AC中点O,连接BO.则BO⊥平面.故为与平面所成角.又在中,,.∴,∴.类型四、二面角4.如图所示,在四面体ABCD中,△ABD、△ACD、△BCD、△ABC都全等,且,,求以BC为棱,以面BCD和面BCA为面的二面角大小.解析:取BC的中点E,连接AE、DE,∵AB=AC,∴AE⊥BC.又∵△ABD≌△ACD,AB=AC,∴DB=DC,∴DE⊥BC.∴∠AED为二面角的平面角.又∵△ABC≌△BDC,∴AD=BC=2,在Rt△DEB中,DB=,BE=1,∴,同理.在△AED中,∵,,∴,∴∠AED=90°.∴以面BCD和面ABC为面的二面角大小为90°.总结升华:确定二面角的平面角,常常用定义来确定.举一反三:【变式1】已知D、E分别是正三棱柱的侧棱和上的点,且.求过D、E、C1的平面与棱柱的下底面所成的二面角的大小.解析:如图,在平面内延长DE和交于点F,则F是面与面的公共点,为这两个平面的交线,∴所求二面角就是的平面角.∵,且,∴E、分别DF和A1F的中点.∵,∴.又面,面,∴面,而面.∴.∴是二面角的平面角,由已知,∴.总结升华:当所求的二面角没有给出它的棱时,找出二面角的两个面的两个公共点,从而找出它的棱,进而求其平面角的大小即可.类型五、平面与平面垂直的判定5.在四面体ABCD中,,AB=AD=CB=CD=AC=,如图所示.求证:平面ABD⊥平面BCD.证明:∵△ABD与△BCD是全等的等腰三角形,∴取BD的中点E,连接AE、CE,则AE⊥BD,BD⊥CE,∴∠AEC为二面角A-BD-C的平面角.在△ABD中,,,∴.同理.在△AEC中,,,由于,∴AE⊥CE,即∠AEC=90°,即二面角A-BD-C的平面角为90°.∴平面ABD⊥平面BCD.总结升华:利用两个平面互相垂直的定义可以直接判定两个平面垂直,判定的方法是(1)找出两个相交平面的平面角;(2)证明这个平面角是直角;(3)根据定义,这两个平面互相垂直.举一反三:【变式1】如图所示,在空间四边形ABCD中,AB=BC,CD=DA,E、F、G分别为CD、DA和对角线AC的中点,求证:平面BEF⊥平面BGD.证明:∵AB=BC,CD=AD,G是AC的中点,∴BG⊥AC,DG⊥AC,∴AC⊥平面BGD.又EF∥AC,∴EF⊥平面BGD.∵EF平面BEF,∴平面BDG⊥平面BEF.总结升华:证面面垂直的方法:(1)证明两平面构成的二面角的平面角为90°;(2)证明一个平面经过另一个平面的一条垂线,将证明“面面垂直”的问题转化为证明线面垂直的问题.【变式2】如图所示,在Rt△AOB中,,斜边AB=4.Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C是直二面角.D是AB的中点.求证:平面COD⊥平面AOB;证明:由题意,CO⊥AO,BO⊥AO,∴∠BOC是二面角B-AO-C的平面角.又∵二面角B-AO-C是直二面角.∴CO⊥BO.又∵AO∩BO=O,∴CO⊥平面AOB.又CO平面COD,∴平面COD⊥平面AOB.【变式3】过点P引三条长度相等但不共面的线段PA、PB、PC,有∠APB=∠APC=60°,∠BPC=90°,求证:平面ABC⊥平面BPC.证明:如图,已知PA=PB=PC=a,由∠APB=∠APC=60°,△PAC,△PAB为正三角形,则有:PA=PB=PC=AB=AC=a,取BC中点为E直角△BPC中,,,由AB=AC,AE⊥BC,直角△ABE中,,,,在△PEA中,,,∴,平面ABC⊥平面BPC.类型六、综合应用6.如图所示,△ABC为正三角形,CE⊥平面ABC,BD∥CE,且CE=AC=2BD,M是AE的中点,求证:(1)DE=DA;(2)平面BDM⊥平面ECA;(3)平面DEA⊥平面ECA.证明:(1)取EC的中点F,连接DF.∵CE⊥平面ABC,∴CE⊥BC.易知DF∥BC,CE⊥DF.∵BD∥CE,∴BD⊥平面ABC.在Rt△EFD和Rt△DBA中,∵,,∴Rt△EFD≌Rt△DBA.故DE=AD.(2)取AC的中点N,连接MN、BN,MN CF.∵BD CF,∴MN BD.N平面BDM.∵EC⊥平面ABC,∴EC⊥BN.又∵AC⊥BN,∴BN⊥平面ECA.又∵BN平面MNBD,∴平面BDM⊥平面ECA.(3)∵DM∥BN,BN⊥平面ECA,∴DM⊥平面ECA.又∵DM平面DEA,∴平面DEA⊥平面ECA.总结升华:本题涉及线面垂直、面面垂直的性质和判定,这里证明的关键是BN⊥平面ECA,应充分体会线线垂直、线面垂直与面面垂直的关系.7.如图所示,已知PA⊥矩形ABCD所在平面,M、N分别是AB、PC的中点.(1)求证:MN∥平面PAD;(2)求证:MN⊥CD;(3)若∠PDA=45°,求证:MN⊥平面PCD.思路点拨:要证明MN∥平面PAD,须证MN平行于平面PAD内某一条直线.注意到M、N分别为AB,PC的中点,可取PD的中点E,从而只须证明MN∥AE即可.证明如下.证明:(1)取PD的中点E,连接AE、EN,则,故AMNE为平行四边形,∴MN∥AE.∵AE平面PAD,MN平面PAD,∴MN∥平面PAD.(2)要证MN⊥CD,可证MN⊥AB.由(1)知,需证AE⊥AB.∵PA⊥平面ABCD,∴PA⊥AB.又AD⊥AB,∴AB⊥平面PAD.∴AB⊥AE.即AB⊥MN.又CD∥AB,∴MN⊥CD.(3)由(2)知,MN⊥CD,即AE⊥CD,再证AE⊥PD即可.∵PA⊥平面ABCD,∴PA⊥AD.又∠PDA=45°,E为PD的中点.∴AE⊥PD,即MN⊥PD.又MN⊥CD,∴MN⊥平面PCD.总结升华:本题是涉及线面垂直、线面平行、线线垂直诸多知识点的一道综合题.(1)的关键是选取PD的中点E,所作的辅助线使问题处理的方向明朗化.线线垂直→线面垂直→线线垂直是转化规律.。
直线、平面垂直的判定及其性质_练习题1(答案)
直线、平面垂直的判定及其性质一、选择题1、“直线l垂直于平面α内的无数条直线”是“l⊥α”的()A、充分条件B、必要条件C、充要条件D、既不充分也不必要条件2、如果一条直线l与平面α的一条垂线垂直,那么直线l与平面α的位置关系是()A、l⊂αB、l⊥αC、l∥αD、l⊂α或l∥α3、若两直线a⊥b,且a⊥平面α,则b与α的位置关系是()A、相交B、b∥αC、b⊂αD、b∥α,或b⊂α4、a∥α,则a平行于α内的( )A、一条确定的直线B、任意一条直线C、所有直线D、无数多条平行线5、如果直线a∥平面α,那么直线a与平面α内的 ( )A、一条直线不相交B、两条直线不相交C、无数条直线不相交D、任意一条直线都不相交6、若直线l上有两点P、Q到平面α的距离相等,则直线l与平面α的位置关系是( )A、平行B、相交C、平行或相交D、平行、相交或在平面α内二、填空题7、过直线外一点作直线的垂线有条;垂面有个;平行线有条;平行平面有个.8、过平面外一点作该平面的垂线有条;垂面有个;平行线有条;平行平面有个.9、过一点可作________个平面与已知平面垂直.10、过平面α的一条斜线可作_________个平面与平面α垂直.11、过平面α的一条平行线可作_________个平面与平面α垂直.三、解答题12、求证:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面13、过一点和已知平面垂直的直线只有一条14、有一根旗杆AB高8m,它的顶端A挂一条长10m的绳子,拉紧绳子并把它的下端放在地面上的两点(和旗杆脚不在同一直线上),C D,如果这两点都和旗杆脚B的距离是6m,那么旗杆就和地面垂直,为什么?15、已知直线l⊥平面α,垂足为A,直线AP⊥l求证:AP在α内参考答案一、选择题1、B ;2、D ;3、D ;4、D ;5、D ;6、D二、填空题7、无数,一,一,无数8、一,无数,无数,一9、无数10、一个11、一个三、解答题12、已知:a∥b,a⊥α 求证:b⊥α证明:设m 是α内的任意一条直线αααα⊥⇒⎭⎬⎫⊂⊥⇒⎭⎬⎫⊥⇒⎭⎬⎫⊂⊥b m m b b a m a m a //13、已知:平面α和一点P 求证:过点P 与α垂直的直线只有一条证明:不论P 在平面α内或外,设直线PA α⊥,垂足为A(或P ) 若另一直线PB α⊥,设,PA PB 确定的平面为β,且a αβ=I ∴,PA a PB a ⊥⊥又∵,PA PB 在平面β内,与平面几何中的定理矛盾 所以过点P 与α垂直的直线只有一条βαa P B A14、解:在ABC∆和ABD∆中,∵8,6,10=====AB m BC BD m AC AD m Array∴222222+=+==6810AB BC AC222222+=+==AB BD AD6810∴90ABC ABD∠=∠=o即,⊥⊥AB BC AB BD又∵,,B C D不共线∴AB⊥平面BCD,即旗杆和地面垂直;15、证明:设AP与l确定的平面为β如果AP不在α内,则可设α与β相交于直线AM∵l⊥α,∴l⊥AM又AP⊥l,于是在平面β内过点A有两条直线垂直于l,这是不可能的所以AP一定在α。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.3直线平面垂直的判定及其性质练习题
一、选择题:本大题共10小题,每小题5分,满分50分.
1. 已知直线a ,b 和平面α,有以下四个命题:
若a α//,a b //,则b α//; 若a α⊂,b A α= ,则a 与b 异面; 若a b //,b α⊥,则a α⊥; 若a b ⊥,a α⊥,则b α//.
其中真命题的个数是( )
A.0 B.1 C.2 D.3
2.在空间,下列哪些命题是正确的( )
①平行于同一条直线的两条直线互相平行;
②垂直于同一条直线的两条直线互相平行;
③平行于同一个平面的两条直线互相平行;
④垂直于同—个平面的两条直线互相平行.
A .仅②不正确
B .仅①、④正确
C .仅①正确
D .四个命题都正确
3. 已知直线l α⊥平面,有以下几个判断:①若m l ⊥,则m α//;②若m α⊥,m l //; ③若m α//,则m l ⊥;④若m l //,则m α⊥.上述判断中正确的是( ) A.①②③ B.②③④ C.①③④ D.①②④
4. 直线a 不垂直于平面α,则α内与a 垂直的直线有( )
A.0条 B.1条 C.无数条 D.α内所有直线
5.在下列四个命题中,假命题为( )
A .如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直
B .垂直于三角形两边的直线必垂直于第三边
C .过点A 垂直于直线a 的所有直线都在过点A 垂直于a 的平面内
D .如果三条共点直线两两垂直,那么其中一条直线垂直于另两条直线确定的平面
6. 已知三条直线m ,n ,l ,三个平面α,β,γ.下面四个命题中,正确的是( )
A.αγαββγ⊥⎫⇒⎬⊥⎭
// B.m l l m ββ⎫⇒⊥⎬⊥⎭// C.m m n n γγ⎫⇒⎬⎭////// D.m m n n γγ⊥⎫⇒⎬⊥⎭
// 7. 在空间四边形ABCD 中,若AB BC =,AD CD =,E 为对角线AC 的中点,下列判断正确的是( )
A.平面ABD ⊥平面BDC B.平面ABC ⊥平面ABD
C.平面ABC ⊥平面ADC D.平面ABC ⊥平面BED
8.在二面角βα-l -的棱l 上任选一点O,若AOB ∠是二面角βα-l -的平面角,则必须具有条件( )
βαβ
αβ
α⊂⊂⊥⊥⊂⊂⊥⊥⊥⊂⊂⊥BO AO l BO l AO D BO AO l AB C l
BO l AO B BO AO BO AO A ,,,.,,.,.,,.且
9. 设a ,b 是异面直线,下列命题正确的是( )
A.过不在a ,b 上的一点P 一定可以作一条直线和a ,b 都相交
B.过不在a ,b 上的一点P 一定可以作一个平面和a ,b 垂直
C.过a 一定可以作一个平面与b 垂直
D.过a 一定可以作一个平面与b 平行
10.如图,三棱锥ABC P -中,,,PB PA ABC PA =⊥平面则直线PB 与
平面ABC 所成的角是( )
30456090. ;. ;. ;.
D C B A
二、填空题:本大题共4小题,每小题5分,满分20分.
11.已知直线a ,b 和平面α,且a b ⊥,a α⊥,则b 与α的位置关系是___________.
12.如图所示,AB 是圆O 的直径,C 是异于A ,B 两点的圆周
上的任意一点,PA 垂直于圆O 所在的平面,则PAB △,PAC △, ABC △,PBC △中,直角三角形的个数是_________.
13. 设O 为平行四边形ABCD 对角线的交点,P 为平面AC 外一点
且有PA PC =,PB PD =,则PO 与平面ABCD 的关系是
_____________.
14.已知直线:,,,,给出下列说法平面βαl m ①若;,αα⊥l l 则内两条相交直线垂直与②;,,,βαβα⊥⊥⊂⊂则且m l l m
③;,,βααβ⊥⊥⊂则且若l l ④.//,//,m l l m 则且若βαβα⊂⊂
其中正确____________.
三,解答题
15.已知四棱锥ABCD P -的地面是菱形,且PA=PC,PB=PD 若O 是AC 与BD
的 交点,求证PO ⊥平面ABCD.
O
P
A B C。
