三余弦定理
高考数学-三余弦(正弦)定理的妙用

三余弦(正弦)定理的妙用一、三余弦定理(最小角定理、爪子定理)(1)定理:设点A 为平面α上一点,过A 点的斜线在平面α上的射影为BO ,BC 为平面α上的任意直线,那么OBA OBC ABC ∠⋅∠=∠cos cos cos即斜线与平面一条直线夹角β的余弦值等于斜线与平面所成角α的余弦值乘以射影与平面内直线夹角θ的余弦值,θαβcos cos cos ⋅=(为了便于记忆,我们约定:β为斜线角,α为线面角,θ为射影角)(2)定理证明:如上图,OAB ∆、OBC ∆、ABC ∆均为直角三角形,AB BC =βcos ,AB BO =αcos ,BOBC =θcos ,易知θαβcos cos cos ⋅=,得证 (3)定理说明:这三个角中,角β是最大的,其余弦值最小,等于另外两个角的余弦值之积。
斜线与平面所成角α是斜线与平面内所有直线所成的角中最小的角。
二、三正弦定理(最大角定理):(1)定理:设二面角N AB M --的度数为γ,在平面M 上有一条射线AC ,它和棱AB 所成的角为β,和平面N 所成的角为α,则γβαsin sin sin ⋅=(为了便于记忆,我们约定:β为线棱角,α为线面角,γ为二面角)(2)定理证明:如图,⊥CO 平面N ,AB OB ⊥,AB BC ⊥,OBC ∆、OAC ∆、ABC ∆均为直角三角形,BC OC =γsin ,ACBC =βsin ,ACOC =αsin ,易得:γβαsin sin sin ⋅=。
(3)定理说明:由γβαsin sin sin ⋅=且1sin ≤β知:γαsin sin ≤,γα≤,所以二面角的半平面M 内的任意一条直线与另一个半平面N 所成的线面角不大于二面角,即二面角是线面角中最大的角。
知识应用:例1.(2016年4月浙江省数学学考试题第16题)如图,在侧棱垂直于底面的三棱柱111C B A ABC -中,P 是棱BC 上的动点。
高考数学立体几何中与角有关的四大定理及其证明
则 cosθ = cos2β + cos2γ - 2cosαcosβcosγ sinα
证明:设 ∠HAC = θ1,∠HAB = θ2 ⇒ α = θ1 + θ2,
由三余弦定理得:
cos β cosγ
= =
cosθ cosθ
cosθ1 cosθ2
① ②
由①和②得 cosθ = cosβ = cosγ ③ cosθ1 cosθ2
α
Aβ
γ
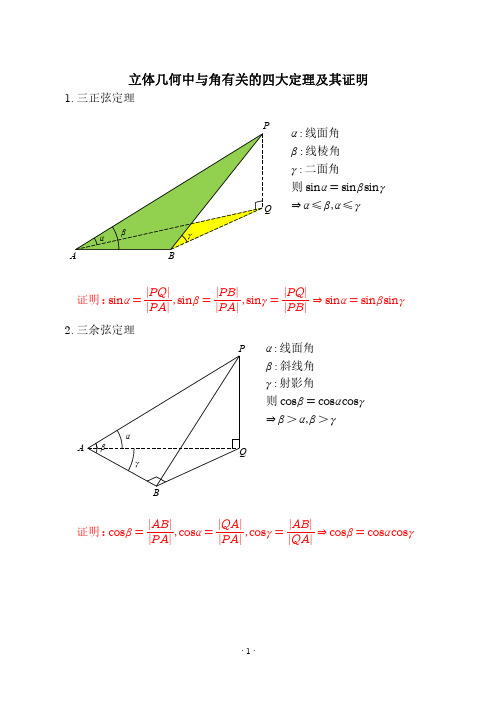
P α : 线面角 β : 斜线角 γ : 射影角 则 cosβ = cosαcosγ ⇒ β > α,β > γ
Q
B
证明:cosβ =
AB PA
,cosα =
QA PA
,cosγ =
AB QA
⇒ cosβ = cosαcosγ
·1·
3. 三夹角公式
P
θ
Aβ
γ
α
C H
B
若 θ 为 PA 与平面 ABC 的夹角
⋅
HO BO
AH AO
⋅
BH BO
= cosθ - cosθ1cosθ2 sinθ1sinθ2
注:若 φ =
π 2
,
则该定理退化为三余弦定理
·3·
立体几何中与角有关的四大定理及其证明
1. 三正弦定理
β α
A
γ
B
P
α : 线面角 β : 线棱角 γ : 二面角 则 sinα = sinβsinγ Q ⇒ α ≤ β,α ≤ γ
证明:sinα =
PQ PA
,sinβ =
PB PA
,sinγ =
PQ PB
⇒ sinα = sinβsinγ
三余弦定理·三垂线定理·三正弦定理

三余弦定理·三垂线定理·三正弦定理三余弦定理(最小角定理或爪子定理)设A 为面上一点,过A 的直线AO 在面上的射影为AB ,AC 为面上的一条直线,那么∠OAC,∠BAC,∠OAB 三角的余弦关系为: cos ∠OAC=cos ∠BAC ×cos ∠OAB(cos ∠BAC 和cos ∠OAB 只能是锐角)斜线与平面内一条直线夹角的余弦值=斜线与平面所成角的余弦值射影与平面内直线夹角的余弦值. 证明:如上图,自点O 作OB ⊥AB 于点B ,过B 作BC ⊥AC 于C ,连OC ,则易知△ABC 、△AOC 、△ABO 均为直角三角形.OA AC AB AC OA AB ===θθθcos ,cos ,cos 21∴ 21cos cos cos θθθ⨯=辅助记忆:这三个角中,角θ是最大的,其余弦值最小,等于另外两个角的余弦值之积。
斜线与平面所成角1θ是斜线与平面内所有直线所成的角中最小的角。
三垂线定理(三余弦定理的特殊情况)平面内的一条直线,如果与穿过这个平面的一条斜线在这个平面上的射影垂直,那么它也和这条斜线垂直。
逆定理:如果平面内一条直线和穿过该平面的一条斜线垂直,那么这条直线也垂直于这条斜线在平面内的射影。
三正弦定理设二面角M -AB -N 的度数为α,在平面M 上有一条射线AC ,它和棱AB 所成角为β,和平面N所成的角为γ,则 sin γ=sin α·sin β(如图)证明:如上图,过C 作CO ⊥平面N 于点O ,过O 作直线OB ⊥二面角的棱于点B ,连OA ,CB ,则易知△CAO ,△CBO ,△ABC 均为直角三角形.于是,sin=AC CO,sin=BC CO ,sin β=AC BC∴ sin γ=sin α·sin β附:β。
三角形的余弦定理

三角形的余弦定理三角形的余弦定理,也称作Cosine定理,是解决三角形问题时常用的重要定理之一。
它可以用来计算三角形中缺失的一边长度,或者计算三个角中的某一个角的大小。
通过余弦定理,我们可以更加灵活地处理三角形相关的计算和分析。
余弦定理可以用于任意一个三角形,不仅限于直角三角形。
该定理的表达方式如下:在一个三角形中,设边长分别为a、b、c,对应的角度为A、B、C,则余弦定理可以表述为:c² = a² + b² - 2ab * cosC (1)a² = b² + c² - 2bc * cosA (2)b² = a² + c² - 2ac * cosB (3)在这三个表达式中,c是第三边的长度,A、B、C是三个角的大小,a、b、c是对应的边长。
通过这三个方程,我们可以互相推导计算。
通过余弦定理,我们可以解决各种与三角形相关的问题。
首先,我们可以计算三角形的某个边的长度,只要已知其他两边的长度和夹角的大小即可。
其次,我们也可以计算三角形中某个角的大小,只要已知其他两条边的长度和这个角的对边即可。
在实际问题中,余弦定理经常被用来解决测量和计算问题。
例如,当我们需要测量一个不规则的三角形中的一条边时,可以利用余弦定理进行计算。
又或者,当我们需要计算两个天线之间的距离时,如果我们知道了两个天线之间的夹角,以及与这个夹角对应的两边长度,就可以利用余弦定理进行计算。
此外,余弦定理也常常与正弦定理结合使用。
这两个定理配合使用可以解决更为复杂的三角形问题,例如计算一个三角形的面积。
正弦定理可以用来计算三角形的面积,而余弦定理则可以用来计算三角形的边长和角度。
总结而言,余弦定理是解决三角形问题时非常有用的工具之一。
它可以应用于各种类型的三角形,并且可以计算三角形的边长和角度。
通过掌握和应用这个定理,我们可以更加方便地解决与三角形相关的计算和分析问题。
三角形余弦定理

三角形余弦定理
三角形余弦定理是一個在數學中常用來計算三角形三邊長度的基本定理。
它是針對一
個三角形三個邊提出的關係式,即此三角形邊長a和b之間以及a和c之間的關係式。
此
定理也稱為秦九韶定理,受到德國數學家安德烈·卡斯特勒的啟發而成立的。
三角形余弦定理的公式為:a2=b2+c2-2bc*cosA。
其中a、b、c為三角形其三個邊的
長度,A為這三個邊之間的夾角。
如果已知其中的b和c以及A的大小,那麼就可以使用
三角形余弦定理來求得a的值,也就是最末端的為未知的邊。
由於三角形余弦定理在數學上極其重要,很多應用也都建立在此定理之上。
例如,三
角形余弦定理用於求出在非正式空間上線段的長度。
它也可以用於求出多邊形的面積大小,和求出多邊形結構整體分級面積大小等。
另外,在物理中,三角形余弦定理也被廣泛應用
於許多對象的運動路徑計算上,例如求出一個形狀的質點的運動路徑。
此外,在數值分析
與電腦視覺領域中,三角形余弦定理也有許多應用,例如利用三角形余弦定理求出影像特
徵變換模型中參數最佳值等。
舉例來說,假設有一個三角形,其a(右側)為3,b(上側)為4,A為60度,則三角形
余弦定理的計算結果如下:
c^2=a^2+b^2-2ab*cosA
=9+16-2*3*4*cos60
=25-24
=1
因此,三個邊的長度為a=3,b=4,c=1。
三角形的余弦定理

三角形的余弦定理在数学几何学中,三角形是一个基础而重要的概念。
而在研究三角形的性质和关系时,我们经常会遇到需要计算三角形边长或角度的问题。
为了解决这些问题,数学家们提出了一系列的三角定理,其中最著名的之一就是三角形的余弦定理。
三角形的余弦定理给出了在一个任意三角形中,任意两边和它们夹角之间的关系。
它的数学表达式如下:c^2 = a^2 + b^2 - 2ab * cos(C)其中,a、b为三角形的两边长度,c为三角形的斜边长度,C为夹角C的度数。
三角形的余弦定理告诉我们,如果我们已知了三角形的两边长度和它们夹角的度数,那么我们可以通过这个定理求解三角形的斜边长度。
这个定理的应用非常广泛,不仅可以用于计算任意三角形的边长,还可以用于解决各种与三角形有关的问题。
下面我们来看几个例子。
例1:求解三角形边长已知一个三角形,其中两边的长度分别为4和6,夹角的度数为60。
利用余弦定理,我们可以计算出第三边的长度。
根据余弦定理,我们有:c^2 = 4^2 + 6^2 - 2*4*6*cos(60)= 16 + 36 - 48*cos(60)= 52 - 48 * 0.5= 52 - 24= 28因此,这个三角形的第三边的长度为√28。
例2:求解三角形夹角已知一个三角形,其中三边的长度分别为5、7和9。
我们可以通过余弦定理来计算任意两条边之间的夹角。
假设我们要求解夹角A的度数。
根据余弦定理,我们有:cos(A) = (b^2 + c^2 - a^2) / (2*b*c)= (7^2 + 9^2 - 5^2) / (2*7*9)= (49 + 81 - 25) / 126= 105 / 126≈ 0.833通过反余弦函数,我们可以求得夹角A的度数为cos⁻¹(0.833) ≈ 33.6度。
例3:验证三边关系余弦定理还可以用于验证三边之间的关系。
例如,我们知道当一个三角形的两边之和大于第三边时,这个三角形是合法的。
三余弦公式的推理与证明

三余弦公式的推理与证明三余弦公式是解决三角形中角度和边长之间关系的重要公式。
它可以用来计算三角形中的任意角度或边长,对于数学和工程学来说都是非常重要的。
下面我们来推导和证明三余弦公式。
首先,我们考虑一个任意三角形ABC,其中AB=c, BC=a, AC=b 是三边的长度,∠A, ∠B, ∠C是对应的内角。
我们可以利用余弦定理来推导三余弦公式。
余弦定理指出,对于任意三角形ABC,有以下关系:c^2 = a^2 + b^2 2abcos∠C.a^2 = b^2 + c^2 2bccos∠A.b^2 = a^2 + c^2 2accos∠B.将上述三个式子进行整理,可以得到:cos∠C = (a^2 + b^2 c^2) / 2ab.cos∠A = (b^2 + c^2 a^2) / 2bc.cos∠B = (a^2 + c^2 b^2) / 2ac.这样我们就得到了三余弦公式的推导过程。
接下来,我们来证明三余弦公式。
证明:我们可以利用单位圆上的点和三角函数的定义来证明三余弦公式。
假设在单位圆上,点P(x,y)对应于角θ,那么有以下关系:x = cosθ。
y = sinθ。
然后我们考虑单位圆上的三个点A(a,0), B(b,0), C(c,0),它们分别对应于角∠A, ∠B, ∠C。
根据单位圆上的点和三角函数的定义,我们可以得到:a = cos∠A.b = cos∠B.c = cos∠C.接下来,我们利用向量的内积来证明三余弦公式。
假设向量AB的长度为c,向量AC的长度为b,那么有以下关系:AB·AC = |AB||AC|cos∠BAC.AB·AC = cbcos∠A.同理,利用向量BC的长度为a,向量BA的长度为c,可以得到:BC·BA = accos∠B.最后,利用向量CA的长度为b,向量CB的长度为a,可以得到:CA·CB = bacos∠C.将上述三个式子整理,可以得到三余弦公式:cos∠A = (b^2 + c^2 a^2) / 2bc.cos∠B = (a^2 + c^2 b^2) / 2ac.cos∠C = (a^2 + b^2 c^2) / 2ab.因此,我们成功地推导和证明了三余弦公式。
三角形余弦定理公式大全

三角形余弦定理公式大全三角形余弦定理是解决三角形相关问题时常用的定理之一。
它能帮助我们在已知两边和夹角的情况下求解第三边的长度,或者在已知三边长度时求解夹角的大小。
下面将介绍一些常见的三角形余弦定理公式。
公式1:已知两边及夹角,求解第三边长度对于一个三角形ABC,已知边AB和AC的长度分别为a和b,夹角∠BAC的大小为θ,我们可以根据三角形余弦定理计算边BC的长度c:c² = a² + b² - 2abcosθ公式2:已知三边长度,求解夹角的大小如果我们已知三角形ABC的边长a、b和c,请根据三角形余弦定理计算∠BAC的大小θ:cosθ = (b² + c² - a²) / (2bc)cosθ = (a² + c² - b²) / (2ac)cosθ = (a² + b² - c²) / (2ab)公式3:正弦函数与余弦函数的关系在三角形中,正弦函数与余弦函数有着密切的关系。
根据正弦函数的定义,我们可以将余弦函数表示为正弦函数的倒数:sinθ = √(1 - cos²θ)cosθ = √(1 - sin²θ)公式4:应用示例假设一个三角形ABC,已知边AB和BC的长度分别为12cm和8cm,夹角∠ABC的大小为60°,我们可以使用公式1来计算边AC的长度:AC² = AB² + BC² - 2 × AB × BC × cos∠ABCAC² = (12)² + (8)² - 2 × 12 × 8 × cos60°AC² = 144 + 64 - 2 × 12 × 8 × 0.5AC² = 208 - 96AC² = 112AC ≈ √112AC ≈ 10.58cm通过计算,我们得知边AC的长度约为10.58cm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三余弦定理
设A为面上一点,过A的斜线AO在面上的射影为AB,AC为面上的一条直线,那么∠OAC,∠BAC,∠OAB三角的余弦关系为:
cos∠OAC=cos∠BAC×cos∠OAB (∠BAC和∠OAB只能是锐角)
平面α的一条斜线l与α所成角为θ1,α内的直线m与l在α上的射影l‘夹角为θ2,l与m所成角为θ,则cosθ=cosθ1*cosθ2.又叫最小角定理或爪子定理,用于求平面斜线与平面内直线成的最小角.表达式cos∠OAC=cos∠BAC×cos∠OAB 过平面的斜线和它在平面内的射影所成的角,是这条斜线和这个平面内任一条直线所成的角中最小的角。
过一个平面的斜线和它在这个平面内的射影的夹角,叫做斜线和平面所成的角(或斜线和平面的夹角)。
两个小角的余弦积等于最大角的余弦值。
如果一个角所在平面外一点到角的两边的距离相等,那么这个点在平面内的射影在这个角的平分线上。
经过一个角的顶点引这个角所在平面的斜线,设它和已知角的两边的夹角为锐角且相等,则这条斜线在平面的射影是这个角的平分线。
若三棱锥的三条侧棱相等,则其顶点在底面上的射影是底面三角形的外心。
