初三几何证明练习题100
初三几何证明练习题和答案

初三几何证明练习题和答案几何证明是初中数学中的重要内容,通过练习不同类型的几何证明题,可以帮助学生理解并掌握几何证明的基本方法与技巧。
本文将为大家提供一些初三几何证明的练习题和答案,希望对同学们的学习有所帮助。
1. 题目:已知ABCD是平行四边形,证明∠ABC + ∠ADC = 180°。
证明:解:连接AC,根据平行四边形的性质可知∠ADC = ∠ACB,所以要证明∠ABC + ∠ADC = 180°,只需证明∠ABC + ∠ACB = 180°。
由角的内外(对顶、同旁)定理可知∠ACB + ∠ABC = 180°,即∠ABC + ∠ACB = 180°。
所以,∠ABC + ∠ADC = 180°得证。
2. 题目:已知直角三角形ABC中,∠ACB = 90°,AC = 5cm,BC= 12cm,证明AB = 13cm。
证明:解:根据勾股定理可得AB² = AC² + BC²。
代入已知条件,即可得AB² = 5² + 12² = 25 + 144 = 169。
开方可得AB = 13cm。
所以,AB = 13cm得证。
3. 题目:已知直角三角形ABC中,∠ACB = 90°,AC = BC,证明∠ABC = 45°。
证明:解:连接AB,根据等腰直角三角形的性质可知∠ACB = ∠CAB。
所以,∠ABC = 180° - ∠ACB - ∠CAB = 180° - ∠ACB - ∠ACB = 180° - 2∠ACB。
由于∠ACB = 90°,代入得∠ABC = 180° - 2 × 90° = 0°。
所以,∠ABC = 0°,即∠ABC = 45°得证。
4. 题目:已知ABCD是一个平行四边形,E为AD的中点,证明BE平分∠CBD。
中考几何证明题及答案

中考几何证明题及答案几何证明练题及答案知识要点:1.掌握直角三角形的性质并能熟练应用;2.能写出较难证明的求证;3.证明要合乎逻辑,能应用综合法证明几何命题。
概念回顾:1.全等三角形的性质:对应边、对应角、对应高线、对应中线、对应角的角平分线。
2.在Rt△ABC中,∠C=90°,∠A=30°,则BC:AC:AB=?例题解析:题1:已知在ΔABC中,A=108°,AB=AC,BD平分ABC。
求证:___。
题2:如图,点E为正方形ABCD的边CD上一点,点F 为CB的延长线上的一点,且EA⊥AF。
求证:DE=BF。
题3:如图,AD为ΔABC的角平分线且BCBD=CD。
求证:AB=AC。
题4:已知:如图,点B、F、C、E在同一直线上,BF=CE,AB∥ED,AC∥FD,证明AB=DE,AC=DF。
题5:已知:如图,△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.求∠APB的度数。
题6:如图:△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足是F,过B作BD⊥BC交CF的延长线于D。
1)求证:AE=CD;2)若AC=12 cm,求BD的长。
题7:等边三角形CEF于菱形ABCD边长相等。
求证:(1)∠AEF=∠AFE;(2)角B的度数。
题8:如图,在△ABC中,∠C=2∠B,AD是△ABC的角平分线,∠1=∠B。
求证:___。
题9:如图,在三角形ABC中,AD是BC边上的中线,E是AD的中点,BE的延长线交AC于点F。
求证:___。
题10:如图,将边长为1的正方形ABCD绕点C旋转到A'B'CD'的位置,若∠B'CB=30°,求AE的长。
题11:AD,BE分别是等边△ABC中BC,AC上的高。
M,N 分别在AD,BE的延长线上,∠___∠ACN。
求证:AM=BN。
题12:已知:如图,AD、BC相交于点O,OA=OD,OB=OC,点E、F在AD上,且AE=DF,∠ABE=∠DCF。
初中数学几何证明题及参考答案

初中数学几何证明题及参考答案初中数学几何证明题及参考答案几何证明题是初中学生在学习数学时需要掌握的重点知识。
为了帮助初中生学会几何证明题,下面就是店铺给大家整理的初中数学几何证明题及参考答案,希望大家喜欢。
初中数学几何证明题及参考答案1己知M是△ABC边BC上的中点,,D,E分别为AB,AC上的点,且DM⊥EM。
求证:BD+CE≥DE。
延长EM至F,使MF=EM,连BF.∵BM=CM,∠BMF=∠CME,∴△BFM≌△CEM(SAS),∴BF=CE,又DM⊥EM,MF=EM,∴DE=DF而∠DBF=∠ABC+∠MBF=∠ABC+∠ACB<180°,∴BD+BF>DF,∴BD+CE>DE。
初中数学几何证明题及参考答案2己知M是△ABC边BC上的中点,,D,E分别为AB,AC上的点,且DM⊥EM。
求证:BD+CE≥DE过点C作AB的'平行线,交DM的延长线于点F;连接EF因为CF//AB所以,∠B=∠FCM已知M为BC中点,所以BM=CM又,∠BMD=∠CMF所以,△BMD≌△CMF(ASA)所以,BD=CF那么,BD+CE=CF+CE (1)且,DM=FM而,EM⊥DM所以,EM为线段DF的中垂线所以,DE=EF在△CEF中,很明显有CE+CF>EF (2)所以,BD+CE>DE当点D与点B重合,或者点E与点C重合时,仍然采用上述方法,可以得到BD+CE=DE综上就有:BD+CE≥DE。
初中数学几何证明题及参考答案3证明因为∠DME=90°,∠BMD<90°,过M作∠BMD=∠FMD,则∠CME=∠FME。
截取BF=BC/2=BM=CM。
连结DF,EF。
易证△BMD≌△FMD,△CME≌△FME所以BD=DF,CE=EF。
在△DFE中,DF+EF≥DE,即BD+CE≥DE。
当F点落在DE时取等号。
另证延长EM到F使MF=ME,连结DF,BF。
初三几何证明练习题

初三几何证明练习题1. 证明:直角三角形的斜边是直角边的倍数。
解析:设直角三角形的两条直角边分别为a和b,斜边为c。
根据勾股定理:c² = a² + b²要证明c是a的倍数或b的倍数,我们可以假设c是a的倍数,并证明c也是b的倍数。
设c = ka,其中k为常数。
代入勾股定理:(k⋅a)² = a² + b²k²⋅a² = a² + b²(k²-1)⋅a² = b²由于k²-1是一个常数,所以(k²-1)⋅a²必定是一个正数。
而b²也是一个正数。
根据数学定理:如果两个正数相等,那么它们的平方根也相等。
因此,我们可以得出结论:如果(k²-1)⋅a² = b²,那么b也必定是a 的倍数。
所以,直角三角形的斜边c可以是直角边a的倍数。
综上所述,直角三角形的斜边是直角边的倍数。
2. 证明:三角形内角和等于180度。
解析:设三角形的三个内角分别为A、B、C。
根据三角形的定义,任意三个点都能构成一个三角形,且三角形的内角和恒等于180度,即A + B + C = 180°。
为了证明这个定理,我们可以通过以下步骤进行推理。
步骤一:构造直线段AD,使其与线段BC重合。
步骤二:根据性质,如果一条直线段与另一条直线段重合,那么它们的内角和相等。
所以∠BAD + ∠CAD = ∠B + ∠C。
步骤三:根据性质,如果一条直线段与自身重合,那么它们的内角和等于180度。
所以∠BAD + ∠CAD = 180°。
步骤四:由于∠BAD + ∠CAD = ∠B + ∠C,且∠BAD + ∠CAD = 180°,所以∠B + ∠C = 180°。
综上所述,三角形内角和等于180度。
总结:通过以上两个几何证明练习题,我们得到了初三几何学中的两个重要结论:直角三角形的斜边是直角边的倍数,三角形的内角和等于180度。
初中数学几何证明题经典例题(超全)
完整版ppt
9
• 已知:如图正方形ABCD,P、Q分别是BC、 DC上的点,若∠1=∠2 求证:PB+QD=PA
完整版ppt
10
• 已知:如图正方形ABCD,AC、BD交于点 O,E、F分别是BC、OD的中点 求证: AF⊥EF
完整版ppt
11
• 已知:如图,,AB=BC,D、E分别是AB、 BC上一点,DM⊥AE交AC于M, BN⊥AE 交AC于N,若BD=BE求证:MN=NC。
完整版ppt
20
• 如图,在四边形ABCD中,AB=DC,E、F 分别是AD、BC的中点,G、H分别是BD、 AC的中点,猜一猜EF与GH的位置关系, 并证明你的结论.
完整版ppt
21
• 如图,分别以△ABC的三边为边长,在BC 的同侧作等边三角形ABD,等边三角形 BCE,等边三角形ACF,连接DE,EF。求 证:四边形ADE 2,AB=3AC,BE⊥AD,
求证:AD=DE
完整版ppt
15
• 已知:如图,AB//CD, D=90 o, BE=EC=DC,求证: AEC=3 BAE
完整版ppt
16
• 已知如图,AB=DC,AE=DE,BF=FC,
FE交BA、CD的延长线于G、H,求证:1= 2。
完整版ppt
17
• 已知:如图,正方形ABCD中,E是DC上一 点,DF⊥AE交BC于F 求证:OE⊥OF
完整版ppt
18
• 已知:如图,AB//CD, ADC=90o , BE=EC,求证: AED=2 EDC
完整版ppt
19
• 已知:如图,正方形ABCD中,E是DC上一 点,DF⊥AE交BC于F 求证:OE⊥OF
初三经典几何证明练习题(含问题详解)

初三几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.2、已知:如图,P是正方形ABCD部的一点,∠PAD=∠PDA=15°。
求证:△PBC是正三角形.(初二)3、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.经典题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.2、设MN是圆O外一条直线,过O作OA⊥MN于A,自A引圆的两条割线交圆O于B、C及D、E,连接CD并延长交MN于Q,连接EB并延长交MN于P.求证:AP=AQ.3、如图,分别以△ABC的AB和AC为一边,在△ABC的外侧作正方形ABFG和正方形ACDE,点O是DF的中点,OP⊥BC求证:BC=2OP证明:分别过F、A、D作直线BC的垂线,垂足分别是L、M、N∵OF=OD,DN∥OP∥FL∴PN=PL∴OP是梯形DFLN的中位线∴DN+FL=2OP∵ABFG是正方形∴∠ABM+∠FBL=90°又∠BFL+∠FBL=90°∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB∴△BFL≌△ABM∴FL=BM同理△AMC≌△CND∴CM=DN∴BM+CN=FL+DN∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE与CD相交于F.求证:CE=CF.证明:连接BD 交AC 于O 。
过点E 作EG ⊥AC 于G ∵ABCD 是正方形 ∴BD ⊥AC 又EG ⊥AC ∴BD ∥EG 又DE ∥AC ∴ODEG 是平行四边形 又∠COD=90° ∴ODEG 是矩形 ∴EG=OD=21BD=21AC=21AE ∴∠EAG=30°∵AC=AE∴∠ACE=∠AEC=75° 又∠AFD=90°-15°=75° ∴∠CFE=∠AFD=75°=∠AEC ∴CE=CF2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F . 求证:AE =AF .证明:连接BD ,过点E 作EG ⊥AC 于G ∵ABCD 是正方形 ∴BD ⊥AC ,又EG ⊥AC ∴BD ∥EG 又DE ∥AC∴ODEG 是平行四边形又∠COD=90° ∴ODEG 是矩形∴EG =OD =21BD=21AC=21CE∴∠GCE=30°∵AC=EC3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE . 求证:PA =PF .(初二)证明:过点F 作FG ⊥CE 于G ,FH ⊥CD 于H ∵CD ⊥CG ∴HCGF 是矩形 ∵∠HCF=∠GCF ∴FH=FG ∴HCGF 是正方形 ∴CG=GF ∵AP ⊥FP ∴∠APB+∠FPG=90° ∵∠APB+∠BAP=90° ∴∠FPG=∠BAP 又∠FGP=∠PBA ∴△FGP ∽△PBA 设AB=x ,BP=y ,CG=z z :y=(x-y+z ):x 化简得(x-y )·y =(x-y )·z ∵x-y ≠0 ∴y=z 即BP=FG∴△ABP ≌△PGF∴∠CAE=∠CEA=21∠GCE=15°在△AFC 中∠F =180°-∠FAC-∠ACF =180°-∠FAC-∠GCE =180°-135°-30°=15° ∴∠F=∠CEA ∴AE=AFPE PB A∴FG :PB=PG :AB4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D . 求证:AB =DC ,BC =AD .(初三)证明:过点E 作EK ∥BD ,分别交AC 、AF 于M 、K ,取EF 的中点H , 连接OH 、MH 、EC ∵EH=FH∴OH ⊥EF ,∴∠PHO=90° 又PC ⊥OC ,∴∠POC=90° ∴P 、C 、H 、O 四点共圆 ∴∠HCO=∠HPO 又EK ∥BD ,∴∠HPO=∠HEK ∴∠HCM=∠HEM ∴H 、C 、E 、M 四点共圆 ∴∠ECM=∠EHM 又∠ECM=∠EFA ∴∠EHM=∠EFA ∴HM ∥AC ∵EH=FH经典题(四)1、已知:△ABC 是正三角形,P 是三角形一点,PA =3,PB =4,PC =5. 求∠APB 的度数.(初二)解:将△ABP 绕点B 顺时针方向旋转60°得△BCQ ,连接PQ 则△BPQ 是正三角形 ∴∠BQP=60°,PQ=PB=3在△PQC 中,PQ=4,CQ=AP=3,PC=5 ∴△PQC 是直角三角形 ∴∠PQC=90°∴∠BQC=∠BQP+∠PQC=60°+90°=150° ∴∠APB=∠BQC=150°2、设P 是平行四边形ABCD 部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)证明:过点P 作AD 的平行线,过点A 作PD 的平行线, 两平行线相交于点E ,连接BE ∵PE ∥AD ,AE ∥PD∴ADPE 是平行四边形∴PE=AD ,又ABCD 是平行四边形∴AD=BC∴PE=BC又PE ∥AD ,AD ∥BC ∴PE ∥BC ∴BCPE 是平行四边形 ∴∠BEP=∠PCB ∵ADPE 是平行四边形 ∴∠ADP=∠AEP∴EM=KM ∵EK ∥BD ∴KMODAM AO EM OB == ∴OB=OD 又AO=CO ∴四边形ABCD 的对角线互相平分 ∴ABCD 是平行四边形 ∴AB=DC ,BC=AD 又∠ADP=∠ABP ∴∠AEP=∠ABP ∴A 、E 、B 、P 四点共圆 ∴∠BEP=∠PAB ∴∠PAB=∠PCB3、设ABCD 为圆接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三) 证明:在BD 上去一点E ,使∠BCE=∠ACD ∵CD⌒ =CD ⌒ ∴∠CAD=∠CBD ∴△BEC ∽△ADC∴ACBC AD BE = ∴AD ·BC=BE ·AC ……………………① ∵∠BCE=∠ACD∴∠BCE+∠ACE=∠ACD+∠ACE 即∠BCA=∠ECD ∵BC⌒=BC ⌒,∴∠BAC=∠BDC △BAC ∽△EDC ∴CDACDE AB =∴AB ·CD=DE ·AC ……………………②4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)证明:过点D 作DG ⊥AE 于G ,作DH ⊥FC 于H ,连接DF 、∴S △ADE =12AE ·DG ,S △FDC =12FC ·DH又S △ADE =S △FDC =12S □ABCD∴AE ·DG=FC ·DH 又AE=CF ∴DG=DH∴点D 在∠APC 的角平分线上 ∴∠DPA =∠DPC经典题(五)1、设P 是边长为1的正△ABC 任一点,L =PA +PB +PC ,求证:3≤L <2. 证明:(1)将△BPC 绕B 点顺时针旋转60°的△BEF ,连接PE , ∵BP=BE ,∠PBE=60° ∴△PBE 是正三角形。
初三几何证明题精选及答案
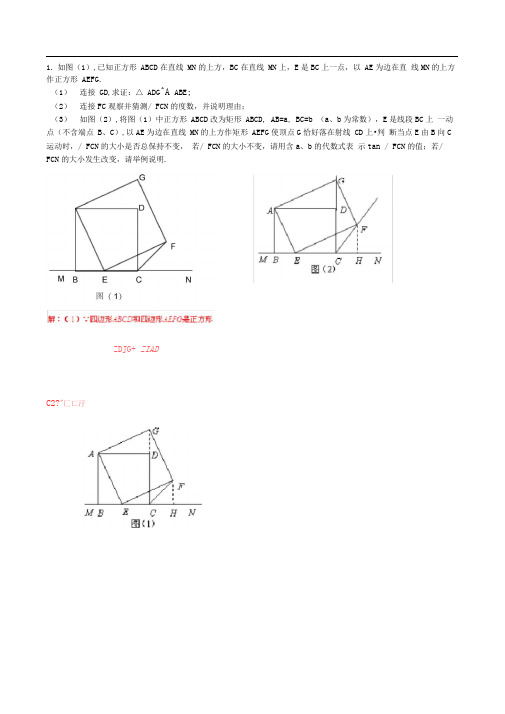
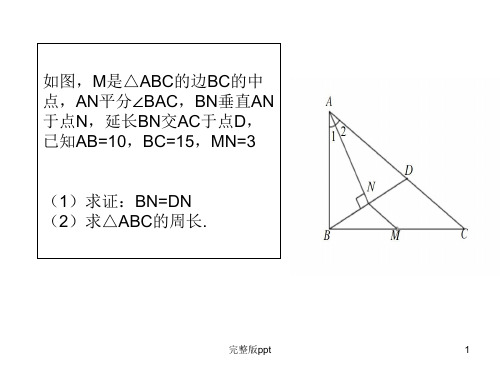
1. 如图(1),已知正方形 ABCD 在直线 MN 的上方,BC 在直线 MN 上,E 是BC 上一点,以 AE 为边在直 线MN 的上方作正方形 AEFG.(1) 连接 GD ,求证:△ ADG ^A ABE ;(2) 连接FC 观察并猜测/ FCN 的度数,并说明理由;(3) 如图(2),将图(1)中正方形 ABCD 改为矩形 ABCD, AB=a , BC=b (a 、b 为常数),E 是线段BC 上 一动点(不含端点 B 、C ),以AE 为边在直线 MN 的上方作矩形 AEFG 使顶点G 恰好落在射线 CD 上•判 断当点E 由B 向C 运动时,/ FCN 的大小是否总保持不变, 若/ FCN 的大小不变,请用含a 、b 的代数式表 示tan / FCN 的值;若/ FCN 的大小发生改变,请举例说明.ZDJG+ ZIADC2?"匚匸汙理由是;作用f丄于弓・・・厶27= 厶迅90°90S 乙FEE■乙肚3二90°:・HH= ZJ.iZ又•• AI€F・ ZS^7= ZI3^= 2△三丘T:・F4 3E,辱曲SC. A CH二51= FH••• "HC二90S ••• ZlrCn= 4FC 3 )当总■由訥C运动时,“G酌大小总保持不吏C 3 )当点三由訥C运动时 > 乙芯、的大小总保持不变理由是;作FF丄于耳由已知可得厶打G= ZJ.W= Zd= 9(f结合Cl) C2)得Z5EH二ZLBAE- ZLDAG又T G在射銭Ct上ZG2>J=厶EHF=ZSSJ=90°••• \EFH盜△ Gd △ EFHs A.i5z证F=AD= 3C= b i CH= BE JEH FH FH-,7B= ~BE = CHFH EH b ・••在泌心中八少"U\•二OH二AB = ab ・••当点三由S冋C运动时丿乙心的夫小总保持不喪门泯“c:\工82.如图,在平面直角坐标系中,矩形AOBC在第一象限内,E是边0B上的动点(不包括端点),作/ AEF=90,使EF交矩形的外角平分线BF于点F,设C(m,n).(1 )若m = n时,如图,求证:E F= AE;(2)若m丰n时,如图,试问边0B上是否还存在点E,使得EF= AE若存在,请求出点E的坐标;若不存在,请说明理由.(3 )若m = tn (t >时,试探究点E在边0B的何处时,使得EF= (t + 1)AE成立并求出点E的坐C3))如C2)圈.设E佃,R ,币二陥0]ijEH=OH-OE=h+m-a,由ZAEF=90e, ZEAO=ZFEH.得803厶创&/.EF= (t+ 1) AE等价于FH二(t+ 1) OE P (t+ 1) a>且空二OE_9即_冬_二兰,EH FH h +^i—<s h整理得nh=ahYnn-f・.?am- a(rn-a)把h=(tJL)耳代入得/刪一町=徉+ 1比’^m-3- (t+ 1)而皿血81ttn-a= (t+1) (r)-a),1ttt!8ta=e解得"f,T t>l,・;-<n<m)枚EEOSLhi•'•当防00辺上卫离聚点距監九?处対満足条隔!t时E(t 0. t t3 .在边长为5的正方形ABCD中,点E、F分别是BC、DC边上的点,且AE EF , BE 2.(1)求EC : CF的值;(2)延长EF交正方形外角平分线CP于点P (如图-2),试判断AE与EP的大小关系,并说明理由;(3)在图-2的AB边上是否存在一点M,使得四边形DMEP是平行四边形若存在,请给予证明;若不存在,请说明理由.D BE C 图-1B EC 图-2解:⑴如图(一)VAEXEF,/.Z2+Z3=90%•••四边形ABCD为正片形,-•.2B=ZC=90°,VZ1+Z3=90%•mz2,.■•△ABES^ECF,/.AB; CE=BE; CF,・・・EC; CF=AB; BE=5S2(2)如图(二〉在AB上取BM=BE,连接EM VABCD为正方形,-•-AB=BC,VBE=BM,Z1 = Z2? ZAME=ZECP=135OA AME^A ECP,.'.AE=EP.;⑶存在-如图(二)在BE取点【儿^AM = BE,TAE 丄EF,Z2+Z3=eo°,T四边理ABC□次正育形,.'.ZB=ZC=90S/. Z5 + 23=90°, 4二Z2T.'ZDAM=ZA9E=90% DA=AB,/.A DAMQ A ABB二DM~AE JTAE=EP,「・Dh1吨・m/5, 十上4二gy,.'.Z4+Z5=90%*\DM±AE S二DM II FE二四SIK DMEP是平行四边形.4,如图:抛物线经过A (-3, 0)、B (0, 4)、C (4, 0)三点.(1)求抛物线的解析式•(2)已知AD = AB ( D在线段AC上),有一动点P从点A沿线段AC以每秒1个单位长度的速度移动;同时另一个动点Q以某一速度从点B沿线段BC移动,经过t秒的移动,线段PQ被BD垂直平分,求t的值;(3)在(2)的情况下,抛物线的对称轴上是否存在一点M,使MQ+MC的值最小若存在,请求出点M的坐标;若不存在,请说明理由。
初中几何证明题【绝对经典】

几何证明1.点A 、B 、C 在同一直线上,在直线AC 的同侧作ABE ∆和BCF ∆,连接AF ,CE .取AF 、CE 的中点M 、N ,连接BM ,BN , MN .(1)若ABE ∆和FBC ∆是等腰直角三角形,且090=∠=∠FBC ABE (如图1),则M B N ∆是三角形.(2)在ABE ∆和BCF ∆中,若BA =BE ,BC =BF ,且α=∠=∠FBC ABE ,(如图2),则M B N∆是 三角形,且=∠MBN .(3)若将(2)中的ABE ∆绕点B 旋转一定角度,(如同3),其他条件不变,那么(2)中的结论是否成立? 若成立,给出你的证明;若不成立,写出正确的结论并给出证明.2.如图,将一三角板放在边长为1的正方形ABCD 上,并使它的直角顶点P 在对角线AC 上滑动,直角的一边始终经过点B,另一边与射线DC 相交于Q .探究:设A 、P 两点间的距离为x .(1)当点Q 在边CD 上时,线段PQ 与PB 之间有怎样的数量关系?试证明你的猜想;(2)当点Q 在边CD 上时,设四边形PBCQ 的面积为y ,求y 与x 之间的函数关系,并写出函数自变量x 的取值范围;(3)当点P 在线段AC 上滑动时,△PCQ 是否可能成为等腰三角形?如果可能,指出所有能使△PCQ 成为等腰三角形的点Q 的位置.并求出相应的x 值,如果不可能,试说明理由.3.(1)如图1,四边形ABCD 中,CB AB =,︒=∠60ABC ,︒=∠120ADC ,请你猜想线段DA 、DC 之和与线段BD 的数量关系,并证明你的结论;(2)如图2,四边形ABCD 中,BC AB =,︒=∠60ABC ,若点P 为四边形ABCD 内一点,且︒=∠120APD ,请你猜想线段PA 、PD 、PC 之和与线段BD 的数量关系,并证明你的结论.4. (1)如图1,在四边形ABCD 中,AB =AD ,∠B =∠D =90°,E 、F 分别是边BC 、CD 上的点,且∠EAF =12∠BAD .求证:EF =BE +FD ; 图1 图2 图3 (2) 如图2在四边形ABCD 中,AB =AD ,∠B +∠D =180°,E 、F 分别是边BC 、CD 上的点,且∠EAF =12∠BAD , (1)中的结论是否仍然成立?不用证明.(3) 如图25-3在四边形ABCD 中,AB =AD ,∠B +∠ADC =180°,E 、F 分别是边BC 、CD 延长线上的点,且∠EAF =12∠BAD , (1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.5. 以ABC ∆的两边AB 、AC 为腰分别向外作等腰Rt ABD ∆和等腰Rt ACE ∆,90,BAD CAE ∠=∠=︒连接DE ,M 、N 分别是BC 、DE的中点.探究:AM 与DE 的位置及数量关系.(1)如图① 当ABC ∆为直角三角形时,AM 与DE 的位置关系是 ,线段AM 与DE 的数量关系是 ;图2图1(2)将图①中的等腰Rt ABD ∆绕点A 沿逆时针方向旋转︒θ(0<θ<90)后,如图②所示,(1)问中得到的两个结论是否发生改变?并说明理由.6.如图,在平面直角坐标系中,矩形AOBC 在第一象限内,E 是边OB 上的动点(不包括端点),作∠AEF = 90?,使EF 交矩形的外角平分线BF 于点F ,设C (m ,n ).(1)若m = n 时,如图,求证:EF = AE ;(2)若m ≠n 时,如图,试问边OB 上是否还存在点E ,使得EF = AE ?若存在,请求出点E 的坐标;若不存在,请说明理由.(3)若m = tn (t >1)时,试探究点E 在边OB 的何处时,使得EF =(t + 1)AE 成立?并求出点E 的坐标.7.B AP ((2)如图1,当点P 为射线BC 上任意一点时,猜想∠QFC 的度数,并加以证明;(3)已知线段AB =32,设BP =x ,点Q 到射线BC 的距离为y ,求y 关于x 的函数关系式.8. 如图,直角梯形ABCD 中,AD ∥BC ,∠ABC =90°,已知AD =AB =3,BC =4,动点P 从B 点出发,沿线段BC 向点C 作匀速运动;动点Q 从点D 出发,沿线段DA 向点A 作匀速运动.过Q 点垂直于AD 的射线交AC 于点M ,交BC 于点N .P 、Q 两点同时出发,速度都为每秒1个单位长度.当Q 点运动到A 点,P 、Q 两点同时停止运动.设点Q 运动的时间为t 秒.(1)求NC ,MC 的长(用t 的代数式表示); (2)当t 为何值时,四边形PCDQ 构成平行四边形?(3)是否存在某一时刻,使射线QN 恰好将△ABC 的面积和周长同时平分?若存在,求出此时t 的值;若不存在,请说明理由;(4)探究:t 为何值时,△PMC 为等腰三角形?9.如图所示,在△ABC 中,D 、E 分别是AB 、AC 上的点,DE ∥BC ,如图①,然后将△ADE 绕A 点顺时针旋转一定角度,得到图②,然后将BD 、CE 分别延长至M 、N ,使DM =21BD ,EN 图1 AC B EQF P 图2A B E QP F C(如图3)CB=21CE ,得到图③,请解答下列问题: (1)若AB =AC ,请探究下列数量关系:①在图②中,BD 与CE 的数量关系是________________;②在图③中,猜想AM 与AN 的数量关系、∠MAN 与∠BAC 的数量关系,并证明你的猜想; (2)若AB =k·AC(k>1),按上述操作方法,得到图④,请继续探究:AM 与AN 的数量关系、∠MAN 与∠BAC 的数量关系,直接写出你的猜想,不必证明. 1、解:(1)等腰直角 (2)等腰 α (3)结论仍然成立 证明: 在ABF EBC ∆∆和中, ∴△ABF ≌△EBC. ∴AF=CE. ∠AFB=∠ECB ∵M,N 分别是AF 、CE 的中点, ∴FM=CN. ∴△MFB ≌△NCB.∴BM=BN. ∠MBF=∠NBC∴∠MBN=∠MBF+∠FBN=∠FBN+∠NBC=∠FBC= 2、解:(1) PQ =PB过P 点作MN ∥BC 分别交AB 、DC 于点M 、N 在正方形ABCD 中,AC 为对角线 ∴AM =PM 又∵AB =MN ∴MB=PN ∵∠BPQ =900∴∠BPM +∠NPQ =900 又∵∠MBP +∠BPM =900∴∠MBP = ∠N PQ ∴Rt △MBP ≌Rt △NPQ, ∴PB =PQ(2)∵S 四边形PBCQ =S △PBC +S △PCQ ∵ AP =x ∴ AM =22x N MQ PDC B A∴CQ=C D -2NQ =1-2x 又∵S △PBC =21BC ·BM =21·1·(1-22x )= 21-42xS △PCQ =21CQ ·PN =21(1-2x )·(1-22x )=221x -x 423+21 ∴S 四边形PBCQ =221x -2x +1 . (0≤x ≤22)(3)△PCQ 可能成为等腰三角形.① 当点P 与点A 重合时,点Q 与点D 重合, PQ=QC ,此时,x=0.② 当点Q 在DC 的延长线上,且CP=CQ 时, 有:QN=AM=PM =x 22,CP =2-x , CN =CP 22=1-x 22 CQ=Q N -CN =x 22-(1-x 22) =2x -1 ∴ 当2-x =x 2-1时 ,x =13、解:(1)如图1,延长CD 至E ,使DA DE =.可证明EAD ∆是等边三角形. 联结AC ,可证明BAD ∆≌CAE ∆. 故BD CE CD DE CD AD ==+=+.(2)如图2,在四边形ABCD 外侧作正三角形D B A ',可证明C B A '∆≌ADB ∆,得DB C B ='. ∵ 四边形DP B A '符合(1)中条件, ∴ PD AP P B +='. 联结C B ',N M QPDCBA 图 1图2ⅰ)若满足题中条件的点P 在C B '上, 则PC B P C B +'='. ∴ PC PD AP C B ++='.∴ PC PD PA BD ++= . ⅱ)若满足题中条件的点P 不在C B '上, ∵ PC B P C B +'<', ∴ PC PD AP C B ++<'.∴ PC PD PA BD ++<.综上,PC PD PA BD ++≤. 4、答案(1)证明:延长EB 到G ,使BG=DF ,联结AG .∵∠ABG =∠ABC=∠D =90°, AB =AD , ∴△ABG ≌△ADF .∴AG =AF, ∠1=∠2.∴∠1+∠3=∠2+∠3=∠EAF=12∠BAD .∴∠GAE=∠EAF . 又AE =AE ,∴△AEG ≌△AEF .∴EG =EF . ∵EG=BE+BG .∴EF= BE +FD(2) (1)中的结论EF= BE +FD 仍然成立.(3)结论EF=BE +FD 不成立,应当是EF=B E -FD . 证明:在BE 上截取BG ,使BG=DF ,连接AG . ∵∠B+∠ADC =180°,∠ADF+∠ADC =180°, ∴∠B =∠ADF . ∵AB =AD ,∴△ABG ≌△ADF .∴∠BAG =∠DAF,AG =AF . ∴∠BAG+∠EAD =∠DAF+∠EAD=∠EAF =12∠BAD .∴∠GAE=∠EAF . ∵AE =AE ,∴△AEG ≌△AEF . ∴EG =EF ∵EG=BE -BG ∴EF=B E -FD .5、答案:解:(1)DE AM ⊥,12AM DE =(2)结论仍然成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三几何证明练习题100
1、如图,△ABC 中,∠ACB=90°,CD ⊥AB 于点D ,E 是AC 的中点,DE 的延长线交BC 的延长线于点F ,EF=5,∠B 的正切值为
2
1 〔1〕求证:△BDF ∽△DCF ;〔2〕求BC 的长
2、:如图,在△ABC 中,BD ⊥AC 于点D ,CE ⊥AB 于点E ,EC 和BD 相交于点O ,联接DE . 〔1〕求证:△EOD ∽△BOC ;
〔2〕假设S △EOD =16,S △BOC =36,求AE
AC
的值.
3、如图,点E 是矩形ABCD 的边BC 上一点,EF ⊥AE ,EF 分别交 AC 、CD 于点M 、F ,BG ⊥AC ,垂足为点G ,BG 交AE 于点H . 〔1〕求证:△ABE ∽△ECF ;
〔2〕找出与△ABH 相似的三角形,并证明;
〔3〕假设E 是BC 中点,BC =2AB ,AB =2,求EM 的长.
4、如图,点D 是
Rt △ABC 斜边AB 上一点,点E 是直线AC 左侧一点,且EC ⊥CD ,∠EAC =∠B . 〔1〕求证:△CDE ∽△CBA ; 〔2〕如果点D 是斜边AB 的中点,且2
3
tan =∠BAC , 试求
CBA
CDE
S S ∆∆的值. 〔CDE S ∆表示△CDE 的面积,CBA S ∆表示△CBA 的面积〕
5、在△ABC 中,∠BAC = 90°,∠EAF = 90°,AB AF AC AE ⋅=⋅. 〔1〕求证:△AGC ∽△DGB ;
〔2〕假设点F 为CG 的中点,AB = 3,AC = 4,1
tan 2
DBG ∠=
,求DF 的长. G
F
E D C
B A
E
O
D A
B
C
E
D
A
F A B D C
E G 6、:如图,在△ABC 中,AB =AC ,点D 、E 分别是边AC 、AB 的中点,D
F ⊥AC ,DF 与CE 相交于点F ,AF 的延长线与BD 相交于点
G .
〔1〕求证:BD DG AD ⋅=2;
〔2〕联结CG ,求证:∠ECB =∠DCG .
7、如图E 为正方形ABCD 边BC 延长线上一点,AE 交DC 于F ,FG ∥BE 交DE 于G . 〔1〕求证:FG FC =;
〔2〕假设1FG =,3AD =,求tan GFE ∠的值.
8、如图,△ABC 中,点D 、E 分别在BC 和AC 边上,点G 是BE 边上一点,且∠BAD =∠BGD =∠C ,联结AG 。
〔1〕求证:BD BC BG BE ⋅=⋅; 〔2〕求证:∠BGA =∠BAC 。
D G
9、如图,在等腰三角形ABC 中,AB =AC ,点E 、D 是底边所在直线上的两点,联接AE 、AD ,假设2
AD DC DE =⋅。
求证:〔1〕△ADC ∽△EDA 〔2〕22AE EB
CD
AD =
第23题图
C
B
A
B C D
E G
F
E
B
D C
A 10、四边形ABCD 是平行四边形,E 是对角线AC 上一点,射线DE 分别交射线C
B 、AB 于点F 、G 。
〔1〕如图8,如果点F 在CB 边上,点G 在AB 边的延长线上,求证:1EF FG
DE DG
+=。
〔2〕如果点F 在CB 边的延长线上,点G 在AB 边上,试写出EF DE 与FG
DG
之间的一种等量关系,并给出证明。
图8F
G A
D
B
C
E
备用图
A
D B
C
11、如图,在□ABCD 中,E 是AB 的中点,ED 和AC 相交于点F ,过点F 作FG ∥AB ,交AD 于点G . 〔1〕求证:AB =3FG ;
〔2〕假设AB :AC =2:3,求证:2DF DG DA =⋅.
12、:如图,在梯形ABCD 中,AD ∥BC ,∠BCD=90°.对角线AC 、BD 相交于点E 。
且AC ⊥BD 。
(1)求证:CD ²=BC ·AD ;
〔2〕点F 是边BC 上一点,连接AF ,与BD 相交于点G ,如果∠BAF=∠DBF ,求证:
22AG BG
AD BD =。
13、如图,CD 是△ABC 中ACB ∠的角平分线,E 是AC 上的一点,
且2CD BC CE =⋅,6AD =,4AE =. 〔1〕求证:△BCD ∽△DCE ;
〔2〕求证:△ADE ∽△ACD ; 〔3〕求CE 的长.
14、在△ABC 中,D 是BC 的中点,且AD=AC ,DE ⊥BC ,与AB 相交于点E ,EC 与AD 相交于点F .
A B
C
D
E
F
G
F
E
A
C
D
B
图10
C B
A
〔1〕求证:△ABC ∽△FCD ;
〔2〕假设DE =3,BC =8,求△FCD 的面积.
15、如图,在夕阳西下的黄昏,某人看见高压电线的铁 塔在阳光的照射下,铁塔的影子的一局部落在小山的斜坡 上,为了测得铁塔的高度,他测得铁塔底部B 到小山坡脚 D 的距离为2米,铁塔在小山斜坡上的影长DC 为米,
斜坡的坡度11.875i =:,同时他测得自己的影长NH ﹦336cm , 而他的身长MN 为168cm ,求铁塔的高度.
16、:如图,在△ABC 中,点D 在BC 上,联结AD ,使得CAD B ∠=∠,DC =3且ACD ADB S S ∆∆:﹦1﹕2. 〔1〕求AC 的值;
〔2〕假设将△ADC 沿着直线AD 翻折,使点C 落点E 处,
AE 交边BC 于点F ,且AB ∥DE ,求EFD ADC
S
S ∆∆的值.
17、小华同学学习了锐角三角比后,对求三角形的面积方法进展了研究,得到了新的结论: 〔1〕如图10,锐角△ABC .求证:1
sin 2
ABC S AB AC A ∆=
; 〔2〕根据题〔1〕得到的信息,请完成下题:如图11,在等腰 △ABC 中,AB=AC =12厘米,点P 从A 点出发,沿着边AB 移动, 点Q 从C 点出发沿着边CA 移动,点Q 的速度是1厘米/秒,点P 的速度是点Q 速度的2倍,假设它们同时出发,设移动时间为t 秒,
问:当t 为何值时,
38
APQ ABC
S S ∆∆=
A
B
C
D
M
C
B
A
图11
F E
D
C
B
A。
