杆件的内力.截面法.
杆件的内力

x
N F 0
NF
6
目录
4. 轴力图
用 平行于杆轴线的坐标 表示横截面的位置,用垂直于杆轴线
的坐标表示横截面上的轴力数值,从而绘出表示轴力与横截
面位置关系的图线,称为 轴力图 。将正的轴力画在上侧,
负的画在下侧。
N
x
7
例题 :一等直杆其受力情况如图所示,作杆的轴力图。
40KN
55KN
25KN
10
求CD段内的轴力
R
55KN 25KN 20KN
40KN
A
B
C
D
E
3
N3
25KN
20KN
N3 25 20 0
N3 5KN
( )
11
求DE段内的轴力
R
40KN
55KN
25KN
20KN
A
B
C
D
E
4
N4
20KN
N 4 20KN
( )
12
40KN
55KN
25KN
20KN
3. 剪力Q=0处,弯矩取极值(Q图由正变负,M取极大值;
Q图由负变正,M取极小值)。
4. 集中力作用处,剪力图突变,突变之值为该处载荷值;M图有尖角。
集中力偶作用处,Q图无影响;弯矩图突变,突变之值为该处集中力偶值。
目录
57
各种形式荷载作用下的剪力、弯矩图
载荷情况
无 载 荷 ( q=0)
剪力图
Q 0
3
§ 5-2 轴向拉压时的内力
特点:
作用在杆件上的外力合力的作用线与 杆件轴线重合,杆件变形是沿轴线方向的伸 长或缩短。
杆的受力简图为 拉伸
截面法求杆件的内力

截面法求杆件的内力教学目标:1、理解和掌握求杆件内力的方法——截面法;2、熟练运用截面法求不同杆件受到拉伸时的内力。
教学重点:截面法求杆件内力的步骤。
教学难点:如何运用截面法求内力的方法解决工程力学中求内力的实际问题。
教学方法:提出问题——实例演示——练习点拨——归纳总结教学过程:一、复习旧知1、杆件有哪几种基本变形?2、拉伸和压缩的受力特点是什么?3、拉伸和压缩的变形特点是什么?二、新课讲解思考:当杆件受到拉伸、压缩时,就会在杆件内部产生力的作用,怎样才能确定杆件的内部会产生多大的力?(引出课题)出示本节课的学习目标。
(一)、教学什么是杆件的内力?内力:杆件在外力作用下产生变形,其内部相互间的作用力称为内力。
一般情况下,内力将随外力增加而增大。
当内力增大到一定限度时,杆件就会发生破坏。
内力是与构件的强度密切相关的,拉压杆上的内力又称为轴力。
(二)、教学截面法求杆件的内力。
1、什么是截面法?截面法:将受外力作用的杆件假想地切开,用以显示内力的大小,并以平衡条件确定其合力的方法,称为截面法。
它是分析杆件内力的唯一方法。
2、实例演示:如图AB 杆受两个力,一个向左,一个向右,大小均为F 。
作用点分别为A 和B 。
①、确定要截开的次数和位置(要根据杆件的受力情况而定) ②、选取一半截面为研究对象(一般选取受力较少的一段作为研究对象)③、假设出截面上的内力(取左段内力向右设,取右段内力向左设,方向跟坐标轴方向一致,左负右正、下负上正)④、用平衡方程求出截面上的内力(求出的内力为正值为拉力,负值为压力)取左段 ∑Fx=O -F +FN =0 取右段 ∑Fx=O F -FN =0FN =F FN =F 3、总结截面法求杆件内力的步骤:(1)截:在需求内力的截面处,沿该截面假想地把构件切开。
(2)取:选取其中一部分为研究对象。
(3)代:将截去部分对研究对象的作用,以截面上的未知内力F F N来代替。
(4)平:根据研究对象的平衡条件,建立平衡方程,以确定未知内力的大小和方向。
第二章 杆件的内力.截面法(第1、2、3节)
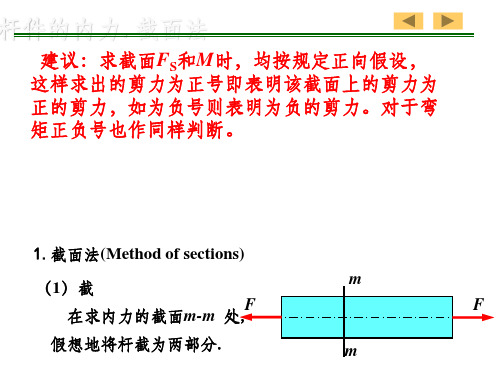
外 无外力段
力
q=0
均布载荷段
q>0
q<0
集中力
P C
集中力偶
m
C
水平直线
斜直线
自左向右突变 无变化
FS 图
FS
特
征
x
FS >0
FS
FS
x
x
FS <0 增函数
FS
FS FS1
C
x
FS2
x
降函数 FS1–FS2=P
FS
C x
M
斜直线
曲线
自左向右折角 自左向右突变
图M
M
M
M
M
与 M M1
特
x
x
x
x
xm
x
求:外力偶矩Me ( N·m)
解:PMe
n 30
P1000Me3n0
由此求得外力偶矩:
Me
Me
P103 00 P
M e
n
954 (N .9 m) n
若传递功率单位为马力(PS)时, 由于PS=735.5N·m/s
Me
702P4(N.m) n
杆件的内力.截面法
对称弯曲:工程中最常见的梁,其横截面一般至少有一根对称 轴,因而整个杆件有一个包含轴线的纵向对称面。 若所有外力都作用在该纵向对称面内时,梁弯曲变 形后的轴线将是位于该平面内的一条曲线,这种弯 曲形式称为对称弯曲。
注意 1、用截面法求轴力时,在切开的截面上建议假设正 的轴力,由平衡方程得出的FN值为正,说明轴力为正 (拉力); FN值为负,说明轴力为负(压力)。
2、在画轴力图时,填充为下画线或无填充,不要画剖 面线形式;并注上 符号 或 。
杆件的内力截面法
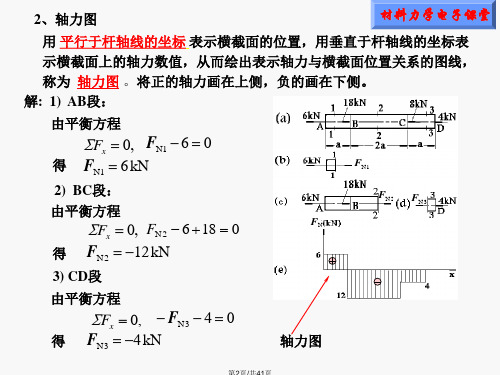
33mm
FN
44mm
150kN
材料力学电子课堂
§5-2 扭转的概念.扭矩与扭矩图
一、扭转的概念
1.受力特征:在杆件两端垂直于杆轴线的平面 内作用一对大小相等,方向相反 的外力偶。
2.变形特征:横截面形状大小未变,只是绕轴 线发生相对转动。
轴:以扭转为主要变形的构件称为轴 。
从动轮B 轴
主动轮A
M
FAy
FS1 1
M
2
FS
2
FS
FBy
2.求内力
得
FAy
FBy
m0 l
在AC段内
FS1 ( x)
FAy
m0 l
, 0
x
a
M1(x)
FAy
x
m0 l
x, 0
x
a
在BC段内
FS2 (x)
FBy
m0 l
, a
x
l
FBy
M
2
(x)
FBy
l
x
m0 l
l
x, a
x
l
3.画剪力图和弯矩图
在集中力偶作用处,弯矩图上发生突变,
Fy M
0, FA
A (F ) 0,
FB FB
l
F
0 Fl
3
0
得
FA
2 3
F,
FB
1 3
F
2.求截面1-1上的内力
FS D MD
FA FA
2F
3 a
2
3
Fa
同理,对于C左截面:
FSC左
FA
2 3
F
,
M
C左=
试述求杆件横截面上内力的截面法步骤和方法

试述求杆件横截面上内力的截面法步骤和方法1. 了解截面法哎,说到工程力学里的截面法,别让这些名字吓坏了,其实就是一种找出杆件内部力量的简单方法。
咱们平常接触的建筑物、桥梁,或者一些机械构件,都是通过这种方法来确保它们的稳固和安全的。
这个方法简单来说就是用“剪刀”切一刀,把杆件“分尸”,然后分析切面上受力的情况。
好比是咱们剥苹果皮,剥开之后看里面的果肉,这样能更清楚地了解苹果的质量。
2. 截面法的步骤2.1 选取截面首先,挑选一个合适的截面,瞅准了方向之后,就下手了。
这个步骤就像在你脑子里画出一条切割线。
你得选择一个合适的位置,把杆件从中间“切开”。
这里要注意,选取的位置一定要使得切面上的力易于计算。
如果这个位置选错了,结果就像你在黑暗中找钥匙一样,费劲不讨好。
2.2 画出受力图接下来,别忘了给这片“切面”画上图。
要把杆件切开后,分离出的部分的受力情况画出来。
图上得标明各种内力,比如剪力、轴力和弯矩等等。
这些力就像是在打游戏时,你需要记录你的角色的状态和装备一样,你要准确记录这些力的情况,这样才能确保你计算的准确。
2.3 列出平衡方程然后,你就要写平衡方程了。
平衡方程是用来保证杆件在切开时的受力状态是平衡的,不会乱七八糟。
这些方程包括了力的平衡、力矩的平衡等。
就像你玩积木,如果要保持积木塔不倒,就得仔细计算每一块积木的放置位置。
2.4 解方程找内力最后,你要解这些方程,找出杆件内部的力量。
就像做数学题一样,把方程算出来,你就能得到具体的内力数值。
这个步骤可不能马虎,不然得到的结果就像是空话,没有实际意义。
3. 截面法的应用3.1 结构分析截面法在结构分析中的应用非常广泛。
无论是大桥、小楼,还是家里的门框,都是用这个方法来确保结构的安全性。
就像是大厨做菜,得先知道每种材料的用量和比例,才能做出美味的菜肴。
工程师用截面法就像是这个大厨,通过计算内力,确保建筑的稳定性和安全性。
3.2 机械设计在机械设计中,截面法也是必不可少的。
第二章 杆件的内力·截面法讲解

F
FN (+)FN
F
F
FN (-)FN
F
轴力图: 轴力沿轴线变化的图形
F
F
FN
轴力图的意义
+ x
① 直观反映轴力与截面位置变化关系; ② 确定出最大轴力的数值及其所在位置,即确定危险截面位置,为 强度计算提供依据。
例 图示杆的A、B、C、D点分别作用着大小为FA = 5 F、 FB = 8 F、 FC = 4 F、 FD= F 的力,方向如图,试求各段内力并画出杆 的轴力图。
应变
一、正应变(线应变)定义
av
Du Ds
棱边 ka 的平均正应变
lim
Du k点沿棱边 ka 方向的正应变
Ds0 Ds
正应变特点
1、 正应变是无量纲量 2、 过同一点不同方位的正应变一般不同
二、切应变定义 微体相邻棱边所夹直角的
改变量 g ,称为切应变
切应变量纲与单位
切应变为无量纲量 切应变单位为 弧度(rad)
BC
D
FN 2 FB FC FD 0
FB
FC
FD
FN2= –3F,
求BC段内力:
FN3
C
D
Fx 0 FN3 FC FD 0 FN3= 5F,
FC
FD
FN4
D
求CD段内力:
Fx 0 FN 4 FD 0
FN4= F
FD
FN1 2F, FN2= –3F, FN3= 5F, FN4= F
M
M
取左段为研究对象:
M 0, T M 0 M x
Tx
T M
取右段为研究对象:
试述求杆件横截面上内力的截面法步骤和方法

试述求杆件横截面上内力的截面法步骤和方法哎呀,这可是个不简单的问题啊!不过别着急,我这个“知识小百科”可是见过世面的,一定能帮你解决。
今天我们就来聊聊:试述求杆件横截面上内力的截面法步骤和方法。
我们要知道杆件横截面上的内力是什么。
简单来说,就是杆件在受力时,由于各个部位的材料不同,所以产生的应力也不一样。
这些应力就会在杆件内部形成一种力量,我们称之为内力。
而求解这种内力的过程,就叫做截面法。
那么,截面法有哪些步骤呢?其实很简单,可以分为以下几步:
第一步:确定截面形状和尺寸。
这是非常重要的一步,因为不同的截面形状和尺寸会影响到内力的分布情况。
所以我们需要根据实际情况来选择合适的截面形状和尺寸。
第二步:建立坐标系。
这个步骤的目的是为了方便我们进行计算。
我们可以将杆件看作一个长方体,然后在这个长方体上建立一个坐标系,用来表示各个部位的位置和方向。
第三步:确定材料的性质和截面几何参数。
这一步也是非常关键的,因为不同的材料有着不同的弹性模量、泊松比等性质参数,而这些参数又会影响到内力的计算结果。
第四步:应用胡克定律和其他力学公式进行计算。
这一步需要我们掌握一定的力学知识和技巧,才能够正确地求解出内力的大小和方向。
好了,以上就是求解杆件横截面上内力的截面法步骤和方法了。
看起来有点复杂吧?但是只要认真学习,相信你也能轻松掌握哦!
希望我的回答对你有所帮助!如果你还有其他问题或者疑问,欢迎随时提出哦!。
截面法是求杆件内力的基本方法

一、概述截面法是工程力学中用于求解杆件内力的基本方法之一。
在工程结构分析和设计中,了解截面法的原理和应用是至关重要的。
本文将深入探讨截面法的基本概念、原理和应用,以帮助读者更好地理解和应用这一方法。
二、截面法的基本概念1.1 概念简介截面法是工程力学中用于分析杆件内力的一种方法,它基于杆件内力平衡的原理,通过考察杆件的截面上的内力分布情况来求解杆件的内力。
1.2 截面法的基本原理截面法基于力的平衡原理,即在杆件的截面上,杆件的内力必须满足横向平衡和转矩平衡的条件。
通过分析截面上的内力分布情况,可以确定杆件内的弯矩、剪力和轴力。
1.3 截面法的应用范围截面法适用于各种杆件的内力分析,包括梁、柱、桁架等结构中的杆件。
在工程实践中,截面法常常用于分析结构内部的受力情况,为结构设计和分析提供重要依据。
三、截面法的具体步骤2.1 确定截面在应用截面法时,首先需要确定分析的截面位置。
通常情况下,选择距离受力部位较近的位置作为截面。
2.2 绘制内力图在截面上绘制出杆件内的剪力图和弯矩图,根据平衡条件和力学原理,确定内力的方向和大小。
2.3 计算内力根据绘制的剪力图和弯矩图,可以直接求解出截面上的剪力、弯矩和轴力大小。
这些内力是杆件在该截面上的受力情况的表示。
2.4 检验平衡通过检验内力图的平衡条件,验证所得的内力是否符合力学平衡定律。
如果内力满足平衡条件,则认为截面法计算是正确的。
四、截面法的应用举例3.1 梁的截面力分析以简支梁为例,说明如何利用截面法分析梁的内力情况。
根据距离支座较近的位置选择截面,绘制剪力图和弯矩图,并计算出截面上的内力情况。
3.2 柱的截面力分析以等截面柱为例,说明如何利用截面法分析柱的内力情况。
通过选择适当位置的截面,绘制出内力图,计算出截面上的轴力和弯矩。
五、截面法的优缺点4.1 优点截面法简单直观,易于理解和应用。
通过截面法可以直接得到截面上的内力分布情况,为结构的受力分析提供了重要依据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章杆件的内力.截面法一、基本要求1.了解轴向拉伸与压缩、扭转、弯曲的概念;2.掌握用截面法计算基本变形杆件截面上的内力;3.熟练掌握基本变形杆件内力图的绘制方法。
表示轴力沿杆件轴线变化规律的图线。
该图一般以平行于杆件轴线的横坐标x轴表示横截面位置,纵轴表示对应横截面上轴力的大小。
正的轴力画在x轴上方,负的轴力画在x轴下方。
当功率P单位为马力(PS),转速为n(r/min)时,外力偶矩为的变形,则该力或力偶在截面上产生正的弯矩,反之为负的弯矩(上挑为正,下压为负)。
4)剪力方程和弯矩方程一般情况下,梁横截面上的剪力和弯矩随截面位置不同而变化。
若以坐标x 表示横截面在梁轴线上的位置,则横截面上的剪力和弯矩可以表示为x 的函数,即)()(S S x M M x F F ==上述函数表达式称为梁的剪力方程和弯矩方程。
5)剪力图和弯矩图为了直观地表达剪力F S 和弯矩M 沿梁轴线的变化规律,以平行于梁轴线的横坐标x 表示横截面的位置,以纵坐标按适当的比例表示响应横截面上的剪力和弯矩,所绘出的图形分别称为剪力图和弯矩图。
剪力图和弯矩图的绘制方法有以下两种:(1)剪力、弯矩方程法:即根据剪力方程和弯矩方程作图。
其步骤为:第一,求支座反力。
第二,根据截荷情况分段列出F S (x )和M (x )。
在集中力(包括支座反力)、集中力偶和分布载荷的起止点处,剪力方程和弯矩方程可能发生变化,所以这些点均为剪力方程和弯矩方程的分段点。
第三,求控制截面内力,作F S 、M 图。
一般每段的两个端点截面为控制截面。
在有均布载荷的段内,F S =0的截面处弯矩为极值,也作为控制截面求出其弯矩值。
将控制截面的内力值标在的相应位置处。
分段点之间的图形可根据剪力方程和弯矩方程绘出。
并注明m a xm a xMF S、的数值。
(2)微分关系法:即利用载荷集度、剪力与弯矩之间的关系绘制剪力图和弯矩图。
载荷集度q (x )、剪力F S (x )与弯矩M (x )之间的关系为:)()(S x q dxx dF = )()(S x F dxx dM = )()()(S 22x q dx x dF dxx M d == 根据上述微分关系,由梁上载荷的变化即可推知剪力图和弯矩图的形状。
(a)若某段梁上无分布载荷,即0)(=x q ,则该段梁的剪力F S (x )为常量,剪力图为平行于x 轴的直线;而弯矩)(x M 为x 的一次函数,弯矩图为斜直线。
(b)若某段梁上的分布载荷q x q =)((常量),则该段梁的剪力F S (x )为x 的一次函数,剪力图为斜直线;而)(x M 为x 的二次函数,弯矩图为抛物线。
当0>q (q 向上)时,弯矩图为向下凸的曲线;当0<q (q 向下)时,弯矩图为向上凸的曲线。
(c)若某截面的剪力F S (x )=0,根据0)(=dxx dM ,该截面的弯矩为极值。
利用以上各点,除可以校核已作出的剪力图和弯矩图是否正确外,还可以利用微分关系直接绘制剪力图和弯矩图,而不必再建立剪力方程和弯矩方程,其步骤如下:第一,求支座反力(对悬臂梁,若从自由端画起,可省去求支反力);第二,分段确定剪力图和弯矩图的形状;第三,求控制截面内力,根据微分关系绘剪力图和弯矩图; 第四,确定maxSF 和max M 。
maxSF 可能出现的地方:①集中力F 作用处;②支座处。
max M 可能出现的地方:①剪力F S =0的截面;②集中力F 作用处;③集中力偶M 作用处。
6)平面刚架和平面曲杆的弯曲内力刚架:杆系结构若在节点处为刚性连接,则这种结构称为刚架。
平面刚架:由在同一平面内、不同取向的杆件,通过杆端相互刚性连接而组成的结构。
各杆连接处称为刚节点。
刚架变形时,刚节点处各杆轴线之间的夹角保持不变。
静定刚架:凡未知反力和内力能由静力学平衡条件确定的刚架。
平面刚架各杆的内力,除了剪力和弯矩外,一般还有轴力。
作刚架内力图的方法和步骤与梁相同,但因刚架是由不同取向的杆件组成,习惯上按下列约定:弯矩图画在各杆的受压一侧,且不注明正、负号。
剪力图及轴力图可画在刚架轴线的任一侧(通常正值画在刚架外侧),且必须注明正负号;剪力正负号的规定与梁相同,轴力仍以拉伸为正,压缩为负。
平面曲杆:轴线为一平面曲线的杆。
平面曲杆横截面上的内力情况及其内力图的绘制方法,与刚架相类似。
三、典型例题分析例2-1 在图2-6F 2、F 3、F 4。
已知:F F 4=4kN 解:1AC 段:以截面(图(b ))。
由0=∑x F 得1N F CD 段:以截面(图(c))。
由0=∑x F 得N F 2N F DB 段:以截面(图(d))。
由0=∑x F 得N F 3N F 2.绘轴力图以横坐标x 表示横截面位置,纵轴表示对应横截面上的轴力N F ,选取适当比例,绘出轴力图(图(e ))。
在轴力图中正的轴力(拉力)画在x 轴上侧,负的轴力(压力)画在x 轴下侧。
例2-2输出功率分别为P B =解:1=M A =M M B =M D 2.计算各段扭矩BC 段:以截面I 分(图(b))得负号说明1T 同理,在CA 在AD 段内,03=-D M T m N 4463⋅==D M T3.以横坐标x 表示横截面位置,纵轴表示对应横截面上的扭矩大小,选取适当比例,绘例2-3 弯矩图。
解:1.由,0=∑∑F y F A =2.在AC段内,x F (S()a x x lFbx F x M A ≤≤=⋅=0,)( 在BC 段内()l x a lFaF x F B <<-=-=,)(S ()()()l x a x l lFax l F x M B ≤≤-=-=,)( 3.求控制截面内力,作剪力图、弯矩图。
S F 图:在AC 、CB 段内,剪力方程均为常数,因此两段剪力图均为平行于x 轴的直线。
在集中力F 作用处,lFb F l Fa F C C ==右左,-S S ,左、右两侧截面的剪力值发生突变,突变量F lFal Fb =--=)(;M 图:在AC 、CB 段内,弯矩方程)(x M 均是x 的一次函数,因此两段弯矩图均为斜直线。
求出控制截面弯矩lFabM M M C B A ===,0,标在x M -坐标系中,并分别连成直线,即得该梁的弯矩图。
显然在集中力F 作用处左、右两侧截面上弯矩值不变,但在该截面处弯矩图斜率发生突变,因此在集中力F 作用处弯矩图上为折角点。
例2.3.()()82,0,002qll M l M M =⎪⎭⎫ ⎝⎛== 8,22max max S ql M ql F ==在某一段上作用分布载荷,剪力图为一斜直线,弯矩图为一抛物线。
且在F S =0处弯矩M 取得极值。
例2-5 如图2-10所示简支梁,在C 点处受矩为M e 的集中力偶作用,试作梁的剪力图和弯矩图。
解:1.求支反力2.在在3.()()bM M l a M M l M M e e =,=-,右左00== 变。
例2-6 如图2-11解:1.求支反力。
由平衡方程∑=0)(F M B 和∑=0)(F M Aql F A 83=,ql F B 81= 2.列剪力、弯矩方程 AC 段:qx ql qx F x F A -=-=83)(S 0(x <22218321)(qx qlx qx x F x M A -=-=)20(lx ≤≤CB 段:ql F x F B 81)(S -=-= )2(l x l<≤)(81)()(x l ql x l F x M B -=-= )2(l x l≤≤3.求控制截面内力,绘Q 、M 图S F 图:AC 段内,剪力方程)(S x F 是x 的一次函数,剪力图为斜直线,求出两个端截面的剪力值,ql F A 83S =,ql F C 81S -=,标在x F -S 坐标系中,连接两点即得该段的剪力图。
CB 段内,剪力方程为常数,求出其中任一截面的内力值,连一水平线即为该段剪力图。
梁AB 的剪力图如图2-11(b)所示。
M 图:AC 段内,弯矩方程)(x M 是x 的二次函数,弯矩图为二次曲线,求出两个端截面的弯矩,0=A M ,2161ql M C =,分别标在x M -坐标系中。
在0S =F 处弯矩取得极值。
令剪力方程0)(S =x F ,解得l x 83=,求得21289)83(ql l M =,标在x M -坐标系中。
根据上面三点绘出该段的弯矩图。
CB 段内,弯矩方程)(x M 是x 的一次函数,分别求出两个端点的弯矩,标在x M -坐标系中,并连成直线。
AB 梁的M 图如图2-11(c)所示。
例2-7解:1.由平衡方程∑F A 2.由于载荷在A 内力图。
根据微分关系)()(S 22dx x dF dx x M d =剪力图为水平常数=q 3.S S F 图:kN 3S -=右C F ,kN 7S =右A F ,据此可作出CA 和AD 两段S F 图的水平线。
kN 7S =右D F ,kN 5S -=左B F ,据此作出DB 段S F 图的斜直线。
M 图:0=C M ,m KN 8.1⋅-=左A M ,据此可以作出CA 段弯矩图的斜直线。
A 支座的约束反力A F 只会使截面A 左右两侧剪力发生突变,不改变两侧的弯矩值,故m KN 8.1⋅-===A A A M M M 右左,m kN 4.2⋅=左D M ,据此可作出AD 段弯矩图的斜直线。
D 处的集中力偶会使D 截面左右两侧的弯矩发生突变,故需求出m KN 2.1⋅-=右D M ,0=B M ;由DB 段的剪力图知在E 处0S =F ,该处弯矩为极值。
根据BE 段的平衡条件∑=0y F ,知BE 段的长度为0.5m ,于是求得m kN 25.1⋅=E M 。
根据上述三个截面的弯矩值可作出DB 段的M 图。
对作出的S F 、M 图要利用微分关系和突变规律、端点规律作进一步的校核。
如DB 段内AD 段的S F D 自由端C例2-7 解:1.对CA 对BA 段距B 端为x 2的截面()F x F =2N ,()22S qx x F =,())0(212222l x qx Fa x M <≤-=。
