第七讲 图像形态学处理分析
第7章 形态学图像处理(08) 数字图像处理课件

第七章 形态学图像处理
S+x3 x
S+x1
S+x2
图7-6 S+x的三种可能的状态
第七章 形态学图像处理 第一种情形说明S+x与X相关最大,因而满足式(7-1)的点x的
全体构成结构元素与图像最大相关点集,这个点集称为S对X的 腐蚀(简称腐蚀,有时也称X用S腐蚀),记为X S。
腐蚀定义
XS {x | S x X}
即取出A中的每个点a的坐标值,将其与点b的坐标值相加,得到 一个新的点的坐标值a+b,所有这些新点所构成的图像就是A被 b平移的结果,记为A+b,或(A)b如图7-4(a-c)所示。 反射:A关于图像原点的反射结果为
Av={- a∣a∈A}
即将A中的每个点取相反数后所得的:如果两个物体之间有细小的连通,那 么当结构元素足够大时, 通过腐蚀可以将两个物体分开。
第七章 形态学图像处理
7.2.2 膨胀(Dilation)——最基本的一种运算
腐蚀可以看作是将图像X中每一与结构元素S全等的子集S+x 收缩为点x。反之,也可以将X中的每一个点x扩大为S+x,这就
结构元素的原点:实际上结构元素本身也是一个图像集合。对 每个结构元素可以指定一个原点,它是结构元素参与形态学运 算的参考点。应注意,原点可以包含在结构元素中,也可以不 包含在结构元素中,但运算的结果常不相同。
以下用阴影代表值为1的区域,白色代表值为0的区域,运 算是对值为1的区域进行的。二值形态学中两个最基本的运算— —腐蚀与膨胀。
第七章 形态学图像处理
b a
A (a)
B
A
(b)
图7-1 元素与集合间的关系 (a) a∈A, b∈A, (b)B A, B是A的子集
图像分析与处理数学形态学

• 如果B不是对称的,X被B膨胀的结 果和X被 Bv膨胀的结果不同。
膨胀
膨胀
• 左边是被处理的图象X(二值图象,针对的是黑点),中间 是结构元素B。
• 膨胀的方法是:
– 拿B的中心点和X上的点及X周围的点一个一个地对; – 如果B上有一个点落在X的范围内,则该点就为黑; – 右边是膨胀后的结果。
– 根据某点(当然是要处理的黑色点了)的八个相邻点的情况查表, 若表中的元素是1,则表示该点可删,否则保留。
细化
static int erasetable[256]= {
0,0,1,1,0,0,1,1, 1,1,0,0,1,1,1,1, 0,0,1,1,0,0,1,1, 1,1,0,0,1,1,1,1, 1,1,0,0,1,1,0,0, 0,0,0,0,0,0,0,0, 1,1,0,0,1,1,0,0, 0,0,0,0,0,0,0,0, 0,0,1,1,0,0,1,1, 1,1,0,0,1,1,1,1, 0,0,1,1,0,0,1,1, 1,1,0,0,1,1,1,1, 1,1,0,0,1,1,0,0, 1,1,0,0,1,1,1,1, 1,1,0,0,1,1,0,0, 1,1,0,0,1,1,1,0, };
二值形态学滤除条码噪声
• 通过闭操作,将条上的划痕和瑕疵填充掉
闭
• 开和闭也是对偶运算。
– 用公式表示为
• (OPEN(X))c=CLOSE((Xc))
– X 开运算的补集等于X的补集的闭运算。
• (CLOSE(X))c =OPEN((Xc))
– X 闭运算的补集等于X的补集的开运算。
• 可以这样理解:
– 在两个小岛之间有一座小桥,把岛和桥看做是处理对 象X,则X的补集为大海。
形态学图像处理

2024/5/8
25
Hit/Miss——形状检测的基本工具
• 在不同尺寸的图形中检测出想要的形状 • 严格的模版匹配。指出被匹配点所应满足的性质(模板形
状)的同时也指出这些点所不应满足的性质,即对周围环 境背景的要求。
形态学的主要应用
• 处理图像的类型:二值图像
边界提取举例
2024/5/8
29
边界提取 Boundary Extraction
区域填充 Region Filling
X k ( X k 1 B) Ac
k 1,2,3,
连通分量提取 Extraction of connected components
连通分量举例
2024/5/8
33
• 补集。A的补集记为
Ac {w | w A}
• 差集:记为A-B,定义为:
A B {w | w A, w B} A Bc
集合的基本运算
集合的基本运算
二值图像的逻辑运算
二值图像的逻辑运算
结构元素
• 形态学图像处理表现为一种邻域运算形式;
• 一种特殊定义的邻域称之为“结构元素” (Structure Element),在每个像素位置上它与 二值图像对应的区域进行特定的逻辑运算,逻辑运 算的结果为输出图像的相应像素。
细化 Thinning
• Your subtopic goes here
A B A ( A B) A ( A B)c
{B} {B1, B2, B3,, Bn} A B ((((A B1 ) B2 )) Bn )
细化 Thinning
• Your subtopic goes here
图像分析与处理数学形态学PPT课件
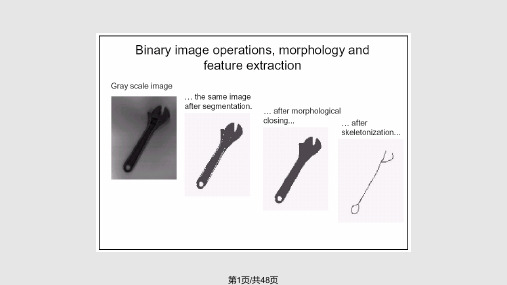
第21页/共48页
开 • 先腐蚀后膨胀称为开(open),即OPEN(X)=D(E(X))。
第22页/共48页
开 • 上面的两幅图中,左边是被处理的图象X(二值图象,针对的是黑点),右
边是结构元素B。 • 下面的两幅图中左边是腐蚀后的结果,右边是在此基础上膨胀的结果。 • 可以看到,原图经过开运算后,一些孤立的小点被去掉了。 • 一般来说,开运算能够去除孤立的小点,毛刺和小桥(即连通两块区域的
• 如果B不是对称的, X被B腐蚀的结果和 X被 Bv腐蚀的结果 不同。
第9页/共48页
腐蚀
第10页/共48页
腐蚀
• 左边是被处理的图象X(二值图象,针对的是黑点)。 • 中间是结构元素B,标有origin的点是中心点,即当前
处理元素的位置。 • 腐蚀的方法是:
• 拿B的中心点和X上的点一个一个地对比; • 如果B上的所有点都在X的范围内,则该点保留,否则将该点
第17页/共48页
膨胀
原图
膨胀后的 结果图
第18页/共48页
膨胀
• 腐蚀运算和膨胀运算互为对偶的,用公式表示 为
• 即X 被B腐蚀后的补集等于X的补集被B膨胀。
• 可以形象的理解为:
• 河岸的补集为河面,河岸的腐蚀等价于河面的膨胀。
• 对偶关系是非常有用的。
第19页/共48页
第20页/共48页
第34页/共48页
• 区域骨架问题:计算量大 算法改进思想
• 在保证产生正确的骨架的同时,改进算法的 效率。比较典型的是一类细化算法,它们不 断删去边缘,但保证删除满足:
1)不移去端点;2)不破坏连通性;(3)不 引起区域的过度腐蚀。
p
第35页/共48页
医学图像中的形态学分析方法

医学图像中的形态学分析方法随着科技的迅猛发展,医学成像技术也得到了越来越广泛的应用。
医学图像是一种非常重要的医学信息,从中医生可以了解一位患者的身体结构和病情。
形态学是一种研究物体形态的方法,是一门涉及数学和图像学的学科。
在医学图像的处理中,形态学分析是一种非常有用的工具。
当医生获得一个医学图像时,他们需要根据图像的外形和结构来判断可能的疾病类型。
形态学分析技术可以帮助医生更好地理解图像中所存在的疾病特征。
本文将介绍在医学图像处理中的形态学分析方法。
二值图像处理形态学分析涉及到二值图像处理技术,即通过二值图像处理使得图像中的某一部分变为黑色或白色。
这一过程可以通过阈值分割来实现,即将图像的像素分为两部分,超过阈值的部分变为白色,否则为黑色。
二值图像处理有时候还会使用一些滤波方法,来消除一些噪点或者细节。
形态学分析基础形态学分析的基础是基本的形态学操作:膨胀(dilate)和腐蚀(erode)。
在医学图像分析中,这些形态学操作被用于去除噪声、分割图像、检测血管、分离组织间空隙等。
图像膨胀操作的原理是将对象内的像素点向外部扩张,腐蚀操作与之相反,即将对象内的像素点向内部收缩。
几何学滤波器通常也用于形态学分析,这些滤波器包括开合运算、顶帽、底帽等。
进一步的形态学操作包括骨架提取、形态学重建等,作为形状分析的基础。
骨架提取是将二值形态分析的图像图形化为一条线,以便更好地分析所表示的病状态的特征。
形态学重建则是一种图像恢复技术,它可以恢复受损的或者已移除的部分,可用于恢复病变前的一种形态。
医学图像的应用形态学分析在医学图像处理中有着广泛的应用,其中最常见的是用于医学图像处理的分割,也就是将图像中的一部分分出来。
常用的分割方法有基于阈值、区域增长等,而基于形态学的分割方法通常是使用形态学的膨胀和腐蚀操作,以及一些形态学滤波器和种子点算法等。
医学图像处理中还经常需要处理图像中的边缘,这通常是通过形态学的操作来实现的。
7-图像分割-形态学图像处理

集合的平移图示
8.2 二值形态学的基本运算
8.2.1 腐蚀
1、概念
设A为目标图像,B为结构元素,则目标图像A被
结构元素B腐蚀可定义为:
AB x | ( B) y A
(8.9)
其中,y是一个表示集合平移的位移量。
8.2.1 腐蚀
腐蚀运算的含义是:每当在目标图像A中找到一个
与结构元素B相同的子图像时,就把该子图像中与B的 原点位置对应的那个像素位置标注为1,图像A上标注
A B {x | x A且x B}
(8.3)
集合的交
2.3.1 简单的图像成像模型
2、集合的基本运算等 (3) 集合的补
A {x | x A}
c
(8.4)
集合的补
2.3.1 简单的图像成像模型
2、集合的基本运算等 (4) 集合的差
A B {x | x A且x B}
70年代
1973年,Mathron的《随机集和积分几何》为数学 形态学奠定了基础。 1982 由Serra主编完成的《Image Analysis and Mathematical Morphology》是里程碑,表明数学形 态学在理论上已趋于完备。 此后,该书的第二版和第三版相继出版。1986, CVGIP(computer vision graphics and image processing) 发表了MM专辑,使MM的研究呈现新景 象。 提出基于MM的纹理分析模型系列。
卷积模板,每当结构元素平移到其原点位置与目标图 像A中那些像素值为“1”的位置重合时,就判断被结构
元素覆盖的子图像的其它像素的值是否都与结构元素 相应位置的像素值相同;只有当其都相同时,就将结 果图像中的那个与原点位置对应的像素位置的值置为 “1”,否则置为0。 注意:当结构元素在目标图像上平移时,结构元素中 的任何元素不能超出目标图像的范围。
图像形态学处理的概念

cvDilate(src,dst,element,1); } cvReleaseStructuringElement(&element); cvShowImage("Erode/Dilate",dst); }
int main(int argc,char **argv) { char *filename =argc ==2?argv[1]:(char *)"lena.jpg"; if( (src = cvLoadImage(filename,1)) == 0 ) return -1; dst=cvCloneImage(src); cvNamedWindow("Open/Close",1); cvNamedWindow("Erode/Dilate",1); open_close_pos = erode_dilate_pos = max_iters;
检测完整幅图像后一次性去除要细化的点。 常用的图像细化算法有 hilditch 算法,pavlidis 算法和 rosenfeld 算法等。 注:进行细化算法前要先对图像进行二值化,即图像中只包含“黑”和“白”两 种颜色。 二、OpenCv 形态学操作相关函数 1、MorphologyEx 高级形态学变换
void cvDilate( const CvArr* src, CvArr* dst, IplConvKernel* element=NULL, int iterations=1 ); src 输入图像. dst 输出图像. element 用于膨胀的结构元素。若为 NULL, 则使用 3×3 长方形的结构元素 iterations 膨胀的次数 函数 cvDilate 对输入图像使用指定的结构元进行膨胀, 该结构决定每个具有最 小值象素点的邻域形状: dst=dilate(src,element): dst(x,y)=max((x',y') in element))src(x+x',y+y') 函数支持 (in-place) 模式。 膨胀可以重复进行 (iterations) 次. 对彩色图像, 每个彩色通道单独处理。 3、Erode 使用任意结构元素腐蚀图像
形态学图像处理实验

形态学图像处理实验1.算法原理1)提取与图像边界融合的颗粒可利用区域填充算法。
如图1所示为源图像,可将图像先转换为二值图像,然后对其进行取反,这样进行区域填充的结果将为与边界相连的颗粒,再与源图像进行比较,即可得出在源图像中与边界相连的颗粒图像。
2)提取彼此交叠的颗粒可利用图像的腐蚀与膨胀操作。
先用模板对图像进行腐蚀操作,由于相交叠的颗粒面积必然比独立的颗粒大,因此腐蚀操作之后剩下的部分为交叠颗粒的部分,再对其进行膨胀,将其与源图像进行比较操作,则可得出交叠的颗粒图像。
3)提取不交叠的颗粒得出交叠的颗粒之后,用源图像对其相减,则得出的为独立分布的颗粒图像。
2.Matlab源代码clear allclcorigin = imread('E:\Documents\BUPT\DIP\第三次作业\grain.jpg');imshow(origin);title('原图');origin = rgb2gray(origin);filterResult = medfilt2(origin);[m,n] = size(origin);%%%%%%%%%%%%取与边界融合的粒子%%%%%%%%%%%%%binaryIm = im2bw(origin);tmp = ~binary Im; %tmp为取反图像fieldFilling = imfill(tmp,'holes');figure, imshow(fieldFilling);title('区域填充结果');boudaryGrains = origin;for i = 1:mfor j = 1:nif fieldFilling(i,j) ==1boudaryGrains(i,j) = 0;endendendfigure, imshow(boudaryGrains);title('与边界融合的粒子结果');%%%%%%%%%%%取交叠与未交叠的粒子%%%%%%%%%%%%mask1 = strel('ball',12,12);%mask2 = ones(13,13);mask2 = strel('ball',7,7);mask3 = strel('disk',4);mask4 = strel('ball',6,6);result1 = imerode(filterResult,ones(15,15));result2 = filter2(fspecial('average',7),im2double(result1)); result2 = medfilt2(result2);result2 = im2uint8(result2);result3 = imdilate(result2,mask1);figure,imshow(result2);title('第一次腐蚀结果'); figure,imshow(result3);title('第一次膨胀结果');result4 = origin;for i = 1:mfor j = 1:nif result3(i,j) <=20result4(i,j) = 0;elseresult4(i,j) = origin(i,j);endendendfigure,imshow(result4);title('阈值处理结果');result5 = imerode(result4,mask4);result6 = imdilate(result5,mask4);figure,imshow(result6);title('交叠粒子结果');result7 = origin-result4;result8 = imerode(result7,mask4);result9 = imdilate(result8,mask4);figure,imshow(result9);title('未交叠粒子结果');3. 运行结果分析1) 提取与边界融合的颗粒原图区域填充结果与边界融合的粒子结果第一次腐蚀所示结果为在腐蚀之后进行了一次中值滤波和一次5X5均值滤波的结果,为使腐蚀的结果更好,去除独立颗粒的腐蚀残留图像。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
它们基本的形状特性,并除去不相干的结构。 数学形态学的基本运算:膨胀、腐蚀、开启和闭合,击中
击不中变换。
二、基本概念 形态学:从图像出发,研究物体目标的结构和拓扑关系 结构元素:任意大小,包含任意0、1组合的一个区域。
结构元素中的任意一点都可以成为结构元的原点。
形态学图像处理:结构元素与图像进行逻辑运算产生新 的图像的处理方法。 结构元与图像的运算:类似卷积,但用逻辑运算代替乘 加运算,结果为处理后图像的像素值。 形态学处理效果:取决于结构元素的大小、形状与逻辑 运算的方法。
A 相对位移B
删除的点 ? 保留的点
原点位于结构元素中的膨胀操作
+
图像 A
结构元 B
A 相对位移B
原点不在结构元素中的膨胀操作
增加的点
删除的点
+
?
? ?
增加的点
图像 A
结构元 B
此时膨胀的结果与A没有任何关系,即:
( A B) A
第 七 讲 图像形态学处理
西安电子科技大学机电工程学院
王
义
敏
一、数学形态学图像处理 形态学:生物学的分支,研究动植物的形态和结构 数学形态学:分析几何形状和结构的数学方法,建立在 集合代数的基础上,用集合论方法定量描述集合结构的学 科。1985年以后成为分析图像几何特征的工具。
数学形态学是一门交叉学科,有严格的数学理论(集合
{(1 , 1), (1 , 2), (2 , 1), (2 , 2), (2 , 3), (2 , 4), (3 , 1), (3 , 2), (3 , 3), (3 , 4), (4 , 2), (4 , 3), (5 , 2) }
c、基于位移运算的膨胀操作
+
保留的点
增加的点
图像 A
结构元 B
bB
膨胀的算法:
1、用结构元素,扫描图像的每一个像素; 2、用结构元素与其覆盖的二值图像做“与”运算 3、如果都为0,结果图像的该像素为0,否则为1
膨胀的作用:
1、用3x3的结构元时,物体的边界沿周边增加一个像素 2、把目标周围的背景点合并到目标中,目标之间存 在细小的缝隙,膨胀可能将不同目标连通在一起
解释:A 被 B 膨胀是所有位移 x 的集合, B 的映射与A至少
有一个元素是重叠的。换言之,用 B 膨胀 A 得到的集合是B 的映射的位移与 A 至少有一个非零元素相交时 B 的原点 x 位置的集合。从而上式变为:
ˆ ) A] A} A B {x | [(B x
膨胀的另外定义为:
A B {x | x a b, a A, b B} A B ( A) b
3、若物体之间有细小的连通,选择适当的结构元,
可以将物体分开。 4、不同的结构元及其不同的原点,产生不同的结果
3、膨胀的运算
a、基于膨胀定义本身的运算
+ +
保留的点
图像 A
结构元 B 原点位于结构元素中的膨胀操作
增加的点
删除的点 ? 保留的点
+
图像 A
结构元 B 原点不在结构元素中的膨胀操作
&理论基础艰深,但基本观念比较简单。 理论基础和所用语言为:集合论。 图像中的集合:代表二值图像或者灰度(彩色)图像的
形状。如:黑白图像中的黑像素集合是图像的完全描述,
感兴趣目标区域的像素集合。
数学形态学图像处理的基本思想:使用具有一定形态 的结构元素,去度量和提取图像中的对应形状,如边界、 骨架、凸壳等,以达到对图像进行分析和识别的目的。 数学形态学图像处理意义:可以简化图像数据,保持
A B ( A) b
bB
向量的观点
位移的观点
腐蚀的算法:
1、用结构元素,扫描图像的每一个像素;
2、用结构元素与其覆盖的二值图像做与运算 3、如果结果都为1,结果图像的该像素为1,否则为0
腐蚀的作用:
1、用3x3的结构元时,物体的边界沿周边减少一个像素 2、消除掉图像中小于结构元大小的目标物体
三、集合论的基本概念
1、集合的定义: 具有某种性质的、确定的、有区别的事物的全集,
用大写字母表示。不包含任何元素的集合称为空集,规
定任何空集都只是同一个集合,记作 Φ 。 在数字图像处理中,集合是图像中描述的对象或其他
感兴趣特征的像素坐标。
2、子集: 3、并集:
a A , aB A B
8、映像(集合的反射):
ˆ {x | x a , a A } A
集合的图解表示:
A
B Z
c
A B
x1
A B
x2
x1
( A)
x2
A B
( A) x ( x ( x1 , x2 ))
ˆ A
四、膨胀与腐蚀
1、膨胀(使图像扩大)
ˆ ) A] } A B {x | [(B x
C {c | c A or c B}
C A B
4、交集:
C {c | c A and c B}
C A B
5、补集: 6、集合的差:
A {x | x A }
c
A B {x | x A , x B } A Bc
7、位移:
( A) x { y | y a x , a A }
b、基于向量运算的膨胀操作 设图像左上角的坐标为(0,0),则:A ={(1,1), (2,1), (2,2), (2,3), (3,2), (3,3), (4,3)},B={(0,0),
(1,0), (0,1)}
A B {(1 , 1), (2 , 1), (2 , 2), (2 , 3), (3 , 2), (3 , 3), (4 , 3), (2 , 1), (3 , 1), (3 , 2), (3 , 3), (4 , 2), (4 , 3), (5 , 3), (1 , 2), (2 , 2), (2 , 3), (2 , 4), (3 , 3), (3 , 4), (4 , 4), }
3、填补分割后物体中的空洞
2、腐蚀(使图像缩小)
A B {x | ( B) x A}
解释:A 被 B 腐蚀是所有位移 x 的集合, 其中 B 平移 x 后 仍包含于 A 中。换言之,用 B 腐蚀 A 得到的集合是B 完全 包含在 A 中时 B 的原点位置的集合。 腐蚀的另外定义为:
A
B {x | x b A, b B}
