材料科学基础第六章 单组元相图及纯晶体的凝固
第6章 单组元相图及纯晶体的凝固 笔记及课后习题详解 (已整理 袁圆 2014.8.6)

第6章单组元相图及纯晶体的凝固6.1 复习笔记一、单元系相变的热力学及相平衡1.相平衡条件和相律组元:组成一个体系的基本单元,如单质(元素)和稳定化合物,称为组元。
相:体系中具有相同物理与化学性质的且与其他部分以界面分开的均匀部分,称为相。
相律:F=C-P+2;式中,F为体系的自由度数,它是指不影响体系平衡状态的独立可变参数(如温度、压力、浓度等)的数目;C为体系的组元数;P为相数。
常压下,F=C-P+1。
2.单元系相图单元系相图是通过几何图像描述由单一组元构成的体系在不同温度和压条件下可能存在的相及多相的平衡。
图6-1 水的相图图6-2 Fe在温度下的同素异构转变上述相图中的曲线所表示的是两相平衡时温度和压力的定量关系,可由克劳修斯(Clausius)一克拉珀龙(Clapeyron)方程决定,即式中,为相变潜热;为摩尔体积变化;T是两相平衡温度。
有些物质在稳定相形成前,先行成自由能较稳定相高地亚稳定相。
二、纯晶体的凝固1.液态结构(1)液体中原子间的平均距离比固体中略大;(2)液体中原子的配位数比密排结构晶体的配位数减小;(3)液态结构的最重要特征是原子排列为长程无序,短程有序,存在结构起伏。
2.晶体凝固的热力学条件(6.1)式中,,是熔点T m与实际凝固温度T之差;L m是熔化热。
晶体凝固的热力学条件表明,实际凝固温度应低于熔点T m,即需要有过冷度△T。
3.形核晶体的凝固是通过形核与长大两个过程进行的,形核方式可以分为两类:均匀形核和非均匀形核。
(1)均匀形核①晶核形成时的能量变化和临界晶核新相晶核是在母相中均匀地生成的,即晶核由液相中的一些原子团直接形成,不受杂质粒子或外表面的影响假定晶胚为球形,半径为r,当过冷液中出现一个晶胚时,总的自由能变化:(6.2)由,可得晶核临界半径:(6.3)代入公式(1),可得:(6.4)由式可知,过冷度△T越大,临界半径则越小,则形核的几率越大,晶核数目增多。
06第六章单组元相图及纯晶体的凝固
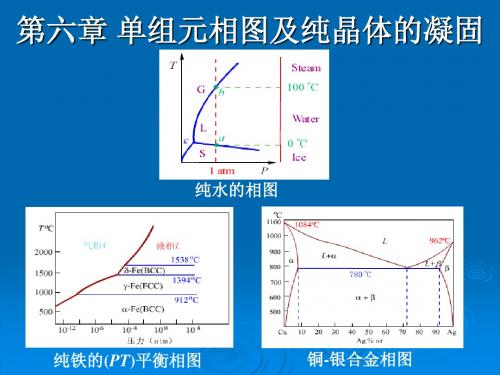
纯铁的(PT)平衡相图
铜-银合金相图
利用相图可以: 1 告知在不同温度、成分情况下合金中能够稳定存在的相; 2 了解各种成分合金的熔点和发生固态转变的温度; 3 用于研究合金的凝固过程和凝固后的组织,从而预测材料性能; 4 是制定合金熔铸、压力加工、热处理工艺的重要依据。
组织结构 相图 加工处理 特性 性能
第六章 单组元相图及纯晶体的凝固
纯水Байду номын сангаас相图
纯铁的(PT)平衡相图
铜-银合金相图
基本概念 ●组元:组成一个体系的,且相互独立的基本单元。 可以是单质也可以是化合物( 如:Fe3C) ●单组元系统(单元系):由一种元素或化合物组成的材料或体系 金刚石、 二氧化碳(CO2)、石英(SiO2)、纯铁、纯铜…… 二组元系统(二元系): Cu和Zn ——黄铜 Fe和C ——碳钢 MgO 和Al2O3 ——陶瓷 多组元系统(三元系及多元系) : 00Cr17Ni14Mo2 ——不锈钢 Ti6Al4V——钛合金
凝固的必要条件: GV 0 则, T Tm T 0 (过冷度)
GV 称为凝固驱动力
●冷却曲线与过冷 1.冷却曲线 金属结晶时温度与时间的 关系曲线称冷却曲线。 水平阶段所对应的温度称 实际结晶温度T1。此水平阶段 是由于结晶时放出结晶潜热引 起的。 2.过冷与过冷度 纯金属都有一个理论结晶 温度Tm(熔点或平衡结晶温 度)。在该温度下, 液体和晶 体处于动平衡状态。 结晶只有在Tm以下的实际 结晶温度下才能进行。
●相:是指体系中具有相同物理与化学性质的、且与其他部分以 界面分开的均匀部分。 单相合金 固溶体或纯金属 多相合金 每个相可以是纯金属、固溶体或化合物
●相变:随着温度和压力的变化(对于合金,还有成分的变化), 材料的组成相会随之变化,从一种相到另一种相的转变 称为相变。 ●凝固:由液相至固相的转变,如果凝固后的固体是晶体,则又 可称之为结晶。 ●固态相变:不同固相之间的转变。
第六章单组元相图及纯晶体的凝固

P ——系统中能够同时存在的相(如:固相、液相、α相等)数。 2 ——表示温度和压力两个变量。
对于绝大多数的常规材料系统而言,压力的影响极小, 可看作常量(1个大气压),因此自由度数减少一个,相律 的表达式为:
(1 相) 组元:Fe
(1 相) 组元:Fe和C
(2相) 组元:Fe和C
●相图(Phase diagrams):是一个材料系统在不同的化学成分、 温度、压力条件下所处状态的图形表示,因此,相图也称为状态 图。由于相图都是在平衡条件(极缓慢冷却)下测得的,所以,相 图也称为平衡相(状态)图。
对于常用的合金相图,因为压力的影响很小,况且一般都是
等温等压下
……
……
如果体系中只有a和b两相,当极少量(dn2)的组元2从a相转到b
相,以dGa和dGb分别代表此时a相和b相的自由能变化,则引 起的总的自由能变化为:
由于 故 因此,组元2从a相自发转到b相的条件是:
当dG=0,即 内没有物质传输。
,a相和b相处于平衡状态,此时体系
同理,其他组元也应有同样的属性。 对于多元系的多相平衡条件可普遍写成:
2.过冷与过冷度 纯金属都有一个理论结晶
温度Tm(熔点或平衡结晶温度 )。在该温度下, 液体和晶体 处于动平衡状态。
结晶只有在Tm以下的实际 结晶温度下才能进行。
●凝固:由液相至固相的转变,如果凝固后的固体是晶体,则又 可称之为结晶。
●固态相变:不同固相之间的转变。
例1:糖水
相与组元的关系
第六章单组元相图及纯金

不同的是液态金属原子不象固态金属原子那 样作长程有序规则排列。由于液态金属所处的 温度较高,原子活动能力较强,所以它只能作 短程(近程)有序长程(远程)无序分布。其 结构示意图如右:
液态金属为什么会具有短程有序,长程无 序的结构?这主要是因为在液态金属内部存 在着较大的能量起伏和结构起伏所造成的。 ①能量起伏:由于液态金属所处的温度较高, 原子的热运动比较强烈,使各原子的能量 不相等,一些原子的能量高于整个体系原 子的平均能量,而另一些原子的能量低于 整个体系原子的平均能量,并且这种现象 瞬息万变,此起彼伏。 我们把这种原子能量的不均匀性称为能量 起伏。
2.纯金属凝固的一般过程
由于液态金属是不透明的,所以目前还无法直 接观察到它的凝固过程。但人们在显微镜下可直接 观察到透明物质的凝固过程,如观察到有机物氯化 铵饱和水溶液的凝固过程如下图:
该图可用来近似地描述纯金属的凝固过程,由 图可知纯金属的凝固过程,主要是通过形核和长大 两个步骤来完成。
①形核:液态金属通过能量起伏和结构起 伏,形成具有一定尺寸的晶胚的过 程。该一定尺寸的晶胚称为晶核。 ②长大:液态金属原子不断地迁移到晶核表 面上去的过程。
另外由纯金属的凝固过程示意图还可以看 出,液态金属在凝固后是由许多晶粒和晶界 组成的多晶体。 晶粒:由一个晶核长大形成的小晶体。 晶界:是晶粒与晶粒之间的交界面。 液态金属在凝固过程中形成的晶核数目越 多,晶粒越细小,晶界总面积就越大。
6.2.3纯金属凝固的热力学条件
1.液、固态金属的自由能-温度曲线 由物理化学可知,体系的自由能G可用下式 表示:G=H-TS。H-热焓,T-绝对温度,S-熵, 求体系的自由能与温度的关系曲线,只需求 出自由能随温度的变化率,即自由能对温度的 一阶导数。
第六章 单组元相图及纯晶体的凝固

L. Baykal
Dnieper
nu MA E ON A CD I be A AIA LB N B LGA I A U R
GR E E EC
Da
MOLD A OV
Sea of Japan
JA A PN
N TH K E OR OR A
MA LI
Black Sea
K ZA H TA A KS N
Irtysh
组元:基本单元- 单质或化合物 单质或化合物) ⅰ 组元:基本单元-(单质或化合物 ⅱ 相:相同的物理与化学性质;与其他部 相同的物理与化学性质; 分之间有界面 分之间有界面 元系: 个组元都是独立的体系 ⅲ n元系:n个组元都是独立的体系 元系
CND AAA
Hudson Bay Gulf of Alaska
Ar abian Sea
INIA D
C GO ON
Bay of Bengal
TH I LA D A N
K MP C E A UHA
I N ON S A D EI
BUE RNI MA Y I A LA S
L. Victoria
KNA EY S I LA K R NA TA ZA I A N N MA Y I A LA S SN P E I GA OR
B LGI U E M C anary I sl ands S AN PI AD R N OR A FR N E AC LU . X GE MA Y R N
Sea Baltic
Ob'
E TON A S I
ne Rhi
C C ZE H
S TZE LA D WI R N P N OLA D
LA I A TV LI TH A I A UN
第6章单组元相图及纯晶体的凝固

纯铁在固态下 有三种同素异 构体, -Fe 、 -Fe 体心立方 结构, -Fe 面 心立方结构。
6
6.2 纯晶体的凝固
6.2.1、液态结构
晶体材料的液态结构从长程上来说是无序的,而在近程范 围内却存在着晶态的原子排列情况即近程有序;而且由于 原子的热运动,这种排列是在不断变动的,称为“结构起 伏”。
(3)振动和搅拌: 在浇注和结晶过程中实施振动和搅拌,可以达到细化晶 粒的目的。 这是因为振动和搅拌可使结晶的枝晶碎化,增加晶核数 量;另外还能向液体中输入额外能量以提供形核功。
25
2、单晶的制备 (1)垂直提拉法: 先用感应加热或电阻加热方法熔化坩埚中的材料,使液 体保持稍高于熔点的温度,然后将夹有一个籽晶的杆下 移,使籽晶与液面接触。缓慢降低炉内温度,将籽晶杆 一边旋转一边提拉,使籽晶作为唯一的晶核在液相中结 晶,最后成为一块单晶体。 (2)尖端形核法:
8
6.2.3、形核
晶体的凝固是通过形核与长大两个过程进行的,即固相 核心的形成与晶核生长至液相耗尽为止。 形核的方式有两类: (1)均匀形核:新相晶核在母相中均匀地生成。 ( 2 )非均匀形核:新相优先在母相中存在的异质处形核。
实际溶液的凝固方式主要是非均匀形核。非均匀形核的 原理是建立在均匀形核基础上的。
(2)必须具备与一定过冷度相适应的能量起伏( G* )和 结构起伏( r* )。
12
形核率 N:当温度低于熔点时,单位体积液体内,在单位
时间所形成的晶核数。 形核率受两个因素控制,形核功因子和原子扩散的几率因子。
G * Q N K exp( ) exp( ) kT kT
形核率先随过冷度增大 而增大,有一极大值, 超过极大值后,形核率 又随过冷度进一步增大 而减小。
第6章 单元系相图
第6章单组元相图及纯晶体的凝固物质由液态转变为固态的过程称为凝固。
物质由液态转变为晶态的过程称为结晶材料的性能组织结构相种类数量尺寸形状分布C ONTENTS6.1 单元系相变的热力学及相平衡6.2纯晶体的凝固6.1单元系相变的热力学及相平衡1. 相(Phase)在一个系统中,成分、结构相同,性能一致的均匀的组成部分叫做相,不同相之间有明显的界面分开,该界面称为相界面。
注意:相在物理性能和化学性能上是均匀的。
相界面和晶界的区别。
6.1单元系相变的热力学及相平衡2. 组元(Component)组元通常是指系统中每一个可以单独分离出来,并能独立存在的化学纯物质,在一个给定的系统中,组元就是构成系统的各种化学元素或化合物。
按组元数目,将系统分为:一元系二元系三元系……化学元素:Cu, Ni, Fe 等化合物:Al 2O 3, MgO, Na 2O, SiO 2等6.1单元系相变的热力学及相平衡3. 相平衡在某一温度下,系统中各个相经过很长时间也不互相转变,处于平衡状态,这种平衡称为相平衡。
各组元在各相中的温度、压力和化学势相同。
A B热力学动态平衡6.1单元系相变的热力学及相平衡4.吉布斯相律(Gibbs Phase Rule)处于热力学平衡状态的系统中自由度与组元数和相数之间的关系定律,通常简称为相律。
f = C-P+N只考虑温度和压力对系统平衡状态的影响:f = C-P+2凝聚系统:f = C-P+1式中:f(freedom)是自由度数;C(component)是组成材料系统的独立组元数;P(phase)是平衡相的数目。
吉布斯相律的应用和局限性相律是检验、分析和使用相图的重要工具,利用它可以分析和确定系统中可能存在的相数,检验和研究相图。
注意使用相律有一些限制:(1)只适用于热力学平衡状态,各相温度相等、压力相等、化学势相等(化学平衡)。
(2)只表示体系中组元和相的数目,不能指明组元和相的类型和含量。
上海交通大学_材料科学基础第六章
GS AL L AW W AW LW
在三相交叉点,表面张力应达到平衡: LW L cos W
式中θ为晶核和型壁的接触角。由于
AL 2r 2 (1 cos )
AW R2 r 2 sin 2n 2 (L cos W )
Page 7
相率的应用
• 可以确定系统中可能存在的最多平衡相数
例:恒压下,单元系,因f ≥0,故P≤1-0+1=2,平衡相最大为二个。 注意
:这并不是说,单元系中能够出现的相数不能超过二个,而是说,某一 固定T下,单元系中不同的相只能有两个同时存在,而其它相则在别的 条件下存在。
• 可解释纯金属与二元合金结晶时的差别
– 原子由液态的聚集状态转变为晶态的排列状态,使体系 △Gv降低;
• 阻力:
– 晶胚形成新的表面,引起表面自由能升高; – 体积应变能,此阻力可在液相中释放,可忽略。
Page 25
临界晶核形成
假定晶胚为球形,半径为r,当过冷液 中出现一个晶胚(Embryo)时,总的自 由能变化△G应为
G
4 3 r GV 4 r 2 3
• 从一种相转变为另一种相的过程称为相变(phase transformation)。若转变前后均为固相,则成为固态相变 (solid-solid phase transformation )。 • 从液相转变为固相的过程称为凝固(solidification)。若凝固 后的产物为晶体称为结晶(crystallization)。
dP H dT T Vm
式中, H 为相变潜热; Vm 为摩尔体积变化;T是两相平衡温度。
当高温相转变为低温相时,H 0 , 如果相变后体积收缩,即 V 0 , 则 如果相变后体积膨胀,即 V 0 ,则
第六章、单组元相图及纯晶体的凝固
凝固4.1.2相律4.1 相图的基本知识相律:在平衡条件下,一个系统的组成物的组元数、相数、和自由度数之间的关系可以由相律来确定。
相律的数学表达式如下:F ——系统的自由度数C ——组成物的组元数P ——系统中能够同时存在的相数2 ——表示温度和压力两个变量,对于不含气相的凝聚体系,压力的影响极小,可以不把压力当作变量而看作常量:1个大气压(atm),因此自由度数减少一个,相律的表达式为:4.1.2 相律☐在压力不变(1atm )的条件下,F = C –P +1 = 2–P。
F = 0的含义是:在保持系统平衡状态不变的条件下,没有可以独立变化的变量。
即,任何变量的变化都会造成系统平衡状态的变化。
◼自由度数F 的最小值为0,当F = 0时,P = 2。
◼这说明,在压力不变(1atm)条件下,单元系统最多只能有二相同时存在。
(表现为??图形)☐如果压力可变,◼F = 0时,由公式F = C -P + 2 可知P = 3,◼单元系统最多可以有三相共存。
(表现为??图形)4.1.2 相律☐在压力不变(1atm)的条件下,F = C–P+1 = 3–P。
◼自由度数F的最小值为0,当F= 0时,P= 3。
◼这说明,当二元合金系统同时出现三个相时,就没有可以变化的因素了☐也就是说,只有在一定的温度、成分所确定的某一点才会出现三相同时存在的状态。
☐表现为??图形4.1.2 相律☐在压力不变(1atm)的条件下,F = C–P+1 = 3–P。
◼可以推断出,二元合金系统存在“三相共存状态”的平衡反应,仅有二大类型:A→B+C,A+B→C。
☐由于自由度数为0,这些平衡反应都是恒温反应,并且反应中的三个相(无论是反应相,还是生成相)的化学成分都是固定的。
☐只有当反应结束后(相数小于3时),随着温度的变化,相的化学成分才可能发生变化。
❶液体中原子间的平均距离比固体中略大;液态结构的特征❷液体中原子的配位数•对于密排结构晶体,液态时配位数减小——导致熔化时体积略为增加,•但对非密排结构的晶体,则液态时配位数反而增大,故熔化时体积略为收缩。
15材料科学基础第六章__单组元相图及纯晶体的凝固01
在熔点(Tm) Gs =Gl, △G = 0 △Gv =-Lm ·△ T/Tm △T= Tm-T △Gv < 0 △T>0 才能发生凝固。
即凝固热力学条件是:需要有过冷度
6.2.3 形 核
凝固过程包括形核和长大
形核方式分为: (1) 均匀形核 新相晶核在母相中均匀生成,
(5)熔融过程出现升温现象(边熔融边升温)。
6.2.6 高分子的结晶特征
高分子结晶与低分子结晶的异同性。
高分子中的晶体像金属、陶瓷及低分子有机物一样 ,三维方向长程有序,与低分子结晶具有相似性。
高分子是长链结构,使高分子长链排入晶格要困难 得多,呈现出不完全性和不完善性、熔融升温和结 晶速度慢的特点。
1. 相似性 (1) 晶粒尺寸受过冷度影响。△T越大,形核率升 高,球晶尺寸小,密度大。 (2) 包括形核和长大两个过程。
生长形态为树枝状长大:
a 光滑界面,树枝晶不明显 b 粗糙界面,树枝晶明显
负温度梯度下的界面形状
树枝晶长大 具有一定的 晶体取向, 与晶体结构 类型有关。
面心立方 <100> 体心立方 <100> 密排六方 1010
钢中的树枝状晶体
Ni-Ta-Mn-Cr合金中的树枝状晶体
3. 凝固后晶粒大小控制
即晶核由液相中的一些原子团直接形成。
(2) 非均匀形核 新相晶核优先在母相中的异 质处形核,即依附于液相中的杂质或表面形核。
1. 均匀形核
A. 晶核形成时能量变化 B. 临界晶核 只有达到临界半径时才能使晶胚成为稳定晶核 过冷度越大,临界半径越小,则形核几率增大, 晶核的数目增多。
C. 形核率
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
书上210页,又给出了Cu非均匀形核所需要的原子个数,20个。 远小于均匀形核的692个。为什么? 表面能的增量变小,需要用来降低能量的体积也变小。
ห้องสมุดไป่ตู้36
b、形核率
单位体积液体内单位时间所形成的晶核数;
原子扩散经过液固界面,到固相形核;
受两个因素的控制
固-液界面的微观结构必 然影响晶体的长大方式。 而液固界面的构造又由 界面热力学决定。
44
透明水样苯酯晶体的小面形态 透明环己烷凝固成树枝形晶体
45
1. 固-液界面(solid-liquid interface)结构 按微观结构可分为:
光滑界面(smooth interface) 粗糙界面(rough interface)
40
练习题
任意形状晶核的临界晶核形核功△G*与临 界晶核体积V*的关系:
△GV---液固相单位体积自由能差。
41
答案
均匀形核:G Ar 3G V Br 2
A和B:晶核的形状因子
对(1)求极值,即 d G 0 r * 2B
dr
2AG V
V * A r * 3
G * Ar * 3 G V B r * 2
6.2、纯晶体的凝固
6.2.1、液态结构 长程无序,短程有序,不稳定,瞬息万变。
结构起伏:液态金属中存在着原子排列规则(有序)的小区域 (原子集团),但是不稳定,存在原子重新聚集clustering,此 起彼伏。 能量起伏:造成结构起伏的原因是液态金属中存在着能量起伏, 能量低的地方形成cluster,遇到能量高峰又散开成无序状态。 结构起伏与能量起伏是对应的。
G V
Lm
T
Lm Tm
Lm T
T
m
G
V
0
T
0
T T m T
T称为过冷度。实际凝固温度应低于
熔点Tm,即需要一定的过冷度。
23
6.2、纯晶体的凝固 6.2.1、液态结构 6.2.2、晶体凝固的热力学条件
6.2.3、形核
凝固过程:形核、长大。直到液相被耗尽
形核分为两类:
• 均匀形核:母相中均匀生成核心,晶核由液相 中的一些原子团直接形成。
20
6.2、纯晶体的凝固 6.2.1、液态结构
6.2.2、晶体凝固的热力学条件
G H TS dG Vdp SdT
在等压时,dp 0, dG S dT
S 0,自由能随温度增加而减小。
熔化后,组态熵和振动熵都增大,
则S
L
S
。
S
理论凝固温度:Tm
21
T
T m ,G
S
G
,固相稳定。
L
T
Tm
,G
L
G
,液相稳定。
S
T =T m ,G
L
G
,状态稳定。
S
从图中也可以看出, 两线的差值即相变的 驱动力。只有T<Tm时 才会凝固。
22
由于G V G S G L H T S
在T m时,G 0,则S m 在恒压下,H L m
H Tm
Lm Tm
G V
H
TS
其中L m为熔化潜热,S为熔化熵。
形核功因子
38
对于流动性很好的液体
当下降到一温度T*时,N突然增大。 此温度称为均匀形核的有效形核温度。 未达上图7的峰值,结晶已完毕。
有效形核过冷度 T*=0.2Tm (K) 均匀形核所需过冷度较大
39
非均匀形核功要小。 到最大值时,结晶并没有
结束,形核率会逐渐下降 至凝固完毕。原因:基底 减少,导致形核率降低。
一般,H
0,V m
0,则有 dP dT
0。
少数,H
0,V m
0,则有
dP dT
0。
一般情况下:V
很小,则固相线几乎垂直。
m
12
位移型相转变和重构型相转变。
• 位移型相变快,体积变化较小 • 重构型相变慢,体积变化较大
一般相图表示的是一种平衡状态,不论相变多 么的慢。
亚(介)稳态:自由能较高。
r>r*,自由能↓,稳定
r*为一临界尺寸。
一定温度下
26
临界半径
G
4r
3
3G V
4 r
2
dG 0 r * 2
dr
G V
r=r*时,G*>0
一定温度下
27
r* G V
2
G V L mT
Tm
r
*
2 T m
L mT
T↑, r*↓ T=0, r*=∞
G* r*
4r
3
2
3G V
粗糙界面上,约有50 %的结晶位 置空着,液相原子可以直接进入 这些位置,从而使整个固-液界面 垂直地向液相中推进,即晶体沿 界面的法线方向向液相中生长。 这种长大方式叫做垂直长大 (vertical growth),或连续长大, 这样的晶体生长速率很快。
vg u1TK
u1为比例常数,视材料而定
54
能用于非平衡状态下过冷度的凝固。
52
2. 晶体长大方式和长大速率
➢ 晶体长大也需要一定的过冷度。长大所需的界 面过冷度称为动态过冷度,用∆Tk表示。
➢ 具有光滑界面的物质,其∆Tk约为1~2℃。具有 粗糙界面的物质,∆Tk仅为0.01~0.05℃。
➢ 不同结构类型的界面,具有不同的长大机制。
53
粗糙界面晶体长大机制 ——连续长大
• 非均匀(异质)形核:在异质处形核,液相 中的原子依附于杂质或外来表面形核。
24
1、均匀形核
核
能量变化
液相
(1)核所处的体积,从液→固,△Gv<0;驱动力 (2)出现新的表面,使体系表面能升高;阻力
(3)体积应变能,忽略。
G
4r
3
3G V
4 r
2
25
G
4r
3
3G V
4 r
2
一定温度下,GV和为定值 r<r*,自由能↑,不稳
材料科学基础 第六章 单组元相图及纯晶体的凝固
1
本章章节结构
6.1 单元系相变的热力学及相平衡 6.2 纯晶体的凝固(重点) 6.3 气-固相变与薄膜生长 6.4 高分子的结晶特征
2
内容简介
相变规律:相律、相平衡 纯晶体的凝固的热力学及动力学:形核、长大 凝固后组织结构及其影响因素
3
4
6.1 单元系相变的热力学及相平衡
33
总的自由能变化
G G t G S
4r
3
3G V
4 r
2
L
2
3cos
4
cos
3
均匀形核:G hom
4r
3
3G V
4 r
2
G het G hom f ( )
34
d G het 0 r * 2 L
dr
G V
G
* het
G
* hom
2 3cos cos
4
3
G
* hom
G
*
V* 2
G V
同样对于非均匀形核也成立
42
6.2、纯晶体的凝固 6.2.1、液态结构 6.2.2、晶体凝固的热力学条件 6.2.3、形核
6.2.4、长大
涉及的问题 长大的形态 长大的方式 长大速率
43
6.2.4 晶体长大 crystal growth
晶体长大就是液相原子向固相转移的过程,即液体 原子依附到晶体的表面上,并按照晶面原子排列的 要求与晶体表面原子结合起来。
18
Structure data comparison between liquid and solid of metals by XRD diffraction
特点: 1)平均距离:液体中略大; 2)配位数CN:液体少, 熔化时体积略微膨胀; 3)液态中原子排列混乱的程度增加。
19
6.1 单元系相变的热力学及相平衡
9
纯铁同素异构转变
α-Fe、δ-Fe为体心立方结构 γ-Fe为面心立方结构 A2磁性转变点:
由铁磁性变为顺磁性
10
两相平衡曲线的斜率 dP
dT
11
克劳修斯-克拉珀龙方程:
dP H 描述两相共存曲线的斜率 dT T V m
其中:H为相变潜热;V
为摩尔体积变化。
m
当液 固,或高温相 低温相时,
4 r
2
G*
4r
3
3G V
4 r
2
G V
2 16
3
3
G V
2
16
3
G V
2
1 16
3
3
G V
2
1 A*
3
形核功
28
G*
4r
3
3G V
4 r
2
2 16
3
3
G V
2
16
3
G V
2
驱动力 < 阻力
讨论:
阻力的1/3怎么办?
• 液相自身存在的结构起伏和能量起伏!
29
2、非均匀形核 实际液体中存在表界面,在这些表面上形核,
13
亚稳态-处于过冷状态的水1
14
亚稳态-处于过冷状态的水2
15
亚稳态一般用虚线表示
16
熔体
熔体
急冷 加热
石英玻璃
常温下稳定的相有 低温石英,低温鳞石英 低温方石英
17
6.1 单元系相变的热力学及相平衡
6.2、纯晶体的凝固
