塑性力学-第二章 应力状态和应变状态
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用下标表示法, ij (i,j =1,2,3) 。令 x=x1,y=x2,z=x3,应力张量可表示为:
11 12 13 ij = 21 22 23 31 32 33
(2—1)
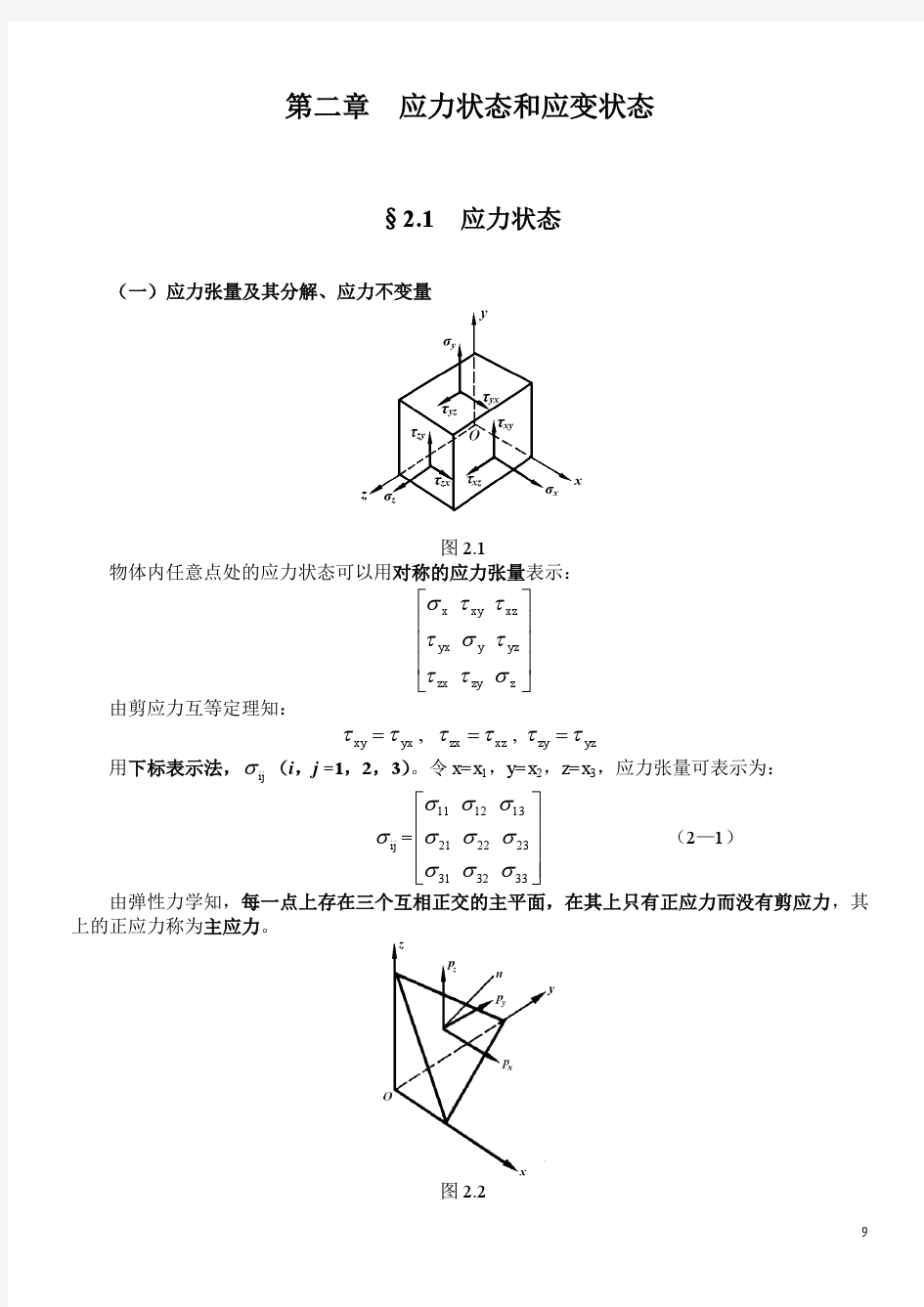
由弹性力学知,每一点上存在三个互相正交的主平面,在其上只有正应力而没有剪应力,其 上的正应力称为主应力。
图 2.3
p1 1l1 p2 2l2 p3 3 l3
图 2.4 (2—27)
则斜截面上总应力沿法线 n 的分量(即斜截面上的正应力 σn)应等于 p1、p2、p3 在法线 n 方向投 影之和,即
n p1l1 p2l2 p3l3 1l12 2l22 3l32 (2—28) (2—27)式也可直接由(2—4)式令 x 1 , y 2 , z 3 , xy yz zx 0 得到。
(2—15)
(2—14)
则(2—14)变成:
ij m ij sij
ij
1, 0 当i j 当i j
(2—16)
ij :Kronecker 符号,其定义为:
(2—17)
m ij :应力球张量,表示三向相等的正应力;
sij :应力偏张量,简称应力偏量。
1 3
1 9
所以
(2—33)
以(2—33)式和(2—19)式第二式对比可得
8
在这里还可以定义几个有关的量,定义
2J 2 3
(2—34)
i
3 1 8 3J 2 ( 1 2 ) 2 ( 2 3 ) 2 ( 3 2 ) 2 2 2 1 2 2 2 ( x y ) 2 ( y z ) 2 ( z x ) 2 6( xy yz zx ) 2
第二章
应力状态和应变状态
§2.1
(一)应力张量及其分解、应力不变量
应力状态
图 2.1 物体内任意点处的应力状态可以用对称的应力张量表示:
x xy xz yx y yz zx zy z
由剪应力互等定理知:
xy yx , zx xz , zy yz
13
表 2.1
(2—25) 在后面的第三章可以看到,应力偏量的第二不变量在研究塑性本构关系时具有特殊的重要意 义。由于 sij 是对称张量, (2—24)式也可以写为:
1 J 2 sij sij 2
(2—26)
(二)几种特定截面上的应力 求得一点处的主平面的方向和主应力大小以后,可以求得通过该点任意倾斜方向截面上的正 应力和剪应力。选三个主应力方向 1、2、3 为坐标轴,设任意斜截面的法线为 n,它对于 1、2、3 轴的方向余弦为 l1,l2,l3。图 2.3 所示的微元四面体即由三个与主平面一致的坐标面及一个斜截 面组成。设斜截面上的总应力 p 分解为沿三个主轴的分量 p1,p2,p3,由微元体的平衡得到
x
I 3 yx
xy
xz
y yz zy z
(2—11)
zx
2 2 2 x y z 2 xy yz zx z yz y zx z xy (2—10)有三个实根,对应三个主应力 1, 2, 3 。
显然,这些根仅与该点的应力状态有关,与坐标轴的选择无关。∴I1,I2,I3 也与坐标轴的选 择无关。分别称为应力张量(2—1)式的第一、第二、第三不变量。 以任一个主应力σj(j = 1,2,3)代入(2—7) ,三个方程只有两个独立,利用其中的任意两 个方程与(2—8)联立可解出主应力σj(j = 1,2,3)的方向余弦,从而确定σj 所在的主平面的
应力偏张量也是一种可能单独存在的应力状态,也有自己的不变量。 J1 , J2 , J3 表 示 应 力 偏 张 量 的 第 一 、 第 二 、 第 三 不 变 量 , 仿 照 ( 2 — 11 ) 式 可 得 :
J 1 s x s y s z x y z 3 m
2 2 2 J 2 ( s x s y s y s z s z s x ) xy yz zx
1 2 2 2 [( x y ) 2 ( y z ) 2 ( z x ) 2 6( xy yz zx )] 6 2 2 2 J 3 s x s y s z 2 xy yz zx s z yz s y zx s z xy
2 2 2
(2—8)
x xy yx zx
由此得:
xz
=0 (2—9)
y yz zy z
3 I1 2 I 2 I 3 = 0
式中,
(2—10)
I1 x y z
2 2 2 I 2 ( x y y z z x ) xy yz zx
(2—20) (2—21) (2—22)
1 2 2 (s x s y s y s z s z s x ) (s x sy s z2 ) 2源自文库
1 3 3 1 3 3 3 (2—23) sx s y sz sx s y ( sx s y ) [ sx s y ( s x s y )3 ] ( s x s y sz ) 3 3 利用(2—21) 、 (2—22)及(2—23)式还可将(2—18)式的后两式写为较简单的张量表示 形式:
当 x,y,z 轴方向和主轴重合时:
(2—18)
J1 0
1 J 2 [( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 ] 6 J 3 s1 s2 s3
而应力偏张量第一不变量为零,即
(2—19)
11
可得:
sx s y sz 0 s z (s x s y )
(2—36)
T~等效剪应力或剪应力强度。 其意义是,原来的应力状态,在某种意义上可以用等效的,大小为 T 的纯剪切应力状态来代 替。 也就是说,纯剪切状态 1 T , 2 0, 3 T ,的剪应力强度等于 T,而实际应力状态的 剪应力强度也等于 T。 8, 、σi、T 和 J2 一样,在塑性本构关系中起重要作用。 ,它们之间的换算关系如下:
斜截面上的剪应力 τn 可由下式求得:
2 2 n p2 n
(2—29)
12
现在来研究几种特定截面上的正应力和剪应力。 在图 2.4 中,主平面用Ⅰ表示,Ⅱ表示与三个主轴成相等倾斜角的斜截面,称为八面体面(或 等倾面) 。其方向余弦为:
1 3 1 l2 3 1 l3 3 l1
(2—35)
为等效应力或应力强度。也就是说,原来的复杂应力状态,在某种意义上可以用等效的,大 小为 σi 的单向应力状态来代替。在单向拉伸时 σ1≠0,σ2 =σ3 =0,代入(2—35)式即得 σi =σ1。还 可以定义
T
3 1 8 ( 1 2 ) 2 ( 2 3 ) 2 ( 3 2 ) 2 2 6
1 3
(2—30)
设八面体面上的正应力、总应力和剪应力分别为 σ8、 p8 和 τ8。将(2—29)式代入(2—27) 式得:
8 ( 1 2 3 ) m
1 2 2 2 2 2 2 2 2 2 p8 p12 p2 p3 12l12 2 l2 3 l3 ( 12 2 3 ) 3
(2—31)式和(2—32)式代入(2—29)式,得
(2—31) (2—32)
82 p82 82 ( 12 22 32 ) ( 1 2 3 ) 2
1 [( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 ] 9 1 8 ( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 3
1 2 1 2 2 2 2 J 2 [s x sy s z2 2( xy yz zx )] sij s ji 2 2
(2—24)
1 3 1 3 2 2 2 J 3 [sx s3 xy yz zx 3 xy ( s x s y ) 3 yz ( s y s z ) 3 zx ( s z s x )] sij s jk skj y sz 6 3 3
pj=σijli
σn= pjlj
(2—2)代入(2—3)得:
(2—3) (2—4)
n = ij lilj= xl12 y l22 z l32 2 xyl1l2 2 yzl2l3 2 zx l3l1
斜截面上的剪应力 τn 为:
2 2 2 2 2 2 n p2 n px py pz n
由§1.4 中 Bridgman 的试验结果可知,在各方向同时作用有大小为 m 的应力时,相当于静水
I 3 1 2 3 1 1 1 m I1 1 2 3 x y z 3 3 3
(2—13)
令:
x xy xz m 0 0 x m xy xz y m yz yx y yz 0 m 0 yx 0 0 zy z m m zx zy z zx s x s xy s xz x m xy xz sij s yx s y syz yx y m yz s s s zy z m zx zy z zx
图 2.2
9
图 2.2 所示微元四面体由三个坐标面和一个斜面所组成。其中: dF:斜面面积, lx,ly,lz:法线 n 的方向余弦,简记为 li(i=1,2,3) 。 p:斜面上的总应力。 px,py,pz:p 沿三个坐标轴的分量,简记为 pj(j=1,2,3) 。 l1dF,l2dF,l3dF:微元体三个坐标面的面积 由微元四面体的平衡方程可得: (2—2) 斜面上的正应力 σn 为总应力 P 沿法线 n 方向的分量, 它应当等于各分量 pj 沿 n 方向投影之和, 即
(2—5)
若斜截面是主平面,则 τn = 0 p =σn=σ,即 p 沿 n 的方向,且等于 σ。故每一 pj 等于 σ 在该 方向上的投影: pj=σlj (2—6) (2—6)代入(2—2) ,得到对于方向余弦的一组齐次线性方程: σijli-σlj=0 (2—7) ∵ l1 l2 l3 li li =1 ∴l1,l2,l3 不能同时为零。∴(2—7)式的系数行列式必为零。即
10
方位。 可以证明,三个主平面的方位互相垂直。 当 x,y,z 轴和三个主轴方向一致时:
I1 1 2 3 I 2 ( 1 2 2 3 3 1 )
(2—12)
平均应力:
压力(或反向的静水压力) ,它不产生塑性变形,所以从应力张量中将各向相同的 m 分离出来, 对于研究塑性变形更为方便,即
11 12 13 ij = 21 22 23 31 32 33
(2—1)
由弹性力学知,每一点上存在三个互相正交的主平面,在其上只有正应力而没有剪应力,其 上的正应力称为主应力。
图 2.3
p1 1l1 p2 2l2 p3 3 l3
图 2.4 (2—27)
则斜截面上总应力沿法线 n 的分量(即斜截面上的正应力 σn)应等于 p1、p2、p3 在法线 n 方向投 影之和,即
n p1l1 p2l2 p3l3 1l12 2l22 3l32 (2—28) (2—27)式也可直接由(2—4)式令 x 1 , y 2 , z 3 , xy yz zx 0 得到。
(2—15)
(2—14)
则(2—14)变成:
ij m ij sij
ij
1, 0 当i j 当i j
(2—16)
ij :Kronecker 符号,其定义为:
(2—17)
m ij :应力球张量,表示三向相等的正应力;
sij :应力偏张量,简称应力偏量。
1 3
1 9
所以
(2—33)
以(2—33)式和(2—19)式第二式对比可得
8
在这里还可以定义几个有关的量,定义
2J 2 3
(2—34)
i
3 1 8 3J 2 ( 1 2 ) 2 ( 2 3 ) 2 ( 3 2 ) 2 2 2 1 2 2 2 ( x y ) 2 ( y z ) 2 ( z x ) 2 6( xy yz zx ) 2
第二章
应力状态和应变状态
§2.1
(一)应力张量及其分解、应力不变量
应力状态
图 2.1 物体内任意点处的应力状态可以用对称的应力张量表示:
x xy xz yx y yz zx zy z
由剪应力互等定理知:
xy yx , zx xz , zy yz
13
表 2.1
(2—25) 在后面的第三章可以看到,应力偏量的第二不变量在研究塑性本构关系时具有特殊的重要意 义。由于 sij 是对称张量, (2—24)式也可以写为:
1 J 2 sij sij 2
(2—26)
(二)几种特定截面上的应力 求得一点处的主平面的方向和主应力大小以后,可以求得通过该点任意倾斜方向截面上的正 应力和剪应力。选三个主应力方向 1、2、3 为坐标轴,设任意斜截面的法线为 n,它对于 1、2、3 轴的方向余弦为 l1,l2,l3。图 2.3 所示的微元四面体即由三个与主平面一致的坐标面及一个斜截 面组成。设斜截面上的总应力 p 分解为沿三个主轴的分量 p1,p2,p3,由微元体的平衡得到
x
I 3 yx
xy
xz
y yz zy z
(2—11)
zx
2 2 2 x y z 2 xy yz zx z yz y zx z xy (2—10)有三个实根,对应三个主应力 1, 2, 3 。
显然,这些根仅与该点的应力状态有关,与坐标轴的选择无关。∴I1,I2,I3 也与坐标轴的选 择无关。分别称为应力张量(2—1)式的第一、第二、第三不变量。 以任一个主应力σj(j = 1,2,3)代入(2—7) ,三个方程只有两个独立,利用其中的任意两 个方程与(2—8)联立可解出主应力σj(j = 1,2,3)的方向余弦,从而确定σj 所在的主平面的
应力偏张量也是一种可能单独存在的应力状态,也有自己的不变量。 J1 , J2 , J3 表 示 应 力 偏 张 量 的 第 一 、 第 二 、 第 三 不 变 量 , 仿 照 ( 2 — 11 ) 式 可 得 :
J 1 s x s y s z x y z 3 m
2 2 2 J 2 ( s x s y s y s z s z s x ) xy yz zx
1 2 2 2 [( x y ) 2 ( y z ) 2 ( z x ) 2 6( xy yz zx )] 6 2 2 2 J 3 s x s y s z 2 xy yz zx s z yz s y zx s z xy
2 2 2
(2—8)
x xy yx zx
由此得:
xz
=0 (2—9)
y yz zy z
3 I1 2 I 2 I 3 = 0
式中,
(2—10)
I1 x y z
2 2 2 I 2 ( x y y z z x ) xy yz zx
(2—20) (2—21) (2—22)
1 2 2 (s x s y s y s z s z s x ) (s x sy s z2 ) 2源自文库
1 3 3 1 3 3 3 (2—23) sx s y sz sx s y ( sx s y ) [ sx s y ( s x s y )3 ] ( s x s y sz ) 3 3 利用(2—21) 、 (2—22)及(2—23)式还可将(2—18)式的后两式写为较简单的张量表示 形式:
当 x,y,z 轴方向和主轴重合时:
(2—18)
J1 0
1 J 2 [( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 ] 6 J 3 s1 s2 s3
而应力偏张量第一不变量为零,即
(2—19)
11
可得:
sx s y sz 0 s z (s x s y )
(2—36)
T~等效剪应力或剪应力强度。 其意义是,原来的应力状态,在某种意义上可以用等效的,大小为 T 的纯剪切应力状态来代 替。 也就是说,纯剪切状态 1 T , 2 0, 3 T ,的剪应力强度等于 T,而实际应力状态的 剪应力强度也等于 T。 8, 、σi、T 和 J2 一样,在塑性本构关系中起重要作用。 ,它们之间的换算关系如下:
斜截面上的剪应力 τn 可由下式求得:
2 2 n p2 n
(2—29)
12
现在来研究几种特定截面上的正应力和剪应力。 在图 2.4 中,主平面用Ⅰ表示,Ⅱ表示与三个主轴成相等倾斜角的斜截面,称为八面体面(或 等倾面) 。其方向余弦为:
1 3 1 l2 3 1 l3 3 l1
(2—35)
为等效应力或应力强度。也就是说,原来的复杂应力状态,在某种意义上可以用等效的,大 小为 σi 的单向应力状态来代替。在单向拉伸时 σ1≠0,σ2 =σ3 =0,代入(2—35)式即得 σi =σ1。还 可以定义
T
3 1 8 ( 1 2 ) 2 ( 2 3 ) 2 ( 3 2 ) 2 2 6
1 3
(2—30)
设八面体面上的正应力、总应力和剪应力分别为 σ8、 p8 和 τ8。将(2—29)式代入(2—27) 式得:
8 ( 1 2 3 ) m
1 2 2 2 2 2 2 2 2 2 p8 p12 p2 p3 12l12 2 l2 3 l3 ( 12 2 3 ) 3
(2—31)式和(2—32)式代入(2—29)式,得
(2—31) (2—32)
82 p82 82 ( 12 22 32 ) ( 1 2 3 ) 2
1 [( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 ] 9 1 8 ( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 3
1 2 1 2 2 2 2 J 2 [s x sy s z2 2( xy yz zx )] sij s ji 2 2
(2—24)
1 3 1 3 2 2 2 J 3 [sx s3 xy yz zx 3 xy ( s x s y ) 3 yz ( s y s z ) 3 zx ( s z s x )] sij s jk skj y sz 6 3 3
pj=σijli
σn= pjlj
(2—2)代入(2—3)得:
(2—3) (2—4)
n = ij lilj= xl12 y l22 z l32 2 xyl1l2 2 yzl2l3 2 zx l3l1
斜截面上的剪应力 τn 为:
2 2 2 2 2 2 n p2 n px py pz n
由§1.4 中 Bridgman 的试验结果可知,在各方向同时作用有大小为 m 的应力时,相当于静水
I 3 1 2 3 1 1 1 m I1 1 2 3 x y z 3 3 3
(2—13)
令:
x xy xz m 0 0 x m xy xz y m yz yx y yz 0 m 0 yx 0 0 zy z m m zx zy z zx s x s xy s xz x m xy xz sij s yx s y syz yx y m yz s s s zy z m zx zy z zx
图 2.2
9
图 2.2 所示微元四面体由三个坐标面和一个斜面所组成。其中: dF:斜面面积, lx,ly,lz:法线 n 的方向余弦,简记为 li(i=1,2,3) 。 p:斜面上的总应力。 px,py,pz:p 沿三个坐标轴的分量,简记为 pj(j=1,2,3) 。 l1dF,l2dF,l3dF:微元体三个坐标面的面积 由微元四面体的平衡方程可得: (2—2) 斜面上的正应力 σn 为总应力 P 沿法线 n 方向的分量, 它应当等于各分量 pj 沿 n 方向投影之和, 即
(2—5)
若斜截面是主平面,则 τn = 0 p =σn=σ,即 p 沿 n 的方向,且等于 σ。故每一 pj 等于 σ 在该 方向上的投影: pj=σlj (2—6) (2—6)代入(2—2) ,得到对于方向余弦的一组齐次线性方程: σijli-σlj=0 (2—7) ∵ l1 l2 l3 li li =1 ∴l1,l2,l3 不能同时为零。∴(2—7)式的系数行列式必为零。即
10
方位。 可以证明,三个主平面的方位互相垂直。 当 x,y,z 轴和三个主轴方向一致时:
I1 1 2 3 I 2 ( 1 2 2 3 3 1 )
(2—12)
平均应力:
压力(或反向的静水压力) ,它不产生塑性变形,所以从应力张量中将各向相同的 m 分离出来, 对于研究塑性变形更为方便,即
