圆的二元方程
二元二次方程表示圆的充要条件是

二元二次方程表示圆的充要条件是一个非常重要且基础的数学概念。
在数学中,二元二次方程和圆有着密切的联系,它们之间的关系可以帮助我们更深入地理解圆的特性和性质。
在本文中,我将以从简到繁的方式探讨二元二次方程表示圆的充要条件,并共享我的个人观点和理解。
让我们回顾一下二元二次方程的一般形式:$Ax^2 + By^2 + Cx +Dy + E = 0$。
这是一个关于$x$和$y$的二次方程,其中$A$、$B$、$C$、$D$和$E$都是常数且$A$和$B$不全为零。
而圆的一般方程可以表示为$(x - a)^2 + (y - b)^2 = r^2$,其中$(a, b)$是圆心的坐标,$r$是圆的半径。
那么,二元二次方程可以表示圆的充要条件是什么呢?其实,二元二次方程表示圆的充要条件包括两个方面:其一是通过几何推导,我们可以得出一个方程为圆的充分条件并证明其必要性;其二是通过代数推导,我们可以利用二次方程的特性来表示圆并证明其充分必要性。
从几何的角度来看,我们知道圆是由到圆心距离相等的所有点构成的几何图形。
如果一个二元二次方程能够表示一个圆,那么这个方程能够描述所有到圆心距离相等的点。
这意味着,对于圆上的任意一点$(x, y)$,它到圆心$(a, b)$的距离应该等于半径$r$。
通过这个几何特性,我们可以得出二元二次方程表示圆的一种充分条件。
另通过代数推导,我们可以将圆的方程$(x - a)^2 + (y - b)^2 =r^2$展开得到$x^2 - 2ax + a^2 + y^2 - 2by + b^2 - r^2 = 0$,然后比较系数得到$A = B = 1$,$C = -2a$,$D = -2b$和$E = a^2 + b^2 - r^2$。
这样,我们就可以将圆的方程转化为二元二次方程的一般形式。
反过来,如果一个二元二次方程的系数满足$A = B$且$C = D$,而且满足$(C/2A, D/2A)$是圆心且$E = a^2 + b^2 - r^2$,那么这个二元二次方程就能表示一个圆。
圆 的 方 程

2 2
C.30°
D.120°
解析:⊙C:(x-1) +(y-1) =1,∵PA、PB 是⊙C 的 两条切线, ∴△PAC≌△PBC, ∴四边形 PACB 面积最小, 即△PAC 面积最小,∵AC 为⊙C 的半径,∴只要 PA 取 最小值,从而 PC 取最小值,∴PC 与已知直线垂直, ∴|PC|=2,∴∠APB=2∠APC=60°.
2 2
2 与 x 轴相切的圆方程: x a y b b r b ;
2 与 y 轴相切的圆方程: x a y b a r a ; 2 2
(2)一般式:x2+y2+Dx+Ey+F=0(D2+E2-4F>0),
把 x +y +Dx+Ey+F=0
二元二次方程表示圆当且仅当 2 2 A=C≠0,B=0 ,D +E -4AF>0。
3、点与圆的位置关系: 2 2 2 若圆(x-a) +(y-b) =r ,那么点(x0,y0)在
圆上 x0 a 2 y 0 b 2 r 2 2 2 2 圆内 x0 a y 0 b r 圆外 x a 2 y b 2 r 2 0 0
二、典例讨论: 1.圆的基本概念
例1、(1)一束光线从A(-1,1)出发经x轴反射 到圆C:(x-2)2+(y-3)2=1上的最短路程是____.
(2)圆x2+y2+2x+4y-3=0上到直线l:x+y+b=0之
距离为
2
的点有2 个,则b 的范围为
.
2、求圆方程
例2、根据下列条件,求圆的方程。 (1)圆心在直线2x+y=0上,且与直线x+y-1=0切于 点(2,-1). (2)已知一圆过P(4,-2)、Q(-1,3)两点,且在y轴 上截得的线段长为4 3 ,求圆的方程。
第三节 圆的方程

第三节圆的方程1.圆的定义及方程如果没给出r>0,则圆的半径为|r|.当D2+E2-4F=0时,方程x2+y2+Dx+Ey+F=0表示一个点⎝⎛⎭⎫-D2,-E2;当D2+E2-4F<0时,方程x2+y2+Dx+Ey+F=0没有意义,不表示任何图形.2.点与圆的位置关系点M(x0,y0)与圆(x-a)2+(y-b)2=r2的位置关系:(1)若M(x0,y0)在圆外,则(x0-a)2+(y0-b)2>r2.(2)若M(x0,y0)在圆上,则(x0-a)2+(y0-b)2=r2.(3)若M(x0,y0)在圆内,则(x0-a)2+(y0-b)2<r2.[熟记常用结论](1)二元二次方程Ax2+Bxy+Cy2+Dx+Ey+F=0表示圆的充要条件是⎩⎪⎨⎪⎧A=C≠0,B=0,D2+E2-4AF>0.(2)以A(x1,y1),B(x2,y2)为直径端点的圆的方程为(x-x1)·(x-x2)+(y-y1)(y-y2)=0.[小题查验基础]一、判断题(对的打“√”,错的打“×”)(1)确定圆的几何要素是圆心与半径.()(2)方程(x-a)2+(y-b)2=t2(t∈R)表示圆心为(a,b),半径为t的一个圆.()(3)方程x2+y2+4mx-2y=0不一定表示圆.()(4)若点M(x0,y0)在圆x2+y2+Dx+Ey+F=0外,则x20+y20+Dx0+Ey0+F>0.()答案:(1)√ (2)× (3)× (4)√ 二、选填题1.圆心坐标为(1,1)且过原点的圆的方程是( ) A .(x -1)2+(y -1)2=1 B .(x +1)2+(y +1)2=1 C .(x +1)2+(y +1)2=2D .(x -1)2+(y -1)2=2解析:选D 由题意得圆的半径为2,故该圆的方程为(x -1)2+(y -1)2=2,故选D. 2.圆x 2+y 2-4x +6y =0的圆心坐标是( ) A .(2,3) B.(-2,3) C .(-2,-3)D .(2,-3)解析:选D 圆的方程可化为(x -2)2+(y +3)2=13,所以圆心坐标是(2,-3). 3.若点(2a ,a -1)在圆x 2+(y -1)2=5的内部,则a 的取值范围是( ) A .(-1,1) B.(0,1) C.⎝⎛⎭⎫-1,15 D.⎝⎛⎭⎫-15,1 解析:选D 由(2a )2+(a -2)2<5,得-15<a <1.4.若方程x 2+y 2+ax +2ay +2a 2+a -1=0表示圆,则a 的取值范围是________. 解析:若方程x 2+y 2+ax +2ay +2a 2+a -1=0表示圆,则a 2+4a 2-4(2a 2+a -1)>0,即3a 2+4a -4<0,解得-2<a <23.答案:⎝⎛⎭⎫-2,23 5.圆心在y 轴上,半径长为1,且过点A (1,2)的圆的方程是________.解析:根据题意可设圆的方程为x 2+(y -b )2=1,因为圆过点A (1,2),所以12+(2-b )2=1,解得b =2,所以所求圆的方程为x 2+(y -2)2=1.答案:x 2+(y -2)2=1考点一 求圆的方程[师生共研过关][典例精析][例1] 已知圆E 经过三点A (0,1),B (2,0),C (0,-1),且圆心在x 轴的正半轴上,则圆E 的标准方程为( )A.⎝⎛⎭⎫x -322+y 2=254B.⎝⎛⎭⎫x +342+y 2=2516C.⎝⎛⎭⎫x -342+y 2=2516D.⎝⎛⎭⎫x -342+y 2=254[解析] 法一:(待定系数法)设圆E 的一般方程为x 2+y 2+Dx +Ey +F =0(D 2+E 2-4F>0),则由题意得⎩⎪⎨⎪⎧1+E +F =0,4+2D +F =0,1-E +F =0,解得⎩⎪⎨⎪⎧D =-32,E =0,F =-1,所以圆E 的一般方程为x 2+y 2-32x -1=0,即⎝⎛⎭⎫x -342+y 2=2516. 法二:(几何法)因为圆E 经过点A (0,1),B (2,0),所以圆E 的圆心在线段AB 的垂直平分线y -12=2(x -1)上.又圆E 的圆心在x 轴的正半轴上,所以圆E 的圆心坐标为⎝⎛⎭⎫34,0. 则圆E 的半径为|EB |= ⎝⎛⎭⎫2-342+(0-0)2=54,所以圆E 的标准方程为⎝⎛⎭⎫x -342+y 2=2516. [答案] C[例2] 圆心在直线x -2y -3=0上,且过点A (2,-3),B (-2,-5)的圆的方程为________________________.[解析] 法一:(几何法)设点C 为圆心,因为点C 在直线x -2y -3=0上,所以可设点C 的坐标为(2a +3,a ).又该圆经过A ,B 两点,所以|CA |=|CB |, 即(2a +3-2)2+(a +3)2=(2a +3+2)2+(a +5)2,解得a =-2,所以圆心C 的坐标为(-1,-2),半径r =10, 故所求圆的方程为(x +1)2+(y +2)2=10.法二:(待定系数法)设所求圆的标准方程为(x -a )2+(y -b )2=r 2,由题意得⎩⎪⎨⎪⎧(2-a )2+(-3-b )2=r 2,(-2-a )2+(-5-b )2=r 2,a -2b -3=0,解得a =-1,b =-2,r 2=10,故所求圆的方程为(x +1)2+(y +2)2=10. [答案] (x +1)2+(y +2)2=10[解题技法]1.求圆的方程的两种方法[提醒] 解答圆的有关问题时,应注意数形结合,充分运用圆的几何性质. 2.确定圆心位置的方法(1)圆心在过切点且与切线垂直的直线上. (2)圆心在圆的任意弦的垂直平分线上. (3)两圆相切时,切点与两圆圆心共线.[过关训练]1.若不同的四点A (5,0),B (-1,0),C (-3,3),D (a,3)共圆,则a 的值为________. 解析:设圆的方程为x 2+y 2+Dx +Ey +F =0(D 2+E 2-4F >0), 分别代入A ,B ,C 三点坐标,得⎩⎪⎨⎪⎧25+5D +F =0,1-D +F =0,9+9-3D +3E +F =0,解得⎩⎪⎨⎪⎧D =-4,E =-253,F =-5.所以A ,B ,C 三点确定的圆的方程为x 2+y 2-4x -253y -5=0.因为D (a,3)也在此圆上,所以a 2+9-4a -25-5=0. 所以a =7或a =-3(舍去).即a 的值为7. 答案:72.已知圆心在直线y =-x +1上,且与直线x +y -2=0相切于点(1,1)的圆的方程为________________________.解析:设圆的方程为(x -a )2+(y -b )2=r 2(r >0),则⎩⎨⎧b =-a +1,(a -1)2+(b -1)2=|a +b -2|2,解得⎩⎨⎧a =12,b =12.所以r =⎝⎛⎭⎫1-122+⎝⎛⎭⎫1-122=22. 故所求圆的方程为⎝⎛⎭⎫x -122+⎝⎛⎭⎫y -122=12. 答案:⎝⎛⎭⎫x -122+⎝⎛⎭⎫y -122=12考点二 与圆有关的最值问题 [全析考法过关][考法全析]考法(一) 斜率型最值问题[例1] 已知实数x ,y 满足方程x 2+y 2-4x +1=0,求yx 的最大值和最小值.[解] 原方程可化为(x -2)2+y 2=3, 表示以(2,0)为圆心,3为半径的圆. yx 的几何意义是圆上一点与原点连线的斜率,所以设yx=k ,即y =kx .当直线y =kx 与圆相切时(如图),斜率k 取最大值或最小值, 此时|2k -0|k 2+1=3,解得k =±3.所以yx 的最大值为3,最小值为- 3.考法(二) 截距型最值问题[例2] 已知点P (x ,y )在圆C :x 2+y 2-6x -6y +14=0上,求x +y 的最大值与最小值.[解] (转化为截距的最值问题求解)设x +y =b ,则b 表示动直线y =-x +b 在y 轴上的截距,显然当动直线y =-x +b 与圆C 相切时,b 取得最大值或最小值,如图所示.由圆心C (3,3)到切线x +y =b 的距离等于圆C 的半径,可得|3+3-b |12+12=2,即|b -6|=22,解得b =6±22,所以x +y 的最大值为6+22,最小值为6-2 2.考法(三) 距离型最值问题[例3] 已知实数x ,y 满足方程x 2+y 2-4x +1=0,求x 2+y 2的最大值和最小值. [解] 如图所示,x 2+y 2表示圆上的一点与原点距离的平方,由平面几何知识知,在原点和圆心连线与圆的两个交点处取得最大值和最小值.又圆心到原点的距离为(2-0)2+(0-0)2=2,所以x 2+y 2的最大值是(2+3)2=7+43, x 2+y 2的最小值是(2-3)2=7-4 3. 考法(四) 利用对称性求最值[例4] 已知A (0,2),点P 在直线x +y +2=0上,点Q 在圆C :x 2+y 2-4x -2y =0上,则|PA |+|P Q |的最小值是________.[解析] 因为圆C :x 2+y 2-4x -2y =0, 故圆C 是以C (2,1)为圆心,半径r =5的圆.设点A (0,2)关于直线x +y +2=0的对称点为A ′(m ,n ), 故⎩⎪⎨⎪⎧m +02+n +22+2=0,n -2m -0=1,解得⎩⎪⎨⎪⎧m =-4,n =-2,故A ′(-4,-2).连接A ′C 交圆C 于Q (图略),由对称性可知|PA |+|P Q |=|A ′P |+|P Q |≥|A ′Q |=|A ′C |-r =2 5.[答案] 2 5[规律探求][过关训练]1.已知点A(-1,0),B(0,2),点P是圆C:(x-1)2+y2=1上任意一点,则△PAB面积的最大值与最小值分别是()A.2,2-52B.2+52,2-52C.5,4- 5D.52+1,52-1解析:选B由题意知|AB|=(-1)2+(-2)2=5,l AB:2x-y+2=0,由题意知圆C的圆心坐标为(1,0),∴圆心到直线l AB的距离d=|2-0+2|4+1=455.∴S △PAB 的最大值为12×5×⎝⎛⎭⎫455+1=2+52,S △PAB 的最小值为12×5×⎝⎛⎭⎫455-1=2-52.2.设P 为直线3x -4y +11=0上的动点,过点P 作圆C :x 2+y 2-2x -2y +1=0的两条切线,切点分别为A ,B ,则四边形PACB 的面积的最小值为________.解析:圆的标准方程为(x -1)2+(y -1)2=1,圆心为C (1,1),半径r =1,根据对称性可知,四边形PACB 的面积为2S △APC =2×12|PA |r =|PA |=|PC |2-r 2,要使四边形PACB 的面积最小,则只需|PC |最小,|PC |最小时为圆心到直线l :3x -4y +11=0的距离d =|3-4+11|32+(-4)2=105=2.所以四边形PACB 面积的最小值为(|PC |min )2-r 2=4-1= 3.答案: 3考点三 与圆有关的轨迹问题 [师生共研过关][典例精析]已知直角三角形ABC 的斜边为AB ,且A (-1,0),B (3,0). (1)求直角顶点C 的轨迹方程;(2)求直角边BC 的中点M 的轨迹方程.[解] (1)设C (x ,y ),因为A ,B ,C 三点不共线,所以y ≠0.因为AC ⊥BC ,所以k AC ·k BC =-1,又k AC =y x +1,k BC =y x -3,所以y x +1·yx -3=-1,化简得x 2+y 2-2x -3=0.因此,直角顶点C 的轨迹方程为x 2+y 2-2x -3=0(y ≠0).(2)设M (x ,y ),C (x 0,y 0),因为B (3,0),M 是线段BC 的中点,由中点坐标公式得x =x 0+32,y =y 0+02,所以x 0=2x -3,y 0=2y .由(1)知,点C 的轨迹方程为(x -1)2+y 2=4(y ≠0), 将x 0=2x -3,y 0=2y 代入得(2x -4)2+(2y )2=4(y ≠0), 即(x -2)2+y 2=1(y ≠0).因此动点M 的轨迹方程为(x -2)2+y 2=1(y ≠0).[解题技法]求与圆有关轨迹问题的3种方法(1)直接法:当题目条件中含有与该点有关的等式时,可设出该点的坐标,用坐标表示等式,直接求解轨迹方程.(2)定义法:当题目条件符合圆的定义时,可直接利用定义确定其圆心和半径,写出圆的方程.(3)代入法:当题目条件中已知某动点的轨迹方程,而要求的点与该动点有关时,常找出要求的点与已知点的关系,代入已知点满足的关系式求轨迹方程.[过关训练]1.自圆C :(x -3)2+(y +4)2=4外一点P (x ,y )引该圆的一条切线,切点为Q ,P Q 的长度等于点P 到原点O 的距离,则点P 的轨迹方程为( )A .8x -6y -21=0B .8x +6y -21=0C .6x +8y -21=0D .6x -8y -21=0解析:选D 由题意得,圆心C 的坐标为(3,-4),半径r =2,如图.因为|P Q |=|PO |,且P Q ⊥C Q ,所以|PO |2+r 2=|PC |2,所以x 2+y 2+4=(x -3)2+(y +4)2,即6x -8y -21=0,所以点P 的轨迹方程为6x -8y -21=0,故选D.2.设定点M (-3,4),动点N 在圆x 2+y 2=4上运动,以OM ,ON 为两边作平行四边形MONP ,求点P 的轨迹.解:如图,设P (x ,y ),N (x 0,y 0), 则线段OP 的中点坐标为⎝⎛⎭⎫x 2,y 2,线段MN 的中点坐标为⎝ ⎛⎭⎪⎫x 0-32,y 0+42.因为平行四边形的对角线互相平分,所以x 2=x 0-32,y 2=y 0+42,整理得⎩⎪⎨⎪⎧x 0=x +3,y 0=y -4.又点N (x +3,y -4)在圆x 2+y 2=4上, 所以(x +3)2+(y -4)2=4. 所以点P的轨迹是以(-3,4)为圆心,2为半径的圆⎝⎛⎭⎫因为O ,M ,P 三点不共线,所以应除去两点⎝⎛⎭⎫-95,125和⎝⎛⎭⎫-215,285.。
二元二次方程表示圆的充要条件在解答题中的应用

②
且 知狓1+狓2=2犽犽(2犽+-33).由 犖 (1,3)是线段 犃犅 的中
点,得狓1+狓2=2,所 以 犽(犽-3)=犽2 +3,解 得 犽= -1,代入②得λ>12,即λ 的 取 值 范 围 是(12,+ ∞).
所以直线 犃犅 的方程为狓+狔-4=0.
(2)易知直线 犆犇 的 方 程 为狓-狔+2=0.则 犃, 犅,犆,犇 在曲线 犕 :(狓+狔-4)(狓-狔+2)=0 上,即 犕 :狓2-狔2 -2狓+6狔-8=0.设 过 椭 圆 3狓2 +狔2 =λ
与曲线 犕 的交点的 曲 线 方 程 为:狓2-狔2-2狓+6狔-
8+犽(3狓2+狔2-λ)=0,即 (1+3犽)狓2+ (犽-1)狔2-
2狓+6狔-8-犽λ=0,若 犃,犅,犆,犇 四点共圆,则
{ { 1+3犽=犽-1,
犽= -1,
ห้องสมุดไป่ตู้
4+36+4(1+3犽)(8+犽λ)>0 λ>3.
故当λ>12时,犃,犅,犆,犇 在同一圆上.
6
该题利用二元二次方程表示圆的充要条件, 降低了 难 度,使 问 题 变 得 更 明 朗,解 答 思 路 更清晰.
例2 已知过狔2=2狆狓 的 焦 点犉 下 作 两 条 互 相 垂直的直线,与抛物线 分 别 交 于 犃,犅,犆,犇 四 点,犃,
犅,犆,犇 四点是否共圆?若共圆,求出圆的方程;若 不
共 圆 ,说 明 理 由 .
们先求出必 要 条 件,再 通 过 增 设 条 件 证 明 其 充 分 性,
这样可以减少解答的复杂性.
通过以上两例可看出:在 解 答 题 中 充 分 利 用 二 元
二次方程表 示 圆 的 充 要 条 件,确 实 可 以 减 少 计 算 量,
圆的方程及其求法

解析:圆 C1:(x+1)2+(y-1)2=1,圆心 C1 为(-1,1),半径为 1.易知点 C1(-1,1)
关于直线 x-y-1=0 对称的点为 C2,设 C2(a,b),则baa- + -2 111= , b=-2,
所以 C2(2,-2),所以圆 C2 的圆心为 C2(2,-2),半径为 1,所以圆
引申探究 1.在本例的条件下,求yx的最大值和最小值. 解:yx可视为点(x,y)与原点连线的斜率,yx的最大值和最小值就是与该圆有公共点 的过原点的直线斜率的最大值和最小值,即直线与圆相切时的斜率.
设过原点的直线的方程为 y=kx,由直线与圆相切得圆心到直线的距离等于半径, 即|2kk2++31|=1,解得 k=-2+233或 k=-2-233,∴yx的最大值为-2+233,最
又∵圆 C 与直线 x-y=0 相切, ∴-D2 +2 E2=12 D2+E2-4F, 即(D-E)2=2(D2+E2-4F), ∴D2+E2+2DE-8F=0.②
又知圆心-D2 ,-E2到直线 x-y-3=0 的距离 d=-D2 +2E2-3, 由已知得 d2+ 262=r2, ∴(D-E+6)2+12=2(D2+E2-4F),③
解析:由于圆心在第一象限且与 x 轴相切,可设圆心为(a,1)(a>0),又圆与直线 4x -3y=0 相切, ∴|4a5-3|=1,解得 a=2 或 a=-12(舍去). ∴圆的标准方程为(x-2)2+(y-1)2=1. 故选 A.
答案:A
题型一 圆的方程
例 1 (1)(2020·湖北名校摸底)过点 A(1,-1),B(-1,1)且圆心在直线 x+y-2=0
题组一 思考辨析 1.判断下列结论是否正确(请在括号中打“√”或“×”) (1)确定圆的几何要素是圆心与半径.( √ ) (2)已知点 A(x1,y1),B(x2,y2),则以 AB 为直径的圆的方程是(x-x1)(x-x2)+(y- y1)(y-y2)=0.( √ )
高中数学圆的标准方程
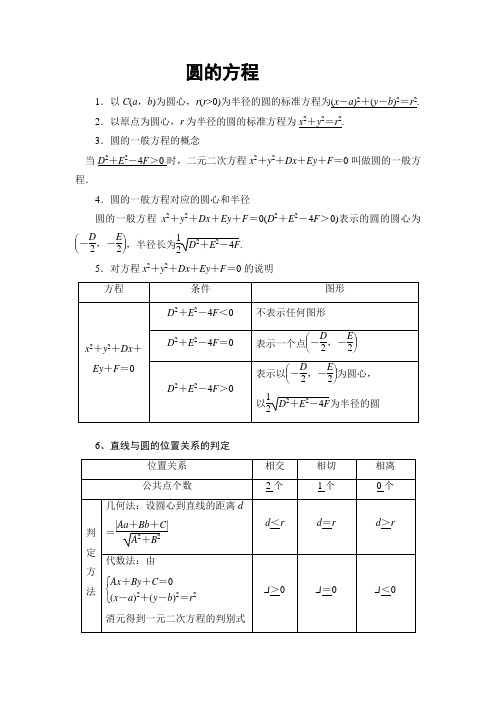
圆的方程1.以C (a ,b )为圆心,r (r >0)为半径的圆的标准方程为(x -a )2+(y -b )2=r 2. 2.以原点为圆心,r 为半径的圆的标准方程为x 2+y 2=r 2. 3.圆的一般方程的概念当D 2+E 2-4F >0时,二元二次方程x 2+y 2+Dx +Ey +F =0叫做圆的一般方程.4.圆的一般方程对应的圆心和半径圆的一般方程x 2+y 2+Dx +Ey +F =0(D 2+E 2-4F >0)表示的圆的圆心为⎝ ⎛⎭⎪⎫-D2,-E 2,半径长为12D 2+E 2-4F .5.对方程x 2+y 2+Dx +Ey +F =0的说明6、直线与圆的位置关系的判定例题讲解1、已知圆的方程是(x-2)2+(y-3)2=4,则点P(3,2)()A.是圆心B.在圆上C.在圆内D.在圆外2、已知一圆的圆心为点(2,-3),一条直径的两个端点分别在x轴和y轴上,则此圆的方程是()A.(x-2)2+(y+3)2=13B.(x+2)2+(y-3)2=13C.(x-2)2+(y+3)2=52D.(x+2)2+(y-3)2=523、以点A(-5,4)为圆心,且与x轴相切的圆的方程是()A.(x+5)2+(y-4)2=25B.(x-5)2+(y+4)2=16C.(x+5)2+(y-4)2=16D.(x-5)2+(y+4)2=25巩固练习1、求圆心在直线x-2y-3=0上,且过点A(2,-3),B(-2,-5)的圆的标准方程.2、求圆心在x轴上,且过点A(5,2)和B(3,-2)的圆的标准方程.3、若P(x,y)是圆C(x-3)2+y2=4上任意一点,请求出P(x,y)到直线x-y +1=0的距离的最大值和最小值.4、已知圆C:(x-3)2+(y-4)2=1,点A(0,-1),B(0,1),设P是圆C上的动点,令d=|P A|2+|PB|2,求d的最大值及最小值.图4-1-15、直线3x+4y+12=0与圆(x-1)2+(y+1)2=9的位置关系是()A.过圆心B.相切C.相离D.相交但不过圆心6、已知直线ax+by+c=0(ab≠0)与圆x2+y2=1相切,则三边长分别为|a|,|b|,|c|的三角形是()A.锐角三角形B.直角三角形C.钝角三角形D.不存在7、已知圆C的圆心是直线x-y+1=0与x轴的交点,且圆C与直线x+y +3=0相切,则圆C的方程为____________________.8、过点P(-1,2)且与圆C:x2+y2=5相切的直线方程是________.课后练习1、圆x2+y2-4x+6y=0的圆心坐标是()A.(2,3) B.(-2,3)C.(-2,-3) D.(2,-3)2、已知方程x 2+y 2-2x +2k +3=0表示圆,则k 的取值范围是( ) A .(-∞,-1)B .(3,+∞)C .(-∞,-1)∪(3,+∞)D.⎝ ⎛⎭⎪⎫-32,+∞ 3、若方程x 2+y 2+Dx +Ey +F =0表示以(2,-4)为圆心,4为半径的圆,则F =________.4、设A 为圆(x -1)2+y 2=1上的动点,P A 是圆的切线且|P A |=1,则P 点的轨迹方程是__________.5、求经过三点A (1,-1),B (1,4),C (4,-2)的圆的一般方程.6、过点(-1,-2)的直线l 被圆x 2+y 2-2x -2y +1=0截得的弦长为2,求直线l 的方程.7、 已知动点M 到点(8,0)的距离等于点M 到点(2,0)的距离的2倍,你能求出点M 的轨迹方程吗?8、 已知直角△ABC 的斜边为AB ,且A (-1,0),B (3,0),请求出直角顶点C 的轨迹方程.9、已知圆心为C 的圆经过点A (1,1)和B (2,-2),且圆心C 在直线l :x -y+1=0上.(1)求圆C 的方程;(2)线段PQ 的端点P 的坐标是(5,0),端点Q 在圆C 上运动,求线段PQ 的中点M 的轨迹方程.。
圆的一般方程 课件

类型二 待定系数法求圆的方程 [例 2] 已知△ABC 的三个顶点为 A(1,4),B(-2,3),C(4,-5), 求△ABC 的外接圆方程、外心坐标和外接圆半径.
又 kAC=x+y 1,kBC=x-y 3,且 kAC·kBC=-1,
所以x+y 1·x-y 3=-1,化简得 x2+y2-2x-3=0. 因此,直角顶点 C 的轨迹方程为 x2+y2-2x-3=0(x≠3 且 x≠ -1).
方法二:同法一得 x≠3 且 x≠-1. 由勾股定理得|AC|2+|BC|2=|AB|2,即(x+1)2+y2+(x-3)2+y2 =16,化简得 x2+y2-2x-3=0.因此,直角顶点 C 的轨迹方程为 x2 +y2-2x-3=0(x≠3 且 x≠-1). 方法三:设 AB 中点为 D,由中点坐标公式得 D(1,0),由直角
因此动点 M 的轨迹方程为(x-2)2+y2=1(x≠3 且 x≠1).
方法归纳
1.一般地,求轨迹方程就是求等式,就是找等量关系,把等 量关系用数学语言表达出来,再进行变形、化简,就会得到相应的 轨迹方程,所以找等量关系是解决问题的关键.
2.求曲线的轨迹方程要注意的三点 (1)根据题目条件,选用适当的求轨迹方程的方法. (2)看准是求轨迹,还是求轨迹方程,轨迹是轨迹方程所表示的 曲线(图形). (3)检查轨迹上是否有应去掉的点或漏掉的点.
【解析】 方法一:设△ABC 的外接圆方程为 x2+y2+Dx+Ey+F=0,
圆的方程

课堂热身训练
(B) 2 a
(C)
2a
(D) 4 a
2.若过点(4,2)总可以作两条直线与圆 (x-3m)2+(y-4m)2=5(m+4)相切,则m的范围是(
D )
19 (A)m 12 9 (C) m 0或 m 5
19 (B) - 4 m 12 9 (D) - 4 m 0或 m 5
又设圆在x轴、y轴上的截距分别是x1、x2、y1、y2, 在圆的方程x2+y2+Dx+Ey+F=0中, 令y=0,得:x2+Dx+F=0,∴x1+x2=-D; 令x=0,得:y2+Ey+F=0,∴y1+y2=-E. ∵x1+x2+y1+y2=2, ∴-D-E=2 …③. 解①、②、③得:D=-2,E=0,F=-12. ∴所求圆的方程为:x2+y2-2x-12=0.
经验体会总结
1.二元二次方程x2+y2+Dx+Ey+F=0, 当D2+E2-4F>0时表示圆.要熟练掌握 用配方法由圆的一般方程求出圆心、半 径.
2.确定圆要有三个条件,那么求圆的方程 也要三个独立条件,求圆的方程通常用待 定系数法,一般来说,与圆心、半径有关的 问题,常用圆的标准方程解决.与圆上的点 有关的问Байду номын сангаас常用圆的一般方程解决.
点A在圆(x +2) 2 + (y -4) 2 = 4上运动.求△ABC的重心G的
8
轨迹方程.
6
【解】:设G(x,y),点A(x0,y0),A
则有:(x0+2) 2 + (y 0-4) 2 = 4…①, 由重心公式x0 -3 +2=3x,y0 -1 +1 =3y. 得x0 =3x+1,y0 =3y,代入①
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于圆的二元方程式的解析
一、表达形式
●圆的二元方程一般形式为:x²+y²+Dx+Ey+F=0,其中D²+E²-4F>0。
●要使二元二次方程Ax²+Bxy+Cy²+Dx+EY+F=0表示圆,需要满足以下条件:A=C≠0,
B=0,且D²+E²-4F>0。
●圆的方程有两种形式的选择:与圆心半径有直接关系时用标准式,无直接关系选一般式。
●圆的二元方程可以用于解决两圆的位置关系(相交、相离、相切、内含)等问题。
二、表达形式的特点
1.x²项和y²项的系数都相等,且不为零。
2.是二元二次方程且没有xy这样的二次项。
3.参数D,E,F满足D²+E²-4F>0。
三、练习题及答案
练习题:
1.写出满足以下条件的圆的二元方程:
(1)圆心坐标为(0, 0),半径为3;
(2)圆心坐标为(1, -1),半径为2;
(3)圆心坐标为(-2, 3),半径为5。
2.判断以下方程是否表示圆,并说明理由:
(1)x²+y²+2x+3y+1=0;
(2)x²+y²-4x-6y+9=0;
(3)x²+y²+2ax+2by+c=0。
3.求出以下方程表示的圆的圆心坐标和半径:
(1)x²+y²-4x-6y+12=0;
(2)(x-3)²+(y-4)²=25;
(3)(x+1)²+(y-2)²=10。
4.根据以下条件,求出所给方程表示的圆的圆心坐标和半径:
(1)圆心坐标为(3, 0),半径为4;
(2)圆心坐标为(0, 0),半径为5;
(3)圆心坐标为(2, 3),半径为1。
答案:
1.x²+y²+6x+9=0 (2) (x-1)²+(y+1)²=4 (3) (x+2)²+(y-3)²=25
2.是圆(2) 是圆(3) 不是圆
3.圆心坐标为(2,3),半径为1 (2) 圆心坐标为(3,4),半径为5 (3) 圆心坐标为(-1,2),半径为√10
4.圆心坐标为(3,0),半径为4 (2) 圆心坐标为(0,0),半径为5 (3) 圆心坐标为(2,3),半径为1。
