图论学生论文
图论论文

课程名称图论入门论文题目图论在物流物配送上的应用指导教师刘颖学院管理学院姓名郭凤午学号2011030284图论在物流货物配送中的应用摘要:最短路径问题对于节约人们的时间成本具有重要意义。
最短路问题是图论理论的一个经典问题。
寻找最短路径就是在指定网络中两结点间找一条距离最小的路。
最短路不仅仅指一般地理意义上的距离最短,还可以引申到其它的度量,如时间、费用、线路容量等。
它可被用来解决厂区布局、管路铺设、线路安装等实际问题。
本文介绍了图论的起源和发展、最短路径问题及其算法,并应用图论最短路径问题的分析方法解决物流货物配送中问题。
1 引言数学是一门古老的学科,它已经有了几千年的历史。
然而,图论作为数学的一个分支,却只有200多年的历史,但是其发展十分迅速。
图论是以图为研究对象,图形中我们用点表示对象,两点之间的连线表示对象之间的某种特定的关系。
事实上,任何一个包含了某种二元关系的系统都可以用图形来模拟,而且它具有形象直观的特点,在图中点的位置和线的长短曲直无关紧要[1]。
图论的发展大力地推进了科学文明的进步,解决了很多实际应用问题。
图论是数学领域中发展最快的分支之一,它以图为研究对象。
图论中的图是有若干给定的点及连接两点的线所构成的图形,这种图形常用来描述某些事物之间的某种特定关系,用来代表事物,用连接两点的线表示相应两个事物间具有这种关系。
图论本身是应用数学的一部分,因此,历史上图论曾经被好多位数学家各自独立的建立过。
关于图论的文字记载最早出现在欧拉1736年的论文中,他所考虑的原始问题有很强的实际背景。
数学史上著名的七桥问题欧拉只用了一步就证明了不重复地通过7座桥的路线是根本不存在的!这是拓扑学研究的先声。
图的染色问题一直是图论研究的焦点问题。
数学家赫伍德成功地运用肯普的方法证明了五色定理,即一张地图能够用五种或者更少的颜色染色。
美国伊利诺斯大学的黑肯和阿佩尔,经过四年的艰苦工作.终于完成了四色猜想的证明。
图论毕业论文

图论毕业论文图论是数学的一个分支,主要研究图的性质和结构。
它对于解决各种实际问题具有重要的意义,如交通网络优化、电子芯片设计等。
本文将就图论的概念、基本性质以及其在实际问题中的应用等方面进行论述。
首先,图论是研究图的性质和结构的数学学科。
图是由节点和边组成的数学结构,可以用来描述各种实际问题,如交通网络、社交关系等。
图由节点和边构成,节点表示图中的元素或对象,边表示节点之间的关系。
图可以分为有向图和无向图,有向图中的边有方向性,无向图中的边没有方向性。
图的回路是指从一个节点出发,沿着边走过一系列节点之后再回到起始节点的路径。
图的连通性是指图中的任意两个节点之间存在一条路径。
其次,图论具有一些基本性质。
首先是图的度数。
图的度数是指图中一个节点与其相邻节点的边的个数。
度数为奇数的节点称为奇节点,度数为偶数的节点称为偶节点。
其次是图的邻接矩阵和关联矩阵。
邻接矩阵是一个n×n的矩阵,其中n是图的节点数,矩阵元素a_ij表示节点i与节点j之间是否存在边。
关联矩阵是一个n×m的矩阵,其中n是图的节点数,m是图的边数,矩阵元素b_ij表示节点i是否与边j相关联。
最后是图的连通性。
图的连通性决定了图中是否存在从一个节点到达另一个节点的路径。
如果图中的任意两个节点之间都存在路径,则图是连通的;否则,图是非连通的。
最后,图论在实际问题中有广泛的应用。
首先是交通网络优化。
图论可以用来优化交通网络中的路径规划和交通流量分析等问题,从而提高交通的效率和安全性。
其次是电子芯片设计。
图论可以用来分析电子芯片中各个元件之间的连接关系,从而提高芯片的性能和可靠性。
此外,图论还可以用来解决诸如社交网络分析、物流规划等实际问题。
综上所述,图论是数学的一个分支,主要研究图的性质和结构。
它对于解决各种实际问题具有重要的意义。
未来,随着科学技术的不断发展,图论在实际问题中的应用将会越来越广泛。
因此,对图论的进一步研究和应用具有重要的意义。
图论论文

课程名称图论入门论文题目图论在物流物配送上的应用指导教师刘颖学院管理学院姓名郭凤午学号2011030284图论在物流货物配送中的应用摘要:最短路径问题对于节约人们的时间成本具有重要意义。
最短路问题是图论理论的一个经典问题。
寻找最短路径就是在指定网络中两结点间找一条距离最小的路。
最短路不仅仅指一般地理意义上的距离最短,还可以引申到其它的度量,如时间、费用、线路容量等。
它可被用来解决厂区布局、管路铺设、线路安装等实际问题。
本文介绍了图论的起源和发展、最短路径问题及其算法,并应用图论最短路径问题的分析方法解决物流货物配送中问题。
1 引言数学是一门古老的学科,它已经有了几千年的历史。
然而,图论作为数学的一个分支,却只有200多年的历史,但是其发展十分迅速。
图论是以图为研究对象,图形中我们用点表示对象,两点之间的连线表示对象之间的某种特定的关系。
事实上,任何一个包含了某种二元关系的系统都可以用图形来模拟,而且它具有形象直观的特点,在图中点的位置和线的长短曲直无关紧要[1]。
图论的发展大力地推进了科学文明的进步,解决了很多实际应用问题。
图论是数学领域中发展最快的分支之一,它以图为研究对象。
图论中的图是有若干给定的点及连接两点的线所构成的图形,这种图形常用来描述某些事物之间的某种特定关系,用来代表事物,用连接两点的线表示相应两个事物间具有这种关系。
图论本身是应用数学的一部分,因此,历史上图论曾经被好多位数学家各自独立的建立过。
关于图论的文字记载最早出现在欧拉1736年的论文中,他所考虑的原始问题有很强的实际背景。
数学史上著名的七桥问题欧拉只用了一步就证明了不重复地通过7座桥的路线是根本不存在的!这是拓扑学研究的先声。
图的染色问题一直是图论研究的焦点问题。
数学家赫伍德成功地运用肯普的方法证明了五色定理,即一张地图能够用五种或者更少的颜色染色。
美国伊利诺斯大学的黑肯和阿佩尔,经过四年的艰苦工作.终于完成了四色猜想的证明。
图的邻接矩阵及其应用——数学专业本科生学年论文

学年论文题目:图的邻接矩阵及其应用学院:数学与信息科学学院专业:数学与应用数学学生姓名:******学号:************指导教师:******图的邻接矩阵及其应用摘要:文章介绍了邻接矩阵的定义及一个重要的定理,揭示了A k 在图论中的实际意义,并运用邻接矩阵的方法解决了锁具装箱和商人过河两个问题[1],使复杂的问题简单易懂,且容易推广,体现出了邻接矩阵在实际生活中的应用价值;另外对邻接矩阵在图的最小生成树和关键路径等算法分析上的应用作了一定的探讨[2]. 关键词:图;有向图;无向图;连通图;邻接矩阵;最小生成树;关键路径1.图论中邻接矩阵(Adjacency Matrix )的定义图的邻接矩阵[3],是表示顶点之间相邻关系的矩阵[4].设G=(V ,E)是一个图,其中V={v 1,v 2,…,v n }.G 的邻接矩阵是一个具有下列性质的n 阶方阵:⑴ 图而言,邻接矩阵一定是对称的,而且对角线一定为零,有向图则不一定如此;⑵ 向图中,任一顶点i 的度为第i 列所有元素的和;在有向图中顶点i 的出度为第i 行所有元素的和,而入度为第i 列所有元素的和.如下图[5]中无向图G 5 和有向图G 6 的邻接矩阵分别为A l 和A2:2.图论中邻接矩阵的一个重要定理设G 是一个图, V(G)为G 的顶点集, E (G)为G 的边集。
G 中有n 个顶点v 1,v 2,…,v n ,A=(a ij )n ×n 为G 的邻接距阵,其中n j i G E v v G E v v a ji j i ij ,...,2,1,)(0)(1=⎪⎩⎪⎨⎧∉∈= 则我们可得到如下定理:定理1 设A(G) 为图G 的邻接距阵,则G 中从顶点v i 到顶点v j ,长度为k 的道路的条数为A k 中的i 行j 列元素.证 对 k 用数学归纳法k =1时,显然结论成立;假设 k 时,定理成立,考虑 k +1的情形.记 A l 的i 行 j 列元素为A (1)ij ≥2,因为A 1#A=A 1+1,所以nj l in j l i j l i l ij a a a a a a a +++=+...2211)1((1)而从v i 到v j 长为 k +1的道路无非是从v i 经 k 步到某顶点v l (1≤l ≤n),再从v l 走一步到v j ;由归纳假设从v i 到v l 长为 k 的道路共计a ij k 而从v l 到v j 长为 1的道路为a ij 条,所以长为k+1的从v i 经过k 步到v l 再经过一步到v j 的道路共有()()nl 1kij il lj l 1a a a +==∑ 条,即定理得证.3.图论中邻接矩阵的应用3.1锁具装箱问题某厂生产一种弹子锁具, 每个锁具的钥匙有5个槽,每个槽的高度从{1,2,3,4,5,6}6个数(单位从略) 中任取一数.由于工艺及其他原因,制造锁具时对5个槽的高度还有两个限制:至少有3个不同的数,相邻两槽的高度之差不能为5,满足以上条件制造出来的所有互不相同的锁具称为一批.销售部门在一批锁具中随意地取每60个装一箱出售.问每一批锁具有多少个,装多少箱.锁具装箱这个问题是一个排列组合的数学问题,但在这里我们用图论中的邻接矩阵方法来解决这个问题.每把锁都有5个槽,每个槽有6个高度,至少有三个不同高度的槽,且相邻槽高差不为5.我们先求出无相邻高差为5的锁具数量,再减去仅有一个两个槽高的锁具数目.先计算由1, 2, 3, 4, 5, 6构成无1, 6相邻的情况的数目.为此,构造一个6节点的图:将1, 2, 3, 4, 5, 6这6 个数作为6个节点,当两个数字可以相邻时,这两个节点之间加一条边,每个节点有自己到自己的一条边.我们得到了锁具各槽之间的关系示意图(图1)1 26 35 4图1该图的邻接矩阵为:邻接矩阵A 的所有元素之和表示两个槽高无1,6相邻的锁具的个数,每个无1, 6相邻的5 位数与图1中长度为4的一条链一一对应,如12345,11111,22335等.A 的k 次方A k 中各元素之和就是长度为k 的链的个数.事实上,从这个具体问题可以看出,A 2中第i 行第j 列的元素指从i 开始经过两条边到达j 的链数,即从i 开始经过一条边到k,再从k 经过一条边达到j, i 和j 就决定了中间顶点k 的数目.于是,利用Matlab 就很容易得到将A 4 中元素求和可得相邻高差不为5的锁具数为6306把,但这6306把锁具中包含了仅有一个两个槽高的锁具,需要从其中减去,需减去的锁具的个数为()()266+C 5122426--=其中,第一个6仅有1个槽高的锁具; 26C 为1, 2, 3, 4, 5,6这6个数中取两个的取法,但扣除1, 6这一种取法; ( 25-2)是5个槽高每个都有两种选择25,再减去都取相同数字的两种情况。
图论小论文
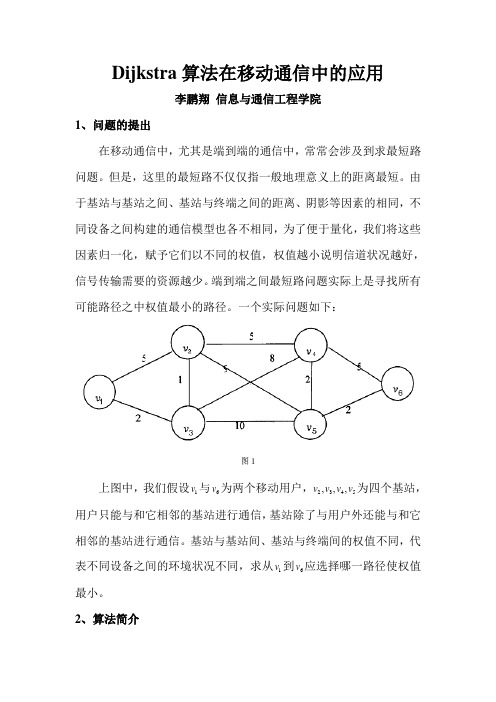
Dijkstra 算法在移动通信中的应用李鹏翔 信息与通信工程学院1、问题的提出在移动通信中,尤其是端到端的通信中,常常会涉及到求最短路问题。
但是,这里的最短路不仅仅指一般地理意义上的距离最短。
由于基站与基站之间、基站与终端之间的距离、阴影等因素的相同,不同设备之间构建的通信模型也各不相同,为了便于量化,我们将这些因素归一化,赋予它们以不同的权值,权值越小说明信道状况越好,信号传输需要的资源越少。
端到端之间最短路问题实际上是寻找所有可能路径之中权值最小的路径。
一个实际问题如下:上图中,我们假设1v 与6v 为两个移动用户,2345,,,v v v v 为四个基站,用户只能与和它相邻的基站进行通信,基站除了与用户外还能与和它相邻的基站进行通信。
基站与基站间、基站与终端间的权值不同,代表不同设备之间的环境状况不同,求从1v 到6v 应选择哪一路径使权值最小。
2、算法简介Dijkstra 算法是图论中确定最短路的基本方法,也是其它算法的基础。
Dijkstra 算法基本步骤: 令:{}{}_23,1,,,,i n s v i s v v v === 并令:{()()10,j j W v T v v s-==∞∈(1)、对j v s -∈,求()(){}()min ,j i ij j T v W v w T v +=。
(2)、求(){}min j j v sT v ∈得()k T v ,使()k T v =(){}min j j v sT v ∈令()()k k W v T v =(3)、若k n v v =则已找到1v 到n v 的最短路距离()k W v ,否则令i k =从s -中删去i v 转(1)。
这样经过有限次迭代则可以求出1v 到n v 的最短路线,可以用一个流程图来表示:第一步:先取()10W v =意即1v 到1v 的距离为0,而()j T v 是对()j T v 所赋的初值。
第二步:利用()1W v 已知,根据()(){}min ,j i ij T v W v w +对()j T v 进行修正。
图论期末论文

1.引言图论是数学的一个分支,并且是组合数学和应用数学的一部分。
它以图做为研究对象,而图是由若干节点和节点之间的边所构成的图型。
在图论中,图往往是某个具体现实生活中问题的数学抽象,可以说,图中的节点代表着生活中的某些特定事物,而节点之间的边则代表着节点之间的特定联系。
图论这门学科需要解决的就是如何利用数学知识去解决它们之间的关系。
图论最早起源于1736年著名的柯尼斯堡七桥问题[1]。
这个问题的内容是:在柯尼斯堡的普莱格尔河上有七座桥将河中的岛屿与河岸连接起来。
问题是要从这四块陆地中任何一块开始,通过每一座桥正好一次,最后再回到起始点。
然而人们无数次的尝试解决却都没有成功。
直到1736年,欧拉解决了这个问题。
他用抽像分析法将这个问题化为世界上第一个图论问题:即把每一块陆地用一个点来代替,将每一座桥用联接相应的两个点的一条边来代替,从而得到了一个“图”。
最终,欧拉成功证明了这个问题是无解的,并且推广了这个问题的意义,给出了对于一个给定的图可以某种方式走遍的判定法则。
这就是后来的欧拉通路、欧拉回路以及欧拉图问题。
于是,欧拉成为了图论学的创始人。
从那以后开始的几百年间,图论开始了飞速的发展。
虽然图论研究的是点和边之间所构成图的问题,但其应用领域还是十分广阔的。
图论的应用不仅仅局限于数学问题和计算机领域,它同时还涵盖了交通管理、通信领域、社会学等诸多其他研究领域。
而最短路径问题是图论应用中的基本问题。
最短路径顾名思义就是在所有的路径中找出一条距离最短的有效路径。
实际上,这里所指的“距离”不仅仅是指地理意义上的距离,还可以引申到时间、费用、等其他度量单位上面。
本文中,以重庆地铁为研究对象,利用图论知识解决在搭乘重庆地铁时的最短路径问题。
可以说,最短路径问题再交通网络结构的分析以及交通路线的选择中都有重要的应用价值。
此外,最短路径问题一直是计算机科学、地理信息学、交通管理学等学科中一个研究的热点问题。
图的着色是指对图的每个节点指定一种颜色,使得相邻的节点的颜色不相同。
图论论文
最小生成树——Prim算法1、算法问题的提出首先介绍生成树的概念连通图G=(V,E)是无向带权图,若一个子图G’是一棵包含G的所有顶点的树,则该子图G’称为G的生成树。
生成树是连通图的极小连通子图。
所谓极小是指:若在树中任意增加一条边,则将出现一个回路;若去掉一条边,将会使之变成非连通图。
生成树各边的权值总和称为生成树的权。
本次设计是求在图G中所有生成树中权值总和(费用/代价)最小的生成树,即最小生成树。
用两个例子进行实例演示。
2、Prim算法思想用哲学的观点来说,每个事物都有自己特有的性质,那么图的最小生成树也是不例外的。
按照生成树的定义,n 个顶点的连通网络的生成树有n 个顶点、n-1 条边。
(1)从树中某一个顶点V0开始,将V0到其他顶点的所有边当作候选边。
(2)重复以下步骤n-1次,使得其他n-1个顶点被并入到生成树中。
○1从候选边挑出权值最小的边输出,并将与该边另一端的相接的顶点V并入生成树中。
○2考察所有剩余顶点V i,如果(V,V i)的权值比lowcost[V i]小,则用(V,V i)的权值更新lowcost[V i]。
其中的vset[i]的值记录顶点V[i]顶点是否被选入最小生成树中,V[i]=0,表示为被选入,V[i]=1,表示已被选入。
用到辅助数组pre[],记录当前所选入顶点的前驱结点,当并入前一个顶点时,剩下顶点到生成树的权值发生了改变时,就需要及时修改剩下顶点V[i]的前驱结点。
3、程序设计(1)所用数据结构,图的存储结构模块(nodetype.h)#define MAXSIZE 7#define INF 100typedef struct{int no;}VertexType; //顶点类型定义typedef struct{int edges[MAXSIZE][MAXSIZE]; //存入边的权值int n; //顶点数int e; //总的边数VertexType vex[MAXSIZE];}MGraph; //图的存储结构MGraph g;(2)主模块(main.cpp)#include#include"nodetype.h"#include"initiate.h"#include"prim.h"void prim(MGraph g,int v0,int &sum);int main(){int sum=0;int v0;initiate(g); //图的初始化printf("请输入起点编号:\n");scanf("%d",&v0);//输入起始节点prim(g,v0,sum); //调用prim算法,构成最小生成树printf("最小生成树的总代价为%d\n",sum);return 0;}(3)读取数据模块,图的初始化(initiate.h)void initiate(MGraph &g){int i,j,v0=0;printf("Please input the Sumnum of MGraph:\n");scanf("%d",&g.n);printf("依次输入各边权值(不相临接的边权值为100)!\n\n"); for(i=1;i<=g.n;i++){g.vex[i].no=i; //节点编号for(j=1;j<=g.n;j++){printf("边[%d][%d]的权值为:",i,j);//各边的权值scanf("%d",&g.edges[i][j]);printf("\n");}}}(4)运用贪心策略——Prim算法构造最小生成树(prim.h)void prim(MGraph g,int v0,int &sum){int lowcost[MAXSIZE],vset[MAXSIZE];int v,pre[MAXSIZE]; //pre[]存入前驱结点数组int i,j,k,min;v=v0; //初始起点for(i=1;i<=g.n;i++){lowcost[i]=g.edges[v0][i]; //lowcost[]的数组pre[i]=v0;vset[i]=0;}vset[v0]=1;sum=0;for(i=1;imin=INF;for(j=1;j<=g.n;j++){if(vset[j]==0&&lowcost[j]min=lowcost[j];k=j;}}vset[k]=1; //将此结点并入到所够造的生成树中v=k;if(min!=INF){printf("边的起点为:%d 终点为:%d 权值为%d\n",pre[v],v,min);sum+=min;}else{break;}for(j=1;j<=g.n;j++){//并入新结点后修改剩下的结点到生成树的权值if(vset[j]==0&&g.edges[v][j]lowcost[j]=g.edges[v][j];pre[j]=v; //并记其下全趋结点}}}}4、算法分析Prim算法的时间复杂度主要是在双重循环构造最小生成树的过程中,设图的顶点数为n,则双重循环的时间复杂度为O(n2),在生成最小生成树的过程中,增加了两个数组,vset[]和lowcost[]数组,同时增加了一个前驱数组prey[],用来记录所选顶点的全趋结点,故空间复杂度为O(3n)。
图论
硕士生毕业论文摘要(25篇)00级(5篇):00-1 邵永强:《网络分析在车辆导航系统中的应用-----及最佳路径搜索软件的开发》Shao Yongqiang: <Application of Network Analysis in Vehicles Navigation>[摘要] 智能交通系统(ITS)是一种自动适应、自动监控的、实时、准确、高效地面交通系统。
智能车辆导航系统是智能交通系统的子系统之一,其重要功能之一是为行驶在道路网中的车辆提供从当前所处位置到目的地的有效、高性能价格比的行车路线,即对交通网络进行路径规划,为行驶车辆提供最佳路径搜索服务。
论文首先系统的介绍了网络分析、图论、地理网络的建模问题等相关理论以及导航电子地图的数据结构、数据模型等理论,接着论述了交通道路网络在电子地图中的表示和网络边的定权问题。
在此基础上论文以图论作为网络分析的主要方法,对导航电子地图的道路网进行网络分析,将最佳路径搜索问题转化为图论中的最短路径搜索问题。
最短路径搜索是图论的经典问题,论文对最短路径搜索问题作了简单的分类,重点介绍了Dijkstra、Moore 等几种经典的最短路径搜索算法,对它们之间时间复杂度进行了简单的比较,并针对传统算法的表达方式、存储结构等方面的缺点讨论了最短路径搜索算法的优化方法,以此为基础论文提出了改进的Moore算法,着重讨论了基于改进Moore算法的次最短路径的搜索、实时动态最短路径搜索以及复杂条件下最短路径搜索等问题。
并运用改进的Moore算法编制了一套最佳路径搜索的软件。
[关键词]智能车辆导航系统GPS导航电子地图网络分析图论最短路径算法优化实时动态最短路径搜索[Abstract] Intelligent Transport System (ITS) is a land traffic system of auto-adapt,auto-watch,real-time, accuracy and high-level efficiency. Intelligent Vehicles Navigation System is a subsystem of ITS. The most important task of Intelligent Vehicles Navigation System is offering effective and highperformance/price drive route from current location to destination for those vehicles which driving in theroad network. That is path planning to traffic network and provide the serving of searching the best path for the driving vehicles.The paper first introduce some theories about network analysis, graph theory and geographic network modeling by the numbers, at the same time the data structure and data model of digital map forcar-navigation is also mentioned. Next this paper discussed the problem that how to express the road network in digital map and how to decide the weight of road network side. Base on those theory, this paper take graph theory as the principal way to analyze the rode network in digital map, and transform the problem of searching the best path in road network to searching the shortest path in graph.Searching shortest path is a classical problem in graph theory. This paper classified the arithmetic of searching shortest path simply, and introduced some classified arithmeticians for example Dijkstra arithmetic and Moore arithmetic emphasisly. Some compare were showed among these arithmeticians with the time complexity in the paper, and some optimize ways were discussed aim at the defect of expression mode and memory structure of traditional arithmeticians. Then a reformed Moore arithmetic was advanced in view of the above discussion. Subsequently, this paper presented the searching way of second shortest path, real-time &dynamic shortest path and the shortest path under complex condition which base on the reformed Moore arithmetic. At last a sort of software about searching best path was programmed with reformed Moore arithmetic.[Key words] Intelligent Vehicles Navigation System, GPS Navigation, Network Analysis, Graph Theory, the Shortest Path, Digital Map, Arithmetic Optimize, the Searching of real-time &dynamic shortest path00-2 祁芳:《卡尔曼滤波算法在GPS非差相位精密单点定位中的应用研究》Qi Fang: <Research on Kalman Filter Algorithm in GPS Precise Point Positioning Usingun-difference Phase[摘要] GPS非差相位精密单点定位是利用GPS精密卫星星历及由一定算法确定的精密卫星钟差,以单台双频GPS接收机采集的非差相位数据作为主要观测值来进行单点定位计算的方法,其精度可达分米级甚至厘米级。
图论 本科毕业论文
图论本科毕业论文近年来,随着社会的发展和科技的进步,图论在各个领域中得到了广泛应用,尤其是网络科学、计算机科学和数学领域。
图论的基础理论和应用研究,也受到越来越多的关注。
本文主要介绍了图论的基础理论和应用研究,以及本人在此领域中的研究工作。
一、图论的基础理论图论是一门基础数学学科,它主要研究图的结构、性质和算法等方面的问题。
在图论中,图是由节点和边组成的集合,它可以用来描述各种实际问题,例如社交网络、电子电路、物流运输等。
图可以分为有向图和无向图两种类型。
有向图是由有向边连接节点而成的图,可以描述各种节点之间的方向关系。
而无向图则是由无向边连接节点而成的图,不考虑节点之间的方向关系,可以表示各种关系网络。
图论中的一些基本概念包括节点、边、路径、回路和连通性等。
节点是图中的基本元素,边是节点之间的连接线,路径指的是由一系列连续的边连接的节点序列,回路是一个首尾相接的路径。
而连通性则是描述图中各个节点之间的相互可达性的层次结构。
图论的另外一个重要的概念是图的度数。
节点的度数指与此节点相邻的边的数目,而图的度数则是所有节点度数之和。
在研究图的性质和结构时,度数是一个非常重要的指标,它可以用来刻画图的稠密或稀疏程度。
二、图论的应用研究图论在实际中的应用非常广泛。
例如,图论可以用于描述社交网络中各个节点之间的关系网络。
在这个网络中,节点代表人或组织,边则代表人和组织之间的关系。
通过研究这个网络的结构和性质,可以分析社交网络中的信息传播和节点的影响力等问题。
图论也广泛应用于计算机科学领域中。
例如,在计算机网络中,图论可以用来描述网络拓扑结构,并通过研究图的各种性质和算法,来优化网络的性能和安全性。
图论还可以用于描述物流和运输网络中的各种问题。
例如,在交通运输中,可以通过赋予各个节点和边合适的权重来刻画交通拥堵程度,从而优化交通运输的效率。
三、本人在图论领域的研究工作在本人的毕业论文中,我主要研究了图论中的连通性问题。
图论论文
最短路算法的比较与应用[摘要]本文较详尽地介绍了最短路算法相关的基本概念,给出了Dijkstra 算法、Floyd 算法、SPFA 算法等常用算法及其核心思想,并对各种最短算法做了多角度的比较,阐述了各种算法的应用范围,并对其在运输网络、舰船通道路线设计、工业生产中的应用做出了举例说明,侧重于模型的建立、思考和证明的过程,最后作出总结。
关键词:最短路算法 Dijkstra 算法 Floyd 算法 SPFA 算法1 引言最短路算法是图论中的核心问题之一,他是许多更深层次算法的基础,同时,该问题有着大量的生产实际的背景.很多问题从表面上看与最短问题没有什么关系,却也可以归结为最短路问题,本文通过收集整理关于最短路径的普遍算法,为研究最短路径问题在一些出行问题,工程问题,及实际生活问题中的应用,为企业和个人提供方便的选择方法。
2 最短路2.1 最短路的定义对最短路问题的研究早在上个世纪60年代以前就卓有成效了,其中对赋权)0(≥ij w 的有效算法是由荷兰著名计算机专家E.W.Dijkstra 在1959年首次提出的,该算法能够解决两指定点间的最短路,也可以求解图G 中一特定点到其它各顶点的最短路。
后来海斯在Dijkstra 算法的基础之上提出了海斯算法.但这两种算法都不能解决含有负权的图的最短路问题.因此由Ford 提出了Ford 算法,它能有效地解决含有负权的最短路问题.但在现实生活中,我们所遇到的问题大都不含负权,所以我们在)0(≥ij w 的情况下选择Dijkstra 算法。
定义1 若图),(E V G G =中各边e 都赋有一个实数)(e W ,称为边e 的权,则称这种图为赋权图,记为),,(W E V G G =。
定义2 若图),(E V G G =是赋权图且)(,0)(G E e e W ∈≥,若u 是i v 到jv 的路)(u W 的权,则称)(u W 为u 的长,长最小的i V 到j V 的路)(u W 称为最短路.若要找出从i v 到n v 的通路u ,使全长最短,即()()min ij e uW u W e ∈=∑。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数理与信息工程学院课程论文课程名称图论及其应用题目图论中邻接矩阵的应用姓名沈海华朱国淼学号******** ******** 专业信息与计算科学06(1)指导老师卜月华浅谈图论中邻接矩阵的应用[摘 要] 使用邻接矩阵求解有关实际问题符合数学中数形结合的思想,对于更好地理解问题,思考问题从而求解问题具有现实意义。
图论知识的应用是相当广泛的,它是数学的重要分支,使今年来较为活跃的数学分支。
这个问题其实也是一个数学游戏问题,是源于生活,高于生活。
图论作为组合数学的一分支,与其他数学分支,如矩阵论,概率论,拓扑学数值分析都有着重要的联系。
[关键字] 邻接矩阵、算法、连通性、最小生成树1、引言首先介绍图论中邻接矩阵的一个重要定理:G 是一个图,V (G)为 G 的顶点集, E(G)为 G 的边集。
设G 中有 n 个顶点,v 1,v 2,…,v n ;A=(a ij )n ×n 为 G 的邻接距阵, 其中n j i G E v v G E v v a j i j i ij ,...,2,1,)(0)(1=⎪⎩⎪⎨⎧∉∈= 定理 1:设 A (G)为图 G 的邻接距阵,则 G 中从顶点 vi 到顶点 vj,长度为 k 的道路的A k 条数为中的 i 行 j 列元素。
证:对 k 用数学归纳法k =1时,显然结论成立;假设 k 时,定理A l .A= A l+1成立,考虑 k +1的情形。
记 A l 的 i 行 j 列元素为l ≥2,因为所以nj l in j l i j l i l ij a a a a a a a +++=+...2211)1( (1)而从v i ,v j 到长 k +1的道路无非是从v i 经 k 步到某顶点v l (1≤l ≤n),再从v l 走一步到v j ; 由归纳假设从v l 到v j 长为 k 的道路共计 而从v l 到v j 长为 1的道路为a ij 条,所以长为k+1的v l 经过k 部到v i 再一步到v j 的道路共有∑-+=nl lj k il l ij a a a 1)()1(条故从v i 经 k +1步到v j 的路径共有1、 邻接矩阵现实问题中的运用锁具装箱问题某厂生产一种弹子锁具,每个锁具的钥匙有 5个槽,每个槽的高度从 {1, 2, 3, 4, 5, 6}6个数 (单位略 )中任取一数由于工艺及其他原因,制造锁具时对 5个槽的高度还有两个限制:至少有 3个不同的数,相邻两槽的高度之差不能为 5,满足以上条件制造出来的所有互不相同的锁具称为一批。
销售部门在一批锁具中随意地取每 60个装一箱出售。
问每一批具有多少个,装多少箱。
分析:锁具装箱这个问题是一个排列组合的数学问题,但在这里我们用图论中的邻接矩阵方法来解决这个问题。
每把锁都有 5个槽,每个槽有 6个高度,至少有三个不同高度的槽。
且相邻槽高差不为 。
我们先求出无相邻高5差为 5的锁具数量,再减去仅有一个、两个槽高的锁具数目。
先计算由 1, 2, 3, 4, 5, 6构成无 1, 6相邻的情况的数目。
为此,构造一个 6节点的图:将 1, 2, 3, 4, 5, 6这 6个数作为 6个节点,当两个数字可以相邻时,这两个节点之间加一条边,每个节点有自己到自己的一条边。
我们得到了锁具各槽之间的关系示意图 (见图 1)。
由图我们可以试着画出这个图的邻接矩阵来:⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=111110111111111111111111111111011111A 邻接矩阵 A 的所有元素之和表示两个槽高无 1, 6相邻的锁具的个数,每个无 1, 6相邻的 5位数与图 1中长度为 4的一条链 1 - 1对应,如 12345, 11111, 22335等。
A 的 k 次方中各元素之和就是长度为 k 的链的个数。
事实上,从这2个具体问题可以看出, A 中第 i 行第 j 列的元素指从 i 开始经过两条边到达 j 的链数,即从 i 开始经过一条边到 k,再从k 经过一条边达到 j, i 和 j 就决定了中间顶点 k 的数目。
于是,利用 Matlab 就很容易得到。
⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=1411651651651651401651941941941941651651941941941941651651941941941941651651941941941941651401651651651651414A 将该矩阵中的元素求和可得相邻高差不为 5的锁具数为 6306把。
把。
但这 6306把锁具中包含了仅有一个、两个槽高的锁具,需要从其中减去。
需减去的锁具的个数为6+( C 62-1)(25-2)=426其中,第一个 6仅有 1个槽高的锁具; C 62为 1, 2, 3, 4, 5, 6这 6个数中取两个的取法,但扣除 1, 6这一种取法。
最后得到一批锁具的个数为 6306 - 426 =5880,总共装98箱。
这样,就用图论的知识成功地解决了一批锁具的数量问题,这个方法比用别的方法简单,且容易推广。
问题求解反思:使用邻接矩阵求解有关实际问题符合数学中数形结合的思想,对于更好地理解问题,思考问题从而求解问题具有现实意义。
图论知识的应用是相当广泛的,它是数学的重要分支,使今年来较为活跃的数学分支。
这个问题其实也是一个数学游戏问题,是源于生活,高于生活。
图论作为组合数学的一分支,与其他数学分支,如矩阵论,概率论,拓扑学数值分析都有着重要的联系。
课本中也列举几种图论的矩阵表示法,如关联矩阵,邻接矩阵。
从矩阵的角度分析了图的顶点度的问题等相关知识。
对于这样的一个问题我们可以类似的联想到还有一个比较有特色的问题就是商人过河问题:三名商人各带一个随从乘船渡河,现有一只小船只能容纳两个人,由他们自己划行,若在河的任一岸的随从人数多于商人,他们就可能抢劫财物。
但如何乘船渡河由商人决定,试给出一个商人安全渡河的方案。
同样我们也可以用矩阵的方法加以解决(本题求解将留给读者思考,不作详述)。
3、基于邻接矩阵图的连通性判定性原则图的连通性判定准则:对于矩阵如果存在如下公式;()∑-=⨯==11m k k m m ij A S S 那么可以做出如下判断如果矩阵 中的元素全部为非零元素,则图G 为连通图;否则如果矩阵S 中存在t(t1)个零元素,则图G 为非连通图。
(证明从略) 在上述准则中,对于无向图,A 为图G 的节点邻接矩阵;对于有向图,A 为图G 对应的无向图的节点邻接矩阵。
对于图所示的有向图,对应的无向图的节点,其所定义的邻接矩阵为:⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=0100001011000001100110100011010000101A 根据图的连通性判定准则, ⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛==∑-=621181818421425757401818576061571818576160571818405757422141818182161111m k k A S可见该矩阵中的全部元素为非零元素,即图1为连通图。
同时,第i 行第 j 列元素表示i 节点和 j 节点间连通的路径数。
对于图1所示的有向图,对应于无向图的节点的邻接矩阵为:⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=0100001000000001100010100011010000102A 根据图的连通性判定原则: ⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛==∑-=2300003200000023242912002423291200292930170012121761122m k k A S可见该矩阵中的全部元素存在零元素,即图2为非连通图。
同时,第i 行第 j 列元素表示i 节点和 j 节点间连通的路径数。
定理求解反思:利用图论和集合论的知识,对节点邻接矩阵进行深入分析,提出了有向图和无向图的连通性判定推则及图中任意两节点间不连通的判定准则:对路径及节点邻接矩阵的概念进行了更为严格的数学描述;确定了路径的极限长度。
文中提出的图的连通性判定准则具有程序思想简单、逻辑性强、方便快捷的优点,对于图的连通性判定、连通块的划分等都具有指导意义。
对于这样的方法判定图的连通性简洁,明了,易于接受。
基于课本中未能涉及此类定理求解图的连通性问题,但是我们需要有意识地去研究类似的定理对于我们在平时作业过程中可能需要做出的快速反应。
对于我们学习本课程我们需要将自己看成是一支“快速反应部队”。
那么对于这类定理的应用是至关重要的。
此定理对于连通性的判定和连通块的划分具有指导意义。
4、求最小生成树的邻接矩阵法求最小生成树的邻接矩阵法如下:设图G 为任意的简单图可以是完全的,也可以是不完全的. 图G 有 个 n 结 点,且其边的集合为{(v 1,v 2),(v 1,v 3),…,(v n-1,v n )}。
在该算法执行过程中我们使用一个 桶 存放最小生成树的边一个桶存放最小生成树的结点一个计数器 记录 桶 中边的数 目 开始时 桶 桶 计数器都是空的。
算法的步骤:1) 写出图G 的邻接矩阵M,对于无向简单图G 矩阵M 以对角线为轴对称,我们只取其对角线以上部份的三角形各元素.在所有矩阵元素不为0的边中,选最小权边(v i ,v j )放入E 桶中,该边的两端点v i ,v j 放入V 桶,并记工=1, 若有两个(或两个以上)最小权边,其权值相等,任选其一。
2)矩阵M中,将(vi ,vj)边对应元素改为0,对vi,vj结点所对应的行与列上的矩阵元素做“乘2的模4运算”。
3)检查若有不为0的元素,则转第四步。
否则算法结束。
此时若I=n-1.则E桶中各边构成最小生成树。
I《n-1,则没有最小生成树。
4)将邻接矩阵M中,值为2的各元素对应边作为候选边.在候选边中找出最小权边(vi ,vj),若有两个或两个以上最小权边任取其一。
将该边放入E桶,并将其在V桶外的端点vi+1放入V桶。
同时:I=I+1。
5)将(vi ,vj)边对应元素改为0,将新入V桶的结点vi+1对应的M行列中做“乘2的模4运算”。
6)转第三步。
在关于算法的叙述中应说明两点:第一、算法中规定即乘2的模4运算它的含义是对一个变量乘以2 如果乘积等于4,则改该变量的值为0。
第二、因为在步骤3检查矩阵,如有不为0的元素,才转4,所以在第4步中邻接矩阵中必有值为2的元素.这是因为当一条边进人E桶,它的两端点进人V桶,与该两端点邻接而尚未进入E桶的各边对应的矩阵元素值原来为1经乘2后,其值必为2。
另一方面某一条边成为候选边,则它的矩阵元素值为2,如在下一步它未被选中其值不变,如被选中它的值才会因为乘2的模4运算而变为0.所以只要最小生成树最后未被求出在步骤4,矩阵中必有值为2的元素。
该算法求解反思:1、本算法在此虽然为涉及具体题目,但是这样的算法在实际问题的求解中是非常奏效的。
