基于分数阶Takagi-Sugeno模糊模型的分数阶Chen混沌系统的控制
T-S模糊Markov跳变系统的有限时间H_(∞)异步控制

T-S模糊Markov跳变系统的有限时间H_(∞)异步控制李秀英;姜囡
【期刊名称】《浙江大学学报(理学版)》
【年(卷),期】2024(51)1
【摘要】针对一类在Takagi-Sugeno模糊规则下的Markov跳变系统,研究了基于模糊状态反馈控制器的有限时间H_(∞)异步控制问题。
采用隐Markov模型刻画了模糊控制器与原系统的异步现象。
首先,通过构造Lyapunov函数,运用有限时间有界性和H_(∞)控制理论,得到了闭环系统H_(∞)有限时间有界的充分条件。
其次,设计了模糊状态反馈异步控制器,使得闭环系统H_(∞)有限时间有界。
最后,通过仿真算例验证了方法的有效性和可行性。
【总页数】7页(P14-20)
【作者】李秀英;姜囡
【作者单位】通化师范学院数学学院;中国刑事警察学院声像资料检验技术系【正文语种】中文
【中图分类】TP13;O211
【相关文献】
1.T-S模糊Markov跳变系统控制策略综述
2.网络化Markov跳变系统的事件触发异步控制
3.基于扩展状态观测器的随机隐Markov正跳变系统有限时间异步控制
4.基于观测器的时滞离散时间马尔可夫跳变系统有限时间H_(∞)控制
5.基于状态观测器的广义Markov跳变时滞系统的有限时间鲁棒H_(∞)控制
因版权原因,仅展示原文概要,查看原文内容请购买。
基于T—S模糊模型的网络控制系统稳定性分析

基于T—S模糊模型的网络控制系统稳定性分析一、引言随着网络控制系统在工业自动化领域的广泛应用,其稳定性分析成为了一个重要研究领域。
Takagi-Sugeno(T-S)模糊模型是一种有效的描述非线性系统的方法,已经在控制系统领域得到了广泛的应用。
本文将基于T-S模糊模型,对网络控制系统的稳定性进行深入研究和分析。
文章主要分为五个部分,首先介绍了网络控制系统的基本概念和T-S模糊模型的基本理论,然后对T-S模糊模型在网络控制系统中的应用进行了详细介绍,接着提出了基于T-S模糊模型的网络控制系统稳定性分析方法,并且针对该方法进行了具体的数学推导和例子分析,最后对整个研究工作进行了总结和展望。
二、网络控制系统的基本概念网络控制系统(Networked Control System,NCS)是一种由传感器、执行器、控制器和通信网络组成的控制系统,其特点是传感器信号和执行器信号通过网络进行传输和交换。
NCS的出现为工业自动化系统带来了很多优势,如降低了系统的成本、提高了系统的灵活性和可靠性等。
网络传输的时延、丢包等问题也给NCS的稳定性分析和控制带来了挑战。
三、T-S模糊模型的基本理论Takagi-Sugeno(T-S)模糊模型是20世纪80年代提出的一种描述非线性系统的方法,其基本思想是将非线性系统分解成一系列局部模型,并通过模糊规则进行整合。
T-S模糊模型的基本形式如下:如果x是一个关于输入向量u和输出向量y的非线性系统,那么T-S模糊模型可以表示为:规则1:如果u是A1,v是B1,则y=f1(u,v)规则2:如果u是A2,v是B2,则y=f2(u,v)规则n:如果u是An,v是Bn,则y=fn(u,v)其中A1、A2、...、An和B1、B2、...、Bn是输入向量u和输出向量y的模糊集合,f1、f2、...、fn是对应的线性函数。
四、T-S模糊模型在网络控制系统中的应用T-S模糊模型在网络控制系统中的应用主要有以下几个方面:1.描述非线性系统:NCS中由于网络时延、丢包等问题导致系统的非线性行为变得更加复杂,T-S模糊模型提供了一种有效的描述非线性系统的方法。
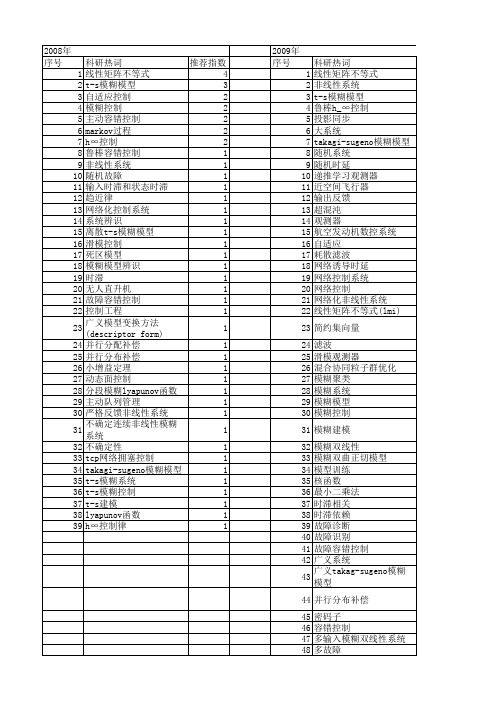
【国家自然科学基金】_takagi-sugeno模糊系统_基金支持热词逐年推荐_【万方软件创新助手】_20140729
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
推荐指数 4 3 3 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
1 1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87
最小二乘法 时滞依赖 时滞 无速度传感器控制 无线传感器网络 控制问题 执行器饱和 截止期错失率 感应电机 并行分布补偿 复杂性 双线性矩阵不等式 参数化线性矩阵不等式(plmi) 参数不确定性 卫星姿态控制系统 功率因数 减法聚类 入侵检测 充要条件 信息安全 仿真 不确定隶属度 不确定连续非线性系统 ts模糊模型 takagi-sugeno模糊系统 t-s模糊神经网络 t-s模糊 pdc o型 nsv姿态系统 lyapunov方法 lq/h_∞控制 l-m算法 h∞最优故障观测器 h_∞控制
53 54 55 56 57 58 59 60 61 62 63 64 65 66
卡尔曼滤波 协同进化 切换 分段 函数 全解耦奇偶方程 takagi-sugeno模糊系统 takagi-sugeno(t-s)模糊系统 takagi-sugeno(t-s)模糊模型 t-s模糊建模 lmi h∞控制 dna序列编码区 chua混沌系统
一类非线性区间时滞随机系统的控制与仿真_解相朋

1 T ∂V 2 (t ) g (t ) g (t ) 2 ∂x 2 + tanh T ( Lx)(Q + R + h1 Z + h12 S ) tanh( Lx) − tanh T ( Lx1 ) R tanh( Lx1 ) −∫ −∫
t t − h1 t − h1
− (1 − τ (t )) tanh T ( Lxτ )Q tanh( Lxτ ) tanh T ( Lx( s )) Z tanh( Lx( s ))ds tanh T ( Lx( s )) S tanh( Lx( s ))ds tanh T ( Lx( s ))dsV (tanh( Lx) − tanh( Lx1 )) tanh T ( Lx( s ))dsW (tanh( Lx1 ) − tanh( Lxτ ))
(4)
t − h1 0
tanh T ( Lx( s)) R tanh( Lx( s ))ds
t
其中 M , N i (i = 1, 2,3, 4) 为适当维数的已知常数矩阵,F (t ) 是
− h1 t + β − h1
∫
tanh T ( Lx( s )) Z tanh( Lx( s ))dsd β tanh T ( Lx( s )) S tanh( Lx( s ))dsd β
如果存在对称正定矩阵 Q ,向量函数 v (t ) 使
得下述各积分都有意义,则不等式 t − h1 t − h1 t − h1 1 − ∫ v T ( s )Qv ( s )ds ≤ − v T ( s )dsQ ∫ v ( s )ds t − h2 t − h2 h2 − h1 ∫t − h2 成立,其中 h 2 ≥ h1 。 引理 2[10] 对于适当维数的矩阵 M, N 和 F (t ) ,若
《2024年空间分数阶Gray-Scott模型和时间分数阶Maxwell系统的有限元方法》范文

《空间分数阶Gray-Scott模型和时间分数阶Maxwell系统的有限元方法》篇一一、引言在数学建模和数值分析领域,空间分数阶Gray-Scott模型和时间分数阶Maxwell系统扮演着重要角色。
随着科学与技术的进步,这两个模型在众多领域如生物学、材料科学和电磁学中得到了广泛应用。
有限元方法作为一种有效的数值计算工具,常被用来解决复杂的数学模型问题。
本文旨在探究如何应用有限元方法来处理这两个复杂系统的数学问题。
二、空间分数阶Gray-Scott模型空间分数阶Gray-Scott模型是一个常用于描述复杂反应扩散系统的偏微分方程模型。
它具有非线性特性和空间分数阶导数,为解决此类问题提供了数学框架。
本文将详细介绍该模型的数学形式、物理背景以及其求解的必要性。
三、时间分数阶Maxwell系统时间分数阶Maxwell系统则是用于描述电磁波传播及物质响应的数学模型。
其方程中的时间分数阶导数使得模型能够更好地反映实际物理现象的复杂性和非局部性。
本部分将详细阐述该系统的数学表达、物理意义及其在电磁学中的应用。
四、有限元方法的基本原理在解决上述两个复杂系统的问题时,有限元方法是一种有效的数值计算工具。
本部分将详细介绍有限元方法的基本原理、步骤和特点,包括其求解过程、计算效率和精度等优势。
五、空间分数阶Gray-Scott模型的有限元方法实现本部分将详细描述如何将有限元方法应用于空间分数阶Gray-Scott模型的求解过程。
包括离散化处理、基函数选择、数值积分等关键步骤的详细解释和实现过程。
此外,还将讨论该方法在求解过程中的稳定性和收敛性等问题。
六、时间分数阶Maxwell系统的有限元方法实现类似地,本部分将详细介绍如何将有限元方法应用于时间分数阶Maxwell系统的求解过程。
包括系统的离散化、时间步长的选择、电磁场量的离散化处理等关键步骤的详细解释和实现过程。
此外,还将讨论该方法在处理复杂电磁现象时的优势和局限性。
T-S模糊系统量化H∞滤波器设计

T-S模糊系统量化H∞滤波器设计赵迪;常晓恒【摘要】This paper considers the problem of H∞filter design for T-S fuzzy system with out-put quantization. Attention is focused on the design of a filter to mitigate the quantization effects, which ensured not only the asymptotical stability but also a prescribed H∞ performance. By using fuzzy Lyapunov function approach and adding slack matrix variables, a sufficient condition is presented in terms of linear matrix inequalities (LMIs) for such filter exists. Finally, a numerical example is provided to demonstrate the effectiveness of the proposed approach.%本文研究了离散T-S模糊系统H∞量化滤波问题。
主要目的是针对存在量化的T-S模糊反馈系统设计可行的滤波器算法使其在消除量化的影响下渐进稳定的并满足给定H∞性能指标。
具体是通过模糊Lyapunov函数及引入松弛变量,提出了比文献中结果保守性低的基于线性矩阵不(LMIs)的滤波器存在的充分条件。
最后,通过数值仿真例子来验证设计方案的有效性。
【期刊名称】《电子设计工程》【年(卷),期】2015(000)016【总页数】4页(P112-115)【关键词】T-S模糊系统;H∞滤波;模糊Lyapunov函数;量化;线性矩阵不等式(LMIs)【作者】赵迪;常晓恒【作者单位】渤海大学数理学院,辽宁锦州 121003;渤海大学工学院,辽宁锦州 121003【正文语种】中文【中图分类】TN964自1985 年Takagi 和Sugeno[1]提出了著名的T-S 模糊系统模型来描述复杂的非线性系统以来,T-S 模糊模型作为处理非线性系统的有效手段吸引了众多学者的关注[1-4]。
分数阶混沌系统的控制与同步研究
分数阶混沌系统的控制与同步探究摘要:分数阶系统具有很好的非线性特性和长记忆能力,在混沌系统的探究中得到广泛应用。
本文主要探讨了分数阶混沌系统的控制与同步问题。
起首介绍了分数阶系统和混沌现象的基本观点,随后分别探讨了分数阶系统的控制方法和同步方法。
通过模拟试验验证了这些方法的有效性。
最后,总结了探究结果并指出了将来的进步方向。
1.引言随着现代科学技术的进步,混沌系统的探究引起了广泛的关注。
混沌系统是一类非线性动力学系统,具有高度复杂的行为和随机性,表现出的熵较高。
分数阶系统是近年来探讨的热点之一,其具有更广泛的记忆特性和非线性特性,能够更好地描述实际系统的动力学行为。
因此,分数阶混沌系统的控制和同步问题成为了探究的重点。
2.分数阶系统的基本观点分数阶系统是指微分与积分阶数不仅仅为整数,而是介于0和1之间的实数。
分数阶微分方程是描述分数阶系统的基本工具。
混沌系统是一类具有无法猜测的行为和极其敏感的初始条件的系统。
分数阶混沌系统介于分数阶系统和混沌系统之间,兼具了两者的特性。
3.分数阶混沌系统的控制方法针对分数阶混沌系统的控制问题,探究者提出了多种方法。
其中一种常用的方法是基于反馈控制理论的方法。
通过在系统中引入适当的反馈控制项,可以有效地控制系统的混沌行为。
另一种方法是基于最优控制理论的方法,通过求解最优控制问题,可以获得使系统行为稳定或特定性能指标最优的控制策略。
4.分数阶混沌系统的同步方法分数阶混沌系统的同步问题是指如何使两个或多个分数阶混沌系统的状态变量在某种意义上达到一致。
同步方法可以分为无控制同步和有控制同步两种。
无控制同步是指系统自身通过耦合作用实现同步,而有控制同步是利用外部控制手段实现同步。
常用的同步方法有时间延迟复杂网络同步、自适应控制同步和非线性控制同步等。
5.模拟试验与结果分析为验证分数阶混沌系统的控制和同步方法的有效性,进行了一系列模拟试验。
通过对分数阶混沌系统进行控制和同步,分析了系统的动力学行为和性能指标。
基于Takagi-Sugeno模糊模型的模糊控制
天津大学硕士学位论文基于Takagi-Sugeno模糊模型的模糊控制姓名:徐妮妮申请学位级别:硕士专业:控制理论与控制工程指导教师:高志伟2002.1.1112陟乒TS模糊模型可以很好地逼近非线性系统,其予模型采用线性动态方程易于用现代控制理论的方法进行分析和控制器的设计。
本文的工作是围绕TS模糊模型展开的。
首先对以往的模糊系统的稳定性分析和模糊控制器的设计成果进行了回顾。
接下来,文中重点讨论了一般模糊系统的模糊控制器的设计和模糊状态观测器的设计。
得出用模糊状态观测一控制器实现的闭环模糊系统的稳定性定理。
文中提出了模糊状态观测器和模糊控制器的相对分离性设计。
仿真结果验证了结论的正确性。
文中通过扩展Ts模糊模型定义了模糊广义系统。
讨论了模糊广义系统的模糊状态观测一控制器的设计。
同样,模糊广义系统的模糊状态观测器和模糊控制器也具有设计的相对分离性。
关键词:Ts模糊模型,模糊控制器,模糊状态观测器,模糊广义系统AbstractThispaperconcentratesontheTSfuzzymodel.ThefuzzymodelproposedbyTakagiandSugenoisdescribedbyfuzzyIF-THENrule,whichrepresentlocallinearinput—outputrelationsofanonlinearsystem.Tobeginwitll.TSfuzzymodelandpreviousstabilityresultsarerecalled.ThenextsectionaddressestheanalysisanddesignofthefuzzycontrollerandthefuzzyobserveronthebasisoftheTSfuzzymodel.Thestabilityconditionfortheclosed-loopsystemisderived,whichshowsthatthefuzzycontrollerandthefuzzyobserverCanbedesignedindependentlywitllsomeconstrains.Thenumericalsimulationonallinvertedpendulumsystemisgiventoillustratetheperformanceoftheclosed-loopsystem.FinallyafuzzydescriptorsystembyextendingtheordinaryTSfuzzymodelisdefined.Thefuzzycontrollerandthefuzzyobserverofthefuzzydescriptorsystemarediscussed.Fourkindsofstabilityconditionsarederived.Simulationresultshowstheutilitiesofthosestabilityconditions.Keywords:TSfuzzymodel,fuzzycontroller,fuzzyobserver,fuzzydescriptorsystem第一章绪论第一章绪论§1.1模糊控制系统近年来的研究与发展美国加利福尼亚大学L.A.Zadeh教授在1965年提出的{FuzzySet>)【1】开创了模糊控制的历史,从此模糊数学科学发展起来了。
7.2-Sugeno模糊模型建模及控制
9
10
9
10
Degree of membership
1
ZR
0.8
0.6
Hale Waihona Puke 0.40.20
-0.25 -0.2 -0.15 -0.1 -0.05 0 0.05 0.1 0.15 0.2 0.25 x
1
ZR
0.8
0.6
0.4
0.2
0
-3
-2
-1
0
1
2
3
dx
Degree of membership
图4 倒立摆的摆角、角速度隶属函数
仿真设计: 根据上述规则设计一个二输入、单输出的
Sugeno模型,可观察到输入输出隶属函数曲线。 仿真结果如图1和图2所示。
仿真程序:chap7_3.m
MF Degree of input 1
1
0.8 little
big
0.6
0.4
0.2
0
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
x
1
0.8 little
big
0.6
0.4
0.2
0
0
1
2
3
4
5
6
7
8
9
10
x
MF Degree of input 2
图1 Sugeno模糊推理系统的输入隶属函数曲线
Z
10
5
0
10
5
5
4 3
2
Y
00
1
X
图2 Sugeno模糊推理系统的输入/输出曲线
第4章 模糊T-S控制(3)
ρ2
P2 P + Q2 2
P Ai + AiT P − ZiC − (ZiC)T + Q2 P 2 2 2 <0 2 P − ρ I 2
(2.13)
首先,由式(2.13)求得P和 i,然后由式(2.12) 2 L 求得 P 和 Ki 。 1
20
二、一类非线性系统的模糊控制方法 一类非线性系统的模糊控制方法 一类非线性系统的模糊控制
2 n1 3 4 n2
(2.1)
其中x , x ∈R , x , x ∈R (n = 2(n1 + n2 ))是系统的状态向量,状 态是可量测的, u∈ Rm 是控制输入向量,y∈Rm 是系 统的可量测输出向量,C ∈R , f 2 , f 4 是光滑非线性函 数,d2 , d4是外部扰动,x =[x1T , x2T , x3T , x4T ]T ∈Rn , m = n1 + n2 ,d =[0, d ,0, d ] .
9
二、一类非线性系统的模糊控制方法 一类非线性系统的模糊控制方法 一类非线性系统的模糊控制
1.一类非线性系统的模糊H∞控制问题 问题描述:考虑如下的非线性系统
& x1 = x2 & x2 = f 2 (x, u) + d2 & x3 = x4 x4 = f 4 (x, u) + d4 &
证明 选取
Lyapunov
5
一、模糊T-S控制简介 模糊T 模糊
从而提出了基于模糊T-S模型的松弛二次稳定控制方 案。Liu等人推广了文[65]的二次稳定充分条件,进 一步降低保守性,提出了一种二次稳定控制方案[66 -67]。Park借助T-S模糊模型,提出一种在线参数估 计方法[68]并研究了参数不确定非线性系统的稳定性 问题[69]。文[70]给出了一种积分模糊模型的系统设 计方案。T-S模糊模型还被用来研究非线性关联系统 的跟踪控制问题[71]、非线性奇异系统的稳定性问题 [72]和带有执行器饱和的非线性系统的鲁棒控制问题 [73]。文[74-75]提出了时延系统的模糊模型,并讨 论了非线性时延系统的分析和综合问题。文[76]给出 了不确定模糊时延系统的二次稳定控制方法。文[77]
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Takagi-Sugeno Fuzzy Model, Fractional Order Chen Chaos System, PDC (Parallel Distributed Compensating)
基于分数阶Takagi-Sugeno模糊模型的分数阶 Chen混沌系统的控制
李玉婷
Copyright © 2020 by author(s) and Hans Publishers Inc. This work is licensed under the Creative Commons Attribution International License (CC BY 4.0). /licenses/by/4.0/
Biu (t )
其中,i = 1, 2,, r ,r 是模糊推理规则的数目,Mij ( j = 1, 2,, p) 是模糊集合,z1 (t ),, zp (t ) 是前件变量, 可以是状态、输入或输出变量。 x (t ) ∈ Rn 是状态变量, u (t ) ∈ Rm 是输入变量, α (0 < α ≤ 1) 是分数阶
本节给出分数阶 Chen 混沌自治系统的分数阶 Takagi-Sugeno 模糊模型。取 x1 ∈[−d, d ] , d > 0 ,根 据混沌系统的有界性可知此假设是合理的。选择 x1 (t ) 作为模糊规则的前件变量,分数阶 Chen 混沌系统
可以表示成如下形式的分数阶 Takagi-Sugeno 模糊模型:
D= α x1 (t ) Dα x2 (t )
a ( x2 (t
= (c − a)
) − x1 x1 (t )
(t
−
)),
x1 (
t
)
x3
(
t
)
+
cx2
(t
)
,
(5)
Dα
x3
(t
)
= −bx3 (
t
)
+
x1
(
t
)
x2
(t
)
.
其中, a = 35 , b = 3 , c = 28 时,取 α = 0.95 时,初值 x (0) = [−9 − 5 14]T 时相应的分数阶 Chen 系统的
Operations Research and Fuzziology 运筹与模糊学, 2020, 10(2), 115-121 Published Online May 2020 in Hans. /journal/orf https:///10.12677/orf.2020.102012
引理 1 [18]:如果存在一个对称正定矩阵 Q,矩阵 Mi ( i = 1, 2,, r ),使得下面的 LMIs 成立
AiQ − Bi Mi + ( AiQ − Bi Mi )T
< 0,
i
= 1, 2, ,
r
,
(3)
( )T
AiQ − Bi M j + AjQ − Bj Mi + AiQ − Bi M j + AjQ − Bj Mi < 0, 1 ≤ i < j ≤ r ,
Dα
表示
C a
Dtα
算子。
2.2. 分数阶 Takagi-Sugeno 模糊系统
Takagi-Sugeno 模糊模型自产生之日起就是处理非线性系统问题的有效方法之一。混沌系统是一类典 型的非线性系统,本文利用分数阶 Takagi-Sugeno 模糊模型来研究非线性分数阶 Chen 混沌系统的控制问 题。首先我们介绍分数阶 Takagi-Sugeno 模糊系统。
义,本文使用 Caputo 型分数阶微积分的概念。
定义 1 [17]:Caputo 型分数阶微分的定义为
= Ca Dtα f (t )
1
Γ(r −α
)
t
∫a
(t
f (r) (τ ) ) −τ α +1−r
dτ ,
(r
−1 ≤
α
<
r)
(1)
其中
Γ (⋅)
是
gamma
函数,
r
∈
N
。为了讨论方便,本文中用
Rule 1: If x1 (t ) is F1 ( x1 (t )) , then Dα x (t ) = A1x (t ) ;
Rule 2: If x1 (t ) is F2 ( x1 (t )) , then Dα x (t ) = A2 x (t ) .
其中 x (t ) = x1 (t ), x2 (t ), x3 (t )T ,
Abstract
The control problem of fractional order Chen chaos system based on fractional order Takagi-Sugeno fuzzy model is studied. The Takagi-Sugeno fuzzy model for fractional order Chen chaos systems is given, and a parallel distributed compensate fuzzy controller is designed to asymptotically stabilize the model. Then effectiveness of the approach is tested on fractional order Chen chaos system with α = 0.95 .
( ) Mij z j (t ) 是 z j (t ) 在模糊集合 Mij 中的隶属度函数,且满足:
∑r wi ( z (t )) > 0
i=1
wi ( z (t )) ≥ 0
∑r hi ( z (t )) = 1
i=1
hi ( z (t )) ≥ 0
下面介绍分数阶 Takagi-Sugeno 模糊闭环系统渐进稳定的结论。
Open Access
1. 引言
混沌是指对初值具有极端敏感性的确定性动力系统的随机行为。1963 年,Lorenz [1]发现了被称为 “蝴蝶效应”的 Lorenz 混沌系统,之后就有许多新的混沌系统被不断的发现。1999 年陈关荣教授发现了 与 Lorenz 混沌系统相关但不拓扑等价且更复杂的 Chen 混沌系统[2] [3]后,有许多关于 Chen 混沌系统的 研究结论[4] [5] [6] [7]产生了。同时分数阶混沌系统的相关动力学性质、控制及同步等问题也得到了广泛 的关注并取得各种成果。如:文献[8]研究了一种新的分数阶超混沌系统的动力学行为、电路实现、混沌 控制及同步问题;分数阶 Chua 系统的混沌与同步问题在文献[9]中进行了探讨;文献[10]讨论了具有输入 饱和的分数阶混沌系统的同步问题;文献[11]分析了分数阶 Chen 混沌系统的局部分叉理论。
状态轨迹如图 1 所示。
DOI: 10.12677/orf.2020.102012Βιβλιοθήκη 117运筹与模糊学
李玉婷
Figure 1. Chaotic behaviors of the fractional order Chen system 图 1. 分数阶 Chen 混沌系统的仿真曲线
3.2. 分数阶 Chen 混沌系统的 Takagi-Sugeno 模糊模型
DOI: 10.12677/orf.2020.102012
116
运筹与模糊学
李玉婷
考虑如下形式的分数阶 Takagi-Sugeno 模糊系统:
Rule i: If z1 (t ) is Mi1 and … zp (t ) is Mip ;
Then
Dα= x (t )
x
(0)
=
x0
Ai x (t ) +
日本学者 Takagi 和 Sugeno 在 1985 年提出了 Takagi-Sugeno 模糊系统[12] [13],其本质是将非线性的 动力学系统通过一系列局部线性系统来描述,线性系统之间通过非线性的隶属度函数来连接。目前利用 Takagi-Sugeno 模糊模型来研究非线性混沌系统的控制与同步等问题目前已经成为研究混沌模型的主要 方法之一。如:文献[14]研究了基于 Takagi-Sugeno 模型的非 PDC 观测器的跟踪控制器在混沌控制中的 应用;文献[15]讨论了降阶模糊控制器对 Lorenz-Stenflo 系统的控制和同步问题;文献[16]考虑了输入未 知的 Takagi-Sugeno 模糊系统在混沌同步中的应用问题;目前这些讨论主要是基于整数阶 Takagi-Sugeno 模糊系统对混沌系统的研究。本文基于分数阶 Takagi-Sugeno 模糊系统理论建立了分数阶 Chen 混沌系统 的 Takagi-Sugeno 模糊模型,讨论了分数阶 Chen 混沌系统的控制问题。
Takagi-Sugeno 模 糊 系 统 的 阶 数 。 Ai ∈ Rn×n 和 Bi ∈ Rn×m 是 系 统 的 已 知 系 数 矩 阵 , 则 全 局 分 数 阶 Takagi-Sugeno 模糊系统模型可以表示为如下形式:
= Dα x (t )
r
∑ hi ( z (t ))( Ai x (t ) + Biu (t ))
i =1
(2)
x (0) = x0
r
p
其 中 , z (t ) = z1 (t ), z2 (t ),, zp (t ) , hi ( z (t )) = wi ( z (t )) ∑ wi ( z (t )) , wi ( z (t )) = ∏ Mij ( z j (t )) ,
i =1
j =1
−a a 0
−a a 0
A1 = c − a
