数学建模-优化问题
最优化问题的建模与解法
最优化问题的建模与解法最优化问题（optimization problem）是指在一组可能的解中寻找最优解的问题。
最优化问题在实际生活中有广泛的应用，例如在工程、经济学、物流等领域中，我们经常需要通过数学模型来描述问题，并利用优化算法来求解最优解。
本文将介绍最优化问题的建模和解法，并通过几个实例来说明具体的应用。
一、最优化问题的数学建模最优化问题的数学建模包括目标函数的定义、约束条件的确定以及变量范围的设定。
1. 目标函数的定义目标函数是一个表达式，用来衡量问题的解的优劣。
例如，对于一个最大化问题，我们可以定义目标函数为：max f(x)其中，f(x)是一个关于变量x的函数，表示问题的解与x的关系。
类似地，对于最小化问题，我们可以定义目标函数为：min f(x)2. 约束条件的确定约束条件是对变量x的一组限制条件，用来定义问题的可行解集合。
约束条件可以是等式或不等式，通常表示为：g(x) ≤ 0h(x) = 0其中，g(x)和h(x)分别表示不等式约束和等式约束。
最优化问题的解必须满足所有的约束条件，即：g(x) ≤ 0, h(x) = 03. 变量范围的设定对于某些变量，可能需要限定其取值的范围。
例如，对于一个实数变量x，可能需要设定其上下界限。
变量范围的设定可以通过添加额外的不等式约束来实现。
二、最优化问题的解法最优化问题的解法包括数学方法和计算方法两种，常见的数学方法有最优性条件、拉格朗日乘子法等，而计算方法主要是通过计算机来求解。
1. 数学方法数学方法是通过数学分析来求解最优化问题。
其中，常见的数学方法包括：（1）最优性条件：例如，对于一些特殊的最优化问题，可以通过最优性条件来判断最优解的存在性和性质。
最优性条件包括可导条件、凸性条件等。
（2）拉格朗日乘子法：对于带有约束条件的最优化问题，可以通过拉格朗日乘子法将原问题转化为无约束最优化问题，从而求解最优解。
2. 计算方法计算方法是通过计算机来求解最优化问题。
数学建模优化问题的求解方法
数学建模优化问题的求解方法
数学建模优化问题的求解方法有很多。
下面列举几种常见的方法：
1. 数学规划方法：包括线性规划、整数规划、非线性规划、动态规划等。
这些方法通过数学模型和约束条件来描述问题，并通过寻找最优解来优化问题。
2. 图论方法：将问题抽象成图或网络，并利用图论算法来求解最优解。
常见的算法有最短路径算法、最小生成树算法、最大流算法等。
3. 近似算法：对于复杂的优化问题，往往很难找到精确的最优解。
近似算法通过寻找接近最优解的解来近似优化问题。
常见的近似算法有贪心算法、近邻算法、模拟退火算法等。
4. 遗传算法：模拟生物进化的过程，通过选择、交叉和变异等操作来搜索问题的解空间，并逐步优化解。
遗传算法适用于复杂问题和无法直接求解的问题。
5. 物理方法：将优化问题转化为物理模型，利用物理规律求解。
比如蚁群算法模拟蚂蚁找食物的行为，粒子群算法模拟鸟群觅食的行为等。
以上只是数学建模优化问题求解方法的几种常见方法，实际问题求解时要根据问题的特点选择适合的方法，并结合领域知识和实际情况进行调整和优化。
2023年全国数学建模题目
2023年全国数学建模题目
一、优化模型
题目：全球能源分配优化问题
问题描述：全球各国对能源的需求不断增长，而能源资源有限。
为了实现可持续发展，需要优化全球能源分配，确保各国都能获得适量的能源供应。
请运用优化模型和方法，设计一个全球能源分配方案，以满足各国能源需求，并尽量减少能源浪费和环境污染。
二、统计分析
题目：社交媒体用户行为分析
问题描述：社交媒体平台上积累了大量用户数据，包括用户发布的内容、关注对象、互动情况等。
请运用统计分析方法，分析社交媒体用户的偏好、行为模式和社交网络结构，为相关企业提供营销策略建议。
三、机器学习
题目：基于机器学习的文本分类问题
问题描述：文本数据包括各种主题，如政治、经济、文化等。
请运用机器学习算法，对给定的文本数据进行分类，并评估分类效果。
同时，请探讨如何提高分类准确率和泛化能力。
四、预测模型
题目：商品价格预测问题
问题描述：商品价格受到多种因素的影响，如市场需求、生产成本、政策因素等。
请运用预测模型和方法，预测未来一段时间内某种商品的价格走势，为投资者和企业提供决策依据。
五、决策分析
题目：企业投资决策问题
问题描述：企业需要在多个项目中做出投资决策，以实现利润最大化。
请运用决策分析方法，评估各项目的风险和收益，为企业制定最优投资策略。
六、系统动力学
题目：城市交通拥堵问题研究
问题描述：城市交通拥堵是一个复杂的问题，涉及多个因素之间的相互作用。
请运用系统动力学方法，建立城市交通拥堵问题的动力学模型，分析各因素之间的因果关系和动态变化规律，提出缓解交通拥堵的策略建议。
数学中的数学建模与优化问题
数学中的数学建模与优化问题数学建模和优化是数学领域中的两个重要概念，它们在解决实际问题中起着关键作用。
本文将探讨数学建模和优化的定义、原理及其在实际中的应用。
一、数学建模数学建模是指将实际问题转化为数学问题，并通过建立数学模型来描述和分析问题。
数学建模的核心是找到问题的本质，抽象出关键因素，并建立合适的数学模型。
通过建模，我们可以利用数学工具和方法来解决问题，预测未来的趋势，制定决策。
在数学建模中，常用的数学工具包括微积分、线性代数、统计学等。
数学建模的过程通常包括问题分析、模型假设、模型建立、模型求解和模型验证等步骤。
通过这些步骤，我们可以得到符合实际情况的数学模型，并进行预测和优化。
二、数学优化数学优化是指在给定的约束条件下，寻找使目标函数达到最大或最小值的一组变量取值。
数学优化在解决实际问题中，通常涉及到决策、资源分配、路径规划等方面。
通过优化，我们可以在有限资源下找到最优解，提高效率和经济性。
数学优化的常用方法包括线性规划、非线性规划、整数规划等。
这些方法通过数学理论和算法，求解最优解或次优解。
在实际应用中，我们可以通过优化来改进生产制造、物流配送、交通规划等领域，提高整体效益。
三、数学建模与优化的应用数学建模和优化在各个领域都有广泛的应用。
以下是数学建模和优化在几个领域的具体应用示例：1. 交通规划：通过数学建模和优化，可以确定最短路径、优化交通信号配时、减少拥堵等，提高城市交通效率。
2. 生产制造：通过数学建模和优化，可以优化工厂生产线布局、减少生产成本、提高生产效率，增加企业竞争力。
3. 资源分配：通过数学建模和优化，可以优化资源的分配，合理规划资源的使用，提高资源利用率和经济效益。
4. 环境保护：通过数学建模和优化，可以优化污染治理方案，减少环境污染，保护生态环境。
5. 金融投资：通过数学建模和优化，可以帮助投资者制定投资组合、分散风险、最大化收益。
通过数学建模和优化，我们可以更好地理解和解决实际问题，提高决策的科学性和准确性。
数学建模优化问题经典练习
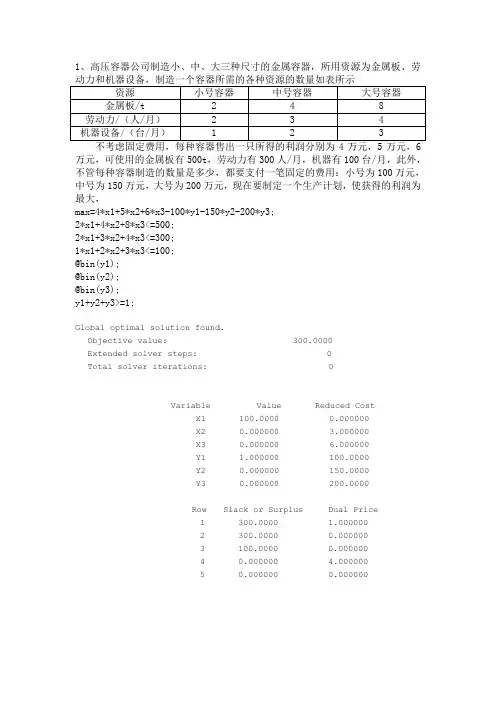
1、高压容器公司制造小、中、大三种尺寸的金属容器，所用资源为金属板、劳万元，可使用的金属板有500t，劳动力有300人/月，机器有100台/月，此外，不管每种容器制造的数量是多少，都要支付一笔固定的费用：小号为100万元，中号为150万元，大号为200万元，现在要制定一个生产计划，使获得的利润为最大，max=4*x1+5*x2+6*x3-100*y1-150*y2-200*y3;2*x1+4*x2+8*x3<=500;2*x1+3*x2+4*x3<=300;1*x1+2*x2+3*x3<=100;@bin(y1);@bin(y2);@bin(y3);y1+y2+y3>=1;Global optimal solution found.Objective value: 300.0000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced CostX1 100.0000 0.000000X2 0.000000 3.000000X3 0.000000 6.000000Y1 1.000000 100.0000Y2 0.000000 150.0000Y3 0.000000 200.0000Row Slack or Surplus Dual Price1 300.0000 1.0000002 300.0000 0.0000003 100.0000 0.0000004 0.000000 4.0000005 0.000000 0.0000002、安排4个人去做4项不同的工作,每个工人完成各项工作所消耗的时间（单位：（2）如果在（1）中在增加一项工作E，甲、乙、丙、丁四人完成工作E的时间分别为17,20,15,16分钟，那么应指派这四人干哪四项工作，使得这四人总的消耗时间为最少？min=20*x11+19*x12+20*x13+28*x14+18*x21+24*x22+27*x23+20*x24+26*x31+16 *x32+15*x33+18*x34+17*x41+20*x42+24*x43+19*x44;x11+x12+x13+x14=1;x21+x22+x23+x24=1;x31+x32+x33+x34=1;x41+x42+x43+x44=1;x11+x21+x31+x41=1;x12+x22+x32+x42=1;x13+x23+x33+x43=1;x14+x24+x34+x44=1;@bin(x11);@bin(x12);@bin(x13);@bin(x14);@bin(x21);@bin(x22);@bin(x23);@bin(x24);@bin(x31);@bin(x32);@bin(x33);@bin(x34);@bin(x41);@bin(x42);@bin(x43);@bin(x44);Global optimal solution found.Objective value: 71.00000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced CostX11 0.000000 20.00000X12 1.000000 19.00000X13 0.000000 20.00000X14 0.000000 28.00000X21 0.000000 18.00000X22 0.000000 24.00000X23 0.000000 27.00000X24 1.000000 20.00000X31 0.000000 26.00000X32 0.000000 16.00000X33 1.000000 15.00000X34 0.000000 18.00000X41 1.000000 17.00000X42 0.000000 20.00000X43 0.000000 24.00000X44 0.000000 19.00000Row Slack or Surplus Dual Price1 71.00000 -1.0000002 0.000000 0.0000003 0.000000 0.0000004 0.000000 0.0000005 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 0.000000 0.0000009 0.000000 0.000000min=20*x11+19*x12+20*x13+28*x14+17*x15+18*x21+24*x22+27*x23+20*x24+20 *x25+26*x31+16*x32+15*x33+18*x34+15*x35+17*x41+20*x42+24*x43+19*x44+1 6*x45;x11+x12+x13+x14+x15=1;x21+x22+x23+x24+x25=1;x31+x32+x33+x34+x35=1;x41+x42+x43+x44+x45=1;x11+x21+x31+x41<=1;x12+x22+x32+x42<=1;x13+x23+x33+x43<=1;x14+x24+x34+x44<=1;x15+x25+x35+x45<=1;@bin(x11);@bin(x12);@bin(x13);@bin(x14);@bin(x15);@bin(x21);@bin(x22);@bin(x23);@bin(x24);@bin(x25);@bin(x31);@bin(x32);@bin(x33);@bin(x34);@bin(x35);@bin(x41);@bin(x42);@bin(x43);@bin(x44);@bin(x45);Objective value: 68.00000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced Cost X11 0.000000 20.00000 X12 1.000000 19.00000 X13 0.000000 20.00000 X14 0.000000 28.00000 X15 0.000000 17.00000 X21 1.000000 18.00000 X22 0.000000 24.00000 X23 0.000000 27.00000 X24 0.000000 20.00000 X25 0.000000 20.00000X31 0.000000 26.00000X32 0.000000 16.00000X33 1.000000 15.00000X34 0.000000 18.00000X35 0.000000 15.00000X41 0.000000 17.00000X42 0.000000 20.00000X43 0.000000 24.00000X44 0.000000 19.00000X45 1.000000 16.00000Row Slack or Surplus Dual Price1 68.00000 -1.0000002 0.000000 0.0000003 0.000000 0.0000004 0.000000 0.0000005 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 0.000000 0.0000009 1.000000 0.00000010 0.000000 0.0000003、一个公司考虑到北京、上海、广州和武汉四个城市设立库房，这些库房负责向华北、华中、华南三个地区供货，每个库房每月可处理货物1000件。
数学建模与优化模型考核试卷
B.约束条件是非线性的
C.决策变量x和y之间是线性关系
D.决策变量x和y之间是非线性关系
5.以下哪个数学工具常用于求解优化问题？()
A. MATLAB
B. Excel
C. SPSS
D. Photoshop
6.在非线性规划模型中，若目标函数为“f(x, y) = x^2 + y^2”，则该模型属于以下哪种类型？()
标准答案
一、单项选择题
1. D
2. C
3. D
4. A
5. A
6. A
7. A
8. B
9. D
10. A
11. D
12. A
13. B
14. A
15. D
16. A
17. D
18. D
19. C
20. C
二、多选题
1. ABCD
2. ABCD
3. ABCD
4. ABC
5. ABC
6. ABC
7. AD
16.以下哪些情况下，非线性规划问题可能存在多个最优解？()
A.目标函数为凸函数
B.目标函数为凹函数
C.约束条件为凸集
D.约束条件为凹集
17.在数学建模中，以下哪些方法可以用于模型验证？()
A.残差分析
B.灵敏度分析
C.拟合优度检验
D.回归分析
18.以下哪些软件工具可以用于统计分析？()
A. MATLAB
A.模型建立
B.模型求解
C.模型分析
D.数据可视化
19.在数学建模过程中，以下哪个步骤是模型建立阶段的内容？()
A.提出问题
B.分析问题
C.求解模型
数学建模作业---优化模型
P104页，复习题题目：考虑以下“食谱问题"：某学校为学生提供营养套餐，希望以最小的费用来满足学生对基本营养的需求按照营养学家的建设，一个人一天要对蛋白质，维生素A和钙的需求如下：50g蛋白质、4000IU维生素A和1000mg的钙，我们只考虑以不食物构成的食谱：苹果，香蕉，胡萝卜，枣汁和鸡蛋，其营养含量见下表。
制定食谱，确定每种食物的用量，以最小费用满足营养学家建议的营养需求，并考虑：（1）对维生素A的需求增加一个单位时是否需要改变食谱？成本增加多少？如果对蛋白质的需求增加1g呢？如果对钙的需求增加1mg呢？（2）胡萝卜的价格增加Ⅰ角时，是否需要改变食谱？成本增加多少？问题分析：（1）此优化问题的目标是使花费最小.（2）所做的决策是选择各种食物的用量，即用多少苹果，香蕉，胡萝卜，枣汁，鸡蛋来制定食谱。
（3）决策所受限制条件：最少应摄入的蛋白质、维生素和钙的含量（4）设置决策变量：用x1表示苹果的个数、x2表示香蕉的个数、x3表示胡萝卜的个数、x4表示枣汁的杯数量、x5表示鸡蛋的个数（5）x1个苹果花费10·x1角x2个香蕉花费15·x2角x3个胡萝卜花费5·x3角x4杯枣汁花费60·x4角x5个鸡蛋花费8·x5角目标函数为总花费金额：z=10·x1+15·x2+5·x3+60·x4+8·x5 (角)（6）约束条件为：最少摄入蛋白质的含量：0.3x1+1.2x2+0.7x3+3.5x4+5.5x5≥50最少摄入维生素A的含量：73x1+96x2+20253x3+890x4+279x5≥4000最少摄入钙的含量：10x1+15x2+5x3+60x4+8x5≥1000非负约束：x 1,x 2,x 3,x 4,x 5≥0优化模型：minz =10x 1+15x 2+5x 3+60x 4+8x 5s.t. 0.3x 1+1.2x 2+0.7x 3+3.5x 4+5.5x 5≥5073x 1+96x 2+20253x 3+890x 4+279x 5≥4000 9.6x 1+7x 2+19x 3+57x 4+22x 5≥1000 x 1,x 2,x 3,x 4,x 5≥0由线性规划模型的定义，容易得到线性规划的性质：1. 比例性 每个决策变量的对目标函数的“贡献”与该决策变量的取值成正比；每个决策变量对每个约束条件右端项的“贡献”，与该决策变量的取值成正比.2. 可加性 各个决策变量对目标函数的“贡献”，与其他决策变量的取值无关；各个决策变量对每个约束条件右端项的“贡献”，与其他决策变量的取值无关.3. 连续性 每个决策变量的取值是连续的. 考察本题，实际上隐含下面的假设 ：1.购买苹果、香蕉、胡萝卜、枣汁、鸡蛋每个（杯）的花费是与各自的用量无关的常数；苹果、香蕉、胡萝卜、枣汁、鸡蛋每个（杯）所包含的蛋白质、维生素、钙的含量是与各自的用量无关的常数.（线性规划性质1—比例性）2.购买苹果、香蕉、胡萝卜、枣汁、鸡蛋每个（杯）的花费是与它们相互间用量无关的常数；苹果、香蕉、胡萝卜、枣汁、鸡蛋每个（杯）所包含的蛋白质、维生素A 、钙的含量是与它们相互间的用量无关的常数. （线性规划性质2—可加性）3. 购买苹果、香蕉、胡萝卜、枣汁、鸡蛋的数量都是实数. (线性规划性质3—连续性) 模型求解：（决策变量是5维的，不适用图解法求解模型）软件求解：线性规划模型：min z=10x1+15x2+5x3+60x4+8x5s.t. 0.3x1+1.2x2+0.7x3+3.5x4+5.5x5≥5073x1+96x2+20253x3+890x4+279x5≥40009.6x1+7x2+19x3+57x4+22x5≥1000x1,x2,x3,x4,x5≥0模型全局最优解：(Global optimal solution)x1=0x2=0x3=49.38272x4=0x5=2.805836z的最优值为269.3603角用LINGO 软件求解，得到如下输出：结果分析：1. 3个约束条件的右端项可视为3种资源：蛋白质含量、维生素A 含量、钙含量.LINGO 的输出项Row Slack or Surplus ，给出了3种资源在最优解下的剩余.2.目标函数可视为“支出（成本）”，紧约束的“资源”增加1单位时，“支出”的增加由LINGO 的输出项 Dual Price 给出。
数学建模中的优化问题求解
数学建模中的优化问题求解在数学建模中，优化问题求解是一个重要的研究领域。
优化问题指的是在给定的约束条件下，寻找使目标函数取得最优值的变量取值。
这一领域涉及到数学、计算机科学、运筹学等多个学科，并在实际应用中起到重要的作用。
首先，我们先来了解什么是数学建模。
数学建模是通过运用数学方法和技巧来解决实际问题的过程。
它的目标是将实际问题转化为数学模型，并通过模型进行分析和求解。
在数学建模中，优化问题是常见的一类问题。
优化问题求解的核心是寻找目标函数的最小值或最大值。
在实际应用中，我们需要考虑不同的约束条件，例如资源限制、时间限制等。
这些约束条件会影响到最优解的取值范围和可能性。
为了解决优化问题，数学建模中常用的方法包括线性规划、非线性规划、整数规划等。
线性规划是在给定的线性约束条件下求解线性目标函数的最优解。
非线性规划则是在一般的约束条件下求解非线性目标函数的最优解。
整数规划是对变量取离散值的情况下的优化问题求解。
在实际应用中，优化问题求解可以应用于各个领域。
例如，在交通规划中，我们可以利用优化方法对交通网络进行优化，提高交通效率。
在生产调度中，我们可以通过优化问题求解来优化生产资源的分配，降低成本。
在金融领域，我们可以利用优化问题求解对投资组合进行优化，降低风险。
除了传统的优化方法，近年来还涌现出了一些基于人工智能的优化算法。
例如，遗传算法、粒子群算法等。
这些算法模拟了自然界中的进化、群体行为等现象，可以在复杂的优化问题中寻找较好的解。
总之，优化问题求解在数学建模中起到了重要的作用。
通过寻找变量取值的最优解，我们可以在实际问题中达到最佳的效果。
不仅仅在理论研究中，优化问题求解也在各个领域得到了广泛的应用。
随着科技的发展，我们相信优化问题求解的方法和技术将会不断地完善和发展，为实际问题的解决提供更加有效的手段。
如何应用数学建模优化问题
如何应用数学建模优化问题数学建模是一种将实际问题转化为数学模型，并通过数学方法来解决问题的过程。
在许多领域中，数学建模都被广泛应用于优化问题的求解。
本文将探讨如何应用数学建模来优化问题，并介绍一些常见的数学优化方法。
一、问题建模在进行数学优化之前，我们首先需要将实际问题转化为数学模型。
这个过程包括以下几个步骤：1. 确定优化目标：明确你想要优化的目标是什么。
比如，你可能要最小化成本、最大化利润，或者使某个指标达到最佳状态等。
2. 确定决策变量：决策变量是影响优化结果的变量。
根据实际问题，选择适当的决策变量。
例如，如果你想要优化某个产品的生产计划，决策变量可以是生产数量、生产时间等。
3. 建立约束条件：约束条件是限制决策变量取值的条件。
根据实际问题，确定约束条件并将其转化为数学形式。
例如，如果你想要优化配送路线，可能会有时间限制、容量限制等。
二、数学优化方法在问题建模完成后，我们可以使用不同的数学优化方法来求解优化问题。
下面介绍几种常见的优化方法：1. 线性规划：线性规划是在给定线性约束条件下求解线性目标函数的优化问题。
使用线性规划可以解决许多实际问题，例如资源分配、生产计划等。
2. 整数规划：整数规划是线性规划的一种扩展形式，其决策变量需要取整数值。
整数规划适用于那些要求决策变量为整数的问题，如生产装配线优化、旅行商问题等。
3. 非线性规划：非线性规划是在给定非线性约束条件下求解非线性目标函数的优化问题。
非线性规划广泛应用于诸如工程优化、金融投资等领域。
4. 动态规划：动态规划是解决具有重叠子问题特性的优化问题的一种方法。
通过将问题划分为一系列子问题，并将子问题的解缓存起来，可以有效地解决很多动态规划问题。
5. 遗传算法：遗传算法是一种模拟自然选择和遗传机制的优化算法。
通过不断地进化和选择，遗传算法可以搜索到优化问题的全局最优解。
三、应用案例下面通过一个应用案例来说明如何应用数学建模优化问题。
假设你是一家互联网电商平台的运营经理，你想要优化产品的价格策略以最大化销售额。
研究生数学建模优化问题
研究生数学建模优化问题
研究生数学建模优化问题可以涉及各种不同的学科和领域。
以下是一些常见的研究生数学建模优化问题的例子：
1. 生产优化问题：如何最大化生产效率，同时最小化生产成本和资源使用。
这包括生产线排程问题、物流和供应链管理等。
2. 资源分配问题：如何最优地分配有限的资源，以满足不同需求。
例如，如何在一所学校中分配教师、教室和学生资源，以实现最佳的学习效果。
3. 运输路径问题：如何找到最短路径或最优路径来满足特定的要求。
这包括最短路径问题、旅行商问题等。
4. 网络优化问题：如何设计最优的网络结构，以实现最大的性能和容量。
例如，如何在一个电信网络中设计最佳的数据传输路由。
5. 风险管理问题：如何评估和管理风险，以保护资产和最小化损失。
这包括投资组合优化、保险精算等问题。
6. 环境优化问题：如何最小化对环境的影响，同时最大化资源保护和可持续发展。
例如，如何设计最优的城市公共交通系统，以减少交通拥堵和空气污染。
以上只是一些研究生数学建模优化问题的例子，实际上，优化问题几乎可以应用于任何领域。
研究生在解决这些问题时，通常需要使用数学模型和优化算法，以寻找最优的解决方案。
数学建模中的优化和反问题求解
数学建模中的优化和反问题求解数学建模是运用数学语言和符号，抽象地描述现实世界中的现象和问题，并通过建立数学模型来分析和解决问题的过程。
在数学建模中，优化问题和反问题求解是两个重要的研究方向。
本文将详细介绍数学建模中的优化和反问题求解。
一、优化问题优化问题是指在一定的约束条件下，找到一个使得目标函数达到最优值（最大值或最小值）的变量取值。
优化问题广泛应用于经济、工程、物理、生物等多个领域。
根据目标函数和约束条件的特点，优化问题可以分为线性优化、非线性优化和整数优化等。
1.线性优化线性优化是指目标函数和约束条件都是线性的优化问题。
线性优化的求解方法有单纯形法、内点法等。
在数学建模中，线性优化可以用于生产计划、物流配送、资源分配等问题。
2.非线性优化非线性优化是指目标函数或约束条件至少有一个是非线性的优化问题。
非线性优化问题的求解方法有梯度法、牛顿法、拟牛顿法、共轭梯度法等。
在数学建模中，非线性优化可以用于参数估计、优化控制、最大熵问题等。
3.整数优化整数优化是指优化问题中的变量取值为整数的优化问题。
整数优化问题的求解方法有割平面法、分支定界法、动态规划法等。
在数学建模中，整数优化可以用于航班调度、设备选址、网络设计等问题。
二、反问题求解反问题是指根据已知的输出数据，推断出输入参数的问题。
反问题求解通常涉及到数值分析和计算数学的方法。
在数学建模中，反问题求解可以用于参数估计、模型识别、图像重建等。
1.参数估计参数估计是指根据已知的观测数据，通过建立数学模型来估计未知参数的方法。
参数估计的方法有最大似然估计、最小二乘估计、贝叶斯估计等。
在数学建模中，参数估计可以用于估计线性回归模型、非线性回归模型、时间序列模型等。
2.模型识别模型识别是指根据已知的输入和输出数据，识别出数学模型的结构和参数。
模型识别的方法有基于统计的方法、基于机器学习的方法、基于优化方法等。
在数学建模中，模型识别可以用于识别神经网络、支持向量机、隐马尔可夫模型等。
数学建模中的优化与控制问题
特点：线性系统 控制具有简单、 易于分析和设计 的优点，适用于 一些较为简单的
系统。
应用场景：在工程、 经济、生物等领域 中，对于一些可以 近似为线性系统的 对象，可以采用线 性系统控制方法进
行优化和控制。
局限性：线性系统 控制对于非线性系 统的描述和控制效 果有限，对于一些 复杂的系统可能需 要采用更为复杂的
特点：整数规划 问题在求解过程 中具有较高的难 度，因为整数约 束使得可行解的 范围大大缩小。
应用领域：整 数规划广泛应 用于组合优化、 生产计划、物 流运输等领域。
求解方法：常 见的整数规划 求解方法包括 穷举法、割平 面法、分支定
界法等。
数学建模中的控制 问题
定义：线性系统控 制是数学建模中的 一种重要方法，通 过建立线性方程组 来描述系统的动态 行为，并采用控制 策略对系统进行调
应用领域：生产计划、物流、金融等
求解方法：单纯形法、分解法等
定义：在数学建模中，非线性规划是寻 找一组变量的最优解，使得某个目标函 数达到最小或最大值，同时满足一系列 约束条件。
应用领域：包括但不限于金融、经济、工 程和科学计算等领域。
特点：目标函数或约束条件至少有一个是 非线性的。
求解方法：常见的求解非线性规划的方法 包括梯度下降法、牛顿法、拟牛顿法等。
案例背景：交通信号灯在城市交通中起着至关重要的作用，如何实现高效、合理的控制 是关键问题。
建模过程：通过建立数学模型，对交通信号灯的配时进行优化，提高道路通行效率。
控制策略：采用智能控制算法，如模糊控制、神经网络等，实现自适应调节。
案例结论：通过实际应用，证明优化后的交通信号灯控制能够有效提高道路通行效率， 减少拥堵。
数学建模中的优化与 控制问题
单目标优化数学建模
单目标优化数学建模
单目标优化问题（Single-Objective Optimization Problem）是指所评测的目标只有一个，只需要根据具体的满足函数条件，求得最值。
在数学建模中，单目标优化问题通常使用一些特定的算法来寻找最优解。
以下是一些常见的单目标优化问题的数学建模方法：
1. 梯度下降法：梯度下降法是一种迭代方法，通过不断地沿着函数梯度的负方向移动，逐渐逼近函数的极小值点。
在数学建模中，我们可以利用梯度下降法来求解一些单目标优化问题，例如最小二乘回归问题、最大似然估计问题等。
2. 牛顿法：牛顿法是一种基于牛顿定理的优化算法，通过不断地沿着函数的负梯度方向移动，逐渐逼近函数的极小值点。
在数学建模中，我们可以利用牛顿法来求解一些单目标优化问题，例如求解非线性方程的根等。
3. 共轭梯度法：共轭梯度法是一种结合了梯度下降法和牛顿法的迭代算法，通过不断地沿着当前点的共轭方向移动，逐渐逼近函数的极小值点。
在数学建模中，我们可以利用共轭梯度法来求解一些单目标优化问题，例如大规模的机器学习问题等。
4. 模拟退火算法：模拟退火算法是一种随机搜索算法，通过模拟物理中的退火过程，在解空间中随机搜索最优解。
在数学建模中，我们可以利用模拟退火算法来求解一些单目标优化问题，例如旅行商问题、组合优化问题等。
以上是一些常见的单目标优化问题的数学建模方法，具体使用哪种方法需要根据问题的性质和要求来选择。
《数学建模-优化》课件
数学建模广泛应用于自然科学、工程技术、社会科学等多个领域，帮助解决各种实际问题， 优化决策和提高效率。
数学建模的意义
数学建模能够培养学生的综合思考和问题解决能力，提高数学知识的实际运用能力。
优化问题概述
1 什么是优化问题？
优化问题是在满足特定 约束条件下，寻找使目 标函数达到最优或最大 值的解。
4
数值优化问题可以采用模拟退火、爬 山算法和遗传算法等方法来寻找最优
解。
单目标优化问题
单目标优化问题包括最小二乘法、线 性规划、非线性规划和动态规划等方 法。
非线性规划问题
非线性规划问题可以使用一阶可导方 法、二阶可导方法和非平滑优化方法 进行求解。
优化工具使用
MATLAB
MATLAB是一种功能强大的数值计算和数据可 视化软件，经常用于数学建模和优化问题的求 解。
数学建模和优化在社会管理领 域起到重要作用，可以帮助解 决各种社会问题和提高社会管 理效率。
Python
Python是一种流行的编程语言，拥有丰富的数 值计算、优化和数据分析库，适用于数学建模 和优化问题的处理。
应用案例
工业应用
数学建模和优化在工业生产中 有广泛的应用，可以帮助优化 生产流程、减少资源消耗和提 高产品质量。
经济决策
社会管理
数学建模和优化被广泛应用于 经济领域，帮助制定经济决策、 优化资源配置和提高经济效益。
《数学建模－优化》PPT 课件
数学建模-优化课程介绍了数学建模的概念、优化问题的概述以及各种优化方 法的分类和应用。通过本课程，您将深入了解数学建模和优化的重要性。
数学建模简介
数学建模的定义
数学建模是利用数学方法解决实际问题的过程。它将现实问题抽象为数学模型，并通过数 学求解方法得到问题的解决方案。
数学建模优化类问题例子
数学建模优化类问题例子
1.最佳生产计划：有一家汽车零部件制造公司，需要决定该如何安排生产计划以最大化利润。
该公司需要考虑每个零部件的生产成本、供应链的延迟和运输成本等因素，以确定最佳的生产数量和交付时间。
2.最优投资组合：一位投资者有一定资金，希望通过合理的资产配置来最大化投资回报。
该投资者需要考虑不同资产类别的风险和回报率，并使用数学建模优化方法来确定最佳的资产配置比例。
3.旅行销售员问题：一位旅行销售员需要在多个城市之间进行访问，并希望以最小的总行驶距离完成所有访问任务。
通过使用数学建模和优化算法，销售员可以确定最佳的访问顺序，从而减少总行驶距离和时间。
4.最佳路径规划：在一个迷宫中，有一只小老鼠需要找到从起点到终点的最短路径。
通过将迷宫与数学模型相关联，可以使用图论和最短路径算法来确定小老鼠应该采取的最佳行动策略。
以上只是一些例子中的几个，实际上数学建模和优化方法可以应用于各种不同的问题领域，包括金融、物流、能源管理、医疗决策等。
通过数学建模和优化，可以帮助人们做出更明智的决策，提高效率和效果。
数学建模与优化最优化问题的求解
数学建模与优化最优化问题的求解在现代科学与工程领域中，数学模型广泛用于解决各种实际问题。
而为了更好地应对实际问题的复杂性和多样性，我们常常需要对数学模型进行最优化问题的求解。
最优化问题是指在一定限制条件下，寻求使得目标函数取得最小（或最大）值的一组变量取值。
本文将介绍数学建模中最优化问题的求解方法。
一、最优化问题的分类最优化问题可分为无约束最优化问题和约束最优化问题两类。
无约束最优化问题是指不受任何约束条件限制的情况下，寻求目标函数的最优解。
而约束最优化问题则需要在一定的约束条件下，求解满足条件的最优解。
二、最优化问题的数学描述无论是无约束最优化问题还是约束最优化问题，我们都可以通过数学模型来描述。
通常情况下，最优化问题可以表示为以下形式：\[ \begin{align*}\text{minimize } &f(x)\\\text{subject to } &g_i(x) \leq 0, \text{ for } i=1,2,\ldots,m\\&h_j(x) = 0, \text{ for } j=1,2,\ldots,p\end{align*} \]其中，\(x=(x_1,x_2,\ldots,x_n)\)为自变量向量，\(f(x)\)为目标函数，\(g_i(x)\)为不等式约束条件，\(h_j(x)\)为等式约束条件。
三、最优化问题的解法1. 无约束最优化问题的求解无约束最优化问题的求解方法有很多种，常见的有梯度下降法、共轭梯度法、牛顿法和拟牛顿法等。
这些方法的基本思想是通过不断迭代，更新自变量的取值，逐渐接近最优解。
2. 约束最优化问题的求解约束最优化问题的求解相对复杂，需要考虑目标函数和约束条件的特点。
一般来说，可以采用等式约束鲁棒法、罚函数法、拉格朗日乘子法、KKT条件等方法来求解。
这些方法的核心思想是将约束条件引入目标函数，将约束最优化问题转化为无约束最优化问题，再应用无约束最优化问题的求解方法。
最优化问题的数学建模步骤
最优化问题的数学建模步骤
最优化问题的数学建模步骤可以分为以下几个步骤：
1. 指定目标函数：首先需要明确最优化问题的目标函数，即要优化的量。
这个函数通常是与实际问题相关的一些指标，例如成本、收益、效率等等。
2. 确定决策变量：在确定目标函数后，需要确定决策变量，即可以控制或调整的参数或变量。
这些变量的取值可以影响目标函数的值，因此需要选择最优的取值。
3. 建立约束条件：除了目标函数和决策变量外，还需要考虑一些约束条件。
这些约束条件通常是实际问题的限制条件，例如资源限制、技术限制、法规限制等等。
4. 建立数学模型：将目标函数、决策变量和约束条件用数学语言表达出来，建立数学模型。
这个模型通常是一个优化问题的数学表示形式，可以使用线性规划、非线性规划、整数规划等方法进行求解。
5. 求解最优解：根据建立的数学模型，使用相应的优化方法求解最优解。
这个最优解是指在满足约束条件的前提下，使目标函数取得最大值或最小值的决策变量取值。
6. 验证和分析：最后需要对求解结果进行验证和分析，看看是否符合实际需求，是否满足实际约束条件等等。
如果结果不满足要求，需要重新调整模型或重新选择优化方法进行求解。
以上是最优化问题的数学建模步骤，通过这些步骤可以将实际问题转化为数学问题，并使用数学方法进行求解，得到最优的决策方案。
数学建模中的优化问题与约束条件的求解
数学建模中的优化问题与约束条件的求解数学建模是一门研究如何将实际问题抽象为数学模型，并利用数学方法解决这些问题的学科。
在数学建模中，优化问题是一类常见且重要的问题。
优化问题的目标是在给定的约束条件下，找到使某个指标达到最优的解。
而约束条件则是对解的限制，限制了解的取值范围。
在数学建模中，优化问题的求解可以通过多种方法来实现。
其中，最常用的方法之一是数学规划。
数学规划是一种通过建立数学模型来描述优化问题，并利用数学方法求解的技术。
常见的数学规划方法包括线性规划、非线性规划、整数规划等。
线性规划是一种常见且简单的数学规划方法。
线性规划的目标函数和约束条件都是线性的，因此可以通过线性代数的方法进行求解。
线性规划的求解过程可以通过图形法、单纯形法等方法来实现。
图形法通过绘制目标函数和约束条件的图形来找到最优解。
而单纯形法则是一种通过迭代计算来逐步逼近最优解的方法。
非线性规划是一种更为复杂的数学规划方法。
非线性规划的目标函数和约束条件可以是非线性的，因此求解过程需要使用更为复杂的数学方法。
常见的非线性规划方法包括梯度下降法、牛顿法、拟牛顿法等。
这些方法通过计算目标函数的梯度或者黑塞矩阵来实现迭代求解。
除了数学规划方法外，还有一些其他的优化方法可以用于求解优化问题。
其中，遗传算法是一种常见的启发式优化方法。
遗传算法通过模拟生物进化的过程，利用选择、交叉和变异等操作来搜索最优解。
遗传算法适用于一些复杂的优化问题，尤其是那些没有明确的数学模型的问题。
在数学建模中，约束条件的求解也是一个重要的问题。
约束条件可以分为等式约束和不等式约束两种。
等式约束是指解必须满足的等式条件，而不等式约束则是指解必须满足的不等式条件。
约束条件的求解可以通过拉格朗日乘子法来实现。
拉格朗日乘子法通过引入拉格朗日乘子，将约束条件转化为目标函数的一部分，从而将含约束的优化问题转化为无约束的优化问题。
除了拉格朗日乘子法外，还有一些其他的约束条件求解方法。
数学建模中的优化问题
奥运会临时超市网点设计
23
奥运会临时超市网点设计
（找关键性语句）
2008 年北京奥运会的建设工作已经进入全面设计 和实施阶段。奥运会期间，在比赛主场馆的周边 地区需要建设由小型商亭构建的临时商业网点， 称为迷你超市（ Mini Supermarket, 以下记做 MS ） 网，以满足观众、游客、工作人员等在奥运会期 间的购物需求，主要经营食品、奥运纪念品、旅 游用品、文体用品和小日用品等。在比赛主场馆 周边地区设置的这种 MS ，在地点、大小类型和总 量方面有三个基本要求：满足奥运会期间的购物 需求、分布基本均衡和商业上赢利。
22
奥运会临时超市网点设计
（找关键性语句）
2008 年北京奥运会的建设工作已经进入全面设计 和实施阶段。奥运会期间，在比赛主场馆的周边 地区需要建设由小型商亭构建的临时商业网点， 称为迷你超市（ Mini Supermarket, 以下记做 MS ） 网，以满足观众、游客、工作人员等在奥运会期 间的购物需求，主要经营食品、奥运纪念品、旅 游用品、文体用品和小日用品等。在比赛主场馆 周边地区设置的这种 MS ，在地点、大小类型和总 量方面有三个基本要求：满足奥运会期间的购物 需求、分布基本均衡和商业上赢利。
20
奥运会临时超市网点设计
（找关键性语句）
2008 年北京奥运会的建设工作已经进入全面设计 和实施阶段。奥运会期间，在比赛主场馆的周边 地区需要建设由小型商亭构建的临时商业网点， 称为迷你超市（ Mini Supermarket, 以下记做 MS ） 网，以满足观众、游客、工作人员等在奥运会期 间的购物需求，主要经营食品、奥运纪念品、旅 游用品、文体用品和小日用品等。在比赛主场馆 周边地区设置的这种 MS ，在地点、大小类型和总 量方面有三个基本要求：满足奥运会期间的购物 需求、分布基本均衡和商业上赢利。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一般优化问题概述
离散优化discrete optimization 或组合优化combinatorial optimization
整数规划(IP) 决策变量(全部或部分)为整数 Integer programming
s.t.AX<=b
x=fminbnd(‘F’,x1,x2) X=fminunc(‘F’,X0)
X=fminsearch(‘F’,X0)
X=linprog(c,A,b)
二次规划
Min 1 xTHx+cTx
2
s.t. Ax<=b
X=quadprog(H,c,A,b)
约束极小 （非线性规划）
Min F(X) s.t. G(X)<=0
✓ 整数线性规划(ILP)，整数非线性规划(INLP) ✓ 纯整数规划(PIP), 混合整数规划(MIP) Pure (mixed) Integer programming 一般整数规划，0-1（整数）规划 Zero-one programming
无约束最优化问题
求解无约束最优化问题的的基本思想 *无约束最优化问题的基本算法
慢，最速下降法适用于寻优过程的前期迭代或作为间插步骤，当接近极值
点时，宜选用别种收敛快的算法.
2．牛顿法算法步骤：
(1) 选定初始点 X 0 E n ，给定允许误差 0 ，令 k=0；
(2) 求f X k , 2 f X k 1 ,检验：若 f X k ,则
停止迭代, X * X k .否则, 转向(3)；
A矩阵和b向量分别为线性不等式约束：
AX b 中的系数矩阵和右端向量
Aeq矩阵和beq向量分别为线性等式约束：
Aeq X beq 中的系数矩阵和右端向量
X的下限和上限向量：vlb≤X≤vub
迭代初始点坐标 函数最小化的区间 优化选项参数结构，定义用于优化函数的参数
调用函数
linprog,quadprog
⑷ 令 S k f X k ，从X k 出发，沿S k 进行一维搜索，
即求k 使得：
min f
0
X k S k
f
X k k S k
；
⑸ 令 X k 1 X k k S k ，k=k+1 返回⑵.
最速下降法是一种最基本的算法，它在最优化方法中占有重要地位.最
速下降法的优点是工作量小，存储变量较少,初始点要求不高；缺点是收敛
X=fmincon(‘FG’,X0)
达到目标问题
Min r s.t. F(x)-wr<=goal
X=fgoalattain(‘F’,x,goal,w)
极小极大问题
Min max {Fi(x)}
X {Fi(x)}
s.t. G(x)<=0
X=fminimax(‘FG’,x0)
2. 优化函数的输入变量
使用优化函数或优化工具箱中其它优化函数时, 输入变量见下表:
0.9997 0.9998 1E-8
最优点 (1 1) 初始点 (-1 1)
返回
无约束优化问题的基本算法
1．最速下降法（共轭梯度法）算法步骤：
⑴ 给定初始点 X 0 E n ，允许误差 0 ,令 k=0；
⑵ 计算f X k ；
⑶ 检验是否满足收敛性的判别准则：
f X k ，
若满足，则停止迭代，得点X * X k ，否则进行⑷；
牛顿法的收敛速度虽然较快，但要求Hessian矩阵要可逆， 要计算二阶导数和逆矩阵，就加大了计算机计算量和存储量.
Matlab优化工具箱简介
1.MATLAB求解优化问题的主要函数
类型
模
型
基本函数名
一元函数极小 无约束极小 线性规划
Min F（x）s.t.x1<x<x2
Min F(X)
Min cT X
返回
求解无约束最优化问题的基本思想
标准形式：
其中
min f X
X E n
f : En E1
max f X = min [ f X ]
X E n
X E n
求解的基本思想 ( 以二元函数为例 )
f (x1 x2 )
连 续 可 微
0
x1
x2
f (X0) f (X1) f (X2)
X0
31
X1
X2
变量 f
fun
H A,b
Aeq,beq
vlb,பைடு நூலகம்ub X0
x1,x2 options
描述 线性规划的目标函数f*X 或二次规划的目标函
数X’*H*X+f*X 中线性项的系数向量
非线性优化的目标函数.fun必须为行命令对象 或M文件、嵌入函数、或MEX文件的名称
二次规划的目标函数X’*H*X+f*X 中二次项的系 数矩阵
(3) 令 S k [ 2 f X k ]1f X k （牛顿方向）；
(4) X k1 X k S k , k k 1 ,转回(2).
如果f是对称正定矩阵A的二次函数，则用牛顿法经过一次迭代 就可达到最优点,如不是二次函数，则牛顿法不能一步达到极值点， 但由于这种函数在极值点附近和二次函数很近似,因此牛顿法的收 敛速度还是很快的.
一般优化问题概述
约束优化constrained optimization的简单分类
数学规划mathematical programming 或连续优化continuous optmization • 线性规划(LP) 目标和约束均为线性函数
Linear programming • 非线性规划(NLP) 目标或约束中存在非线性函数
x2
5
0
x1
唯一极小 (全局极小)
f 0.298
f 0
f (x1 x2 ) 2x12 2x1x2 x22 3x1 x2
多局部极小
f 0.298
搜索过程 min f (x1 x2 ) 100 (x2 x12 )2 (1 x1)2
x1 x2 f
-1 1 4.00 -0.79 0.58 3.39 -0.53 0.23 2.60 -0.18 0.00 1.50 0.09 -0.03 0.98 0.37 0.11 0.47 0.59 0.33 0.20 0.80 0.63 0.05 0.95 0.90 0.003 0.99 0.99 1E-4 0.999 0.998 1E-5
fminbnd,fminsearch,fminunc, fmincon,lsqcurvefit,lsqnonlin,