无应力状态控制法-III
无应力索长控制法在斜拉桥调索中的应用

无应力索长控制法在斜拉桥调索中的应用周国玲;丁少凌;顾双春【摘要】@@%针对斜拉桥施工过程中出现结构体系不明确(如索张拉时结构中存在支架等)和索力控制偏差及结构计算本身就设置了调索阶段3种在运营之前需要调索的情况,介绍了以无应力长度为基础通过控制调索时张拉端拔出量来调整索力的方法,并对该方法的理论基础、实际操作要求及特点进行了说明.【期刊名称】《公路与汽运》【年(卷),期】2012(000)004【总页数】3页(P198-200)【关键词】桥梁;斜拉桥;调索;无应力索长;张拉端拔出量【作者】周国玲;丁少凌;顾双春【作者单位】中交第二公路勘察设计研究院有限公司,湖北武汉430056;中交第二公路勘察设计研究院有限公司,湖北武汉430056;湖北省交通规划设计院,湖北武汉430051【正文语种】中文【中图分类】U448.271 调索理论基础结构构件单元的内力和节点位移随着结构的加载、体系转换和斜拉索的张拉而变化,而单元的无应力长度和无应力曲率不会发生改变。
斜拉索单元的无应力长度只有在调整自身索力(文中所提索力均为该阶段发生后斜拉索索力,并非模型计算中桁架单元的初张力。
因计算中仅涉及斜拉索索力增量,故统一选塔端索力或梁端索力均可)时才会发生变化,存在一一对应的关系。
假设有如图1所示结构,结构体系温度t1℃,状态A各索力AFi为当前索力状态,状态B各索力BFi为目标索力状态。
结构在A、B状态下各斜拉索索力、索截面面积、索单位重均为已知参数,若能确定A、B状态下各斜拉索锚点坐标即可通过悬链线方程求出A、B状态下各斜拉索的无应力长度(t1℃),两种状态下的无应力索长(t1℃)之差即为调索时张拉端拔出量。
状态A、状态B为施工过程中的两种状态,受施工误差、结构变形影响,实际坐标确切的数值很难确定。
斜拉桥结构刚度比较大,以上原因引起的坐标变化属于小位移问题,所以认为状态A坐标即为设计坐标;状态B坐标按如下方法确定:模型计算状态A→状态B过程中各斜拉索锚点变化位移图1 斜拉索无应力索长调索法示意图2 实际计算模型中的操作2.1 张拉端拔出量计算斜拉桥总体结构计算通常采用空间杆元程序,梁、塔采用梁单元,斜拉索采用桁架单元。
2012无应力状态法在东江大桥监控中的应用_张合清

公路 2012年5月 第5期HIGHWAY May.2012 No.5 文章编号:0451-0712(2012)05-0140-03 中图分类号:U446.2 文献标识码:B无应力状态法在东江大桥监控中的应用张合清,罗嗣碧(中国公路工程咨询集团有限公司 北京市 100097)摘 要:对东桥大桥主桥钢桁梁架设施工监控进行研究,在仿真计算过程中采用无应力状态法进行分析计算,对监测结果进行分析,优化了钢桁梁合龙时机和方法。
此方法在实际工程中的应用,简化了监控繁琐的计算、提高了工作效率和监控精度,保证本项目钢桁梁的顺利合龙。
关键词:三桁结构;加劲;施工监控;无应力状态法1 工程概况东江大桥主桥采用上加劲弦的三跨连续钢桁梁,结构新颖、技术先进、功能合理、造型美观,填补了我国双层公路桥梁建设的空白。
东江大桥主桥桥跨布置为112m+208m+112m,主桁立面采用有竖杆的华伦式桁架,上加劲弦采用二次抛物线,上弦与上加劲弦之间采用吊杆连接。
主桁横向采用三桁结构,桁高10m,桁间距2×18m,中间支点处上加劲弦中心到上弦中心高度28m,上加劲弦(刚性悬索)与上弦在跨中合成上弦; 节间长度8m。
主桁三片桁之间仅在中间支点上加劲弦与上弦间的大竖杆处设有横向连接系,其他位置将竖杆与横梁联结为框架。
桥梁效果图如图1所示,全桥结构图如图2所示。
图1 桥梁效果单位:m图2 全桥结构示意2 无应力状态法原理[1,2]无应力状态法[3]分析的基本思路:采用完全线性理论对桥梁结构进行解体,只要保证单元无应力长度和曲率不变,无论按照何种程序恢复还原后的结构内力和线形将与原结构一致。
应用这一原理,建立施工阶段和成桥状态的联系[4]。
钢桁梁的制造是按照钢桁梁无应力长度来设计生产的,要使钢桁梁架设后的受力状态和结构线形满足设计要求,施工架设过程必须满足如下要求:收稿日期:2012-03-12(1)膺架上和利用全回转吊机安装的钢梁杆件必须实现无应力安装;(2)钢桁梁合龙时,合龙口杆件必须采用技术措施实现合龙杆件无应力安装;(3)钢桁梁合龙后,支座必须调整到设计高程。
浅谈分阶段施工桥梁的无应力状态控制法

P
P‘
P。
种 方式 进行 应 用 的时候 应 当 对其 有一 个较 好 的 掌控 , 从 而 能够将 这种 经验 实现 到桥 梁 的实 际建 设 中去 。 同时 , 在桥
梁 施 工 的过 程 中 , 还 应 当对桥 梁 上 设 置相 应 的温 度 、 索力 测 量点 。 而在 监控 的特 殊 时段 中 , 则 应 当选 择 气 温较 为稳 定 的时 间 对桥 梁 的 温度 、 索力 等 因素 进行 测 试 , 而 当桥 梁 图 1 分 阶段 施 工 的 斜 拉 桥 我们 将 分阶 段施 工 桥 梁 最 终 的 状 态节 点 位 移 分 别 为 中存在 临 时荷 载 则应 当也 对其位 置 以及 大小 进行 记录 。由 u i 、 V . 以及 e. , 其中 , i 的值 为 1 , 2 , 3, …, n 。 那 么其 最 终 状 于 在 测 试 的过 程 中 , 桥 梁 索力 、 应力 等都 具 有 与其 对 应 的 态结 构 的总势 能 即为每 一个 单元 变形 势 能之和 。 临时荷 载 以及 温度 , 所 以在 计 算 的过程 中很容 易将 其 实 测 而在 桥 梁建 设 的过程 中 , 一定 要 对其 荷 载给 到 足够 的 值 改变 成在标 准 荷载 条件 以及 温度 之下 的数 值。而 当这 些 重视 。在 很 多 已经建 成 的桥 梁 中 , 都 是 因 为对荷 载 问题没 经过 处 理过 后 的数 值 同桥 梁施 工过 程 中 的状态 值相 比后 , 有进 行充 分 的考 虑 , 从 而导 致桥 梁 的整体 质 量 不合格 。在 就 可 以对桥 梁 目前 的状 态 进行 判定 , 并 以此 为依据 开展 下 分 阶段施 工桥 梁 的 无应力 状 态控 制 法 中 , 桥 梁荷 载 的位 置 步 的操作 。
无应力状态控制法综述

文章编号:1003-4722(2010)01-0071-04无应力状态控制法综述黄晓航1,高宗余2(1.中铁大桥局集团有限公司,湖北武汉430050; 2.中铁大桥勘测设计院有限公司,湖北武汉430050)摘 要:无应力状态控制法是解决桥梁结构分阶段施工的理论方法。
通过建立分阶段施工结构的力学平衡方程,从理论上阐明桥梁构件单元的无应力状态量是影响分阶段施工结构内力和位移的本质因素,并得出无应力状态控制法原理:在结构外荷载、结构体系、支承边界条件、单元无应力长度、无应力曲率一定的情况下,其对应的结构内力和位移是惟一的,与结构的形成过程无关。
采用无应力状态控制法,在斜拉桥安装计算时可由成桥最终状态直接解算施工中间状态;可分析杆件工厂制造长度偏差对桥梁结构内力和线形的影响;可实现调索与其他工序并行作业等运用传统方法解决较困难或无法解决的工程问题。
关键词:桥梁工程;分阶段施工;无应力状态量;安装计算;施工监控;原理;应用中图分类号:TU311.4文献标志码:AA Summarized Account of Unstressed State Control MethodH U ANG Xiao hang1,GAOZong y u2(1.China Zhongt ie M ajo r Bridge Engineer ing G roup Co.,L td.,W uhan430050,China; 2.ChinaZho ng tie M ajor Br idg e Reconnaissance&Desig n Institute Co.,L td.,W uhan430050,China)Abstract:T he unstressed state co ntro l method is a theoretic m ethod for bridg e structur e con structio n in stages.By establishing the m echanical equilibrium equations for the structure,it is theoretically ex plained that the unstressed state am ount o f the element o f the str ucture is the es sential factor that has influence on the internal force and displacem ent of the structur e constructed in stages and the principle of the unstr essed state control is obtained,that is,under the certain conditions of the ex ternal load,structural system,supporting boundary co ndition,element un stressed leng th and unstressed cur vature,the structur al internal force and displacement co rre spo nding to the conditio ns is sole and has no relatio nship w ith the fo rmation pro cess of the str uc ture.T hrough utilization of the unstressed state contr ol m ethod in the calculatio n fo r erection ofa cable stayed br idge,the construction interm ediate state can be directly solved from the finalcom pletion state,the influences of the shop manufactur ing length to ler ance of structural members on the internal fo rce and geometric shape o f the structure can be analyzed and the parallel o pera tion o f cable adjustment and other w or king procedures that is difficult for the conv entional con structio n methods to be carried out or that can not be car ried out by the m ethods can be realized.Key words:bridg e engineering;co nstructio n in stages;unstr essed state amount;calculation for erection;construction mo nitoring and co ntro l;principle;applicatio n收稿日期:2009-11-13作者简介:黄晓航(1970-),男,高级工程师,1992年毕业于上海交通大学工程力学专业,工学学士(h uangx h@)。
钢管混凝土拱桥无应力状态施工控制技术
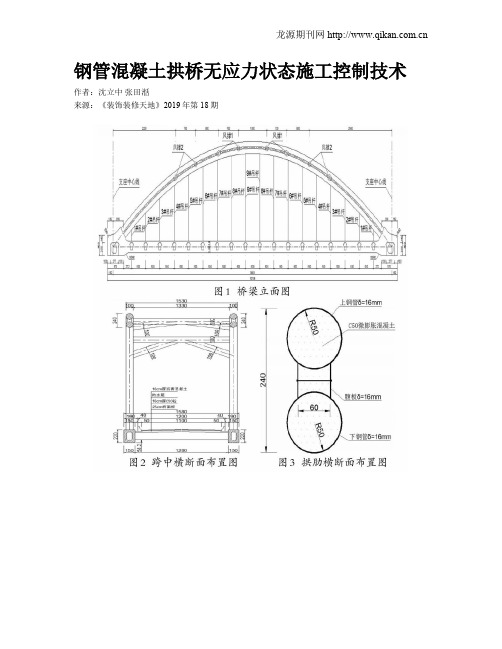
钢管混凝土拱桥无应力状态施工控制技术作者:沈立中张田湉来源:《装饰装修天地》2019年第18期摘; ; 要:钢管混凝土系杆拱属于无推力结构,有明确的传力路径,是一种自架设结构体系,但结构施工过程相对较复杂。
结构形成过程中拱肋分段线形、桥面线形及吊杆索力是其主要的控制目标,而常规采用倒装分析、正装分析、正倒装交互迭代的控制方法实现成桥理想状态,但分析及实施过程较为繁杂。
本文以飞云江大桥为例,采用无应力状态法施工控制原理,对钢管混凝土系杆拱合理成桥状态下的拱肋、吊杆进行无应力长度计算,并应用于拱肋及吊杆安装控制等施工流程,使结构施工控制更加明了清晰,大大减少计算及施工工作量。
关键词:钢管混凝土系杆拱;施工控制;无应力状态法;桥梁线形;无应力长度1; 引言钢管混凝土拱桥的施工控制主要是指在施工过程中对结构的安全和主要构件(拱肋、吊杆、系梁等)的内力、线形控制[1]。
根据正常施工工序拱肋最早形成,裸拱形成后拱轴线基本确定且不易调整,因此裸拱线形是拱桥施工控制过程中的关键因素之一,其次是对吊杆内力及桥面线形的控制。
无应力状态法的核心原理[2]:桥梁结构只要确定最终成桥无应力状态量(无应力长度和曲率)、外部荷载及边界条件,则最终成桥结构的内力及位移状态与结构的形成过程无关。
(即保证结构成形过程中所有构件都能实现无应力安装,则最终成桥的线形与内力状态与设计要求一致)。
该原理较多的应用于斜拉桥,近年来逐步扩展至拱桥结构中,不过应用于钢管混凝土系杆拱桥中的文献较少[3]。
本文以飞云江大桥为背景,建立数值仿真模型,研究无应力线形、吊(系)杆初始张拉力及无应力长度,为此类桥梁施工控制提供依据。
2; 工程概况飞云江大桥主桥全长100m,宽12m,公路等级为高速公路,设计时速为100km/h。
采用钢管混凝土系杆拱结构,拱轴线为二次抛物线,抛物线方程为y=(4/5-2x/245)×x,矢跨比为1/5,矢高19.6m。
无应力状态控制法-III

对于斜拉桥 斜拉桥 设计时无法仔细考虑每一个施 工过程: 工过程:
1)施工阶段多,体系转换过程复杂 )施工阶段多, 2)施工阶段的张拉调索 ) 3)理想成桥状态的要求 )
7
所以
斜拉桥设计时 以理想的恒载成桥状态为基础, 进行结构设计和运营阶段的各种验算。
设计阶段的后期进行安装计算。
1)施工过程结构安全性检算; 施工过程结构安全性检算; 确定满足成桥目标状态要求的中间 满足成桥目标状态要求的 2)确定满足成桥目标状态要求的中间 施工过程的内力和线形 的内力和线形( 施工过程的内力和线形(中间过程 理想状态) 理想状态)
X=0.2938
36
D
考察一斜拉结构
l
B A l/2 P
45°
C l/2 P
ABC 为抗弯刚度为 EI 的主梁, CD 为拉压刚度为 EA 的拉压杆。
结构一次形成,在 B 点和 C 点分别施加外荷载 P 。 ( 荷载未加时, CD 杆长 2 l) 结构内力:
N CD = 21 2 Al 2 16( Al + 6 2 I )
1 2 MA = MB =− ql 2
MC = MC′ = 0
18
两种施工方法形成的最终结构 计算图式相同 外荷载也相同
q
A
C 2l
EI
B
19
内力完全不同! 内力完全不同!
1 3q
l
2
1 3q
l
2
A
C
1 6q
B l
2
1 2q l
2
1 2q l
2
A l
C
C' l
B
为什么?
20
支架上一次形成结构在恒 作用下的挠度曲线: 支架上一次形成结构在恒载 q 作用下的挠度曲线:
大跨度施工桥梁控制

• 斜拉索张拉索力与理论预报值的相对误差应控制 在2%以内; • 挂篮定位标高与预报标高之差控制在1厘米以内; • 斜拉索张拉完后,如梁端测点标高与控制预报标 高之差超过4厘
米,需研究调整方案,确定索力调整措施。
测量值和控制措施
观测变量为:标高、索力、塔顶水平位移、主梁及塔 身的局部温度场和应力场;混凝土徐变系数和弹性模 量测试试验;在悬臂浇筑之前对挂篮进行了现场预压 试验。 控制措施:斜拉索的索力及梁段的立模标高。
参数估计计算原理
影响方程
待估计参数
Z A (S)
可测量变量
调整影响函数
优化目标方程
实际测量值
预计测量值
约束条件
J min f (Z - Z) min f [Z - A(S)]
优化目标
优化目标函数
si si max (i 1,2,,r)
参数估计方法分类
一类是基于误差最小化的算法,如最 小二乘法
施工操作误差的累计误差较大 • 斜拉桥设计规范中把施工控制作为实现设计目
标的必要措施
二.施工控制的思路
开环施工控制——适用于简单桥梁或非循 环式施工桥梁
反馈施工控制——适用于结构参数比较稳 定的桥梁
自适应施工控制——适用于循环式施工桥 梁
目前尚没有一种算法可直接用于施工控制, 控制方法只是一种思路的应用
的影响非常明显, 钢梁的抗拉、抗压能力均较强。
大跨度钢斜拉桥控制对策
在确定施工控制目标时,一般使用无应力状态法。 由于梁段间相对位置不能调整,某一梁段的误差除影
响本节段外,误差的趋势还将影响以后的梁段,因此, 拼装阶段的线形是控制的主要目标,必须在下一节段 拼装前通过斜拉索索力的调整来纠正已建成梁段的线 形误差,而将索力控制在一定误差范围内。
基于无应力状态控制法的钢桁梁桥起拱研究

基于无应力状态控制法的钢桁梁桥起拱研究但启联【摘要】为探讨已知预拱度曲线的钢桁梁桥的预拱度设置方法,将节间相对预拱度作为输入变量,由分阶段成形结构力学平衡方程出发,推导得出各单元杆件伸缩量的数学表达式.针对下承式钢桁梁桥预拱度设置特点,进一步得出了只伸缩上弦杆,同时伸缩上弦杆和斜腹杆,同时伸缩上弦杆、竖杆和斜腹杆三种情况下的杆件伸缩公式,并通过实桥算例说明该方法的应用.分析结果表明:无应力状态起拱法为纯几何起拱法,起拱过程不会产生附加内力和起拱支座反力;计算结果与设计值和文献计算值吻合,说明该方法进行预拱度设置是可靠的.本文方法计算结果可靠,值得同类桥型借鉴.【期刊名称】《哈尔滨工程大学学报》【年(卷),期】2018(039)012【总页数】6页(P1941-1946)【关键词】钢桁梁桥;预拱度曲线;相对预拱度;厂制预拱度;无应力状态起拱法【作者】但启联【作者单位】西南交通大学土木工程学院,四川成都610031【正文语种】中文【中图分类】U448.36桥梁预拱度设置对于保证线路平顺、运行质量至关重要。
我国铁路及公路钢结构设计规范[1-2]均规定,桥跨结构应设置预拱度,以抵消大桥所受恒载和一半活载的挠度。
在钢桁梁的设计中,一般通过伸缩杆件以实现起拱目的。
预拱度设置合理与否,不但影响桥梁的使用功能,甚至影响结构受力。
钢桁梁预拱度设置的科学性首先体现在计算方法上,许多学者对此展开了研究,提出了几何法、温度法及位移荷载法等。
几何法[3-5]是根据主桁杆件间的几何关系计算上弦杆变化量与预拱度值之间关系,通常需反复试算才能得到与理论预拱度曲线吻合较好的线形,该方法仅适用于结构形式简单的钢桁梁桥。
温度法[6-8]是通过升降温的方式调整杆件的无应力长度,使桁架控制点节点位移逼近理论预拱度。
对于超静定结构,采用升降温法起拱会产生起拱次内力及起拱支座反力,通常需建立优化模型,求解约束方程。
对于大型钢桁梁桥,约束方程冗杂,求解困难,甚至无解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ql Pl − =0 6 EI 2 EI
3
2
1 P = ql 3
27
2P
1 M A= 6 q l
2
1 M B= 6 l
2
B
拆除集中荷载弯矩图
2 M=1ql A 3
1 M=3ql
B
2
C A
1 M=6ql
C 2
B
最终结构弯矩图
28
M
A
1 1 1 1 2 2 2 = ql − ql + ql = ql2 2 3 6 3
2
P
MA = −
3 Al 2 + 144 2 I 16( Al + 6 2 I )
2
Pl
37
考虑安装过程:
A l/2 B
D
AB梁段
l
B A l/2
A l/2 B P
45°
C P l/2 P
施加集中荷载P
A l/2
B P l/2
C
安装BC梁段
A B l/2 P l/2 C P
C点施加荷载P
38
D
l A
y1 = qx ( x 3 − 4 lx 24EI
2
+ 4l2 x)
结构形成后, 假设” “ 挠度曲线变化: 结构形成后, 假设”卸除荷载 q ,挠度曲线变化:
y2 = − qx ( x 3 − 4 lx 2 + 4 l 2 x ) 24 EI
卸除荷载后梁体的残余挠度变形: 卸除荷载后梁体的残余挠度变形:
卸除荷载后梁体的残余挠度: 卸除荷载后梁体的残余挠度:
y = y
1
+
y
2
=
q x 2l 2 1 2 E I
22
梁体曲率: 梁体曲率:
一次形成结构 悬臂施工结构
y = 0 ,
y′′ = 0
qx2l 2 ql2 y= , y ′′ = 12EI 6EI
由此可以看出: 由此可以看出:两种方法形成的最终结 内力状态的差异是由于最终结构的 是由于最终结构的“ 构内力状态的差异是由于最终结构的“卸载 曲率”差异造成的 造成的。 曲率”差异造成的。
无应力状态控制法
理论与实践
秦顺全
中铁大桥局集团有限公司
1
一、概述 二、结构形成过程与最终状态的关系 三、斜拉桥无应力状态法 四、无应力状态法的其它应用
2
一、概述
近几十年来,桥梁建设最大的技术进 步是:分阶段形成桥梁结构技术的提出 和发展。
拱桥 :无拱架施工 连续梁(刚构):悬臂施工技术 斜拉桥 :施工过程多次体系转换 … …
1 2 一次落架: (一次落架: ql 3
)
29
3. A、B支点转动
1 2q l
2
1 2q l
2
A l
C
C' l
B
悬臂梁弯矩
1 M = 6 ql
B 2
A
C B
1 M = 12 ql
C 2 2
M = 1 ql 3
A
A点转动弯矩图
EI EI ql 3 1 2 M A = 4 ⋅ ⋅θ A = 4 ⋅ ⋅ = ql 2l 2l 6EI 3
最终弯矩图
31
M
A
1 1 1 1 2 2 2 2 = ql − ql + ql = ql 2 3 6 3
(一次落架:
卸载后的残余曲率?
1 2 ql 3
)
很容易核算,采取三种措施后,形成的最终 结构的卸载曲率与一次形成结构是一致的!
32
从对固端梁的讨论,可以看出: 从对固端梁的讨论,可以看出:
不论结构形成过程如何,只要支承边界条 件正确,最终荷载相同,结构的弹性曲线连续 (卸载曲率相等),则结构最终的内力状态和 变形状态与结构的形成过程无关。
30
1 M = 6ql
A
2
C A M = 112 q l
C 2
B
1 M = 3q l
B 2
EI EI ql 3 1 2 M B = 4 ⋅ ⋅θ B = 4 ⋅ ⋅ = ql 2l 2l 6 EI 3
B点转动弯矩 B
1 M = 3q l
A 2
M = 1q l 3
B
2
C A
1 M = 6ql
C 2
B
q
1 2 3ql
1 2 3ql
A
C 2l
2l EI
B
A
C
1 2 6ql
B
按一次落架施工: 按一次落架施工:
1 2 M A = M B = − ql 3
M
C
1 = ql2 6
17
1 2 2ql
1 2 2ql
A l
C C' l
B
两个悬臂梁, 之间合龙( 若结构先形成 AC , BC ′ 两个悬臂梁,然后在 C 和 C ′ 之间合龙(假定 C , 结构先形成 两点之间的长度为零) C ′ 两点之间的长度为零)
B P l/2
45°
C P
l/2
安装CD杆件
39
1、形成 AB 梁段
A l/2
B
AB 梁段
2、 B 点施加荷载 P ,
M
A 2
= -
1 Pl 2
δ
B 2
=
P l3 24 E I
A l/2
B P
施加集中荷载 P
40
3、安装 BC 梁段
M
A3
= -
1 Pl 2
δ δ
B 3
X=0.2938
36
D
考察一斜拉结构
l
B A l/2 P
45°
C l/2 P
ABC 为抗弯刚度为 EI 的主梁, CD 为拉压刚度为 EA 的拉压杆。
结构一次形成,在 B 点和 C 点分别施加外荷载 P 。 ( 荷载未加时, CD 杆长 2 l) 结构内力:
N CD = 21 2 Al 2 16( Al + 6 2 I )
3
弯矩图
1 2 M = ql 6 1 2 M ′ = ql 6
25
M
A
1 = ql 2
2
1 − ql 6
2
1 = ql 3
2
(一次落架:
1 2 ql 3
)
26
2.施加集中力
1 2q
l
2
1 2q
l
2
A l
C
C ' l
B
悬臂梁弯矩
A P M= 1ql 3
A 2
B P' M= 1ql 3
B 2
施加集中荷载弯矩图
12
正装试算法计算工作量大,对复杂的大跨 度斜拉桥应用难度大,所以发展了一些改进的 算法, 但这些算法对桥型和工序变化的适应性 较差。 。
有无既简单,适应性又强的方法?
13
无应力状态法: 无应力状态法:
无应力状态法是确定分阶段形成桥梁结构 过程状态与最终状态关系的方法
1) 确定满足成桥目标状态要求的中间施工过程的 内力和线形—计算问题; 2) “理论”到 “实际”过程中,临时荷载和温度变 化 影响的处理; 3) 实桥上的多工序同步施工。
14
无应力状态法在实桥上的应用开始 于武汉长江二桥(1992年)。 到目前为止,已在包括混凝土斜拉 桥、钢箱梁斜拉桥、结合梁斜拉桥、混 合型斜拉桥和钢桁梁斜拉桥在内的二十 多座大跨度斜拉桥中应用,均取得了非 常好的效果。
15
二、结构形成过程与 最终状态的关系
16
考察一等截面的两端固端梁, 考察一等截面的两端固端梁,跨度为 2l ,主梁刚度为 EI ,结构 恒载的荷载集度为 恒载的荷载集度为 q 。
6
对于斜拉桥 斜拉桥 设计时无法仔细考虑每一个施 工过程: 工过程:
1)施工阶段多,体系转换过程复杂 )施工阶段多, 2)施工阶段的张拉调索 ) 3)理想成桥状态的要求 )
7
所以
斜拉桥设计时 以理想的恒载成桥状态为基础, 进行结构设计和运营阶段的各种验算。
设计阶段的后期进行安装计算。
1)施工过程结构安全性检算; 施工过程结构安全性检算; 确定满足成桥目标状态要求的中间 满足成桥目标状态要求的 2)确定满足成桥目标状态要求的中间 施工过程的内力和线形 的内力和线形( 施工过程的内力和线形(中间过程 理想状态) 理想状态)
y = y1 + y
2
= 0
21
悬臂施工结构, 作用下的挠度曲线: 悬臂施工结构,恒载 q 作用下的挠度曲线:
y1 qx2 = (6l 24EI
2
− 4 lx + x 2 )
结构形成后(合龙) 假设” 挠度曲线变化为: 结构形成后(合龙)“假设”卸除荷载 q ,挠度曲线变化为: ,
y2 = − qx ( x 3 − 4 lx 2 + 4 l 2 x ) 24EI
34
研究连续梁的施工过程可以得出相 同的结论!
q A 0 .7 l B l C D E I 0 .7 l E
M=0.0763ql
B
2
M=0.0763ql
D
2
A
B
C M=0.0487ql
C
2
D
2
E
1 M= 8ql
B
1 M= 8ql
D
2
A 0.7l
B 0.5l
C
C 'EI 0.5l
D 0.7l
E
0.0357 3 θC ′ = − ql EI
(桥梁结构从开始施工到成桥必须经历一个复杂的多阶段构件施工安装和 体系转换过程 )
3
最终状态: 恒载最终状态: 全部恒载完成后的内力和线形必须 考虑桥梁结构的实际施工过程。 考虑桥梁结构的实际施工过程。
