CH02-平面体系机动分析
平面体系机动分析

目录
• 平面体系机动分析概述 • 平面体系机动分析的基本理论 • 平面体系机动的实例分析 • 平面体系机动分析的应用领域 • 平面体系机动分析的未来展望
01
平面体系机动分析概述
定义与特点
定义
平面体系机动分析是一种研究平面体 系在外部激励或干扰下的动态响应和 稳定性的方法。
特点
该方法主要关注平面体系的几何特性 和物理行为,通过分析其运动规律和 稳定性,为实际工程结构的优化设计 提供理论支持。
船舶工程领域
在船舶工程领域,平面体系机动分析可用于 船体结构的稳定性分析和船舶推进器的动力
学分析。
05
平面体系机动分析的未 来展望
机动分析技术的发展趋势
智能化
随着人工智能和机器学习技术的快速发展,未来机动分析 将更加智能化,能够自动识别结构中的关键因素,提高分 析的效率和准确性。
精细化
随着数值计算方法的不断进步,未来机动分析将更加精细 化,能够更准确地模拟结构的复杂行为和细节特征。
建筑物在受到地震、风等外部作用时,可能 会发生倒塌、损坏等危险情况。需要考虑建 筑物的结构形式、材料特性、支撑条件等因 素对建筑物运动稳定性的影响,以及如何优 化建筑物的结构和设计以提高其抗震和抗风 性能。
04
平面体系机动分析的应 用领域
建筑结构领域
建筑结构的稳定性分析
风载分析
通过平面体系机动分析,可以评估建 筑结构的稳定性,预测结构在不同外 力作用下的响应,从而优化结构设计。
现状
目前,平面体系机动分析已经成为结构工程、航空航天、机械工程等领域的重要研究内容,广泛应用 于桥梁、高层建筑、航空器结构等复杂结构的稳定性分析和优化设计。同时,该方法也在智能材料与 结构、生物医学工程等领 本理论
第二章 平面体系的机动分析

§2-3 几何不变体系的基本组成规则
1、三刚片规则 (基本规则)
三个刚片用不在同一直线上的三个单铰两两铰联,则组成的 体系是几何不变的,而且没有多余联系。 2、二元体规则 二元体:两根不在一直线上的链杆联结一个新结点的构造。 在一个体系上增加或拆除二元体,不会改变原有体系的几何 构造性质。 3、两刚片规则 两个刚片用一个铰和一根不通过此铰的链杆相联(或用三根不 全平行也不交于同一点的链杆相联),则为几何不变体系,而 且没有多余联系。
7
8
1 2 3
4 7 8
5
6
1 2 3 4
(教材题2-15)
5
6
常变
例4(教材例2-1):
1 2 3 4 5
解:
1、结点编号 2、列表分析
地基 杆件1-2
刚片一 杆件2-3
刚片二 杆件3-4
刚片三 杆件4-5
刚片四
3、结论 该体系为几何不变,且无多余联系。
14 13 15 16 8 9 6 4 1 2 10 11 12 7 5 13 8
14 15 16 9 6 4 1 2 10 11 12
1
2
8
9
刚片5-9
刚片二
刚片三
3、结论
地基
该体系为几何不变,且无多余联系。
Байду номын сангаас
4
3
例7:
解: 1、结点编号 2、列表分析
1 2 3
刚片1-2
地基
刚片一 +1-4-2 +1-3-2
刚片二
4
3、结论
该体系为几何不变,且有两个多 余联系。
1
2
4
李廉锟第四版《结构力学》第2章平面体系的机动分析习题+参考答案
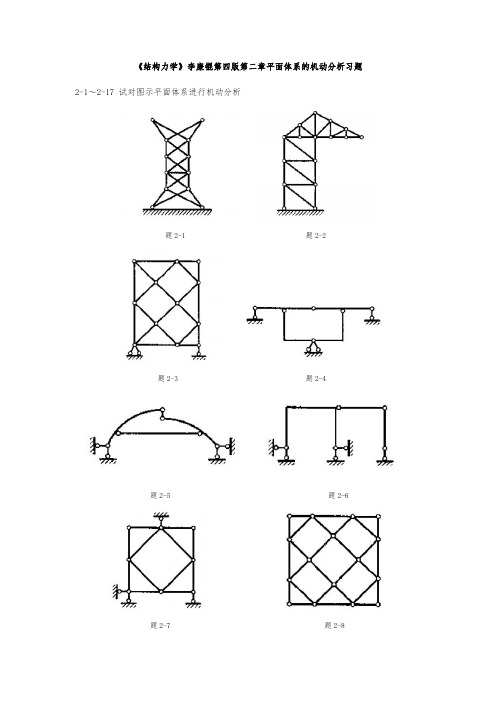
《结构力学》李廉锟第四版第二章平面体系的机动分析习题2-1~2-17试对图示平面体系进行机动分析题2-1题2-2题2-3题2-4题2-5题2-6题2-7题2-8题2-9(a、b处非结点)题2-10(k处非结点)题2-11题2-12题2-13题2-14题2-15(k处非结点)题2-16题2-172-18、2-19添加最少数目的链杆和支承链杆,使体系成为几何不变,而且无多余约束。
题2-18题2-19《结构力学》李廉锟第四版第二章平面体系的机动分析参考答案题2-1说明:自上往下依次拆除二元体,或者自下往上依次添加二元体,故体系为有一个多余约束的几何不变体系(多余约束:中间的横杆或者也可以看成支座上多了一根水平杆)。
题2-2说明:如图所示取刚片1和刚片2,采用二刚片规则(两刚片用一个铰和一根不通过此铰的链杆相联),为几何不变体系,而且没有多余联系。
刚片1由二元体组成,刚片2从大地向上组装二元体组成。
题2-3说明:先不考虑支座的三根链杆,考虑上部几何构造,去掉二元体简化分析,取如上图所示刚片1、刚片2和刚片3。
刚片1和刚片2通过一个实铰联结;刚片1和刚片3通过两根平行链杆联结,交于无穷远处;刚片2和刚片3通过两根平行链杆联结,交于无穷远处;三铰不共线,故上部无多余约束且几何不变。
最后上部与大地通过一个铰和一根不通过此铰的链杆相联,故整个体系为无多余约束的几何不变体系。
题2-4说明:如上图所示取刚片1、刚片2和刚片3,刚片1和刚片2交于铰12O ,刚片1和刚片3交于铰13O ,刚片2和刚片3交于铰23O ,三铰不共线,故原体系为无多余约束的几何不变体系。
题2-5说明:将大地等效成一根链杆,取如图所示刚片1和刚片2,显然两刚片通过三根链杆相联,且三根链杆既不相互平行也不相交于一点,故原体系为无多余约束的几何不变体系。
题2-6说明:先拆除二元体以简化分析,可知右部分为常变部分;左部分为有一个多余约束的几何不变体系,故体系为几何常变体系。
ch02-数学教育的东西方差异

11.“大众数学”与“精英数学”
• 本肖夫的数学网络课堂
• 电影:死亡诗社
• 《卡尔∙威特的教育》
• 卢梭《爱弥尔》
• 资优教育
• 教育的公平性
12. 过滤器与水泵
1. 选拔人才的筛子(拉丁文); 2. 《人人有份》; 3. 多元智力与成功智力
13. 名师与教育家
• 理论与经验; • 教师与研究者; • 学派与流派;
1. 适者生存与统一发展
• 学游泳,
• 导游,
• 建筑,
• 《教育为何是无用的?》
• 灵魂工程师,园丁,蜡烛
• …
2. 双基与创新
• 华人学习者悖论
• 一个美国数学教授的遭遇
• 不会开
49
• 英国提高成人数学素养的计划 • 火星为什么是红色的 • 德国的两堂课 • 花岗岩上盖茅草房 • 吴非《不跪着教书》
A. 3.86 B. 7.73* C. 28.27 D. 32.86 E. 36.00
(正确率:29%)
7.“学问”与“学答”
1. 蔡金法的研究 2. 大胆假设与小心求证
3. 基于问题的教学法
4. 高分低能
问题解决的基本特征(中国)
一题多解 变异空间大 一题多变 变式教学
一法多用
双 (三) 基——化归的基础
初 二
公式 变形
含有字母系数 的一元一次方 程 可化为一元一 次方程的分式 方程 降 次 一元二次 方程 分式 方程 化 简
分式
因式 分解
初 三
求定 义域
求定 义域 零 点 二次 函数 二次函 数图像 图像 解法 分式 函数 无理 函数
二元二次方 程组 函数
一次 函数
一次函 数图像
结构力学习题

2、产生位移的原因主要有三种
3、变形体系的虚功原理:
a)荷载作用 b)温度改变和材料胀缩
c)支座沉降和制造误差
变形体虚功原理:各微段内力在应变上所作的内虚功总和Wv,
等于荷载在位移上以及支座反力在支座位移上所作的外虚功总
和W。
F + FRk ck = FN du + M d + FS ds
M
M
第四章
一、三铰拱的主要受力特点:
静定拱
在竖向荷载作用下,产生水平推力。 优点:水平推力的存在使拱截面弯矩减小,轴力增大; 截面应力分布较梁均匀。节省材料,自重轻能跨越大跨 度;截面一般只有压应力,宜采用耐压不耐拉的材料砖、 石、混凝土。使用空间大。 缺点:施工不便;增大了基础的材料用量。
二、反力计算公式:
FN FN P MM P EI ds + EA ds
8)该公式既用于静定结构和超静定结构。但必须是弹性体系 9)虚拟力状态:在拟求位移处沿着拟求位移的方向,虚设相应 的广义单位荷载。
A B 求A点的 水平位移 P=1 求A截面 的转角
m=1
m=1
m=1
P=1 求AB两点 的相对位移
P=1
教材57页(4-1)
注:1)该组公式仅用于:两底铰在同一水平线上且承受竖向荷载。 2)三铰拱的反力与跨度、矢高(即三铰的位臵)有关, 而与拱轴线的形状无关;水平推力与矢高成反比。
三、内力计算公式: 0 注:1、该组公式仅用于两底铰 FS = FS cos - FH sin 在同一水平线上,且承受 0 FN = - FS sin - FH cos 竖向荷载; 2、仍有 FS=dM/ds 即剪力等零处弯矩达极值; 3、 M、FS、FN图均不再为直线。 4、集中力作用处FS图将发生突变。 5、集中力偶作用处M图将发生突变。 四、三铰拱的合理轴线 在给定荷载作用下使拱内各截面弯矩 剪力等于零,只有轴力的拱轴线。合理拱轴线方程为:
平面两自由度七杆机构位置分析的符号解

平面两自由度七杆机构位置分析的符号解
徐礼矩;宋绍富
【期刊名称】《机械科学与技术》
【年(卷),期】1998(017)001
【摘要】应用数学机械化方法和计算机符号处理技术,地平面两自由度七杆机构位置分析问题进行了符号求解,该法通过对变量的排序、多项式分组、约化、构成基列、求余等运算,将一组非线性多项式方程化简为一个同价的三角化方程组,导出了单变量的8次代数是到了封闭形式的解析解,并给出了一个数字实测来说明这种方法。
【总页数】3页(P51-53)
【作者】徐礼矩;宋绍富
【作者单位】四川联合大学;四川联合大学
【正文语种】中文
【中图分类】TH112
【相关文献】
1.基于Groebner基的平面五杆机构位置分析符号解
2.基于Groebner基的平面两自由度七杆滑块机构位置分析符号解
3.基于Groebner平面两自由度七杆机构位置分析的符号解
4.基于Groebner基法的平面七杆机构位置分析
5.混合驱动平面两自由度七杆机构最优运动规划
因版权原因,仅展示原文概要,查看原文内容请购买。
李廉锟《结构力学》笔记和课后习题(含考研真题)详解-第2章 平面体系的机动分析【圣才出品】
相当于三刚片规则。同理,两刚片规则中链杆仍然可以看作一个刚片。因此三个基本组成
规则实质上只是同一个规则。
5.何谓瞬变体系?为什么土木工程中要避免采用瞬变和接近瞬变的体系? 答:(1)瞬变体系的定义 瞬变体系是指经微小位移后由几何可变转化为几何不变的体系,瞬变体系是一种几何 可变体系。 (2)在土木工程的实际中,由于材料变形,瞬变体系一经受力即偏离原有位置,而 内力通常也很大,甚至可能导致体系的破坏。同时,瞬变体系的位移只是理论上为无穷小, 实际上在很小的荷载作用下也会产生很大的位移。因此,土木工程中要பைடு நூலகம்免采用瞬变和接
二、平面体系的计算自由度 ★★★★★ 1.自由度和约束(见表 2-1-2)
表 2-1-2 自由度和约束
2.平面体系的计算自由度(见表 2-1-3) 表 2-1-3 平面体系的计算自由度
2 / 37
圣才电子书
十万种考研考证电子书、题库视频学习平 台
三、几何不变体系的基本组成规则(见表 2-1-4) ★★★★★ 表 2-1-4 几何不变体系的基本组成规则
9 / 37
圣才电子书
十万种考研考证电子书、题库视频学习平
台
近瞬变的体系,以保证结构的安全和正常使用。
6.试小结机动分析的一般步骤和技巧。 答:(1)机动分析的一般步骤 ①一般先考察体系的计算自由度。如果 W>0,已表明体系是几何可变的;如果 W≤0,进一步做组成分析。 ②运用几何组成的基本规则做几何组成分析。 (2)机动分析的一般技巧 ①对于较复杂的体系,宜先把能直接观察出的几何不变部分当作刚片。 ②以地基或刚片为基础按二元体或两刚片规则逐步扩大刚片范围。 ③拆除二元体使体系的组成简化,以便进一步用基本的组成规则去分析它们。
平面体系的机动分析
使得体系减少自由度的联结装置称约束或联系。在刚片间加入某些联结装置,它们的
自由度将减少,减少一个自由度的装置就称为一个约束,减少n个自由度的装置就称为个约束。
n
2.1.1不同联结装置对体系的约束作用
1.链杆的作用
图2-4(a)表示用一根链杆BC联结的两个刚片Ⅰ和Ⅱ。未联结以前,这两个刚片在平面
(2)自由度。
图2-2所示为平面内一点A的运动情况。一点在平面内可以沿水平方向(x轴方向)移
动,又可以沿竖直方向(y轴方向)移动。当给定x、y坐标值后,A点的位置确定。换句话
说,平面内一点有两种独立运动方式(两个坐标x、y可以独立地改变),即确定平面内一点
的位置需要两个独立的几何参数
(x、y坐标值
),因此我们说一点在平面内有两个自由度。
后的自由度总数为五个(6- 1=5)。由此可见,一根链杆使体系减少了一个自由度,也就是说,
一根链杆相当于一个联系或一个约束。
2.单铰的作用
图2-4(b)表示用一个铰B联结的两个刚片Ⅰ和Ⅱ。在未联结以前, 两个刚片在平面内共
有六个自由度。在用铰B联结以后,刚片Ⅰ仍有三个自由度,而刚片Ⅱ则只能绕铰B作相
EF来看,E点的运E点的这种运动不可能
发生,也就是链杆
EF阻止了刚片Ⅰ和刚片Ⅱ的相对转动。因此,这样组成的体系是几何不
变体系。
图2-7两刚片组成规则
如果在刚片Ⅰ和刚片Ⅱ之间再增加一根链杆,如图2-7(c)所示,显然体系仍是几何不变
的,但从保证几何不变性来看它是多余的。这种可以去掉而不影响体系几何不变性的约束
对转动,即再用一个独立参数(夹角)就可确定它的位置,所以减少了两个自由度。因此,
两个刚片用一个铰联结后的自由度总数为四个(6- 2=4),我们把联结两个刚片的铰称为单铰。
第二章平面体系的机动分析
例2-2-2 求图示体系的计算自由度。 解1: I 1 A II m=2,h=1, r=2×2+3+1=8 4
2
3
5
W=3×2-2-8=-4
例2-3-3 求图示体系的计算自由度。 解:
A 1
B 5 7 E 10
j 5 b 10 W 2 5 10 0
2 3 4 8 C 9 6 D
例2-1
I
1 解: 2 3 II(基础)
4
D 5
1)被约束对象:刚片I, II及结点D。
刚片I、II用链杆1、2、3相连,符合规律4, 组成大刚片I;
大刚片 I、结点D用链杆4、5相连,符合规 律1。故体系为几何不变且无多余约束。
2)被约束对象:刚片I,II,III及结点D,见图 b)。 o D A III B I 4 1 2 3 解: b) II(基础) 刚片I、II用链杆1、2相连(瞬铰o);刚片I、 III用铰B相连;刚片II、III用铰A相连。铰A、 B、o不共线,符合规律3,组成大刚片 I。
例1: I I
II 无多余约束的 几何不变体系
II
瞬变体系
无多余约束的 几何不变体系
有一个多余约束 的几何不变体系
例2:
无多余约束的几何不变体系
无多余约束的 几何不变体系
技巧 1: 对于与地面有着简单联系的体系,可以直接取体系内部出 来,对其进行几何构造分析。
例3:
几何可变体系
例4:
有3个多余约束的
此外应根据几何不变体系的规律设计新结构。 2. 正确区分静定结构与超静定结构。 以选择不同的计算方法
基本概念
杆件体系:不考虑材料变形,几何形状与位置 保持不变的体系为几何不变体系 发生可变的体系为几何可变体系 结构—几何不变体系 机动分析:判别体系是否为几何不变体系的分析 刚片——杆件或几何不变部分(忽略材料变形) 联系(约束)——其余链杆、结点和支座
第02章 酸碱理论与中间体(2015.04.19)
+
H+
KR+ຫໍສະໝຸດ R++ H2O
pKR+
[ R+ ] = lg [ ROH ]
+ HR
一些碳正离子的pKR+值
碳正离子 三芳基甲基正离子 三苯基甲基 4,4’,4’’-三甲基三苯基甲基 4-甲氧基三苯基甲基 4,4’ –二甲氧基三苯基甲基 4,4’,4’’-三甲氧基三苯基甲基 4,4’,4’’-三氯三苯基甲基 4-硝基三苯基甲基 4,4’,4’’-三硝基三苯基甲基 4,4’,4’’-三(二甲氨基)三苯基甲基 倍半占吨氢基 -6.63 -3.56 -3.40 -1.24 0.82 -7.74 -9.15 -16.27 9.36 9.05 pKR+ 碳正离子 二芳基甲基正离子 二苯基甲基 4,4’ –二甲基二苯基甲基 4,4’-二甲氧基二苯基甲基 2,2’,4,4’,6,6’-六甲基二苯基甲基 4,4’ –二氯二苯基甲基 其他种类碳正离子 三环丙基甲基 环庚三烯正离子 三苯基环丙烯基 三甲基环丙烯基 三环丙基环丙烯基 -2.3 4.7 3.1 7.8 9.7 -13.3 -10.4 -5.71 -6.6 -13.96 pKR+
η(eV) 7.0 4.7 4.2 3.7 6.8 4.0 4.9 5.3 5.6 4.5 5.3 4.1 4.5
35.1 21.1 11.7 6.3 6.9 5.7 7.2
软硬酸碱理论(HSAB)应用举例: O NH 例如: Cl CC NH + CH OH
3
O Cl3CC OCH3
( Hb )
用前线轨道理论来理解和解释Lewis 酸碱理论: 所有提供LUMO轨道的物质称为酸。 所有提供HOMO轨道的物质称为碱。 提供SOMO轨道的物质既是酸又是碱。 Lewis 酸碱反应几乎涵盖除周环反应外的所有有 机化学反应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
26
各种几何瞬变体系
三平行不 等长链杆 瞬变体系
三共点链杆 瞬变体系
共线一铰一链 杆瞬变体系
三铰共线瞬变体系
三对平行链 杆瞬变体系
27
§2-5 机动分析示例
28
图示体系是 A.无多余约束的几何不变体系 B.有多余约束的几何不变体系 C.常变体系 D.瞬变体系 答案:C(W = 4)
刚片245与基础用二链杆相连 刚片123与245用一铰相连
几何不变 (三铰不共线)
自由度计算: W = 3m – 2h – r = 24-20-4 = 0
36
例2-5
分析: 刚片:1,2,3 (基础) 刚片 1 与 2 用一对链杆相连(蓝) 刚片 2 与 3 用一对链杆相连(绿) 刚片 3 与 1 用一对链杆相连(红) 结论:三刚片用三对链杆相连,结构几何不变 自由度计算: W = 3m – 2h – r = 24-20-4 = 0
(1)三刚片用不共线三铰两两相连 (2)二刚片用不共线一铰一链杆相连 (3)二刚片用不平行不共点三链杆相连 (4)一刚片上增删一个二元体
25
几何可变体系 ——不符合构造规则的体系
几何瞬变体系
(1)二刚片用共线一铰一链杆相连 (2)二刚片用共点三链杆相连 (3)二刚片用三平行不等长链杆相连
(4)三刚片用共线三铰两两相连
自由度 W = 3m – ( 2h + r ) = 3
若杆 2 固定, 杆 1 绕 A 转动,C点轨迹为圆弧。 杆 2 绕 B 转动,C点轨迹为圆弧。 杆 1 和杆 2 同时存在,C点不动。 结论:3 杆间无相对运动 —— 该体系几何不变
13
二、二元体规则
在一刚片上增加一个二元体,仍为几何不变体系, 且无多余联系。 二元体:两根不共线的链杆联结一个新结点的构造
一、自由度——体系运动时具有的独立运动方式数目
即确定体系位置所需独立坐标的数目。
1、平面内一个点的自由度数:2
2、平面内一刚片的自由度数:3
几何不变体系的自由度应为零
4
——限制运动的装置 二、联系(约束) ◆ 体系的自由度随联系的加入而减少 ◆ 减少一个自由度的装置称为一个联系
链杆 ——仅在两处与其他物体用铰相连 常用的联系
31
图示体系是 A.无多余约束的几何不变体系 B.有一个自由度的可变体系 C.有两个多余约束的几何不变体系 D.瞬变体系
A
答案:D (三铰共线)
32
例2-1
分析: 刚片AB与基础用一铰一链杆相连 刚片EF与基础(AB)用三链杆相连 刚片GH与基础(EF)用一铰一链杆相连 自由度计算: 刚片:4 单铰:3 链杆:6 W = 3m – 2h – r = 12-6-6 = 0 结论: 几何不变
17
对图示体系机动分析
刚片:BCE,基础 链杆:AB,CD,E 不平行,不共点 结论:几何不变
18
几何不变体系构造规则:
(1)三刚片用不共线三铰两两相连 (2)二刚片用不共线一铰一链杆相连 (3)二刚片用不平行不共点三链杆相连 (4)一刚片上增删一个二元体
19
四个规则可归结为一个三角形法则。
20
38
例2-7
F
E
D
CALeabharlann B分析:刚片ACD和BEF用三链杆ED,AF,BC相连
结论:三链杆既不平行也不共点——几何不变
自由度计算: 刚片:8 单铰:10 链杆:4
W = 3m – 2h – r = 27-24-3 = 0
39
几种常用的分析途径
1、由基础开始逐件增删二元体 2、将体系归结为两个刚片或三个刚片相连,再用规则判定。 3、当体系杆件数较多时,将刚片选得分散些,用链杆相连, 而不用单铰相连。 4、如上部体系于基础用满足要求三个约束相联可去掉基础, 只分析上部。 5、刚片的等效代换:在不改变刚片与周围的连结方式的前 提下,可以改变它的大小、形状及内部组成。即用一个等效 (与外部连结等效)刚片代替它。
6
三、平面体系的计算自由度 自由度计算公式: W = 3m – ( 2h + r ) m——刚片数 h ——单铰数
r ——链杆数
体系中若有复铰,则需换算成单铰代入公式计算
7
W = 3m – ( 2h + r ) = 6 – ( 2 + 3 ) = 1
刚片:m = 2 单铰:h = 1 链杆:r = 3 刚片:m = 2 单铰:h = 1 链杆:r = 4
♦ 三虚铰不在同一条直线上
结论:几何不变
42
一、一铰在无穷远处
(2) 组成无穷远虚铰的两平行链杆与另两铰连线平行, 并且组成另二虚铰的两链杆长度不等 分析: ♦ 红链杆虚铰在无穷远处
♦ 蓝,绿虚铰连线与红链杆平行 ♦ 三虚铰在同一条直线上 ♦ 因兰绿链杆不等长,当刚片有相 对位移后,三虚铰便不共线。
刚片:3 单铰:2 链杆:5
分析: AC,BC,基础用三铰两两相联——几何不变 刚片 GED与 链杆组成一二元体
结论:几何不变
自由度计算: W = 3m – 2h – r = 9-4-5 = 0
35
例2-4 刚片:8 单铰:10 链杆:4
分析: 刚片:123,245,基础
刚片123与基础用二链杆相连
A
29
图示体系是 A.无多余约束的几何不变体系 B.有一个自由度的可变体系 C.有两个多余约束的几何不变体系 D.瞬变体系 答案:B(W = 4)
A
30
图示体系是 A.无多余约束的几何不变体系 B.有一个自由度的可变体系 C.有两个多余约束的几何不变体系 D.瞬变体系 答案:C(复铰可改为单铰)
♦ 兰绿链杆组成无穷远虚铰 ♦ 三虚铰不共线
结论:几何不变
46
二、二铰在无穷远处
(2) 组成两无穷远虚铰的两对平行链杆互相平行, 但不等长 分析: ♦ 红链杆组成虚铰
♦ 兰绿链杆组成无穷远虚铰 ♦ 三虚铰共线 ♦ 因组成虚铰蓝绿链杆不等长, 当刚片稍有相对位移,蓝绿链杆 便不再平行,于是三铰不共线。
(2) 两刚片用三平行不全等长链杆相联
若用三平行等长链杆相联则几何常变
(3) 两刚片用三平行等长不同侧链杆相联 (4) 两刚片用共线铰一链杆相联
23
各种几何瞬变体系
(5) 三刚片用共线三铰相联
(6) 三刚片用三对平行链杆相联
24
小结
几何不变体系
体系 几何常变体系 几何可变体系 几何瞬变体系
几何不变体系构造规则:
二、体系的分类
1、几何不变体系:在任何外力作用下,其形状和位置都 不会改变(不计材料变形)。 2、几何可变体系:在外力作用下,其形状或位置会改变。
2
几何不变体系
几何可变体系
说明: 1 机动分析也称几何构造分析。 2 在机动分析中,不考虑材料的变形,每根杆件均可看作 刚体,也称刚片。
3
§2-2 平面体系的计算自由度
结论:几何瞬变
47
二、二铰在无穷远处
(3) 组成两无穷远虚铰的两对平行链杆互相平行且等长 分析: ♦ 红链杆组成虚铰
♦ 兰绿链杆组成无穷远虚铰 ♦ 三虚铰共线 ♦ 因组成虚铰蓝绿链杆等长,刚 片3可作相对平动。
§2-4 瞬变体系
几何常变体系 几何可变体系 几何瞬变体系
常变体系:体系受力后,将产生较大位移 瞬变体系:经微小位移后,体系由几何可变变为几何不变。 但杆件会产生很大内力。
21
几何常变体系
几何瞬变体系
几何常变体系和几何瞬变体系均不能作为建筑结构使用
22
各种几何瞬变体系
(1) 两刚片用三共点链杆相联
例2-2
G F D C E A B
刚片:13 单铰:16 链杆:7
分析: 从基础开始,依次增加二元体G,F,E,D,C,B,A 。 结论:几何不变 同理:依次拆除二元体A,B,C,D,E,F,G 可知 该结构几何不变。 自由度计算: W = 3m – 2h – r = 39-32-7 = 0
例2-3
结论:二元体与刚片无相对运动 —— 该体系几何不变
桁架设计大都遵循此二元体规则
14
桁架设计遵循 二元体规则
同理:在一体系上拆除一个二元体,不改变原有体系 的几何构造性质 结论:在一个体系上增加或拆除二元体,不改变原有 体系的几何构造性质 此结论对于判别桁架的几何构造性质非常有效
15
三、二刚片规则
刚片:m = 12 单铰:h = 16 链杆:r = 4 W = 3m – ( 2h + r ) = 36 – ( 32 + 4 ) = 0
11
§2-3 几何不变体系的基本组成规则
三刚片规则 基本组成规则 二元体规则 两刚片规则
12
一、三刚片规则
三刚片用不共线的三个单铰两两铰联,组成的体系 几何不变且无多余联系。 两两相联:每两个刚片间用一单铰相联。
37
刚片:8 单铰:10 链杆:4
例2-6 刚片:8 单铰:10 链杆:4 分析: 刚片:BCE,DF,基础 刚片BCE与DF用一对链杆BD,EF相连(虚铰无穷远处) 刚片BCE与基础用二链杆AB,CH相连(虚铰C) 刚片DE与基础用二链杆CH,FG相连(虚铰F) 结论:三刚片用三铰两两相连,结构几何不变 自由度计算: W = 3m – 2h – r = 24-20-4 = 0
W = 3m – ( 2h + r ) = 6 – ( 2 + 4 ) = 0
刚片:m = 2 单铰:h = 1 链杆:r = 5 W = 3m – ( 2h + r ) = 6 – ( 2 + 5 ) = -1
8
W=1 W=0 W = -1 W > 0 : 体系缺少足够的联系,肯定几何可变。 W < 0 : 体系具有多余联系,是否可变视联系布置情况。 W = 0 : 若无多余联系,则几何不变; 若有多余联系,则几何可变。 W ≤ 0 是体系几何不变的必要条件。 体系是否可变,除看自由度外,还要看体系的组成规则。
