材料力学-弯曲应力
合集下载
材料力学弯曲应力_图文

§5-3 横力弯曲时的正应力
例题6-1
q=60kN/m
A
1m
FAY
C
l = 3m
FS 90kN
120
1.C 截面上K点正应力 2.C 截面上最大正应力
B
x
180
K
30 3.全梁上最大正应力 z 4.已知E=200GPa,
FBY
C 截面的曲率半径ρ y
解:1. 求支反力
x 90kN M
x
(压应力)
目录
目录
§5-2 纯弯曲时的正应力
正应力分布
z
M
C
zzy
x
dA σ
y
目录
§5-2 纯弯曲时的正应力
常见截面的 IZ 和 WZ
圆截面 空心圆截面
矩形截面 空心矩形截面
目录
§5-3 横力弯曲时的正应力
横力弯曲
6-2
目录
§5-3 横力弯曲时的正应力
横力弯曲正应力公式
弹性力学精确分析表明 ,当跨度 l 与横截面高度 h 之比 l / h > 5 (细长梁)时 ,纯弯曲正应力公式对于横 力弯曲近似成立。 横力弯曲最大正应力
§5-3 横力弯曲时的正应力
q=60kN/m
A
1m
FAY
C
l = 3m
FS 90kN
120
2. C 截面最大正应力
B
x
180
K
30 C 截面弯矩 z
FBY
y
C 截面惯性矩
x 90kN M
x
目录
§5-3 横力弯曲时的正应力
q=60kN/m
A
1m
FAY
C
l = 3m
材料力学5弯曲应力_图文

(1)合理安排载荷 (2)分散载荷(从使用方案考虑) (3)调整支座位置(从设计角度)
1、合理安排梁的受力
(1)合理安排载荷
P
(降低最大弯矩)
P
a
b
l
1、合理安排梁的受力(降低最大弯矩)
(2)分散载荷(从使用方面考虑)
P P
P
若:
l
1、合理安排梁的受力(降低最大弯矩)
(3)调整支座位置(从设计角度)
aP
q
A
C
E
l
P
B D
弯曲切应力强度校核
一般而言,对于等直梁,梁上的最大切应力发生在剪力最大 截面的中性轴上,且
是中性轴一侧的面积对中性轴的静矩 。
型钢可查表
切应力强度条件:
梁上的最大切应力max≤[]
例题4-10 图示梁为工字型截面,跨长2a=4 m、 q=25 KN/m;材
料许用应力[]=160 MPa,[]=100 MPa。试选择工字钢型号。
3950
(3)合理截面要符合材料的力学性能
塑性材料
z
z
采用关于中性轴对称的截面
y
y
脆性材料
z
采用关于中性轴不对称的截面
y
理想情况: 可调整各部分尺寸,使
z
y
y1 z
y2 y
3、采用变截面梁
以危险截面的弯矩设计梁的截面,而在其
他截面的弯矩较小,材料不能被充分利用。
从强度的角度来看,如果在弯矩大的部位采用较大的截面,弯矩较 小的部位采用较小的截面,就比较合理。截面尺寸沿梁轴线变化的梁 叫变截面梁。 若各个截面上的最大应力都等于材料的许用应力,这种梁叫等强度梁。
正应力大小与其到中 性轴距离成正比;
1、合理安排梁的受力
(1)合理安排载荷
P
(降低最大弯矩)
P
a
b
l
1、合理安排梁的受力(降低最大弯矩)
(2)分散载荷(从使用方面考虑)
P P
P
若:
l
1、合理安排梁的受力(降低最大弯矩)
(3)调整支座位置(从设计角度)
aP
q
A
C
E
l
P
B D
弯曲切应力强度校核
一般而言,对于等直梁,梁上的最大切应力发生在剪力最大 截面的中性轴上,且
是中性轴一侧的面积对中性轴的静矩 。
型钢可查表
切应力强度条件:
梁上的最大切应力max≤[]
例题4-10 图示梁为工字型截面,跨长2a=4 m、 q=25 KN/m;材
料许用应力[]=160 MPa,[]=100 MPa。试选择工字钢型号。
3950
(3)合理截面要符合材料的力学性能
塑性材料
z
z
采用关于中性轴对称的截面
y
y
脆性材料
z
采用关于中性轴不对称的截面
y
理想情况: 可调整各部分尺寸,使
z
y
y1 z
y2 y
3、采用变截面梁
以危险截面的弯矩设计梁的截面,而在其
他截面的弯矩较小,材料不能被充分利用。
从强度的角度来看,如果在弯矩大的部位采用较大的截面,弯矩较 小的部位采用较小的截面,就比较合理。截面尺寸沿梁轴线变化的梁 叫变截面梁。 若各个截面上的最大应力都等于材料的许用应力,这种梁叫等强度梁。
正应力大小与其到中 性轴距离成正比;
材料力学-第四章弯曲应力教学

FS
x
dx
0
FS
x
dM x
dx
qx
dM 2x
dx 2
注:q(x)向上为正,反之为负。
●简易法作剪力图和弯矩图
①梁上无分布荷载作用:q(x)=0
qx dFS x 0
dx
FS x cont
剪力图斜率为零,FS(x)图为平行于x轴的直线。
dM x
B 1kN
A FAx
FB
FAy
FAx=-3kN FAy=3kN
FB=5kN
2)剪力图: 简易法 BC杆:取一点(水平线) DC杆:取两点(水平线) DA杆:取两点(斜直线)
D 3kN
C
1kN E
5kN
1kN B
3kN A
q=1kN/m 4m 3m
8kN
1m D
2m C
E
B 1kN
A FAx
A
A
ydA Sz 0 中性轴z必通过截面形心
A
横截面对z轴的静矩
My
z dA 0
A
zE
A
y dA
E
A
zydA
0
zydA I yz 0
A
截面对yz轴的惯性积
*由于y为对称轴, 上式自然满足。
M z
y dA
A
M
例5.作外伸梁的内力图
q
FA
ql 8
A
FB
5ql 8
FA
FS
B
lC
l
FB 2
ql / 2
材料力学——弯曲应力

公式推导
线应变的变化规律 与纤维到中性层的距离成正比。
从横截面上看: 点离开中性轴越远,该点的线应变越大。
2、物理关系
当σ<σP时 虎克定律
E
E
y
y
弯曲正应力的分布规律 a、与点到中性轴的距离成正比; 沿截面高度 线性分布; b、沿截面宽度 均匀分布; c、正弯矩作用下, 上压下拉; d、危险点的位置, 离开中性轴最远处.
M max ymax IZ
x
67.5 103 90 103 5.832 105
104.17MPa
6、已知E=200GPa,C 截面的曲率半径ρ q=60KN/m A FAY B 1m C 3m FBY
M C 60kN m
I z 5.832 105 m 4
M EI
4 103 88 103 46.1MPa 6 7.64 10
9KN
4KN
C截面应力计算
A FA
M 1m
C 1m
B
1m FB
C截面应力分布 应用公式
t ,max
My Iz
2.5KNm
2.5 103 88 103 28.8MPa 6 7.64 10
Fb Fa
C截面: max M C Fb3 62.5 160 32 46.4MPa d W 3
zC
2
0.13
32
(5)结论 轮轴满足强度条件
一简支梁受力如图所示。已知 [ ] 12MPa ,空心圆截面 的内外径之比 一倍,比值不变,则载荷 q 可增加到多大? q=0.5KN/m A B
反映了截面的几何形状、尺寸对强度的影响
最大弯曲正应力计算公式
材料力学-弯曲应力

对于宽为b高为h的矩形截面:
W
bh3 12
bh2
h
6
2
对于直径为d的圆形截面:
W d 4 64 d 3
d
32
2
限定最大弯曲正应力不得超过许用应力,于是强度条件为:
max
M max W
设σt 表示拉应力,σc 表示压应力,则:
t max t
cmax c
塑性材料, [σt]= [σc]= [σ];
所以由(1)式:
A
d
A
A E
y
d
A
E
A y d
A
E
Sz
0
由(2)式:
说明中性轴过形心
A z
d
A
A zE
y
d
A
E
A
yz d
A
E
I yz
0
由于y轴是对称轴,此 式自然满足。
由(3)式:
A
y
d
A
A
yE
y
d
A
E
A
y2
d
A
E
Iz
M
1 M
EI z
1 为梁轴线变形后的曲率 ;
由变形几何关系得到 y
由物理关系得到
bh2 2b3 W
63
故: b 121.6 mm
h 2b 243.2 mm
选取截面为: 125 250 mm 2
e.g.3 已知:l=1.2m,[σ]=170MPa, 18号工字钢,不计自重。
求:P 的最大许可值。
P A
解:作弯矩图, 由图可得:
M
| M |max Pl 1.2P N m
材料力学第六章弯曲应力
但相应的最大弯矩值变为
Fl ql2
M max
4
8
375 kN m 13 kN m 388 kN m
而危险截面上的最大正应力变为
max
388103 N m 2342106 m3
165.7106
Pa
165.7
MPa
显然,梁的自重引起的最大正应力仅为
165.7 160 MPa 5.7 MPa
<2>. 相邻横向线mm和nn,在梁弯曲后仍为直线,只是
相对旋转了一个角度,且与弧线aa和bb保持正交。
根据表面变形情况,并设想梁的侧面上的横向线mm和 nn是梁的横截面与侧表面的交线,可作出如下推论(假设):
平面假设 梁在纯弯曲时,其原来的横截面仍保持为平面, 只是绕垂直于弯曲平面(纵向平面)的某一轴转动,转动后 的横截面与梁弯曲后的轴线保持正交。
力的值max为
max
M ym a x Iz
M
Iz ymax
M Wz
式中,Wz为截面的几何性质,称为弯曲截面系数(对Z轴)
(section modulus in bending),其单位为m3。
b
h d
o
z
o
z
y
y
中性轴 z 不是横截面的对称轴时(参见图c),其横截面 上最大拉应力值和最大压应力值为
A
r
(b)
M z
y d A E
A
r
y2 d A EI z M
A
r
(c)
由于式(a),(b)中的
E
r
不可能等于零,因而该两式要求:
1. 横截面对于中性轴 z 的静矩等于零,A y d A 0 ;显
弯曲应力-材料力学
弯曲应力的计算方法
根据材料力学的基本原理,弯曲应力 的计算公式为:σ=M/Wz,其中σ为 弯曲应力,M为弯曲力矩,Wz为截面 对中性轴的抗弯截面系数。
另外,根据不同的弯曲形式和受力情 况,还可以采用其他计算公式来求解 弯曲应力,如均布载荷下的简支梁、 集中载荷下的悬臂梁等。
弯曲应力的计算方法
根据材料力学的基本原理,弯曲应力 的计算公式为:σ=M/Wz,其中σ为 弯曲应力,M为弯曲力矩,Wz为截面 对中性轴的抗弯截面系数。
弯曲应力可能导致材料发生弯曲变形,影响结构的稳定性和精度。
弯曲应力对材料刚度的影响
弯曲应力对材料的刚度有影响,材料的刚度随着弯曲应力的增大而 减小。
弯曲应力与剪切应力的关系
1 2
剪切应力在弯曲应力中的作用
在弯曲过程中,剪切应力会在材料截面的边缘产 生,它与弯曲应力相互作用,影响梁的承载能力 和稳定性。
弯曲应力
材料的韧性和强度都会影响其弯曲应力的大小和分布。韧性好的材料能够更好地分散和 吸收弯曲应力,而高强度的材料则能够承受更大的弯曲应力而不发生断裂。
材料韧性、强度与弯曲应力的关系
韧性
是指材料在受到外力作用时吸收能量的能力。韧性好的材料能够吸收更多的能量,从而 减少因弯曲应力而产生的脆性断裂。
强度
剪切应力的分布
剪切应力在材料截面的边缘最大,向中性轴方向 逐渐减小。
3
剪切应力和弯曲应力的关系
剪切应力和弯曲应力共同作用,影响梁的承载能 力和稳定性,在设计时需要考虑两者的相互作用。
弯曲应力与剪切应力的关系
1 2
剪切应力在弯曲应力中的作用
在弯曲过程中,剪切应力会在材料截面的边缘产 生,它与弯曲应力相互作用,影响梁的承载能力 和稳定性。
材料力学第五章 弯曲应力
x
F F d F 0 N 2 N 1 S
将FN2、FN1和dFS′的表达式带入上式,可得
* M M d M * S S b d x 0 z z
I z I z
简化后可得
dM S z* dx I z b
dM F S ,代入上式得 由公式(4-2), dx
* 式中 S z
A1
y1dA ,是横截面距中性轴为 y 的横线 pq 以下的面积对中性轴的静矩。同理,
可以求得左侧面 rn 上的内力系的合力 FN 1 为
M * FN 1 S z Iz
在顶面rp上,与顶面相切的内力系的合力是
d F b d x S
根据水平方向的静平衡方程
F 0 ,可得
综上所述,对于各横截面剪力相同的梁和剪力不相同的
细长梁(l>5h),在纯弯曲情况下推导的弯曲正应力公式 (5-2)仍然适用。
例5-1
图5-10(a)所示悬臂梁,受集中力F与集中力
偶Me作用,其中F=5kN,Me=7.5kN· m,试求梁上B点左邻 面1-1上的最大弯曲正应力、该截面K点处正应力及全梁的 最大弯曲正应力。
第五章 弯曲应力
5.1 弯曲正应力 5.2 弯曲切应力简介 5.3 弯曲强度条件及其应用 5.4 提高梁弯曲强度的主要措施
5.1 弯曲正应力
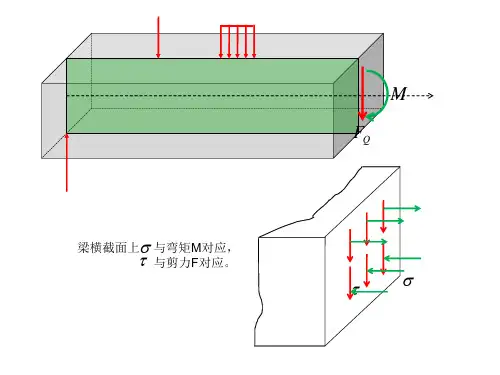
上一章研究表明,一般情况下,梁横截面上同时存在
剪力FS和弯矩M。由于只有切向微内力τ dA才可能构成剪力, 也只有法向微内力σdA才可能构成弯矩,如图5-1(a)所示。 因此,在梁的横截面上将同时存在正应力σ和切应力τ(见图 5-1(b))。梁弯曲时横截面上的正应力与切应力分别称为 弯曲正应力与弯曲切应力。
F F d F 0 N 2 N 1 S
将FN2、FN1和dFS′的表达式带入上式,可得
* M M d M * S S b d x 0 z z
I z I z
简化后可得
dM S z* dx I z b
dM F S ,代入上式得 由公式(4-2), dx
* 式中 S z
A1
y1dA ,是横截面距中性轴为 y 的横线 pq 以下的面积对中性轴的静矩。同理,
可以求得左侧面 rn 上的内力系的合力 FN 1 为
M * FN 1 S z Iz
在顶面rp上,与顶面相切的内力系的合力是
d F b d x S
根据水平方向的静平衡方程
F 0 ,可得
综上所述,对于各横截面剪力相同的梁和剪力不相同的
细长梁(l>5h),在纯弯曲情况下推导的弯曲正应力公式 (5-2)仍然适用。
例5-1
图5-10(a)所示悬臂梁,受集中力F与集中力
偶Me作用,其中F=5kN,Me=7.5kN· m,试求梁上B点左邻 面1-1上的最大弯曲正应力、该截面K点处正应力及全梁的 最大弯曲正应力。
第五章 弯曲应力
5.1 弯曲正应力 5.2 弯曲切应力简介 5.3 弯曲强度条件及其应用 5.4 提高梁弯曲强度的主要措施
5.1 弯曲正应力
上一章研究表明,一般情况下,梁横截面上同时存在
剪力FS和弯矩M。由于只有切向微内力τ dA才可能构成剪力, 也只有法向微内力σdA才可能构成弯矩,如图5-1(a)所示。 因此,在梁的横截面上将同时存在正应力σ和切应力τ(见图 5-1(b))。梁弯曲时横截面上的正应力与切应力分别称为 弯曲正应力与弯曲切应力。
材料力学第5章弯曲应力
3 R2
4)
最大切应力: max
k
FS A
矩形:k =3/2 工字形:k =1 圆形:k =4/3
5)
切应力强度条件: max
F S* S max z max Izb
[
]
梁的强度条件小结:
1)应力公式:
正应力: My
Iz
最大值在距中 性轴最远处 max
M W
切应力:
FS Sz* Izb
最大值在 中性轴处
。 F位于跨中时,M最大
FRA
F
FRB
Mmax=Fl/4 F靠近支座时,FS最大 Qmax=F 按弯曲正应力强度条件选择截面
Wz
Fl
4
3.0 104 m3
300cm 3
max
FS z max Izd
14.11MPa
选择 22a工字钢
Iz / Szmax 18.9cm
d=7.5mm
5.16 铸铁梁的载荷及横截面尺寸如图所示。许用 拉应力[ t ] 40,MP许a 用压应力 [ c ] 。 1试60按MP正a 应力
My Iz
My
zdA
E
yzdA
E
I yz
0——y为主惯轴
总结: • 应力应变沿高度线性变化,中间有零应力应变层
• 应力应变公式的适用范围 • 最大应力、应变点在哪里
§5.3 横力弯曲时的正应力
1)横力弯曲时的正应力公式
横力弯曲时,基本假设不成立,但
My 满足精度要求,可使用。
Iz
max
Mmax ymax Iz
应变: (bb bb) / bb
(
y)d d
d
y
2)物理方程: E Ey /
4)
最大切应力: max
k
FS A
矩形:k =3/2 工字形:k =1 圆形:k =4/3
5)
切应力强度条件: max
F S* S max z max Izb
[
]
梁的强度条件小结:
1)应力公式:
正应力: My
Iz
最大值在距中 性轴最远处 max
M W
切应力:
FS Sz* Izb
最大值在 中性轴处
。 F位于跨中时,M最大
FRA
F
FRB
Mmax=Fl/4 F靠近支座时,FS最大 Qmax=F 按弯曲正应力强度条件选择截面
Wz
Fl
4
3.0 104 m3
300cm 3
max
FS z max Izd
14.11MPa
选择 22a工字钢
Iz / Szmax 18.9cm
d=7.5mm
5.16 铸铁梁的载荷及横截面尺寸如图所示。许用 拉应力[ t ] 40,MP许a 用压应力 [ c ] 。 1试60按MP正a 应力
My Iz
My
zdA
E
yzdA
E
I yz
0——y为主惯轴
总结: • 应力应变沿高度线性变化,中间有零应力应变层
• 应力应变公式的适用范围 • 最大应力、应变点在哪里
§5.3 横力弯曲时的正应力
1)横力弯曲时的正应力公式
横力弯曲时,基本假设不成立,但
My 满足精度要求,可使用。
Iz
max
Mmax ymax Iz
应变: (bb bb) / bb
(
y)d d
d
y
2)物理方程: E Ey /
材料力学(给排水)第四章-弯曲应力
弯曲应力的计算方法
1 梁弯曲公式
常用于计算直梁受弯时的应力分布和最大应 力值。
2 等强度法
常用于计算不同形状截面的梁受弯时的应力 分布。
弯曲应力的分布特点
1 最大应力出现在最远离中性轴的位置
2 中性轴附近应力应变
2 下表面拉应变
3 中性面应变为0
弯曲应力的应力-应变关系
1 胡克定律
当弯曲应力小于材料的弹性极限时,应力与 应变成正比关系。
2 弹性模量
描述了材料在受力时的变形程度。
材料力学中常见的弯曲应力计算问题
1 悬臂梁的最大弯曲应力计算
2 叠木梁的弯曲应力分布计算
3 榀形梁的弯曲应力计算
弯曲应力的工程应用及实例
1 建筑结构设计
弯曲应力的分析和计算对 于设计坚固和稳定的建筑 结构至关重要。
2 桥梁工程
弯曲应力的研究可以帮助 工程师设计和评估桥梁的 结构和安全性。
3 车辆设计
在汽车和飞机等交通工具 的设计过程中,弯曲应力 是一个重要的考虑因素。
材料力学(给排水)第四章 -弯曲应力
在材料力学中,弯曲应力是一个重要的概念,它涉及到物体在受力时的弯曲 情况。本章将介绍弯曲应力的定义、计算方法、分布特点、应变状态、应力应变关系以及其工程应用及实例。
弯曲应力的定义
1 弯曲应力
当一个物体受到外力作用而发生弯曲时,物体内部会出现垂直于弯曲面的应力,这种应 力即为弯曲应力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
横截面上的正应力
3、静力学关系
FN = ∫ σ dA = 0,
A
代入
M y = ∫ zσ dA = 0,
A
σ = Eε = E
y
ρ
目前未解决问题: 目前未解决问题
M z = ∫ yσ dA = M
A
得到 中性轴where? ①z轴-中性轴 轴 中性轴
∫ ydA = 0,
A
∫ yz dA = 0,
A
E
材 料 力 学
Mechanics of Materials
横截面上的正应力
1、几何方面 、
取长度为dx的一段微梁, 取长度为 的一段微梁, 的一段微梁 变形后的形状如图。 变形后的形状如图。记长度不变 中性层) 轴线o 中性层 轴线 ´o´(中性层)的曲率半径 两横截面的夹角为dθ 为ρ,两横截面的夹角为 θ,则 变形后, 变形后,距o´o´为y处纤维的长 处纤维的长 度为 ( ρ + y)dθ 注意到o 于是, 注意到 ´o´= dx =ρ dθ,于是, 距o´o´为y处的纤维的线应变为 处的纤维的线应变为
已知:矩形截面 × 已知:矩形截面b× h 求:Iy, Iz
y
dA
dy
轴和y轴的微元面积 解:取平行于x轴和 轴的微元面积 取平行于 轴和
dA = bdy
z
dA
y
h C z dz
I z = ∫ y dA = ∫
2 A
h 2 h − 2
bh y bdy = 12
2
3
b
dA = hdz
I y = ∫ z 2dA = ∫
dx
材 料 力 学
Mechanics of Materials
到 中 性 层 的 距 离 成 正 比 它 与 变 应 线 的 维 纤 向 纵
即
b b − bb ( ρ + y)dθ − dx ( ρ + y)dθ − ρdθ y ε= = = = dx ρdθ ρ bb
' '
材 料 力 学
Mechanics of Materials
2
常见横截面的惯性矩 和抗弯截面系数
b h C y D d z y z
bh3 Iz = 12 bh2 Wz = 6
d z y
I =
z
πd
4
64
C
W =
z
πd
3
32
C
Iz =
πD 4
64
(1 − α 4 ),
Wz =
πD 3
32
(1 − α 4 ),
α=
d . D
材 料 力 学
Mechanics of Materials
A b 2 b − 2
hb3 z 2 hdz = 12
材 料 力 学
Mechanics of Materials
惯性矩、极惯性矩 惯性矩、
y
z
I y = ∫ z dA
2 A
dA
I z = ∫ y dA
2 A
A
OrΒιβλιοθήκη yzI P = ∫ r dA
2 A
IP = I y + Iz
材 料 力 学
Mechanics of Materials
–
材 料 力 学
Mechanics of Materials
横截面上的正应力
变形假设(里 变形假设 里)
1、弯曲变形的平面假设 、弯曲变形的平面假设 变形后, 变形后,横截面仍保 持为平面, 持为平面,并且仍与 弯曲后的纵向线正交, 弯曲后的纵向线正交, 纵向线正交 各截面间作相对转动。 各截面间作相对转动。
材 料 力 学
Mechanics of Materials
横截面上的正应力
M σ= y Iz
–
最大正应力发生在离中 性轴最远的点上, 性轴最远的点上,即
σ max
Mymax = Iz
I z ——抗弯截面系数,则 ——抗弯截面系数, 令 Wz = ymax M 抗弯截面系数综合反映了横 σ max = 截面形状和尺寸对弯曲正应 Wz
–
对于具有对称截面的一般细长梁(梁的跨 对于具有对称截面的一般细长梁( 对称截面的一般细长梁 与高度h之比 ),剪力 度l与高度 之比 ≥5),剪力对正应力的 与高度 之比l/h≥ ),剪力对正应力的 分布规律影响很小, 分布规律影响很小,上述计算正应力的公 式仍然可用, 式仍然可用,并且具有足够的精度
材 料 力 学
Mechanics of Materials
横截面上的正应力
研究梁横截面上应力的分布, 研究梁横截面上应力的分布,必须 几何(变形)、物理(本构) )、物理 从几何(变形)、物理(本构)和静力 平衡) 学(平衡)三方面进行综合分析 下面依次分析梁纯弯曲时, 下面依次分析梁纯弯曲时,这三个 方面的特征
1 M = ρ EIz
M σ= y Iz
梁横截面上的正应力分布公式
1
ρ
→ 梁变形剧烈程度 EI z → 抗弯刚度
材 料 力 学
Mechanics of Materials
附录: 附录:截面图形的几何性质
z y A dA z y
静矩: 静矩:
S y = ∫ zdA, Sz = ∫ ydA
形心公式
A A
惯性矩、 惯性矩、惯性半径
y
z
iy =
dA
y
Iy A
——图形对 轴的惯性半径 ——图形对 y 轴的惯性半径 z
O
iz =
Iz A
——图形对 轴的惯性半径 ——图形对 z 轴的惯性半径
材 料 力 学
Mechanics of Materials
已知:圆截面直径 已知:圆截面直径d 求:Iy, Iz, IP
材 料 力 学
Mechanics of Materials
组合图形的惯性矩
o z1
(2)组合图形的惯性矩 组合图形的惯性矩
Iyc=ΣIyci= Iy Σ
Izc=? 平行轴公式
Izc=Σ( zci+di2Ai) Σ(I Σ(
2
o’ zc
惯性矩平行轴定理: 惯性矩平行轴定理
I z = ∫ y dA = ∫ ( y0 + a) dA
ρ
ρ=?与弯矩有何关系 与弯矩有何关系? y 2 dA = M ②ρ=?与弯矩有何关系? ∫
A
材 料 力 学
Mechanics of Materials
∫ ydA = 0,
A
∫ yz dA = 0,
A
E
ρ
y 2 dA = M ∫
A
ρ的确定
E 2 ∫ y dA = M ρA
I z = ∫ y dA
2 A
材 料 力 学
Mechanics of Materials
第六章 弯曲应力
材 料 力 学
Mechanics of Materials
回顾
σ
Fs M
τ
上一章任务:合力 横截面上整体情况
本章任务:分力 横截面上每一点情况
材 料 力 学
Mechanics of Materials
几个基本概念
横力弯曲——横截面上 横截面上 横力弯曲 既存在弯矩, 既存在弯矩,又存在横 向剪力的梁的弯曲,称为 向剪力的梁的弯曲 称为 横力弯曲 纯弯曲——横截面上仅 纯弯曲 横截面上仅 存在弯矩的梁的弯曲 图示简直梁中 BC 段为纯弯曲 AB,CD段为横力弯曲 段为横力弯曲
材 料 力 学
Mechanics of Materials
正应力强度条件
对于一般的弯曲梁, 对于一般的弯曲梁,其弯矩是截面 位置的函数。因此计算等截面直梁 等截面直梁的最 位置的函数。因此计算等截面直梁的最 大正应力的公式为
σ max
M max ymax = Iz
即横截面上的最大正应力发生在全梁最大弯 横截面上的最大正应力发生在全梁最大弯 最大正应力 所在横截面的最外边缘各点 最外边缘各点处 矩Mmax所在横截面的最外边缘各点处
y
解:取圆环微元面积 dA
dr
r C
dA = 2 rdr π
z
IP 1 2 I y = Iz = = ∫ r dA 2 2 A
1 πd 4 = ∫ r 2 (2πr )dr = 2 64
d 2 0
d
I p = 2I y =
πd
4
32
材 料 力 学
Mechanics of Materials
组合图形的惯性矩
力的影响。 力的影响。
材 料 力 学
Mechanics of Materials
附录: 附录:截面图形的几何性质
惯性矩
z
I y = ∫ z dA,
2 A
I z = ∫ y dA,
2 A
y
A dA z y
材 料 力 学
Mechanics of Materials
Iz I z = ∫ y dA, Wz = ymax A
2 A 2 A 2
y z0 z y a b y0 A dA z0 z y0 y
= ∫ y0 dA + 2a∫ y0dA + Aa
A A
I z = I z 0 + Aa
2
I y = I y 0 + Ab2
材 料 力 学
Mechanics of Materials
横截面上的正应力
横力弯曲
是在纯弯曲 纯弯曲条件下 尽管公式 σ = Mzy/Iz 是在纯弯曲条件下 建立的。 弹性理论和实验表明 表明: 建立的。但弹性理论和实验表明:
横截面上的正应力
即对给定的横截面,其上 任一点的正应力与该点到 中性轴的距离成正比
