高等数学实验报告matlab参考答案
Matlab实验指导书(含答案)详解

实验一:Matlab操作环境熟悉一、实验目的1.初步了解Matlab操作环境。
2.学习使用图形函数计算器命令funtool及其环境。
二、实验内容熟悉Matlab操作环境,认识命令窗口、内存工作区窗口、历史命令窗口;学会使用format命令调整命令窗口的数据显示格式;学会使用变量和矩阵的输入,并进行简单的计算;学会使用who和whos命令查看内存变量信息;学会使用图形函数计算器funtool,并进行下列计算:1.单函数运算操作。
➢求下列函数的符号导数(1) y=sin(x);(2)y=(1+x)^3*(2-x);➢求下列函数的符号积分(1) y=cos(x);(2) y=1/(1+x^2);(3)y=1/sqrt(1—x^2);(4) y=(x-1)/(x+1)/(x+2);➢求反函数(1) y=(x—1)/(2*x+3);(2) y=exp(x);(3)y=log(x+sqrt(1+x^2));➢代数式的化简(1) (x+1)*(x—1)*(x—2)/(x—3)/(x-4);(2) sin(x)^2+cos(x)^2;(3)x+sin(x)+2*x—3*cos(x)+4*x*sin(x);2.函数与参数的运算操作。
➢从y=x^2通过参数的选择去观察下列函数的图形变化(1)y1=(x+1)^2(2)y2=(x+2)^2(3) y3=2*x^2(4)y4=x^2+2(5)y5=x^4(6)y6=x^2/23.两个函数之间的操作➢求和(1) sin(x)+cos(x)(2) 1+x+x^2+x^3+x^4+x^5➢乘积(1) exp(—x)*sin(x)(2)sin(x)*x➢商(1)sin(x)/cos(x);(2)x/(1+x^2);(3)1/(x-1)/(x-2);➢求复合函数(1) y=exp(u) u=sin(x)(2)y=sqrt(u) u=1+exp(x^2)(3)y=sin(u)u=asin(x)(4) y=sinh(u)u=—x三、设计提示1.初次接触Matlab应该注意函数表达式的文本式描述。
MATLAB全部实验及答案

MATLAB全部实验及答案实验一、MATLAB基本操作实验内容及步骤4、有关向量、矩阵或数组的一些运算(1)设A=15;B=20;求C=A+B与c=a+b?(2)设A=[1 2 3;4 5 6;7 8 9],B=[9 8 7;6 5 4;3 2 1];求A*B与A.*B?A*B就是线代里面的矩阵相乘 A.*B是对应位置的元素相乘(3)设a=10,b=20;求i=a/b=0.5与j=a\b=2?(4)设a=[1 -2 3;4 5 -4;5 -6 7]请设计出程序,分别找出小于0的矩阵元素及其位置(单下标、全下标的形式),并将其单下标转换成全下标。
clear,clca=[1 -2 3;4 5 -4;5 -6 7];[x,y]=find(a<0);c=[];for i=1:length(x)c(i,1)=a(x(i),y(i));c(i,2)=x(i);c(i,3)=y(i);c(i,4)=(y(i)-1)*size(a,2)+x(i);endc(5)在MATLAB命令行窗口运行A=[1,2;3,4]+i*[5,6;7,8];看结果如何?如果改成运行A=[1,2;3,4]+i[5,6;7,8],结果又如何?前面那个是虚数矩阵,后面那个出错(6)请写出完成下列计算的指令:a=[1 2 3;3 4 2;5 2 3],求a^2=?,a.^2=?a^2= 22 16 1625 26 2326 24 28a.^2=1 4 99 16 425 4 9(7)有一段指令如下,请思考并说明运行结果及其原因clearX=[1 2;8 9;3 6];X( : ) 转化为列向量(8)使用三元组方法,创建下列稀疏矩阵2 0 8 00 0 0 10 4 0 06 0 0 0方法一:clear,clcdata=[2 8 1 4 6];ir=[1 1 2 3 4 ];jc=[1 3 4 2 1];s=sparse(ir,jc,data,4,4);full(s)方法二:不用三元组法clear,clca=zeros(4,4);a(1,[1,3])=[2,8];a(2,4)=1;a(3,2)=4;a(4,1)=6;a(9) 写出下列指令的运行结果>> A = [ 1 2 3 ]; B = [ 4 5 6 ];>> C = 3.^A>> D = A.^B5、 已知⎪⎭⎫⎝⎛+⋅=-334sin 234πt e y t 若需要计算t ∈[-1,1],取间隔为0.01,试计算出相对应的y 值。
MATLAB实验三参考答案

how =collect(x)
4、求下列函数的极限(写出命令) (1) lim
cos x e x 0 x4
x2 2
syms x; limit('(cos(x)-exp(-1/2*x^2))/(x^4)',x,0) -1/12 (2) lim
2 x ln 2 x 1 x 0 1 cos x
syms n; S=symsum(1/((3*n-2)*(3*n+1)),n,1,inf) 8、试求出函数 f ( x )
sin x 的麦克劳林幂级数展开式的前 9 项,并求出关于 x=2 x 3x 2
2
的 Taylor 幂级数展开式的前 5 项。(命令 taylor 或者 taylortool)
河南财经政法大学数学与信息科学学院 1
实验报告
结果: EXPR =(x^2+x*exp(-t)+1)*(x+exp(-t)) expr1 =x^3+2*exp(-t)*x^2+(1+exp(-t)^2)*x+exp(-t) expr2 =x*exp(-t)^2+(2*x^2+1)*exp(-t)+(x^2+1)*x 3、factor(因式分解),simple(简化运算,对表达式尝试多种不同的算法进行简化,并以最 简化形式给出,How 中记录的为简化过程中使用的方法, )指令的使用 syms a x; f1=x^4-5*x^3+x^2+5*x-6; factor(f1) x^4-5*x^3+x^2+5*x-6 f2=x^2-a^2; factor(f2) (x-a)*(x+a) f3=2*sin(x)^2-cos(x)^2 [y , how]=simple(f3) y 为 f 的最优化简形式,How 中记录的为简化过程中使用的方法 y =-3*cos(x)^2+2 how =simplify [y , how]=simple(f1) y =x^4-5*x^3+x^2+5*x-6
高等数学实验2 微分、积分(含答案)

班级 学号 姓名高等数学实验2 微分、积分一. 用MA TLAB 计算下列导数:diff 函数(1)已知2xy e =,求y '、y ''、(10)y 。
(2)已知nx y e =,求y '''。
(3)已知210x y xe-=,求y '、y ''与(8)y 。
(4)设2sin ()43x f x x x =++,求()f x '、()f x ''及()6f π''。
二.用MA TLAB 解方程。
solve 函数1.一元方程与线性方程(组)(1) 解方程 062=--x x(2)解方程组⎪⎩⎪⎨⎧=-+=-+060622x y y x (3)解方程组⎪⎪⎩⎪⎪⎨⎧=+++=++=++-=++012412324543213214321431x x x x x x x x x x x x x x2.非线性方程(组)(4)解非线性方程组⎩⎨⎧=+-=--0sin 3.0cos 5.00cos 3.0sin 5.0212211x x x x x x 三。
用MA TLAB 计算极值:(1)已知销售额R 是价格P 的函数,且200184R P P ⎛⎫=-⎪+⎝⎭。
当价格P 为何值时, 销售额R 有最大值,且求此最大值。
(2)已知某公司收益函数210xR xe -=,成本函数32(1085)/100C x x =++,其中x 为产(销)量,求最大收益、最低平均成本和最大利润。
四.用MATLAB 计算下列不定积分 int 函数1.ln xdx ⎰; 2。
321x x e dx -⎰; 3. 42(31)sin(21)x x x dx -++⎰; 4.(sin sin cos )ax bx cx dx ⨯⨯⎰; 5.(练习)5(4)ln(32)x x x dx --⎰; 6.(练习)4sin(25)x x e dx +⎰;五.用MATLAB 计算下列定积分 int 函数1.120(1)x xe dx x +⎰ 2。
MATLAB数学实验答案(全)

第一次练习教学要求:熟练掌握Matlab 软件的基本命令和操作,会作二维、三维几何图形,能够用Matlab 软件解决微积分、线性代数与解析几何中的计算问题。
补充命令vpa(x,n) 显示x 的n 位有效数字,教材102页fplot(‘f(x)’,[a,b]) 函数作图命令,画出f(x)在区间[a,b]上的图形 在下面的题目中m 为你的学号的后3位(1-9班)或4位(10班以上) 1.1 计算30sin limx mx mx x →-与3sin limx mx mxx →∞- syms xlimit((902*x-sin(902*x))/x^3) ans =366935404/3limit((902*x-sin(902*x))/x^3,inf)//inf 的意思 ans = 0 1.2 cos1000xmxy e =,求''y syms xdiff(exp(x)*cos(902*x/1000),2)//diff 及其后的2的意思 ans =(46599*cos((451*x)/500)*exp(x))/250000 - (451*sin((451*x)/500)*exp(x))/250 1.3 计算2211x y edxdy +⎰⎰dblquad(@(x,y) exp(x.^2+y.^2),0,1,0,1)//双重积分 ans = 2.13941.4 计算4224x dx m x +⎰ syms xint(x^4/(902^2+4*x^2))//不定积分 ans =(91733851*atan(x/451))/4 - (203401*x)/4 + x^3/12 1.5 (10)cos ,x y e mx y =求//高阶导数syms xdiff(exp(x)*cos(902*x),10) ans =-356485076957717053044344387763*cos(902*x)*exp(x)-3952323024277642494822005884*sin(902*x)*exp(x)1.6 0x =的泰勒展式(最高次幂为4).syms xtaylor(sqrt(902/1000+x),5,x)//泰勒展式 ans =-(9765625*451^(1/2)*500^(1/2)*x^4)/82743933602 +(15625*451^(1/2)*500^(1/2)*x^3)/91733851-(125*451^(1/2)*500^(1/2)*x^2)/406802 + (451^(1/2)*500^(1/2)*x)/902 +(451^(1/2)*500^(1/2))/500 1.7 Fibonacci 数列{}n x 的定义是121,1x x ==12,(3,4,)n n n x x x n --=+=用循环语句编程给出该数列的前20项(要求将结果用向量的形式给出)。
数学实验(MATLAB)课后习题答案
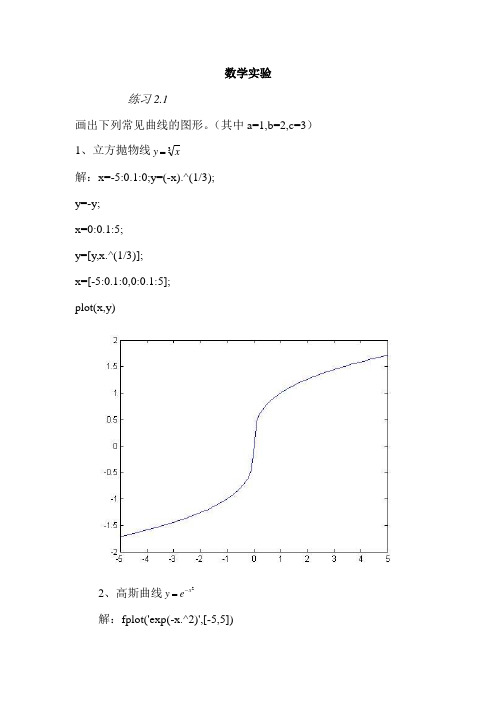
数学实验练习2.1画出下列常见曲线的图形。
(其中a=1,b=2,c=3)1、立方抛物线3xy=解:x=-5:0.1:0;y=(-x).^(1/3);y=-y;x=0:0.1:5;y=[y,x.^(1/3)];x=[-5:0.1:0,0:0.1:5];plot(x,y)2、高斯曲线2x e=y-解:fplot('exp(-x.^2)',[-5,5])3、笛卡儿曲线)3(13,1333222axy y x t at y t at x =++=+=解:ezplot('x.^3+y.^3-3*x*y',[-5,5])xyx.3+y.3-3 x y = 0或t=-5:0.1:5; x=3*t./(1+t.^2); y=3*t.^2./(1+t.^2); plot(x,y)4、蔓叶线)(1,1322322xa x y t at y t at x -=+=+=解:ezplot('y.^2-x.^3/(1-x)',[-5,5])xyy.2-x.3/(1-x) = 0或t=-5:0.1:5; x=t.^2./(1+t.^2); y=t.^3./(1+t.^2); plot(x,y)5、摆线)cos 1(),sin (t b y t t a x -=-= 解:t=0:0.1:2*pi;x=t-sin(t); y=2*(1-cos(t)); plot(x,y)6、星形线)(sin ,cos 32323233a y x t a y t a x =+== 解:t=0:0.1:2*pi; x=cos(t).^3; y=sin(t).^3;plot(x,y)或ezplot('x.^(2/3)+y.^(2/3)-1',[-1,1])xyx.2/3+y.2/3-1 = 07、螺旋线ct z t b y t a x ===,sin ,cos 解:t=0:0.1:2*pi; x=cos(t); y=2*sin(t); z=3*t; plot3(x,y,z) grid on8、阿基米德螺线θa r = 解:x =0:0.1:2*pi; r=x; polar(x,r)902701809、对数螺线θa e r = 解:x =0:0.1:2*pi; r=exp(x); polar(x,r)90270180010、双纽线))()((2cos 22222222y x a y x a r -=+=θ 解:x=0:0.1:2*pi; r=sqrt(cos(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-(x.^2-y.^2)',[-1,1]) grid onxy(x.2+y.2).2-(x.2-y.2) = 011、双纽线)2)((2sin 222222xy a y x a r =+=θ 解:x=0:0.1:2*pi; r=sqrt(sin(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-2*x*y',[-1,1]) grid onxy(x.2+y.2).2-2 x y = 012、心形线)cos 1(θ+=a r 解:x =0:0.1:2*pi; r=1+cos(x); polar(x,r)90270练习2.21、求出下列极限值。
MATLAB)课后实验答案

A = 1.0000 0 0 0 0 0 1.0000 0 0 0 0 0 1.0000 0 0 0.5383 0.9961 0.0782 1.0000 0 0.4427 0.1067 0.9619 0 2.0000
a = 1.0000 0 0 0 0 0 1.0000 0 0 0 0 0 1.0000 0 0 1.0767 1.9923 0.1564 1.0000 0 1.3280 0.3200 2.8857 0 4.0000
P= 1 1 1 1 1 2 3 4 1 3 6 10 1 4 10 20 1 5 15 35
1
5
15
35Βιβλιοθήκη 70Hh = 3.7493e-012
Hp = 1
Th = 4.7661e+005
Tp = 8.5175e+003 因为它们的条件数 Th>>Tp,所以 pascal 矩阵性能更好。 3. 建立一个 5×5 矩阵,求它的行列式值、迹、秩和范数。 解: M 文件如下:
实验一
MATLAB 运算基础
1. 先求下列表达式的值,然后显示 MATLAB 工作空间的使用情 况并保存全部变量。 (1) z1
2sin 850 1 e2
1 2
1 2i 2 5 0.45
(2) z2 ln( x 1 x 2 ) ,其中 x (3) z3
用 if 语句实现,分别输出 x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0 时的 y 值。 解:M 文件如下:
运算结果有: f(-5) y= 14 >> f(-3)
y= 11 >> f(1) y= 2 >> f(2) y= 1 >> f(2.5) y= -0.2500 >> f(3) y= 5 >> f(5) y= 19
高等应用数学问题的MATLAB求解_习题参考解答

= A−1 − A−1 B C −1 + B T A−1 B
B T A−1
试根据上面的算法用 MATLAB 语句编写一个函数对矩阵 M 进行求逆,并通过一个小例子来 检验该程序,并和直接求逆方法进行精度上的比较。 【求解】 编写这个函数 function Minv=part_inv(A,B,C) Minv=inv(A)-inv(A)*B*inv(inv(C)+B’*inv(A)*B)*B’*inv(A);
1)+fib(n − 2) 可以求出数列的 n + 1 项,这可以使用递归调用的功能,而递归调用的出口为
10 由矩阵理论可知,如果一个矩阵 M 可以写成 M = A + BCB T , 并且其中 A, B , C 为相应 阶数的矩阵,则 M 矩阵的逆矩阵可以由下面的算法求出 M −1 = A + BCB T
plot(xxx’,yyy’,’r’), axis(’square’) 13 选择合适的步距绘制出下面的图形 sin 1 t ,其中 t ∈ (−1, 1)。
% 变换成弧度
【求解】 用普通的绘图形式,选择等间距,得出如图 2-3a 所示的曲线,其中 x = 0 左右显得 粗糙。 >> t=-1:0.03:1; y=sin(1./t); plot(t,y) 选择不等间距方法,可以得出如图 2-3b 所示的曲线。 >> t=[-1:0.03: -0.25, -0.248:0.001:0.248, 0.25:.03:1]; y=sin(1./t); plot(t,y) 14 对合适的 θ 范围选取分别绘制出下列极坐标图形 ①ρ = 1.0013θ2 , ②ρ = cos(7θ/2), ③ρ = sin(θ)/θ, ④ρ = 1 − cos3 (7θ) 【求解】 绘制极坐标曲线的方法很简单,用 polar(θ,ρ) 即可以绘制出极坐标图,如图 2-4 所 示。注意绘制图形时的点运算: >> t=0:0.01:2*pi; subplot(221), polar(t,1.0013*t.^2),% (a) subplot(222), t1=0:0.01:4*pi; polar(t1,cos(7*t1/2)) subplot(223), polar(t,sin(t)./t) % (c) subplot(224), polar(t,1-(cos(7*t)).^3) 15 用图解的方式找到下面两个方程构成的联立方程的近似解。 x2 + y 2 = 3xy 2 , x3 − x2 = y 2 − y 【求解】 这两个方程应该用隐式方程绘制函数 ezplot() 来绘制,交点即方程的解,如图 2-5a 所示。 % (b)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
成都大学高等数学实验报告(MATLAB版)班级姓名学号注意:1 这个答案可由教师保存;2 每个班级注意保存实验报告。
成都大学高等数学教研室2011年3月高等数学实验报告1 基本计算与作图班级 姓名 学号 完成时间 成绩一、实验内容基本计算,函数的表示,函数图形的显示.二、预期目标1.熟悉Matlab 软件的基本操作.2.掌握基本计算,函数的表示与函数的作图命令.3.学会利用Matlab 软件对函数进行分析研究.三、练习内容习题一1.计算下列各式的值:(写出格式及执行结果,(1)为例式) (1)1675; >> 75^16ans = 1.0023e+030 (2)i31-; (3)23sin ;>> sqrt(1-3*i) >>sin(23*pi/180) ans = 1.4426 - 1.0398i ans = 0.3907 (4)π2arcsin; (5)!88.>> asin(2/pi) >> factorial(88) ans = 0.6901 ans = 1.8548e+134 2.3tan,2π==b e a e,计算:(1)5332532b a ab a -+; (2))sec(arctana .>> a=sqrt(exp(exp(1))); b=tan(pi^2/3); >> a=sqrt(exp(exp(1))); b=tan(pi^2/3); >> 2*a^2+3*a*b^3-5*a^3*b^5 >> sec(atan(a)) ans =30.3255 ans =4.0192 3.在计算机上练习以下语句的输入:((1)为求解格式)(1)143212-+x bx ax ; (2)13ln 42sin 2+-⎪⎭⎫ ⎝⎛+x x x π;>> syms a b x >> syms x>> (3*a*x^2+4*b*x^(1/2))/(x-1) >> (sin(2*x+pi/4)-log(3*x))/sqrt(x^2+1)ans =(3*a*x^2+4*b*x^(1/2))/(x-1) ans = (sin(2*x+1/4*pi)-log(3*x))/(x^2+1)^(1/2) (3)xex x 22)2sin (cos -.>> syms x>> (cos(x)^2-sin(2*x))*exp(2*x) ans =(cos(x)^2-sin(2*x))*exp(2*x) 习题二(只写出输入格式) 1.作出13y x =的图象>> x=linspace(0,3,100); >> y=x.^(1/3); >> plot(x,y) 参见图12.作出14xy ⎛⎫=⎪⎝⎭的图象 3.作出14log y x =的图象 >> x=linspace(-2,2,50); >> fplot('log(x)/log(1/4)',[0.1,3])>> y= (1/4).^x; >> plot(x,y)参见图2 参见图3图1图2 图34.作出sin(2)4y x π=+在一个周期内的图象 5.作分段函数2,0()1,0x x f x x x ⎧≤=⎨+>⎩的图象。
>> x=linspace(0,pi,100); >> x1=-2:0.1:0;x2=0:0.1:2; >> y=sin(2*x+pi/4); >> y1=x1.^2;y2=x2+1; >> plot(x,y) >> plot(x1,y1,x2,y2) 参见图4 参见图56.在一个坐标系内作y=x,y=cosx,x ∈[0,π]和y=arccosx,x ∈[-1,1]的图象,且要求两坐标轴上的单位比为1:1,y=x 用虚线和红色,y=cosx 用绿色,y=arccosx 用蓝色。
>> x1=linspace(-1,pi,100);y1=x1;>> x2=linspace(0,pi,100);y2=cos(x2);>> x3=linspace(-1,1,100);y3=acos(x3);>> plot(x1,y1,'r:',x2,y2,'g',x3,y3,'b')参见图6四、思考与提高1. 怎样对隐函数的图形进行显示?2. 如何利用软件对函数的连续性进行判断?图4图5图6高等数学实验报告2 极限·导数与微分·极值班级 姓名 学号 完成时间 成绩一、实验内容极限,导数与微分的运算法则,复合函数求导法及参数方程求导法等.二、预期目标1.进一步理解极限,导数及其几何应用.2.学习Matlab 的求极限,求导命令与求导法.三、练习内容习题一求下列函数的极限:1.1lim x x a x→+∞- 2. 222ln(3)lim 32x x x x →--+>> syms a x >> syms x>> limit((a^x-1)/x) >> limit(log(x^2-3)/(x^2-3*x+2),2) ans =log(a) ans =43. 2ln lim ln x x x x x→+∞+ 4. 0tan lim 2x xx →>> syms x >> syms x>> limit((x^2+log(x))/(x*log(x)),+inf) >>limit(tan(x)/(2*x)) ans =Inf ans =1/2 5. 0sin 4limsin 3x x x → 6. 2lim ln(1)x x x→∞+>> syms x >> syms x>> limit(sin(4*x)/(3*x),0) >>limit(x*log(1+2/x),inf) ans =4/3 ans =2习题二求下列函数的导数或微分:(写出命令和结果)1.y =y '.2. ln ,y x =求y '''.>> syms x >> syms x>> diff(asin(sqrt(x))) >>diff(log(x),3) ans =1/2/x^(1/2)/(1-x)^(1/2) ans =2/x^33. 21sincos xy x +=,求y '. 4.211y x x =+求y '.>> syms x >> syms x>> diff((1+sin(x)^2)/cos(x),1) >> diff('1/x+1/x^2+1/x^(2/3)') ans =1/2/x^(1/2)/(1-x)^(1/2) ans = -1/x^2-2/x^3-2/3/x^(5/3)5.(1y =+ ,求y '.6.tan ,xy x=求dx .>> syms x >> syms x>>diff((1+x^(1/2))*(2+x^(1/3))*(3+x^(1/4)),1) >> diff(tan(x)/x) ans =ans=1/2/x^(1/2)*(2+x^(1/3))*(3+x^(1/4))+1/3*(1+x^(1/2))/x^(2/3)*(3+x^(1/4))+1/4*(1+x^(1/2))*(2+x^(1/3))/x^(3/4)7.y =求dx . 8.2(22),x y e x x =-+ 求dx .>> syms x >> syms x>> diff((sqrt(x+1)-sqrt(x+2))/(sqrt(x+1)+sqrt(x+2))) >> diff(exp(x)*(x^2-2*x+2)) ans= (1/2/(x+1)^(1/2)-1/2/(x+2)^(1/2))/((x+1)^(1/2) ans = exp(x)*(x^2-2*x+2) +(x+2)^(1/2))-((x+1)^(1/2)-(x+2)^(1/2))/((x+1)^(1/2) +exp(x)*(2*x-2) +(x+2)^(1/2))^2*(1/2/(x+1)^(1/2)+1/2/(x+2)^(1/2)) 习题三求下列函数的极值:(要求写出输入及结果,可通过计算机的结果画出草图)1.22(1)sin 1y x x =--, 2.y =.输入f='(x^2-1)^2-1'; 输入g='sqrt(2*x-x^2)'; fplot(f,[-3,3]) fplot(g,[0,2])[x1min,y1min]=fminbnd(f,-3,0) g1='-sqrt(2*x-x^2)';[x2min,y2min]=fminbnd(f,0,3) [xmin,ymin]=fminbnd(g1,0.8,1.2); f1='-(x^2-1)^2+1'; xmax=xmin,ymax=-ymin [xmin,ymin]=fminbnd(f1,-0.5,0.5); 结果xmax =1 ymax =1 xmax=xmin,ymax=-ymin结果x1min =-1.0000 y1min =-1.0000 x2min =1.0000 y2min =-1.0000 xmax =-5.5511e-017 ymax =0高等数学实验报告3 积分班级 姓名 学号 完成时间 成绩一、实验内容一元函数的不定积分与定积分的求解二、预期目标1.加深理解积分理论中分割、近似、求和、取极限的思想方法.2.学习求积分的命令int .3.熟悉Matlab 软件在积分运算的重要作用.三、练习内容1.742x dx x +⎰ 2. 131x e dx x⎰ >> int('x^7/(x^4+2)') >> int('exp(1/x)/x^3') ans =1/4*x^4-1/2*log(x^4+2) ans = -exp(1/x)/x+exp(1/x)3. 221sin cos dx x x⎰ 4. 21x x e dx e +⎰ >>int('1/sin(x)^2/cos(x)^2') >>int('exp(x)/(1+exp(2*x))')ans =1/sin(x)/cos(x)-2/sin(x)*cos(x) ans =atan(exp(x))5.24363x x dx x +-+⎰6. 1⎰ >>int('(x^2+x-6)/(x+3)','x',3,4) >>int('sqrt(x^2-1)/x','x',1,2)ans = 3/2 ans =3^(1/2)-1/3*pi 7.2211(1)dx x x +∞+⎰8. 0sin xe xdx +∞-⎰ >> int('1/x^2/(x^2+1)','x',1,+inf) >>int('exp(-x)*sin(x)','x',0,+inf)ans =-1/4*pi+1 ans =1/2高等数学实验报告4 微分方程的计算班级 姓名 学号完成时间 成绩一、实验内容求微分方程的解析解和数值解。
