格 布尔代数的应用
离散数学第6章 格与布尔代数

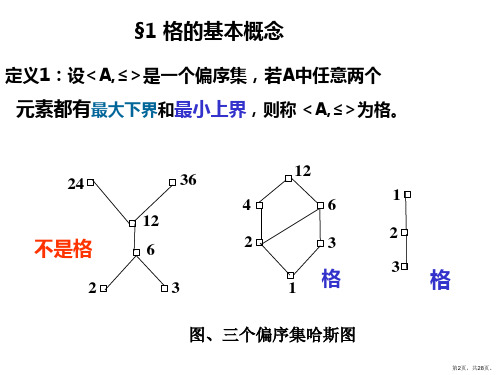
6-1 格的概念
5)下面证明 a∧b=aa∨b=b 若a∧b=a 则 a∨b=(a∧b)∨b=b 反之,若a∨b=b 则 a∧b=a∧(a∨b)=a
b用a∨b代替(∵两式中b是相互独立的) ∴a∨(a∧(a∨b))=a 即 a∨a=a. (2)格的等价定理:〈A,∨,∧〉代数系统,∨.∧满足交换性, 结合性,吸收性,则A上存在偏序关系≤,使〈A,≤〉是一个格
从格可引出代数系统〈A,∨,∧〉; 而从满足三个条件的〈A,∨,∧〉也可导出格〈A,≤〉 证明见书:(格中⑻⑼⑾三个性质很重要,决定了格)
(11) 要证 a≤a∨(a∧b) 第一式显然成立
a∨(a∧b)≤a
a≤a
a∧b≤a
∴a∨(a∧b) ≤a
∴a=a∨(a∧b)
6-1 格的概念
6、格的等价原理:格〈A,≤〉 (1)引理6-1.1:〈A,∨,∧〉代数系统,若∨, ∧满足吸收性,
则∨, ∧满足幂等性 证:a,b∈A. a∨(a∧b)=a a∧(a∨b)=a.
第六章 格与布尔代数
格论是近代数学的一个重要分支,由它所引出的布尔 代数在计算机科学中有很多直接应用。
格的概念 分配格 有补格 布尔代数 布尔表达式
6-1 格的概念
1、回忆偏序集〈A,≤〉,≤偏序关系:满足自反性,反对称性, 传递性。有限集合上的偏序集可用哈斯图来表示:
COV (A) {a,c, b,c, c, d, d,e, d, f }
∧也易求得 ∴ A,∨,∧〉是格〈A,|〉 诱导的代数系统
6-1 格的概念
09-格与布尔代数-8.2

第三节 子布尔代数、积布尔代数、布尔代数同态
定义:给定布尔代数<B, , *, ’ , 0, 1>,≠T B
2015年6月6日星期六
若T对 、* 和 ’ 是封闭的,且:0, 1 T
称<T, , *, ’ , 0, 1>是<B, , *, ’ , 0, 1>的子布尔代 数 显然:<{0, 1}, , *, ’ , 0, 1>和<B, , *, ’ , 0, 1> 都是<B, , *, ’ , 0, 1>的(平凡)子布尔代数
则:<f(B),∨,∧, , f(0), f(1)>是布尔代数 (证明参见教材P170 —— 利用布尔代数的定义证明)
布尔代数同态
结论:
2015年6月6日星期六
若 f 是从布尔代数<B, , *, ’ , 0, 1>到格<S,∨,∧>的 格同态映射,且f是满射的,
则:<S,∨,∧>是布尔代数
并且可以用基本公式来定义布尔代数
布尔代数的定义 从这4个定律,可以推出所有布尔代数的公式
有兴趣的同学可以参阅 R. L. 古德斯坦因 著的
对于a, b B , 有 定义:设<B, , *, ’ >是一个代数结构,其中:
2015年6月6日星期六
和 * 是B上的二元运算,’ 是B上的一元运算,且 0, 1 B
例9.15:设Bn是由0和1形成的n元组集合,且
2015年6月6日星期六
a = <a1, a2, …, an>,b = <b1, b2, …, bn> 0n = <0, 0, …, 0> , 1n = <1, 1, …, 1> 对任意 a, b Bn,定义: a b = < a1∨b1, a2∨b2 , …, an∨bn > a * b = < a1∧b1, a2∧b2 , …, an∧bn > a’ = < a1, a2, …, an> < Bn,∨,∧, , F, T>是布尔代数(开关代数)
格与布尔代数课件2
= {y | y≤x1} ∪ {y | y≤x2} = f(x1) ∨2 f(x2)
存在一个从A1到A2的映射f,使得对 x1,x2 A, 有f(x1∨1x2)=f(x1)∨2f(x2),f(x1∧1x2)=f(x1)∧2f(x2) ∴f 是 A1 到 A2 的格同态。
吸收律:a∨(a∧b) = a、a∧(a∨b) = a
证明:幂等律 ∵ a≤a,∴ a是a的上界,而a∨a是a的最小上界, ∴a∨a≤a ,又 ∵ a≤a ∨a,
由反对称性得:a∨a = a 由对偶原理得,a∧a = a
第15页,共28页。
证明:吸收律 ∵ a ≤a a ∧b ≤a ∴ a∨(a ∧ b)≤a∨a, a∨(a ∧ b)≤a
解:< I+ , D>是格 ∵整除关系是偏序关系,对a,bI, a、b的最小上界等于a、b的最小公倍数, a、b的最大上界等于a、b的最大公约数。
第3页,共28页。
< P(S) , > 是格
∵子集关系是偏序关系,对a,b P(S),
a、b的最小上界等于a∪b,
a、b的最大上界等于a∩b。
<<=S{S<n61, ,D,1D>>>,是<2格,2,>,<偏3,序3>关,<系1,6的>,哈<1斯,2>图,<如1,下3>1:,2<2,6>,<3,6>}
{a,b,c}
a
{a,b} {a,c} {b,c}
格和布尔代数

分三步: 1) 证明’≤’是L上的偏序关系 2)证明 a,bL, {a,b}的下确界存在, 且 a∧b = glb(a,b)。 3)a,bL, {a,b}的上确界存在,且 lub(a,b) a∨b 具体证法见后面
1) 证明’≤’是L上的偏序关系 自反性:aL 由等幂律 a∧a=a, a≤a 反对称性:a,bL, 若a≤b, b≤a 则 a∧b=a, b∧a=b a = a∧b = b∧a = b 传递性:a,b,cL, 若 a≤b,b≤c 则a∧b=a, b∧c=b a∧c=(a∧b)∧c = a∧(b∧c)= a∧b=a a≤c
2、格的对偶原理
① 集合S的偏序关系≤的逆关系≥也是偏序关 系,若AS, 其中 ≤的glb(A) 对应于 ≥的lub(A), ≤的lub(A) 对应于 ≥的glb(A), 所以,若<S,≤>是格,则<S,≥>也是格, 称这两个格互为对偶。
2、格的对偶原理
② 因为<S,≤>的交是<S,≥>的并, <S,≤>的并是<S,≥>的交,
一般格只满足分配不等式: a∨(b∧c)≤(a∨b)∧(a∨c)
一、定义
设<L,∧,∨>是格,若a,b,cL,有: (1) a∧(b∨c)=(a∧b)∨(a∧c), (2) a∨(b∧c)=(a∨b)∧(a∨c), 则称 <L,∧,∨> 为分配格。
注:(1)(2)是互相等价的,由对偶原理,从一式可推
2)证明 a,bL, {a,b}的下确界存在, 且 a∧b=glb(a,b)。
a) 因为 (a∧b)∧a =(a∧a)∧b=a∧b a∧b≤a 同理a∧b≤b a∧b 是a,b的下界。
格与布尔代数

三. 格的性质
5. ∨和∧都满足结合律。即 (a∨b)∨c =a∨(b∨c) , (a∧b)∧c =a∧(b∧c) 。 证明:⑴先证明(a∨b)∨c ≤a∨(b∨c) ∵ a≤ a∨(b∨c) b≤b∨c ≤ a∨(b∨c) (性质1) 即a∨(b∨c) 为{a,b}的上界。 ∴ (a∨b) ≤a∨(b∨c) 又 ∵ c≤b∨c ≤ a∨(b∨c) (性质1) 即a∨(b∨c) 为{a∨b ,c}的上界 ∴ (a∨b)∨c ≤a∨(b∨c) ⑵同理可证 a∨(b∨c)≤(a∨b)∨c 最后由反对称得 (a∨b)∨c =a∨(b∨c) 类似可证 (a∧b)∧c =a∧(b∧c) 。
。 。 。 。
a b
1
a
c
d e
2 4
3 5
b d
c e
6
这三个偏序集,也都不是格,第一个与第三个是同构 的。因为 d和e无下界,也无下确界;b,c虽有下界, 但无下确界。 2,3无下确界,4,5无上确界。 2. 平凡格:所有全序都是格,称之为平凡格。 因为全序中任何两个元素x,y,要么x≤y, 要么y≤x。 如果x≤y,则{x,y}的下确界为x,上确界为y。 如果y≤x,则{x,y}的下确界为y,上确界为 x 。 即这{x,y}的下确界为较小元素,上确界为较大元素.
*9. a≤b a∨b=b a∧b=a
证明:下面只证明a≤b a∨b=b 先证a≤b a∨b=b 设 a≤b,又b≤b ∴ a∨b≤ b 又∵ b≤a∨b 由反对称得 a∨b=b 再证 a∨b=b a≤b 已知 a∨b=b ∵ a≤ a∨b ∴ a≤b。 最后得 a≤b a∨b=b 这是个很重要的定理,我们在以后经常用到此论。
离散数学结构 第十三章 格与布尔代数

第十三章格与布尔代数13.1 格的定义与性质一、格作为偏序集的定义1.格的定义定义13.1设<S,>是偏序集,如果x,y S,{x,y}都有最小上界和最大下界,则称S 关于偏序作成一个格。
由于最小上界和最大下界的唯一性,可以把求{x,y}的最小上界和最大下界看成x与y的二元运算∨和∧,即求x∨y和x∧y分别表示x与y的最小上界和最大下界。
这里要说明一点,本章中出现的∨和∧符号只代表格中的运算,而不再有其它的含义。
2.格的实例例13.1设n是正整数,S n是n的正因子的集合。
D为整除关系,则偏序集<S n,D>构成格。
x,y∈S n,x∨y是lcm(x,y),即x与y的最小公倍数。
x∧y是gcd(x,y),即x与y的最大公约数。
图13.1给出了格<S8,D>,<S6,D>和<S30,D>.图13.1例13.2 判断下列偏序集是否构成格,并说明理由。
(1) <P(B),>,其中P(B)是集合B的幂集。
(2) <Z,≤>,其中Z是整数集,≤为小于或等于关系。
(3) 偏序集的哈斯图分别在图13.2中给出。
二.格的性质1.对偶原理定义13.2设f是含有格中元素以及符号=,,,∨和∧的命题。
令f*是将f中的替换成,替换成,∨替换成∧,∧替换成∨所得到的命题。
称f*为f的对偶命题。
例如,在格中令f是(a∨b)∧c c, 则f*是(a∧b)∨c c .格的对偶原理设f是含有格中元素以及符号=,,,∨和∧等的命题。
若f对一切格为真,则f的对偶命题f*也对一切格为真。
例如,对一切格L都有a,b∈L,a∧b a那么对一切格L都有a,b∈L,a∨b a许多格的性质都是互为对偶命题的。
有了格的对偶原理,在证明格的性质时,只须证明其中的一个命题就可以了。
2. 运算性质定理13.1设<L,>是格,则运算∨和∧适合交换律、结合律、幂等律和吸收律,即(1) a,b ∈L 有a∨b=b∨a, a∧b=b∧a(2) a,b,c∈L 有(a∨b)∨c=a∨(b∨c), (a∧b)∧c=a∧(b∧c)(3) a∈L 有a∨a=a, a∧a=a(4) a,b∈L 有a∨(a∧b)=a, a∧(a∨b)=a证(1)a∨b和b∨a分别是{a,b}和{b,a}的最小上界。
(优选)第篇格与布尔代数

第2式证明由对偶原理从上式直接可得。
定理15-1.6 设<A, >是一个格,那么,对于任意的 a,bA, 都有:
ab(a∧b)=a(a∨b)=b
ab(a∧b)证明思路:
(1)先证 ab (a∧b)=a
由ab和a a ,根据定理15-1.2得 a a∧b
又根据a∧b的定义, 有
a∧b a
由二元关系的反对称性得 :
(优选)第篇格与布尔代数
通常用a∨b 表示{a,b}的上确界,用a∧b 表示{a, b}的下确界,∨和∧分别称为保联(join)和保交(meet) 运算。由于对任何a,b,a∨b及a∧b都是A 中确定 的成员,因此 ∨,∧均为A上的运算。
例3 设S={a,b} , (S) ={, {a},{b},{a,b}} 由格< (S), >诱导的代数系统为< (S),∨,∧> 。 其中∨为集合的并运算和∧为集合的交运算。
a∧b = a
(2) 再证 (a∧b)=a ab
设a∧b=a,则a =a∧bb ,这就证明了
(a∧b)=a ab
综合(1)和(2)得: ab(a∧b)
定理15-1.7 设<A, >是一个格,那么,对于任意的
a,b,cA, 都有: aca∨(b∧c) (a∨b)∧c
证明思路: (1)先证 ac a∨(b∧c) (a∨b)∧c 根据定理15-1.6有 ac (a∨c)=c 根据定理15-1.5有a∨(b∧c)(a∨b)∧(a∨c)
可以证明,若<A,>是格,则<A,R>也是格。 称R是的逆关系。记为。
格对偶原理可以叙述为:设P是对任意格都真的命题, 如果在命题P中把换成 ,∨换成∧,∧换成∨,就
地六章-格和布尔代数(1)

定义6.7 集合 L 中的偏序关系 R 与其逆关系 R1,称为互 相对偶的两个关系。 对任意 x, y∈L,xR1y yRx。 6.1.1 节例 6.4 中的 关系即为蕴涵关系 的逆关系。 因此,对任意 P, Q∈S, (P Q) (Q P)
【例6.7】设 n 是一个正整数,Sn 是 n 的所有因数的集合, 两个正整数的最大公因数 ,最小公倍数 可看作是 Sn 上两个代数运算,于是,(Sn, , ) 是一个格。
定理6.1 关于格的两种定义(以对应一个代数格;任意一个代 数格也都可以对应一个偏序格。
定义中没有要求 , 运算满足等幂律,实际上由 , 满足吸收律即可推出它们一定满足等幂律。任取 L 中元素
a,由 , 满足吸收律知
a(aa)=a
a(aa)=a
故
aa=a(a(aa))
aa=a(a(aa))
又由 , 满足吸收律知,上面两式的等式右端都等于 a。
因此,
aa=a
aa=a
即定义 6.3 中的 , 运算亦满足等幂律。
【例6.4】设 S 是所有的命题集合,定义 “” 关系如下: A B 当且仅当 B 蕴涵 A
则 (S, ) 是一个格。对 A, B∈S, sup{A, B}=A∧B∈S inf{A, B}=A∨B∈S
定义6.2 若格 L 的一个子集 M≠Ф 对于运算 和 封闭, 则 M 称作子格。
例如:a 是格 L 的一个固定元素,则使 X≥a(或 X≤a) 的 L 中元素 X 的集合,显然是一个子格。若 a≥b,则使 a≥X≥b 的 L 中元素 X 的集合是一个子格,这样的子格 叫作一个闭区间(商),记作 M(a,b)。
例如,S6={1, 2, 3, 6}, S24={1, 2, 3, 4, 6, 8, 12, 24}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
格布尔代数的应用
布尔代数起源于数学领域,是一个用于集合运算和逻辑运算的公式:〈B,∨,∧,¬ 〉。
其中B为一个非空集合,∨,∧为定义在B上的两个二元运算,¬为定义在B上的一个一元运算。
通过布尔代数进行集合运算可以获取到不同集合之间的交集、并集或补集,进行逻辑运算可以对不同集合进行与、或、非。
应用
布尔代数不仅可以在数学领域内实现集合运算,更广泛应用于电子学、计算机硬件、计算机软件等领域的逻辑运算:当集合内只包含两个元素(1和0)时,分别对应{真}和{假},可以用于实现对逻辑的判断。
常见的应用包括:
•数字电路设计,0和1与数字电路中某个位的状态对应,例如:高电平、低电平。
•计算机的网络设置,利用计算机的二进制特性,将子网掩码与本机IP地址进行逻辑与运算,可以得到计算机的网络地址和主机地址。
•数据库应用,通过SQL语句查询数据库时需要进行逻辑运算,确定具体的查询目标。
