热力学函数的基本关系式
合集下载
热力学状态函数及其关系式.完整版PPT资料

dFSdT pdV dGSdTVdp
由于U、H、F、G为状态函数 U=U(S,V),H=(S,p),F=F(T,V),G=G(T,p)
dU U dS U dV
S V
V S
dH H dS H dp
S V
V S
dF F dT F dV
T V
V T
dG
G dT T VLeabharlann G pTdp
dUTdSpdV
dHTdSVdp
dFSdT pdV dGSdTVdp
U H T S V S p U F p V S S T
T p 2 u V S S V SV
T p
S
V S
p
2H Sp
由于U、H、F、G为状态函数
麦U=克U斯(S韦,(MV)a,xwHe=ll ()S关,系五p式),个F=F状(T,态V),函G=数G(TU,p、) H、S、F、G,以及可以直接测量p、
吉热布力斯 学-状亥态姆函霍V数滋及(、G其ib关bTs系-、H式elmChopltz、)方程Cv等函数,为重要的热力学性质;其中基本
定义:
T
1 V V T p
SpT
V Tp
TV
dHTdSVdp H pTT S pTVV(1TT)
由于膨胀系数αT可以通过测量得到,因此可用上两式 得到某温度下材料的S和H随压力的变化。
吉布斯-亥姆霍滋(Gibbs-Helmholtz)方程
GH-TS
G= H S
TT
G T T p H T T p T S p = T 1 H T p H 1 T T p T S p
热力学状态函数及其关系 式
状态函数关系式 麦克斯韦(Maxwell )关系式 吉布斯-亥姆霍滋(Gibbs-Helmholtz)方程 基尔霍夫(Kirchhoff )公式 克劳修斯-克拉配龙(Clausius-Glapeyron)方程 埃阑菲斯特(Ehrenfest)方程 理查德(Richard)规则和楚顿(Trouton)规则
由于U、H、F、G为状态函数 U=U(S,V),H=(S,p),F=F(T,V),G=G(T,p)
dU U dS U dV
S V
V S
dH H dS H dp
S V
V S
dF F dT F dV
T V
V T
dG
G dT T VLeabharlann G pTdp
dUTdSpdV
dHTdSVdp
dFSdT pdV dGSdTVdp
U H T S V S p U F p V S S T
T p 2 u V S S V SV
T p
S
V S
p
2H Sp
由于U、H、F、G为状态函数
麦U=克U斯(S韦,(MV)a,xwHe=ll ()S关,系五p式),个F=F状(T,态V),函G=数G(TU,p、) H、S、F、G,以及可以直接测量p、
吉热布力斯 学-状亥态姆函霍V数滋及(、G其ib关bTs系-、H式elmChopltz、)方程Cv等函数,为重要的热力学性质;其中基本
定义:
T
1 V V T p
SpT
V Tp
TV
dHTdSVdp H pTT S pTVV(1TT)
由于膨胀系数αT可以通过测量得到,因此可用上两式 得到某温度下材料的S和H随压力的变化。
吉布斯-亥姆霍滋(Gibbs-Helmholtz)方程
GH-TS
G= H S
TT
G T T p H T T p T S p = T 1 H T p H 1 T T p T S p
热力学状态函数及其关系 式
状态函数关系式 麦克斯韦(Maxwell )关系式 吉布斯-亥姆霍滋(Gibbs-Helmholtz)方程 基尔霍夫(Kirchhoff )公式 克劳修斯-克拉配龙(Clausius-Glapeyron)方程 埃阑菲斯特(Ehrenfest)方程 理查德(Richard)规则和楚顿(Trouton)规则
热力学函数的基本关系式

dU = TdS- pdV
(1-108)
dH = TdS + Vdp
(1-109)
dA = -SdT- pdV
(1-110)
dG = -SdT + Vdp
(1-111)
式(1-108),(1-109),(1-110),(1-111)称为热力学基本方程
dU = TdS- pdV dH = TdS + Vdp dA = -SdT- pdV dG = -SdT + Vdp
常用的是式(1-120)及式(1-121),这两等式右边的变化率是可以由 实验直接测定的,而左边则不能。可用等式右边的变化率代替左
4.热力学状态方程
由dU=TdS-pdV
定温下, dUT=TdST-pdVT
等式两边除以dVT 即
dUT T dST p
dVT
dVT
由麦克斯韦方程 于是
U T S p V T V T S p V T T V
式(1-116)及 (1-117)叫吉布斯 - 亥姆霍茨方程。
(1-117)
G-H方程常用的形式为:
即
(G / T )
T p
H T2
加△
(1-116)
Gibbs自由能随压力的变化
因
(эG/эP)T,n=V
(э△G/эP)T,n=△V 此即G---V关系式
只要知道△V--p关系式,在定温下P1的△G1就可求算出P2的△G2。
在定压下从T1到 T2积分得: (△G)2/ T2- (△G)1/ T1=- =∫T1 T2 △H/T2dT 若知△H--T关系以及T1时的△G1就可求算T2时的△G2 而: △H= △H T0+∫ T0 T △CpdT △H T0是T0时的焓变。
热力学基本关系式

)S
(V S
)
p
(Sp)T (VT)p
第17页,本讲稿共62页
4.7热力学关系式的应用
18
4.7.1材料热力学中一些常见的定义公式
U T
V
CV
H T
P
CP
CI
T S T I
S C p T p T
S CV T V T
恒压膨胀 V 系 V 1数 V TP
恒容压力 系 1数 P
U T p p V T T V
对理想气体而言:
U VT
Tp TV
pTTnVRTV
p
TnRppp0 V
由U=U(T,V),已证明理想气体的热力学能在定温下与 体积无关,所以U只是温度的函数。
第27页,本讲稿共62页
28
4.7.6理想气体的内能和焓
同理:
H p
T
T V T
p
V
对应系数关系式讲的是特性函数与其某一特征变
量的偏微商关系,脚标为该特性函数的另一特征变量 ,结果等于偏微特征变量的共轭变量。
U H T S V S p
U F p V S V T
H p
S
G p
T
V
F G S T V T p
第16页,本讲稿共62页
dG -SdT VdP
G S T P
G V P T
H G TS G T G T P
U H - PV G - T G P G T P P T
F G PV G P G P T
常用的特性函数与特征变量为:
G(T ,P ) F(T ,V ) U( S ,V )
和教材 P52的推导 进行比较
H p T G p T T T 2 G p V T T G p T p V T V T p
热力学函数的基本关系式

dG = -SdT + Vdp
S p
T
V T
p
麦克斯韦关系式 :表示的是系统在同一状态的两种
变化率数值相等。 9
二阶混合偏导数
T p V S S V 麦氏方程记忆法:
T p
S
V S
p
① 对角乘积永远是pV,TS;
② 等式两边分母与外角标互换;
S p
T
V T
4
由四个热力学基本方程,分别加上相应的条件,可得到
8个派生公式:
dU = TdS- pdV
U S
V
T
U V
S
p
dH = TdS + Vdp
T V H
S p
H p S
dA = -SdT- pdV
A T
V
S
A V
T
p
dG = -SdT + Vdp
G T
P
S
G P
则
U T p p
V T T V
11
练习:由热力学基本方程出发证明,
H p
T
T
V T
p
V
证明:
dH=TdS+Vdp
定温下,等式两边除以dp
H p
T
T
S p
T
V
由麦克斯韦方程
S p
T
V T
p
返回
H p
T
T
V T
p
V
12
U T p p V T T V
S T p
T
T
定容
S CV T V T
S T V
15
T
V
5
2. 吉布斯 - 亥姆霍茨方程
热力学第二定律(4)
dH TdS Vdp
(3) dA SdT pdV (4)
A(T ,V )
G(T , p)
dG SdT Vdp
适用条件:(1)无相变化和化学变化(恒定组成)的均 相封闭系统发生单纯pVT变化的可逆或不可逆过程(2) 对于化学反应和相变化只适用于非体积功为零的可逆过程 即非体积功为零的恒定组成的封闭系统
解:对理想气体,
pV nRT
p nRT /V
p nR ( )V T V
p nR U ( )T T ( )V p T p 0 V T V
所以,理想气体的热力学能只是温度的函数。
§3.8 热力学基本方程
8、偏微分运算规则: z f ( x, y ) 循环关系式:
=
2U U V S SV V S T V S
S一定时对V 微分 U T ; S V
§3.8 热力学基本方程 (1) dU TdS pdV
§3.8 热力学基本方程 3、热力学方程的简单应用
例:试证明理想气体恒温过程ΔA=ΔG
dT 0 dA pdV A
V2 V1
dT 0 dG Vdp G Vdp nRT ln
p1 p2
V1 pdV nRT ln V2
p2 V nRT ln 1 p1 V2
H G / T 2 T T p
积分:
G2
G1
T2 G H d( ) 2 dT T1 T T
T2 H G2 G1 dT 2 T1 T T2 T1
§3.8 热力学基本方程
物理化学(机材类第四版,ppt课件)2.9 热力学基本关系式

适用条件:组成不变,W′= 0 的封闭系统或 封闭系统,W′= 0,可逆过程。
4
2、热力学函数的基本关系式
由热力学基本方程
热力学恒等式
dU = TdS- pdV dH = TdS + Vdp
U T ; U p
S V
V S
H T; S p
H p
S
V
dA = -SdT- pdV dG = -SdT + Vdp
再将dU = TdS – pdV 式代入得到 dH = TdS +Vdp
(c) A=U-TS 微分,并用上式代入得到
dA = -SdT- pdV
(d) G = H – T S微分,并用上式代入得到 dG = -SdT + Vdp
3
四个热力学基本方程
dU = TdS- pdV dH = TdS + Vdp dA = -SdT- pdV dG = -SdT + Vdp
G p3 p2 p1
p3>p2>p1
T Tm
T
26
(1)求U随V的变化关系 (2)求H随p的变化关系 (3)求S与Cp的变化关系 (4)求G或Δr G与温度的关系 (5)求G随p的变化关系
27
关于U,H, S, G,A与T、p、V的关系
(一定量、一定组成的单相系统)
➢理想气体 U、H 只是T 的函数,与p、V 无关;S与T、p、V 均有关。
-p -S
G T p
麦克斯韦关系式中不含熵与温度的偏微商。
问题
S T p
S T V
Cp/T CV/T
10
思考题
1、对于只作膨胀功的封闭系统 ()
A T
V
4
2、热力学函数的基本关系式
由热力学基本方程
热力学恒等式
dU = TdS- pdV dH = TdS + Vdp
U T ; U p
S V
V S
H T; S p
H p
S
V
dA = -SdT- pdV dG = -SdT + Vdp
再将dU = TdS – pdV 式代入得到 dH = TdS +Vdp
(c) A=U-TS 微分,并用上式代入得到
dA = -SdT- pdV
(d) G = H – T S微分,并用上式代入得到 dG = -SdT + Vdp
3
四个热力学基本方程
dU = TdS- pdV dH = TdS + Vdp dA = -SdT- pdV dG = -SdT + Vdp
G p3 p2 p1
p3>p2>p1
T Tm
T
26
(1)求U随V的变化关系 (2)求H随p的变化关系 (3)求S与Cp的变化关系 (4)求G或Δr G与温度的关系 (5)求G随p的变化关系
27
关于U,H, S, G,A与T、p、V的关系
(一定量、一定组成的单相系统)
➢理想气体 U、H 只是T 的函数,与p、V 无关;S与T、p、V 均有关。
-p -S
G T p
麦克斯韦关系式中不含熵与温度的偏微商。
问题
S T p
S T V
Cp/T CV/T
10
思考题
1、对于只作膨胀功的封闭系统 ()
A T
V
2.7 热力学函数基本关系式

T
U )T 的关系式,可以求出气体在状 V
知道气体的状态方程,求出 ( p )V 的值,就可计算U 值。
上一内容
下一内容 回主目录 返回
1/30/2019
Maxwell 关系式的应用
(2)求H 随 p 的变化关系
物化课件
已知基本公式
dH TdS Vdp
p p
S V )T ( ) p p T
上一内容
下一内容 回主目录 返回
1/30/2019
四个基本公式
物化课件
(2) 因为
dH TdS Vdp
H U pV
dH dU pdV Vdp
dU TdS pdV
所以
dH TdS Vdp
上一内容
下一内容
回主目录
返回
1/30/2019
四个基本公式
z z ( x, y )
z z dz ( ) y dx ( ) x dy Mdx Ndy x y M 和N也是 x,y 的函数 M 2 z N 2 z ( )x , ( )y y xy x xy M N 所以 ( )x ( ) y y x
V =C p dT [V T ( ) p ]dp T
V H C p dT [V T ( ) p ]dp T
知道气体状态方程,求出( V ) p 值,就可计算 H值。
T
上一内容
下一内容 回主目录 返回
1/30/2019
Maxwell 关系式的应用
例3 解: 利用 ( H )T 的关系式求 J-T 。
1/30/2019
Maxwell 关系式的应用
利用 (
物化课件
例2 态变化时的 U 值。设某气体从P1,V1,T1至P2,V2,T2, 求U ? U U (T ,V ) 解: U U dU ( )V dT ( ) T dV T V p =CV dT [T ( )V p ]dV T p U CV dT [T ( )V p ]dV T
U )T 的关系式,可以求出气体在状 V
知道气体的状态方程,求出 ( p )V 的值,就可计算U 值。
上一内容
下一内容 回主目录 返回
1/30/2019
Maxwell 关系式的应用
(2)求H 随 p 的变化关系
物化课件
已知基本公式
dH TdS Vdp
p p
S V )T ( ) p p T
上一内容
下一内容 回主目录 返回
1/30/2019
四个基本公式
物化课件
(2) 因为
dH TdS Vdp
H U pV
dH dU pdV Vdp
dU TdS pdV
所以
dH TdS Vdp
上一内容
下一内容
回主目录
返回
1/30/2019
四个基本公式
z z ( x, y )
z z dz ( ) y dx ( ) x dy Mdx Ndy x y M 和N也是 x,y 的函数 M 2 z N 2 z ( )x , ( )y y xy x xy M N 所以 ( )x ( ) y y x
V =C p dT [V T ( ) p ]dp T
V H C p dT [V T ( ) p ]dp T
知道气体状态方程,求出( V ) p 值,就可计算 H值。
T
上一内容
下一内容 回主目录 返回
1/30/2019
Maxwell 关系式的应用
例3 解: 利用 ( H )T 的关系式求 J-T 。
1/30/2019
Maxwell 关系式的应用
利用 (
物化课件
例2 态变化时的 U 值。设某气体从P1,V1,T1至P2,V2,T2, 求U ? U U (T ,V ) 解: U U dU ( )V dT ( ) T dV T V p =CV dT [T ( )V p ]dV T p U CV dT [T ( )V p ]dV T
工程热力学第12讲-第7章-1热力学基本关系式、稀溶液

T
求U ? 解:
Maxwell 关系式的应用二
(2)求H 随 p 的变化关系 已知基本公式 等温对p求偏微分
dH TdS Vdp
H S ( )T T ( )T V p p
S V ( )T ( ) p p T
S 不易测定,据Maxwell关系式 ( )T p
从公式(2),(4)导出
U H T ( )V ( )p S S U A p ( ) S ( )T V V H G V ( ) S ( )T p p
从公式(3),(4)导出
A G S ( )V ( ) p T T
Maxwell 关系式
2.热力学基本关系式
热力学基本关系式 特性函数 Maxwell 关系式
变组成的热力学性质关系式
状态参数的全微分条件
设函数 z 的独立变量为x,y, z具有全微分性质
z z ( x, y )
z z dz ( ) y dx ( ) x dy Mdx Ndy x y
M 和N也是 x,y 的函数
z z M N dz ( ) y dx ( ) x dy Mdx Ndy ( )x ( ) y x y y x p T ( ) S ( )V (1) dU TdS pdV V S T V ( ) ( )p (2) S dH TdS Vdp p S
(3) (4)
dA SdT pdV
dG SdT Vdp
S p ( )T ( )V V T S V ( )T ( ) p p T
每个麦克斯韦关系式表示系统在同一状态的两种变化率数值相等。利用该关系 式可将实验可测偏微商来代替那些不易直接测定的偏微商。
Maxwell 关系式的应用一
求U ? 解:
Maxwell 关系式的应用二
(2)求H 随 p 的变化关系 已知基本公式 等温对p求偏微分
dH TdS Vdp
H S ( )T T ( )T V p p
S V ( )T ( ) p p T
S 不易测定,据Maxwell关系式 ( )T p
从公式(2),(4)导出
U H T ( )V ( )p S S U A p ( ) S ( )T V V H G V ( ) S ( )T p p
从公式(3),(4)导出
A G S ( )V ( ) p T T
Maxwell 关系式
2.热力学基本关系式
热力学基本关系式 特性函数 Maxwell 关系式
变组成的热力学性质关系式
状态参数的全微分条件
设函数 z 的独立变量为x,y, z具有全微分性质
z z ( x, y )
z z dz ( ) y dx ( ) x dy Mdx Ndy x y
M 和N也是 x,y 的函数
z z M N dz ( ) y dx ( ) x dy Mdx Ndy ( )x ( ) y x y y x p T ( ) S ( )V (1) dU TdS pdV V S T V ( ) ( )p (2) S dH TdS Vdp p S
(3) (4)
dA SdT pdV
dG SdT Vdp
S p ( )T ( )V V T S V ( )T ( ) p p T
每个麦克斯韦关系式表示系统在同一状态的两种变化率数值相等。利用该关系 式可将实验可测偏微商来代替那些不易直接测定的偏微商。
Maxwell 关系式的应用一
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
△S=QR/T; T △S= QR 故△G= △H- T △S=0- T △S= QR= WR=-RTlnP1/P2=5744Jmol-1 解法二: △G=∫ p1 p2Vdp = RTlnP2/P1=5744Jmol-1.
⑵等温等压相变△G 对于等温等压的可逆相变,直接可得(△G)T,P=0.对于非等温 等压的非可逆相变或同温同压下两个相态的△G,可以通过设计可 逆过程进行计算,也可根据G---P关系公式求算。
1.8 热力学函数的基本关系式
H
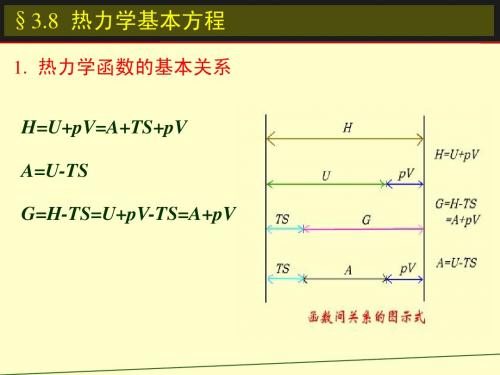
U、H、S、A、G 、 p、V、T H =U+pV,A =U-TS,G =H-TS 1. 热力学基本方程
U
pV
TS A pV
TS
G
δWr ′=0时,则δWr=-pdV,于是
一微小可逆过程
dU=δQr+δWr,
dS δ Qr T
δWr ′ =0时,则δWr=-pdV,于是
=8586Jmol-1 故△G= △G1+ △G2 + △G3=8584Jmol-1 依Gibbs自由能减少原理,298K,1atm水不能经等温等压过程转变 为同温 同压的水蒸气,但其逆过程则是可以的。因此在298K, 1atm下液态水是稳定态。
⒊应用Gibbs--helmholtz方程求△G 将 G--H方程:{э(△G/T)/эT}P=- △H/T2
△S=0,△T=0,△H=0,
△G=0
⑵理气在等温等压的Gibbs自由能改变 △G = △H-T △S (△H=0) △S=-R∑nilnXi △G= RT∑nilnXi 其中ni为组分i的量,Xi为理想混合气中
为组分I的摩尔数。
⒌非等温等压两态的△G 若体系的两态温度,压力都不相等,根据G的定义:
p
,
H p
T
T V T
p
V
(1-123)
式(1-122), (1-123)都叫热力学状态方程。
⒈9△G的 求算及Gibbs自由能减少原理的应用 ⒈体系在同温两态的△G
G≡H-TS 当两态温度相等时,则有 △G= △H-T △S 于是求出△H,△S也就求出了△G。
T p
(G / T ) T p
1 T
G T p
G T2
S G T T2
(TS G)
T2
H T2
即
(G / T )
T
p
H T2
(1-116)
同理,有
(A/T) T V
U T2
1.8 热力学函数的基本关系式
U、H、S、A、G 、 p、V、T H =U+pV,A =U-TS,G =H-TS=A+PV
H
U
pV
TS
A
pV
TS
G
1. 热力学基本方程
δWr ′=0时,则δWr=-pdV,于是
一微小可逆过程
dU=δQr+δWr,
dS δ Qr T
dU=TdS-pdV
微分H=U-PV
H p
S
V
式(1-110),若dV=0
A T
V
S
;若dT=0
A
V T
p
式(1-111),若dp=0
G T
p
S
;-112) (1-113) (1-114) (1‐115)
dU=TdS-pdV
dS=0
dV=0
U p V S ↓V一定时对S 微分
U T S V
↓ S一定时对V 微分
2U VS
p S
V
2U SV
T V
S
↓
p T S V V S
例:求算1mol水经下列相变后的△G。
H2O(l,298K,1atm)
H2O(g,298K,1atm)
并判断该相变能否在等温等压下进行? 298K,1atm下的水与水蒸汽
何者稳定?已知298K时水的蒸汽压为3.126×10-2atm,假设水蒸汽
为理气, 298K下水的Vm,L=0.01809L. mol-1
常用的是式(1-120)及式(1-121),这两等式右边的变化率是可以由 实验直接测定的,而左边则不能。可用等式右边的变化率代替左
4.热力学状态方程
由dU=TdS-pdV
定温下, dUT=TdST-pdVT
等式两边除以dVT 即
dUT T dST p
dVT
dVT
由麦克斯韦方程 于是
U T S p V T V T S p V T T V
(1-108)
微分A=U-TS
等式两边减d(pV)
等式两边加d(TS)
结合式(1-108),得
结合式(1-108),得
dH=TdS+Vdp
(1-109)
dA=-SdT-pdV
微 等分 式两 G=边 H-T加Sd(TS)(1-110)
结合式(1-109),得
dG=-SdT+Vdp
(1-111)
式(1-108),(1-109),(1-110),(1-111)称为热力学基本方程。
(1-108) (1-109) (1-110) (1-111)
由四个热力学基本方程,分别加上相应的条件,则
式(1-108),若dV=0
U S
V
T
;若dS=0
U V
S
p
式(1-109),若dp=0
H S
p
T
;若dS=0
△G= △G1+ △G2 + △G3 其中 △G1=∫ p1 p2Vm.Ldp= Vm.L(P2 - P1)=0.01809*(3.126×10-2-1)
=-1.78Jmol-1 △G2=0 △G3=∫ p1 p2Vm.gdp=RTln P1/ P2=8.3148298ln1/ 3.126×10-2
式(1-116)及 (1-117)叫吉布斯 - 亥姆霍茨方程。
(1-117)
G-H方程常用的形式为:
即
(G / T )
T p
H T2
加△
(1-116)
Gibbs自由能随压力的变化
因
(эG/эP)T,n=V
(э△G/эP)T,n=△V 此即G---V关系式
只要知道△V--p关系式,在定温下P1的△G1就可求算出P2的△G2。
U T p p V T T V
(1-122)
U T p p V T T V
(1-122)
同理,由dH=TdS+Vdp,并用麦克斯韦方程 可得
S p
T
V T
1mol H2O(l)
△G
298K,1atm
1mol H2O(g) 298K,1atm
等温可逆 膨胀
△G1=∫ p1 p2Vm.Ldp
△G3=∫ p1 p2Vm.gdp 等温可 逆压缩
1mol H2O(l)
△G2=0
298K, 3.126×10-2atm
1mol H2O(g) 298K, 3.126×10-2atm
在定压下从T1到 T2积分得: (△G)2/ T2- (△G)1/ T1=- =∫T1 T2 △H/T2dT 若知△H--T关系以及T1时的△G1就可求算T2时的△G2 而: △H= △H T0+∫ T0 T △CpdT △H T0是T0时的焓变。
⒋理想气体混合的Gibbs自由能改变
⑴理气在等温等容的Gibbs自由能改变
dU = TdS- pdV
(1-108)
dH = TdS + Vdp
(1-109)
dA = -SdT- pdV
(1-110)
dG = -SdT + Vdp
(1-111)
式(1-108),(1-109),(1-110),(1-111)称为热力学基本方程
dU = TdS- pdV dH = TdS + Vdp dA = -SdT- pdV dG = -SdT + Vdp
(1-118)
3.麦克斯韦关系式
T p
S
V S
p
(1-119)
S p V T T V
S p
T
V T
p
(1-120) (1-121)
麦克斯韦关系式 [式(1-118)~式(1-121)]各式表示的是系统在 同一状态的两种变化率数值相等。因此应用于某种场合等式右左 可以代换。
△G=G2-G1=(H2-T2S2)- (H1-T1S1)= △H-(T2S2 - T1S1) (不要忘了,最基本的东西--定义)
3.麦克斯韦关系式
若Z=f(x,y),且Z有连续的二阶偏微商,则必有
y
Z x
y x
x
Z y
x
y
即
2Z 2Z
xy yx
因Z是状态函数,具有二级偏导数求导次序无关的性质。
把以上结论应用于热力学基本方程有
其次,对于均相,无其他功的封闭体系,根据热力学基本方程: dG=-SdT+Vdp=0+vdp(因同温,dT=0) 从而 △G=∫ p1 p2Vdp (只要知道V---P关系或物态方程即可求 △G)
⑵等温等压相变△G 对于等温等压的可逆相变,直接可得(△G)T,P=0.对于非等温 等压的非可逆相变或同温同压下两个相态的△G,可以通过设计可 逆过程进行计算,也可根据G---P关系公式求算。
1.8 热力学函数的基本关系式
H
U、H、S、A、G 、 p、V、T H =U+pV,A =U-TS,G =H-TS 1. 热力学基本方程
U
pV
TS A pV
TS
G
δWr ′=0时,则δWr=-pdV,于是
一微小可逆过程
dU=δQr+δWr,
dS δ Qr T
δWr ′ =0时,则δWr=-pdV,于是
=8586Jmol-1 故△G= △G1+ △G2 + △G3=8584Jmol-1 依Gibbs自由能减少原理,298K,1atm水不能经等温等压过程转变 为同温 同压的水蒸气,但其逆过程则是可以的。因此在298K, 1atm下液态水是稳定态。
⒊应用Gibbs--helmholtz方程求△G 将 G--H方程:{э(△G/T)/эT}P=- △H/T2
△S=0,△T=0,△H=0,
△G=0
⑵理气在等温等压的Gibbs自由能改变 △G = △H-T △S (△H=0) △S=-R∑nilnXi △G= RT∑nilnXi 其中ni为组分i的量,Xi为理想混合气中
为组分I的摩尔数。
⒌非等温等压两态的△G 若体系的两态温度,压力都不相等,根据G的定义:
p
,
H p
T
T V T
p
V
(1-123)
式(1-122), (1-123)都叫热力学状态方程。
⒈9△G的 求算及Gibbs自由能减少原理的应用 ⒈体系在同温两态的△G
G≡H-TS 当两态温度相等时,则有 △G= △H-T △S 于是求出△H,△S也就求出了△G。
T p
(G / T ) T p
1 T
G T p
G T2
S G T T2
(TS G)
T2
H T2
即
(G / T )
T
p
H T2
(1-116)
同理,有
(A/T) T V
U T2
1.8 热力学函数的基本关系式
U、H、S、A、G 、 p、V、T H =U+pV,A =U-TS,G =H-TS=A+PV
H
U
pV
TS
A
pV
TS
G
1. 热力学基本方程
δWr ′=0时,则δWr=-pdV,于是
一微小可逆过程
dU=δQr+δWr,
dS δ Qr T
dU=TdS-pdV
微分H=U-PV
H p
S
V
式(1-110),若dV=0
A T
V
S
;若dT=0
A
V T
p
式(1-111),若dp=0
G T
p
S
;-112) (1-113) (1-114) (1‐115)
dU=TdS-pdV
dS=0
dV=0
U p V S ↓V一定时对S 微分
U T S V
↓ S一定时对V 微分
2U VS
p S
V
2U SV
T V
S
↓
p T S V V S
例:求算1mol水经下列相变后的△G。
H2O(l,298K,1atm)
H2O(g,298K,1atm)
并判断该相变能否在等温等压下进行? 298K,1atm下的水与水蒸汽
何者稳定?已知298K时水的蒸汽压为3.126×10-2atm,假设水蒸汽
为理气, 298K下水的Vm,L=0.01809L. mol-1
常用的是式(1-120)及式(1-121),这两等式右边的变化率是可以由 实验直接测定的,而左边则不能。可用等式右边的变化率代替左
4.热力学状态方程
由dU=TdS-pdV
定温下, dUT=TdST-pdVT
等式两边除以dVT 即
dUT T dST p
dVT
dVT
由麦克斯韦方程 于是
U T S p V T V T S p V T T V
(1-108)
微分A=U-TS
等式两边减d(pV)
等式两边加d(TS)
结合式(1-108),得
结合式(1-108),得
dH=TdS+Vdp
(1-109)
dA=-SdT-pdV
微 等分 式两 G=边 H-T加Sd(TS)(1-110)
结合式(1-109),得
dG=-SdT+Vdp
(1-111)
式(1-108),(1-109),(1-110),(1-111)称为热力学基本方程。
(1-108) (1-109) (1-110) (1-111)
由四个热力学基本方程,分别加上相应的条件,则
式(1-108),若dV=0
U S
V
T
;若dS=0
U V
S
p
式(1-109),若dp=0
H S
p
T
;若dS=0
△G= △G1+ △G2 + △G3 其中 △G1=∫ p1 p2Vm.Ldp= Vm.L(P2 - P1)=0.01809*(3.126×10-2-1)
=-1.78Jmol-1 △G2=0 △G3=∫ p1 p2Vm.gdp=RTln P1/ P2=8.3148298ln1/ 3.126×10-2
式(1-116)及 (1-117)叫吉布斯 - 亥姆霍茨方程。
(1-117)
G-H方程常用的形式为:
即
(G / T )
T p
H T2
加△
(1-116)
Gibbs自由能随压力的变化
因
(эG/эP)T,n=V
(э△G/эP)T,n=△V 此即G---V关系式
只要知道△V--p关系式,在定温下P1的△G1就可求算出P2的△G2。
U T p p V T T V
(1-122)
U T p p V T T V
(1-122)
同理,由dH=TdS+Vdp,并用麦克斯韦方程 可得
S p
T
V T
1mol H2O(l)
△G
298K,1atm
1mol H2O(g) 298K,1atm
等温可逆 膨胀
△G1=∫ p1 p2Vm.Ldp
△G3=∫ p1 p2Vm.gdp 等温可 逆压缩
1mol H2O(l)
△G2=0
298K, 3.126×10-2atm
1mol H2O(g) 298K, 3.126×10-2atm
在定压下从T1到 T2积分得: (△G)2/ T2- (△G)1/ T1=- =∫T1 T2 △H/T2dT 若知△H--T关系以及T1时的△G1就可求算T2时的△G2 而: △H= △H T0+∫ T0 T △CpdT △H T0是T0时的焓变。
⒋理想气体混合的Gibbs自由能改变
⑴理气在等温等容的Gibbs自由能改变
dU = TdS- pdV
(1-108)
dH = TdS + Vdp
(1-109)
dA = -SdT- pdV
(1-110)
dG = -SdT + Vdp
(1-111)
式(1-108),(1-109),(1-110),(1-111)称为热力学基本方程
dU = TdS- pdV dH = TdS + Vdp dA = -SdT- pdV dG = -SdT + Vdp
(1-118)
3.麦克斯韦关系式
T p
S
V S
p
(1-119)
S p V T T V
S p
T
V T
p
(1-120) (1-121)
麦克斯韦关系式 [式(1-118)~式(1-121)]各式表示的是系统在 同一状态的两种变化率数值相等。因此应用于某种场合等式右左 可以代换。
△G=G2-G1=(H2-T2S2)- (H1-T1S1)= △H-(T2S2 - T1S1) (不要忘了,最基本的东西--定义)
3.麦克斯韦关系式
若Z=f(x,y),且Z有连续的二阶偏微商,则必有
y
Z x
y x
x
Z y
x
y
即
2Z 2Z
xy yx
因Z是状态函数,具有二级偏导数求导次序无关的性质。
把以上结论应用于热力学基本方程有
其次,对于均相,无其他功的封闭体系,根据热力学基本方程: dG=-SdT+Vdp=0+vdp(因同温,dT=0) 从而 △G=∫ p1 p2Vdp (只要知道V---P关系或物态方程即可求 △G)
