梯形面积公式的不同推导方式Word版
梯 形 面 积 公 式 的 推 导

梯形面积公式的推导梯形的面积公式是在平行四边形面积公式的基础上进行推导的。
在此之前,已建立了梯形的概念,因此,在教学前,可先让学生自制两个全等梯形。
铺垫性的准备练习后,拿出4平方厘米的测量板,用数方格的方法,算出梯形面积是多少。
(梯形面积占满8个方格,每个方格是4平方厘米,梯形面积为32平方厘米。
)方法一:将两个全等梯形,一个正放,一个倒放拼在一起,组成一个平行四边形。
提出点拔题:这个平行四边形的底是由梯形的什么组成的?②怎样求出平行四边形的面积?③怎样求出一个梯形的面积?如图:由此得出:梯形面积=(上底+下底)×高÷ 2。
方法二:将一个梯形通过割、拼的方法,转化成平行四边形。
如图:通过上图可以清楚地推导出:方法三:一个梯形的割、补,使其转化为三角形,运用求三角形面积的公式,对照观察,从而推导出求梯形面积的公式。
对转化后的图观察可知,三角形的底为梯形上底加下底的和,三角形的高相当于原来梯形的高。
由此可以推导出梯形面积公式:在此基础上,抽象成求梯形面积的字母公式为: S=(a+b)×h÷2。
方法四:当推导求梯形面积的第二个公式时,找出两腰的中点,画出中位线,然后把右下角剪下来,拼在右上方,使梯形转化为平行四边形。
如图:割、补后,梯形已转化成平行四边形,面积大小未变。
梯形的中位线相当于平行四边形的底,梯形的高也是平行四边形的高。
用字母公式表示为:S=m×h。
第二个公式除转化成平行四边形推导外,还可以转化成长方形进行推导。
有了前面的推导基础,这个推导过程,应以学生自己思考为主。
由此也可以推导出梯形面积公式:。
梯形的面积推导公式

梯形的面积推导公式有多种,以下是其中四种:
1. 梯形面积公式推导一:
两个完全相同的梯形可以拼成一个平行四边形,这个平行四边形的底等于梯形的上底与下底的和,高等于梯形的高。
因为平行四边形的面积等于底×高,所以梯形的面积等于上底与下底和的一半乘以高,即(上底+下底)×高÷2。
2. 梯形面积公式推导二:
将梯形对角线右半部分顺次连接,可以将梯形分成两个三角形,其中一个是小三角形,另一个是大三角形的面积是小三角形的两倍。
因此,梯形的面积等于两个三角形的面积的和,即(上底+下底)×高÷2=1/2(上底+下底)×高+1/2(上底+下底)×高。
3. 梯形面积公式推导三:
在梯形内连接顶点到一腰中点的线段,将梯形分为两个等高不同底的三角形。
根据等高三角形的面积比等于底边的比,可以得出梯形的面积等于两个三角形的面积的和,即(上底+下底)×高÷2=1/2(上底+下底)×高+1/2(上底+下底)×高。
4. 梯形面积公式推导四:
在梯形内作一虚线,将梯形分为一个平行四边形和一个三角形。
根据
平行四边形和三角形的面积公式,可以得出梯形的面积等于平行四边形的面积和三角形的面积的和,即(上底+下底)×高÷2=1/2(上底+下底)×高+1/2(上底+下底)×高-1/2上底×高。
梯形面积公式的推导演示
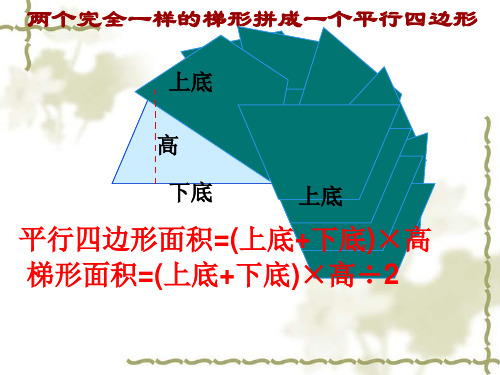
上底 高 下底 上底
平行四边形面积=(上底+下底)×高 梯形面积=(上底+下底)×高÷2
上底 高
因为:大三角形的面积 =(上底+下底)×高÷2 所以:梯形的面积
下底
上底 =(上底+下底)×高÷2
把一个梯形分割成两个三角形
上底
高
下底
绿三角形面积=下底×高÷2 红三角形面积=上底×高÷2 梯形面积=绿三角形面积+红三角形面积 =下底×高÷2 +上底×高÷2 =(上底+下底)×高÷2
把一个梯形转化成一个平行四边形
因为:平行四边形的面积 =(上底+下底)×高÷2 所以:梯形的面积=(上底+下底)×高÷2
梯形的面积公式 梯形的面积 = (上底+下底)×高÷2 如果用字母s表示梯形的面积,a、b、h 分别表示梯形的上底、下底和 高,哪用 字母怎样表示梯形的面积公式呢?
S=(a+b) h÷2
(完整word版)面积公式和周长公式

(完整word版)面积公式和周长公式
面积公式
梯形面积公式公式描述:公式中a,c分别为梯形上下底,h 为梯形的高,S为梯形的面积。
长方形:S=ab{长方形面积=长×宽}
正方形:S=a^2{正方形面积=边长×边长}
平行四边形:S=ab{平行四边形面积=底×高}
三角形:S=ab÷2{三角形面积=底×高÷2}
长方体表面积:S=2(ab+ac+bc){长方体表面积=(长×宽+长×高+宽×高)×2}
正方体表面积:S=6a^2{正方体表面积=棱长×棱长×6}
三角形(一般三角形,海伦公式) 周长L = a + b + c(a,b,c为三角形的三个边的长)
周长公式
长方形周长L = 2(a + b)(a,b为长方形相邻边的长)
正方形周长L = 4a
梯形周长L = a + b + c + d(a:上底,b:下底,c,d两个腰的长,下同)
圆周长L = 2πr(π:圆周率,r:圆的半径)
半圆的周长=πr+2r=πd/2+d。
梯形的面积公式推导

梯形的面积公式推导梯形是一种四边形,它有两条平行边,这使得它与其他四边形不同。
我们可以通过推导梯形的面积公式来更好地理解它。
首先我们假设梯形的两条平行边分别为a和b,而梯形的高为h。
接下来,我们将梯形分割成一个大三角形和一个小三角形,这样我们就能更好地处理。
我们假设大三角形的底边为a,高为h,小三角形的底边为b,高为h。
首先,我们计算大三角形的面积。
根据三角形的面积公式,我们有:大三角形的面积等于底边乘以高的一半,即S1 = (a * h) / 2。
接下来,我们计算小三角形的面积。
同样地,根据三角形的面积公式,小三角形的面积等于底边乘以高的一半,即S2 = (b * h) / 2。
现在,我们将两个三角形的面积相加,即S1 + S2 = ((a * h) / 2) + ((b * h) / 2)。
我们可以使用公因式法则将这个等式简化为S1 + S2 = (a + b) * h / 2。
我们知道,梯形的面积等于两个三角形的面积之和,所以我们可以将上述等式表示为整个梯形的面积公式,即S = (a + b) * h / 2。
通过这个推导过程,我们得到了梯形的面积公式:S = (a + b) * h / 2。
这个公式告诉我们,要计算梯形的面积,我们只需要知道它的两条平行边和高就可以了。
这个推导过程不仅帮助我们理解了梯形的面积公式,还为我们提供了一种方法,可以将梯形的计算分解为计算两个简单三角形的面积。
这使得我们能更轻松地解决与梯形相关的问题。
总之,梯形的面积公式推导为S = (a + b) * h / 2,这个公式是基于两个三角形的面积之和。
通过这个公式,我们可以更好地理解梯形以及如何计算它的面积。
希望本文的内容能对你有所帮助!。
梯形面积公式的推导方法

梯形面积公式的推导方法梯形是一种拥有两个平行底边的四边形,它的面积可以通过梯形面积公式来计算。
本文将详细介绍梯形面积公式的推导方法。
我们需要明确梯形的定义和特点。
梯形是一种四边形,它有两个平行的底边和两条不平行的侧边。
梯形的面积可以看作是两个平行底边之间的平均高度与底边长度的乘积。
我们可以通过将梯形分割成两个三角形来推导梯形面积公式。
假设梯形的上底边长为a,下底边长为b,高为h。
我们可以将梯形分割成一个上底边为a,下底边为b,高为h的小三角形和一个上底边为a,下底边为b,高为0的大三角形。
我们计算小三角形的面积。
小三角形的面积等于底边长度乘以高再除以2,即S1 = (a * h) / 2。
接下来,我们计算大三角形的面积。
大三角形的面积等于底边长度乘以高再除以2,即S2 = (b * h) / 2。
将小三角形和大三角形的面积相加,即可得到整个梯形的面积。
即S = S1 + S2 = (a * h) / 2 + (b * h) / 2 = (a + b) * h / 2。
梯形的面积公式可以表示为S = (a + b) * h / 2。
其中,a和b分别代表梯形的上底边和下底边的长度,h代表梯形的高。
通过这种推导方法,我们可以清晰地理解梯形面积公式的来源和计算过程。
梯形面积公式是数学中的基本公式之一,在解决实际问题中具有广泛的应用。
无论是计算几何还是实际工程中的面积计算,梯形面积公式都是必备的知识点。
在实际应用中,我们可以根据梯形的具体参数,直接套用梯形面积公式进行计算。
通过掌握和理解梯形面积公式的推导方法,我们可以更好地应用它解决各种实际问题。
总结起来,梯形面积公式的推导方法是通过将梯形分割成两个三角形,计算每个三角形的面积,然后将两个三角形的面积相加得到整个梯形的面积。
这种推导方法简单直观,可以帮助我们深入理解梯形面积的计算原理。
掌握了梯形面积公式的推导方法,我们可以更加灵活地运用它解决各种实际问题。
梯形面积公式的四种推导方法

梯形面积公式的四种推导方法一、引言梯形是一个只有两对平行边的四边形,其中上底和下底是平行的,而两腰不平行。
梯形的面积公式为(上底+下底)*高/2。
本篇文档将详细介绍如何通过不同的方式推导出这个公式。
二、平行线分割法首先,我们可以将梯形分割成两个三角形。
假设上底长为a,下底长为b,高为h,那么这两个三角形的面积分别为1/2ah和1/2bh。
因此,梯形的总面积就是这两个三角形的面积之和,即1/2ah + 1/2bh = (1/2)(a+b)h,这就是梯形面积公式。
三、矩形与三角形组合法另一种方法是将梯形视为一个矩形和两个等高的三角形的组合。
假设矩形的宽为(a-b)/2,那么矩形的面积就是((a-b)/2)*h。
另外两个等高的三角形的面积分别为1/2ah和1/2bh。
所以,梯形的总面积就是这三个图形的面积之和,即((a-b)/2)*h + 1/2ah + 1/2bh = (1/2)(a+b)h。
四、割补法第三种方法是利用割补法。
我们可以在梯形中画一条平行于上底和下底的线,将其分割成一个矩形和两个等高的三角形。
假设这条线离上底的距离为x,则矩形的宽为x,面积为xh;两个等高的三角形的面积分别为1/2( a-x)h 和1/2(b-x)h。
所以,梯形的总面积就是这三个图形的面积之和,即xh + 1/2( a-x)h + 1/2(b-x)h = (1/2)(a+b)h。
五、相似三角形法最后一种方法是利用相似三角形的性质。
我们可以发现,梯形中的任意一个小三角形都与整个梯形是相似的。
因此,它们的面积比等于对应的边长的平方比。
设小三角形的面积为S,那么有S/h^2=(a+b)/2h。
解得S=1/2(a+b)h,这就是梯形的面积。
六、结论以上就是推导梯形面积公式的四种方法,分别是平行线分割法、矩形与三角形组合法、割补法以及相似三角形法。
每种方法都有其独特的思路和应用场景,希望读者能从中受益,更深入地理解和掌握梯形面积的计算方法。
梯形的面积公式推导

梯形的面积公式推导梯形是一个具有两个平行边的四边形,它的面积公式是很多学生在学习几何的时候都会接触到的一个重要的内容。
在这篇文章中,我们将推导出梯形的面积公式,并通过几个例子来加深对这个公式的理解。
假设有一个梯形,它的上底长为a,下底长为b,高为h。
我们的目标是推导出这个梯形的面积公式。
首先,我们可以将这个梯形分为一个大矩形和两个小三角形。
大矩形的长为b,宽为h,面积为bh。
两个小三角形分别由大矩形的两个边和梯形上底连接而成。
设其中一个小三角形的底边长为x,高为h1,那么这个小三角形的面积为1/2 * x * h1。
根据梯形的定义,我们可以知道两个小三角形的底边长分别为a和b,高都为h1。
因为两个小三角形是等高的,所以它们的面积相等,即1/2 * a * h1 = 1/2 * b * h1。
将上面这个等式变形,可以得到a * h1 = b * h1。
我们将这个等式代入一个小三角形的面积公式,即1/2 * x * h1 =1/2 * b * h1,两个h1可以约掉,那么就得到了一个小三角形的面积公式:1/2 * x * h = 1/2 * b * h1。
将两个小三角形的面积相加,可以得到整个梯形的面积:bh + 1/2 * x * h = (b + x) * h / 2。
我们可以看到,公式中的(b + x)实际上就是梯形的上底和下底之和,也即梯形的平均底长。
现在,我们已经推导出了梯形的面积公式。
根据这个公式,当我们已知梯形的上底、下底和高时,就可以轻松地计算出梯形的面积。
让我们通过几个例子来进一步加深对这个公式的理解。
例子一:已知梯形的上底长为8cm,下底长为12cm,高为5cm。
根据面积公式,我们可以计算出这个梯形的面积为(8 + 12) * 5 / 2 = 50平方厘米。
例子二:已知梯形的上底长为10cm,下底长为15cm,高为6cm。
根据面积公式,我们可以计算出这个梯形的面积为(10 + 15) * 6 / 2 = 75平方厘米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
梯形面积公式的不同推导方式
课本中介绍梯形面积公式推导的方法,通常只有一种方法,那就是用两个相同梯形拼成一个平行四边形,然后用这个平行四边形的面积推得其中梯形的面积。
这种方法很简洁,实际上梯形面积公式推导还有其它方法,现介绍如下:
方法一:把梯形分成两个三角形,分别算面积,然后计算它们的和。
把梯形分成两个三角形,如图所示,一个在左下,一个在右上。
右上三角形的面积= 上底×高÷2
左下三角形的面积= 下底×高÷2
所以梯形的面积= 上底×高÷2+下底×高÷2
= (上底+下底)×高÷2
因此梯形的面积=(上底+下底)×高÷2
方法二:如图所示,分别沿梯形两
腰中点向下底作垂线,与腰、下底正好
围成两个直角三角形,把这两个三角形
分别按逆时针或顺时针旋转1800角,使
得原来的梯形被拼组成一个长方形。
梯
形的上下底总长度,正好等于现在长方
形两个长的总长度,即长方形的长=(上底+下底)÷2。
长方形的宽正好等于梯形的高。
长方形的面积= 长×宽
所以梯形的面积=[(上底+下底)÷2 ]×高
=(上底+下底)×高÷2
因此梯形的面积=(上底+下底)×高÷2
方法三:如图所示,把梯形切割成两块,一块是平行四边形,一块是三角形。
平行四边形的底就是原梯形的上底,三角形的底是梯形的下底与上底之差,而平行四边形和三角形的高都等于梯形的高。
所以梯形的面积
= 平行四边形的面积+三角形的面积
= 上底×高+(下底-上底)×高÷2
=(2×上底)×高÷2+(下底-上底)×高÷2
=(2×上底+下底-上底)×高÷2
=(上底+下底)×高÷2
因此梯形的面积=(上底+下底)×高÷2
方法四:如图所示,把梯形的缺角补上,
正好补成一个长方形,则:
长方形的面积=下底×高
而补上的两个小三角形的总面积为:
小三角形面积和=(下底-上底)×高÷2
所以梯形面积
= 长方形的面积-小三角形面积和
=下底×高-(下底-上底)×高÷2
= [下底-(下底-上底)÷2] ×高
= [2×下底-(下底-上底)] ×高÷2
=(上底+下底)×高÷2
方法五:如图所示,在梯形的
一侧补上一个三角形,使整个图形成
为一个平行四边形。
平行四边形的底
就是梯形的下底,三角形的底恰好是
梯形的下底与上底之差。
它们的高都
是析梯形的高。
所以梯形的面积为:
下底×高-(下底-上底)×高÷2
= [下底-(下底-上底)÷2] ×高
= [2×下底-(下底-上底)] ×高÷2
=(上底+下底)×高÷2
因此梯形的面积=(上底+下底)×高÷2
作者:江苏省滨海县振东中心小学张钦
邮编:224544。
