四年级数学下《平均数与条形统计图》知识点归纳总结复习用
人教版四年级数学下册 平均数与条形统计图 知识点 填空

《平均数与条形统计图》知识点归纳
知识点一、平均数
1、平均数是描述一组数据()的量,它指的是一组数据中所有数据之和再除以这组数据的个数。
2、平均数的公式:
①()=()÷()
②()×()=()
③()=()÷()
3、平均数与平均分是()的概念。
平均分是分物时所用的一种思想,它是指在分物的时候,要尽可能地分完,而且还要使每一份分得的数相等。
4、在比赛时,一般要先去掉一个()分和一个()分,再计算平均的分数。
这样做可减少极端值对平均分的影响。
知识点二、条形统计图
1、条形统计图分为()条形统计图和()条形统计图。
2、复式条形统计图分为()复式条形统计图和()复式条形统计图。
3、条形统计图可以看出()。
4、单式条形统计图能反映出()种类型的数据的数量,复式条形统计图能反映()数据的数量,能更清楚地看出各种数据不同的地方。
四年级数学下册8平均数与条形统计图知识清单素材新人教版
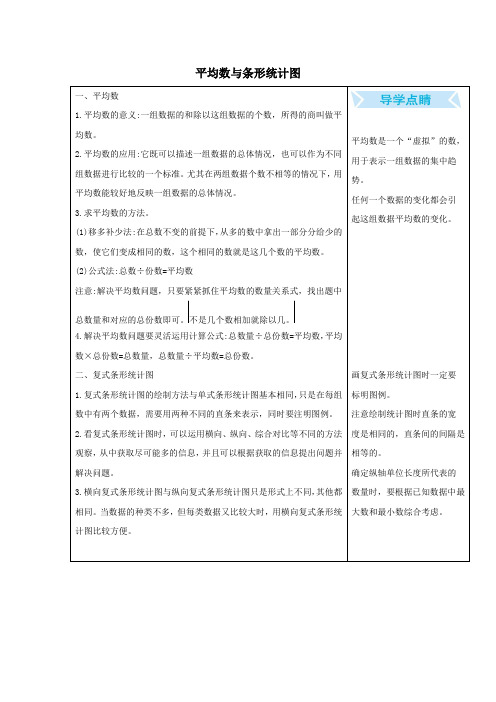
一、平均数
1.平均数的意义:一组数据的和除以这组数据的个数,所得的商叫做平均数。
2.平均数的应用:它既可以描述一组数据的总体情况,也可以作为不同组数据进行比较的一个标准。尤其在体情况。
3.求平均数的方法。
(1)移多补少法:在总数不变的前提下,从多的数中拿出一部分分给少的数,使它们变成相同的数,这个相同的数就是这几个数的平均数。
2.看复式条形统计图时,可以运用横向、纵向、综合对比等不同的方法观察,从中获取尽可能多的信息,并且可以根据获取的信息提出问题并解决问题。
3.横向复式条形统计图与纵向复式条形统计图只是形式上不同,其他都相同。当数据的种类不多,但每类数据又比较大时,用横向复式条形统计图比较方便。
平均数是一个“虚拟”的数,用于表示一组数据的集中趋势。
任何一个数据的变化都会引起这组数据平均数的变化。
画复式条形统计图时一定要标明图例。
注意绘制统计图时直条的宽度是相同的,直条间的间隔是相等的。
确定纵轴单位长度所代表的数量时,要根据已知数据中最大数和最小数综合考虑。
(2)公式法:总数÷份数=平均数
注意:解决平均数问题,只要紧紧抓住平均数的数量关系式,找出题中总数量和对应的总份数即可。不是几个数相加就除以几。
4.解决平均数问题要灵活运用计算公式:总数量÷总份数=平均数,平均数×总份数=总数量,总数量÷平均数=总份数。
二、复式条形统计图
1.复式条形统计图的绘制方法与单式条形统计图基本相同,只是在每组数中有两个数据,需要用两种不同的直条来表示,同时要注明图例。
四年级下数学《平均数与条形统计图》知识点总结归纳

四年级下数学《平均数与条形统计图》知识点总结归纳
一、平均数
1.定义:平均数是所有数的和除以数的个数。
2.计算方法:
•直接相加法:将所有数值相加,然后除以数值的数量。
•移多补少法:将多的数值移到较少的数值上,使所有数值相等。
1.平均数的性质:
•平均数大于或等于最小值,小于或等于最大值。
•当所有数值相等时,平均数等于所有数值中的任何一个。
•平均数可以反映一组数据的总体“平均水平”。
1.平均数的应用:
•比较不同类别的数据大小和它们之间的对比关系。
•表示数据的分布情况。
•在实际生活中,可以用平均数来估算平均水平。
二、条形统计图
1.定义:条形统计图是用直条的长短来表示相互独立的统计指标数值大小和它们
之间的对比关系。
2.制作方法:
•确定统计指标和数据。
•确定直条的分类和间隔。
•绘制直条并标注数据。
•写上标题和时间。
1.条形统计图的优点:
•可以直观地看出各类别的数据大小和它们之间的对比关系。
•可以比较不同类别的数据,便于分析和比较。
•可以表示出数据的分布情况。
1.条形统计图的局限性:
•不容易表示数据的变化趋势。
•容易受到直条间隔的影响,可能导致误导。
•如果数据量很大,制作会比较困难和繁琐。
1.条形统计图的应用:
•展示不同类别数据的数量和对比关系。
•比较不同时间段或不同地区的同类数据。
•分析数据的分布情况,了解数据的集中趋势和离散程度。
人教版小学四年级下学期平均数与条形统计图复习讲义

平均数与条形统计图一.平均数的意义及求平均数的方法:1.平均数的意义:一组数据的和除以这组数据的个数,所得的商叫做平均数,它是描述数据集中程度的一个统计量。
2.求平均数的方法:(1)移多补少法:从多的数量中拿出一部分给少的数量,使它们变成相等的数。
(2)公式法:总数量÷总分数=平均数二.用平均数比较两组或几组数据的总体情况的方法:1.先计算出每组数据的平均数;2.再对比各个平均数,综合分析;3.最后进行正确判断,解决问题。
容易出错的题:小米所在班级的平均身高是140厘米,小刚所在班级的平均身高是145厘米,由此判断小米一定比小刚矮。
(×)分析:小米和小刚所在班级的平均身高代表不了他们实际的身高,他们的实际身高可能高于平均值,也可能低于平均值。
在这里无法确定他们的身高。
三.复式条形统计图的知识点:(一)能绘制纵向复式条形统计图:复式条形统计图的制作和表示方法与单式条形统计图基本相同,只是有两组(或多组)数据,需要用两种(或多种)不同颜色的直条来表示,同时要标明图例。
(二)根据复式条形统计图进行数据分析。
(三)绘制复式条形统计图。
注意:绘制统计图时直条的宽度是相同的,直条间的间隔是相等的。
第九单元:数学广角:鸡兔同笼9.工人运青瓷花瓶250个,规定完整运一个到目的地给运费20元,损坏一个倒赔100元,运完这批花瓶后,工人共得4400元,则损坏了___只.10.有2角,5角和1元人民币20张,共计12元,则1元有_______张,5角有______张,2角有_______张.二、分析与解答题:1.班主任张老师带五年级(2)班50名同学栽树,张老师一人栽5棵,男生一人栽3棵,女生一人栽2棵,总共栽树120棵,问几名男生,几名女生?2.大油瓶一瓶装4千克,小油瓶2瓶装1千克.现有100千克油装了共60个瓶子.问大、小油瓶各多少个?3.乐乐参加数学竞赛,共做20道题,得76分,已知做对一道得5分,错一题扣1分.问小毛做对几道题?4. 小红的储钱罐里有面值2元和5元的人民币共65张,总钱数为205元,两种面值的人民币各多少张?5. 朱老师带了41名同学去北海公园划船,共租了10条船.每条大船坐6人,每条小船坐4人,问大船、小船各租几条?6. 鸡、兔共笼,鸡比兔多26只,足数共274只,问鸡、兔各几只?7. 幼儿园买来20张小桌和30张小凳共用去1860元,已知每张小桌比小凳贵8元,问小桌、小凳的价格各多少?8. 瓷器商店委托搬运站运送800只花瓶,双方商定每只运费是0.35元,如果打破1只,不但不计运费,而且要赔偿2.50元,结果运到目的地后,搬运站共得运费268.6元,求打破了几只花瓶?。
人教版-分章节全视角系列讲学案-4下第26讲:第8章平均数和条形统计图-平均数-知识点梳理-教师版

人教版-4下第26讲:平均数和条形统计图-平均数-知识点梳理平均数与条形统计图――知识点一、平均数:平均数是统计中的一个重要概念。
小学数学里所讲的一般指算术平均数,是一组数据的和除以这组数据的个数所得的商。
算术平均数常用于表示统计对象的一般水平,它是描述数据集中位置的一个统计量。
既可以用它来反映一组数据的一般情况、和平均水平,也可以用它进行不同组数据的比较,以看出组与组之间的差别.用平均数表示一组数据的情况,有直观、简明的特点,所以在日常生活中经常用到,如平均速度、平均身高、平均产量、平均成绩等等。
理解:1、算术平均数的本质:将一组数移多补少后,得到的近似的中间数。
2、算术平均数指一组数据的和除以这组数据的个数所得的商。
3、平均数是表示这一组数据整体情况的数据。
4、算术平均数常用于表示统计对象的一般水平,描述数据集中位置。
5、可以自比,反映一组数据的一般情况、和平均水平。
6、可以对比。
进行不同组数据的比较,以看出组与组之间的差别。
7、平均数表示数据的特点:直观、简明。
二、平均数的计算方法。
公式:总数量÷总份数=平均数如:班级数学平均分=班级数学总分÷班级总人数平均速度=总路程÷总时间平均单价=物品总价钱÷物品总数量每天的平均气温=24小时的气温和÷24本班男生的平均身高=本班男生身高之和÷本班男生人数注1:一定是总数量÷总份数注2:根据平均数公式可以求:总数量=平均数×总份数;总份数=总数量÷平均数三、生活中的平均数。
平均数在生活中应用非常广泛,渗透在我们的生活、工作、学习各个环境中。
如:1、本周平均最高气温6摄氏度。
2、三年级学生的平均身高是140厘米。
3、四年级2班五位同学平均每人捐10本图书。
4、李莉同学平均每天上学路上花费15分钟。
典型例题【例1、加深理解平均数的意义:移多补少】书架上层有12本书,下层有10本书,请重新整理一下,使每层书架上的书一样多。
四年级下册数学课件-8.3 平均数与条形统计图 单元总结 人教版(共14张PPT)

谢谢!
14
四年级(下册)
平均数与条形统计图 单元总结
1
知识总结
一、平均数: 1、能较好地反映一组数据的总体情况,而不能代表 其中某个个体的情况。它表示统计对象的一般水平。 2、它比一组数据中最大的数要小,比最小的数要大。 3、求平均数的计算方法:总数量÷总份数=平均数 4、平均分:平均数和平均分不一样,是两个不同的 概念。比赛时,计算平均得分时,一般要去掉一个最 高分和一个最低分。
6
例题讲解
例题3.丁丁期末考试语文、数学、英语、体育、美术五门功课的平均成绩 是90分。其中语文、数学、英语三门功课的平均成绩是92分,英语、体育、 美术三门功课的平均成绩是88分。请问,丁丁的英语成绩是多少分?
解析:根据“五门功课的平均分是90分”可得五门功课的总分是 90×5=450(分);根据“语文、数学、英语的平均分数是92分”可得三门功 课的总分是92×3=276(分);根据“英语、体育、美术的平均分数是88分” 可得三门功课的总分是88×3=264(分)。 用算式表示: 语文+数学+英语+体育+美术=90×5=450(分)① 语文+数学+英语=92×3=276(分)② 英语+体育+美术=88×3=264(分)③ ②③两个算式相加,英语成绩被加了2次,即英语成绩被多算了1次, ②③两式和比五门功课的总分数多了:276+264–450=90(分), 所以英语是90分。答:丁丁的英语成绩是90分。 答案:90分
4
空气质量 良 轻度污染 中度污染 重度污染
9
例题讲解
例题5.下表是郑州、北京两座城市2016年12月1日-15日的空气 质量等级情况。
天数(天) 等级
人教部编版四年级数学下册《10.4 总复习:平均数与复式条形统计图》PPT课件

平均数与复式条形统计图
这学期“统计与概率” 学了哪些知识?
我认识了平均数,还会 求一组数据的平均数。
还认识了复式条形统计图,还 会绘制复式条形统计图。
平均数=总数÷份数
画复式条形统计图时,要先确定图例,按照 图例画。 复式条形统计图可以清楚地表示多个物体的 情况。
实验小学二至五年级学生参加公益活动情况如下表:
男生喜欢小汽车的人数 多,女生喜欢布娃娃的 人数多。
22
24
18
1513
14
85
(2)喜欢什么玩具的人 数最多?
18+14=32(人) 答:喜欢拼图的人最多。
22
24
18
1513
14
85
(3)你还能发现什么信息? 答:喜欢跳棋的人最少。
答案不唯一
小明三次跳绳练习的平均成绩是70下,他第一次跳 了64下,第二次跳了68下,第三次跳了多少下?
三次平均跳70下,可以求 出三次的总成绩,再减去 前两次的,就可以求出第 三次的成绩。
70×3-(64+68) =210-132 =78(下) 答:第三次跳了78下。
课堂作业
1.从书本练习中选择题目, 完成与本课时相关练习;
2.完成练习册本课时内容。
学习体会 1、本节课你学到了哪些基本知识? 2、本节课你学到了哪些解题方法? 3、还有哪些知识和方法上的问题?
李兵说得对吗?
李兵说得不对。
因为平均水深1.1m,并不能反映出整 个小河中每一处的水深数值,有的地 方会深一些,有的地方会浅一些。所 以身高1.4m的李兵要下河游泳是会有 危险的。
四年级学生喜欢各图。
22
24
18
1513
四年级数学下册期末总复习《8单元平均数与条形统计图》必记知识点

四年级数学下册期末总复习《8单元平均数与条形统计图》必记知识点一、平均数1.定义:1.平均数是一组数据的总和除以这组数据的个数所得的商。
2.公式:平均数= 总数量÷ 总份数2.意义:1.描述一组数据的整体情况或作为不同组数据进行比较的一个标准。
2.尤其在两组数据个数不相等的情况下,平均数能更好地反映一组数据的总体情况。
3.求平均数的方法:1.移多补少法:在总数不变的前提下,从多的数中拿出一部分分给少的数,使它们变成相同的数。
2.公式法:使用上述公式进行计算。
4.应用:1.比赛计分时,一般采取去掉一个最高分和一个最低分,再求剩余数据的平均数。
二、条形统计图1.定义:1.条形统计图是用直条的长短表示数量的多少,能清楚地看出数量的多少。
2.分类:1.单式条形统计图:表示单一项目的数量。
2.复式条形统计图:可以比较多个项目的数量。
3.复式条形统计图又分为纵向和横向两种形式。
3.绘制方法:1.确定单位长度表示的数量。
2.根据数据的多少画出长短不同的直条。
3.注明图例和数据。
4.注意事项:1.直条的宽度应相同,直条间的间隔应相等。
2.单位长度需统一。
3.必须标明图例。
5.应用:1.可以直观地展示不同项目之间的数量关系。
三、平均数与条形统计图的结合•在分析数据时,可以使用条形统计图来展示数据的分布情况,并通过平均数来进一步描述数据的整体情况或进行不同组数据的比较。
四、总结•平均数和条形统计图都是数学中常用的统计工具,它们能帮助我们更好地理解和分析数据。
通过掌握平均数的定义、意义和求法,以及条形统计图的绘制方法和应用,我们可以更准确地理解和表达数据中的信息。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平均数与条形统计图
1、求平均数公式:
总数量=每份数相加平均数=总数量÷总份数
总数量=平均数×总份数总份数=总数量÷平均数
2、平均数和平均分不一样,是两个不同的概念。
3、比赛时,计算平均得分时,一般要去掉一个最高分和一个最低分。
平均数能较好的反映一组数据的总体情况,而不能代表其中某个个体的情况。
4、条形统计图可以看出数量的多少。
复式条形统计图可以更清楚地看出两组数据不同的地方。
5、复式条形统计图可分为:纵向复式条形统计图和横向复式条形统计图,必须要有图例。
单位长度需统一。
1。
