人教版九年级数学上册知识点总结:第二十三章旋转
人教版九上第二十三章旋转第讲_图形的旋转

初中九年级数学上册第15讲:图形的旋转一:思维导图二:知识点讲解知识点一:旋转的定义➢ 旋转:把一个平面图形绕着平面内某一点O 转动一个角度,叫做图形的旋转,点O 叫做旋转中心,转动的角叫做旋转角。
➢ 旋转角:转动的角叫做选择角,且任意一对对应点与旋转中心所连线段的夹角都是旋转角。
➢ 旋转三要素:旋转中心,旋转角,旋转方向➢ 旋转中心既可以在图形的外部,也可以在图形的内部,还可以在图形上➢ 确定旋转角时,其关键是确定旋转中心和旋转前、后对应点的位置。
例1:如下图所示,△ABC 为等边三角形,D 为BC 边上一点,△ABD 经过旋转后到达△ACP 的位置。
1) 旋转中心是点 ;2) 旋转角度是 ;3) △ADP 是 三角形知识点二:旋转的性质➢ 性质:✧ 对应点到旋转中心的距离相等✧ 对应点与旋转中心所连线段的夹角等于旋转角✧ 旋转前、后的图形全等➢ 注意:✧ 图形中的每一个点都绕旋转中心旋转了同样大小的角度✧ 对应点到旋转中心的距离相等,对应线段相等,对应角相等✧ 图形的大小和形状都没有发生变化,只改变了图形的位置例2:如下图,已知△ABC 中,AC=BC ,∠ACB=90°,直角∠DFE 的顶点F 是AB 中点,两边FD ,FE 分别交AC ,BC 于D ,E 两点,当∠DFE 在△ABC 内绕顶点F 旋转时(点D 不与A ,C 重合),给出以下结论:①CD=BE ;②四边形CDFE 不可能是正方形;③△DFE 是等腰直角三角形;④ABC CDFE S S ∆=21。
上述结论中始终正确的是( ) A. ①②③ B. ②③④C. ①③④D. ①②④ 知识点三:旋转作图➢ 旋转作图的依据✧ 任意一对对应点与旋转中心所连线段的夹角等于旋转角✧ 对应点到旋转中心的距离相等➢ 作图要素:原图、旋转中心、旋转方向、旋转角、一对对应点➢ 作图步骤:✧ 连:连接原图形中一个关键点与旋转中心✧ 转:根据旋转方向与旋转角度,以“连”中关键点与旋转中心的连线为一边作一个旋转角✧ 截:在该旋转角的另一边上,从旋转中心开始截取此关键点到旋转中心的长度,得到该点的对应点。
九年级数学上册第二十三章旋转知识点汇总(带答案)

九年级数学上册第二十三章旋转知识点汇总单选题1、下列图形中,是中心对称图形但不是轴对称图形的是()A.B.C.D.答案:B分析:根据中心对称图形和轴对称图形的定义判断即可.解:∵A中的图形旋转180°后不能与原图形重合,∴A中的图象不是中心对称图形,∴选项A不正确;∵B中的图形旋转180°后能与原图形重合,∴B中的图形是中心对称图形,但不是轴对称图形,∴选项B正确;∵C中的图形旋转180°后能与原图形重合,∴C中的图形是中心对称图形,也是轴对称图形,∴选项C不正确;∵D中的图形旋转180°后不能与原图形重合,∴D中的图形不是中心对称图形,∴选项D不正确;故选:B.小提示:本题考查了轴对称图形和中心对称图形的定义,熟练掌握轴对称图形和中心对称图形的定义是解题的关键.2、有一个正n边形旋转90∘后与自身重合,则n为()A.6B.9C.12D.15答案:C分析:根据选项求出每个选项对应的正多边形的中心角度数,与90∘一致或有倍数关系的则符合题意.如图所示,计算出每个正多边形的中心角,90∘是30∘的3倍,则可以旋转得到.A.B.C.D.观察四个正多边形的中心角,可以发现正12边形旋转90°后能与自身重合故选C.小提示:本题考查正多边形中心角与旋转的知识,解决本题的关键是求出中心角的度数并与旋转度数建立关系.3、如图,在边长为6的正方形ABCD中,点E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF 的长为()A.2B.3√2C.3D.2√22答案:A分析:把△ABF绕点A逆时针旋转90°至△ADG,可使AB与AD重合,首先证明△AFE≌△AGE,进而得到EF=FG,问题即可解决.解:∵四边形ABCD是正方形,∴AB=AD,∴把△ABF绕点A逆时针旋转90°至△ADG,可使AB与AD重合,如图:∴∠BAF=∠DAG,AB=AG∵∠BAD=90°,∠EAF=45°,∴∠BAF+∠DAE=∠DAG+∠DAE=45°,∴∠EAF=∠EAG,∵∠ADG=∠ADC=∠B=90°,∴∠EDG=180°,点E、D、G共线,在△A FE和△AGE中,AG=AF,∠FAE=∠EAG,AE=AE,∴△AFE≌△AGE(SAS),∴EF=EG,即:EF=EG=ED+DG,∵E为CD的中点,边长为6的正方形ABCD,∴CD=BC=6,DE=CE=3,∠C=90°,∴设BF=x,则CF=6−x,EF=3+x,在Rt△CFE中,由勾股定理得:EF2=CE2+CF2,∴(3+x)2=32+(6−x)2,解得:x=2,即BF=2,故选:A.小提示:本题考查了正方形的性质、全等三角形的判定及其性质的应用,解题的关键是作辅助线,构造全等三角形.4、如图,将直角三角板ABC绕顶点A顺时针旋转到△AB′C′,点B′恰好落在CA的延长线上,∠B=30°,∠C= 90°,则∠BAC′为()A.90°B.60°C.45°D.30°答案:B分析:根据直角三角形两锐角互余,求出∠BAC的度数,由旋转可知∠BAC=∠B′AC′,在根据平角的定义求出∠BAC′的度数即可.∵∠B=30°,∠C=90°,∴∠BAC=90°−∠B=90°−30°=60°,∵由旋转可知∠BAC=∠B′AC′=60°,∴∠BAC′=180°−∠BAC−∠B′AC′=180°−60°−60°=60°,故答案选:B.小提示:本题考查直角三角形的性质以及图形的旋转的性质,找出旋转前后的对应角是解答本题的关键.5、将△AOB绕点O旋转180∘得到△DOE,则下列作图正确的是()A.B.C.D.答案:D分析:把一个图形绕某一点O转动一个角度的图形变换叫做旋转.解:观察选项中的图形,只有D选项为△ABO绕O点旋转了180°.小提示:本题考察了旋转的定义.6、如图,在方格纸中,将Rt△AOB绕点B按顺时针方向旋转90°后得到Rt△A′O′B,则下列四个图形中正确的是()A.B.C.D.答案:B分析:根据绕点B按顺时针方向旋转90°逐项分析即可.A、Rt△A′O′B是由Rt△AOB关于过B点与OB垂直的直线对称得到,故A选项不符合题意;B、Rt△A′O′B是由Rt△AOB绕点B按顺时针方向旋转90°后得到,故B选项符合题意;C、Rt△A′O′B与Rt△AOB对应点发生了变化,故C选项不符合题意;D、Rt△AOB是由Rt△AOB绕点B按逆时针方向旋转90°后得到,故D选项不符合题意.故选:B.小提示:本题考查旋转变换.解题的关键是弄清旋转的方向和旋转的度数.7、如图,先将该图沿着它自己的右边缘翻折,再绕着右下角的一个端点按顺时针方向旋转180°,之后所得到的图形是()A.B.C.D.答案:A分析:将图沿着它自己的右边缘翻折,则圆在正方形图形的右上角,然后绕着右下角的一个端点按顺时针方向旋转180°,则圆在正方形的左下角,利用此特征可对四个选项进行判断.先将图沿着它自己的右边缘翻折,得到,再绕着右下角的一个端点按顺时针方向旋转180°,之后所得到的图形为.故选:A小提示:本题考查了利用旋转设计图案:由一个基本图案可以通过平移、旋转和轴对称以及中心对称等方法变换一些复合图案.8、在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,-300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是()A.Q(3,240°)B.Q(3,−450°)C.Q(3,600°)D.(3,−120°)答案:B分析:根据中心对称的性质解答即可.解:∵P(3,60°)或P(3,-300°)或P(3,420°),由点P关于点O成中心对称的点Q可得:点Q的极坐标为(3,240°),(3,-120°),(3,600°),故选:B.小提示:本题考查了中心对称的问题,关键是根据中心对称的性质解答.9、如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A'B'C,连接AA',若∠1=25°,则∠BAA'的度数是()A.70°B.65°C.60°D.55°答案:B分析:根据旋转的性质可得AC=A′C,然后判断出△ACA′是等腰直角三角形,根据等腰直角三角形的性质可得∠CAA′=45°,再根据三角形的内角和定理可得结果.∵Rt△ABC绕直角顶点C顺时针旋转90°得到△A′B′C,∴AC=A′C,∴△ACA′是等腰直角三角形,∴∠CA′A=45°,∠CA′B′=20°=∠BAC∴∠BAA′=180°-70°-45°=65°,故选:B.小提示:本题考查了旋转的性质,等腰直角三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并准确识图是解题的关键.10、如图,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,若点D恰好在BC的延长线上,则∠BDE的度数为()A.100°B.80°C.70°D.60°答案:B分析:由旋转的性质可知∠B=∠ADE,AB=AD,由等腰三角形的性质和三角形的内角和定理可求得∠B=∠BDA=∠ADE=40°,从而可求得∠BDE=80°.解:由旋转的性质可知:∠B=∠ADE,AB=AD,∠BAD=100°.∵AB=AD,∠BAD=100°,∴∠B=∠BDA=40°,∴∠ADE=40°,∴∠BDE=∠BDA+∠ADE=40°+40°=80°.故选B.小提示:本题考查旋转的性质,等腰三角形的性质,三角形内角和定理.由旋转的性质得到△ABD为等腰三角形是解题的关键.填空题11、如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是__.答案:38°分析:根据旋转变换的性质得到∠AOD=31°,∠BOC=31°,结合图形,计算即可.解:由旋转的性质可知,∠AOD=31°,∠BOC=31°,∴∠DOB=∠AOC−∠AOD−∠BOC=38°,所以答案是:38°.小提示:本题考查的是旋转变换的性质,掌握对应点与旋转中心所连线段的夹角等于旋转角是解题的关键.12、在平面直角坐标系内,点P(−3,2)关于原点的对称点Q的坐标为______.答案:(3,−2)分析:根据平面直角坐标系中任意一点P(x,y),关于原点的对称点是(−x,−y),即可直接作答.根据中心对称性质可知:点P (−3,2)关于原点的对称点Q 的坐标为(3,−2),故答案为(3,−2).小提示:本题考查了关于原点对称点的坐标,属于基础问题,熟记知识点是解题关键.13、点O 是平行四边形ABCD 的对称中心,AD >AB ,E 、F 分别是AB 边上的点,且EF =12AB ;G 、H 分别是BC 边上的点,且GH =13BC ;若S 1,S 2分别表示∆EOF 和∆GOH 的面积,则S 1,S 2之间的等量关系是______________答案:2S 1=3S 2分析:过点O 分别作OM ⊥BC ,垂足为M ,作ON ⊥AB ,垂足为N ,根据点O 是平行四边形ABCD 的对称中心以及平行四边形的面积公式可得AB•ON=BC•OM ,再根据S 1=12EF•ON ,S 2=12GH•OM ,EF =12AB ,GH =13BC ,则可得到答案.过点O 分别作OM ⊥BC ,垂足为M ,作ON ⊥AB ,垂足为N ,∵点O 是平行四边形ABCD 的对称中心,∴S 平行四边形ABCD =AB •2ON , S 平行四边形ABCD =BC•2OM ,∴AB•ON=BC•OM ,∵S 1=12EF•ON ,S 2=12GH•OM ,EF =12AB ,GH =13BC ,∴S 1=14AB•ON ,S 2=16BC•OM , ∴2S 1=3S 2,故答案为2S 1=3S 2.小提示:本题考查了平行四边形的面积,中心对称的性质,正确添加辅助线、准确表示出图形面积是解题的关键.14、如图,在直角坐标系中,边长为2个单位长度的正方形ABCO绕原点O逆时针旋转75°,再沿y轴方向向上平移1个单位长度,则点B″的坐标为___________.答案:(−√2,√6+1)##(−√2,1+√6)分析:连接OB,OB′由题意可得∠BOB′=75°,可得出∠COB′=30°,可求出B′的坐标,即可得出点B″的坐标.解:如图:连接OB,OB′,作B′M⊥y轴∵ABCO是正方形,OA=2∴∠COB=45°,OB=2√2∵绕原点O逆时针旋转75°∴∠BOB′=75°∴∠COB′=30°∵OB′=OB=2√2∴MB′=√2,MO=√6∴B′(−√2,√6)∵沿y轴方向向上平移1个单位长度∴B″(−√2,√6+1)所以答案是:(−√2,√6+1)小提示:本题考查了坐标与图形变化﹣旋转,坐标与图形变化﹣平移,熟练掌握网格结构,准确确定出对应点的位置是解题的关键.15、如图,P是正△ABC内的一点,若将△PAB绕点A逆时针旋转到△P1AC,则∠PAP1等于________度.答案:60分析:利用旋转的性质即可得出答案.解:∵△ABC是正三角形,∴∠CAB=60°,由旋转的性质可知,∠PAP1=∠CAB=60°.所以答案是:60.小提示:本题考查正三角形的性质和旋转的性质,由旋转的性质得出∠PAP1=∠CAB是解题的关键.解答题16、如图1,二次函数y=a(x+3)(x﹣4)的图象交坐标轴于点A,B(0,﹣2),点P为x轴上一动点.(1)求该二次函数的解析式;(2)过点P作PQ⊥x轴,分别交线段AB、抛物线于点Q,C,连接AC.若OP=1,求△ACQ的面积;(3)如图2,连接PB,将线段PB绕点P逆时针旋转90°得到线段PD.当点D在抛物线上时,求点D的坐标.答案:(1)y=16x2−16x−2;(2)SΔACQ=34;(3)D(3,−1)或D(−8,10)分析:(1)将B(0,−2)代入y=a(x+3)(x−4),即可求解;(2)先求直线AB的解析式为y=12x−2,则Q(1,−32),C(1,−2),可求SΔACQ=SΔACP−SΔAPQ=34;(3)设P(t,0),过点D作x轴垂线交于点N,可证明ΔPND≅ΔBOP(AAS),则D(t+2,−t),将D点代入抛物线解析式得−t=16(t+2+3)(t+2−4),求得D(3,−1)或D(−8,10).解:(1)将B(0,−2)代入y=a(x+3)(x−4),∴a=16,∴y=16(x+3)(x−4)=16x2−16x−2;(2)令y=0,则16(x+3)(x−4)=0,∴x=−3或x=4,∴A(4,0),设直线AB的解析式为y=kx+b,∴{b=−24k+b=0,∴{k=1 2b=−2,∴y=12x−2,∵OP=1,∴P(1,0),∵PQ⊥x轴,∴Q(1,−32),C(1,−2),∴AP=3,∴SΔACQ=SΔACP−SΔAPQ=12×3×2−12×3×32=34;(3)设P(t,0),如图2,过点D作x轴垂线交于点N,∵∠BPD=90°,∴∠OPB+∠NPD=90°,∠OPB+∠OBP=90°,∴∠NPD=∠OBP,∵BP=PD,∴ΔPND≅ΔBOP(AAS),∴OP=ND,BO=PN,∴D(t+2,−t),∴−t=16(t+2+3)(t+2−4),解得t=1或t=−10,∴D(3,−1)或D(−8,10).小提示:本题是二次函数综合题,考查了二次函数图象和性质,待定系数法求抛物线解析式,三角形面积,全等三角形判定和性质,旋转的性质等,解题的关键是熟练掌握二次函数的图象及性质,分类讨论,数形结合.17、如图1,正方形ABCD的边长为4,点P在边AD上(P不与A,D重合),连接PB,PC.将线段PB绕点P顺时针旋转90°得到PE,将线段PC绕点P逆时针旋转90°得到PF.连接EF,EA,FD.(1)求证:PD2;①ΔPDF的面积S=12②EA=FD;(2)如图2,EA.FD的延长线交于点M,取EF的中点N,连接MN,求MN的取值范围.答案:(1)①见详解;②见详解;(2)4≤MN<2√5分析:(1)①过点F作FG⊥AD交AD的延长线于点G,证明△PFG≌△CPD,即可得到结论;②过点E作EH⊥DA交DA的延长线于点H,证明△PEH≌△BPA,结合△PFG≌△CPD,可得GD=EH,同理:FG=AH,从而得△AHE≌△FGD,进而即可得到结论;(2)过点F作FG⊥AD交AD的延长线于点G,过点E作EH⊥DA交DA的延长线于点H,可得∠AMD=90°,EF,HG= 2AD=8,EH+FG=AD=4,然后求出当点P与点D重合时,EF最大值=4√5,当点P与AD的中点重合MN=12时,EF最小值= HG=8,进而即可得到答案.(1)①证明:过点F作FG⊥AD交AD的延长线于点G,∵∠FPG+∠PFG=90°,∠FPG+∠CPD=90°,∴∠FPG=∠CPD,又∵∠PGF=∠CDP=90°,PC=PF,∴△PFG≌△CPD(AAS),∴FG=PD,∴ΔPDF的面积S=12PD⋅FG=12PD2;②过点E作EH⊥DA交DA的延长线于点H,∵∠EPH+∠PEH=90°,∠EPH +∠BPA=90°,∴∠PEH =∠BPA,又∵∠PHE=∠BAP=90°,PB=PE,∴△PEH≌△BPA(AAS),∴EH=PA,由①得:FG=PD,∴EH+FG=PA+PD=AD=CD,由①得:△PFG≌△CPD,∴PG=CD,∴PD+GD= CD= EH+FG,∴FG+GD= EH+FG,∴GD=EH,同理:FG=AH,又∵∠AHE=∠FGD,∴△AHE≌△FGD,∴EA=FD;(2)过点F作FG⊥AD交AD的延长线于点G,过点E作EH⊥DA交DA的延长线于点H,由(1)得:△AHE≌△FGD,∴∠HAE=∠GFD,∵∠GFD+∠GDF=90°,∴∠HAE+∠GDF=90°,∵∠HAE=∠MAD,∠GDF=∠MDA,∴∠MAD+∠MDA=90°,∴∠AMD=90°,∵点N是EF的中点,∴MN=1EF,2∵EH=DG=AP,AH=FG=PD,∴HG=AH+DG+AD=PD+AP+AD=2AD=8,EH+FG=AP+PD=AD=4,当点P与点D重合时,FG=0,EH=4,HG=8,此时EF最大值=√42+82=4√5,当点P与AD的中点重合时,FG=2,EH=2,HG=8,此时EF最小值= HG=8,∴MN的取值范围是:4≤MN<2√5.小提示:本题主要考查全等三角形的判定和性质,正方形的性质,勾股定理,旋转的性质,添加辅助线,构造直角全等的直角三角形,是解题的关键.18、如图,△AOB中,OA=OB=6,将△AOB绕点O逆时针旋转得到△COD.OC与AB交于点G,CD分别交OB、AB 于点E、F.(1)∠A与∠D的数量关系是:∠A______∠D;(2)求证:△AOG≌△DOE;(3)当A,O,D三点共线时,恰好OB⊥CD,求此时CD的长.答案:(1)=(2)证明见解析(3)6√3,详见解析分析:(1)根据旋转性质及等腰三角形性质即可得答案;(2)由旋转性质知∠AOB=∠DOC,可证得∠AOG=∠DOE,结合OA=OB及(1)中结论,得证;(3)分两种情况讨论,设∠A=x°,先利用三角形内角和求出x的值,再借助勾股定理求出CD的长度即可.(1)解:由旋转知,∠A=∠C,∠B=∠D,∵OA=OB,∴OC=OD,∠A=∠B=∠C=∠D∴∠A=∠D,所以答案是:=.(2)证明:由旋转知,OA=OC,OB=OD,∠AOB=∠COD,∴∠AOB-∠BOC=∠COD-∠BOC,即∠AOG=∠DOE,∵OA=OB,∴OA=OB=OC=OD,又∵∠A=∠D,∴△AOG≌△DOE.(3)解:分两种情况讨论,①如图所示,设∠A=∠B=∠C=∠D=x°,则∠DOB=2x°,∵OB⊥CD,∴∠OED=90°,∴x+2x=90°,解得:x=30,即∠D=30°,在Rt△ODE中,OE=3,由勾股定理得:DE=√62−32=3√3,∵OC=OD,OE⊥CD,∴CD=2DE=6√3.②当D与A重合时,如图所示,同理,得:CD=6√3.综上所述,当A,O,D三点共线时,OB⊥CD,此时CD的长为6√3.小提示:本题考查了旋转的性质、等腰三角形性质、全等三角形的判定、勾股定理等知识点,解题关键是利用旋转性质得到边、角的关系.。
最新人教版数学九年级上册第二十三章—旋转知识点总结及其练习

第二十三章—旋转一、旋转变换1、旋转的定义把一个图形绕着某一点O转动一个角度的图形变换叫做旋转。
点O叫做旋转中心,转动的角叫做旋转角,如果图形上的点P经过旋转变为点P',那么这两个点叫做这个旋转的对应点。
2、旋转的性质(1)对应点到旋转中心的距离相等。
(旋转中心就是各对应点所连线段的垂直平分线的交点。
)(2)对应点与旋转中心所连线段的夹角等于旋转角。
(3)旋转前、后的图形全等。
3、作旋转后的图形的一般步骤(1)明确三个条件:旋转中心,旋转方向,旋转角度;(2)确定关键点,作出关键点旋转后的对应点;(3)顺次连结。
4、欣赏较复杂旋转图形图形是由什么基本图形,以哪个点为中心,按哪个方向(顺时针或逆时针)旋转多少度,连续旋转几次,便得到美丽的图案。
5、有关图形旋转的一些计算题和证明题例题练习1.将叶片图案旋转180°后,得到的图形是( )2.如图,在等腰直角△ABC中,B=90°,将△ABC绕顶点A逆时针方向旋转60°后得到△AB′C′,则等于()A.60°B.105°C.120°D.135°3.如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在位置,A点落在位置,若,则的度数是()A.50°B.60°C.70°D.80°4.数学来源于生活,下列生活中的运动属于旋转的是 ( )A.国旗上升的过程B.球场上滚动的足球C.工作中的风力发电机叶片D.传输带运输东西5.如图,将方格纸中的图形绕点O逆时针旋转90°后得到的图形是 ( )6.如图,在△ABC中,AB=AC,∠ABC=30°,点D、E分别为AB、AC上的点,且DE∥BC.将△ADE绕点A逆时针旋转至点B、A、E在同一条直线上,连接BD、EC.下列结论:①△ADE的旋转角为120°;②BD=EC;③BE=AD+AC;④DE⊥AC.其中正确的为( )A.②③B.②③④C.①②③D.①②③④7.如图,将△ABC绕点A顺时针旋转得到△ADE,且点D恰好在AC上,∠BAE=∠CDE=136°,则∠C的度数是()8.如图,以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连接BE、CF.(1)求证:△FAC≌△BAE;(2)图中可以通过旋转△BAE而得到△FAC,请你说出旋转中心、旋转方向和旋转角的度数.9.如图,四边形ABCD是正方形,点E是边BC上的动点(不与B,C重合),将线段AE 绕点E顺时针旋转90°得到线段EF,连接AF,EF、AF分别与CD交于点M、N,连接EN,作FG⊥BC交BC的延长线于点G.(1)求证:BE=CG;(2)若BE=2,DN=3,求EN的长.二、中心对称图形1、中心对称的定义把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点。
2024九年级数学上册“第二十三章 旋转”必背知识点

2024九年级数学上册“第二十三章旋转”必背知识点一、旋转的基本概念定义:将一个图形绕着某点O转动一个角度的变换叫做旋转。
其中,O叫做旋转中心,转动的角度叫做旋转角。
旋转三要素:旋转中心、旋转角度、旋转方向。
二、旋转的性质旋转后的图形与原图形的关系:旋转后的图形与原图形全等。
对应点与旋转中心的距离:对应点到旋转中心的距离相等。
对应点与旋转中心所连线段的夹角:对应点与旋转中心所连线段的夹角等于旋转角。
图形变化:图形的大小和形状都没有发生改变,只改变了图形的位置。
三、中心对称定义:若一个图形绕着某个点O旋转180°,能够与另一个图形完全重合,则这两个图形关于这个点对称或中心对称。
这个点叫做对称中心。
中心对称图形:若一个图形绕着某个点O旋转180°,能够与原来的图形完全重合,则这个图形叫做中心对称图形。
这个点叫做该图形的对称中心。
性质:1. 关于中心对称的两个图形上的对应点的连线都经过对称中心,并且都被对称中心平分。
2. 关于中心对称的两个图形能够互相重合,是全等形。
3. 关于中心对称的两个图形,对应线段平行(或共线)且相等。
四、关于原点对称的点的坐标在平面直角坐标系中,如果两个点关于原点对称,它们的坐标符号相反。
即点P(x,y)关于原点对称的点的坐标为P'(-x,-y)。
五、作图与应用利用旋转性质作图:关键是连接图形中的每一个关键点与旋转中心,并按要求绕旋转中心转过一定角度,然后在新的位置上截取与原来等长的线段,连接各点得到新的图形。
旋转的应用:旋转在几何图形的变换、证明以及解决实际问题中都有广泛的应用,如通过旋转构造全等图形、证明角相等或线段相等。
六、例题与练习为了加深对旋转知识点的理解和记忆,可以通过做一些相关的例题和练习题来巩固所学内容。
这些题目通常会涉及到旋转的基本概念、性质以及应用等方面的知识点。
综上所述,九年级数学上册 “第二十三章 旋转”的必背知识点主要包括旋转的基本概念、性质、中心对称及其性质、关于原点对称的点的坐标以及作图与应用等方面。
九年级数学上册第二十三章旋转笔记重点大全(带答案)

九年级数学上册第二十三章旋转笔记重点大全单选题1、平面直角坐标系中,O为坐标原点,点A的坐标为(−5,1),将OA绕原点按逆时针方向旋转90°得OB,则点B 的坐标为()A.(−5,1)B.(−1,−5)C.(−5,−1)D.(−1,5)答案:B分析:根据题意证得△AOC≌△OBD,可得结论.解:如图,根据题意得∶∠AOB=90°,∠ACO=∠BDO=90°,OA=OB,∴∠AOC+∠BOD=90°,∠AOC+∠OAC=90°,∴∠BOD=∠OAC,∴△AOC≌△OBD,∴BD=OC,OD=AC,∵点A的坐标为(−5,1),∴BD=OC=1,OD=AC=5,∴B(−1,−5).故选:B.小提示:本题考查坐标与图形变化−旋转,解题的关键是熟练掌握旋转的性质,属于中考常考题型.2、如图,正方形OABC的边长为√2,将正方形OABC绕原点O顺时针旋转45°,则点B的对应点B1的坐标为()A.(−√2,0)B.(−√2,0)C.(0,√2)D.(0,2)答案:D分析:连接OB,由正方形ABCD绕原点O顺时针旋转45°,推出∠A1OB1=45°,得到△A1OB1为等腰直角三角形,点B1在y轴上,利用勾股定理求出O B1即可.解:连接OB,∵正方形ABCD绕原点O顺时针旋转45°,∴∠AOA1=45°,∠AOB=45°,∴∠A1OB1=45°,∴△A1OB1为等腰直角三角形,点B1在y轴上,∵∠B1A1O=90°,A1B1=OA1=√2,∴OB1=√A1B12+OA12=√2+2=2,∴B1(0,2),故选:D.小提示:本题考查了正方形的性质,旋转的性质,特殊三角形的性质.关键是根据旋转角证明点B1在y轴上.3、在平面直角坐标系中,点(3,2)关于原点对称的点的坐标是()A.(2,3)B.(−3,2)C.(−3,−2)D.(−2,−3)答案:C分析:根据坐标系中对称点与原点的关系判断即可.关于原点对称的一组坐标横纵坐标互为相反数,所以(3,2)关于原点对称的点是(-3,-2),故选C.小提示:本题考查原点对称的性质,关键在于牢记基础知识.4、以图(1)(以O为圆心,半径为1的半圆)作为“基本图形”,分别经历如下变换,不能得到图(2)的是()A.绕着OB的中点旋转180°即可B.先绕着点O旋转180°,再向右平移1个单位C.先以直线AB为对称轴进行翻折,再向右平移1个单位D.只要向右平移1个单位答案:D分析:根据旋转、平移和轴对称的定义进行分析即可.由旋转、平移和轴对称的性质可知:经过A、B、C的变化,图(1)均可得到图(2),经过D的变化不能得到图(2);故选:D小提示:本题主要考查了旋转、平移和轴对称的性质,熟练地掌握各个性质是解题的关键.5、如图,在平面直角坐标系中,OA1=OB1,∠A1OB1=120°,将ΔA1OB1绕点O顺时针旋转并且按一定规律放大,每次变化后得到的图形仍是顶角为120°的等腰三角形.第一次变化后得到等腰三角形A2OB2,点A1(1,0)的对应点为A2(−1,−√3);第二次变化后得到等腰三角形A3OB3,点A2的对应点为A3(−32,3√32);第三次变化后得到等腰三角形A4OB4,点A3的对应点为A4(4,0)⋯⋯依此规律,则第2022个等腰三角形中,点B2022的坐标是()A.(2022,0)B.(−2022,−2022√3)C.(−1011,1011√3)D.(−1011,−1011√3)答案:D分析:利用循环的规律,找到第2022个等腰三角形与第一个循环的图形的第几个位置相同,再根据第一个循环中的点坐标进行求值即可.解:由题意可知,旋转规律为4次一个循环,即第2022次为:505个循环余2,∴点B2022位置与B3相同,在第三象限,∵B3坐标为(−32,−3√32),∴点B2022坐标为(−20222,−2022√32),即为(−1011,−1011√3).故选:D.小提示:本题主要考查的是坐标系与几何图形的规律问题,准确找到循环规律是解题的关键.6、如图,在△ABC中,AB=AC,若M是BC边上任意一点,将△ABM绕点A逆时针旋转得到△ACN,点M的对应点为点N,连接MN,则下列结论一定正确的是()A.AB=AN B.AB∥NC C.∠AMN=∠ACN D.MN⊥AC答案:C分析:根据旋转的性质,对每个选项逐一判断即可.解:∵将△ABM绕点A逆时针旋转得到△ACN,∴△ABM≌△ACN,∴AB=AC,AM=AN,∴AB不一定等于AN,故选项A不符合题意;∵△ABM≌△ACN,∴∠ACN=∠B,而∠CAB不一定等于∠B,∴∠ACN不一定等于∠CAB,∴AB与CN不一定平行,故选项B不符合题意;∵△ABM≌△ACN,∴∠BAM=∠CAN,∠ACN=∠B,∴∠BAC=∠MAN,∵AM=AN,AB=AC,∴△ABC和△AMN都是等腰三角形,且顶角相等,∴∠B=∠AMN,∴∠AMN=∠ACN,故选项C符合题意;∵AM=AN,而AC不一定平分∠MAN,∴AC与MN不一定垂直,故选项D不符合题意;故选:C.小提示:本题考查了旋转的性质,等腰三角形的判定与性质.旋转变换是全等变换,利用旋转不变性是解题的关键.7、在平面直角坐标系中,抛物线y=x2−4x+5与y轴交于点C,则该抛物线关于点C成中心对称的抛物线的表达式为()A.y=−x2−4x+5B.y=x2+4x+5C.y=−x2+4x−5D.y=−x2−4x−5答案:A分析:先求出C点坐标,再设新抛物线上的点的坐标为(x,y),求出它关于点C对称的点的坐标,代入到原抛物线解析式中去,即可得到新抛物线的解析式.解:当x=0时,y=5,∴C(0,5);设新抛物线上的点的坐标为(x,y),∵原抛物线与新抛物线关于点C成中心对称,由2×0−x=−x,2×5−y=10−y;∴对应的原抛物线上点的坐标为(−x,10−y);代入原抛物线解析式可得:10−y=(−x)2−4⋅(−x)+5,∴新抛物线的解析式为:y=−x2−4x+5;故选:A.小提示:本题综合考查了求抛物线上点的坐标、中心对称在平面直角坐标系中的运用以及求抛物线的解析式等内容,解决本题的关键是设出新抛物线上的点的坐标,求出其在原抛物线上的对应点坐标,再代入原抛物线解析式中求新抛物线解析式,本题属于中等难度题目,蕴含了数形结合的思想方法等.8、将△OBA按如图方式放在平面直角坐标系中,其中∠OBA=90°,∠A=30°,顶点A的坐标为(1,√3),将△OBA绕原点逆时针旋转,每次旋转60°,则第2023次旋转结束时,点A对应点的坐标为()A.(−1,√3)B.(−√3,1)C.(−√33,1)D.(−1,√33)答案:A分析:根据旋转性质,可知6次旋转为1个循环,故先需要求出前6次循环对应的A点坐标即可,利用全等三角形性质求出第一次旋转对应的A点坐标,之后第2次旋转,根据图形位置以及OA长,即可求出,第3、4、5次分别利用关于原点中心对称,即可求出,最后一次和A点重合,再判断第2023次属于循环中的第1次,最后即可得出答案.解:由题意可知:6次旋转为1个循环,故只需要求出前6次循环对应的A点坐标即可第一次旋转时:过点A′作x轴的垂线,垂足为C,如下图所示:由A的坐标为(1,√3)可知:OB=1,AB=√3,在RtΔAOB中,∠AOB=90°−∠A=60°,OA=2由旋转性质可知:ΔAOB≌ΔA′OB′,∴∠A′OB′=∠AOB=60°,OA′=OA,∴∠A′OC=180°−∠A′OB′−∠AOB=60°,在ΔA′OC与ΔAOB中:{∠A′OC′=∠AOB=60°∠A′CO=∠ABO=90°OA′=OA∴ΔA′OC′≌ΔAOC(AAS),∴OC =OB =1,A ′C =AB =√3,∴此时点A 对应坐标为(−1,√3),当第二次旋转时,如下图所示:此时A 点对应点的坐标为(−2,0).当第3次旋转时,第3次的点A 对应点与A 点中心对称,故坐标为(−1,−√3).当第4次旋转时,第4次的点A 对应点与第1次旋转的A 点对应点中心对称,故坐标为(1,−√3). 当第5次旋转时,第5次的点A 对应点与第2次旋转的A 点对应点中心对称,故坐标为(2,0). 第6次旋转时,与A 点重合.故前6次旋转,点A 对应点的坐标分别为:(−1,√3)、(−2,0)、(−1,−√3)、(1,−√3)、(2,0)、(1,√3).由于2023÷6=337⋅⋅⋅⋅⋅⋅1,故第2023次旋转时,A 点的对应点为(−1,√3).故选:A .小提示:本题主要是考查了旋转性质、中心对称求点坐标、三角形全等以及点的坐标特征,熟练利用条件证明全等三角形,;通过旋转和中心对称求解对应点坐标,是求解该题的关键.9、如图,点O 是等边三角形ABC 内一点,OA =2,OB =1,OC =√3,则ΔAOB 与ΔBOC 的面积之和为( )A .√34B .√32C .3√34D .√3答案:C分析:将ΔAOB绕点B顺时针旋转60°得ΔBCD,连接OD,得到△BOD是等边三角形,再利用勾股定理的逆定理可得∠COD=90°,从而求解.解:将ΔAOB绕点B顺时针旋转60°得ΔBCD,连接OD,∴OB=OD,∠BOD=60°,CD=OA=2,∴ΔBOD是等边三角形,∴OD=OB=1,∵OD2+OC2=12+(√3)2=4,CD2=22=4,∴OD2+OC2=CD2,∴∠DOC=90°,∴ΔAOB与ΔBOC的面积之和为S△BOC+S△BCD=S△BOD+S△COD=√34×12+12×1×√3=3√34.故选:C.小提示:本题主要考查了等边三角形的判定与性质,勾股定理的逆定理,旋转的性质等知识,利用旋转将ΔAOB与ΔBOC的面积之和转化为S△BOC+S△BCD,是解题的关键.10、已知点P(m−3,m−1)关于原点的对称点P′在第四象限,则m的取值范围在数轴上表示正确的是()A.B.C.D.答案:D分析:先确定点P 所在的象限,然后根据点所在象限的坐标特点列不等式组求解即可.解:∵点P(m −3,m −1)关于原点的对称点P′在第四象限,∴点P 在第二象限,∴ {m −3<0m −1>0, 解得:1<m <3,故选:D .小提示:本题主要考查了点的坐标特征,掌握第二象限的点的横坐标小于零、纵坐标大于零是解答本题的关键.填空题11、△ABC 中,AB =8,AC =6,AD 是BC 边上的中线,则AD 长度的范围是__________.答案:1<AD <7分析:延长AD 至E ,使DE =AD ,连接CE .根据SAS 证明△ABD ≌△ECD ,得CE =AB ,再根据三角形的三边关系即可求解.解:延长AD 至E ,使DE =AD ,连接CE .在△ABD 和△ECD 中,{DE =AD∠ADB =∠CDE DB =DC,∴△ABD ≌△ECD (SAS ),∴CE =AB .在△ACE 中,CE -AC <AE <CE +AC ,即2<2AD <14,故1<AD<7.故答数为:1<AD<7.小提示:本题主要考查了全等三角形的判定和性质、三角形的三边关系.注意:倍长中线是常见的辅助线之一.12、如图,正方形OABC的边长为2,将正方形OABC绕点O逆时针旋转角α(0°<α<180°)得到正方形OA′B′C′,连接BC′,当点A′恰好落在线段BC′上时,线段BC′的长度是 ___.答案:√6+√2分析:连接OB,过点O作OE⊥C'B于E,则∠OEC'=∠OEB=90°,由正方形OABC绕点O逆时针旋转角α(0°<α<180°)得到正方形OA′B′C′,所以∠OC'E=45°,OA=OC'=AB=2,∠A=90°,根据勾股定理得到BE的长,从而得到BC'.解:如图,连接OB,过点O作OE⊥C'B于E,则∠OEC'=∠OEB=90°,∵将正方形OABC绕点O逆时针旋转角α(0°<α<180°)得到正方形OA′B′C′,点A′恰好落在线段BC′上,∴∠OC'E=45°,OA=OC'=AB=2,∠A=90°,∴OB=2√2,OE=EC'=√2,在Rt△OBE中,由勾股定理得:BE=√OB2−OE2=√(2√2)2−(√2)2=√6,∴BC'=BE+EC'=√6+√2.所以答案是:√6+√2小提示:本题考查了旋转的性质、正方形的性质以及勾股定理,解题的关键是作辅助线构造特殊三角形.13、已知坐标系中点A(−2,a)和点B(b,3)关于原点中心对称,则a+b=__________.答案:-1分析:直接利用关于原点对称点的性质,得出a,b的值,即可得出答案.解:∵坐标系中点A(-2,a)和点B(b,3)关于原点中心对称,∴b=2,a=-3,则a+b=2-3=-1.所以答案是:-1.小提示:此题主要考查了关于原点对称点的性质,正确掌握横纵坐标的符号关系是解题关键.14、如图,在直角坐标系中,△ABC的顶点坐标分别为A(1,2),B(-2,2),C(-1,0).将△ABC绕某点顺时针旋转90°得到△DEF,则旋转中心的坐标是_____________.答案:(1,-1)分析:由旋转的性质可得A的对应点为D,B的对应点为E,C的对应点为F,同时旋转中心在AD和BE的垂直平分线上,进而求出旋转中心坐标.解:由旋转的性质,得A的对应点为D,B的对应点为E,C的对应点为F作BE和AD的垂直平分线,交点为P∴点P的坐标为(1,-1)所以答案是:(1,-1)小提示:本题考查坐标与图形变化—旋转,图形的旋转需结合旋转角求旋转后的坐标,常见的旋转角有30°,45°,60°,90°,180°.15、若点P(a-1,5)与点Q(5,1-b)关于原点成中心对称,则a+b=___.答案:2分析:根据关于原点对称的性质得到a-1+5=0,5+1-b=0,求出a、b,问题得解.解:∵点P(a-1,5)与点Q(5,1-b)关于原点成中心对称,∴a-1+5=0,5+1-b=0,∴a=-4,b=6,∴a+b=2.所以答案是:2小提示:本题考查了关于原点对称的点的坐标特点,熟知“两个点关于原点对称,则这两个点的横纵坐标都互为相反数”是解题关键.解答题16、如图,已知等边△ABC中,点D、E、F分别为边AB、AC、BC的中点,M为直线BC上一动点,△DMN为等边三角形(点M的位置改变时,△DMN也随之整体移动).(1)如图1,当点M在点B左侧时,请你连结EN,并判断EN与MF有怎样的数量关系?点F是否在直线NE 上?请写出结论,并说明理由;(2)如图2,当点M在BC上时,其它条件不变,(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请利用图2证明;若不成立,请说明理由;(3)如图3,若点M在点C右侧时,请你判断(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请直接写出结论:若不成立,请说明理由.答案:(1)相等,在,理由见解析;(2)成立,证明见解析;(3)成立.分析:(1)连接DE、DF、EF,NF,根据等边三角形的性质和三角形中位线的性质,先证得△DBF是等边三角形,可得△DMB≌△DNF,可得∠DBM=∠DFN,从而得到∠NFD+∠DFE=180°,再由△DMN是等边三角形,从而证得△DMF≌△DNE,得到EN=MF,即可求证;(2)连接DF,NF,EF,等边三角形的性质,可证得△DMB≌△DNF,得到BM=FN,∠DFN=∠FDB=60°,从而NF∥BD,再由EF是△ABC的中位线,可得EF∥BD,从而F在直线NE上,即可求证;(3)连接DF、DE,EF,根据等边三角形的性质和三角形中位线的性质,可得△DBF是等边三角形,从而证得△DNE≌△DMF,即可求证.解:(1)EN=MF,点F在直线NE上,理由如下:如图1,连接DE、DF、EF,NF,∴AB=AC=BC,∠ABC=60°,又∵点D、E、F分别为边AB、AC、BC的中点,∴DE、DF、EF为等边△ABC的中位线,DE=12BC,EF=12AB,DF=12AC,∴DE=DF=EF,∴∠FDE=∠DFE=60°∵D、F分别是AB、BC的中点,∴BD=BF,∴△DBF是等边三角形,∴∠BDF=60°,∵△DMN是等边三角形,∴∠MDN=60°,DM=DN,∴∠MDN=∠BDF=60°,DB=DF,∴∠MDN-∠BDN=∠BDF-∠BDN,即∠MDB=∠NDF,在△DMB和△DNF中,∵DM=DN,∠MDB=∠NDF,DB=DF,∴△DMB≌△DNF,∴∠DBM=∠DFN,∵∠ABC=60°,∴∠DBM=120°,∴∠NFD=120°,∴∠NFD+∠DFE=120°+60°=180°,∴N、F、E三点共线,∴F在直线NE上;∴∠MDN=60°,DM=DN,∴∠FDE+∠NDF=∠MDN+∠NDF,∴∠MDF=∠NDE,在△DMF和△DNE中,∵DF=DE,∠MDF=∠NDE,DM=DN,∴△DMF≌△DNE,∴MF=NE,(2)成立,理由如下:如图2,连接DF,NF,EF,∵△ABC是等边三角形且D、F分别是AB、BC的中点,∴∠ABC=60°,BD=BF,∴△DBF是等边三角形,∴∠BDF=∠DBF=60°,∵△DMN是等边三角形,∴∠MDN=60°,DM=DN,∴∠MDN=∠BDF=60°,DB=DF,∴∠MDN-∠FDM=∠BDF-∠FDM,即∠MDB=∠NDF,在△DMB和△DNF中,∵DM=DN,∠MDB=∠NDF,DB=DF,∴△DMB≌△DNF,∴∠DBM=∠DFN=60°,BM=FN,∴∠DFN=∠FDB=60°,∴NF∥BD,∵E,F分别为边AC,BC的中点,∴EF是△ABC的中位线,BF=12BC=12AB,∴EF∥BD,EF=12AB,∴F在直线NE上,BF=EF,∴MF=EN;(3)MF与EN相等的结论仍然成立,理由如下:如图3,连接DF、DE,EF,∵△ABC是等边三角形,∴AB=AC=BC,又∵点D、E、F分别为边AB、AC、BC的中点,∴DE、DF、EF为等边△ABC的中位线,DE=12BC,EF=12AB,DF=12AC,∴DE=DF=EF,∴△DEF是等边三角形,∴∠FDE=60°,∵△DMN是等边三角形,∴∠MDN=∠FDE=60°,DM=DN,∴∠EDM+∠NDE=∠EDM+∠FDM,∴∠NDE=∠FDM,在△DNE和△DMF中,∵DE=DF,∠NDE=∠FDM,DN=DM,△DNE≌△DMF,∴MF=NE.小提示:本题主要考查了等边三角形的性质和判定,全等三角形的性质和判定,熟练掌握等边三角形的性质和判定,全等三角形的性质和判定是解题的关键.17、已知△ABC是等边三角形,点B,D关于直线AC对称,连接AD,CD.(1)求证:四边形ABCD是菱形;(2)在线段AC上任取一点Р(端点除外),连接PD.将线段PD绕点Р逆时针旋转,使点D落在BA延长线上的点Q处.请探究:当点Р在线段AC上的位置发生变化时,∠DPQ的大小是否发生变化?说明理由.(3)在满足(2)的条件下,探究线段AQ与CP之间的数量关系,并加以证明.答案:(1)见解析(2)∠DPQ大小不变,理由见解析(3)CP=AQ,证明见解析分析:(1)连接BD,由等边三角形的性质可得AC垂直平分BD,继而得出AB=BC=CD=AD,便可证明;(2)连接PB,过点P作PE∥CB交AB于点E,PF⊥AB于点F,可证明△APE是等边三角形,由等腰三角形三线合一证明∠APF=∠EPF,∠QPF=∠BPF,即可求解;(3)由等腰三角形三线合一的性质可得AF = FE,QF = BF,即可证明.(1)连接BD,∵△ABC是等边三角形,∴AB=BC=AC,∵点B,D关于直线AC对称,∴AC垂直平分BD,∴DC=BC,AD=AB,∴AB=BC=CD=AD,∴四边形ABCD是菱形;(2)当点Р在线段AC上的位置发生变化时,∠DPQ的大小不发生变化,始终等于60°,理由如下:∵将线段PD绕点Р逆时针旋转,使点D落在BA延长线上的点Q处,∴PQ=PD,∵△ABC是等边三角形,∴AB=BC=AC,∠BAC=∠ABC=∠ACB=60°,连接PB,过点P作PE∥CB交AB于点E,PF⊥AB于点F,则∠APE=∠ACB=60°,∠AEP=∠ABC=60°,∴∠APE=∠BAC=60°=∠AEP,∴△APE是等边三角形,∴AP=EP=AE,∵PF⊥AB,∴∠APF=∠EPF,∵点B,D关于直线AC对称,点P在线段AC上,∴PB = PD,∠DPA =∠BPA,∴PQ = PD,∵PF⊥AB,∴∠QPF=∠BPF,∴∠QPF -∠APF=∠BPF -∠EPF,即∠QPA = ∠BPE,∴∠DPQ =∠DPA - ∠QPA=∠BPA-∠BPE = ∠APE= 60°;(3)AQ= CP,证明如下:∵AC = AB,AP= AE,∴AC - AP = AB–AE,即CP= BE,∵AP = EP,PF⊥AB,∴AF = FE,∵PQ= PD,PF⊥AB,∴QF = BF,∴QF - AF = BF–EF,即AQ= BE,∴AQ= CP.小提示:本题考查了图形的旋转,等边三角形的判定和性质,等腰三角形的性质,菱形的判定等,熟练掌握知识点是解题的关键.18、如图所示的两个图形成中心对称,请找出它的对称中点.答案:见解析.分析:根据关于中心对称的两个图形,对应点的连线都经过对称中心作图.连接CC′,BB′,两条线段相交于当O,则点O即为对称中点.小提示:本题考查的是中心对称的性质,掌握关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分是解题的关键.。
人教版九年级上册23.旋转作图课件

• (3)作旋转后的对应点,方法如下: •①连:连接图形的每个关键点与旋转中心; • ②转:把连线绕旋转中心按旋转方向旋转相同的角 度(作旋转角); • ③截:在作得的角的另一边截取与关键点到旋转中 心的距离相等的线段,得到各个关键点的对应点.
• (4)按原图形的顺序连接这些对应点,所得到的图形就 是旋转后的图形.
①请按要求画图:将△ABC绕点A顺时针方向旋转90°,点B的 对应点为点B′,点C的对应点为点C′.连接BB′. 解:如图①,△AB′C′即为所求.
②在①中所画图形中,∠AB′B=___4_5____°.
(2)【问题解决】 如图②,在Rt△ABC中,BC=1,∠C=90°,延长CA到点 D,使CD=1,将斜边AB绕点A顺时针旋转90°到AE,连接 DE,求∠ADE的度数.
B.(2,-2)
C.(3,-2) D.(-1,4)
4.把一个图案进行旋转变换,选择不同的旋转中心、不同 的旋转方向、不同的__旋__转__角__度_____,会有不同的效果.
5.(202X·赤峰)下列图形绕某一点旋转一定角度都能与原图形 重合,其中旋转角度最··小的是( C )
6.(202X·鄂尔多斯)(1)【操作发现】 如图①,在边长为1个单位长度的小正方形组成的网格中, △ABC的三个顶点均在格点上.
2.把图中的交通标志图案绕着它的中心旋转一定角度后与 自身重合,则这个旋转角度至少为( C ) A.30° B.90° C.120° D.180°
3.(202X·青岛)如图,将△ABC先向上平移1个单位长度,再
绕点P按逆时针方向旋转90°,得到△A′B′C′,则点A的对
应点A′的坐标是( D)
A.(0,4)
(1)旋转中心不变,改变旋转角(如图).
九年级上册数学第23章《旋转》知识点梳理完整版
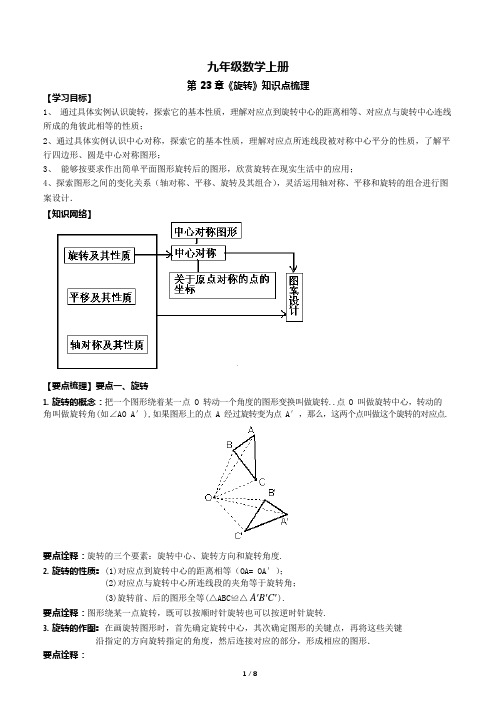
【学习目标】九年级数学上册第 23 章《旋转》知识点梳理1、通过具体实例认识旋转,探索它的基本性质,理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角彼此相等的性质;2、通过具体实例认识中心对称,探索它的基本性质,理解对应点所连线段被对称中心平分的性质,了解平行四边形、圆是中心对称图形;3、能够按要求作出简单平面图形旋转后的图形,欣赏旋转在现实生活中的应用;4、探索图形之间的变化关系(轴对称、平移、旋转及其组合),灵活运用轴对称、平移和旋转的组合进行图案设计.【知识网络】【要点梳理】要点一、旋转1.旋转的概念:把一个图形绕着某一点 O 转动一个角度的图形变换叫做旋转..点 O 叫做旋转中心,转动的角叫做旋转角(如∠AO A′),如果图形上的点 A 经过旋转变为点A′,那么,这两个点叫做这个旋转的对应点.要点诠释:旋转的三个要素:旋转中心、旋转方向和旋转角度.2.旋转的性质: (1)对应点到旋转中心的距离相等(OA= OA′);(2)对应点与旋转中心所连线段的夹角等于旋转角;(3)旋转前、后的图形全等(△ABC≌△A'B'C').要点诠释:图形绕某一点旋转,既可以按顺时针旋转也可以按逆时针旋转.3.旋转的作图: 在画旋转图形时,首先确定旋转中心,其次确定图形的关键点,再将这些关键沿指定的方向旋转指定的角度,然后连接对应的部分,形成相应的图形.要点诠释:作图的步骤:(1)连接图形中的每一个关键点与旋转中心;(2)把连线按要求(顺时针或逆时针)绕旋转中心旋转一定的角度(旋转角);(3)在角的一边上截取关键点到旋转中心的距离,得到各点的对应点;(4)连接所得到的各对应点.要点二、特殊的旋转—中心对称1.中心对称:把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心.这两个图形中的对应点叫做关于中心的对称点.要点诠释:(1)有两个图形,能够完全重合,即形状大小都相同;(2)位置必须满足一个条件:将其中一个图形绕着某一个点旋转180°能够与另一个图形重合 (全等图形不一定是中心对称的,而中心对称的两个图形一定是全等的) .2.中心对称图形:把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.要点诠释:(1)中心对称图形指的是一个图形;(2)线段,平行四边形,圆等等都是中心对称图形.要点三、平移、轴对称、旋转类型一、旋转1.数学课上,老师让同学们观察如图所示的图形,问:它绕着圆心 O 旋转多少度后和它自身重合?甲同学说:45°;乙同学说:60°;丙同学说:90°;丁同学说:135°. 以上四位同学的回答中,错误的是().A.甲 B. 乙 C. 丙 D. 丁【答案】B.【解析】因为圆被平分为 8 部分,所以旋转45°,90°,135°均能与原图形重合.【总结升华】同一图形的旋转角可以是多个.举一反三:【变式】以图 1 的边缘所在直线为轴将该图案向右翻折180°后,再按顺时针方向旋转180°,所得到图形是().【答案】A.类型二、中心对称2.如图,△A′B′C′是△ABC旋转后得到的图形,请确定旋转中心、旋转角.【答案与解析】∵对应点到旋转中心的距离相等,即OA=OA′∴O点在AA′的垂直平分线上同理 O 点也在BB′的垂直平分线上∴两条垂直平分线的交点 O 就是旋转中心,∠AOA′的度数就是旋转角.【总结升华】中心对称的对应点到对称中心的距离相等,所以对称中心在对应点的垂直平分线上.举一反三:【变式】下列图形中,既是中心对称图形又是轴对称图形的是().A.B.C.D.【答案】A.类型三、平移、轴对称、旋转3.(2015•裕华区模拟)如图,点 O 是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C 按顺时针方向旋转60°得△ADC,连接 OD.(1)求证:△COD是等边三角形;(2)当a=150°时,试判断△AOD 的形状,并说明理由;(3)探究:当 a 为多少度时,△AOD是等腰三角形?【思路点拨】(1)根据旋转的性质可得出 OC=OD,结合题意即可证得结论;(2)结合(1)的结论可作出判断;(3)找到变化中的不变量,然后利用旋转及全等的性质即可做出解答.【答案与解析】(1)证明:∵将△BOC绕点 C 按顺时针方向旋转60°得△ADC,∴CO=CD,∠OCD=60°,∴△COD是等边三角形.(2)解:当α=150°时,△AOD是直角三角形.理由是:∵将△BOC绕点 C 按顺时针方向旋转60°得△ADC,∴△BOC≌△ADC,∴∠ADC=∠BOC=150°,又∵△COD是等边三角形,∴∠ODC=60°,∴∠ADO=∠ADC﹣∠ODC=90°,∵∠α=150°∠AOB=110°,∠COD=60°,∴∠AOD=360°﹣∠α﹣∠AOB﹣∠COD=360°﹣150°﹣110°﹣60°=40°,∴△AOD 不是等腰直角三角形,即△AOD是直角三角形.(3)解:①要使AO=AD,需∠AOD=∠ADO,∵∠AOD=360°﹣110°﹣60°﹣α=190°﹣α,∠ADO=α﹣60°,∴190°﹣α=α﹣60°,∴α=125°;②要使 OA=OD,需∠OAD=∠ADO.∵∠OAD=180°﹣(∠AOD+∠ADO)=180°﹣(190°﹣α+α﹣60°)=50°,∴α﹣60°=50°,∴α=110°;③要使 OD=AD,需∠OAD=∠AOD.∵∠OAD=360°﹣110°﹣60°﹣α=190°﹣α,∠AOD==120°﹣,∴190°﹣α=120°﹣,解得α=140°.综上所述:当α的度数为125°或110°或140°时,△AOD是等腰三角形.【总结升华】本题以“空间与图形”中的核心知识(如等边三角形的性质、全等三角形的性质与证明等)为载体,内容由浅入深,层层递进.试题中几何演绎推理的难度适宜,蕴含着丰富的思想方法(如运动变化、数形结合、分类讨论、方程思想等),能较好地考查学生的推理、探究及解决问题的能力.举一反三:【变式】已知 D 是等边△ABC外一点,∠BDC=120º.求证:AD=BD+DC.【答案】∵△ABC为等边三角形,∴AB=AC,∠BAC=60°.将△ABD绕点A 逆时针旋转60°,得到△EAC,∴△DAB≌△EAC,即∠ABD=∠ACE,∵四边形 ABCD 中,∠BDC=120º,∠BAC=60°,∴∠DBA+∠DCA=180°,即∠ACE+∠DCA=180°,点 D,C,E 三点共线.∴BD+DC=CE+DC=DE.又∵∠DAE=60°.∴△ADE是等边三角形,即DE=AD.∴BD+DC=AD.4.如图,在四边形 ABCD 中,∠ABC=30°,∠ADC=60°,AD=CD. 求证:BD2=AB2+BC2.【思路点拨】利用 AD=CD 可以将△BCD绕点D 逆时针旋转60°,从而把条件集中到一个三角形中.【答案与解析】证明: ∵AD=CD,∠ADC=60°,∴△BCD 绕点 D 逆时针旋转 60°,得到△EAD, ∴∠BDE=∠CDA=60°,△BCD≌△EAD. ∴BC=AE, BD=DE ,∠DAE=∠DCB, ∴△BDE 为等边三角形. ∴BE=BD.∵在四边形 ABCD 中,∠ABC=30°,∠ADC=60°, ∴∠DCB+∠DAB=270°,即∠DAE+∠DAB=270°. ∴∠BAE=90°. ∵在 Rt△BAE 中, ,∴.【总结升华】由求证可知应该建立一个直角三角形,再由已知知道有 30°,60°的角,有等线段,可以构想通过旋转构建直角三角形.5 、正方形 ABCD 和正方形 AEFG 有一个公共点 A ,点 G 、E 分别在线段 AD 、AB 上(1) 如图连结 DF 、BF ,试问:当正方形 AEFG 绕点 A 旋转时,DF 、BF 的长度是否始终相等?若相等请证明;若不相等请举出反例.(2) 若将正方形 AEFG 绕点 A 顺时针方向旋转,连结 DG ,在旋转过程中,能否找到一条线段的长度与线段 DG的长度相等,并画图加以说明. 【答案与解析】(1) 如图, DF 、BF 的长度不是始终相等,当点 F 旋转到 AB 边上时,DF>AD>BF.(2)线段BE=DG如图: ∵正方形 ABCD 和正方形 AEFG∴AD=AB,AG=AE, ∠1+∠2=∠2+∠3 ∴∠DAG=∠BAE ∴△ADG≌△ABE ∴ DG=BE【总结升华】利用旋转图形的不变性确定全等三角形. 举一反三:【变式】(2015•沈阳)如图,正方形 ABCD 绕点 B 逆时针旋转 30°后得到正方形 BEFG ,EF 与 AD 相交于点 H ,延长DA 交 GF 于点 K .若正方形 ABCD 边长为,求 AK 的长?【答案与解析】 解:连接 BH ,如图所示:∵四边形 ABCD 和四边形 BEFG 是正方形, ∴∠BAH=∠ABC=∠BEH=∠F=90°, 由旋转的性质得:AB=EB ,∠CBE=30°, ∴∠ABE=60°,在 Rt△ABH 和 Rt△EBH 中,,∴Rt△ABH≌△Rt△EBH(HL ), ∴∠ABH=∠EBH=∠ABE=30°,AH=EH , ∴AH= ×=1,∴EH=1, ∴FH=﹣1,在 Rt△FKH 中,∠FKH=30°, ∴KH=2FH=2(﹣1),∴AK=KH﹣AH=2( ﹣1)﹣1=2 ﹣3; 故答案为: 2 3 .6. 如图,已知△ABC 为等腰直角三角形,∠BAC=900,E 、F 是 BC 边上点且∠EAF=45°.求证: .3【思路点拨】通过求证可以猜测要证得直角三角形,所以可以考虑旋转.【答案与解析】∵ △ABC为等腰直角三角形且∠BAC=90°∴ AB=AC,将△CAF 绕点 A 顺时针旋转90°,如图,得到∴∴ ,,,,∴ ,连结,则在,中,∴ ①,又∵ ,∵ .又∵∴ 在与,中,.∴ ②,∴ 由①②得:. 【总结升华】旋转性质:旋转前,后的图形全等.。
九年级数学上册第二十三章旋转知识归纳新版新人教版

第二十三章旋转23.1 图形的旋转1. 图形的旋转(1)定义:在平面内,将一个圆形绕一个定点沿某个方向(顺时针或逆时针)转动一个角度,这样的图形运动叫做旋转,这个定点叫做旋转中心,转动的角称为旋转角。
(2)生活中的旋转现象大致有两大类:一类是物体的旋转运动,如时钟的时针、分针、秒针的转动,风车的转动等;另一类则是由某一基本图形通过旋转而形成的图案,如香港特别行政区区旗上的紫荆花图案。
(3)图形的旋转不改变图形的大小和形状,旋转是由旋转中心和旋转角所决定,旋转中心可以在图形上也可以在图形外。
(4)会找对应点,对应线段和对应角。
2. 旋转的基本特征:(1)图形在旋转时,图形中的每一个点都绕旋转中心旋转了同样大小的角度。
(2)图形在旋转时,对应点到旋转中心的距离相等,对应线段相等,对应角相等;(3)图形在旋转时,图形的大小和形状都没有发生改变。
3. 几点说明:(1)在理解旋转特征时,首先要对照图形,找出旋转中心、旋转方向、对应点、旋转角。
(2)旋转的角度是对应线段的夹角或对应顶点与旋转中心连线的夹角。
(3)旋转中心的确定分两种情况,即在图形上或在图形外,若在图形上,哪一点旋转过程中位置没有改变,哪一点就是旋转中心;若在图形外,对应点连线的垂直平分线的交点就是旋转中心。
23.2 中心对称中心对称:把一个图形绕着某一点旋转180°,假如它能够与另一个图形重合,那么这刘遇图形关于这个点对称或中心对称。
中心对称的性质:①关于中心对称的刘遇图形,对应点所连线段都经过对称中心,而且被对称中心所平分。
②关于中心对称的刘遇图形是全等形。
中心对称图形:把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形。
对称点的坐标规律:①关于x轴对称:横坐标不变,纵坐标互为相反数,②关于y轴对称:横坐标互为相反数,纵坐标不变,③关于原点对称:横坐标、纵坐标都互为相反数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版九年级数学上册知识点总结
第二十三章旋转
23.1 图形的旋转
知识点一旋转的定义
在平面内,把一个平面图形绕着平面内某一点O转动一个角度,就叫做图形的旋转,点O叫做旋转中心,转动的角叫做旋转角。
我们把旋转中心、旋转角度、旋转方向称为旋转的三要素。
知识点二旋转的性质
旋转的特征:(1)对应点到旋转中心的距离相等;(2)对应点与旋转中心所连线段的夹角等于旋转角;(3)旋转前后的图形全等。
理解以下几点:
(1)图形中的每一个点都绕旋转中心旋转了同样大小的角度。
(2)对应点到旋转中心的距离相等,对应线段相等,对应角相等。
(3)图形的大小和形状都没有发生改变,只改变了图形的位置。
知识点三利用旋转性质作图
旋转有两条重要性质:(1)任意一对对应点与旋转中心所连线段的夹角等于旋转角;(2)对应点到旋转中心的距离相等,它是利用旋转的性质作图的关键。
步骤可分为:
①连:即连接图形中每一个关键点与旋转中心;
②转:即把直线按要求绕旋转中心转过一定角度(作旋转角)
③截:即在角的另一边上截取关键点到旋转中心的距离,得到各点的对应点;
④接:即连接到所连接的各点。
23.2 中心对称
知识点一中心对称的定义
中心对称:把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心。
注意以下几点:
中心对称指的是两个图形的位置关系;
只有一个对称中心;绕对称中心旋转180°两个图形能够完全重合。
知识点二作一个图形关于某点对称的图形
要作出一个图形关于某一点的成中心对称的图形,关键是作出该图形上关键点关于对称中心的对称点。
最后将对称点按照原图形的形状连接起来,即可得出成中心对称图形。
知识点三中心对称的性质
有以下几点:
(1)关于中心对称的两个图形上的对应点的连线都经过对称中心,并且都被对称中心平分;
(2)关于中心对称的两个图形能够互相重合,是全等形;
(3)关于中心对称的两个图形,对应线段平行(或共线)且相等。
知识点四中心对称图形的定义
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心。
知识点五关于原点对称的点的坐标
在平面直角坐标系中,如果两个点关于原点对称,它们的坐标符号相反,即点p(x,y)关于原点对称点为(-x,-y)。
中考回顾
1.(2017四川绵阳中考)下列图案中,属于轴对称图形的是(A)
2.(2017天津中考)在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( C )
3.(2017内蒙古呼和浩特中考)图中序号①②③④对应的四个三角形,都是△ABC这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是(:A)
A.①
B.②
C.③
D.④
解析:∵轴对称是沿着某条直线翻转得到新图形,
∴通过轴对称得到的是①.故选A.
4.(2017西宁中考)下列图形中,是轴对称图形但不是中心对称图形的是(A)
A.等边三角形
B.平行四边形
C.正六边形
D.圆
5.(2017江苏淮安中考)点P(1,-2)关于y轴对称的点的坐标是(C)
A.(1,2)
B.(-1,2)
C.(-1,-2)
D.(-2,1)
解析:P(1,-2)关于y轴对称的点的坐标是(-1,-2),故选C.
6.(2017四川宜宾中考)如图,在矩形ABCD中,BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上的点F处,则DE的长是(C)
A.3
B.
C.5
D.
解析:∵在矩形ABCD中,∠BAE=90°,
且由折叠可得△BEF≌△BEA,
∴∠BFE=90°,AE=EF,AB=BF,
在Rt△ABD中,AB=CD=6,BC=AD=8,
根据勾股定理得BD=10,即FD=10-6=4,
设EF=AE=x,则有ED=8-x,
根据勾股定理得x2+42=(8-x)2,
解得x=3,所以DE=8-3=5,故选C.
7.(2017山东枣庄中考)如图,把正方形纸片ABCD先沿对边中点所在的直线对折后展开,折痕为MN,再过点B 折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( B )
A.2
B.
C.
D.1
解析:∵四边形ABCD为正方形,AB=2,过点B折叠纸片,使点A落在MN上的点F处,∴FB=AB=2,BM=1,则在Rt△BMF中,FM=,故选B.
8.(2017湖南长沙中考)如图,将正方形ABCD折叠,使顶点A与CD边上的一点H重合(H
不与端点C,D重合),折痕交AD于点E,交BC于点F,边AB折叠后与边BC交于点G.设正
方形ABCD的周长为m,△CHG的周长为n,则的值为( B )
A. B. C. D.随H点位置的变化而变化
解析:设CH=x,DE=y,则DH=-x,EH=EA=-y,∵∠EHG=90°,∴∠DHE+∠CHG=90°.
∵∠DHE+∠DEH=90°,
∴∠DEH=∠CHG,
又∵∠D=∠C=90°,△DEH∽△CHG,
∴,即,
∴CG=,HG=,
△CHG的周长n=CH+CG+HG=,
在Rt△DEH中,DH2+DE2=EH2,
即+y2=,
整理得-x2=,
∴n=CH+HG+CG=.
故.故选B.
模拟预测
1.下列标志中,可以看作是中心对称图形的是(D)
2.下列图形中,是轴对称图形,但不是中心对称图形的是(B)
3.如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B',AB'与DC相交于点E,则下列结论一定正确的是()
A.∠DAB'=∠CAB'
B.∠ACD=∠B'CD
C.AD=AE
D.AE=CE
答案:D
4.如图,把一张长方形纸片对折,折痕为AB,再以AB的中点O为顶点把平角∠AOB三等分,沿平角的三等分线折叠,将折叠后的图形剪出一个以O为顶点的等腰三角形,那么剪出的等腰三角形全部展开铺平后得到的平面图形一定是(D)
A.正三角形
B.正方形
C.正五边形
D.正六边形
解析:根据第一次对折以及三等分平角可知将360°进行6等分,即多边形的中心角为60°,由最后的剪切可知所得图形符合正六边形特征.故选D.
5.如图,直线l是四边形ABCD的对称轴.若AB=CD,有下面的结论:①AB∥CD;②AC⊥BD;③AO=OC;④AB⊥BC.其中正确的结论有.(填序号)
答案:①②③
6.如图,在四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B=95°
.
解析:∵FN∥DC,∴∠BNF=∠C=70°.
∵MF∥AD,∴∠BMF=∠A=100°.
由翻折知,∠F=∠B.
又∵∠BMF+∠B+∠BNF+∠F=360°,
∴100°+∠B+70°+∠F=360°,
∴∠F=∠B==95°.
7.如图,在平面直角坐标系中,若△ABC与△A1B1C1关于点E成中心对称,则对称中心点E的坐标是(3,-1)
8.在Rt△ABC中,∠BAC=90°,AB=3,M为边BC上的点,连接AM(如图).如果△ABM沿直线AM翻折后,点B恰好落在边AC的中点处,那么点M到AC的距离是2.
解析:如图,过点M作MN⊥AC于N,
由折叠性质可知,∠BAM=∠CAM=45°.
∵点B恰好落在边AC的中点处,
∴AC=2AB=6.
∵∠ANM=90°,
∴∠CAM=∠AMN=45°.
∴MN=AN.
由Rt△CNM∽Rt△CAB,得,
∴.
∴MN=2.
9.△ABC在平面直角坐标系中的位置如图.
(1)作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C1与△A2B2C2,它们是否关于某直线对称?若是,请在图上画出这条对称轴.
解:(1)△A1B1C1如图,A1(0,4),B1(2,2),C1(1,1).(2)△A2B2C2如图.A2(6,4),B2(4,2),C2(5,1).(3)△A1B1C1与△A2B2C2关于直线x=3对称.如图.。
