工程力学习题册第八章 - 答案
工程力学(山东理工大学)智慧树知到课后章节答案2023年下山东理工大学

工程力学(山东理工大学)智慧树知到课后章节答案2023年下山东理工大学第一章测试1.物体的平衡状态是指物体静止不动。
A:对 B:错答案:错2.柔索只能承拉,不能承压。
A:错 B:对答案:对3.在物体上加上或减去任意的平衡力系,不改变原力系对物体的效应。
A:对 B:错答案:错4.静力学研究的物体都是处于平衡状态的。
A:错 B:对答案:对5.力平行四边形法则只适用于刚体。
A:对 B:错答案:错6.平衡是相对的,是物体运动的一种特殊形式。
A:对 B:错答案:对7.力只能沿力线在自身刚体上传递。
A:错 B:对答案:对8.刚体的平衡条件是变形体平衡的必要条件,而非充分条件。
A:对 B:错答案:对9.作用力与反作用力不是一对平衡力。
A:错 B:对答案:对10.作用于刚体上的力是滑移矢量。
滑动矢量。
A:错 B:对答案:对第二章测试1.汇交力系一定是共点力系。
A:错 B:对答案:错2.一般力系向一点简化得到的主矢是一般力系中各力的向量和,主矢与原力系来说一般不等效。
A:对 B:错答案:对3.图示中的力偶臂等于AB两点间距离。
A:错 B:对答案:错4.作用在刚体上同一个平面内的力偶,不能合成为一个合力偶。
A:错 B:对答案:错5.只要保证力偶矩不变,可以改变力偶中力的大小和力偶臂的长短,不改变力偶对刚体的效应。
A:错 B:对答案:对6.力偶对其作用面内任一点的矩恒等于力偶矩本身。
A:错 B:对答案:对7.力偶不能合成为一个力。
A:错 B:对答案:对8.力的投影是代数量,力的分量也是代数量。
A:错 B:对答案:错9.在任意坐标系下,力在坐标轴上投影的大小都等于分量的大小。
A:对 B:错答案:错10.汇交力系平衡的必要和充分条件是:力多边形首尾相连。
A:错 B:对答案:对第三章测试1.可以根据对称性确定物体的重心。
A:错 B:对答案:对2.任何物体的重心必然与其形状中心重合。
A:对 B:错答案:错3.空间平行力系的平衡方程共有三个,此三个方程都可以采用力的投影方程。
工程力学课后答案(第二版少学时)

第一章静力学基本概念1.1 解F=F x+F y=F x i+F y jF1=1000N=-1000Cos30ºi-1000Sin30ºjF2=1500N=1500Cos90ºi- 1500Sin90ºjF3=3000N=3000 Cos45ºi+3000Sin45ºjF4=2000N=2000 Cos60ºi-2000Sin60ºj1.2因为前进方向与力F A,F B之间均为45º夹角,要保证二力的合力为前进方向,则必须F A=F B。
所以:F B=F A=400N1.3解:M O(F)=F l解:M O(F)=0解: M O(F)=F l sinβ解: M O(F)=F l sinθ解: M O(F)= -F a解:M O(F)= F(l+r)解:1.4解:1.5解:1位置:M A(G)=02位置:M A(G)=-G l sinθ3位置:M A(G)=-G l1.6解:M O(F n)=-F n cosθ·D/2=-75.2N·m 1.71.8第二章平面力系2.1 力系简化解:(1)主矢大小与方位:F/R x=∑F x=F1cos45º+F3+F4cos60º=100Ncos45º+200N+250cos60º=395.7N F/R y=∑F y=F1sin45º-F2-F4sin60º=100Nsin45º-150N-250sin60º=-295.8N(2)主矩大小和转向:M O=∑M O(F)=M O(F1)+M O(F2)+M O(F3)+M O(F4)+m=0-F2×0.3m+F3×0.2m+F4sin60×0.1m+F×0.1m=0-150N×0.3m+200N×0.2m+250Nsin60×0.1m+50N×0.1m =21.65N·m( )向O点的简化结果如图所示。
工程力学第8章答案
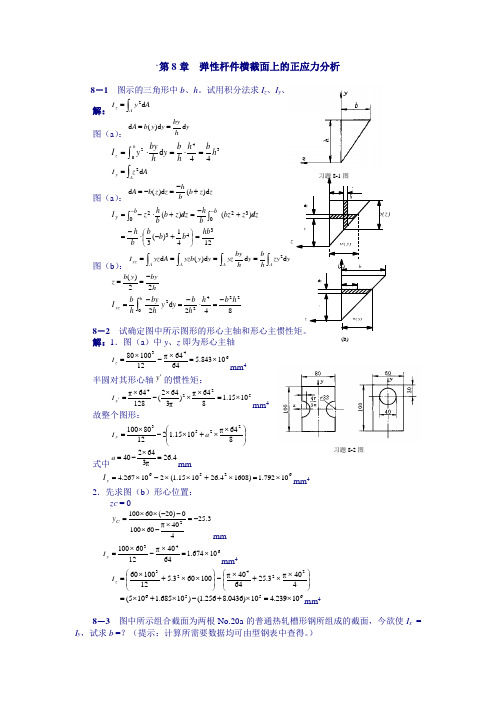
`第8章 弹性杆件横截面上的正应力分析8-1 图示的三角形中b 、h 。
试用积分法求I z 、I y 、I yz 。
解:⎰=Az Ay I d 2图(a ):yh by y y b A d d )(d ==34244d hb h h b y h byy I h z =⋅=⋅=⎰⎰=AyAzId 2图(a ):zz b bh z z b A d )(d )(d +-=-=1241)(3)()(3433202hb b b b b h zz bz bh z z b bh z I bby =⎪⎭⎫ ⎝⎛+-⋅-=+-=+⋅-=⎰⎰--d d图(b ):⎰⎰⎰⎰====AAA A yz yzy h by hby yzy y yzb A yz I d d d )(d 2hby y b z 22)(-==842d 2224220hb hh by y h by h b I hyz -=⋅-=-=⎰8-2解:1.图(a )中y 、z 即为形心主轴64310843.56464π1210080⨯=⨯-⨯=z I mm 4半圆对其形心轴y '的惯性矩:52241015.1864π)π3642(12864π⨯=⨯⨯⨯-⨯='y I mm 4故整个图形:⎪⎪⎭⎫⎝⎛⨯⨯+⨯-⨯=864π1015.1212801002253a I y式中4.26π364240=⨯-=a mm625610792.1)16084.261015.1(210267.4⨯=⨯+⨯⨯-⨯=y I mm 42.先求图(b )形心位置: z C = 03.25440π601000)20(601002-=⨯-⨯--⨯⨯=C y mm64310674.16440π1260100⨯=⨯-⨯=y I mm 4⎪⎪⎭⎫⎝⎛⨯⨯+⨯-⎪⎪⎭⎫⎝⎛⨯⨯+⨯=440π3.256440π100603.5121006022423z I655610239.410)0436.8256.1()10685.1105(⨯=⨯+-⨯+⨯=mm 48-3 图中所示组合截面为两根No.20a 的普通热轧槽形钢所组成的截面,今欲使I x = I y ,试求b =?(提示:计算所需要数据均可由型钢表中查得。
《工程力学》课后习题与答案全集

由 ,作出速度平行四边形,如图示:
即:
7.图示平行连杆机构中, mm, 。曲柄 以匀角速度 2rad/s绕 轴转动,通过连杆AB上的套筒C带动杆CD沿垂直于 的导轨运动。试示当 时杆CD的速度和加速度。
解:取CD杆上的点C为动点,AB杆为动系。对动点作速度分析和加速度分析,如图(a)、(b)所示。图中:
解:设该力系主矢为 ,其在两坐标轴上的投影分别为 、 。由合力投影定理有:
=-1.5kN
kN
kN
;
由合力矩定理可求出主矩:
合力大小为: kN,方向
位置: m cm,位于O点的右侧。
2.火箭沿与水平面成 角的方向作匀速直线运动,如图所示。火箭的推力 kN与运动方向成 角。如火箭重 kN,求空气动力 和它与飞行方向的交角 。
(d)由于不计杆重,杆AB在A、C两处受绳索作用的拉力 和 ,在B点受到支座反力 。 和 相交于O点,
根据三力平衡汇交定理,
可以判断 必沿通过
B、O两点的连线。
见图(d).
第二章力系的简化与平衡
思考题:1.√;2.×;3.×;4.×;5.√;6.×;7.×;8.×;9.√.
1.平面力系由三个力和两个力偶组成,它们的大小和作用位置如图示,长度单位为cm,求此力系向O点简化的结果,并确定其合力位置。
则
(mm/s)
故 =100(mm/s)
又有: ,因
故:
即:
第四章刚体的平面运动
思考题
1.×;2.√; 3.√;4.√;5.×.
习题四
1.图示自行车的车速 m/s,此瞬时后轮角速度 rad/s,车轮接触点A打滑,试求点A的速度。
工程力学--第八章_圆轴的扭转

df /dx ,称为单位扭转角。
对半径为r的其它各处,可作类 似的分析。
1. 变形几何条件
MT
A
r
B r
rr
C
df
C O D
D
dx
对半径为r的其它各处,作类 似的分析。 同样有:
CC= dx=rdf
即得变形几何条件为:
rdf / dx --(1)
剪应变的大小与半径r成
2
TBC 2
B mx C
2 TBC
2
T
A
用假想截面2将圆轴切开 ,取左段或右段为隔离 体,根据平衡条件求得 :
TBC=-mx
(3)作扭矩图
2mx +
B
–
Cx mx
[例8-2]图示为一装岩机的后车轴,已知其行走的功率 PK=10.5kW,额定转速n=680r/min,机体上的荷载通过轴承 传到车轴上,不计摩擦,画出车轴的扭矩图
4.78
6.37
15.9
4.78
简捷画法:
MT图 10kN m 10kN m
FN图(轴力)
2kN 8kN
5kN
o
x
A
C B 20kN m
5kN 2kN 8kN
5kN
向 按右手法确定
向
MT / kN m
20
5kN
3kN
10
N图
5kN
A
B
C
在左端取参考正向,按载荷大小画水平线;遇集 中载荷作用则内力相应增减;至右端回到零。
G
df
dx
A
r 2dA
MT
3. 力的平衡关系
令:
工程力学(第二版)习题册答案

一、填空题
1. 相 对 滑 动 相 对 滑 动 趋 势 接触面的切线 相反 2. 10N 20N 30N 30N 30N 3. 100N 竖直向上 平衡 4. 平稳无冲击 自锁
阻碍物体相对滑动
相对滑动趋势
二、选择题
1. A
三、简答题
1. ①问题中含有可能发生相对滑动的摩擦面,因此,存在摩擦力; ②受力图中要画出摩擦力,摩擦力总是沿着接触面的切线方向并与物体相对滑
7.
8.
9.
第二章 平面力系
第一节 共线力系的合成与平衡
一、填空题
1. 在同一条直线上
2. FR Fi FR 0
二、计算题
设向右为正方向。 则 FR=120+40-80-200=-120N 方向:水平向左
第二节 平面汇交力系的合成
一、填空题
1. 作用于同一平面内且各力作用线相交于一点的力系 共线力系 力的作用点 2. -F 或 F 0 0 -F 或 F 3. 合力在任一坐标轴上的投影 各分力在同一轴上投影的代数和 4. F4 F3 5. 自行封闭 6. 所有各力在 x 轴上投影的代数和为零 所有各力在 y 轴上投影的代数和为零 Fx 0 Fy 0
3. 后轮:摩擦力向前 前轮:摩擦力向后
4. 不下滑,处于自锁状态
四、计算题
FT 60 18 3N
五、应用题
1. (提示)从摩擦力与 F 对 B 点的力矩大小的比较进行考虑
第三章 空间力系 第一节 力在空间坐标轴上的投影与合成
一、填空题
1. 力的作用线不都在同一平面内呈空间分布的力系 2. 一次投影法 二次投影法
二、选择题
1. A 2.B
它所限制物体
三、简答题
1.柔性体约束只能承受拉力,不能承受压力。 2.被约束物体可以沿约束的水平方向自由滑动,也可以向离开约束的方向运动, 但不能向垂直指向约束的方向运动。 3.剪刀的两半部分可以绕销钉轴线相对转动,但不能在垂直销钉轴线的平面内沿 任意方向做相对移动。 4.木条不能沿圆柱销半径方向移动,但可以绕销轴做相对转动。 5.固定端约束既限制物体在约束处沿任何方向的移动,也限制物体在约束处的转 动。
工程力学—点的合成运动习题及解答

第八章 点的合成运动习题及解答P189 8-5. 已知 OA=l ,曲杆BCD 的速度为v ,BC=a; 求:A 点的速度与x 的关系。
解:取曲杆上的点B 为动点,OA 杆为动系,则r e a v v v +=v v a =,得22a e a x a .v sin .v v +==φ,a x a.v OB v 22e0+==ω=A v .v l .0=ωl ,a x a .22+P190 8-7. 已知 两种机构中2m .0a O O 21==, 杆 A O 1的角速度1ω=3rad/s,030=θ;求:杆A O 2A O 1的角速度2ω.解: 图 (a) , 取杆A O 1上的A 点为动点,杆A O 2为动系,图 (b) , 取杆A O 2上的A 点为动点,杆A O 1为动系,由: r e av v v += 分别作速度矢量图。
由图 (a) 解出23a.cos30.v v 10a e ω==,,s /rad 5.12A O v 12e 2===ωω由图 (b) 解出32.a .cos30v v 10e a ω==, ,s /5rad .12A O v 12e 2===ωω.s /rad 232A O v 12a 2===ωωP190 8-9. 已知 ==V v AB 常数,当t=0时,0=ϕ;求:045=ϕ时,点C 的速度的大小。
解: 取杆AB 上的A 点为动点,杆OC 为动系,由: r e av v v += 作速度矢量图。
ϕϕcos .v cos .v v a e ==,lcos .a OA OC .v v e c ϕ==解出 l a.cos vv 2c ϕ=,当045=ϕ时, 2l av v c =P190 8-10. 已知,轮C 半径为R ,偏心距OC=e, 角速度 ω=常数;求:00=ϕ时,平底杆AB 的速度。
解: 取轮心C 为动点,平底杆AB 为动系,由: r e av v v += 作速度矢量图。
清华出版社工程力学答案-第8章弯曲强度问题

eBook工程力学习题详细解答教师用书(第8章)2011-10-1范 钦 珊 教 育 教 学 工 作 室FAN Qin-Shan ,s Education & Teaching Studio习题8-1 习题8-2 习题8-3 习题8-4 习题8-5 习题8-6 习题8-7 习题8-8 习题8-9 习题8-10 习题8-9 习题8-10习题8-11 习题8-12 习题8-13 习题8-14 习题8-15 习题8-16 习题8-17 习题8-18 习题8-19 习题8-20习题8-21工程力学习题详细解答之八第8章 弯曲强度问题8-1 直径为d 的圆截面梁,两端在对称面内承受力偶矩为M 的力偶作用,如图所示。
若已知变形后中性层的曲率半径为ρ;材料的弹性模量为E 。
根据d 、ρ、E 可以求得梁所承受的力偶矩M 。
现在有4种答案,请判断哪一种是正确的。
(A) ρ64π4d E M =(B) 4π64d E M ρ=(C) ρ32π3d E M =(D) 3π32dE M ρ=正确答案是 A 。
8-2 矩形截面梁在截面B 处铅垂对称轴和水平对称轴方向上分别作用有F P1和F P2,且F P1=F P2,如图所示。
关于最大拉应力和最大压应力发生在危险截面A 的哪些点上,有4种答案,请判断哪一种是正确的。
(A) +max σ发生在a 点,−max σ发生在b 点M习题8-1图A Ba b cd P2z固定端习题8-2图(B) +max σ发生在c 点,−max σ发生在d 点 (C) +max σ发生在b 点,−max σ发生在a 点 (D) +max σ发生在d 点,−max σ发生在b 点正确答案是 D 。
8-3 关于平面弯曲正应力公式的应用条件,有以下4种答案,请判断哪一种是正确的。
(A) 细长梁、弹性范围内加载;(B) 弹性范围内加载、载荷加在对称面或主轴平面内;(C) 细长梁、弹性范围内加载、载荷加在对称面或主轴平面内;(D) 细长梁、载荷加在对称面或主轴平面内。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八章 直梁弯曲一、填空题1.工程中 发生弯曲 或以 弯曲变形 为主的杆件称为梁。
2.常见梁的力学模型有 简支梁 、 外伸梁 和 悬臂梁 。
3.平面弯曲变形的受力特点是 外力垂直于杆件的轴线,且外力和力偶都作用在梁的纵向对称面内 ;平面弯曲变形的变形特点是 梁的轴线由直线变成了在外力作用面内的一条曲线 ;发生平面弯曲变形的构件特征是 具有一个以上对称面的等截面直梁 。
4.作用在梁上的载荷有 集中力 、 集中力偶 和 分布载荷 。
5.梁弯曲时,横截面上的内力一般包括 剪力 和 弯矩 两个分量,其中对梁的强度影响较大的是 弯矩 。
6.在计算梁的内力时,当梁的长度大于横截面尺寸 五 倍以上时,可将剪力略去不计。
7.梁弯曲时,某一截面上的弯矩,在数值上等于 该截面左侧或右侧梁上各外力对截面形心的力矩 的代数和。
其正负号规定为:当梁弯曲成 凹面向上 时,截面上弯矩为正;当梁弯曲成凸面向上 时,截面上弯矩为负。
8.在集中力偶作用处,弯矩发生突变,突变值等于 集中力偶矩 。
9.横截面上弯矩为 常数 而剪力为 零 的平面弯曲变形称为 纯弯曲变形 。
10.梁纯弯曲变形实验中,横向线仍为直线,且仍与 梁轴线 正交,但两线不再 平行 ,相对倾斜角度θ。
纵向线变为 弧线 ,轴线以上的纵向线缩短,称为 缩短 区,此区梁的宽度 增大 ;轴线以下的纵向线伸长,称为 伸长 区,此区梁的宽度 减小 。
情况与轴向拉伸、压缩时的变形相似。
11.中性层与横截面的交线称为 中性轴 ,变形时梁的 所有横截面 均绕此线相对旋转。
12.在中性层凸出一侧的梁内各点,其正应力均为 正 值,即为 拉 应力。
13.根据弯曲强度条件可以解决 强度校核 、 截面选取 和 确定许可载荷 等三类问题。
14.产生最大正应力的截面又称为 危险截面 ,最大正应力所在的点称为 危险点 。
15.在截面积A 相同的条件下, 抗弯截面系数 越大,则梁的承载能力就越高。
当截面的形状不同时,可以用 W Z /A 来衡量截面形状的合理性和经济性。
16.为减轻自重和节省材料,将梁做成变截面梁,使所有横截面上的 最大正应力 都近似等于 许用应力[σ] ,这样的梁称为等强度梁。
二、判断题(正确的打“√”,错误的打“×”)1.一端(或两端)向支座外伸出的简支梁叫做外伸梁。
( × )2.悬臂梁的一端固定,另一端为自由端。
( √ )3.悬臂梁受固定端约束,简支梁受铰链约束。
( √ )4.弯矩的作用面于梁的横截面垂直,它们的大小及正负由截面一侧的外力确定。
( √ )5.弯曲时剪力对细长梁的强度影响很小,所以在一般工程的计算中可忽略。
( √ )6.凡弯矩图曲线折点处,梁上必有对应点受集中外力作用。
( √ )7.式σmax =ZWM W 中,σmax 值一般随横截面位置不同而异。
( × ) 8.梁弯曲变形时,弯矩最大的截面一定是危险截面。
( √ ) 9.钢梁和木梁的截面形状和尺寸相同,在受同样大的弯矩时,木梁的应力一定大于钢梁的应力。
( × )10.梁的合理截面形状应是不增加横截面积,而使其ZW A数值尽可能大的形状。
( √ )三、选择题( B )1.平面弯曲时,梁上的外力(或力偶)均作用在梁的 。
A.轴线上B.纵向对称平面内C.轴面内( C )2.当梁的纵向对称平面内只有力偶作用时,梁将产生 。
A.平面弯曲B.一般弯曲C.纯弯曲( A )3.梁纯弯曲时,截面上得内力是 。
A.弯矩B.扭矩C.剪力D.轴力E.剪力和弯矩( A )4.如图8-1所示,悬臂梁的B 端作用一集中力,使梁产生平面弯曲的是图 。
( A 、C )5.图8-2所示的简支梁中,弯矩最大的梁是 ;弯矩最小的梁是 。
( C )6.当梁上的载荷只有集中力时,弯矩图为 。
A.水平直线B.曲线C.斜直线( A )7.纯弯曲梁的横截面上 。
A.只有正应力B.只有切应力C.既有切应力又有正应力( B 、A )8.图8-3表示横截面上得应力分布图,其中属于直梁弯曲的是图 。
属于圆轴扭转的图是 。
( A )9.在图8-4中所示各梁中,属于纯弯曲的节段是。
A.图a中的AB,图b中的BC,图c中的BCB.图a中的AC,图b中的AD,图c中的BCC.图a中的AB,图b中的AC,图c中的BC( A )10.矩形截面梁发生平面弯曲时,横截面的最大正应力分布在。
A.上下边缘处B.左右边缘处C.中性轴处( A )11.梁横截面上得正应力与有关。
A.截面形状B.截面位置C.截面尺寸D.外载荷大小E.材料性质( C )12.梁平面弯曲时,横截面上最大拉应力与最大压应力不相等的梁是。
A.圆形截面梁B.矩形截面梁C.T形截面梁13.已知图8-5所示梁的尺寸及载荷。
( C )(1)AB段各截面的弯矩。
A.相等且为正B. 相等且为负C. 不等且为正D. 不等且为负( A )(2)弯矩图线过B截面时。
A.有折点B.有突变C.无变化( B )(3)段为纯弯曲梁。
A. ABB. BCC. AC( A )14.图8-6所示的矩形截面梁,放置正确的是图。
( B )15.如图8-7所示,用工字钢作简支梁,从提高弯曲强度考虑,图。
是正确的。
( B )16.如图8-8所示,用T形截面形状的铸铁材料作悬臂梁,从提高梁的弯曲强度考虑,图的方案是合理的。
( C )17.等强度梁各横截面上数值相等。
A.最大正应力B.弯矩C.面积D.抗弯截面系数四、简答题1.试述弯曲变形的受力特点和变形特点。
答:平面弯曲变形的受力特点:外力垂直于杆件的轴线,且外力和力偶都作用在梁的纵向对称面内。
平面弯曲变形的特点是:梁的轴线由直线变成在外力作用面内的一条曲线。
2.什么是梁的纵向对称平面?什么是平面弯曲?答:梁的纵向对称面是梁的轴线与横截面的对称轴组成的平面。
梁弯曲变形后,其轴线在纵向对称面内由直线变成平面曲线,这种情况称为平面弯曲。
3.绘制弯矩图的规律有哪些?答:(1)无载荷作用的梁段上,弯矩图为斜直线。
(2)在均布载荷作用的梁端上,弯矩图为抛物线。
载荷指向向下,抛物线为凸曲线,反之为凹曲线。
(3)在集中力作用处,弯矩图出现折角。
(4)在集中力偶作用处,弯矩发生突变,突变值等于集中力偶句。
4.试述弯曲正应力的分布规律。
答:正应力的分布规律:横截面上各点正应力的大小与改点到中性轴的距离成正比。
5.什么是中性层?什么是中性轴?答:中性层是指弯曲变形中,由于变形的连续性,伸长和缩短的长度是逐渐变化的。
从伸长区过渡到缩短区,中间必有一层纤维既不伸长也不缩短,即长度不变的纵向纤维。
中性轴是指中性层与横截面的交线,中性轴通过截面形心。
梁弯曲变形时,所有横截面均绕各自的中性轴回转。
6.提高梁弯曲强度的主要措施有哪些?答:(1)降低最大弯矩值。
(2)选择合理的截面形状。
(3)采用等强度梁。
五、作图题1.求作图8-9所示各梁的弯矩图。
2.绘出图8-10所示各梁的弯矩图。
六、计算题1.如图8-12所示为矩形截面的悬臂梁,在B 端受力F 的作用。
已知b =200mm ,h =600mm,l =6000mm ,梁的许用应力[σ] =120MPa ,试求力F 的最大许用值。
解:(1)计算最大弯矩值M wmax由截面法可求得max w M Fl = (2)计算抗弯截面系数W z23120000006z bh W mm == (3)确定许可载荷F由[]maxw zM W σ≤与max w M Fl =,得:[]240zW F kN lσ≤∙= 故力F 的最大许用值为240kN 。
2.齿轮轴AD 的受力情况如图8-13所示,已知直径d =60mm ,载荷F =5kN 。
l =300mm ,试求轴上的最大正应力。
解:(1)计算支座反力取AD 轴为研究对象,其受力分析如图所示。
由()0Ai MF =∑得:2()023B l lF F l F l -∙+∙-∙+=解得:196B F F =(方向与图示方向相同) 由()0B i M F =∑得:2023A l lF F l F ∙-∙-∙=解得:6A FF =-(方向与图示方向相反)(2)计算弯矩值0wA M =125262wC A l F lM F N m =-∙=-∙=-∙ 210003wBlM F N m =-∙=-∙0wD M =(3)绘制弯矩图,如图所示。
(4)计算抗弯截面系数W Z3333.1460211953232z d W mm π⨯===(5)计算最大正应力3max max10001047.1821195w z M MPa W σ⨯===故轴上的最大正应力为47.18MPa 。
3.在建筑工地上,常用到截面尺寸宽B =300mm ,厚H =80mm ,长L =6000mm 的木板。
现将它平放在相距为4m 的两个建筑物上作为临时搭板,让一个重为700N 的工人走过,若木板的许用应力[σ] =5MPa ,是否有危险? 解:(1)建立力学模型依题意建立如图力学模型,由经验可知人在板中间行进为最危险情形。
(2)求支座反力以木板为研究对象,其受力图如图所示。
由()0Ai MF =∑得:0B F AC F AB -∙+∙=2B FF =(方向与图示方向相同) 同理可以求得:2A FF =(方向与图示方向相同)(3)计算最大弯矩值Mwmax由截面法可知在C 处由最大弯矩值:max 70027002wC w A M M F AC N m ==∙=⨯=∙ (4)计算抗弯截面系数W Z2233008032000066z BH W mm ⨯===(5)校核强度3max max70010 2.19320000w z M MPa W σ⨯===因为[]max σσ≤,故木板的强度符合弯曲强度要求,重为700N 的人可以安全走过。
