第5章 概率分布 医学统计学
研究生医学统计学概率分布ppt课件

2) 百分位数法
⑴适用资料:适用于任意分布类型的资料, 主要用于偏态分布或分布类型不清楚的资 料。
⑵计算: 以95%正常值范围为例 双侧: P2.5~P97.5
单侧:< P95(上限) > P5(下限)
2020/2/22
正态分布应用
200例血铅值频数表及Px计算表
组段
3~ 8~ 13~ 18~ 23~ 28~ 33~ 38~ 43~ 48~ 53~ 58~62
2020/2/22
2.用途
1.划分正常与异常的界限。如作诊断 指标。
2.反映某人群的某项指标的动态变化。 如某地不同时期发汞值的正常范围 可反映环境污染的变化或环境保护 的效果。
2020/2/22
3.确定医学参考值范围的方法
⑴确定一批样本含量足够大(n>100)的 “正常人”或动物作为研究对象。
❖ 很多其他分布的极限为正态分布。二项分布和 Poission分布样本含量足够大时近似正态分布。
2020/2/22
医学参考值范围 1. 正态分布法 2. 百分位数法 3. 对数正态分布法
2020/2/22
1.医学参考值概念
是指大多数处于相同生理状态下的“正常人” 的某项指标(形态、机能及代谢产物等) 数值变化波动的范围。由于正常个体间存 在变异、机体内外环境改变,时间、地点、 条件的不同,使这些生理指标有一定的波 动范围,因此,实际应用中,一般采用正 常值范围.
标准正态分布变换 标准正态分布曲线下面积的分布规律 标准正态分布表的使用
2020/2/22
1、标准正态分布变换
一般正态分布为一个分布族:N(μ,σ2)。 为
卫管卫法卫统教案教案:第五章常用概率分布2-2学时.doc

复习:二项分布及泊松分布的特征 第五章常用概率分布——正态分布及其应用一、正态分布的概念和特征止态分布又称Gauss 分布,是--种很重要的连续型分布1. 正态分布的图形已知正态分布的方程,即可绘其图形2. 正态分布的特征(1) 正态曲线在横轴上方、均数处最高(2) 以均数为中心,左右对称。
对称轴是? (3) 正态分布山两个参数决定,即均数和标准差。
均数为位置参数,标准差为变异参数。
当标准弟恒定时,均数越人,曲线沿横轴越向右移;反之则向左移。
当均数恒定时,标准差越大,数据越分散,曲线授高点越向下・•・(4) 正态曲线下的而积分布有一定的规律。
二、标准正态分布将止态分布的方程作如下变量变换u 二(x -口)/o 即将原正态分布曲线图的原点 移到U 的位置,横轴尺度以。
为单位,就可将正态分布变换为标准正态分布N ( 0, 1 ), u 称为标准正态变量或标准正态(离)差。
⑴10,多媒体演 示正态分布的形成频数分布逐渐接近正态分布示意图10'图示参数 变化与图 形的关系10'三、正态曲线下面积的分布规律:实际工作中,常需要了解止态曲线下横轴上某一区间的而积占・总而积的百分数,以便估计该区间的例数書总例数的百分数(频数分布)或观察值落在该区间的概率。
正态曲线下一定区间的而积可以通过附表1求得。
对于正态或近似正态分布的资料,已知均数和标准差,就町对其频数分布作出概率估计。
杳附表1标准正态分布曲线下左侧尾部面积,e (u)值注意:(1)当卩、。
和xD知时,先按U二(x-u) /。
求U值,再查附表1;当》、。
未知时,分别用兀和S來估计;(2)曲线下对称于0的区间,面积相等,.••附表1只列出(-□)值。
(3)曲线下横轴上的总面积为100%或1。
正态分布Illi线下有三个区间的面积应用较多,应熟记:①标准正态分布时区间(-1,1) 或正态分布时区间(u-10, u+lo)的而积占总面积的68.27%;②标准正态分布时区间(-1.96, 1.96)或正态分布时区间(U-1.96 0, y+1.96o )的面积占总面积的95%;③标准正态分布时区间(-2.58, 2. 58)或正态分布时区间(»-2.58。
医学统计学 常用概率分布-正态分布

N (123.02,4.792)
(2)身高在120~128者占该地8岁男孩总数的百分比;
解析:
58.65%
58.65%
120cm 128cm N (123.02,4.792)
-0.63 1.46 N (0,1)
(3)该地80%男孩的身高集中在哪个范围?
解析:
80%
10%
10%
10% Z1
80%
10% Z2
任意正态分布曲线 X~N(μ,σ2)
标准正态分布曲线 X~N(0,1)
采用定积分的办法,对函数式 (1) 或 (2) 定积分, 算得从 -∞ 到 x累计面积,从而推算出该区间事件发 生的概率值。 .
j(Z )
1 2
Z
e
Z
2
/ 2
dZ
图 6 正态分布(左)及标准正态曲线下(右)的累计面积
1.2 正态概率密度曲线下的面积 1.3 正态分布的应用
1.4 正态分布的判断
一、正态分布的概念
正态分布(normal distribution)
德莫佛最早发现了二项概率
的一个近似公式,这一公式被 认为是正态分布的首次露面。
德莫佛
正态分布在十九世纪前叶由
高斯加以推广,所以通常称为 高斯分布(Gauss distribution)。
单侧临界值:标准正态分布单侧尾部面积等于α 时所对应 的正侧变量值,记作Zα 。
若按左单侧算,则是 97.5% 参考值范围
按左单侧算,是 95% 参考值范围
举例2: 某地调查120名健康成年男性的第一秒肺通 气量得均数 X =4.2(L), 标准差S =0.7(L),试据此估 计其第一秒肺通气量的95%参考值范围。 解析: 分布近似正态 1. 2. 仅过低为异常 3. 求下界值
统计学第五章概率与概率分布
再用各概率乘以学生总人数,即为各等级 人数。
3. 将能力、品行等的等级评定转化为数量化分数
计算步骤:
计算各等级人数的概率;
求各等级中点所对应的Z值
求各等级中点以下(上)的累加概率,并 求出其与0.5的差;
根据计算出的概率查找相应的Z值,该值 就是各等级的数量化分数;
男
女
可能结果 0
1
2
3
次数x
1
3
3
1
概率P 1/8 3/8 3/8 1/8
随机抽查的4个婴儿中男孩的概率分布 男女
X=0 X =1 X =2 X =3 X =4
可能结果 0
1
2
3
4
次数x 概率p
14 6 4 1 1/16 4/16 6/16 4/16 1/16
二项展开式的通式就是二项分布函
数,运用这一函数式可以直接求出 在n次二项试验中成功事件恰好出 现X次的概率
概率与概率分布基础 正态分布 二项分布 抽样分布
教学目的与要求:了解概率的基础知识;
掌握正态分布的特点及其应用;掌握二项分 布的性质与应用;掌握常见抽样分布的主要 特点及性质
教学重点与教学难点:重点——正态分布、
二项分布和抽样分布;难点——二项分布与 抽样分布
第一节 概率与概率分布基础
一、概率基础
的面积,找出相应的Z值; 根据公式Z=X-/ 计算出原始分数X
X= +Z
2.在能力分组或等级评定时确定人数
例如:假设对100名报考研究生的学生按 能力分为甲、乙、丙、丁四个组,问各组 应有多少人才能使分组构成等距量尺?
计算步骤:
将正态分布基线上Z=-3至Z=3之间6个标准 差的距离分成相等的几份;
医学统计学之概率分布的概念

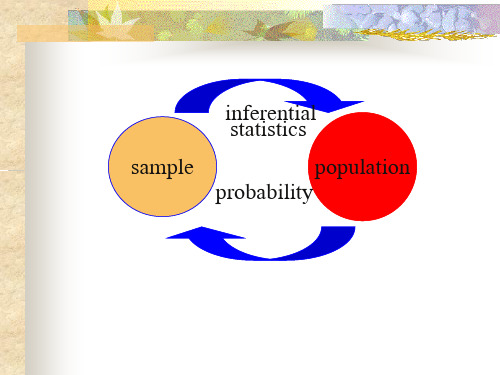
医学统计学之概率分布的概念医学统计学之概率分布的概念众所周知,统计分析可以分为描述性统计分析(descriptive statistics)和推断性统计分析 (inferential statistics)。
下面是yjbys店铺为大家带来的关于医学统计学的知识,欢迎阅读。
对于推断性统计分析来说,要抓住其本质,就必须对其背后最根本的概率分布(probability distribution)有个清楚的理解。
概率分布是很多统计推断方法的基础,最典型的例子就是正态分布,很多统计检验方法都会涉及到正态分布。
而有些统计检验则是直接建立在统计量值服从某种概率分布的基础上的,比如t检验的t值服从t分布,方差分析的F值服从F分布,卡方检验的卡方值服从卡方分布等。
因此在展开推断性统计分析或统计检验之前,先和大家一起熟悉一下概率分布。
首先简单介绍一下几个常见的概念:1、Random variable (随机变量):假设我们掷硬币,那么出现的结果有两种:正面或反面。
我们换个角度,把正面和反面的结果与数字联系起来,将结果数量化,比如我们掷10次硬币,出现5正5反。
这时我们就把掷硬币的结果(正或反)与出现正或反结果的数字联系起来了。
而随机变量就是一种function,它把每一种结果都与一个唯一的数值联系起来。
对于随机变量的定义,版本有很多,我们来看一下其中的一个定义:一个随机试验的可能结果(称为基本事件)的全体组成一个基本空间Ω 。
随机变量X是定义在基本空间Ω上的取值为实数的函数,即基本空间Ω中每一个点,也就是每个基本事件都有实轴上的点与之对应。
随机变量一般可分为离散型随机变量(discrete)和连续性随机变量(continuous)。
所谓离散型随机变量是指随机变量X的取值是有限个或可列无限个。
比如我们掷硬币,我们定义随机变量是正面的次数,那么我们掷10次,那么X的取值只能是0,1,2,3,4,5,6,7,8,9,10,这时我们就称X是个离散型随机变量。
统计学课件 (05)第5章 概率与概率分布

5 - 11
B A
A∩B
统计学
事件的关系和运算 (互斥事件)
事件A与事件B中,若有一个发生,另一个必定不发生, 则称事件A与事件B是互斥的,否则称两个事 件是相容的。显然,事件A与事件B互斥的充分必要条件是事件A与事件B没有公共的样本点
5 - 12
A
B
A 与 B互不相容
统计学
事件的关系和运算 (事件的逆)
5 - 28
统计学
概率的加法法则 (例题分析)
【例】根据钢铁公司职工的例子,随机抽取一名职工,计算该职工为炼钢厂或轧钢厂职工的概率
解:用A表示“抽中的为炼钢厂职工”这一事件;B表示“抽中的为轧钢厂职工”这一事件。随机 抽取一人为炼钢厂或轧钢厂职工的事件为互斥事件A与B 的和,其发生的概率为
P (A B ) P (A ) P (B )48 1 05 0 0 0 .50 04 121 52 05 000
统计学课件 (05)第5 章 概率与概率分布
统计学
第 5 章 概率与概率分布
§5.1 随机事件及其概率 §5.2 概率的性质与运算法则 §5.3 离散型随机变量及其分布 §5.4 连续型随机变量及其分布
5 -2
统计学
学习目标
1.
定义试验、结果、事件、样本空间、概率
2.
描述和使用概率的运算法则
3.
解:设A={读甲报纸},B={读乙报纸},C={至少读一种报纸}。则 P ( C ) =P ( A∪B )
= P ( A ) + P ( B ) - P ( A∩B ) =0.2 + 0.16 - 0.08 = 0.28
5 - 31
统计学
条件概率、乘法公式与独立事件
常用概率分布
有拐点,表现为钟形 靠近 x 处曲线下面积较为集中,两边减少,意味
着正态分布变量取值靠近 x处 的概率较大,两 边逐渐减少 正态分布的总体偏度系数和峰度系数均为0
8
正态分布曲线下面积
正态分布变量X的取值为(-∞,∞)
23
四、二项分布的图形
24
图形特点:两个轴意义,对称、偏态、与 正态分布的关系
决定图形的两个参数:n,
25
五、样本率的均数和标准差
样本率的总体均数p:
p
1 n
x
1 n
(n )
样本率的总体标准差p:
p
1 n
x
(1 )
n
样本率的标准差(标准误)Sp:
Sp
p(1 p) n
26
根据中心极限定理,在n较大,n(1- )均大于5时,二项分 布接近于正态分布。当n → ∞ , 二项分布B(n,)的极限分布 是总体均数为X = n、总体方差 X2 = n(1-)的正态分布 N(n, n(1-))。这个时候可以用正态分布N(n, n(1-)) 作近似计算。
16
确定医学参考值范围
例 估计某地健康成年女子的血红蛋白的95% 医学参考值范围
具体步骤如下: 1. 根据研究背景确定研究对象的入选标准和排
除标准。这类研究一般要求参加体检并且要 求除研究指标血红蛋白指标外,其他指标均 正常的对象。 2. 根据研究背景,确定血红蛋白过高或过低均 属于不正常(双侧范围)。
6. 如果受检指标血红蛋白呈偏态分布,则可 以用百分位数P2.5~P97.5确定95%参考值 范围,但样本量要充分大。
7. 样本量充分大是相对与指标的变异程度, 指标变异大,要求样本量大;指标变异程 度小,要求样本量可以相对小一些。
医学统计学((概率分布(正态分布))资料
99%
0.5%
0.5%
2.58
X 2.58
曲线下对称于μ的区间面积相等,如区间(-∞,-1.96) 与(1.96 ,+∞)的面积相等。
【例3-1】 已知某地120例正常人血浆铜含量(μM)的
均数 =14.48、s=2.27,试估计该地120例正常
人血浆铜含量(μmol/L)在14.20~15.60范围内的人数。 ⑴计算z值:按μ,σ未知时的标准正态变换
4.正态分布的特征*
(1)正态分布具有集中性、对称性和均匀变动性。 (2)正态分布的图形由参数μ和σ确定。
4.正态分布的特征
(3)任何均数为μ、标准差为σ的正态分布N
(μ, σ ),都可通过式(3-9)变换为均数为 0、 σ为1的标准正态分布N(0,1)。
x
Z=
5.正态曲线下面积的分布规律*
z=(x― )/s: x1=14.20,z1 = (14.20-14.48)/2.27 =-0.1233 x2=15.60,z2 = (15.60-14.48)/2.27=0.4934
⑵查附表5,标准正态曲线下面积表:
z= -0.12时,在表的左侧找到-0.1,在表的上方找 到0.02,二者相交处为0.4522,标准正态曲线下, 横轴上z值小于-0.12的面积Ф(-0.12)=45.22%,即 标准正态变量z值小于-0.12的概率为0.4522;
μ-σ μ+σ
3. 正态变量的分布函数F (x)
F (x)= P (X<x)=
1
e dX X ( X )2 /(2 2 )
2
正态变量在(-∞,x) 内取值的累计概率。
不同变量的正态分布曲线
二、标准正态分布
1.标准正态分布的密度函数
卫生统计学题库(6版)
第一章绪论第二章(一)A1型:1.下面的变量中,属于分类变量的是_____。
A.脉搏B.血型C.肺活量D.红细胞计数E.血压2.下面的变量中,属于定量变量的是_____。
A.性别 B.体重 C.血型 D.职业 E.民族3.某人记录了50名病人体重的测定结果:小于50kg的13人,介于50kg和70kg间的20人,大于70kg的17人,此种资料属于_____。
A.定量资料B.分类资料C.有序资料D.二分类资料E.名义变量资料4.上述资料可以进一步转换为_____。
A.定量资料B.分类资料C.有序资料D.二分类资料E.名义变量资料5.若要通过样本作统计推断,样本应是_____。
A.总体中典型的一部分B.总体中任一部分C.总体中随机抽取的一部分D.总体中选取的有意义的一部分E.总体中信息明确的一部分6.统计量_____。
A.是统计总体数据得到的量 B.反映总体统计特征的量C.是根据总体中的全部数据计算出的统计指标D.是用参数估计出来的E.是由样本数据计算出的统计指标7.因果关系_____。
A.就是变量间数量上的联系 B.可以用统计方法证明 C.必定表现为数量间的联系D.可以通过单独考察两个变量间关系得出E.可以通过变量间数量上的联系来证明(二)A2型:1.教材中提及美国人1954年实施了旨在评价索尔克(Salk)疫苗预防小儿麻痹或死于脊髓灰质炎效果的临床试验。
有180万儿童参与,约有1/4参与者得到了随机化。
这180万儿童是_____。
A.目标总体B.研究总体C.1份样本D.1份随机样本E.180万份样本2.上述试验最终肯定了索尔克疫苗的效果。
请问此结论是针对_____而言。
A.180万儿童B.每个儿童C.所有使用索尔克疫苗的儿童D.所有儿童E.180万儿童中随机化的1/4二、是非题 1.定量变量、分类变量和有序变量可以相互转换。
2.假变量可以参与计算,所以假变量是定量变量。
3.离散变量在数值很大时,单位为“千”或“万”时可以取小数值,此时可近似地视为连续型变量。
南方医科大学·医学统计学·简答题总结
第四章·资料分布特征与描述统计量1.统计描述主要从哪几个方面发现和描述数据特征?统计描述可以从样本含量n,集中趋势(算术均数、几何均数、中位数),离散趋势(极差、四分位数间距、方差和标准差)以及通过绘制统计图,编制统计表来发现和描述数据特征。
2.频数表的主要用途有哪些?(1)描述频数分布的类型;(2)描述频数分布的特征;(3)便于发现一些特大或特小的可疑值;(4)便于进一步做统计分析和处理。
3.算数均数、几何均数和中位数各有什么适用条件?算术均数主要适合描述对称分布资料的集中位置;几何均数适合描述当资料呈倍数关系或对数正态分布时的集中趋势;当大部分观测值比较集中,少数观测值偏向一侧时,或资料分布情况不清楚时,或数据的最大值(最小值)无准确测量数据时,宜用中位数来表示其平均水平。
4.标准差有何用途?(1)表示变量分布的离散程度。
两组资料(总体或样本)均数相近,度量单位相同的条件下,标准差较大,说明变量值的变异度较大,即各变量值较分散(较远离均数),因而均数的代表性较差;反之标准差较小,说明变异度x 来较小,即各变量值较集中在均数周围,因而均数对各变量值的代表性较好,在用数字作统计描述时常用符号s反映均数代表性的好坏。
(2)可用来计算变异系数。
当两组资料单位不同,或单位相同,均数相差较大时,不能直接用标准差比较它们的变异程度,须用变异系数进行比较。
(3)结合均数描述正态分布的特征,并利用正态曲线下面积分布规律,来计算医学上各种生化、生理的参考值范围。
(4)在单纯随机抽样调查中,是计量资料估计样本大小的不可缺的重要依据之一。
(5)可用来计算抽样误差的大小。
5.变异系数与标准差有何异同?同:变异系数与标准差都可反映数据的变异度大小,异:标准差是一组同质数据间变异度大小的量度指标,它带有单位,因而不同单位的数据间的变异度大小不可用标准差作比较;而变异系数是一种不带单位的反映变异度大小的相对数值,因而它可对不同单位数据间的变异度大小作比较。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
-x1 -x2
+x2 + x1
27
正态曲线下的面积规律
S(-, )=0.5 S(-, -1)=0.1587 S(-, -2)=0.0228 S(-, -3)=0.0013 S(-, )=1 S(-, +1)=0.8413 S(-, +2)=0.9772 S(-, +3)=0.9987
Z 0
25
正态曲线下的面积规律
X轴与正态曲线所夹面积恒等于1 。 对称区域面积相等。
S(-, -X)
S( +X,)=S(-, -X)
26
正态曲线下的面积规律
对称区域面积相等。
S( -x1, -x2) S( -x1, -x2)= S( +x1, +x2)
0 1 3 2
0.008 0.096
2 3
1 0
0.384 0.512 1.000
46
二项分布的概率
设事件A出现的概率为。则在n次独立试 验中,事件A恰好出现 k 次的概率为:
P( X k ) C (1 )
k n k
n k
对应于二项展开式:
(1 )
2
e
(-∞< X <+∞)
则称X服从正态分布,记作X~N(,2),其中, 为分布的均数, 为分布的标准差。
17
正态分布图示
.4
f(x)
.3
.2
.1
0
x
18
方差相等、均数不等的正态分布图示
2 1 3
3
1
2
19
均数相等、方差不等的正态分布图示
2 3 1 2 1
14
正态分布的概念及图形
(a)
(b)
(c)
(d)
15
正态分布的概念及图形
Normal distribution Gauss发现 最早用于物理学、天文学 Gaussian distribution
16
正态分布的概率密度函数
如果随机变量X的概率密度函数
f (X )
1
( X )2 2 2
0.0013 0.0013 0.0012 0.0011 0.0010 0.0062 0.0059 0.0055 0.0052 0.0049 0.0228 0.0217 0.0207 0.0197 0.0188 0.0287 0.0274 0.0262 0.0250 0.0239 0.0548 0.0526 0.0505 0.0485 0.0465 0.1587 0.1539 0.1492 0.1446 0.1401 0.3085 0.3015 0.2946 0.2877 0.2810 0.5000 0.4920 0.4840 0.4761 0.4681
40
5.1.4 正态分布的应用
正态分布是许多统计方法的理论基础
估计频数分布( frequency distribution) (自学)
确定临床参考值范围(reference interval) (自学)
41
作 业
阅读内容:(P51-54) 查阅文献,介绍某项参考值范围(reference interval)的制定过程(最新进展) 每人准备5-10张ppt (中英文均可), 我会给 你10-20分钟时间.
离散型:性别、血型、子女数、事故数、菌
落数 连续型:身高、体重
10
5.1 正态分布
正态分布的特征 标准正态分布 正态分布曲线下面积的规律 正态分布的应用
11
例:密度函数和分布函数
抛两枚硬币,
P 两枚均正面朝上 0.25 P 两枚均反面朝上 0.25 P A正面B反面朝上 0.25 P A反面B正面朝上 0.25 P 至少有一枚正面朝上 0.75 P 恰好有一枚正面朝上 0.5
-2
-1
0
1
2
3
4
29
正态曲线下的面积规律
S(-, )=0.5 S(-, -1)=0.1587 S(-, -2)=0.0228 S(-, -3)=0.0013
S(-, )=1 S(-, +1)=0.8413 S(-, +2)=0.9772 S(-, +3)=0.9987
35
常用正态曲线下的面积规律
例5.4 求正态分布N(119.41,4.382)曲线下区间 (110.83,127.99)内的面积
⑴ 先用求对应的u值 uL = (110.83-119.41)/4.38 = -1.96 uU = (127.99-119.41)/4.38 = 1.96 ⑵查u界值表,得面积 (-1.96,1.96)的面积 = 1-2×标准正态分布曲线下区间(-∞,1.96) 的面积 =1-2×0.025 =0.95
甲乙丙
生生生 生生死 生死生 死生生 生死死 死生死 死死生 死死死
0.2×0.2×0.2 0.2×0.2×0.8 0.2×0.8×0.2 0.8×0.2×0.2 0.2×0.8×0.8 0.8×0.2×0.8 0.8×0.8×0.2 0.8×0.8×0.8 1
n X X
(1 )
X n-X
33
正态曲线下的面积规律
例5.2 求标准正态分布曲线下区间(-∞,-2.58)的面积与区 间(2.58,∞)的面积
(-∞,-2.58)的面积是0.0049,约为0.5%。区间(2.58,∞)的面积亦为0.5%
34
正态曲线下的面积规律
例5.3 求标准正态分布曲线下区间(-1,1)的面积
区间(-1,1)的面积 =1-2×(-∞,-1)的面积 =1-2×0.1587 =0.6826
n
k 0 (1 )n n 1 (1 )n1 Cn k (1 )n k
n n1 (1 )1 n (1 )0
47
二项展开
( 0.2 +0.8 )3 = 0.23 + 3×0.22×0.8 + 3×0.2×0.82 + 0.83
医学统计学
余小金 xiaojinyu@ 东南大学公共卫生学院 流行病与卫生统计学教研室
内容复习
基本概念 研究设计基础 统计描述
2
基本概念汇总
总体
个体、个体变异
随机 抽样
样本
代表性、抽样误差
总体参数
未知
统计推 断
样本统计量已
知
风 险
3
研究设计基础
抽样研究的科学性 如何保障抽样研究的合理性?
-3 -2 -
+ +2 +3
-4
-3
-2
-1
0
1
2
3
4
30
正态曲线下的面积规律
正态分布的一个显著特点 曲线下面积完全决定于以标准差为单位从点x 到µ的离差。
31
X2=-σ X1=-σ X3=-σ
2
2 1
0.1587 0.1587 0.1587
1
3
3
X3 X1 X2
3
20
正态分布的特征
单峰分布且峰在均数处; 以均数为中心,均数两侧完全对称。 正态分布有两个参数(parameter),即位置参数 (均数)和变异度参数(标准差)。 有些指标服从正态分布; 有些指标本身不服从正 态分布,但经过数值变换之后服从正态分布。 正态曲线下的面积分布有一定的规律。
密度函数
分布函数
12
例:密度函数和分布函数
x
13
随机变量的概率分布
概率函数(Probability Function),或者说概率密度函 数(Probability Density Function) 、密度函数。 在统计学中,分布函数(Distribution Function)。说明 变量取某些值的可能性。 当变量的取值包括了所有可能的取值时,分布函数为1。 密度函数和分布函数构成某种分布(Distribution)
生存 死亡 概率 概率
三生
二生一死
一生二死
三死
48
累=1)+…+P(X=k) P(X≥k) = P(X=k)+P(X=k+1)+…+P(X=n)
P(X≤k) = 1- P(X≥k+1)
49
5.2.2 二项分布的性质
如果X~B(n,p),则:
X的均数:
X n n (1 )
36
常用正态曲线下的面积规律
95%
2.5%
2.5%
-1.96
+1.96
37
常用正态曲线下的面积规律
90%
5%
5%
-1.64
+1.64
38
常用正态曲线下的面积规律
99%
0.5%
0.5%
-2.58
+2.58
39
正态曲线下的面积规律
正态曲线下面积总和为1; 正态曲线关于均数对称;对称的区域内面积相等; 对任意正态曲线,按标准差为单位,对应的面积相等; -1.64~ +1.64内面积为90%; -1.96~ +1.96内面积为95%; -2.58~ +2.58内面积为99%。
正态分布转换为标准正态分布
若 X~N(,2),作变换:
Z
X
则Z服从标准正态分布。 Z称为标准正态离差(standard normal
deviation)
24
标准正态分布曲线下面积(Z)
