《高数》第十章习题课-线面积分的计算
高数线面积分

10 沿D内任何一闭路L上的积分为零,即 Pdx Qdy 0 ;
L
20 曲线积分 Pdx Qdy与路径无关,只与起点 A与终点B有关;
L( AB )
30 P Q 在D内恒成立; y x
40 在D内存在二元函数 u( x, y),使du Pdx Qdy .
.
等价的意义是: 若其中一个成立,另外三个也成立。
I a 2 x 2 y 2 dxdy a 2 x 2 y 2 (dxdy)
.
.
Dxy
Dxy
.
2
a 2 x 2 y 2 dxdy 2
2π
d
a
a 2 r 2 rdr
4π a3
.
Dxy
0
0
3
二4 :球面 x 2 y 2 z 2 a 2的外侧表面,Dxy为xOy平面上的圆域:
一型:对面积
二型:对坐标
三重积分
高斯公式
1. 第Ⅰ型、第Ⅱ型曲线积分的比较
曲线积分 标准形式 物理意义
计算方法
相似处
不同处
第一型 (对弧长)
第二型 (对坐标)
f ( x, y)ds
L
f ( x, y, z)ds
L
L指曲线
⌒
AB
当 f ( x, y) 0,
f ( x, y)ds表示
L
线密度为 f ( x,
y)的曲线型构
件的质量 M .
设曲线
L: x y
φ(t) (t)
t
1.都是化曲线积分为 定积分计算。
Pdx Qdy W Pdx Qdy 2.都要把曲线表示式 L
L
Pdx Qdy Rdz
表示力F P,Q
高数第十章线面积分习题和答案

第十章曲线积分曲面积分练习题A 组一.填空题1. 设L 是 122=+y x 上从)0,1(A 经)1,0(E 到)0,1(-B 的曲线段,则⎰Lydy e 2=2.设⋂MN 是从M(1,3) 沿圆 2)2()2(22=-+-y x 至点 )1,3(N 的半圆,则积分⎰⋂+MNxdy ydx =3. L 是从)6,1(A 沿6=xy 至点)2,3(B 的曲线段,则⎰++Ly x xdy ydx e )( =4. 设L 是从)0,1(A 沿1222=+y x 至点2,0(B )的曲线段,则⎰+Ly x y x dy ye dx xe 222 =5. 设L 是 2x y = 及 1=y 所围成的区域D 的正向边界,则⎰+Ldx y x xy )(33 + dy y x x )(242+ = 6. 设L 是任意简单闭曲线,b a ,为常数,则⎰++L bdy adx )( =7. 设L 是xoy 平面上沿逆时针方向绕行的简单闭曲线,且9)34()2(=++-⎰dy y x dx y x L,则L 所围成的平面区域D 的面积等于8. 常数 k = 时, 曲线积分⎰+Ldy x kxydx 2与路径无关。
9.设是球面 1222=++z y x ,则对面积的曲面积分⎰⎰∑++ds z y x 222 =10.设L 为)0,0(o , )0,1(A 和)1,0(B 为顶点的三角形围成的线, 则对弧长的曲线积分⎰Lds =11. 设L 是从点)1,1(到)3,2(的一条线,则⎰-++Ldy y x dx y x )()(=12. 设L 是圆周 t a x cos =, t a y sin = )20(π≤≤t ,则⎰+LdS y x 322)(=13. 设为曲面2222a z y x =++, 则⎰⎰∑dS z y x222=二、选择题1.设→→+=j y x Q i y x P A ),(),(,D y x ∈),(且P,Q 在域D 内具有一阶连续偏导数,又L :⋂AB 是D 内任一曲线,则以下四个命题中,错误的是( )A .若⎰+LQdy Pdx 与路径无关,则在D 内必有yPx Q ∂∂≡∂∂ B .若⎰⋅Lds A 与路径无关,则在D 内必有单值函数),(y x u ,使得dy y x Q dx y x P y x du ),(),(),(+=C .若在D 内yPx Q ∂∂≡∂∂,则必有⎰L ds A ·与路径无关。
第10章线面积分2

即
∫∫ f ( x, y, z)dS = lim∑ f (ξi ,ηi ,ζ i )∆Si λ→0 i =1
Σ
n
叫被积函数, 其中f ( x, y, z)叫被积函数,Σ叫积分曲面.
2.对面积的曲面积分的性质 2.对面积的曲面积分的性质
若Σ可分为分片光滑的曲面Σ1及Σ2 , 则
∫∫ f ( x, y, z)dS =∫∫ f ( x, y, z)dS +∫∫ f ( x, y, z)dS. Σ
思考题
在对面积的曲面积分化为二重积分 2 2 的公式中, 的公式中 有因子 1+ zx + zy , 试说明 这个因子的几何意义. 这个因子的几何意义
思考题解答
是曲面元的面积, dS是曲面元的面积
2 x 2 y
cos(n, z) =
1
2 1+ zx + z2 y
故 1+ z + z 是曲面法线与z 轴夹角的余弦
( 其中 ∆σ )xy 表示投影区域的面积.
二、概念的引入
实例: 流向曲面一侧的流量. 实例: 流向曲面一侧的流量.
(1) 流 速场 为常向 v ,有 量 向平 面区域 A,求单位 假定密度为1) 1). 时间流过 A 的流体的质量Φ(假定密度为 1).
v
θ
A
n
0
流量 Φ = A v cosθ = Av ⋅ n = v ⋅ A
都在Σ上连续, 都在Σ上连续, 求在单位 时间内流向Σ 时间内流向Σ指定侧的流 体的质量Φ.
x
z
Σ
o
y
1. 分割 把 面 分 n 小 ∆s (∆s 同 也 表 曲 Σ 成 块 i 时 代 i 第i 小 曲 的 积 块 面 面 ), vi 在∆si 上 取 点 任 一 z ∆Si ni (ξi ,ηi ,ς i ) (ξi ,ηi ,ζ i ), 则该点流速为 vi . 法向量为 ni .
线面积分复习JD.docx

高数下册第十章-曲线积分与曲面积分练习题(一)・复2填1・设曲线L:x2 +y2 =4 ,则曲线积分j(x- y + V)^x2 + y2ds = 8兀・2 2复3填1・设椭圆厶:—1的周长为Q,且椭圆厶上任意一点处的质量密度为3 4厂(兀,刃=4兀2+3尸+2心,则该椭圆构件的质量M = \2a・2 21 •设椭圆厶:—+ ^- = 1的周长为°,则L(1+4兀2 + 3y2 + 3兀2y)ds = 13a・3.设曲线厶:,+)/=]上任意一点处的质量密度p(x,y) = (x+y)2,则该曲线构件的质量M = 27V ・复5填1・设曲线厶:/+)'二]上任意一点处的质量密度。
(兀,刃=X2 4- y2 + 2 ,则该曲线构件的质量M= _______________ ・(二)・复1选1・设有向曲线厶为y = x2,从点(1,1)到点(0,0),则J /(x, y)dy = ( C )・J厶A . f(x,x2)clx; B. ^2xf(x,x2)clx ;C. J:/(V7,y)dy;D. 芳・复2选1.设有向曲线厶为『=仮,从点(1,1)到点(0,0),则\L y)dx = ( B ).A. [/(兀仮)如D.复1三、(5分〉计算曲线积分J/Fyh,其中厶为连接两点(1,0)及(0,1)的直线段.解:厶的方程为y = \-x( 0 < x < 1 ), y = -1 (1分)『厶x2yds = J。
%2(1 - x)y[2 dx(3 分)复2三、(6分)设曲线L:y = 2x+l (0<x<l )上任意一点处的质量密度为p (x, y ) = xy ,求 该曲线构件的质量M. 解:_/ = 2 , ds = yfidx ,M = j xy ds= 7A /5 复5三•计算曲线积分£ y(l - x)ds , 三角形的整个边界.解:OA:y = 0 (0 < x< 1)AB \ y = \- x (0 < x < 1) , ds - 4^dx ,L y(1 一 x)d$ = J ; (1 一 x) 2 y[2dx = ¥ ' OB : x = 0 (0 < y < 1) , ds = dy, \oB y(\-x)ds = \\)y dy=^1 J? 所以 $ y(l - x)ds =——i--—・2 3复3三、计算曲线积分削xds,其中厶为由及所围成区域的边界. 解:厶:y =兀(0 井 x 1) , ds -4^dx,(3分)L 2 : y= x 2 (01) , ds = Jl + 4x 2 dx,12(5分)(1分)J ()x (2x+1)亦心(5分) (6分)其中厶为0(0,0),A (1,0),B (0,1)三点所^xds=xj 1 + 4x 2 dxo=J1+ 4才 d(l+ 4x 2)(3分)1 2 护+4“5A /5- 1 12y(l - x)ds = 0 ,所以 51 xds =竺5—I +. (1 分)5 1226. 计算\L Jyds,其中厶是抛物线y = X 2上点0(0,0)与点B (l,l )之间的一段弧.解厶的方程y = x 2(0 < x < 1),ds = y]l + (x 2 )fl dx = 71 + 4x 2 dx. 因此J y[yds = j V? • J1 + 4” dx=J xy) 1 + 4x 2 dx= ±(575-1).0丄厶7.设曲线厶是y = 2x, y = 2和x = 0所围三角形区域的边界,求线积分7 =xyds .解令厶=/j + /2 + /3 ,其中厶为 y = 2%, 0 < x < 1 , ds = y[5dx ;厶为 = 2, 0 < x < 1, ds - dx ; 厶为 x = 0, 1 < y < 2 , ds - dy /二 J x2x>/5dx + j 2xdx + 0 二—V5 +0 0(三)・复2四、(6分)求质点在平面力场F (x, y ) =y7 + 2xy 作用下沿抛物线L : y = \-x 2从点(1,0)移 动到点(0,1)所做的功W 的值.=|] [1 - x 2 + 2^(-2x)]t/x =j (l-5x 2)rfx(6分)复1四、(7分〉验证平面力场F (x,y ) =cosxsin y ~i + sinxcosy;所做的功与路径无关,并求质所以解:W = ^yclx + lxdy(2分) (4分) (5分)点在力戸的作用下沿直线厶从点(。
线面积分总结

圆Γ的形心 在原点, 故
X =0
机动 目录 上页 下页 返回 结束
例. 计算
其中Γ 为曲线
z
解: 利用对称性 , 有
Γ
Γ
o
y
∫Γ
x2 ds = ∫ y2 ds = ∫ z2 ds
Γ
x
(Γ的重心在原点)
利用重心公式知
2 2 2 2 ∴ I = ∫ (x + y + z )ds 3 Γ 4 3 = πa 3
2
解: 显然球心为 (1 1 1) , 半径为 3 ,, 利用对称性可知
2 4 2 2 2 ∴ I = ∫∫ (x + y + z ) d S = ∫∫ (x + y + z) d S 3 ∑ 3 ∑ ∫∫∑ xd S = ∫∫∑ yd S = ∫∫∑ zd S 利用形心公式
= 4∫∫ xd S = 4⋅ x ⋅ ∫∫ d S
= 4∫
π
0
4 a2 cosθ dθ
机动
目录
上页
下页
返回
结束
的圆弧 L 对于它的对 例. 计算半径为 R ,中心角为 称轴的转动惯量I (设线密度µ = 1). 解:
y
I = ∫ y ds
2 L
x = Rcosθ ( −α ≤θ ≤α ) L: y = Rsinθ
α
−α
L α o R x
∫ P(x, y, z)dx = ∫
(c)
b大
a小 b终
P(x, y(x), z(x)) d x
= ∫ P(x, y(x), z(x)) d x
a起
(S )
∫∫ f (x, y, z) d S = σ f (x, y, z(x, y)) ∫∫
线面积分整章课件
且L P( x, y)dx Q( x, y)dy
{P[ (t), (t)](t) Q[ (t), (t)] (t)}dt
特殊情形
(1) L : y y( x) x起点为a,终点为b.
则
b
Pdx Qdy {P[ x, y( x)] Q[ x, y( x)]y( x)}dx.
L
a
(2) L : x x( y) y起点为c,终点为d .
i 1
n
[P(i ,i ) xi Q(i ,i ) yi ].
i 1
n
取极限
W
lim
0
i 1
[ P ( i
,i
)
xi
Q( i
,i
)
yi
].
精确值
二、对坐标的曲线积分的概念
1.定义 设L为 xoy面内从点A到点B的一条有 向光滑曲线弧, 函数 P( x, y), Q( x, y)在 L 上有界. 用L上的点M1( x1, y1 ), M2( x2 , y2 ), , Mn1( xn1, yn1 )把 L分成n个有向小弧段 Mi1Mi (i 1,2,, n; M0 A, Mn B). 设xi xi xi1, yi yi yi1, 点(i ,i )为 Mi1Mi 上任意取定的点. 如果当各小弧段 长度的最大值 0时,
L Pdx Qdy L1 Pdx Qdy L2 Pdx Qdy.
(2) 设 L是有向曲线弧,L是与L方向相反的 有向曲线弧, 则
L P( x, y)dx Q( x, y)dy L P( x, y)dx Q( x, y)dy
即对坐标的曲线积分与曲线的方向有关.
三、对坐标的曲线积分的计算
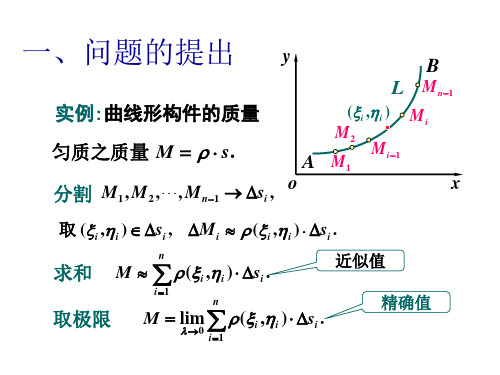
一、问题的提出 y
实例:曲线形构件的质量
D10_习题课--★【汉魅HanMei—课程讲义】

其中由平面 y = z 截球面 从 z 轴正向看沿逆时针方向. 故
o x
z
1y
原式 =
1 3 1 2 2 2 4 2 2
机动 目录 上页 下页 返回 结束
2. 基本技巧
(1) 利用对称性及重心公式简化计算 ;
(2) 利用积分与路径无关的等价条件;
(3) 利用格林公式 (注意加辅助线的技巧) ; (4) 利用斯托克斯公式 ; (5) 利用两类曲线积分的联系公式 .
2
z
o x
0
xd ydz ydzdx zdxd y
y
3 d x d y d z
3
0
3 R 0 2 R 3
3
P185 题4(2) , P185 题 9 同样可利用高斯公式计算.
机动 目录 上页 下页 返回 结束
例3. 设 为简单闭曲面, a 为任意固定向量, n 为的 单位外法向向量, 试证 证明: 设 n (cos , cos , cos )
I
L BA
( x y ) d x ( y x) d y ( x y ) d x ( y x) d y
a 2
2
2
y
C
2
2
L
BA
D
B
o
0 d x d y x d x a a D 3
2
3
Ax
(利用格林公式)
思考: (1) 若L 改为顺时针方向,如何计算下述积分:
习题课 线面积分的计算
一、 曲线积分的计算法 二、曲面积分的计算法
第十章
机动
目录
上页
高数 第十章 曲线积分与曲面积分

计算
定积分
计算
Stokes公式 计算 曲面积分 Gauss公式
重积分
16
积分概念的联系
定积分
f ( M )d lim f ( M ) i , f ( M )点函数
0
i 1
n
当 R1上区间 a, b]时, f ( M )d f ( x )dx. [
5
基本问题: 如何熟练掌握各种积分的计算
首先判断准确要求的是哪一类积分 重要的是牢牢记住各种积分的计算方法
1、I
L
f ( x , y )ds 代入曲线的方程以及ds,从而化为定积分解之
2、I Pdx Qdy 代入曲线的方程,化为定积分解之 L
P Q 闭合 y x 非闭
( y 2 z 2 ) dS; I z
( x 2 y 2 ) dS
曲面质心: 曲面形心:
x
x
dS ; y
S
;y
ydS ydS
dS ; z
S
;z
dS S
dS zzdS
15
(二)各种积分之间的联系
积分是
P cos Q cos R cos ds
,其中, ,为有向曲面上点
x, y, z 处的
法方向 的方向角。
20
2.选择以下各题中给出的四个结论中一个正确的结论:
(1)设曲面是上半球面 : x 2 y 2 z 2 R 2 , z 0, 曲面 1 是 曲面在第一卦限中的部分 , 则有 C .
条 件 等
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12
练习题: P184 题 3(5) ; P185 题6; 10 3(5). 计算
其中L为上半圆周 提示:
沿逆时针方向.
I ex sin y d x (ex cos y 2)dy 2 ydx
L
L
2 ydx
L AB AB
L
L
:
xy
a a
(1 cos sin t
其中L为上半圆周
沿逆时针方向.
P185 6 . 设在右半平面 x > 0 内, 力
构成力场,其中k 为常数,
场力所作的功与所取的路径无关.
证明在此力场中
P185 10. 求力
沿有向闭曲线 所作的
功, 其中 为平面 x + y + z = 1 被三个坐标面所截成三
角形的整个边界, 从 z 轴正向看去沿顺时针方向.
3
16
二、曲面积分的计算法
1. 基本方法
曲面积分
第一类( 第二类(
对面积 对坐标
) )
转化
二重积分
(1) 统一积分变量 — 代入曲面方程
(2)
积分元素投影
第一类: 第二类:
始终非负 有向投影
(3) 确定二重积分域
— 把曲面积分域投影到相关坐标面
17
2. 基本技巧
(1) 利用对称性及重心公式简化计算 重心公式
20
例4. 设 为简单闭曲面, a 为任意固定向量, n 为的 单位外法向向量, 试证
证明: 设 n (cos , cos , cos )
(常向量)
则 cos( n ,a ) d S n a 0 dS
cos cos cos cos cos cos d S cosdydz cos dzdx cos dxdy
应如何
提示: 在椭球面内作辅助小球面 x2 y2 z2 2 取
内侧, 然后用高斯公式 .
22
这说明积分与路径无关, 故
I AB (x2 y) d x ( y2 x)dy B
a
a
x
2
d
x
y
C
L
o Ax
9
解法2 添加辅助线段 BA,它与L所围区域为D, 则
I LBA(x2 y) d x ( y2 x) d y
BA(x2 y) d x ( y2 x) d y
P184 3 (1) 计算
其中L为圆周
P184 3(3). 计算
其中L为摆线
上对应 t 从 0 到 2 的一段弧.
P184 3(6). 计算
其中由平面 y = z 截球面 从 z 轴正向看沿逆时针方向.
3
解答提示: P184 3 (1)
计算
其中L为圆周
提示: 利用极坐标 ,
ds r2 r2 d a d
y
x
3 x d z AB
1
30 (1 z)dz
15
方法2 利用斯托克斯公式 设三角形区域为 , 方向向上, 则
1
1
3
3
x
y
yz
1 3
(3)
d
S
1
3
z
dS
x
3 2
z
B n
oC
A
y
x
:x y z 1
n 1 (1, 1, 1)
原式 = L ax ds
说明: 若用参数方程计算, 则
y
r
t
o
ax
d s x2 y 2 d t
4
P184 3(3).计算
上对应 t 从 0 到 2 的一段弧. 提示:
其中L为摆线
原式
a
2
2
0
t
sin
td
t
a2 t cos t sin t 02
5
P184 3(6). 计算
D 0 d x d y
a x2 dx 2 a3
a
3
y
C
L
D
B o Ax
(利用格林公式)
思考:
(1) 若L 改为顺时针方向,如何计算下述积分:
I1 L (x2 3 y) d x ( y2 x) d y
(2) 若 L 同例2 , 如何计算下述积分:
I2
(x2 y y 2 )d x (y2 x)d y
L
10
思考题解答:
y
(1) I1
(x2 3 y)d x (y2 x)d y
L
L AB AB
C
L
D
B o Ax
2 d x d y 2 a3 a2 (2 a )
D
3
3
(2)I2 L (x2 y y 2 ) d x ( y2 x) d y
0
21
例5. 计算曲面积分
其中, r x2 y2 z2 , : x2 y2 z2 R2 取外侧.
解:
1 R3
3
d
x
d
y
d
z
思考: 1. 为什么不考虑(0,0,0)点的可导性,不考虑行吗?
2. 本题 改为椭球面 计算 ?
x2 a2
y2 b2
z2 c2
1时,
z
的上侧.
提示: 以半球底面 0 为辅助面,
且取下侧 , 记半球域为 , 利用 高斯公式有
o
y
x 0
原式 =
3d x d y d z 0 xdydz ydzdx zdxdy
3 2 R3 0 2 R3
3
P185 题4(2) , P185 题 9 同样可利用高斯公式计算.
x xd S d S
注意公式使用条件
(2)
利用高斯公式
添加辅助面的技巧
(辅助面一般取平行坐标面的平面)
(3) 两类曲面积分的转化
18
例3. 计算曲面积分
中 是球面 x2 y2 z2 2x 2z .
解: I (x2 y2 z2 ) 2xy 2 yz dS
7
例1. 计算
其中 为曲线
z
解: 利用轮换对称性 , 有
x2 ds y2 ds z2 ds
利用重心公式知
I
2 3
(x2
y2
z2 )ds
4 a3
3
y
o
x
(的重心在原点)
8
例2. 计算
其中L 是沿逆
时针方向以原点为中心, a 为半径的上半圆周.
解法1 令 P x2 y, Q y2 x, 则
t)
t :0
y L
D
oA a B x
D 0d x d y
2a
0d
x
2a2
0
sin2 td t
0
a2
13
P185 6 . 设在右半平面 x > 0 内, 力
构成力场,其中k 为常数, 场力所作的功与所取的路径无关.
证明在此力场中
提示: F 沿右半平面内任意有向路径 L 所作的功为
提示: 因在 上有
其中由平面 y = z 截球面
从 z 轴正向看沿逆时针方向.
故
z
原式 =
o 1y
x
2
1 2
2
3 4
1 2
2
6
2.线积分基本技巧
(1) 利用对称性及重心公式简化计算 ; y y ds ds
(2) 利用积分与路径无关的等价条件; (3) 利用格林公式 (注意加辅助线的技巧) ; (4) 利用斯托克斯公式 ; (5) 利用两类曲线积分的联系公式 .
令
P
k
x
3
,
Q
k
y
3
易证
14
P185 10. 求力
沿有向闭曲线 所作的
功, 其中 为平面 x + y + z = 1 被三个坐标面所截成三
角形的整个边界, 从 z 轴正向看去沿顺时针方向.
提示: 方法1
z
B
利用对称性
3 y d x z d y xdz AB
oC
A
(2x 2z) d S 2 (x z)ydS
用重心公式
利用对称性 z
R2
2(x z) d S 0
(1,0,1)
oy
x
19
练习: P185 题4(3)
计算 x d y d z y d z d x z d x d y,其中 为半球面
(x2 y) d x (y2 x)dy y2 dx
L
L
L : x a cost, y a sin t, t : 0
I a3 sin3 t d t 2 a3
0
3
2a3
11
练习题: P184 题 3(5) ; P185 题6; 10 3(5). 计算
习题课
线面积分的计算
第十章
一、 曲线积分的计算法 二、曲面积分的计算法
1
一、曲线积分的计算法
1. 基本方法 曲线积分
