角平分线、中线和高
高考数学二轮复习三角形中的中线、高线、角平分线问题ppt课件

三角形中的中线、高线、
角平分线问题
一、中线
2
2
2
2
1.中线长定理:在△ABC 中,AD 是边 BC 上的中线,则 AB +AC =2(BD +AD )
推导过程:在△ABD 中,cos B=
在△ABC 中,cos B=
+ -
+ -
·
·
,求 c.
解:(2)设 BC 边上的高为 h,由三角形的面积公式得 S△ABC= ah= ×
bcsin A=×5c×sin=
c,所以
a=
c,即 a=
a=
c,
由余弦定理得 a2=25+c2-5c,
将 a=
c 代入上式得 c2+16c-80=0,解得 c=4 或-20(舍去),所以 c=4.
→
→ → →
+ +||·||·cos∠ADB,解得
cos∠ADB=.
三角形的角平分线性质定理将分对边所成的线段比转化为对应的两边之比,
再结合共线定理的推论,就可以转化为向量.一般地,涉及三角形中“定比”
类问题,运用向量知识解决起来都较为简捷.
触类旁通2 如图,在△ABC中,内角A,B,C的对边分别为a,b,c.已知b=3,c=6,
→
→
→
→
→
两边平方得 4 = + +2·,
2
2
2
三角形的高、中线与角平分线
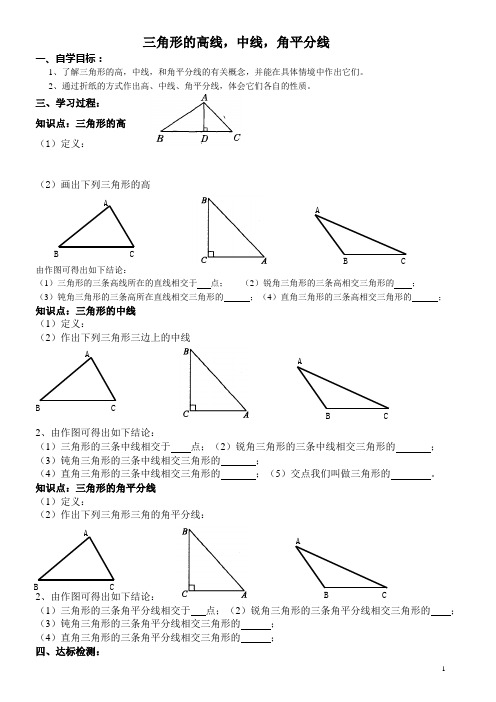
三角形的高线,中线,角平分线一、自学目标:1、了解三角形的高,中线,和角平分线的有关概念,并能在具体情境中作出它们。
2、通过折纸的方式作出高、中线、角平分线,体会它们各自的性质。
三、学习过程:知识点:三角形的高(1)定义:(2)画出下列三角形的高由作图可得出如下结论: (1)三角形的三条高线所在的直线相交于 点; (2)锐角三角形的三条高相交三角形的 ;(3)钝角三角形的三条高所在直线相交三角形的 ;(4)直角三角形的三条高相交三角形的 ;知识点:三角形的中线(1)定义:(2)作出下列三角形三边上的中线2、由作图可得出如下结论: (1)三角形的三条中线相交于点;(2)锐角三角形的三条中线相交三角形的 ;(3)钝角三角形的三条中线相交三角形的 ;(4)直角三角形的三条中线相交三角形的 ;(5)交点我们叫做三角形的 。
知识点:三角形的角平分线(1)定义:(2)作出下列三角形三角的角平分线:2、由作图可得出如下结论:(1)三角形的三条角平分线相交于 点;(2)锐角三角形的三条角平分线相交三角形的 ;(3)钝角三角形的三条角平分线相交三角形的 ;(4)直角三角形的三条角平分线相交三角形的 ;A CB A CB AC B A C B A C B A C B四、达标检测:1.三角形的三条高在( )A.三角形的内部B. 三角形的外部C.三角形的边上D.三角形的内部,外部或边上2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )A.锐角三角形B.直角三角形C.钝角三角形D.锐角三角形3.下列说法:①三角形的角平分线、中线、高线都是线段;•②直角三角形只有一条高线;③三角形的中线可能在三角形的外部;④三角形的高线都在三角形的内部,并且相交于一点,其中说法正确的有( ).A .1个B .2个C .3个D .4个4.下列说法正确的是( )①平分三角形内角的射线叫做三角形的角平分线;②三角形的中线,角平分线都是线段,而高是直线;③每个三角形都有三条中线,高和角平分线;④三角形的中线是经过顶点和对边中点的直线。
三角形的角平分线、中线和高课件冀教版七年级数学下册

E
B
D
C
五、当堂检测
3.如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=50°,
∠C=60°,求∠DAE和∠BOA的度数.
Aபைடு நூலகம்
解:∵∠CAB=50°,∠C=60°,
∴∠ABC=180°-50°-60°=70°, 又∵AD是高,∴∠ADC=90°,∠DAC=180°-90°-∠C=30°, F
∵AD是△ABC的中线
∴BD=CD
1
1
又∵S△ABD= 2 BD×AE , S△ACD= 2 CD×AE
∴S△ABD=S△ACD
E
三角形的中线将三角形分成 面积相等的两部分.
四、合作探究
探究二 运用三角形的角平分线和高计算角度
问题提出:如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平
分线,已知∠BAC=82°,∠C=40°,求∠DAE的大小.
∵AE是△ABC的角平分线,且∠BAC=82°, ∴∠CAE= ∠BAC=41°,
∴∠DAE=∠DAC-∠CAE=50°-41°= 9°.
四、合作探究
练一练
3.如图,在△ABC中,∠ABC=62°,BD是角平分线,CE是高,BD与CE交于点O,
求∠BOC的大小. A
解: ∵ CE是△ABC的高,
∴∠BEC=90°, ∵BD是△ABC的角平分线,且∠ABC=62°,
E
O
D
∴∠ABD=∠OBC= ∠ABC=31°,
B
C
∴∠BOC=∠BEC+∠ABD=121°.
五、当堂检测
1.在ΔABC中,CD是中线,已知BC-AC=5cm,ΔDBC的周长为25cm,则ΔADC的
三角形的中线、高线、角平分线
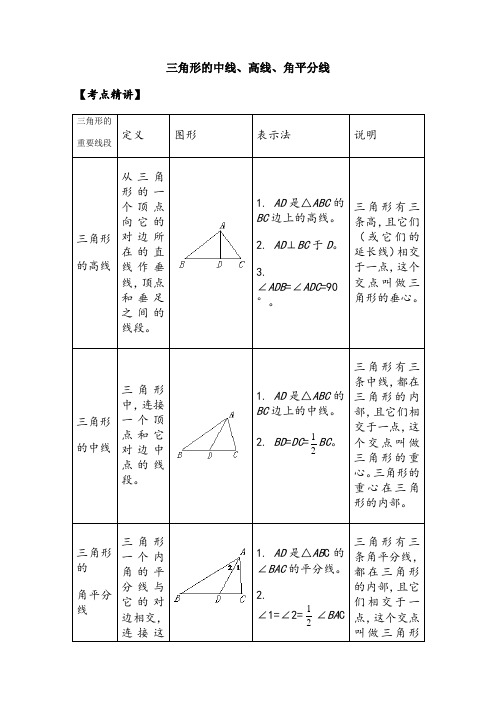
三角形的中线、高线、角平分线【考点精讲】三角形的重要线段定义图形表示法说明三角形的高线从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段。
1. AD是△ABC的BC边上的高线。
2. AD⊥BC于D。
3.∠ADB=∠ADC=90°。
三角形有三条高,且它们(或它们的延长线)相交于一点,这个交点叫做三角形的垂心。
三角形的中线三角形中,连接一个顶点和它对边中点的线段。
1. AD是△ABC的BC边上的中线。
2. BD=DC=12BC。
三角形有三条中线,都在三角形的内部,且它们相交于一点,这个交点叫做三角形的重心。
三角形的重心在三角形的内部。
三角形的角平分线三角形一个内角的平分线与它的对边相交,连接这1. AD是△AB C的∠BAC的平分线。
2.∠1=∠2=12∠BA C三角形有三条角平分线,都在三角形的内部,且它们相交于一点,这个交点叫做三角形个角的顶点与交点之间的线段。
的内心。
三角形的内心在三角形的内部。
【典例精析】例题1 如图,是甲、乙、丙、丁四位同学画的钝角△ABC 的高BE ,其中画对的是_______。
甲 乙 丙 丁思路导航:根据三角形的高是过一个顶点向对边引垂线,顶点与垂足之间的线段是该三角形的高,对各图形作出判断。
答案:丁点评:这是学生在画图时的一个易错点,通过本题理解画高时的两个注意点:一是过哪个点;二是垂直于哪条边。
这道题是过B 点,垂直于AC 边。
例题 2 等腰三角形一腰上的中线把这个三角形的周长分成12cm 和21cm 两部分,则这个等腰三角形的底边长是______。
思路导航:根据等腰三角形的性质和已知条件求出腰长和底边长,然后根据三边关系进行讨论,即可得出结论。
答案:设等腰三角形的腰长是x cm ,底边是y cm 。
根据题意,得:⎪⎪⎩⎪⎪⎨⎧=+=+212122x y x x 或⎪⎪⎩⎪⎪⎨⎧=+=+122212x y x x , 解得:⎩⎨⎧==178y x 或⎩⎨⎧==514y x根据三角形的三边关系,知:8,8,17不能组成三角形,应舍去。
三角形的高、中线与角平分线(ppt课件)

复习提问
1.什么叫线段的中点?
把一条线段分成两条相等的线段的点叫线段的中点
A
B
2.什么叫角平分线?
一条射线把一个角分成两个相等的角,这条射线叫做
这个角的平分线
B
O
A
复习提问 3.你还记得“过一点画已知直线的垂线”吗?
放、靠、过、画.
01
01
01
23
23
23
0
1 0 2 1 03 21 3 2
3
探究新知
B
C
探究新知
3.钝角三角形的三条高
(1)你能画出钝角三角形的三条高吗?
AF
(2)AC边上的高是__B_F__; BC边上的高是__A__D_;
DB
C
AB边上的高是__C_E__;
E
(3)钝角三角形的三条高交于一点吗?
钝角三角形的三条高不相交于一点.
O
(4)它们所在的直线交于一点吗?
钝角三角形的三条高所在直线交于一点.
三角形的中线
B
D
C
定义:连接三角形的一个顶点和它所对的边的中 点,所得线段叫做三角形的这条边上的中线.
三角形中线的符号语言:
∵AD是△ABC的中线
∴BD=CD =12 BC
探究新知
思考2.如图,在△ABC中,还能画出几条中 线呢?你发现了什么特征?
还能画出2条,3条中线交于一点.
B
重心:三角形的三条中线相交于一点,三 角形三条中线的交点叫做三角形的重心.
重心
A
O C
D
探究新知
1.如图,有一块三角形的菜地,现要求分成面积比为1:1:2
三块,且图中A处是三块菜地的共同水源处,应该怎么分?
三角形及其角平分线、中线和高线

三角形及其角平分线、中线和高线知识导引1、三角形的有关概念:定义:由不在通一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
外角:三角形一条边的延长线和另一条相邻的边组成的角。
三角形的中线:连结三角形的一个顶点与该顶点的对边中点的线段,叫做三角形的中线。
三角形的高线:从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高线。
三角形的角平分线:在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。
注意:三角形的中线、高线、角平分线都是线段。
2、三角形的边角关系:边与边的关系:三角形的任意一边大于另外两边之差,并小于另外两边之和。
角与角的关系:三角形的内角和等于180°,外角和等于360°;三角形的一个外角等于和它不相邻的两个内角的和,且大于任何一个和它不相邻的内角。
边与角的关系:在一个三角形中,等角对等边,等边对等角,大角对大边,大边对大角。
3三角形的分类:按角分:三角形可分为锐角三角形、直角三角形、钝角三角形。
按边分:三角形可分为不等边三角形、等腰三角形。
典例精析例1:现有2cm,4cm,5cm,8cm长的四根木棒,任意选取三根组成一个三角形,那么可以组成三角形的个数为()A、1个B、2个C、3个D、4个例2:如图,AD是△ABC的角平分线,AE是BC边上的高线,∠B=20°,∠C=40°,求∠DAE 的度数。
例3:如图所示,平面上的六个点A、B、C、D、E、F构成一个封闭的折线图形。
求∠A+∠B +∠C+∠D+∠E+∠F的值。
例3—1:求如图1所示图形中∠A+∠B+∠C+∠D+∠E 的大小。
例3—2:如图所示,(∠1+∠2-∠3)+(∠4+∠5-∠6)+(∠7+∠8-∠9)=例4:如图所示,在△ABC 中,∠ABC 的平分线与∠ACB 的外角平分线交于点D ,且∠D=30°,求∠A 的度数。
解三角形之中线、角平分线、高线问题+课件-高2025届高三数学一轮复习
( +
- )
.
(1)求∠ACB;
(2)若∠A= ,∠ACB 的平分线 CE 与边 AB 相交于点 E,延长 CE 至点 D,使得 CE=DE,求 cos∠ADB.
解:(2)不妨令 AC=3,因为∠ACB= ,可得 AB=3
1
1
1
:
:
sin A sin B sin C
2、求高一般采用等面积法,即求某边上的高,需要求出面积和底边长度
高线两个作用:(1)产生直角三角形;(2)与三角形的面积相关。
例题讲解
三角形的中线问题
【例 1】在 ABC 中, AD 是 BC 边的中线,
, BAC 120 且 AB AC
知识梳理
知识梳理
3、等面积法:
因为
所以
+
∆
+
=
∆
=2
1
1
,所以2 ∙
∆
2
整理的:
2
=
+2 ∙
2
2
+
2
(角平分线长公式)
【作用】
: ①利用角度关系建立各三角形之间的面积关系
②通过面积关系式求解角分线长度
1
=2
,
知识梳理
三、垂线
1 1 1
a b c
1、 h1,h2,h3 分别为 ABC 边 a,b,c 上的高,则 h1 : h2 : h3 : :
+ -
=
= ,
C,
例题讲解
三角形的高线问题
【例3】在△ABC中,内角A,B,C的对边分别为a,b,c,且(sin B-sin C)2=sin2A-sin Bsin C.
三角形的高、中线与角平分线课件
边BC于点D,所得线段AD叫做 ABC
的角平分线.
B
D
C
你能画出三角形另外的两条角平分线吗?
思考: (1)三角形的角平分线是什么线?与角平分线有什么区别? (2)一个三角形有几条角平分线?在位置上有什么关系?
探究二: 三角形的中线与角平分线 活动4 集思广益,探究新知
A
F E
B
D
C
任何三角形都有三条角平分线; 任何三角形的三条角平分线都在三角形内部交于一点, 我们把这个点称为三角形的内心(内切圆的圆心). 三角形的角平分线是一条线段,而角平分线是一条射线.
这个方法合理吗?
探究二: 三角形的中线与角平分线
活动2 反思过程,发现新概念
在三角形中,连接一个顶点和它的对边中点的线段叫做
三角形的中线.
A
思考:
D
(1)三角形的中线是什么线? 线段
B
C
(2)一个三角形有几条中线? 三条中线
(3)三角形的中线所分成的两个三角形面积有什么关系?
三角形的中线所分成的两个三角形的面积相等,因为等 底等高的三角形面积相等.
12 E F
3
B
D
4C
(2)
两个小角相等.
探究三: 利用三角形的高、中线及角平分线的概念解决问题
活动1
练习:如图,在 ABC中,AE是中线,AD是角平分线,
AF是高.则BE=C__E__=1 _B_C__;∠BAD=_∠_C__A__D__=1__∠_B__A_C__;
2
2
∠AFB=_∠__A_F__C__=90°.
练习:如图,点D、E、F分别是BC、AD、BE的中点,且
S△ABF=1,求 S△ABC .
13.1.3三角形的角平分线、中线和高线
任意画一个三角形,你能画出它的 一个角的平分线吗?
A
B
D
C
A
三角形的角平分线
B
D C
三角形中,一个角的平分线与这个角 的对边相交,顶点与交点之间的线段 叫做三角形的角平分线。
∵AD是 △ ABC的角平分线
1 ∴∠ BAD = ∠ CAD = — ∠BAC 反之也成立 2
任意画出一个三角形,并画出它所有的角平分线,你 有什么发现?并与同学交流。
④三角形的三条高线的交点,叫做三角形的垂心。
本
三角形的 重要线段 概念
课 小 结
图形 表示法
三角形 的高线
从三角形的一个 顶点向它的对边 所在的直线作垂 线,顶点和垂足之 间的线段 三角形中,连结一 个顶点和它对边 中的 线段 三角形一个内角 的平分线与它的 对边相交,这个角 顶点与交点之间 的线段
5、如图,AD是△ABC的角平分线, DE∥AC, DE交AB于E, DF∥AB ,DF交AC 于F,图中∠ADE与∠ADF有什么关系?为 什么?
A
E
B D
F C
张大爷有一块三角形的菜园, 想把它分成形状也是三角形的两块 给他的两个儿子,应该怎样分才公 平呢?
A
B
C
本节课 你学到了什 么?
任意画出一个三角形,并画出它所有的 中线,你有什么发现?并与同学交流。
O O O
●
●
●
三角形中线的性质: 一个三角形有三条中线,它们都在三角形的内 部,并且相交于一点.
交点O叫做三角形的重心
如图在△ABC中,AD是BC 边上的中线
猜想:△ABD的面积和△ADC的面积有什么 关系?试说明。 A
B D
E
《三角形的高、中线与角平分线》PPT教学课文课件
所以∠BAD
=∠CAD
=
1 2
∠BAC.
新知讲解
任意剪一个三角形,用折叠的方法,画出这个三角形的三条角平分线,你发现 了什么?
三角形的三条角平分线交于同一点.
课堂练习
1. 如图,在△ABC中,若∠BAD=∠DAE=∠EAF=∠FAC,则_____是△ABC的角
平分线( B )
A. AD
B. AE
课堂练习
7. 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°. 求: (1)∠BAE的度数;
解:(1)∵∠B+∠C+∠BAC=180°, ∴∠BAC=180°-∠B-∠C=180°-70°-30°=80°. ∵AE平分∠BAC, ∴∠BAE= ∠BAC=40°.
课堂练习
并观察它们中线的交点有什么规律?
A
A
F OE
F
O
E
A F OE
B
CB
D
CB
D
C
如图,三角形的三条中线相交于一点.三角形三条中线的交 点叫做三角形的重心.
针对训练
如图,AD,BE,CF 是△ABC 的三条中线. (1)AC = 2 ; AE = 2 EC;
CD = BD ;AG= 2 GD. (2)若S△ABC = 12 cm2,
C. AF
D. AC
2. 如图,在△ABC中,BC边上的高为( D )
A. BF
B. CF
C. BD
D. AE
课堂练习
3. 下列说法错误的是( C ) A.锐角三角形的三条高、三条中线、三条角平分线分别交于一点 B.钝角三角形有两条高线三角形外部 C.直角三角形只有一条高 D.任意三角形都有三条高、三条中线、三条角平分线
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1)如图,在Δ ABC 中,AE⊥BC 于点 E,BD 是∠ABC 的平分线,与 AE 交于点 0,已知∠ABC=40°,∠C=60°,则∠A0B 的度数.
0
2)如图所示,在Δ ABC 中,∠B 和∠C 的平分线相交于点 F,过点 F 作
E
DE‖BC,交 AB 于点 D,交 AC 于点 E,若 BD+CE=9,则线段 DE 的长为 ( )
教具媒体组合应用
导学案
教学过程(内容及步骤)
教法与学法
一、三角形的角平分线
A
1、知识点金(口述定义并画图)
特性:( )=( 三条角平分线交于( )=( ) )
巩固基础 运用角平
2、运用于求角的度数
B A
D B E C D
C
分线性质 做题
1)如图 AB∥传递,AD 与 BC 交于点 E EF 是∠BED 的角平分线,若∠1=30 度 ∠2=40 度,则∠BEF=( ).
教学过程(内容及步骤)
教法与学法 提升能力, 激 发学习热情
A D F E
B
C
以提问方式 总结学习心 得, 进行归纳 小结
教
学 后
记
三角形的角平分线、中线和高———复习课 题组+分组 一知识点金 对比总结 总结角平分线、中线和高的特性及口述定义并画图 二求角的度数 三求周长和面积 四综合小测
特性:(
)=(
)=(
)
理解。
( )=( ) (关于面积) ( )(关于周长) 三条中线交于一点 2 运用于周长和面积 1)如图,已知 BD 是 ABC 的中线,AB=5cm,AC=3cm.则Δ ABD 与Δ BCD 的周 长差( ),若Δ ABC 的面积为 10cm,则 SΔ ABD=( )。
E
2)如图,在Δ ABC 中,D、E 分别是 AC、BD 的中点,SΔ ABE=(
激发学生
F
运用知识 的愿望和 学习兴 趣。
2)已知:如图,在 ABC 中,BE、CF 分别平分 ABC 、ACB ,且交于点 O, ∠A=50 度,则∠BOC=( ). A F O E C
B
3)如图,已知:在 ABC 中,外角 CBD 和 BCE 的平分线 BF,CF 相交于 点 F 则∠BFC 的度数( ) D B F
F E
三、三角形的高线 1、知识点金
A
B
特性:( )=( )=90° ( )+( 锐角三角形的三条高交于( 直角三角形的三条高交于(
C
)=90° ) )、钝角三角形的三条高交于( )
2、常与角平分线或高线综合运用,求角的的度数或求三角形的面积
1)如图在Δ ABC 中,∠A=50 度,高 BE、CF 所在的直线交于点 0, 求∠BOC 的度数
2)有一块三角形空地, 要在这块空地种植某种草皮以美化环境。 已知这种草皮 每平方米的售价为 a 元,根据图上所标尺寸,购买这种草皮至少需要( )
15cm 20cm 3)在 Rt Δ ABC 中 , ∠ ACB=90
度 , CD 是 边 AB 上 的 高 ,
AB=13cm,BC=12cm,AC=5cm.1)求Δ ABC 的面积
东新庄镇中学
课 题
李红艳
三角形的角平分线、中线和高
教学设计 回顾三角形的角平分线中线和高 教 学 目 标 知识与能力 运用三条线段的特性,解决有关角度周 长和面积问题 通过对问题的探索,适当渗透变量知识, 让学生发现三条线段的区别和几何规 律。 过程与方法 通过经历实际问题中数量关系的分析抽 象过程,体会现实世界各种各样的数量 关系。 认识到角平分线Байду номын сангаас中线和高在现实生活 情感、态度、价值观 中的作用,通过讨论、交流的过程体验 数学活动充满着探索性和创造性。 教法选择 教 学 策 略 课堂组织形式 学生探索、共同讨论、交流,老师点拨 学法选择 以小组学习探究的形式 互动教学
)。
3)如图,某村有一块三角形的空地(Δ ABC),其中点 A 处靠近水源,现村长准 备将它分给甲乙两户耕种,分配方案规定,按每户人口数量来平均分配,且甲
联系实际, 运 用数学知识
A
乙两户所分的土地都要靠近水源(点 A),已知甲农户有 1 人,乙农户有 3 人, 解决问题 请你把它分出来。
B
C
4)如图,在Δ ABC 中,E 是 BC 上的一点,EC=2BE,D 是 AC 的中点,设Δ ABC、 Δ ABF、Δ BEF 的面积分别为 SΔ ABC、SΔ ADF、SΔ BEF,且 SΔ ABC=12 则 SΔ ADF—SΔ BEF=( )。
通 过 归 纳,巩固 概念,加 深理解。
A
C
E
教学过程(内容及步骤) 4)已知△ABC 中,BE 平分∠ABC,CE 平分∠ACD,BE、CE 相交于点 E,
教法与学法
若∠E=40 度,则∠A 的度数(
)
二、三角形的中线 1、知识点金(口述定义,并画图)
运用三角形 中线的概念 进行判别, 加 深对概念的
