第一章_波动方程
第一章 三类典型方程和定解条件
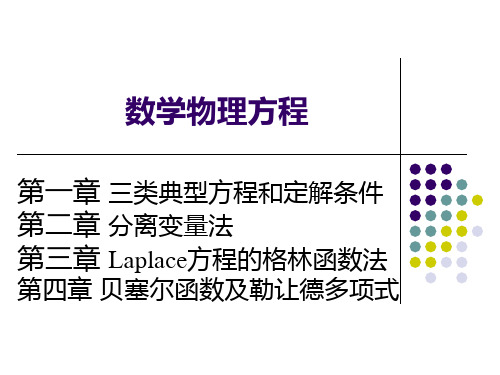
a 其中,ij (x), bi (x), c x , f (x)都只是 x1 , x2, , xm 的已知 函数,与未知函数无关。
若一个函数具有某偏微分方程中所需 要的各阶连续偏导数,并且代入该方程中 能使它变成恒等式,则此函数称为该方程 的解(古典解)。 初始条件和边界条件都称为定解条件。 把某个偏微分方程和相应的定解条件 结合在一起,就构成了一个定解问题。 只有初始条件,没有边界条件的定解问题 称为始值问题(或柯西问题)。反之,只 有边界条件,没有初始条件的定解问题称 为边值问题。既有初始条件又有边界条件 的定解问题,称为混合问题。
数学物理方程
第一章 三类典型方程和定解条件 第二章 分离变量法 第三章 Laplace方程的格林函数法
第四章 贝塞尔函数及勒让德多项式
第一章 三类典型方程和定解条件
数学物理方程的研究对象——定解问题。 一个定解问题是由偏微分方程和相应的定解 条件组成。我们先来介绍三类典型的方程:
三类典型方程
一、波动方程 二、热传导方程
用以说明初始状态的条件称为初始条件。 用以说明边界上的约束情况的条件称为边 界条件。
一、初始条件
比如说波动方程(1.3)其初始条件有两 个,一个是参数u,一个是u的一阶导数。 即: u u t 0 及 都已知。 t
t 0
而热传导方程(1.7)其初始条件只有一 个,就是参数u。即:
Байду номын сангаасu t 0 是已知。
一个定解问题提的是否符合实际情况,从 数学角度来看,有三方面可以加以检验:
1、解的存在性,看定解问题是否有解。
2、解的唯一性,看是否只有一个解。
3、解的稳定性,看当定解条件有微小
变动时,解是否相应地只有微小的变 动,若确实如此,则称此解是稳定的。
波动方程_精品文档
l
=
=
12
50
600
s
=
1
(
)
υ
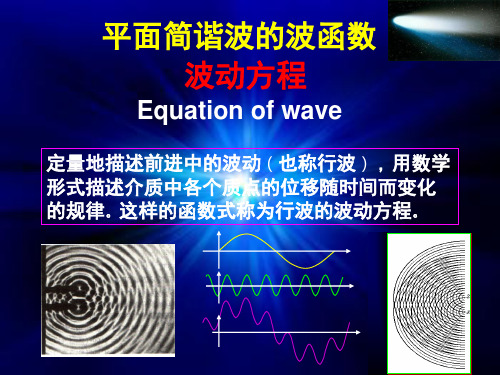
例题:有一列向x 轴正方向传播的平面简谐波,
它在t = 0 时刻的波形如图所示其波速为:
u = 600m/s 。试写出波动方程。
=
5m
A
24m
l
=
从波形图中可知:
ω
=
π
2
=
π
50
(
)
rad.
s
1
υ
原点处质点的振动方程为:
波动方程为:
y
0
2
π
由旋转矢量法:
u
l
=
=
=
t
+
cos
(
)
y
A
ω
0
1.时间推迟方法
x
x
u
y
o
P
·
A
已知振源(波源)的振动方程为:
振源的振动状态从0点以传播速度u传送到P 点,显然时间要落后:
´
u
x
=
t
u
x
j
=
t
+
cos
(
)
A
ω
-
j
=
t
+
cos
(
)
y
A
ω
0
´
t
j
=
t
+
cos
(
)
y
A
ω
-
P
介质中任一质点(坐标为 x)相对其平衡位
置的位移(坐标为 y)随时间t 的变化关系。
=
0
数学物理方程答案谷超豪

数学物理方程答案谷超豪数学物理方程答案谷超豪【篇一:数学物理方程第二版答案(平时课后习题作业)】>第一章.波动方程1 方程的导出。
定解条件4. 绝对柔软逐条而均匀的弦线有一端固定,在它本身重力作用下,此线处于铅垂平衡位置,试导出此线的微小横振动方程。
解:如图2,设弦长为l,弦的线密度为?,则x点处的张力t(x)为t(x)??g(l?x)且t(x)的方向总是沿着弦在x点处的切线方向。
仍以u(x,t)表示弦上各点在时刻t沿垂直于x轴方向的位移,取弦段(x,x??x),则弦段两端张力在u轴方向的投影分别为g(l?x)sin?(x);?g(l?(x??x))sin?(x??x)其中?(x)表示t(x)方向与x轴的夹角又sin??tg??于是得运动方程u ?x.u?2u?ux2?[l?(x??x)]∣x??x?g?[l?x]∣?gxx?x?t利用微分中值定理,消去?x,再令?x?0得2u??ug[(l?x)]。
x?x?t25. 验证u(x,y,t)?1t2?x2?y2在锥t?x?y0中都满足波动方程2222u?2u?2u1222证:函数在锥0内对变量t?x?y??u(x,y,t)?222222?t?x?y?x?y x,y,t有二阶连续偏导数。
且232u(t2?x2?y2)?tt35u(t2?x2?y2)2?3(t2?x2?y2)2?t22t(t2x2?y2)32(2t2?x2?y2)u(t2?x2?y2)?x32x2u?x2t?x22352?2222?22?y?3t?x?yx52??u同理 ??t2?x2?y2?2?t2?x2?2y2?2y所以即得所证。
2 达朗贝尔公式、波的传抪3.利用传播波法,求解波动方程的特征问题(又称古尔沙问题) 2 2u2?u?2?a2t?x?ux?at?0??(x) ??(0)??(0)? ?u??(x).?x?at?0?5?t2?x2?y22t2?2x2?y22u?x22u?y2t?x?225?y222t2x?y22t2.2u解:u(x,t)=f(x-at)+g(x+at) 令 x-at=0 得 ?(x)=f(0)+g(2x)令x+at=0 得 ?(x)=f(2x)+g(0) 所以 f(x)=?()-g(0). g(x)=?()-f(0). 且 f(0)+g(0)=?(0)??(0). 所以 u(x,t)=?(x2x2x?atx?at)+?()-?(0). 22即为古尔沙问题的解。
数学物理方程习题讲义

t
=
0
:
v
=
(h
−
x)ϕ(x),
∂v ∂t
=
(h
−
x)ψ(x)
因此
v(x, t)
=
1 2
((h
−
x
+
at)ϕ(x − at) + (h
−
x
−
at)ϕ(x + at))
+
1 2a
x+at
(h − ξ)ψ(ξ)dξ,
x−at
从而
u(x, t)
=
1 2(h − x)
((h
−
x
+
at)ϕ(x
−
at)
+
(h
−
(x
+
∆x,
t)
−
E
(x)
S
(x)
∂u ∂x
(x,
t)
=
∂ ∂x
E
(x∗)
S
(x∗)
∂u ∂x
(x∗,
t)
∆x
-1-
1.2 习题选讲
其中x∗ ∈ (x, x + ∆x).约去∆x并令∆x → 0,即得
∂ ∂t
ρ
(x)
S
(x)
∂u ∂t
=
∂ ∂x
E
(x)
S
(x)
∂u ∂x
当S(x)为常数时,即为
∂ ∂t
第四章 二阶线性偏微分方程的分类与总结. . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
4.1 学习要求 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38 4.2 习题选讲 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
第一章----波动方程

总之:
无外力作用的一维弦振动方程:
2u t 2
a2
2u x2
0
外力作用下的弦振动方程:
(1.4)
2u t 2
a2
2u x2
f (x,t)
(1.5)
其中 a2 T , f F , f 称为非齐次项(自由项)。
注:弦振动方程也叫波动方程,因为它描述的是一种 振动或波动现象,后面将给出解释。
1973年布莱克(Black)和休尔斯(Scholes)建立了倒向 微分方程决定欧式期权的无套利价格:
f t
rS
f S
1 2S2
2
2 f S 2
rf
这里,对买入期权有 f (S,t) |tT max{ST X ,0} ;对卖出期权有
f (S,t) |tT max{X ST ,0} 。其中 r 为无风险利率, S 为股票价格,
一般步骤(从宇宙探星谈起): 1、将物理问题归结为数学上的定解问题; 2、求解定解问题; 3、对求得的解给出物理解释。
四、偏微分方程的研究内容-适定性的概念
1、存在性 2、唯一性 3、稳定性
如果一个定解问题的解是存在的、 唯一的,而且是稳定的,则称该定 解问题是适定的。
五、微分方程的重要作用
可以说有了微积分,就有了微分方程 (微积分是17世纪为了解决物理、力学、 天体问题而产生的,而这些问题多为数学 物理方程)。
1 (tan )2 dx 1 2 dx dx
(2)弦上各点的张力是常数
由于弦做横振动,弦沿 x 轴无运动,所以合力为零
T1 cos1 T2 cos2 T1 T2 T
数学物理方程答案谷超豪

数学物理方程答案谷超豪【篇一:数学物理方程第二版答案(平时课后习题作业)】>第一章.波动方程1 方程的导出。
定解条件4. 绝对柔软逐条而均匀的弦线有一端固定,在它本身重力作用下,此线处于铅垂平衡位置,试导出此线的微小横振动方程。
解:如图2,设弦长为l,弦的线密度为?,则x点处的张力t(x)为t(x)??g(l?x)且t(x)的方向总是沿着弦在x点处的切线方向。
仍以u(x,t)表示弦上各点在时刻t沿垂直于x轴方向的位移,取弦段(x,x??x),则弦段两端张力在u轴方向的投影分别为?g(l?x)sin?(x);?g(l?(x??x))sin?(x??x)其中?(x)表示t(x)方向与x轴的夹角又sin??tg??于是得运动方程?u ?x.?u?2u?u??x2?[l?(x??x)]∣x??x?g?[l?x]∣?g?xx?x?t利用微分中值定理,消去?x,再令?x?0得?2u??u?g[(l?x)]。
?x?x?t25. 验证u(x,y,t)?1t2?x2?y2在锥t?x?y0中都满足波动方程222?2u?2u?2u1222证:函数在锥0内对变量t?x?y??u(x,y,t)?222222?t?x?y?x?yx,y,t有二阶连续偏导数。
且232?u??(t2?x2?y2)?t??t35??u(t2?x2?y2)2?3(t2?x2?y2)2?t22?t?(t2?x2?y2)?32?(2t2?x2?y2)?u?(t2?x2?y2)?x?32?x?2u?x2?t?x?22352?2222?22?y?3t?x?yx??????52??u同理 ??t2?x2?y2?2?t2?x2?2y2?2?y所以即得所证。
2 达朗贝尔公式、波的传抪3.利用传播波法,求解波动方程的特征问题(又称古尔沙问题) 2??2u2?u?2?a2t?x??ux?at?0??(x) ??(0)??(0)? ?u??(x).?x?at?0?5??t2?x2?y22t2?2x2?y2??2u?x2?2u?y2?t?x??225?y22??2t2?x?y22???t2.?2u解:u(x,t)=f(x-at)+g(x+at) 令 x-at=0 得 ?(x)=f(0)+g(2x)令x+at=0 得 ?(x)=f(2x)+g(0) 所以 f(x)=?()-g(0). g(x)=?()-f(0). 且 f(0)+g(0)=?(0)??(0). 所以 u(x,t)=?(x2x2x?atx?at)+?()-?(0). 22即为古尔沙问题的解。
微分方程波动方程

2u u ∣ x 2 [l ( x x)] x t
∣ x g
运动方程为:
x sx x
2u
u u ES xx ES x b x s x t t 2
利用微分中值定理,消去 x ,再令 x 0 得
o
x
所
以
证明: (1) 如果初始条件在 x 轴的区间[x 1 ,x 2 ]上发生变化,那末 对应的解在区间[ x1 ,
令 x-at=0 得 ( x) =F(0)+G(2x)
(1)
以
令 x+at=0 得 ( x) =F(2x)+G(0) 所以 F(x)= ( ) -G(0). G(x)= ( ) -F(0). 且 所以 F(0)+G(0)= (0) (0). u(x,t)= (
所
x 2
利用微分中值定理,消去 x ,再令 x 0 得
2u u g [(l x) ] 。 2 x x t
5. 验证
x sx 2ຫໍສະໝຸດ u ( x, y , t )
1 t x y
2 2
2u u u ES b x s x 2 t x x t
其中 h 为圆锥的高(如图 1) 证:如图,不妨设枢轴底面的半径为 1,则 x 点处截面的半径 l 为:
E ( x)S ( x)u x ( x, t ); E ( x x)S ( x x)u x ( x x, t ).
于 是 得 运 动 方 程
l 1 x h
x h
2
( x)s( x) x utt ( x, t ) ESu x ( x x) | x x ESu x ( x) | x
第一章_波动方程

假定有垂直于x轴方向的外力存在,并设其线密度为F(x,t),则 弦段(x, x+Δx)上的外力为:
x x
x
F ( x ,t) dx
它在时间段(t, t+Δt)内的冲量为:
t x
t t x x
F ( x , t ) dx dt
数学物理方程
第一章 波动方程
于是有:
2 2 u ( x , t ) u ( x , t ) [ 2 T F ( x , t )] dx dt 0 2 t x t x t t x x
数学物理方程
第一章 波动方程
回 答 下 列 方 程 是 线 性、 的非 线 性 的 ? 齐 次 非次 齐? 阶 数 ?
(1)
4u
4
x x y y u u ( 2)u xy 0 x x
2u
2
2
4u
2 2
4u
4
0
四阶线性齐次 一阶非线性,拟线性的 二阶线性齐次的 二阶线性非齐次的 三阶非线性
要在区域 ( 0 x l ,t 0 )上(见右上图)求上述定解问题的解,就是
要求这样的连续函数u(x, t) ,它在区域0<x<l,t>0中满足波动方程(2.1);在x 轴上的区间[0,l]上满足初始条件(2.2);并在边界x=0和x=l上满足边界条件 (2.3)和 (2.4)。 一般称形如(2.3)和(2.4)的边界条件为第一类边界条件,也叫狄利克雷 (Dirichlet)边界条件。
非均匀弦的强迫横振动方程
一维波动方程不仅可以描述弦的振动,还可以描述: 弹性杆的纵向振动 管道中气体小扰动的传播 ………等等 因此,一个方程反应的不止是一个物理现象, 而是一类问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学物理方程
第一章 波动方程
u 2 ( x, t ) 2 u ( x, t ) T x 2 g dx t 2 dx
T u 2 ( x, t ) 2u ( x, t ) g 2 x t 2
t t
另一方面,在时间段(t, t+Δt)内弦段(x, x+Δx)的动量变化为:
x x x
u ( x , t t ) u ( x , t ) [ ] dx t t
于是由冲量定理:
t t
x u ( x x , t ) u ( x , t )x u ( x , t t ) u ( x , t ) T [ ] dt [ ] d t x x x t t
u ( x x, t ) u ( x, t ) T ( sin 2 sin1 ) T (tg 2 tg1 ) T [ ] x x
假设2和假设3
数学物理方程 在时间段(t, t+Δt)内该合力产生的冲量为:
第一章 波动方程
u ( x x , t ) u ( x , t ) T [ ] dt t x x
非均匀弦的强迫横振动方程
一维波动方程不仅可以描述弦的振动,还可以描述: 弹性杆的纵向振动 管道中气体小扰动的传播 ………等等 因此,一个方程反应的不止是一个物理现象, 而是一类问题。
数学物理方程
第一章 波动方程
§1.2 定解条件
列出微分方程的目的是要从微分方程中求得具体问题的解或者研究 解的性质。前面我们看到,弦振动方程描述的是弦作微小横振动时的位 移函数u(x, t)所应满足的一般性规律。仅仅利用它并不能完全确定一条弦 的具体运动状况。这是因为弦的运动还与其初始状态以及边界所处的状 况有关系,因此对于具体的弦振动问题而言,还需要结合实际问题附加 某些特定条件。 例如: 在前面的推导中,弦的两端被固定在x=0和x=l两点,即 u(0, t)=0 , u(l, t)=0,
数学物理方程
第一章 波动方程
§1.1 弦振动方程的导出
基本假设: 1. 弦的质量是均匀的,弦的截面直径与长度相比可以忽略。 弦可以视为一条曲线,线密度为常数。 2. 弦在某一个平面内作微小横振动。 弦的位置始终在一直线段附近,弦上各点在同一平面内垂 直于该直线的方向上作微小振动。 (微幅) 3. 弦是柔软的,它在形变时不抵抗弯曲。 弦上各质点的张力方向与弦的切线方向一致,而弦的伸长 变形与张力的关系服从虎克定律。 (横振动) 基本规律: 牛顿第二定律(冲量定律) (细弦)
y
M'
T'
u ( x, t ) sin tan x u ( x dx, t ) sin ' tan ' x
ds
'
T
M
gds
x x dx x
数学物理方程
第一章 波动方程
T T '
其中: m
ds
u ( x dx, t ) u( x, t ) T gds ma x x
要在区域 ( 0 x l ,t 0 )上(见右上图)求上述定解问题的解,就是
要求这样的连续函数u(x, t) ,它在区域0<x<l,t>0中满足波动方程(2.1);在x 轴上的区间[0,l]上满足初始条件(2.2);并在边界x=0和x=l上满足边界条件 (2.3)和 (2.4)。 一般称形如(2.3)和(2.4)的边界条件为第一类边界条件,也叫狄利克雷 (Dirichlet)边界条件。
u |x0 0,
或: u (a, t ) 0
狄利克雷(Dirichlet) 边界条件
(2)自由端:x=a 端既不固定,又不受位移方向力的作用。
u T x
0
xa
u x
0
xa
ux (a, t ) 0
诺依曼(Neumann) 边界条件
(3) 弹性支承端:在x=a端受到弹性系数为k 的弹簧的支承。
数学物理方程
第一章 波动方程
§1.2 定解条件
1、初始条件——描述系统的初始状态
波动方程的初始条件
u |t 0 ( x) u ( x) t t 0
系统各点的初位移 系统各点的初速度
数学物理方程
第一章 波动方程
2、边界条件——描述系统在边界上的状况
波动方程的三类边界条件 (1)固定端:对于两端固定的弦的横振动,其为:
u ( 3) 2 x 0 y x 2u 2u 2u ( 4) 2 2 2 sin x xy
3u x y
数学物理方程
第一章 波动方程
简化假设:
(1)弦是柔软的,弦上的任意一点的张力沿弦的切线方向。
(2)振幅极小, 张力与水平方向的夹角很小。 牛顿运动定律: 横向: T cos T 'cos ' 纵向: T sin T 'sin ' gds ma 其中:cos 1 cos ' 1
数学物理方程
第一章 波动方程
§1.3 定解问题适定性概念
定解问题的存在性、唯一性和稳定性统称为定解问题的适 定性。如果一个定解问题的解是存在的,唯一的,而且是稳定 的,我们就称这个问题是适定的,即认为这样的定解问题的提 法是合适的。对定解问题的适定性进行一定的分析,可以帮助 我们初步判定所归结的定解问题是否合理、所附加的定解条件 是否合适以及对一个偏微分方程应该如何指定定解条件等问题 ,同时也可以对求解定解问题起到一定的指导作用。 除了研究定解问题的适定性外,数理方程中还经常研究的 问题包括:解的正则性(光滑性)、解的渐近性(包括衰减性 )和定解问题的求解方法(精确解、渐近解、数值解)等。
令: a
2
T
2 2u u 2 a g ………一维波动方程 2 2 t x
自由项 忽略重力作用:
------非齐次方程
u 2 u a 2 t x 2
2
2
------齐次方程
数学物理方程
第一章 波动方程
§1.1 弦振动方程的导出
如果弦非均匀,则 和T为x的函数,
(T ( x )u x ) F ( x )utt ( x, t ) x
这两个等式称为边界条件。此外,设弦在初始时刻t=0时的位置和速度为
u ( x , 0 ) u ( x , 0 ) ( x ), ( x )( 0 x l ) t 这两个等式称为初始条件。边界条件和初始条件总称为定解条件。把微分 方程和定解条件结合起来,就得到了与实际问题相对应的定解问题。
数学物理方程
第一章 波动方程
y
M'
研究对象: u ( x, t ) 弦线上任意一点在 t 时刻沿y轴上的位移
T'
ds
'
在右图所示的坐标系,用u(x, t)表示弦 上各点在时刻t沿垂直于x方向的位移。在 这条弦上任意取一弦段(x, x+Δx),它的 弧长为 :
T
M
gds
x
x dx x
由假设3,弦线张力T(x)总是沿着弦在x处的切线方向.由于弦只在垂直x 轴的方向进行横振动,因此可以把弦线的张力T(x)在x轴的方向的分量看成 常数T。对于图中选取的弦段而言,张力在x轴的垂直方向上的合力为:
数学物理方程
第一章 波动方程
§1 方程的导出、定解条件
§1.1 弦振动方程的导出 §1.2 定解条件 §1.3 定解问题适定性概念
数学物理方程
第一章 波动方程
物理背景: 波的传播和弹性体振动。 §1.1 弦振动方程的导出 首先,考察弦横振动这个物理问题:
给定一根两端固定的拉紧的均匀柔软的弦线,设其 长度为l ,它在外力作用下在平衡位置附近作微小的横 振动,求弦上各点的运动规律。 把实际问题提炼为数学模型时必须做一定的理想化 假设,以便抓住问题的最本质特征。
2 2 u ( x , t ) u ( x , t ) 2 2 a f ( x , t ), a T / , f ( x , t ) F ( x , t ) / 2 2 t x
类似地,三维波动方程可以表示为:
2 2 2 2 u u u u 2 a ( ) f ( x , y , z , t ) 2 2 2 2 t x y z
u T x
x a
k u x a
或
u u 0 x xa
数学物理方程
第一章 波动方程
§1.2 定解条件
同一类物理现象中,各个具体问题又各有其特殊性。边
界条件和初始条件反映了具体问题的特殊环境和历史,即
个性。 初始条件:够用来说明某一具体物理现象初始状态的条件。 边界条件:能够用来说明某一具体物理现象边界上的约束 情况的条件。 其他条件:能够用来说明某一具体物理现象情况的条件。
数学物理方程
第一章 波动方程
回 答 下 列 方 程 是 线 性、 的非 线 性 的 ? 齐 次 非次 齐? 阶 数 ?
(1)
4u
4
x x y y u u ( 2)u xy 0 x x
2u
2
2
4u
2 2
4u
4
0
四阶线性齐次 一阶非线性,拟线性的 二阶线性齐次的 二阶线性非齐次的 三阶非线性
数学物理方程
第一章 波动方程
§1.3 定解问题适定性概念 定解问题
把某种物理现象满足的偏微分方程和其相应的定解 条件结合在一起,就构成了一个定解问题。 (1) 初始问题:只有初始条件,没有边界条件的定解问题;
