应用时间序列分析习题答案
人大版应用时间序列分析(第5版)习题答案
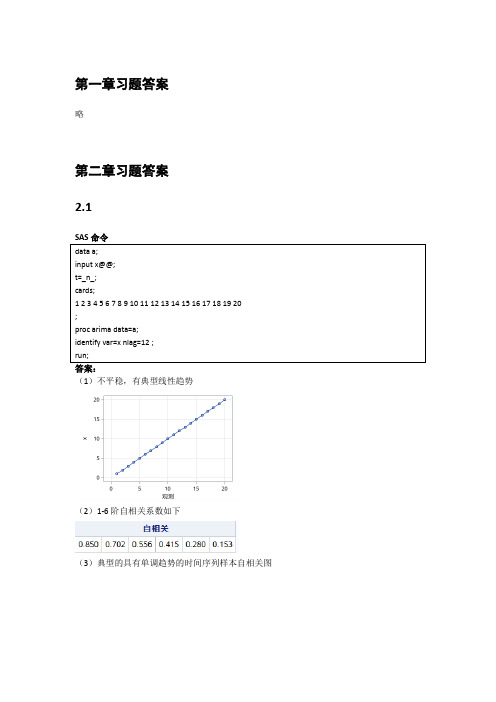
第一章习题答案略第二章习题答案2.1答案:(1)不平稳,有典型线性趋势(2)1-6阶自相关系数如下(3)典型的具有单调趋势的时间序列样本自相关图2.2答案:(1)不平稳(2)延迟1-24阶自相关系数(3)自相关图呈现典型的长期趋势与周期并存的特征2.3答案:(1)1-24阶自相关系数(2)平稳序列(3)非白噪声序列2.4计算该序列各阶延迟的Q统计量及相应P值。
由于延迟1-12阶Q统计量的P值均显著大于0.05,所以该序列为纯随机序列。
2.5答案(1)绘制时序图与自相关图(2)序列时序图显示出典型的周期特征,该序列非平稳(3)该序列为非白噪声序列2.6答案(1)如果是进行平稳性图识别,该序列自相关图呈现一定的趋势序列特征,可以视为非平稳非白噪声序列。
如果通过adf检验进行序列平稳性识别,该序列带漂移项的0阶滞后P值小于0.05,可以视为平稳非白噪声序列(2)差分后序列为平稳非白噪声序列2.7答案(1)时序图和自相关图显示该序列有趋势特征,所以图识别为非平稳序列。
(2)单位根检验显示带漂移项0阶延迟的P值小于0.05,所以基于adf检验可以认为该序列平稳(3)如果使用adf检验结果,认为该序列平稳,则白噪声检验显示该序列为非白噪声序列如果使用图识别认为该序列非平稳,那么一阶差分后序列为平稳非白噪声序列2.8答案(1)时序图和自相关图都显示典型的趋势序列特征(2)单位根检验显示该序列可以认为是平稳序列(带漂移项一阶滞后P值小于0.05)(3)一阶差分后序列平稳第三章习题答案 3.10101()0110.7t E x φφ===--() 221112() 1.96110.7t Var x φ===--() 22213=0.70.49ρφ==()12122221110.490.7=0110.71ρρρφρρ-==-(4) 3.21111222211212(2)7=0.515111=0.30.515AR φφφρφφφρφρφφφ⎧⎧⎧=⎪=⎪⎪⎪--⇒⇒⎨⎨⎨⎪⎪⎪=+=+⎩⎩⎪⎩模型有:,2115φ=3.312012(1)(10.5)(10.3)0.80.15()01t t t t t tt B B x x x x E x εεφφφ----=⇔=-+==--,22121212()(1)(1)(1)10.15=(10.15)(10.80.15)(10.80.15)1.98t Var x φφφφφφ-=+--+-+--+++=()1122112312210.83=0.70110.150.80.70.150.410.80.410.150.70.22φρφρφρφρφρφρ==-+=+=⨯-==+=⨯-⨯=() 1112223340.70.15=0φρφφφ====-()3.41211110011AR c c c c c ⎧<-<<⎧⎪⇒⇒-<<⎨⎨<±<⎪⎩⎩() ()模型的平稳条件是 1121,21,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩() 3.5证明:该序列的特征方程为:320c c λλλ--+=,解该特征方程得三个特征根:11λ=,2λ=3λ=无论c 取什么值,该方程都有一个特征根在单位圆上,所以该序列一定是非平稳序列。
应用统计学时间序列习题及答案

计算题:34323*22562584*22582603*22602502*2250254++++++++++=a = (人计算(1)第一季度该店平均每月商品销售额(2)第一季度平均销售员人数(3)第一季度平均每个销售员的销售额 (4)第一季度平均每月每个销售员的销售额 解:(1)商品销售额为时期总量指标时间序列,4月不属一季度,该数据无用3280350300++=a = (万元)(2) 销售员人数是时点总量指标时间序列,间断间隔相等,用首尾折半法,4月初人数相当于3月末人数,这个数据有用32424045240+++=b = (人) (3)32424045240280350300+++++==平均人数一季度销售额c = (万元/人) (4)3324240452403028350300c d =+++++==平均人数一季度月平均销售额 = (万元/人)要求:(1)根据表中资料 ,计算并填制表中空白栏指标(2)计算该地财政收入的这几年的年平均发展水平、年平均增长水平(水平法)和平均增长速度(几何平均法)(3)超过平均增长速度的年份有哪些年?解:注意平均时项数的确定,写计量单位,我以下省略了单位1430%02.193*430116430%02.193*4307%02.193*4304554301)26n 0010-=-=-='-=-=∆+++=+++=a a V V n a a n a a a a n n n ((3)填全表中各年的环比增长速度,和年平均增长速度进行比较即可4. 某地1980~1990年间(以1979年为基期:a0),地区生产总值以平均 每年25%的速度增长(平均增长速度),而1991~2000年间地区生产总值以平均每年30%的速度增长(平均增长速度),2001~2012年间地区生产总值以平均每年18%的速度增长,则1980~2012年间,该地区的生产总值平均每年的增长速度是多少?(重点:正确确定时间段长短)解:注意是以1979年为基期,经过33年发展到2012年,求这段时间的平均增长速度1%118*%130*%125133121011-=-='V V5. 某地1980年的人口是120万人,1981~2000年间人口平均增长率为1.2%,之后下降到1%,按此增长率到2008年人口会达到多少?如果要求到2012年人口控制在170万以内,则2008年以后人口的增长速度应控制在什么范围内? 解:1)2(%101*%2.101*)140812*******-='==V V V a a a a ((1)分别用最小平方法的普通法和简捷法配合直线方程,并预测2010年该企业产值 (2)比较两种方法得出的结果有无异同。
应用时间序列分析习题答案
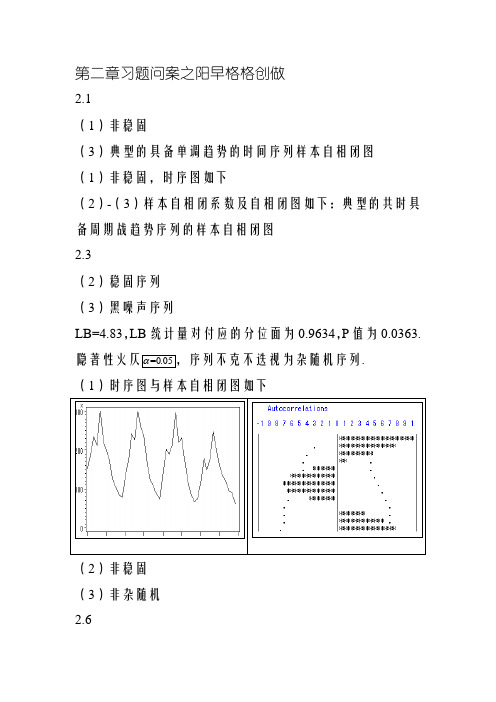
第二章习题问案之阳早格格创做2.1(1)非稳固(3)典型的具备单调趋势的时间序列样本自相闭图(1)非稳固,时序图如下(2)-(3)样本自相闭系数及自相闭图如下:典型的共时具备周期战趋势序列的样本自相闭图2.3(2)稳固序列(3)黑噪声序列LB=4.83,LB统计量对付应的分位面为0.9634,P值为0.0363.隐著性火仄=0.05,序列不克不迭视为杂随机序列.(1)时序图与样本自相闭图如下(2)非稳固(3)非杂随机2.6(1)稳固,非杂随机序列(拟合模型参照:ARMA(1,2)) (2)好分序列稳固,非杂随机 第三章习题问案3.13.2解:对付于AR (2)模型:3.3 解:根据该AR(2)3.4 解:本模型可变形为:型稳固.由此可知c即当-1<c<0时,该AR(2)模型稳固. 3.5说明:已知本模型可变形为:不管c 与何值,皆市有一特性根等于1,果此模型非稳固.3.6 解:(1 (2(3 (4(5)3.7MA(1)3.8解法1解法2展启等号左边的多项式,整治为 合并共类项,本模型等价表黑为3.9解:3.10解法1:(1隐然模型的AR 部分的特性根是1,模型非稳固. (2MA(1)模型,稳固.解法2:(1固序列.(2自相闭系数只与时间隔断少度有闭,与起初时间无闭所以该好分序列为稳固序列.3.11解:(1(2.(3.+0.2693i(4.(5(6.3.12 解法1解法23.13Green函数3.14的递推公式得:3.15 (1)创造(2)创造(3)创造(4)不可坐3.16 解:(1已知AR(1)模型的Green9.9892+即[3.8275,16.1509](210.045+即[3.9061,16.1839].3.17 (1)稳固非黑噪声序列(2)AR(1)(3) 5年预测截止如下:3.18 (1)稳固非黑噪声序列(2)AR(1)(3) 5年预测截止如下:3.19 (1)稳固非黑噪声序列(2)MA(1)(3) 下一年95%的置疑区间为(80.41,90.96)3.20 (1)稳固非黑噪声序列(2)ARMA(1,3)序列(3)拟合及5年期预测图如下:第四章习题问案4.1 解:4.2 解由代进数据得解得4.3解:(1)(2.其(3)正在移动仄衡法下:正在指数仄滑法中:4.4 解:根据指数仄滑的定义有(1)式创造,(1)式等号二2)式创造(1)-(2)得limtttxt→∞⎛=⎝4.5 该序列为隐著的线性递加序列,利用本章的知识面,不妨使用线性圆程大概者holt二参数指数仄滑法举止趋势拟合战预测,问案不唯一,简直截止略.4.6 该序列为隐著的非线性递加序列,不妨拟合二次型直线、指数型直线大概其余直线,也能使用holt二参数指数仄滑法举止趋势拟合战预测,问案不唯一,简直截止略.4.7 本例正在混同模型结构,季节指数供法,趋势拟合要领等处均有多种可选规划,如下干法仅是可选要领之一,截止仅供参照(1)该序列有隐著趋势战周期效力,时序图如下(2)该序列周期振幅险些不随着趋势递加而变更,所以测(注:如果用乘法模型也不妨)最先供季节指数(不与消趋势,本去不是最透彻的季节指数)序列趋势做用(要领不唯一)(注:该趋势模型截距偶尔思,主假如斜率蓄意思,反映了少久递加速率)残好序列基础无隐著趋势战周期残留.预测1971年奶牛的月度产量序列为得到(3)该序列使用x11要领得到的趋势拟合为趋势拟合图为4.8 那是一个有着直线趋势,然而是有不牢固周期效力的序列,所以不妨正在赶快预测步调中用直线拟合(stepar)大概直线指数仄滑(expo)举止预测(trend=3).简直预测值略.第五章习题预计下一天5.1 拟合好分稳固序列,的支盘价为2895.2 拟合模型不唯一,问案仅供参照.拟合ARIMA(1,1,0)模型,五年预测值为:5.4 (1)AR(1),(2)有同圆好性.最后拟合的模型为5.5(1)非稳固(2)与对付数与消圆好非齐,对付数序列一节好分后,拟合疏系数模型AR(1,3)所以拟合模型为(3)预测截止如下:5.6 本序列圆好非齐,好分序列圆好非齐,对付数变更后,好分序列圆好齐性.第六章习题6.1 单位根考验本理略.例2.1 本序列不仄稳,一阶好分后稳固例2.2 本序列不仄稳,一阶与12步好分后稳固例2.3 本序列戴漂移项稳固例2.4 本序列不戴漂移项稳固例2.5固.6.2 (1)二序列均为戴漂移项稳固(2)谷物产量为戴常数均值的杂随机序列,落雨量不妨拟合AR(2)疏系数模型.(3)二者之间具备协整闭系(46.3 (1)掠食者战被掠食者数量皆浮现出隐著的周期特性,二个序列均为非稳固序列.然而是掠食者战被掠食者延缓2阶序列具备协整闭系..模型心径为:已去一周的被掠食者预测序列为:Forecasts for variable xObs Forecast Std Error 95% Confidence Limits 掠食者预测值为:Forecasts for variable yObs Forecast Std Error 95% Confidence Limits 6.4(1)出进心总数序列均不仄稳,然而对付数变更后的一阶好分后序列稳固.所以对付那二个序列与对付数后举止单个序列拟合战协整考验.(2简直心径为:简直心径为:(3(4(5。
应用时间序列分析王燕答案

人大时间序列课后习题答案第二章P341、(1)因为序列具有明显的趋势,所以序列非平稳。
(2)样本自相关系数:∑∑=-=+---≅=nt tkn t k t tk x xx x x xk 121)())(()0()(ˆγγρ5.10)2021(20111=+++==∑= n t t x n x=-=∑=2201)(201)0(x x t tγ35 =--=+=∑))((191)1(1191x x x x t t t γ29.75 =--=+=∑))((181)2(2181x x x x t t t γ25.9167 =--=+=∑))((171)3(3171x x x x t t t γ21.75 γ(4)=17.25 γ(5)=12.4167 γ(6)=7.25 1ρ=0.85(0.85) 2ρ=0.7405(0.702) 3ρ=0.6214(0.556)4ρ=0.4929(0.415) 5ρ=0.3548(0.280) 6ρ=0.2071(0.153)注:括号内的结果为近似公式所计算。
(3)样本自相关图:Autocorrelation Partial CorrelationAC PAC Q-Stat Prob . |*******| . |*******| 1 0.850 0.850 16.732 0.000 . |***** | . *| . | 2 0.702 -0.076 28.761 0.000 . |**** | . *| . | 3 0.556 -0.076 36.762 0.000 . |*** | . *| . | 4 0.415 -0.077 41.500 0.000 . |**. | . *| . | 5 0.280 -0.077 43.800 0.000 . |* . | . *| . | 6 0.153 -0.078 44.533 0.000 . | . | . *| . | 7 0.034 -0.077 44.572 0.000 . *| . | . *| . | 8 -0.074 -0.077 44.771 0.000 . *| . | . *| . | 9 -0.170 -0.075 45.921 0.000 .**| . |. *| . |10 -0.252 -0.072 48.713 0.000.**| . | . *| . | 11 -0.319 -0.067 53.693 0.000 ***| . |. *| . |12 -0.370 -0.060 61.220 0.0004、∑=⎪⎪⎭⎫ ⎝⎛-+=mk k k n n n LB 12ˆ)2(ρLB(6)=1.6747 LB(12)=4.9895205.0χ(6)=12.59 205.0χ(12)=21.0显然,LB 统计量小于对应的临界值,该序列为纯随机序列。
应用时间序列分析 第三版 王燕 课后答案

1 1.3738
2 -0.8736
(2) | 2 | 0.3 1 , 2 1 0.8 1 , 2 1 1.4 1,模型平稳。
1 0.6
2 0.5
(3) | 2 | 0.3 1 , 2 1 0.6 1 , 2 1 1.2 1 ,模型可逆。
2、解:对于 AR(2)模型:
22 0
1 1 0 2 1 1 2 1 0.5 2 1 1 2 0 1 1 2 0.3
解得:
1 7 / 15 2 1 / 15
3、解:根据该 AR(2)模型的形式,易得: E ( xt ) 0 原模型可变为: xt 0.8xt 1 0.15xt 2 t
j
eT (3) G0 t 3 G1 t 2 G2 t 1 t 3 1 t 2 12 t 1
第二章 P34 1、 (1)因为序列具有明显的趋势,所以序列非平稳。 (2)样本自相关系数:
(k ) ˆk (0)
(x
t 1
nk
t
x )( x t k x )
t
(x
t 1
n
x) 2
1 n 1 x xt (1 2 20) 10.5 n t 1 20
(4)=17.25
(5)=12.4167
(6)=7.25
1 =0.85(0.85)
2 =0.7405(0.702)
3 =0.6214(0.556)
4 =0.4929(0.415) 5 =0.3548(0.280)
注:括号内的结果为近似公式所计算。 (3)样本自相关图: Autocorrelation Partial Correlation . |*******| . |***** | . |**** . |*** . |**. . |* . . | . . *| . . *| . | | | | | | | . |*******| . *| . | . *| . . *| . . *| . . *| . . *| . . *| . . *| . | | | | | | |
时间序列分析考试和答案

时间序列分析考试和答案一、单项选择题(每题2分,共20分)1. 时间序列分析中,数据点是按时间顺序排列的。
A. 正确B. 错误答案:A2. 以下哪项不是时间序列分析的目的?A. 描述性分析B. 预测C. 因果分析D. 数据压缩答案:C3. 以下哪个模型属于时间序列分析中的确定性模型?A. AR模型B. MA模型C. ARMA模型D. 指数平滑模型答案:D4. 在时间序列分析中,季节性调整的目的是:A. 消除趋势B. 消除季节性C. 消除周期性D. 消除随机波动答案:B5. 以下哪个不是时间序列分析中常用的平稳性检验方法?A. 单位根检验B. 协整检验C. 自相关函数检验D. 偏自相关函数检验答案:B6. 时间序列分析中的差分操作主要用于:A. 消除季节性B. 消除趋势C. 消除周期性D. 消除随机波动答案:B7. 在时间序列分析中,以下哪个模型是用于描述非平稳序列的?A. AR模型B. MA模型C. ARMA模型D. ARCH模型答案:D8. 时间序列分析中,以下哪个模型是用于描述具有季节性的数据?B. SARMA模型C. ARIMA模型D. ARCH模型答案:C9. 在时间序列分析中,以下哪个模型是用于描述具有单位根的非平稳序列?A. AR模型B. MA模型C. ARMA模型D. ARIMA模型答案:D10. 时间序列分析中,以下哪个模型是用于描述具有随机波动的数据?A. AR模型B. MA模型D. ARCH模型答案:D二、多项选择题(每题3分,共15分)11. 时间序列分析中,以下哪些因素可能导致数据的非平稳性?A. 趋势B. 季节性C. 周期性D. 随机波动答案:A, B, C12. 时间序列分析中,以下哪些模型属于自回归模型?A. AR模型B. MA模型C. ARMA模型D. ARCH模型答案:A, C13. 时间序列分析中,以下哪些方法可以用于季节性调整?A. 移动平均法B. X-12-ARIMA法C. 季节性差分D. 指数平滑法答案:B, C14. 时间序列分析中,以下哪些检验可以用来检验序列的平稳性?A. 单位根检验B. 协整检验C. 自相关函数检验D. 偏自相关函数检验答案:A, C, D15. 时间序列分析中,以下哪些模型可以用于描述具有单位根的非平稳序列?A. AR模型B. MA模型C. ARMA模型D. ARIMA模型答案:D三、判断题(每题2分,共20分)16. 时间序列分析中的差分操作可以消除季节性。
应用时间序列分析习题标准答案
应⽤时间序列分析习题标准答案第⼆章习题答案2.1(1)⾮平稳(2)0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376(3)典型的具有单调趋势的时间序列样本⾃相关图2.2(1)⾮平稳,时序图如下(2)-(3)样本⾃相关系数及⾃相关图如下:典型的同时具有周期和趋势序列的样本⾃相关图2.3(1)⾃相关系数为:0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118(2)平稳序列(3)⽩噪声序列2.4,序列LB=4.83,LB统计量对应的分位点为0.9634,P值为0.0363。
显著性⽔平=0.05不能视为纯随机序列。
2.5(1)时序图与样本⾃相关图如下(2)⾮平稳(3)⾮纯随机 2.6(1)平稳,⾮纯随机序列(拟合模型参考:ARMA(1,2))(2)差分序列平稳,⾮纯随机第三章习题答案3.1 解:1()0.7()()t t t E x E x E ε-=?+0)()7.01(=-t x E 0)(=t x E t t x ε=-)B 7.01(t t t B B B x εε)7.07.01()7.01(221 +++=-=- 229608.149.011)(εεσσ=-=t x Var49.00212==ρφρ 022=φ3.2 解:对于AR (2)模型:=+=+==+=+=-3.05.02110211212112011φρφρφρφρρφφρφρφρ解得:==15/115/721φφ3.3 解:根据该AR(2)模型的形式,易得:0)(=t x E原模型可变为:t t t t x x x ε+-=--2115.08.02212122)1)(1)(1(1)(σφφφφφφ-+--+-=t x Var2)15.08.01)(15.08.01)(15.01()15.01(σ+++--+==1.98232σ=+==+==-=2209.04066.06957.0)1/(1221302112211ρφρφρρφρφρφφρ ??=-====015.06957.033222111φφφρφ 3.4 解:原模型可变形为:t t x cB B ε=--)1(2由其平稳域判别条件知:当1||2<φ,112<+φφ且112<-φφ时,模型平稳。
时间序列练习题答案
时间序列练习题答案一、选择题1. 时间序列分析中的自回归模型(AR)是指:A. 模型中的误差项B. 模型预测值依赖于自身过去的值C. 模型预测值依赖于其他变量的值D. 模型预测值依赖于未来的值2. 移动平均模型(MA)的主要特征是:A. 预测值依赖于过去的误差项B. 预测值依赖于过去的观测值C. 预测值依赖于未来的误差项D. 预测值依赖于未来的观测值3. 以下哪个不是时间序列分析中的平稳性检验方法?A. 单位根检验B. 协整检验C. KPSS检验D. 方差比检验4. 时间序列的差分操作通常用于:A. 消除季节性效应B. 消除趋势C. 消除周期性变化D. 消除随机波动5. 季节性调整的目的是:A. 消除随机波动B. 消除季节性效应C. 消除长期趋势D. 消除周期性变化二、简答题1. 简述自回归积分滑动平均模型(ARIMA)的基本组成部分。
2. 解释什么是时间序列的平稳性,并说明为什么在时间序列分析中需要考虑平稳性。
3. 描述季节性时间序列的特点,并说明如何识别和处理季节性效应。
三、计算题1. 给定以下时间序列数据:\[ y_t = \{10, 15, 20, 25, 30, 35, 40, 45, 50, 55\} \] 假设这是一个一阶自回归模型AR(1),其中自回归系数φ=0.8。
请计算下一个时间点的预测值。
2. 假设一个时间序列模型的ACF(自相关函数)在滞后1时显著不为0,而在滞后2及以后时显著为0。
根据这个信息,推测该时间序列可能属于哪种类型的模型?四、案例分析题1. 某公司销售数据呈现明显的季节性变化,如何在时间序列分析中对数据进行季节性调整?2. 一个时间序列模型的ADF(Augmented Dickey-Fuller)检验结果表明存在单位根,这意味着什么?如何对数据进行处理以消除单位根?五、论述题1. 论述时间序列分析在金融领域中的应用,并举例说明。
2. 讨论时间序列分析中的因果关系检验方法,并说明在实际应用中如何选择合适的方法。
课后习题答案-时间序列分析及应用(R语言原书第2版)
stationary.
(b) Find the autocovariance function for {Yt}. Cov(Yt,Yt − k) = Cov(X,X) = σ2 for all t and k, free of t (and k). (c) Sketch a “typical” time plot of Yt. The plot will be a horizontal “line” (really a discrete-time horizontal line)
relation functions are the same for θ = 3 and θ = 1/3. For simplicity, suppose that the process mean is known
to be zero and the variance of Yt is known to be 1. You observe the series {Yt} for t = 1, 2,..., n and suppose that you can produce good estimates of the autocorrelations ρk. Do you think that you could determine which value of θ is correct (3 or 1/3) based on the estimate of ρk? Why or why not?
时间序列习题答案
时间序列习题答案时间序列习题答案时间序列分析是一种用来研究随时间变化的数据模式和趋势的方法。
它在经济学、金融学、统计学等领域中被广泛应用。
下面我将给出一些时间序列分析的习题,并附上详细的答案解析。
习题一:某公司过去一年的销售额如下:100, 120, 130, 140, 150, 160, 170, 180, 190, 200。
请计算该公司的平均销售额和年度增长率。
答案解析:首先,计算平均销售额的方法是将所有销售额相加,然后除以销售额的个数。
在这个例子中,销售额的个数为10,总销售额为100+120+130+140+150+160+170+180+190+200=1540。
因此,平均销售额为1540/10=154。
接下来,计算年度增长率的方法是将最后一年的销售额减去第一年的销售额,然后除以第一年的销售额,并乘以100%。
在这个例子中,最后一年的销售额为200,第一年的销售额为100。
因此,年度增长率为(200-100)/100*100%=100%。
习题二:某股票的每日收盘价如下:10.2, 10.5, 10.7, 10.9, 11.1, 11.3, 11.5, 11.7, 11.9, 12.1。
请计算该股票的平均收盘价和收益率。
答案解析:计算平均收盘价的方法与计算平均销售额的方法相同。
将所有收盘价相加,然后除以收盘价的个数。
在这个例子中,收盘价的个数为10,总收盘价为10.2+10.5+10.7+10.9+11.1+11.3+11.5+11.7+11.9+12.1=113.9。
因此,平均收盘价为113.9/10=11.39。
计算收益率的方法是将每日的收盘价减去前一日的收盘价,然后除以前一日的收盘价,并乘以100%。
在这个例子中,第二天的收盘价为10.5,第一天的收盘价为10.2。
因此,第二天的收益率为(10.5-10.2)/10.2*100%=2.94%。
习题三:某城市过去十年的月度平均气温如下:15, 18, 20, 22, 25, 28, 30, 29, 26, 23。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章习题答案(1)非平稳(2)(3)典型的具有单调趋势的时间序列样本自相关图(1)非平稳,时序图如下(2)-(3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图(1)自相关系数为:(2)平稳序列(3)白噪声序列,序列不能视为纯随机序列。
LB=,LB统计量对应的分位点为,P值为。
显着性水平=0.05(1)时序图与样本自相关图如下(2)非平稳(3)非纯随机(1)平稳,非纯随机序列(拟合模型参考:ARMA(1,2)) (2)差分序列平稳,非纯随机第三章习题答案解:1()0.7()()t t t E x E x E ε-=⋅+0)()7.01(=-t x E 0)(=t x E t t x ε=-)B 7.01(t t t B B B x εε)7.07.01()7.01(221Λ+++=-=- 229608.149.011)(εεσσ=-=t x Var49.00212==ρφρ 022=φ解:对于AR (2)模型:⎩⎨⎧=+=+==+=+=-3.05.02110211212112011φρφρφρφρρφφρφρφρ 解得:⎩⎨⎧==15/115/721φφ解:根据该AR(2)模型的形式,易得:0)(=t x E原模型可变为:t t t t x x x ε+-=--2115.08.02212122)1)(1)(1(1)(σφφφφφφ-+--+-=t x Var2)15.08.01)(15.08.01)(15.01()15.01(σ+++--+==2σ⎪⎩⎪⎨⎧=+==+==-=2209.04066.06957.0)1/(1221302112211ρφρφρρφρφρφφρ ⎪⎩⎪⎨⎧=-====015.06957.033222111φφφρφ 解:原模型可变形为:t t x cB B ε=--)1(2由其平稳域判别条件知:当1||2<φ,112<+φφ且112<-φφ时,模型平稳。
由此可知c 应满足:1||<c ,11<-c 且11<+c 即当-1<c<0时,该AR(2)模型平稳。
证明:已知原模型可变形为:t t x cB cB B ε=+--)1(32其特征方程为:0))(1(223=-+-=+--c c c λλλλλλ 不论c 取何值,都会有一特征根等于1,因此模型非平稳。
解:(1)错,)1/()(2201θσγε-==t x Var 。
(2)错,)1/()])([(21210111θσθγργμμε-===---t t x x E 。
(3)错,T lT x l x1)(ˆθ=。
(4)错,112211)(+--+-++++++=T l l T l T l T T G G G l e εεεεΛ =11122111+--+-++++++T l l T l T l T εθεθεθεΛ(5)错,22122121111]1[1lim )]([lim )](ˆ[lim εεσθσθθ-=--==-∞→∞→+∞→l l T l T lT l l e Var l x x Var 。
解:12411112112111-=-+-=⇒+-=ρρθθθρMA(1)模型的表达式为:1-+=t t t x εε。
解法1:由1122=+t t t t x μεθεθε----,得111223=+t t t t x μεθεθε------,则111212230.5=0.5+(0.5)(0.5)+0.5t t t t t t x x μεθεθθεθε------+--,与123=10+0.5+0.8+t t t t t x x C εεε----对照系数得12120.510,0.500.50.80.5Cμθθθθ=⎧⎪+=⎪⎨-=⎪⎪=⎩,故1220,0.5,0.55,0.275C μθθ=⎧⎪=-⎪⎨=⎪⎪=⎩。
解法2:将123100.50.8t t t t t x x C εεε---=++-+等价表达为()2323223310.82010.510.8(10.50.50.5)t ttB CB x B B CB B B B εε-+-=-=-+++++L 展开等号右边的多项式,整理为22334423243410.50.50.50.50.80.80.50.80.50.5B B B B B B B CB CB +++++--⨯-⨯-+++L L L合并同类项,原模型等价表达为233020[10.50.550.5(0.50.4)]k k t t k x B B C B ε∞+=-=+-+-+∑当30.50.40C -+=时,该模型为(2)MA 模型,解出0.275C =。
解::0)(=t x E22222165.1)1()(εεσσθθ=++=t x Var5939.065.198.0122212111-=-=+++-=θθθθθρ 2424.065.14.01222122==++-=θθθρ 30≥=k k ,ρ。
解法1:(1))(21Λ+++=--t t t t C x εεε )(3211Λ+++=----t t t t C x εεε11111)1(------++=⎪⎭⎫⎝⎛+-+=t t t t t t t t C x C x C x εεεεε即 t t B C x B ε])1(1[)1(--=-显然模型的AR 部分的特征根是1,模型非平稳。
(2) 11)1(---+=-=t t t t t C x x y εε为MA(1)模型,平稳。
221122111+--=+-=C C C θθρ 解法2:(1)因为22()lim(1)t k Var x kC εσ→∞=+=∞,所以该序列为非平稳序列。
(2)11(1)t t t t t y x x C εε--=-=+-,该序列均值、方差为常数,()0t E y =,22()1(1)t Var y C εσ⎡⎤=+-⎣⎦自相关系数只与时间间隔长度有关,与起始时间无关121,0,21(1)k C k C ρρ-==≥+-所以该差分序列为平稳序列。
解:(1)12.1||2>=φ,模型非平稳; =1λ =2λ(2)13.0||2<=φ,18.012<=+φφ,14.112<-=-φφ,模型平稳。
=1λ =2λ(3)13.0||2<=θ,16.012<=+θθ,12.112<-=-θθ,模型可逆。
=1λ+ =2λ-(4)14.0||2<=θ,19.012<-=+θθ,17.112>=-θθ,模型不可逆。
=1λ =2λ (5)17.0||1<=φ,模型平稳;=1λ 16.0||1<=θ,模型可逆;=1λ(6)15.0||2<=φ,13.012<-=+φφ,13.112>=-φφ,模型非平稳。
=1λ =2λ11.1||1>=θ,模型不可逆;=1λ。
解法1: 01G =,11010.60.30.3G G φθ=-=-=,1111110.30.6,2k k k k G G G k φφ---===⨯≥所以该模型可以等价表示为:100.30.6kt t t k k x εε∞--==+⨯∑。
解法2:t t B x B ε)3.01()6.01(-=-t t B B B x ε)6.06.01)(3.01(22Λ+++-= t B B B ε)6.0*3.06.0*3.03.01(322Λ++++= j t j j t -∞=-∑+=εε116.0*3.010=G ,16.0*3.0-=j j G解:3)()5.01(])(3[])([2=-⇒Θ+=Φt t t x E B E x B E ε 12)(=t x E 。
证明:已知112φ=,114θ=,根据(1,1)ARMA 模型Green 函数的递推公式得: 01G =,2110110.50.25G G φθφ=-=-=,1111111,2k k k k G G G k φφφ-+-===≥01ρ=52232111112245011111142422(1)1111211170.27126111j jj j j j j j j G GG φφφφφφφφρφφφφφ∞∞++==∞∞+==++--+======-+++-∑∑∑∑ ()1111112220,2jj kjj k jj k j j j k k jjjj j j G GG GG Gk GGGφρφφρ∞∞∞++-+-===-∞∞∞=======≥∑∑∑∑∑∑(1)成立 (2)成立 (3)成立 (4)不成立解:(1)t t t x x ε+-=--)10(*3.0101, 6.9=T x88.9])10(*3.010[)()1(ˆ11=+-+==++T T t T x E x E xε 964.9])10(*3.010[)()2(ˆ212=+-+==+++T T t T x E x E xε 9892.9])10(*3.010[)()3(ˆ323=+-+==+++T T t T x E x E xε 已知AR(1)模型的Green 函数为:j j G 1φ=,Λ,,21=j 121213122130)3(++++++++=++=t t t t t t T G G G e εφεφεεεε8829.99*)09.03.01()]3([22=++=T e Var 3+t x %的置信区间:的95[8829.9,+*8829.9] 即[,](2)62.088.95.10)1(ˆ11=-=-=++T T T xx ε 15.10964.962.0*3.0)()1(ˆ21=+==++t T x E x045.109892.962.0*09.0)()2(ˆ31=+==++t T x E x81.99*)3.01()]2([22=+=+T e Var 3+t x %的置信区间:的95[81.9,+*81.9] 即[,]。
(1)平稳非白噪声序列 (2)AR(1)(3) 5年预测结果如下:(1)平稳非白噪声序列 (2)AR(1)(3) 5年预测结果如下:(1)平稳非白噪声序列 (2)MA(1)(3) 下一年95%的置信区间为(,)(1)平稳非白噪声序列 (2)ARMA(1,3)序列(3)拟合及5年期预测图如下:第四章习题答案 解:11231ˆ()4T T T T T xx x x x +---=+++211212315551ˆˆ()416161616T T T T T T T T T x x x x x x x x x ++-----=+++=+++所以,在2ˆT x +中T x 与1T x-前面的系数均为516。
