决胜2021年中考数学压轴题全揭秘精品(上海专版) 专题19 计算题专项训练(教师版含解析)
2021年上海中考数学压轴题

2021年上海中考数学压轴题一、在直角坐标系中,点A(3,4)关于原点对称的点B的坐标是?A. (-3,-4)B. (3,-4)C. (-3,4)D. (4,3)(答案:A。
解析:关于原点对称的点,横纵坐标都取反。
)二、若一元二次方程x2 - 2x - 3 = 0的两个根为x1和x2,则x1 * x2的值为?A. -3B. 2C. 3D. -2(答案:A。
解析:根据一元二次方程的根与系数的关系,x1 * x2 = c/a = -3/1 = -3。
)三、一个正方体的表面积是24平方厘米,那么它的体积是?A. 4立方厘米B. 6立方厘米C. 8立方厘米D. 12立方厘米(答案:C。
解析:正方体一个面的面积为24/6=4平方厘米,边长为2厘米,体积为23=8立方厘米。
)四、函数y = 2x + 1与y = -x + 4的交点坐标是?A. (1,3)B. (2,3)C. (3,1)D. (3,2)(答案:A。
解析:联立两个方程解得x=1,y=3。
)五、若一个长方形的长是宽的2倍,且面积为128平方厘米,则它的周长是?A. 32厘米B. 48厘米C. 64厘米D. 96厘米(答案:B。
解析:设宽为x,则长为2x,x * 2x = 128,解得x=8,周长为2(8+16)=48厘米。
)六、下列哪个数是无理数?A. 3.14B. √2C. 22/7D. 1.5(答案:B。
解析:无理数是不能表示为两个整数之比的数,√2是无理数。
)七、在三角形ABC中,若∠A = 60°,∠B = 45°,则∠C = ?A. 45°B. 60°C. 75°D. 90°(答案:C。
解析:三角形内角和为180°,∠C = 180° - 60° - 45° = 75°。
)八、若一组数据1,2,x,4,5的平均数为3,则x = ?A. 1B. 2C. 3D. 4(答案:C。
决胜2021年中考数学压轴题全揭秘精品(上海专版) 专题19 计算题专项训练(教师版含解析)

专题19 计算题专项训练1.(2020·上海中考真题)解不等式组:1076713x xxx>+⎧⎪+⎨-<⎪⎩【答案】2<x<5.【分析】先求出不等式组中每一个不等式的解集,再求出它们的公共部分即可求解.【详解】解:由题意知:1076713①②>+⎧⎪⎨+-<⎪⎩x xxx,解不等式①,移项得:3x>6,系数化为1得:x>2,解不等式②,去分母得:3x-3<x+7.移项得:2x<10,系数化为1得:x<5,∴原不等式组的解集是2<x<5.故答案为:2<x<5.【点睛】本题考查解一元一次不等式组,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.2.(2020·上海中考真题)计算:1327(12)﹣2+|3.【答案】0.【分析】利用分数的指数幂的意义,分母有理化,负指数幂的意义,绝对值的性质计算后合并即可.【详解】原式=133(3)+2﹣4+32﹣4+3=0.【点睛】本题考查了分数指数幂的运算,负指数幂的运算,绝对值的意义以及分母有理化运算,熟练掌握实数的运算法则是解题的关键.3.(2020·上海九年级一模)计算:()2232cos 453tan 302sin 60cos60cot 30-︒+︒︒-︒-︒【答案】2-【分析】利用特殊锐角三角函数值计算求解即可.【详解】解:原式=223232122⎛-+ ⎝⎭=-⨯--⎝⎭ 【点睛】本题考查了特殊锐角三角函数值的计算,熟知特殊锐角三角函数值是解题的关键. 4.(2020·上海大学附属学校九年级三模)解方程组:222-620x y x xy y =⎧⎨--=⎩【答案】121242,22x x y y ==⎧⎧⎨⎨==-⎩⎩ 【分析】将第二个方程进行因式分解得到()(2)0+-=x y x y ,然后令因式2x y -和因式x y +分别为0即可求解.【详解】解:由题意可知: 222-620x y x xy y =⎧⎨--=⎩①② 对方程②进行因式分解得:()(2)0+-=x y x y即20x y -=或0x y +=∴原方程组化为2620x y x y -=⎧⎨-=⎩ 或 260x y x y -=⎧⎨+=⎩解得1142x y =⎧⎨=⎩或2222x y =⎧⎨=-⎩ 故原方程组的解为:1142x y =⎧⎨=⎩或2222x y =⎧⎨=-⎩. 【点睛】本题考查了因式分解的方法及二元方程组,熟练掌握常见的二元一次方程组的解法是解决此类题的关键.5.(2020·上海九年级二模)解不等式组:3(2)8(6)121123x x x x -≤-+⎧⎪+-⎨<+⎪⎩,并把解集在数轴上表示出来.【答案】﹣1<x ≤2,数轴见解析【分析】先求出每个不等式的解集,再求出不等式组的解集即可.【详解】解:()()3286121123x x x x ⎧--+⎪⎨+-<+⎪⎩①②,解不等式∴,得:2x ,解不等式∴,得:1x >-,将不等式解集表示在数轴上如下:所以不等式组的解集为12x -<.【点睛】本题考查了解一元一次不等式组和在数轴上表示不等式组的解集,能根据不等式的解集求出不等式组的解集是解此题的关键.6.(2020·上海九年级二模)先化简,再求值:2224112a a a a a -÷----,其中2a =. 【答案】12a -. 【分析】先根据分式的运算法则化简分式,再将a 的值代入计算即可.【详解】解:原式=2(1)(1)12(2)2a a a a a a +-⨯---- =122a a a a +--- =12a -,将2a =代入上式得,原式=. 【点睛】本题考查了分式的化简求值,掌握基本运算法则是解题的关键.1.(2020·上海九年级二模)解不等式组:26233122x x x x ⎧⎛⎫-<- ⎪⎪⎪⎝⎭⎨-⎪-⎪⎩并把解集在数轴上表示出来.【答案】﹣1≤x <3,见解析【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【详解】解不等式①,得:x <3,解不等式②,得:x≥﹣1,则不等式组的解集为﹣1≤x <3,将不等式组的解集表示在数轴上如下:【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.2.(2020·上海九年级二模)计算:12012()122tan 601)3π-+--+︒-(【答案】4【分析】原式利用零指数幂、负整数指数幂法则,分数指数幂法则,以及特殊角的三角函数值计算即可得到结果.【详解】原式)1=2121-+-3=-3=-=4.【点睛】此题考查了实数的运算,零指数幂、负整数指数幂,分数指数幂以及特殊角的三角函数值,熟练掌握运算法则是解本题的关键.3.(2020·上海九年级二模)计算:110311)183-⎛⎫-+++ ⎪⎝⎭. 【答案】【分析】先利用零次幂的运算法则,绝对值的意义,负整指数的运算法则以及分数指数幂的运算法则进行化简,再进行加减运算即可.【详解】解:原式.【点睛】本题是实数的混合运算,考查了零次幂的运算法则,绝对值的意义,负整指数的运算法则以及分数指数幂的运算法则,掌握基本运算法则是解题的关键.4.(2020·上海九年级二模)方程组22205x y x y -=⎧⎨+=⎩的解是_______. 【答案】12x y =⎧⎨=⎩或12x y =-⎧⎨=-⎩ 【分析】先将y 用含x 的式子表示,再代入解一元二次方程即可.【详解】22205x y x y -=⎧⎨+=⎩①②由①得:2y x =③将③代入②得:()2225x x +=解得:1x =± ,将1x =±代入③得: 2y =±∴12x y =⎧⎨=⎩或12x y =-⎧⎨=-⎩ 故答案为:12x y =⎧⎨=⎩或12x y =-⎧⎨=-⎩ 【点睛】本题考查二元二次方程组的解法,掌握代入消元是解题关键.5.(2020·上海九年级二模)解方程组:222;1.x y x xy y -=⎧⎨--=⎩【答案】121251,31x x y y ==⎧⎧⎨⎨==-⎩⎩ 【分析】用代入法解方程.【详解】,由①得x=2+y ③,将③代入②得22(2(2))1y y y y -+-=+, 解得13y =,21y =-,将13y =、21y =-分别代入③,得 15=x ,21x =,∴原方程组的解是 121251,31x x y y ==⎧⎧⎨⎨==-⎩⎩. 【点睛】此题考查解二元二次方程组,根据方程组的特点选择恰当的解法是解题的关键. 6.(2020·上海九年级二模)解方程组:222,{230.x y x xy y -=--=【答案】1111x y =⎧⎨=-⎩2231x y =⎧⎨=⎩【详解】x 2-2xy -3y 2="0"(x -y)2-4y 2=0又因:x -y=2代入上式4-4y 2=0y=1或y=-1再将y=1、y=-1分别代入x -y=2则 x=1、x=3∴1111x y =⎧⎨=-⎩2231x y =⎧⎨=⎩ 7.(2020·上海九年级一模)解方程组:2228560x y x xy y +=⎧⎨+-=⎩【答案】11122x y =⎧⎨=-⎩,228383x y ⎧=⎪⎪⎨⎪=⎪⎩【分析】先将第2个方程变形为x +6y =0,x ﹣y =0,从而得到两个二元一次方程组,再分别求解即可.【详解】解:2228560x y x xy y +=⎧⎨+-=⎩①②, 由∴得:x +6y =0,x ﹣y =0,原方程组可化为2860x y x y +=⎧⎨+=⎩或280x y x y +=⎧⎨-=⎩,故原方程组的解为11122x y =⎧⎨=-⎩,228383x y ⎧=⎪⎪⎨⎪=⎪⎩. 【点睛】本题考查的是高次方程,关键是通过分解,把高次方程降次,得到二元一次方程组,用到的知识点是因式分解、加减法.8.(2020·上海九年级一模)计算:24sin 30tan 60cot 30tan45--【分析】把特殊的锐角三角函数值代入计算即可.21432⨯-=;【点睛】本题主要考查了特殊的锐角三角函数值,掌握特殊的锐角三角函数值是解题的关键.9.(2020·上海)计算:22sin 30tan 60cot 45cos 60cos30sin 45︒︒︒︒︒︒⋅-+-+1.【分析】直接利用特殊角的三角函数值进而分别代入求出答案.【详解】解:原式=11122222⨯-+⎛- ⎝⎭22. 【点睛】本题主要考查特殊三角函数值的相关运算,牢记特殊三角函数值是解题的关键. 10.(2020·上海市民办协和双语学校九年级一模)计算:13tan 3045cos60︒︒︒-【答案】1.【分析】将特殊角的三角函数值代入,根据实数的运算法则求值即可.【详解】原式=131221=1.【点睛】本题考查了特殊角的三角函数值以及实数的混合运算,熟记特殊角的三角函数值、熟练掌握实数的运算法则是解题的关键. 11.(2020·上海)计算:22cot 602tan 30tan 60sin 452sin 30︒︒︒︒︒++-【答案】52【分析】根据特殊角的三角函数值即可代入求解.【详解】解:原式222331222+⎛=+- ⎝⎭⨯ 132=+52=【点睛】此题主要考查实数的运算,解题的关键是熟知特殊角的三角函数值. 12.(2020·上海九年级一模)计算:2tan 45cos60cot 602sin 30︒-︒+︒︒【答案】56【分析】先将特殊三角函数值分别算出原算式中的每一项,然后根据实数混合运算的法则进行计算即可. 【详解】解:2tan 45cos60cot 602sin 30︒-︒+︒︒2112122-=+⎝⎭⨯ 1123=+ 56=【点睛】本题考查的是特殊三角函数值,熟记特殊角度的三角函数值是解答此题的关键. 13.(2020·上海九年级一模)已知:::2:3:5a b c =.(1)求代数式323a b c a b c-++-的值; (2)如果324a b c -+=,求,,a b c 的值.【答案】(1)1;(2)6,9,15a b c ===【分析】(1)设a=2k ,b=3k ,c=5k (k 0)≠,代入代数式323a b c a b c-++-,即可求出答案; (2)把a 、b 、c 的值代入,求出即可.【详解】∵::2:3:5a b c =∴设a=2k ,b=3k ,c=5k (k 0)≠,(1)36358=1234958a b c k k k k a b c k k k k-+-+==+-+-;(2)∵324a b c -+=∴6k -3k+5k=24,∴k=3,∴a=2×3=6,b=3×3=9,c=5×3=15.【点睛】本题考查了比例的性质的应用,主要考查学生的计算能力.14.(2020·上海九年级一模)2sin60°•tan45°+4cos 230°﹣tan60°【答案】3【分析】直接利用特殊角的三角函数值分别代入求出答案.【详解】2sin60°•tan45°+4cos 230°﹣tan60°=×1+4×2=3.【点睛】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键. 15.(2020·上海九年级一模)计算:2cos30°+tan45°-2sin30°-cot30°【答案】0【分析】将特殊角的三角函数值代入即可【详解】2cos30°+tan45°-2sin30°-cot30°+1-2×12-1=0【点睛】本题主要考查特殊角的三角函数值,掌握特殊角的三角函数值是解题的关键. 16.(2020·上海九年级二模)解方程: 24211422xx x x .【答案】x =1.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解.【详解】去分母得:4x ﹣2x ﹣4=x 2﹣4﹣x +2,即x 2﹣3x +2=0,解得:x =1或x =2,经检验x =2是增根,所以,分式方程的解为x =1.【点睛】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.17.(2020·上海九年级一模)2318-【答案】-3.【分析】根据绝对值的性质,二次根式的混合运算,进行运算即可1243-+=-【点睛】此题考查二次根式的混合运算,解题关键在于掌握运算法则18.(2020·上海九年级二模)解方程组:226,320.x y x xy y +=⎧⎨-+=⎩【答案】114,2;x y =⎧⎨=⎩223,3.x y =⎧⎨=⎩【分析】先对x 2-3xy+2y 2=0分解因式转化为两个一元一次方程,然后联立①,组成两个二元一次方程组,解之即可.【详解】将方程22320x xy y -+= 的左边因式分解,得20x y -=或0x y -=. 原方程组可以化为6,20x y x y +=⎧⎨-=⎩或6,0.x y x y +=⎧⎨-=⎩ 解这两个方程组得114,2;x y =⎧⎨=⎩ 223,3.x y =⎧⎨=⎩ 所以原方程组的解是114,2;x y =⎧⎨=⎩ 223,3.x y =⎧⎨=⎩ 【点睛】本题考查了高次方程组,将高次方程化为一次方程是解题的关键.19.(2020·上海九年级三模)解方程:213221x x x x --=-∴ 【答案】11x =-∴213x = 分析:首先21x y x-=,然后将方程转化为y 的一元二次方程,从而求出y 的值,然后根据y 的值求出x 的值. 详解:设21x y x-=,则原方程化为2230y y --=∴ 解得123,1y y ==-∴ 当13y =时,得1x =- , 当11y =-时,得13x =∴ 经检验,11x =-∴213x =是原方程的解. 点睛:本题主要考查的是分式方程的解法以及换元思想的应用,属于中等难度的题型.学会换元思想是解题的关键.20.(2020·上海九年级二模)解不等式组31222236255134x x x x x --+⎧+<⎪⎪⎨-⎪+≤⎪⎩,并把解集在数轴上表示出来. 【答案】47x ≥,数轴见解析 【分析】本题可根据不等式组分别求出x 的取值,然后画出数轴,数轴上相交的点的集合就是该不等式的解集.若没有交点,则不等式无解 【详解】解:31222,2362551,34x x x x x --+⎧+<⎪⎪⎨-⎪+≤⎪⎩①② 解不等式①,得1x <. 解不等式②,得47x ≥. 所以不等式组的解集为47x ≥. 将解集表示在数轴上如下:【点睛】本题可分别解完不等式后可以利用数轴或口诀“比大的小,比小的大,中间找”得到最终结果,此题考查利用数形结合解不等式组,是对学生基本运算方法、运算法则、基本性质的运用能力的考查.21.(2020·上海九年级二模)先化简,再求值:22111121x x x x x x --÷+--+,其中x. 【答案】11x x -+,﹣3【分析】先根据分式的混合运算顺序和运算法则化简原式,再将x 的值代入计算可得.【详解】 解:原式21(1)1(1)(1)1x x x x x x -=-++-- 111x x x =-++ 11x x -=+,当1x =时,原式==3=.【点睛】本题主要考查分式的化简求值,解题的关键是熟练掌握分式的混合运算顺序和运算法则.。
决胜2021年中考数学压轴题全揭秘精品(上海专版) 专题09 面积的存在性问题(学生版)

专题09 面积的存在性问题在求面积时,除了最基本的面积公式外,还需要注意三角形的面积比与底边之比、高之比的关系.在压轴题中,往往是以函数为背景,此时则还需掌握好在坐标系中常用的割补法.模块一:固定面积的存在性问题1、 知识内容:固定面积的存在性问题最为简单,在待求图形中,往往只有一个是变量,此时只需通过方程将其解出即可.2、 解题思路:(1) 根据题目条件,求出相应的固定面积;(2) 找到待求图形合适的底和高;(3) 列出方程,解出相应变量;根据题目实际情况,验证所有可能点是否满足要求并作答.例1.(2020黄浦区一模)已知在平面直角坐标系xOy 中,抛物线()2240y mx mx m =-+≠与x 轴交于点A 、B (点A 在点B 的左侧),且AB =6.(1)求这条抛物线的对称轴及表达式;(2)在y 轴上取点E (0,2),点F 为第一象限内抛物线上一点,联结BF 、EF ,如果10OEFB S =四边形,求点F 的坐标;(3)在第(2)小题的条件下,点F 在抛物线对称轴右侧,点P 在x 轴上且在点B 左侧,如果直线PF 与y 轴的夹角等于∠EBF ,求点P 的坐标.例2.如图,在平面直角坐标系中,点A 的坐标为(8,0),点B 在y 轴的正半轴上,且4cot 3OAB ∠=,抛物线214y x bx c =-++经过A 、B 两点. (1)求b 、c 的值;(2)过点B 作CB ⊥OB ,交这个抛物线于点C ,以点C 为圆心,CB 为半径的圆记作⊙C , 以点A 为圆心,r 为半径的圆记作⊙A .若⊙C 与⊙A 外切,求r 的值;(3)若点D 在这个抛物线上,AOB ∆的面积是OBD ∆面积的8倍,求点D 的坐标.例3.如图,二次函数的图像过点A(6x=-,顶点为C,点-,0)、B(0,6),对称轴为直线2B关于直线2x=-的对称点为D.(1)求二次函数的解析式以及点C和点D的坐标;(2)联结AB、BC、CD、DA,点E在线段AB上,联结DE,若DE平分四边形ABCD的面积,求AE的长;(3)在二次函数的图像上是否存在点P,能够使PCA BAC∠=∠?如果存在,请求出点P的坐标;如果不存在,请说明理由.模块二:有关面积比的存在性问题1、知识内容:有些问题是关于两个未知面积比的,此类问题的难度稍大.一般都需要先通过公共边或公共高,将面积比转化为线段之比,从而进一步列出方程解决问题.2、解题思路:(1)根据题目条件,用函数表示出相关面积;(2) 利用面积比的条件列出方程并求解;(3) 根据题目实际情况,验证所有可能点是否满足要求并作答.例1.(2019上海中考真题)如图1,AD 、BD 分别是△A BC 的内角∠BAC 、∠ABC 的平分线,过点A 作AE 上AD ,交BD 的延长线于点E(1)求证:∠E =12∠C ; (2)如图2,如果AE =AB ,且BD :DE =2:3,求cos ∠ABC 的值;(3)如果∠ABC 是锐角,且△ABC 与△ADE 相似,求∠ABC 的度数,并直接写出ADE ABC SS 的值.例2.如图,在平面直角坐标系中,抛物线22y ax ax c =-+与x 轴正半轴交于点A ,与y 轴正半轴交于点B ,它的对称轴与x 轴交于点C ,且OBC OAB ∠=∠,AC = 3.(1)求此抛物线的表达式;(2)如果点D 在此抛物线上,DF ⊥OA ,垂足为F ,DF 与线段AB 相交于点G ,且32ADG AFG S S =△△,求点D 的坐标.例3.如图,在平面直角坐标系中,已知点A 的坐标为(a ,3)(其中a > 4),射线OA 与反比例函数12y x=的图像交于点P ,点B 、C 分别在函数12y x =的图像上,且AB // x 轴,AC // y 轴.(1)当点P 的横坐标为6时,求直线AO 的表达式;(2)联结BO ,当AB = BO 时,求点A 的坐标;(3)联结BP 、CP ,试猜想ABP ACP S S △△的值是否随a 的变化而变化?如果不变,求出ABP ACP S S △△的值; 如果变化,请说明理由.模块三:隐藏的梯形的存在性问题1、 知识内容:若ABC ADC S S ∆∆=,且B 和D 在AC 的同侧,易证A 、B 、C 、D 构成梯形(或平行四边形),其中AC //BD .2、 解题思路:(1) 根据题目条件,找出相应的平行关系;(2)利用已知直线的解析式求出未知直线;(3)解出相应的点;(4)根据题目实际情况,验证所有可能点是否满足要求并作答.【例1】在平面直角坐标系中(如图),已知抛物线与x轴交于点A(1-,0)和点B,与y轴交于点C(0,2-).(1)求该抛物线的表达式,并写出其对称轴;(2)点E为该抛物线的对称轴与x轴的交点,点F在对称轴上,四边形ACEF为梯形,求点F的坐标;(3)点D为该抛物线的顶点,设点P(t,0),且t> 3,如果BDP∆和CDP∆的面积相等,求t 的值.1.抛物线()2=++与x轴交于A、B两点,顶点M的坐标为(1,4-).y x m k(1)求A、B两点的坐标;(2)设直线AM与y轴交于点C,求BCM∆的面积;(3)在抛物线上是否还存在点P,使得S△PMB = S△BCM,如存在,求出点P的坐标;如果不存在,请说明理由.2.如图,在平面直角坐标系中,O为坐标原点,开口向上的抛物线与x轴交于点A(1-,0)和点B(3,0),D为抛物线的顶点,直线AC与抛物线交于点C(5,6).(1)求抛物线的解析式;(2)点E在x轴上,且AEC∆相似,求点E的坐标;∆和AED(3)若直角坐标平面中的点F和点A、C、D构成直角梯形,且面积为16,试求点F的坐标.3.如图,抛物线2=+-经过直线3y x bx c=-与坐标轴的两个交点A、B,此抛物线与xy x轴的另一个交点为C,抛物线的顶点为D.(1)求此抛物线的解析式;(2)点P为抛物线上的一个动点,求使S△APC : S△ACD = 5 : 4的点P的坐标;(3)点M为平面直角坐标系上一点,写出使点M、A、B、D为平行四边形的点M的坐标.4.如图,已知抛物线22=-+-的顶点A在第四象限,过点A作AB⊥y轴于点B,Cy x tx t22是线段AB上一点(不与A、B重合),过点C作CD⊥x轴于点D,并交抛物线于点P.(1)若点C的横坐标为1,且是线段AB的中点,求点P的坐标;(2)若直线AP交y轴负半轴于点E,且AC = CP,求四边形OEPD的面积S关于t的函数解析式,并写出定义域;(3)在(2)的条件下,当ADE∆的面积等于2S时,求t的值.。
决胜2021年上海市中考数学压轴题全揭秘精品试题三

绝密★启用前决胜2021年上海市中考数学压轴题全揭秘精品试题三数学试题考生注意:1.本试卷共25题。
2.试卷满分150分,考试时间100分钟。
3.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效。
4.除第一、二大题外,其余各题如无特殊说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤。
一.选择题(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确的代号并填涂在答题纸的相应位置上】1.下列四个选项,其中的数不是分数的选项是()(A);(B);(C);(D).2.若a<b,则下列各式中不一定成立的是()A.a﹣1<b﹣1B.3a<3b C.﹣a>﹣b D.ac<bc3.下列说法中不正确的是()A.函数y=2x的图象经过原点B.函数y=1的图象位于第一、三象限xC.函数y=3x﹣1的图象不经过第二象限D.函数y=−3的值随x的值的增大而增大x4.一组数据:3、4、4、5,如果再添加一个数字4,那么会发生变化的统计量是()(A)平均数;(B)中位数;(C)众数;(D)方差.5.下列四个命题中,真命题是()(A)一组对边平行,一条对角线被另一条对角线平分的四边形是平行四边形;(B)一组对角相等,一条对角线被另一条对角线平分的四边形是平行四边形;(C)一组邻边相等,一条对角线被另一条对角线平分的四边形是平行四边形;(D)一组对边相等,一条对角线被另一条对角线平分的四边形是平行四边形.6.在△ABC中,AB=9,BC=2AC=12,点D、E分别在边AB、AC上,且DE∥BC,AD=2BD,以AD为半径的⊙D和以CE为半径的⊙E的位置关系是()A.外离B.外切C.相交D.内含二.填空题(本大题共12题,每题4分,满分48分)【请将结果直接填入答题纸的相应位置上】a2b)3=.7.计算:(−12x2﹣2kx+1﹣4k=0有两个相等的实数根,则代数式10.若关于x的一元二次方程12(k﹣2)2+2k(1﹣k)的值为.11.从1、2、3中任取一个数作为十位上的数字,再从余下的数字中任取一个数作为个位上的数字,那么组成的两位数是4的倍数的概率是12.我国古代数学著作《九章算术》中有一道阐述“盈不足术”的问题,原文是“今有人共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?”大致意思是:“现有几个人共同购买一个物品,每人出8元,则多3元;每人出7元,则差4元.问人数、物品的价格各是多少?”如果设共有x人,物品的价格为y元,那么根据题意可列出方程组为.13.若抛物线y=(x﹣m)2+(m+1)的顶点在第二象限,则m的取值范围为_____.14.如图,点A的坐标是(2,0),△ABO是等边三角形,点B在第一象限,若反比例函数k=yx 的图象经过点B,则k的值是_____.15.如图,点D是△ABC的边AB上一点,如果∠ACD=∠B,并且:AD AC=AD BD=_________.:16.如图,已知D 是△ABC 的边AC 上一点,且AD =2DC ,如果AB →=a →,AC →=b →,那么向量BD →关于a →、b →的分解式是 .17.定义:如果三角形的两个内角∠α与∠β满足∠α=2∠β,那么,我们将这样的三角形称为“倍角三角形”,如果一个等腰三角形是“倍角三角形”,那么这个等腰三角形的腰长与底边18.如图,正方形ABCD 的边长为6,点E ,F 分别为AB 、BC 的中点,点H 是AD 边上一点,将△DCF 沿DF 折叠得△DC ′F ,将△AEH 沿EH 折叠后点A 的对应点A ′刚好落在DC ′上,则cos ∠DA ′H = .三.解答题(共7小题,满分78分)19.(本题满分10分)计算:(√2−1)2√3+√2+|1−√2|.20.(本题满分10分)解方程:21416222+=---+x x x x21.(本题满分10分,每小题满分各5分)在平面直角坐标系中,直线l 1:y =kx +b (k 、b 为常数,且k ≠0)经过A 、B 两点,点A 在y 轴上.(1)若B 点坐标为(﹣1,2).①b = (用含有字母k 的代数式表示)②当△OAB 的面积为2时,求直线l 1的表达式;(2)若B 点坐标为(k ﹣2b ,b ﹣b 2),点C (﹣1,s )也在直线l 1上,①求s 的值;②如果直线l 1:y =kx +b (k ≠0)与直线l 2:y =x 交于点(x 1,y 1),且0<x 1<2,求k 的取值范围.22. (本题满分10分,每小题满分各5分)如图1是某小型汽车的侧面示意图,其中矩形ABCD 表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角为60°时,箱盖ADE落在AD'E'的位置(如图2所示).已知AD=90厘米,DE=30厘米,EC=40厘米.(1)求点D'到BC的距离;(2)求E、E'两点的距离.23.(本题满分12分,第(1)小题满分5分,第(2)小题满分7分)已知:如图,在平行四边形ABCD中,对角线AC与BD相交于点E,过点E作AC的垂线交边BC于点F,与AB的延长线交于点M,且AB AM AE AC⋅=⋅.求证:(1)四边形ABCD矩形;(2)2=⋅.DE EF EM24.在平面直角坐标系xOy中,直线y=﹣1x+5与x轴、y轴分别交于点A、B(如图).抛物线2y=ax2+bx(a≠0)经过点A.(1)求线段AB的长;(2)如果抛物线y=ax2+bx经过线段AB上的另一点C,且BC求这条抛物线的表达式;(3)如果抛物线y=ax2+bx的顶点D位于△AOB内,求a的取值范围.25.如图,△ABC中,AB=AC,⊙O是△ABC的外接圆,BO的延长交边AC于点D.(1)求证:∠BAC=2∠ABD;(2)当△BCD是等腰三角形时,求∠BCD的大小;(3)当AD=2,CD=3时,求边BC的长.。
决胜2021年中考数学压轴题全揭秘精品(上海专版) 专题20 证明题专项训练(教师版含解析)

专题20 证明题专项训练1.(2018·上海中考真题)已知:如图,正方形ABCD 中,P 是边BC 上一点,BE ⊥AP,DF ⊥AP ,垂足分别是点E,F,(1)求证:EF=AE,BE,(2)联结BF ,如果AF BF =DF AD.求证:EF=EP,【分析】(1)利用正方形的性质得AB=AD,∠BAD=90°,根据等角的余角相等得到∠1=∠3,则可判断△ABE ≌△DAF ,则BE=AF ,然后利用等线段代换可得到结论;(2)利用AF DF BF AD =和AF=BE 得到BE BF DF AD=,则可判定Rt △BEF ∽Rt △DFA ,所以∠4=∠3,再证明∠4=∠5,然后根据等腰三角形的性质可判断EF=EP,【详解】(1)∵四边形ABCD 为正方形,∴AB=AD,∠BAD=90°,∵BE ⊥AP,DF ⊥AP,∴∠BEA=∠AFD=90°,∵∠1+∠2=90°,∠2+∠3=90°,∴∠1=∠3,在△ABE 和△DAF 中12BEA AFD AB DA ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABE≌△DAF,∴BE=AF,∴EF=AE,AF=AE,BE,(2)如图,∵AF DFBF AD=,而AF=BE,∴BE DFBF AD=,∴BE BFDF AD=,∴Rt△BEF∽Rt△DFA,∴∠4=∠3,而∠1=∠3,∴∠4=∠1,∵∠5=∠1,∴∠4=∠5,即BE平分∠FBP,而BE⊥EP,∴EF=EP,【点睛】本题考查了正方形的性质、全等三角形的判定与性质、相似三角形的判定与性质,熟练掌握相关的性质与定理、正确添加辅助线是解题的关键.2.(2020·上海九年级二模)如图,四边形ABCD是菱形,点E在AB延长线上,联结AC,DE,DE分别交BC,AC于点F,G,且CD AE AC AG⋅=⋅.求证:(1)ABC∽AGE;(2)2AB GD DE=⋅【分析】(1)只要证明AB ACAG AE=,又∠BAC=∠GAE,即可证明,ABC∽△AGE;(2)只要证明,ADG∽△EDA,可得AD DGDE AD=,推出AD2=DE•DG即可证明;【详解】证明:(1),CD AE AC AG ⋅=⋅,,CD AC AG AE=, ,四边形ABCD 是菱形,,AB CD =, ,AB AC AG AE =,,BAC GAE ∠=∠, ,ABC AGE ∽△△;(2),ABC AGE ∽△△,,ACB E ∠=∠, ,四边形ABCD 是菱形,,AB AD =,//BC AD ,,ACB CAD E ∠=∠=∠,,ADG ADE ∠=∠,,ADG EDA ∽△△,,AD DG DE AD=, ,2AD DE DG =⋅,,2AB DE DG =⋅.【点睛】本题考查相似三角形的性质、菱形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.3.(2020·上海九年级三模)已知:如图,点E 为□ABCD 对角线AC 上的一点,点F 在线段BE 的延长线上,且EF=BE ,线段EF 与边CD 相交于点G .(1)求证:DF //AC ;(2)如果AB=BE ,DG=CG ,联结DE 、CF ,求证:四边形DECF 是矩形.【分析】(1)根据平行四边形的性质得到BO=DO ,根据三角形的中位线定理即可得到结论;(2)根据平行四边形的性质得到AB ∥CD ,由平行线的性质得到∠BAE=∠GCE ,求得∠GEC=∠GCE ,得到GE=CG ,推出四边形DECF 是平行四边形,得到DG=CG=FG=GE ,于是得到结论.【详解】证明:(1)四边形ABCD 是平行四边形,BO DO ∴=.EF BE =,OE ∴是BDF 的中位线. //DF OE ∴,即//AC DF .(2)AB BE =,BAE BEA ∴∠=∠.四边形ABCD 是平行四边形,//AB CD ∴. BAE GCE ∴∠=∠.又BEA GEC ∠=∠,GEC GCE ∴∠=∠. GE CG ∴=.//DF AC ,∴△DFG ∽△CEG ,DG FG CG GE∴=. DG CG =,FG GE ∴=. ∴四边形DECF 是平行四边形.DG CG =,FG GE =,GE CG =. DG CG FG GE ∴===.DC EF ∴=. ∴四边形DECF 是矩形.【点睛】本题考查了矩形的判定和性质,平行四边形的判定和性质,三角形的中位线定理,相似三角形的判定与性质,熟练掌握矩形的判定和性质定理是解题的关键.4.(2020·上海大学附属学校九年级三模)已知:如图,在等腰梯形ABCD 中,AD ∥BC ,AB =DC ,过点D 作AC 的平行线DE ,交BA 的延长线于点E .求证:(1)△ABC ≌△DCB ;(2)DE·DC =AE·BD .【分析】(1)根据三角形全等的判定条件找到相应的条件:AC =DB ,AB =DC ,BC =CB ,即可证明;(2)根据题意证明△ADE∽△CBD,对应边成比即可求证.【详解】证明:(1)∵四边形ABCD是等腰梯形,∴AC=DB,∵AB=DC,BC=CB,∴△ABC≌△BCD,(2)∵△ABC≌△BCD,∴∠ACB=∠DBC,∠ABC=∠DCB,∵AD∥BC,∴∠DAC=∠ACB,∠EAD=∠ABC,∵ED∥AC,∴∠EDA=∠DAC,∴∠EDA=∠DBC,∠EAD=∠DCB,∴△ADE∽△CBD,∴DE︰BD=AE︰CD,∴DE·DC=AE·BD.【点睛】此题考查三角形全等的判定定理,相似三角形的证明及性质.5.(2020·上海九年级二模)已知:如图,在平行四边形ABCD中,对角线AC与BD交于点O,点E是DB延长线上的一点,且EA=EC,分别延长AD、EC交于点F.(1)求证:四边形ABCD为菱形;(2)如果∠AEC=2∠BAC,求证:EC•CF=AF•AD.【分析】(1)由四边形ABCD是平行四边形知OA=OC,结合EA=EC知EO⊥AC,从而得证;(2)先由∠AEB=∠CEB=12∠AEC,平行四边形ABCD为菱形得∠CDF=∠DAC+∠DCA=∠AEF,据此可证△FCD∽△F AE得FC CDFA AE,结合CD=AD,AE=CE可得答案.【详解】(1)∵四边形ABCD是平行四边形,∴OA=OC,又∵EA=EC,∴EO⊥AC,∴四边形ABCD是菱形;(2)∵∠AEB=∠CEB=12∠AEC,平行四边形ABCD为菱形,∴∠AEB=∠CEB=∠BAC=∠BCA=∠DAC=∠DCA,∠CDF=∠DAC+∠DCA=∠AEF,∴△FCD∽△F AE,∴FC CD FA AE=,∵CD=AD,AE=CE,∴FC ADFA CE=,即EC•CF=AF•AD.【点睛】此题考查相似三角形的判定与性质,等腰三角形的性质及相似三角形的判定与性质,解题的关键是掌握判定定理.6.(2020·上海九年级二模)如图,在平行四边形ABCD中,BE、DF分别是平行四边形的两个外角的平分线,∠EAF=12∠BAD,边AE、AF分别交两条角平分线于点E、F.(1)求证:△ABE∽△FDA;(2)联结BD、EF,如果DF2=AD•AB,求证:BD=EF.【分析】(1)根据角平分线的定义得到∠HDF=12∠HDC.根据平行四边形的性质得到AB∥CD.求得∠BAD=∠CDH.等量代换得到∠BAE=∠F,同理∠DAF=∠E,于是得到结论;(2)作AP平分∠DAB交CD于点P,由角平分线的定义得到∠DAP=12∠BAD,求得∠HDF=∠DAP,推出DF∥AP,同理BE∥AP,根据相似三角形的性质得到BE=DF,根据平行四边形的性质即可得到结论.【详解】解:(1)∵∠EAF =12∠BAD ,∴∠DAF+∠BAE =12∠BAD , ∵DF 平分∠HDC ,∴∠HDF =12∠HDC , 又∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴∠BAD =∠CDH ,∴∠HDF =∠EAF ,∴∠HDF =∠DAF+∠BAE ,又∵∠HDF =∠DAF+∠F ,∴∠BAE =∠F ,同理:∠DAF =∠E ,∴△ABE ∽△FDA ;(2)作AP 平分∠DAB 交CD 于点P ,∴∠DAP =12∠BAD , ∵∠HDF =12∠CDH ,且∠BAD =∠CDH ∴∠HDF =∠DAP ,∴DF ∥AP , 同理:BE ∥AP ,∴DF ∥BE ,∵△ABE ∽△FDA ,∴=AD DF BE AB,即BE•DF =AD•AB , 又∵DF 2=AD•AB ,∴BE =DF ,∴四边形DFEB 是平行四边形,∴BD =EF .【点睛】本题考查了相似三角形的判定和性质,平行四边形的性质,角平分线的定义,熟练掌握相似三角形的判定和性质是解题的关键.7.(2020·上海杨浦·九年级二模)如图,已知在正方形ABCD 中,对角线AC 与BD 交于点O ,点M在线段OD上,联结AM并延长交边DC于点E,点N在线段OC上,且ON=OM,联结DN与线段AE交于点H,联结EN、MN.(1)如果EN∥BD,求证:四边形DMNE是菱形;(2)如果EN⊥DC,求证:AN2=NC•AC.【分析】(1)根据正方形性质及ON=OM,求出MN∥CD,进而得出四边形DMNE是平行四边形,在证明出△AOM≌△DON即可得到平行四边形DMNE是菱形;(2)根据MN∥CD得到AN AMNC ME=,再由EN⊥DC得到EN∥AD,AC DCAN DE=,再由AB∥DC,得到AM ABME DE=,即可得到AN ACNC AN=,即为所求.【详解】证明:(1)如图1,∵四边形ABCD是正方形,∴OA=OB=OC=OD,AC⊥BD,∵ON=OM,∴ON OMOC OD=,∴MN∥CD,又∵EN∥BD,∴四边形DMNE是平行四边形,在△AOM和△DON中,∵∠AOM=∠DON=90°,OA=OD,OM=ON,∴△AOM≌△DON(SAS),∴∠OMA=∠OND,∵∠OAM+∠OMA=90°,∴∠OAM+∠OND=90°∴∠AHN=90°.∴DN⊥ME,∴平行四边形DMNE是菱形;(2)如图2,∵MN∥CD,∴AN AM NC ME=,∵四边形ABCD是正方形,∴AB∥DC,AB=DC,∠ADC=90°,∴AD⊥DC,又∵EN⊥DC,∴EN∥AD,∴AC DC AN DE=,∵AB∥DC,∴AM ABME DE=,∴AN ACNC AN=,∴AN2=NC•AC.【点睛】此题考查正方形相关知识,主要是利用平行线分线段成比例求解,难度较大.1.(2020·上海九年级二模)如图,在△ABC中,AB=AC,点D在边BC上,联结AD,以AD 为一边作△ADE ,满足AD =AE ,∠DAE =∠BAC ,联结EC .(1)求证:CA 平分∠DCE ;(2)如果AB 2=BD•BC ,求证:四边形ABDE 是平行四边形.【分析】(1)根据等腰三角形的性质得到∠B =∠ACB ,证明△ABD ≌△ACE ,根据全等三角形的性质得到∠B =∠ACE ,根据角平分线的定义证明结论;(2)根据相似三角形的判定定理得到△ABD ∽△CBA ,得到∠BAD =∠ACB ,分别证明AE ∥BD ,AB ∥DE ,根据平行四边形的判定定理证明.【详解】(1)证明:∵AB =AC ,∴∠B =∠ACB ,∵∠DAE =∠BAC ,∴∠BAC ﹣∠DAC =∠DAE ﹣∠DAC ,即∠BAD =∠CAE , 在△ABD 和△ACE 中,AB AC BAD CAE AD AE =∠=∠=⎧⎪⎨⎪⎩,∴△ABD ≌△ACE (SAS ),∴∠B =∠ACE ,∴∠ACB =∠ACE ,∴CA 平分∠DCE ;(2)证明:∵AB 2=BD•BC ,∴AB BC =BD AB , 又∠B =∠B ,∴△ABD ∽△CBA ,∴∠BAD =∠ACB ,∵△ABD ≌△ACE ,∴∠BAD =∠CAE ,∴∠CAE =∠ACB ,∴AE ∥BD ,∵AB=AC,AD=AE,∠DAE=∠BAC,∴∠ACB=∠ADE,∴∠BAD=∠ADE,∴AB∥DE,∵AE∥BD,AB∥DE,∴四边形ABDE是平行四边形.【点睛】本题考查的是相似三角形的判定和性质、全等三角形的判定和性质、平行四边形的判定,掌握等腰三角形的性质、相似三角形的判定定理和性质定理是解题的关键.2.(2020·上海九年级二模)已知:如图,在梯形ABCD中,CD∥AB,∠DAB=90°,对角线AC、BD相交于点E,AC⊥BC,垂足为点C,且BC2=CE•CA.(1)求证:AD=DE;(2)过点D作AC的垂线,交AC于点F,求证:CE2=AE•AF.【分析】(1)根据相似三角形的判定定理得到△BCE∽△ACB,根据相似三角形的性质得到∠CBE=∠CAB,根据等角的余角相等得到∠BEC=∠DAE,根据等腰三角形的判定定理证明;(2)根据平行线分线段成比例定理得到CE BEEF DE=,BE AEDE CE=,得到CE AEEF CE=,整理得到CE2=AE•EF,根据等腰三角形的三线合一得到AF=EF,证明结论.【详解】证明:(1)∵BC2=CE•CA,∴BC CACE BC=,又∠ECB=∠BCA,∴△BCE∽△ACB,∴∠CBE=∠CAB,∵AC⊥BC,∠DAB=90°,∴∠BEC+∠CBE=90°,∠DAE+∠CAB=90°,∴∠BEC=∠DAE,∵∠BEC=∠DEA,∴∠DAE=∠DEA,∴AD=DE;(2)过点D作AC的垂线,交AC于点F,如图,∵DF ⊥AC ,AC ⊥BC ,∴∠DFE =∠BCA =90°,∴DF ∥BC ,∴CE BE EF DE=, ∵DC ∥AB ,∴BE AE DE CE =,∴CE AE EF CE =,∴CE 2=AE •EF , ∵AD =DE ,DF ⊥AC ,∴AF =EF ,∴CE 2=AE •AF .【点睛】本题考查的是相似三角形的判定和性质、直角梯形的概念,掌握相似三角形的判定定理和性质定理是解题的关键.3.(2020·上海九年级二模)已知:如图,四边形ABCD 是平行四边形,延长BA 至点E ,使得AE =AB ,联结DE 、AC .点F 在线段DE 上,联结BF ,分别交AC 、AD 于点G 、H .(1)求证:BG =GF ;(2)如果AC =2AB ,点F 是DE 的中点,求证:AH 2=GH •BH .【分析】(1)由平行四边形的性质可得AB =CD =AE ,AB ,CD ,可证四边形ACDE 是平行四边形,可得1BG AB GF AE==,可得结论; (2)由“SAS ”可证,BEF ,,DEA ,可得,EBF =,EDA ,通过证明,AHG ,,BHA ,可得结论.【详解】证明:(1),四边形ABCD 是平行四边形,,AB =CD ,AB ,CD ,,AB =AE ,,AE =CD ,,四边形ACDE 是平行四边形,,AC ,DE ,,1BG AB GF AE==,,BG =GF ; (2),AB =AE ,,BE =2AE ,,AC =2AB ,,BE =AC ,,四边形ACDE 是平行四边形,,AC =DE ,,DE =BE ,,点F 是DE 的中点,,DE =2EF ,,AE =EF ,,DE =BE ,,E =,E ,AE =EF ,,,BEF ,,DEA (SAS ),,,EBF =,EDA ,,AC ,DE ,,,GAH =,EDA .,,EBF =,GAH .,,AHG =,BHA ,,,AHG ,,BHA ,,AH GH BH AH=.,AH 2=GH •BH . 【点睛】本题考查了相似三角形的判定和性质,全等三角形的判定和性质,平行四边形的性质,灵活运用相似三角形判定和性质是本题的关键.4.(2020·上海九年级二模)如图,已知AB 、AC 是⊙O 的两条弦,且AO 平分∠BAC .点M 、N 分别在弦AB 、AC 上,满足AM =CN .(1)求证:AB =AC ;(2)联结OM 、ON 、MN ,求证:MN OM AB OA=.【分析】(1)过点O 作OD ⊥AB 于点D ,OE ⊥AC 于点E ,利用角平分线的性质和垂径定理即可得出答案;(2)联结OB ,OM ,ON ,MN ,首先证明BOM AON ≅,然后再证明NOM BOA ,根据相似三角形的性质即可得出答案.【详解】证明:(1)过点O 作OD ⊥AB 于点D ,OE ⊥AC 于点E ,如图所示:∵AO 平分∠BAC .∴OD =OE .222222,AD AO OD AE AO OE =-=-, AD AE ∴=.,OD AB OE AC ⊥⊥,2,2AB AD AC AE ∴==, ∴AB =AC ;(2)联结OB ,OM ,ON ,MN ,如图所示,∵AM =CN ,AB =AC ∴BM =AN .∵OA =OB ,∴∠B =∠BAO .∵∠BAO =∠OAN ,∴∠B =∠OAN ,∴△BOM ≌△AON (SAS ),∴∠BOM =∠AON ,OM =ON ,∴∠AOB =∠MON ,∴△NOM ∽△BOA , ∴MN OM AB OA=. 【点睛】本题主要考查相似三角形的判定及性质,全等三角形的判定及性质及圆的有关性质,熟练掌握相关性质及定理是解题的关键.5.(2020·上海九年级二模)如图,已知四边形ABCD 是矩形,点E 在对角线AC 上,点F 在边CD 上(点F 与点C 、D 不重合),BE EF ⊥,且45ABE CEF ∠+∠=︒.(1)求证:四边形ABCD 是正方形;(2)联结BD ,交EF 于点Q ,求证:DQ BC CE DF ⋅=⋅.【答案】(1)四边形ABCD 是正方形(过程见详解)(2)DQ BC CE DF ⋅=⋅(过程见详解)【分析】(1)本题借助辅助线利用45ABE CEF ∠+∠=︒,45FEM CEF ∠+∠=︒,找出∠DAC=45°得到DA=DC ,即可证明,(2)本题在(1)的条件下证明△CBE ~△DFQ ,即可求证.【详解】(1)分别作EP ⊥BC ,EM ⊥CD ,∵四边形ABCD 为矩形,∴∠ABE=∠BEP ,又BE ⊥EF ,∴∠BEP+∠FEP=∠FEP+∠FEM=90°,∴∠BEP =∠FEM ,∵45ABE CEF ∠+∠=︒,∴45BEP CEF ∠+∠=︒,∴45FEM CEF ∠+∠=︒, 即∠CEM=45°,∴∠DAC=45°,∴DA=DC ,∴矩形ABCD 为正方形.(2)由(1)得:∠QDF=∠BCE=45°,45ABE EBQ ∠+∠=︒,∵45ABE CEF ∠+∠=︒,∴CEF EBQ ∠=∠,∴4545CEF EBQ ∠+=∠+, 即∠EBC=∠DFQ(三角形外角等于与其不相邻两内角和),∴△CBE ~△DFQ ,∴DF DQ BC EC= ,∴DF ⨯EC=DQ ⨯BC , 即DQ BC CE DF ⋅=⋅.【点睛】此题从特殊四边形下手,涵盖知识点包括相似三角形的证明及性质.6.(2020·上海九年级二模)已知:△ABC ,AB =AC ,∠BAC =90°,点D 是边BC 的中点,点E 在边AB 上(点E 不与点A 、B 重合),点F 在边AC 上,联结DE 、DF .(1)如图1,当∠EDF =90°时,求证:BE =AF ;(2)如图2,当∠EDF =45°时,求证:22DE BE DF CF=.【分析】(1)连接AD ,证△BDE ≌△ADF (ASA ),即可得出结论;(2)证明△BDE ∽△CFD .得出BE BD DE CD CF DF ==,得出2()BE BD DE CD CF DF⋅=,由BD =CD ,即可得出结论.【详解】(1)连接AD ,如图1所示:在Rt △ABC 中,∵AB =AC ,∠BAC =90°,∴∠B =∠C =45°.∵点D 是边BC 的中点,∴AD 12=BC =BD ,AD ⊥BC ,∠BAD =∠CAD =45°, ∴∠B =∠CAD .∵∠EDF =90°,∴∠ADF +∠ADE =90°∵∠BDE +∠ADE =90°,∴∠BDE =∠ADF , 在△BDE 和△ADF 中,B CAD BD AD BDE ADF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△BDE ≌△ADF (ASA ),∴BE =AF ;(2)∵∠BDF =∠BDE +∠EDF ,∠BDF =∠C +∠CFD ,∴∠BDE +∠EDF =∠C +∠CFD .又∵∠C =∠EDF =45°,∴∠BDE =∠CFD ,∴△BDE ∽△CFD , ∴BE BD DE CD CF DF ==,∴2()BE BD DE CD CF DF⋅=, 又∵BD =CD ,∴22DE BE DF CF=. 【点睛】本题考查了相似三角形的判定与性质、全等三角形的判定与性质、等腰直角三角形的性质等知识;熟练掌握等腰直角三角形的性质,证明三角形全等和三角形相似是解题的关键.7.(2020·上海九年级二模)如图,已知四边形ABCD 菱形,对角线AC BD 、相交于点O ,DH AB ⊥,垂足为点H ,交AC 于点E ,连接HO 并延长交CD 于点G .(1)求证:12DHO BCD ∠=∠; (2)求证:2HG AE DE CG =.【分析】(1)(1)先根据菱形的性质得OD=OB ,AB ∥CD ,BD ⊥AC ,则利用DH ⊥AB 得到DH ⊥CD ,∠DHB=90°,所以OH 为Rt △DHB 的斜边DB 上的中线,得到OH=OD=OB ,利用等腰三角形的性质得∠1=∠DHO ,然后利用等角的余角相等证明结论;(2)根据//AB CD ,推出12OH OG HG ==,再证AED CGO ∆∆∽,即可推出••OG AE CG DE =,即可证出结论.【详解】(1)∵四边形ABCD 是菱形,//,,,AB CD AB CD AC BD DO BO ∴=⊥=,12ACD BCD ∠=∠, DH AB ⊥,90DHA DHB ∴∠=∠=︒,//AB CD ,90DHA HDC ∴∠=∠=︒,90BDH BDC ∴∠+∠=︒,90COD ∠=︒,90ACD BDC ∴∠+∠=︒,90,DHB DO BO ∴∠=︒=,OD OH ∴=,BDH DHO ∴∠=∠,12DHO BCD ∴∠=∠.(2)//AB CD ,1HO OB OG OD ∴==,12OH OG HG ∴==, AD CD =,DCA DAC ∴∠=∠,,AED HDC DCA HGC HDC DHG ∠=∠+∠∠=∠+∠,又DHO DCA ∠=∠,AED HGC ∴∠=∠,AED ∴∆,CGO ∆,OG CG DE AE ∴=,••OG AE CG DE ∴=,1••2HG AE DE CG ∴=, ∴2HG AE DE CG =.【点睛】本题考查了相似三角形的判定和性质,菱形的性质,直角三角形的性质,熟记个性质定理是解题的关键.8.(2020·上海九年级二模)已知:如图,在平行四边形ABCD 中,对角线AC 与BD 相交于点E ,过点E 作AC 的垂线交边BC 于点F ,与AB 的延长线交于点M ,且AB AM AE AC ⋅=⋅.求证:(1)四边形ABCD 是矩形;(2)2DE EF EM =⋅.【分析】(1)由AB AM AE AC ⋅=⋅可得AB AE AC AM=,又∠CAB=∠EAM ,从而推出△ABC ∽△AEM ,继而推出∠ABC=∠AEM=90°,从而可得出结论;(2)先证明△EFB ∽△EBM ,从而推出EB EF EM EB=,得出2EB EF EM =⋅,又DE=BE ,从而可得出结果.【详解】证明:(1)∵AB AM AE AC ⋅=⋅,∴AB AE AC AM=, 又∠CAB=∠EAM ,∴△ABC ∽△AEM ,∴∠ABC=∠AEM=90°,又四边形ABCD 为平行四边形,∴四边形ABCD 为矩形;(2)∵四边形ABCD 为矩形,∴AE=BE=DE=CE ,∴∠EAB=∠EBA ,又∠EAB+∠M=90°,∠EBA+∠EBF=90°∴∠M=∠EBF , 又∠FEB=∠BEM ,∴△EFB ∽△EBM ,∴EB EF EM EB=, ∴2EB EF EM =⋅,∴2DE EF EM =⋅.【点睛】本题考查了相似三角形的判定与性质,矩形的判定与性质以及等腰三角形的性质等知识,综合运用基本性质进行推理是解题的关键.9.(2020·上海九年级二模)如图,E F 、分别是正方形ABCD 的边DC CB 、的中点,以AE 为边作正方形AEHG ,HE 与BC 交于点Q ,联结AQ DF 、.(1)求证:AE DF ⊥;(2)设123,,,CEQ AED EAQ S S S S S S ∆∆∆===,求证123S S S +=.【分析】(1)先说明△ADE ≌△DCF,然后再利用同角的余角相等以及垂直的定义即可证明;(2)先证△ADE ∽△ECQ ,得出1 2QE CE DE AE AD AD ===,进而可得△AEQ ∽△ADE ∽△ECQ ,然后根据相似三角形的性质即可证明.【详解】(1)证明:∵四边形ABCD 是正方形∴AD=DC ,∠ADE=∠DCF=90°在△ADE 和△DCF 中AD DC ADE DCF DE CF =⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△DCF (SAS )∴∠EAD=∠CDF∵∠AED+∠EAD=90°∴∠AED+∠CDF=90°∴AE ⊥DF ;(2)∵∠ADE=∠C ,∠CEQ=∠EAD ,∴△ADE ∽△ECQ∵E 是CD 的中点∴1 2QE CE DE AE AD AD ===, ∵∠ADE=∠C=90°∴△AEQ ∽△ADE ∽△ECQ设CE DE a ==,则AD=2a ,∴1315S S =,234 5S S =,∴123 S S S +=. 【点睛】本题考查了正方形的性质,全等三角形、相似三角形的判定和性质,灵活应用全等三角形、相似三角形的判定和性质是解答本题的关键.10.(2020·上海九年级二模)如图,已知C 是线段AB 上的一点,分别以AC 、BC 为边在线段AB 同侧作正方形ACDE 和正方形CBGF ,点F 在CD 上,联结AF 、BD ,BD 与FG 交于点M ,点N 是边AC 上的一点,联结EN 交AF 与点H .(1)求证:AF=BD;(2)如果AN GMAC GF=,求证:AF EN⊥.【分析】(1)根据SAS证明△ACF≌△DCB即可得到结论;(2)根据正方形的性质得到AE=AC,GF=GB,由AN GMAC GF=证得AN GMAE GB=得到△EAN∽△BGM,再证明△MBG∽△BDC,由△BDC≌△FAC,得到△EAN∽△ACF,推出∠CAF+∠ANE=90°,即可得到结论.【详解】(1)在正方形ACDE和正方形CBGF中,AC=CD,CF=CB,∠ACD=∠BCD=90°,∴△ACF≌△DCB,∴AF=BD;(2)在正方形ACDE和正方形CBGF中,AE=AC,GF=GB,∵AN GMAC GF=,∴AN GMAE GB=,∵∠EAN=∠G=90°,∴△EAN∽△BGM,∵CD∥BG,∴∠CDB=∠MBG,∵∠DCB=∠G=90°,∴△MBG∽△BDC,∵△BDC≌△FAC,∴△EAN∽△ACF,∴∠AEN=∠CAF,∵∠AEN+∠ANE=90°,∴∠CAF+∠ANE=90°,∴∠AHN=90°,∴AF EN⊥.【点睛】此题考查全等三角形的判定及性质,正方形的性质,相似三角形的判定及性质. 11.(2020·上海九年级二模)如图,已知在平行四边形ABCD 中,AE ⊥BC ,垂足为E ,CE=AB ,点F 为CE 的中点,点G 在线段CD 上,联结DF ,交AG 于点M ,交EG 于点N ,且∠DFC=∠EGC .(1)求证:CG=DG ;(2)求证:2CG GM AG =⋅.【分析】(1)首先证明△ECG ≌△DCF ,则有CG=CF ,因为CF=12CE ,则有CG=12CD ,则结论可证; (2)延长AG 、BC 交于点H ,首先证明△ADG ≌△HCG ,则有AG=HG ,然后根据直角三角形斜边中线有AG=HG=EG ,进而得出∠CDF=∠DAH ,进一步可证△ADG ∽△DMG ,则有MG DG DG AG=,即2DG GM AG =⋅,又因为CG=DG 即可证明结论. 【详解】证明:(1)∵四边形ABCD 是平行四边形,CE=AB ,∴AB=CD=EC .又∵∠DFC=∠EGC ,∠FCD=∠GCE ,∴△ECG ≌△DCF ,∴CG=CF .∵点F 为CE 的中点,∴CF=12CE ,∴CG=12CD ,即:CG=DG . (2)延长AG 、BC 交于点H .∵△ECG≌△DCF,∴∠CEG=∠CDF,DG=CG.∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAH=∠H,∠ADC=∠DCH.∴△ADG≌△HCG,∴AG=HG.∵AE⊥BC,∴∠AEC=90°,∴AG=HG=EG.∴∠CEG=∠H,∴∠CDF=∠DAH.又∵∠AGD=∠DGM,∴△ADG∽△DMG.∴MG DGDG AG=,∴2DG GM AG=⋅又,CG=DG,,2CG GM AG=⋅.【点睛】本题主要考查全等三角形的判定及性质,相似三角形的判定及性质,掌握全等三角形的判定及性质,相似三角形的判定及性质是解题的关键.12.(2020·上海九年级一模)已知:如图,△ABC中,∠ACB=90°,D在斜边AB上,DE⊥AC,DF⊥BC,垂足分别为E,F.(1)当∠ACD=∠BCD时,求证:四边形DECF是正方形;(2)当∠BCD=∠A时,求证:CD CF CA AD=.【分析】(1)由垂直的定义可得出,DEC=,DFC,结合,ECF=90°可得出四边形DECF为矩形,由,ACD =,BCD 可得出CD 平分,ACB ,利用角平分线的性质可得出DE =DF ,再利用“邻边相等的矩形是正方形”可证出四边形DECF 是正方形;(2)由,BCD +,ACD =,ACB =90°,,BCD =,A 可得出,A +,ACD =90°,利用三角形内角和定理可求出,ADC =90°,由,DCF =,A ,,DFC =,ADC =90°可证出,CDF ,,ACD ,再利用相似三角形的性质可证出CD CF CA AD=. 【详解】证明:(1),DE ,AC ,DF ,BC ,,,DEC =,DFC =90°,又,,ECF =90°,,四边形DECF 为矩形.,,ACD =,BCD ,,CD 平分,ACB ,,DE =DF ,,四边形DECF 是正方形.(2),,BCD +,ACD =,ACB =90°,,BCD =,A ,,,A +,ACD =90°,,,ADC =180°﹣90°=90°.,,DCF =,A ,,DFC =,ADC =90°,,,CDF ,,ACD ,,CD CF CA AD=. 【点睛】本题考查了相似三角形的判定与性质以及正方形的判定,解题的关键是:(1)利用“邻边相等的矩形是正方形”,证出四边形DECF 是正方形;(2)利用“两角对应相等两三角形相似”证出△CDF ∽△ACD .13.(2020·上海)如图,在ABC 中,点D 、E 分别在边AB 、BC 上,AE 与CD 交于点F ,若AE 平分BAC ∠,AB AF AC AE ⋅=⋅.(1)求证:AFD AEC ∠=∠;(2)若//EG CD ,交边AC 的延长线于点G ,求证:CD CG FC BD ⋅=⋅.【分析】(1)先证△BAE∽△CAF,推出∠AEB=∠AFC,由等角的补角相等可得出结论;(2)先后证明∠DCB=∠CEG,∠G=∠ACF=∠B,推出△BDC∽△GCE,由相似三角形的性质可得出结论.【详解】(1)证明:∵AB•AF=AC•AE,∴AB AC AE AF=,∵AE平分∠BAC,∴∠BAE=∠CAE,∴△BAE∽△CAF,∴∠AEB=∠AFC,∴180°−∠AEB=180°−∠AFC,∴∠AEC=∠AFD;(2)证明:∵∠CFE=∠AFD=∠CEF,∴CE=CF,∵DC∥EG,∴∠DCB=∠CEG,∠G=∠ACF=∠B,∴△BDC∽△GCE,∴BD GC GCDC CE CF==,∴CD•CG=FC•BD.【点睛】本题考查了相似三角形的判定与性质,解题关键是能够灵活运用相似三角形的判定与性质.14.(2020·上海九年级一模)如图,在Rt△ABC中,∠ACB=90°,点D是边BC的中点,联结AD.过点C作CE⊥AD于点E,联结BE.(1)求证:BD2=DE•AD;(2)如果∠ABC=∠DCE,求证:BD•CE=BE•DE.【分析】(1)证明△CDE∽△ADC推出CD DEAD CD=,可得CD2=DE•DA即可解决问题.(2)利用相似三角形的性质首先证明AC=BE,再证明△ACE∽△CDE,可得AC EC CD DE=,可得BE ECBD DE=即可解决问题.【详解】解:(1)证明:如图1中,∵CE⊥AD,∴∠CED=∠ACD=90︒,∵∠CDE=∠ADC,∴△CDE∽△ADC∴CD DEAD CD=,∴CD2=DE•DA,∵DB=CD,∴BD2=DE•DA.(2)解:如图2中,∵BD2=DE•DA,∴BD DA DE BD=,∵∠CDE=∠ADB,∴△BDE∽△ADB,∴∠DEB=∠ABC,∵∠ABD=∠ECD,∴∠BED=∠BCE,∵∠EBD=∠CBE,∴△EBD∽△CBE,∴BE BDCB BE=,∴BE2=BD•BC,∵CD=BD,∴BE2=2CD2,∵∠DCE+∠ACE=90︒,∠CAD+∠ACE=90︒,∴∠CAD=∠ECD=∠ABC,∵∠ACD=∠BCA,∴△ACD∽△BCA,∴AC CD BC AC=,∴AC2=CD•CB=2CD2,∴AC=BE,∵△ACE∽△CDE,∴AC ECCD DE=,∴BE ECBD DE=,∴BD•CE=BE•DE.【点睛】本题主要考查了相似三角形的判定与性质,掌握相似三角形的判定与性质是解题的关键.15.(2020·上海九年级一模)如图,在△ABC中,点D、E分别在边AB、BC上,AE与CD 交于点F,若AE平分∠BAC,AB•AF=AC•AE.(1)求证:∠AFD=∠AEC;(2)若EG∥CD,交边AC的延长线于点G,求证:CD•CG=FC•BD.【分析】(1)先证△BAE∽△CAF,推出∠AEB=∠AFC,由等角的补角相等可得出结论;(2)先证明∠DCB=∠CEG,∠G=∠ACF=∠B,推出△BDC∽△GCE,由相似三角形的性质可得出结论.【详解】(1)证明:∵AB•AF=AC•AE,∴AB AC AE AF=,∵AE平分∠BAC,∴∠BAE=∠CAE,∴△BAE∽△CAF,∴∠AEB=∠AFC,∴180°﹣∠AEB =180°﹣∠AFC ,∴∠AEC =∠AFD ;(2)证明:∵∠CFE =∠AFD =∠CEF ,∴CE =CF ,∵DC ∥EG ,∴∠DCB =∠CEG ,∠G =∠ACF =∠B ,∴△BDC ∽△GCE , ∴BD GC GC DC CE CF==,∴CD •CG =FC •BD . 【点睛】本题考查了相似三角形的判定与性质,解题关键是能够灵活运用相似三角形的判定与性质.16.(2020·上海九年级一模)已知:如图,在△ABC 中,点D 在边BC 上,AE ∥BC ,BE 与AD 、AC 分别相交于点F 、G , 2AF FG FE =⋅.(1)求证:△CAD ∽△CBG ;(2)联结DG ,求证:DG AE AB AG ⋅=⋅.【分析】(1)由2AF FG FE =⋅及∠AFG =∠EF A ,证得△F AG ∽△FEA ,结合AE ∥BC ,证得∠EBC =∠F AG ,从证得结论;(2)由(1)的结论得到=CA CD CB CG ,证得△CDG ∽△CAB ,结合AE ∥BC ,证得=AG GC AE CB ,继而证得结论.【详解】(1)∵2AF FG FE =⋅,∴=AF FE FG AF. 又∵∠AFG =∠EF A ,∴△F AG ∽△FEA . ∴∠F AG =∠E .∵AE ∥BC ,∴∠E =∠EBC . ∴∠EBC =∠F AG .又∵∠ACD =∠BCG ,∴△CAD ∽△CBG .(2)∵△CAD ∽△CBG ,∴=CA CD CB CG. 又∵∠DCG =∠ACB ,∴△CDG ∽△CAB , ∴=DG CG AB CB. ∵AE ∥BC ,∴=AE AG CB GC . ∴=AG GC AE CB ,∴=DG AG AB AE, ∴DG AE AB AG ⋅=⋅.【点睛】本题考查了相似三角形的判定和性质,平行线分线段成比例定理,灵活运用比例的性质以及中间比是解题的关键.17.(2020·上海九年级一模)如图,△ABC 中,AB =AC ,AM 为BC 边的中线,点D 在边AC 上,联结BD 交AM 于点F ,延长BD 至点E ,使得BD DE =AD DC,联结CE . 求证:(1)∠ECD =2∠BAM ;(2)BF 是DF 和EF 的比例中项.【分析】(1)由等腰三角形的性质可得∠BAC=2∠BAM,通过证明△ADB∽△CDE,可得∠BAC=∠ECD=2∠BAM;(2)由等腰三角形的性质可得BF=CF,通过证明△DCF∽△CEF,可得DF CFCF EF=,可得结论.【详解】证明:(1)∵AB=AC,AM为BC边的中线,∴∠BAC=2∠BAM,∵BDDE=ADDC,∠ADB=∠CDE,∴△ADB∽△CDE,∴∠BAC=∠ECD,∴∠ECD=2∠BAM;(2)如图,连接CF,∵AB=AC,AM为BC边的中线,∴AM是BC的垂直平分线,∴BF=CF,且AB=AC,AF=AF,∵△ABF≌△ACF(SSS)∴∠ABF=∠ACF,由(1)可知:△ADB∽△CDE,∴∠ABF=∠E,∴∠ACF=∠E,且∠EFC=∠DFC,∴△DCF∽△CEF,∴DF CFCF EF=,且BF=CF,∴BF2=DF•EF,∴BF是DF和EF的比例中项.【点睛】主要考查了相似三角形的判定及其性质的应用等几何知识点问题;对综合的分析问题解决问题的能力提出了较高的要求.18.(2020·上海九年级一模)如图,在平行四边形ABCD 中,点E 在边AD 上,点F 在边CB 的延长线上,联结,CE EF ,2CE DE CF =•.(1)求证:D CEF ∠=∠;(2)联结AC ,交EF 于点G ,如果AC 平分ECF ∠,求证:AC AE CB CG •=•.【分析】(1)由∠FCE=∠CED ,2CE DE CF =⋅,可得:∆FCE ~∆CED ,即可得到结论;(2)先证∆ECG~∆DAC ,可得:EC CG DA AC=,结合AE=CE ,DA=CB ,即可得到结论. 【详解】(1)∵在平行四边形ABCD 中,∴AD ∥BC ,∴∠FCE=∠CED ,∵2CE DE CF =⋅,∴CF EC EC DE=,∴∆FCE ~∆CED ,∴D CEF ∠=∠; (2)∵AC 平分ECF ∠,∴∠ACE=∠ACB ,∵AD ∥BC ,∴∠ACB=∠CAE ,∴∠ACE=∠CAE ,∴AE=CE ,∵D CEF ∠=∠,∴∆ECG~∆DAC ,∴EC CG DA AC=,∴AC EC DA CG ⋅=⋅, ∵DA=CB ,∴AC AE CB CG ⋅=⋅【点睛】本题主要考查相似三角形的判定和性质定理,根据题意,找到对应角相等,对应边成比例,以及进行适当的等量代换,是解题的关键.19.(2020·上海)如图, ABC ∆中, AD BC ⊥,E 是 AD 边上一点,联结 BE ,过点 D 作DF BE ⊥,垂足为 F ,且AE DF EF CD ⋅=⋅,联结 AF 、CF , C F 与边 AD 交于点 O .求证:(1)EAF DCF ∠=∠;(2) AF BD AC DF ⋅=⋅.【分析】(1)证明△AEF ∽△CDF ,根据相似三角形的性质证明结论;(2)证明△AOF ∽△COD ,得到AO OC OF OD=,得到△AOC ∽△FOD ,根据相似三角形的性质得到∠ACF =∠EDF ,证明△BFD ∽△CFA ,根据相似三角形的性质证明结论.【详解】(1)证明:,AD BC DF BE ⊥⊥90ADB DFE ︒∴∠=∠=90,90DBE BED DBE BDF ︒︒∴∠+∠=∠+∠=BED BDF ∴∠=∠AEF CDF ∴∠=∠AE DF CD EF ⋅=⋅AE EF CD DF∴=AEF CDF ∴∆∆∽EAF DCF ∴∠=∠(2)证明:AEF CDF ∆∆∽,EFA DFC ∴∠=∠90AFO EFD ︒∴∠=∠=90DFB ︒∠=BFD AFC ∴∠=∠,EAF DCF AOF COD ∠=∠∠=∠AOF COD ∴∆∆∽AO OF OC OD ∴=AO OC OF OD ∴= 又AOC FOD ∠=∠AOC FOD ∴∆∆∽ACF EDF ∴∠=∠90DBE BED FDE BED ︒∠+∠=∠+∠=DBE EDF ∴∠=∠ACF DBE ∴∠=∠又BFD AFO ∠=∠BFD CFA ∴∆∆∽AF AC DF BD ∴=AF BD AC DF ∴⋅=⋅ 【点睛】本题考查的是相似三角形的判定和性质,掌握相似三角形的判定定理和性质定理是解题的关键.20.(2020·上海九年级一模)如图,已知ABC ∆和ADE ∆,点D 在BC 边上,,DA DC ADE B =∠=∠,边DE 与AC 相交于点F .(1)求证:AB AD DF BC ⋅=⋅;(2)如果//AE BC ,求证:BD DF DC FE=. 【分析】(1)根据等边对等角得到ADE B ∠=∠,通过证明△ABC ∽△FDA 得对应边成比例,化比例式为等积式即可;(2)通过证明△AEF ∽△CDF 和△ABD ∽△EDA,根据相似三角形的性质列两个比例式,用等量代换即可得.【详解】(1)证明:∵AD=DC,∴∠DAC=∠C,∵∠ADE=∠B,∴△ABC ∽△FDA,∴AD DF BC AB,∴AB AD DF BC ⋅=⋅. (2)证明:∵AE ∥BC,∴∠E=∠EDC, ∠EAC=∠C,∴△AEF ∽△CDF,∴DF DC FE AE ,∴DF AD FE AE, ∵∠ADC=∠ADE+∠EDC=∠B+∠BAD, ∠ADE=∠B,∴∠BAD=∠EDC,∴∠BAD=∠E,∴△ABD ∽△EDA,∴BD AD AD AE, ∴BD AD CD AE ,∴BD DF DC FE =. 【点睛】本题考查相似三角形的判定和性质的综合应用,借助中间比进行等量代换是解答此题的关键.21.(2020·上海九年级一模)如图,在ABC ∆中,点,,,D E F G 分别在,,AB AC BC 上,3AB AD =,2CE AE =,BF FG CG ==,DG 与EF 交于点H .(1)求证:FH AC HG AB •=•;(2)连接,DF EG ,求证:A FDG GEF ∠=∠+∠.【分析】(1)根据已知条件先证明DG ∥AC ,EF ∥AB ,可得∠HGF=∠C ,∠HFG=∠B ,即可证明△HFG ∽△ABC ,从而可得结论;(2)连接DF ,EG ,DE ,证明四边形DFGE 和ADHE 是平行四边形,即可证得结论.【详解】∵AB=3AD ,BF=FG=CG ,∴BD=2AD ,BG=2CG , ∴2BD BG AD CG==,∴DG ∥AC, 同理可得,EF ∥AB ,∴∠HFG=∠ABC ,∠HGF=∠ACB ,∴△HFG ∽△ABC ,∴FH HG AB AC=,即FH AC HG AB •=•; (2)连接,DF EG ,DE,如图所示,∵EF ∥AB ,∴GH GF HD FB=, ∵GF=FB ∴GH GF HD FB==1,∴GH=HD ,同理可证,FH=EH ,∴四边形DFGE 是平行四边形,∴DF ∥EG ,∴∠FDG=∠EGD ,∴∠FHG=∠EGH+∠HEG ,∵∠DHE=∠FHG ,∴∠DHE=∠EGH+∠HEG=FDG GEF ∠+∠,由EF ∥AB ,DG ∥AC,得四边形ADHE 是平行四边形,∴∠A=∠DHE ,∴A FDG GEF ∠=∠+∠【点睛】此题主要考查了平行线分线段成比例的判定与性质,以及平行四边形的判定与性质,熟练掌握相减的判定与性质是解决此题的关键.22.(2020·上海九年级一模)已知:如图,在△ABC 中,点D ,E 分别在边AB 、 AC 上,DE ∥BC ,∠ABE=∠C ,(1)求证:2BE DE BC =⋅(2)当BE 平分∠ABC 时,求证:BD AE BE AB=【分析】(1)利用平行线的性质可知DEB EBC ∠=∠,则有BED CEB ,利用相似三角形的性质即可得出结论;(2)利用平行线的性质及角平分线的性质可知DAE EAB ,利用相似三角形的性质即可得出结论.【详解】解:(1)DE BC ∥DEB EBC ∴∠=∠ABE C ∠=∠BED CEB ∴BE DE BC BE∴=2BE DE BC ∴= (2)BE 平分ABC ∠ABE EBC ∴∠=∠DE BC ∥,DEB EBC C AED ABE ∴∠=∠∠=∠=∠ABE DEB ∠=∠BD DE ∴=,A A AED ABE ∠=∠∠=∠DAE EAB ∴DE AE BE AB∴= 【点睛】本题主要考查平行线的性质,角平分线定义,相似三角形的判定及性质,掌握三角形相似的判定方法是解题的关键.23.(2020·上海九年级一模)如图,在⊙O 中,AB 、CD 是两条弦,⊙O 的半径长为rcm,弧AB 的长度为1l cm,弧CD 的长度为2l cm(温馨提醒:弧的度数相等,弧的长度相等,弧相等,有联系也有区别) 当1l =2l 时,求证:AB=CD【分析】利用弧长公式得出圆心角相等,再利用圆心角,弧,弦之间的关系即可证明.【详解】解:令∠AOB=α,∠COD=β.∵1l =2l ∴12180180r r απβπ=∵AB 和CD 在同圆中,r 1=r 2 ∴α=β∴AB=CD【点睛】本题主要考查弧长公式及圆心角,弧,弦之间的关系,掌握圆心角,弧,弦之间的关系是解题的关键.。
2019-2021年上海各区数学中考一模压轴题分类汇编18题-图形的旋转含详解
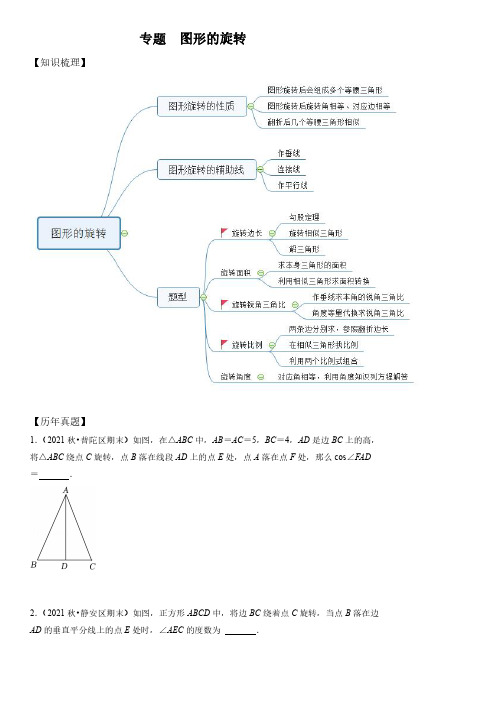
专题图形的旋转【知识梳理】【历年真题】1.(2021秋•普陀区期末)如图,在△ABC中,AB=AC=5,BC=4,AD是边BC上的高,将△ABC绕点C旋转,点B落在线段AD上的点E处,点A落在点F处,那么cos∠FAD =.2.(2021秋•静安区期末)如图,正方形ABCD中,将边BC绕着点C旋转,当点B落在边AD的垂直平分线上的点E处时,∠AEC的度数为.3.(2021秋•杨浦区期末)如图,已知在Rt△ABC中,∠C=90°,tan A=512,将△ABC绕点A逆时针旋转90°后得△ADE,点B落在点D处,点C落在点E处,联结BE、CD,作∠CAD的平分线AN,交线段BE于点M,交线段CD于点N,那么AMAN的值为.4.(2021秋•嘉定区期末)如图,在△ABC中,∠C=90°,BC=2,AB=25D在边AC上,CD:AD=1:3,联结BD,点E在线段BD上,如果∠BCE=∠A,那么CE=.5.(2021秋•松江区期末)如图,已知矩形ABCD中,AD=3,AB=5,E是边DC上一点,将△ADE绕点A顺时针旋转得到△AD′E′,使得点D的对应点D'落在AE上,如果D′E′的延长线恰好经过点B,那么DE的长度等于.6、(2021秋•黄浦区期末17)如图,在△ABC中,AB=4,AC=5,将△ABC绕点A旋转,使点B落在AC边上的点D处,点C落在点E处,如果点E恰好在线段BD的延长线上,那么边BC的长等于.7.(2020秋•嘉定区期末)已知在△ABC 中,∠ACB =90°,AB =10,sin A =55(如图),把△ABC 绕着点C 按顺时针方向旋转α°(0<α<360),将点A 、B 的对应点分别记为点A ′,B ′,如果△AA ′C 为直角三角形,那么点A 与点B '的距离为.8.(2020秋•闵行区期末)如图,在Rt △ABC 中,∠ACB =90°,AB =3,tan B =.将△ABC 绕着点A 顺时针旋转后,点B 恰好落在射线CA 上的点D 处,点C 落在点E 处,射线DE 与边AB 相交于点F ,那么BF =.9.(2020秋•静安区期末)在Rt △ABC 中,∠C =90°,AB =13,tan B =23(如图),将△ABC 绕点C 旋转后,点A 落在斜边AB 上的点A ',点B 落在点B ',A 'B '与边BC 相交于点D ,那么'CD A D 的值为.10.(2020秋•杨浦区期末)如图,已知在△ABC 中,∠B =45°,∠C =60°,将△ABC 绕点A 旋转,点B 、C 分别落在点B 1、C 1处,如果BB 1∥AC ,联结C 1B 1交边AB 于点D ,那么1BD B D 的值为.11.(2020秋•宝山区期末)在Rt △ABC 中,∠ACB =90°,AC =BC ,点E 、F 分别是边CA 、CB 的中点,已知点P 在线段EF 上,联结AP ,将线段AP 绕点P 逆时针旋转90°得到线段DP ,如果点P 、D 、C 在同一直线上,那么tan ∠CAP =.12.(2020秋•奉贤区期末)如图,在Rt △ABC 中,∠ACB =90°,AC =3,BC =4,CD 是△ABC 的角平分线,将Rt △ABC 绕点A 旋转,如果点C 落在射线CD 上,点B 落在点E 处,联结DE ,那么∠AED 的正切值为.13.(2019秋•奉贤区期末)如图,已知矩形ABCD (AB >BC ),将矩形ABCD 绕点B 顺时针旋转90°,点A 、D 分别落在点E 、F 处,连接DF ,如果点G 是DF 的中点,那么∠BEG 的正切值是.14.(2019秋•浦东新区期末)在Rt △ABC 中,∠C =90°,AC =2,BC =4,点D 、E 分别是边BC 、AB 的中点,将△BDE 绕着点B 旋转,点D 、E 旋转后的对应点分别为点D '、E ',当直线D 'E '经过点A 时,线段CD '的长为.15.(2019秋•长宁、金山区期末)如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=4点P在边BC上,联结AP,将△ABP绕着点A旋转,使得点P与边AC的中点M重合,点B的对应点是点B′,则BB′的长等于.16.(2019秋•松江区期末)如图,矩形ABCD中,AD=1,AB=k,将矩形ABCD绕着点B 顺时针旋转90°得到矩形A′BC′D′,联结AD′,分别交边CD,A′B于E、F,如果AE D′F,那么k=.17.(2019秋•嘉定区期末)在△ABC中,∠ACB=90°,AB=10,cos A=35(如图),把△ABC绕着点C按照顺时针的方向旋转,将A、B的对应点分别记为点A'、B'.如果A'B'恰好经过点A,那么点A与点A'的距离为.18.(2019秋•徐汇区期末)如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕着点B顺时针旋转后得到矩形A'BC'D',点A的对应点A'在对角线AC上,点C、D分别与点C'、D'对应,A′D'与边BC交于点E,那么BE的长是.19.(2019秋•普陀区期末)如图,在RtΔABC中,∠C=90°,AC=5,sinB=513,点P为边BC上一点,PC=3,将△ABC绕点P旋转得到△A'B'C'(点A,B、C分别与点A'、B'、C'对应).使B'C'∥AB,边A'C'与边AB交于点G,那么A'G 的长等于.专题图形的旋转【历年真题】1.(2021秋•普陀区期末)如图,在△ABC 中,AB =AC =5,BC =4,AD 是边BC 上的高,将△ABC 绕点C 旋转,点B 落在线段AD 上的点E 处,点A 落在点F 处,那么cos ∠FAD =21332-.【考点】旋转的性质;解直角三角形;等腰三角形的性质;勾股定理.【专题】几何综合题;推理能力.【分析】如图,过点F 作FG ⊥AD 于点G ,由旋转可知:CE =BC =4,CF =EF =AB =AC =5,利用三角函数可得∠ECD =60°,进而可得:DE =AF =EF =5,运用勾股定理可得AD ,AE ﹣,由等腰三角形性质可得AG =EG =21332-,再运用三角函数可得cos ∠FAD =AG AF =.【解答】解:如图,过点F 作FG ⊥AD 于点G ,∵将△ABC 绕点C 旋转,点B 落在线段AD 上的点E 处,点A 落在点F 处,∴CE =BC =4,CF =EF =AB =AC =5,∵AB =AC ,AD 是边BC 上的高,∴BD =CD =2,∴cos ∠ECD =2142CD CE ==,∴∠ECD =60°,∴DE =CE •sin ∠ECD =4×sin60°=,∵∠ACF =∠ECD =60°,∴△ACF 是等边三角形,∴AF =EF =5,在Rt △ACD 中,AD ===,∴AE =AD ﹣DE ﹣∵AF =EF ,FG ⊥AD ,∴AG =EG =21332-,∴cos ∠FAD =AG AF ==2-,故答案为:2.【点评】本题考查了旋转的性质,等腰三角形的性质,等边三角形的判定和性质,勾股定理,三角函数定义,解题关键是要熟练运用等腰三角形性质.2.(2021秋•静安区期末)如图,正方形ABCD中,将边BC绕着点C旋转,当点B落在边AD的垂直平分线上的点E处时,∠AEC的度数为45°或135°..【考点】旋转的性质;线段垂直平分线的性质;正方形的性质.【专题】矩形菱形正方形;平移、旋转与对称;推理能力.【分析】分两种情况讨论,由旋转的性质和线段垂直平分线的性质可得△BEC是等边三角形,由等腰三角形的性质可求解.【解答】解:如图,当点E在BC的上方时,连接BE∵MN是AD的垂直平分线,四边形ABCD是正方形,∴MN垂直平分BC,∴BE=EC,∵将边BC绕着点C旋转,∴BC=CE,∴△BEC是等边三角形,∴∠EBC=∠BEC=60°,∴∠ABE=30°,∵AB=BC=BE,∴∠AEB=75°,∴∠AEC=75°+60°=135°;当点E'在BC的下方时,同理可得△BE'C是等边三角形,∴BC=BE',∠BE'C=60°=∠CBE',∴∠ABE'=150°,∵AB=BC=BE',∴∠AE'B=15°,∴∠AE'C=45°,故答案为:45°或135°.【点评】本题考查了旋转的性质,正方形的性质,等边三角形的性质,利用分类讨论思想解决问题是解题的关键.3.(2021秋•杨浦区期末)如图,已知在Rt△ABC中,∠C=90°,tan A=512,将△ABC绕点A逆时针旋转90°后得△ADE,点B落在点D处,点C落在点E处,联结BE、CD,作∠CAD的平分线AN,交线段BE于点M,交线段CD于点N,那么AMAN的值为23.【考点】相似三角形的判定与性质;解直角三角形;旋转的性质.【专题】三角形;等腰三角形与直角三角形;推理能力.【分析】先根据题目条件作出图象,由∠C=90°和tan A=512,设BC=5k,AC=12k,然后由旋转的性质得到AE =AC=12k,ED=BC=5k,AB=AD=13k,以点C为原点、BC和AC所在直线分别为x轴和y轴建立平面直角坐标系,则A(0,12k),B(﹣5k,0),E(12k,12k),D(12k,7k),过点N作NF⊥AC于点F,交BE于点P,NH ⊥AD于点H,得到NF=NH,得到AMCAMDAC12k==AD13kSS△△,然后由高相等的两个三角形的面积之比为底边长之比得到CNDN的值,进而用含有k的式子表示点N的坐标,再求得直线BE的解析式,然后求得点P的坐标得到NP的长,最后通过△MAE∽△MNP得到AMNM的值,即可得到AMAN的值.【解答】方法一:解:由∠C=90°和tan A=512可设BC=5k,AC=12k,∴AB=13k,由旋转得,AE=AC=12k,ED=BC=5k,AB=AD=13k,如图,以点C为原点,BC和AC所在直线分别为x轴和y轴,建立平面直角坐标系,则A(0,12k),B(﹣5k,0),∵旋转角为90°,∴E(12k,12k),D(12k,7k),过点N作NF⊥AC于点F,交BE于点P,作NH⊥AD于点H,∵AN平分∠CAD,∴NF=NH,∴AMCAMDAC12k==AD13kSS△△,又∵△ANC 在边CN 上的高和△AND 在边DN 上的高相等,∴AMC AMD CN 12==DN 13S S △△,∴点N 的坐标为(144k 25,84k 25),设直线BE 的解析式为y =mx +n ,则-5mk+01212n km n k =⎧⎨+=⎩,解得:12m 176017k n ⎧=⎪⎪⎨⎪=⎪⎩,∴直线BE 的解析式为y =1217x +6017k ,当y =8425k 时,1217x +6017k =8425k ,解得:x =﹣625k ,∴P (﹣625k ,8425k ),∴NP =144k 25﹣(﹣625k )=6k ,∵NF ⊥AC ,∠EAC =90°,∴AE ∥NP ,∴△MAE ∽△MNP ,∴126AM AE k MN NP k ===2,∴23AM AN =,方法二:解:由题可知,∠BAC =∠DAE ,∠CAM =∠MAD ,∴∠BAC +∠CAM =∠DAE +∠MAD ,∴∠BAN =∠NAE ,如图,延长AN ,交BC 的延长线于点F ,∵AE ∥BC ,∴∠EAN =∠AFC ,∴∠BAN =∠AFC ,∴BF =BA ,设BC =5,AC =12,AB =13,∴1213AE BF =,∴△AME ∽△FMB ,∴1213AM AE MF BF ==,∴1225AM AF =,延长AD 与BC 的延长线交于点H ,延长ED 与BH 交于点I ,∵DE =5,∴四边形ACIE 为正方形,∴DI =7,延长CD 与AE 延长线交于点G ,易证△EDG ∽△IDC ,∴EG DE CI DI =,即5127EG =,∴EG =607,∴AG =12+607=1447,易知,△ANG ∽△FNC ,∴AN AG NF FC =,∵BF =13,BC =5,∴CF =8,∴14418787AN NF ==,∴1825AN NF =,∵1225AM NF =,∴122183AM AN ==,故答案为:23.【点评】本题考查了旋转的性质、勾股定理、相似三角形的判定与性质、角平分线的性质定理、三角形的面积,解题的关键是通过旋转的性质建立平面直角坐标系.4.(2021秋•嘉定区期末)如图,在△ABC 中,∠C =90°,BC =2,D 在边AC 上,CD :AD =1:3,联结BD ,点E 在线段BD 上,如果∠BCE =∠A ,那么CE =52.【考点】相似三角形的判定与性质;勾股定理.【专题】图形的相似;运算能力.【分析】根据已知∠BCE =∠A ,想到构造这两个角所在的三角形相似,所以过点E 作EF ⊥BC ,垂足为F ,可得△ABC ∽△CEF ,进而可得CF =2EF ,然后设EF 为a ,则CF 为2a ,BF 为2﹣2a ,最后再证明A 字模型相似△BFE ∽△BCD ,从而解答即可.【解答】解:过点E 作EF ⊥BC ,垂足为F ,∵∠ACB =90°,BC =2,25AB =2222(25)24AC AB BC =-=-,∵CD :AD =1:3,∴CD =1,∵∠BCE =∠A ,∠ACB =∠CFE =90°,∴△ABC ∽△CEF ,∴42AC CF BC EF ===2,∴设EF 为a ,则CF 为2a ,BF 为2﹣2a ,∵∠ACB =∠BFE =90°,∠CBD =∠FBE ,∴△BFE ∽△BCD ,∴BF EF BC CD =,∴2221a a -=,∴a =12,∴EF =12,CF =1,∴CE 22215()122EF CF +=+=,故答案为:52.【点评】本题考查了相似三角形的判定与性质,勾股定理,熟练掌握A 字模型相似是解题的关键.5.(2021秋•松江区期末)如图,已知矩形ABCD 中,AD =3,AB =5,E 是边DC 上一点,将△ADE 绕点A 顺时针旋转得到△AD ′E ′,使得点D 的对应点D '落在AE 上,如果D ′E ′的延长线恰好经过点B ,那么DE 的长度等于94.【考点】旋转的性质;矩形的性质.【专题】平移、旋转与对称;推理能力.【分析】如图,连接BE 、BE ′,根据矩形的性质和旋转变换的性质可得:AD ′=AD =3,∠AD ′E =∠D =90°,利用勾股定理可得BD ′=4,再运用面积法可得:AB •AD =AE •BD ′,求出AE =,再运用勾股定理即可求得答案.【解答】解:如图,连接BE 、BE ′,∵矩形ABCD 中,AD =3,AB =5,∴∠D =90°,由旋转知,△AD ′E ′≌△ADE ,∴AD′=AD=3,∠AD′E=∠D=90°,∵D′E′的延长线恰好经过点B,∴∠AD′B=90°,在Rt△ABD′中,BD4==,∵AB•AD=AE•BD′,∴AE='5315 44AB AD BD⨯==,在Rt△ADE中,DE94 =,方法二:∵△ADE∽△BDA,∴'' DE AD AD BD=∴334DE=∴DE=94故答案为:9 4.【点评】本题考查了矩形的性质,旋转变换的性质,勾股定理,三角形面积等,解题关键是运用面积法求得AE.6、(2021秋•黄浦区期末17)如图,在△ABC中,AB=4,AC=5,将△ABC绕点A旋转,使点B落在AC边上的点D处,点C落在点E处,如果点E恰好在线段BD的延长线上,那么边BC【考点】旋转的性质;相似三角形的判定.【专题】平移、旋转与对称;推理能力.【分析】如图所示,连接CE,由旋转的性质可得:AD=AB=4,BC=DE,∠BCD=∠DEA,AE=AC=5,则CD=AC-AD=1,然后证明△BDC∽△ADE,得到BC DCAE DE=,即15BCBC=,则BC2=5,由此即可得到答案.【解答】解:如图所示,连接CE,由旋转的性质可得:AD=AB=4,BC=DE,∠BCD=∠DEA,AE=AC=5,∴CD=AC-AD=1又∵∠BDC=∠ADE∴△BDC∽△ADE,∴BC DCAE DE=,即15BCBC=,∴BC2=5,∴BC (负值已经舍去),【点评】本题主要考查了旋转的性质,相似三角形的性质与判定,熟知相似三角形的性质与判定条件是解题的关键.7.(2020秋•嘉定区期末)已知在△ABC中,∠ACB=90°,AB=10,sin A=55(如图),把△ABC绕着点C按顺时针方向旋转α°(0<α<360),将点A、B的对应点分别记为点A′,B′,如果△AA′C为直角三角形,那么点A与点B'的距离为【考点】旋转的性质;解直角三角形.【专题】分类讨论;平移、旋转与对称;几何直观.【分析】根据△AA′C为直角三角形,分两种情况:①当点B'在线段AC上时,△AA′C为直角三角形;②当点B'在线段AC的延长线上时,△AA′C为直角三角形,依据线段的和差关系进行计算即可得到点A与点B'的距离.【解答】解:分两种情况:①当点B'在线段AC上时,△AA′C为直角三角形,∵∠ACB=90°,AB=10,sin A=5 5,∴BC=AB×5=10×5=∴B'C=AC=,∴AB'=AC﹣B'C=②当点B'在线段AC的延长线上时,△AA′C为直角三角形,同理可得,B'C=AC=,∴AB'=AC+B'C=综上所述,点A与点B'的距离为故答案为:【点评】本题考查了旋转的性质,勾股定理,锐角三角函数的应用,运用分类思想是本题的关键.8.(2020秋•闵行区期末)如图,在Rt△ABC中,∠ACB=90°,AB=3,tan B=.将△ABC绕着点A顺时针旋转后,点B恰好落在射线CA上的点D处,点C落在点E处,射线DE与边AB相交于点F,那么BF=3【考点】旋转的性质;解直角三角形.【专题】平移、旋转与对称;解直角三角形及其应用;运算能力;推理能力.【分析】过点F作FG⊥AC于点G,由旋转的性质得出∠B=∠D,得出tan∠B=tan∠D=12FGGD=,由平行线的性质得出∠B=∠AFG,设AG=x,则FG=2x,则2132xx=+,求出AG=1,则可得出答案.【解答】解:如图,过点F作FG⊥AC于点G,∵将△ABC 绕着点A 顺时针旋转后,点B 恰好落在射线CA 上的点D 处,∴∠B =∠D ,∴tan ∠B =tan ∠D =12FG GD =,∵∠ACB =∠FGA =90°,∴BC ∥FG ,∴∠B =∠AFG ,∴tan ∠B =tan ∠AFG =12AG FG =,设AG =x ,则FG =2x ,∴2132x x =+,解得x =1,∴AG =1,FG =2,∴AF 225FG AG +=∴BF =AB ﹣AF =35.故答案为:35【点评】本题考查了旋转的性质,直角三角形的性质,锐角三角函数的定义,勾股定理,熟练掌握旋转的性质是解题的关键.9.(2020秋•静安区期末)在Rt △ABC 中,∠C =90°,AB =13,tan B =23(如图),将△ABC 绕点C 旋转后,点A 落在斜边AB 上的点A ',点B 落在点B ',A 'B '与边BC 相交于点D ,那么'CD A D 的值为3135.【考点】旋转的性质;解直角三角形.【专题】等腰三角形与直角三角形;几何直观.【分析】过C 作CE ⊥AB 于E ,根据勾股定理和正切的定义得到AC =213,BC =313,根据三角形面积得到CE =6,再根据旋转的性质和相似三角形的判定与性质即可求解.【解答】解:过C 作CE ⊥AB 于E ,∵tan B =23,∴23AC BC =,设AC =2x ,则BC =3x ,在Rt △ABC 中,AB=13,解得x=AC =,BC =,S △ABC =12AC •BC =12AB •CE ,即12××312×13×CE ,解得CE =6,∵tan B =CE EB =23,∴EB =9,∵将△ABC 绕点C 旋转后,点A 落在斜边AB 上的点A ',点B 落在点B ',∴∠B =∠B ′,AC =AC ′,∵CE ⊥AB ,∴AE ′=AE =AB ﹣BE =13﹣9=4,∴A ′B =AB ﹣A ′E =9﹣4=5,∵∠A ′DB =∠CDB ′,∴△A ′DB ∽△B ′DC ,∴'CD A D =''CB A B ='CB A B..【点评】本题考查了勾股定理,解直角三角形,旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.10.(2020秋•杨浦区期末)如图,已知在△ABC 中,∠B =45°,∠C =60°,将△ABC 绕点A 旋转,点B 、C 分别落在点B 1、C 1处,如果BB 1∥AC ,联结C 1B 1交边AB 于点D ,那么1BD B D 的值为622.【考点】旋转的性质;平行线的性质.【专题】平移、旋转与对称;推理能力.【分析】由旋转的性质和等腰三角形的性质可求∠B1AB=30°,由直角三角形的性质可求DB1=DE,DB=﹣DE,即可求解.【解答】解:如图,过点D作DE⊥AB1于E,∵∠B=45°,∠C=60°,∴∠CAB=75°,∵BB1∥AC,∴∠CAB=∠ABB1=75°,∵将△ABC绕点A旋转,∴AB=AB1,∠AB1C1=∠ABC=45°,∴∠AB1B=∠ABB1=75°,∴∠B1AB=30°,又∵DE⊥AB1,∠AB1C1=45°,∴AD=2DE,AE=DE,DE=B1E,∴AB1DE+DE=AB,DB1DE,∴DB=AB﹣ADDE﹣DE,∴1BDB D622=,故答案为:622.【点评】本题考查了旋转的性质,等腰三角形的性质,直角三角形的性质,灵活运用这些性质进行推理是本题的关键.11.(2020秋•宝山区期末)在Rt△ABC中,∠ACB=90°,AC=BC,点E、F分别是边CA、CB的中点,已知点P在线段EF上,联结AP,将线段AP绕点P逆时针旋转90°得到线段DP,如果点P、D、C在同一直线上,那么tan∠CAP﹣1.【考点】旋转的性质;解直角三角形;等腰直角三角形;三角形中位线定理.【专题】等腰三角形与直角三角形;平移、旋转与对称;图形的相似;解直角三角形及其应用;推理能力.【分析】分两种情形:①当点D在线段PC上时,延长AD交BC的延长线于H.证明AD=DC即可解决问题.②当点P在线段CD上时,同法可证:DA=DC解决问题.【解答】解:如图1,当点D在线段PC上时,延长AD交BC的延长线于H.∵CE=EA,CF=FB,∴EF∥AB,∴∠EFC=∠ABC=45°,∵∠PAO=45°,∴∠PAO=∠OFH,∵∠POA=∠FOH,∴∠H=∠APO,∵∠APC=90°,EA=EC,∴PE=EA=EC,∴∠EPA=∠EAP=∠BAH,∴∠H=∠BAH,∴BH=BA,∵∠ADP=∠BDC=45°,∴∠ADB=90°,∴BD⊥AH,∴∠DBA=∠DBC=22.5°,∵∠ADB=∠ACB=90°,∴A,D,C,B四点共圆,∠DAC=∠DBC=22.5°,∠DCA=∠ABD=22.5°,∴∠DAC=∠DCA=22.5°,∴DA=DC,设AD=a,则DC=AD=a,AP=PD =22a,∴PC=a +22a,∴tan∠CAP=22122a aCPAP+==;如图2中,当点P在线段CD上时,同法可证:DA=DC,设AD=a,则CD=AD=a,PD =2 2 a,∴PC=a ﹣22 a,∴tan∠CAP=22122a aCPAP+==,∵点P在线段EF上,∴情形1,不满足条件,情形2满足条件,﹣1.【点评】本题考查了旋转变换,等边三角形的性质,等腰直角三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质等知识,解题的关键是正确寻找全等三角形或相似三角形解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.12.(2020秋•奉贤区期末)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CD是△ABC的角平分线,将Rt△ABC绕点A旋转,如果点C落在射线CD上,点B落在点E处,联结DE,那么∠AED的正切值为3 7.【考点】旋转的性质;解直角三角形.【专题】等腰三角形与直角三角形;平移、旋转与对称;解直角三角形及其应用;推理能力.【分析】设点C落在射线CD上的点C'处,由勾股定理可求AB=5,由旋转的性质可得∠ACD=∠AC'C=45°=∠DCB,∠EAB=∠CAC',由平行线分线段成比例可求AD的长,即可求解.【解答】解:如图,设点C落在射线CD上的点C'处,∵∠ACB=90°,AC=3,BC=4,∴AB=5,∵CD是△ABC的角平分线,∴∠ACD=∠DCB=45°,∵将Rt△ABC绕点A旋转,∴∠ACD=∠AC'C=45°=∠DCB,∠EAB=∠CAC',∴∠CAC'=90°=∠EAB,∴AC'∥BC,∴'34AD ACDB BC==,∴AD=157,∴tan∠AED=37 ADAE=,故答案为:3 7.【点评】本题考查了旋转的性质,勾股定理,锐角三角函数,平行线的性质等知识,灵活运用这些性质解决问题是本题的关键.13.(2019秋•奉贤区期末)如图,已知矩形ABCD(AB>BC),将矩形ABCD绕点B顺时针旋转90°,点A、D分别落在点E、F处,连接DF,如果点G是DF的中点,那么∠BEG的正切值是1.【考点】旋转的性质;矩形的性质.【专题】平移、旋转与对称;应用意识.【分析】连接BD,BF,EG.利用四点共圆证明∠BEG=∠BFD=45°即可.【解答】解:连接BD,BF,EG.由题意:BD=BF,∠DBF=90°,∵DG=GF,∴BG⊥DF,∴∠BGF=∠BEF=90°,∴B,G,E,F四点共圆,∠BEG=∠BFD=45°,∴∠BEG的正切值是1.故答案为1.【点评】本题考查旋转变换,等腰直角三角形的判定和性质,四点共圆,锐角三角函数等知识,解题的关键是学会添加常用辅助线解决问题,属于中考常考题型.14.(2019秋•浦东新区期末)在Rt△ABC中,∠C=90°,AC=2,BC=4,点D、E分别是边BC、AB的中点,将△BDE绕着点B旋转,点D、E旋转后的对应点分别为点D'、E',当直线D'E'经过点A时,线段CD'的长为【考点】三角形综合题.【专题】图形的全等;等腰三角形与直角三角形;矩形菱形正方形;图形的相似;推理能力.【分析】分两种情况:①点A在E'D'的延长线上时;②点A在线段D'E'的延长线上时;然后分类讨论,求出线段BD的长各是多少即可.【解答】解:如图1,当点A 在E 'D '的延长线上时,∵∠C =90°,AC =2,BC =4,∴AB ==2,∵点D 、E 分别是边BC 、AB 的中点,∴DE ∥AC ,DE =12AC =1,BD =12BC =2,∴∠EDB =∠ACB =90°,∵将△BDE 绕着点B 旋转,∴∠BD 'E '=∠BDE =90°,D 'E '=DE =1,BD =BD '=2,∵在Rt △ABC 和Rt △BAD '中,D 'B =AC =2,AB =BA ,∴Rt △ABC ≌Rt △BAD '(HL ),∴AD '=BC ,且AC =D 'B ,∴四边形ACBD '是平行四边形,且∠ACB =90°,∴四边形ACBD '是矩形,∴CD '=AB =如图2,当点A 在线段D 'E '的延长线上时,∵∠AD 'B =90°,∴AD '==4,∴AE '=AD '﹣D 'E '=3,∵将△BDE 绕着点B 旋转,∴∠ABC =∠E 'BD ',∵'12BE AB ==BD BC ,∴△ABE '∽△CBD ',∴''AE AB CD BC=,∴'3254CD =,∴CD '故答案为:.【点评】本题属于三角形综合题,考查了全等三角形的判定和性质,相似三角形的判定和性质,矩形的判定和性质,勾股定理等知识,解题的关键是理解题意,正确寻找相似三角形解决问题,属于中考常考题型.15.(2019秋•长宁、金山区期末)如图,在Rt △ABC 中,∠ABC =90°,AB =2,BC =4点P在边BC上,联结AP,将△ABP绕着点A旋转,使得点P与边AC的中点M重合,点B的对应点是点B′,则BB′的长等于5.【考点】旋转的性质;相似三角形的判定与性质.【专题】等腰三角形与直角三角形;平移、旋转与对称;图形的相似;推理能力.【分析】如图,延长AB'交BC于E,过点B'作B'D⊥AB于点D,由勾股定理可求AC的长,由旋转的性质可求AP=AM,∠PAB=∠CAE,AB=AB'=2,通过证明△ABP∽△CBA,可得∠PAB=∠C,可得CE=AE,由勾股定理可求CE,BE的长,由相似三角形的性质可求B'D,BD的长,即可求解.【解答】解:如图,延长AB'交BC于E,过点B'作B'D⊥AB于点D,∵∠ABC=90°,AB=2,BC=4,∴AC==∵点M是AC中点,∴AM∵将△ABP绕着点A旋转,使得点P与边AC的中点M重合,∴AP=AM,∠PAB=∠CAE,AB=AB'=2,∵AP2=AB2+PB2,∴PB=1,∵BAPB=2=BCAB,且∠ABP=∠ABC=90°,∴△ABP∽△CBA,∴∠PAB=∠C,∴∠C=∠CAE,∴CE=AE,∵AE2=AB2+BE2,∴CE2=4+(4﹣CE)2,∴CE=AE=52,∴BE=32,∵B'D∥BC,∴△AB'D∽△AEB,∴''AB AD B DAE AB BE==,∴'253222AD B D==,∴AD=85,B'D=65,∴BD=25,∴BB'=2105,故答案为:2105.【点评】本题考查了旋转的性质,相似三角形的判定和性质,等腰三角形的性质,勾股定理等知识,求出CE 的长是本题的关键.16.(2019秋•松江区期末)如图,矩形ABCD 中,AD =1,AB =k ,将矩形ABCD 绕着点B顺时针旋转90°得到矩形A ′BC ′D ′,联结AD ′,分别交边CD ,A ′B 于E 、F ,如果AED ′F ,那么k【考点】旋转的性质;相似三角形的判定与性质;矩形的性质.【专题】矩形菱形正方形;平移、旋转与对称;图形的相似;推理能力.【分析】由矩形的性质和旋转的性质可求AD =A 'D '=1,AB =A 'B =k ,∠A '=∠DAB =90°=∠DCB =∠ABC ,通过证明△ADE ∽△FA 'D ',可得''''AD DE AE A F A D D F ==,可求DE ,A 'F 的长,通过证明△A 'D 'F ∽△CEF ,由相似三角形的性质可求解.【解答】解:∵将矩形ABCD 绕着点B 顺时针旋转90°得到矩形A ′BC ′D ′,∴AD =A 'D '=1,AB =A 'B =k ,∠A '=∠DAB =90°=∠DCB =∠ABC ,∴A 'D '∥BA ∥CD∴∠A 'D 'F =∠FEC =∠DEA ,且∠D =∠A '=90°,∴△ADE ∽△FA 'D ',∴''''AD DE AE A F A D D F==,且AED ′F ,∴DEA 'D ',A 'FAD=2,∵∠A '=∠DCF =90°,∠A 'FD '=∠EFC ,∴△A 'D 'F ∽△CEF ,∴'''EC FC A D A F =,∴''21222k k A D ---=∴k+1,+1.【点评】本题考查了旋转的性质,矩形的性质,相似三角形的判定和性质,利用相似三角形的性质求DE ,A 'F 的长是本题的关键.17.(2019秋•嘉定区期末)在△ABC中,∠ACB=90°,AB=10,cos A=35(如图),把△ABC绕着点C按照顺时针的方向旋转,将A、B的对应点分别记为点A'、B'.如果A'B'恰好经过点A,那么点A与点A'的距离为36 5.【考点】旋转的性质;解直角三角形.【专题】等腰三角形与直角三角形;平移、旋转与对称;解直角三角形及其应用;推理能力.【分析】如图,过点C作CE⊥A'B',由锐角三角函数可求AC=6,由旋转的性质可得AC=A'C=6,∠A'=∠BAC,即可求A'E的长,由等腰三角形的性质可求AA'的长.【解答】解:如图,过点C作CE⊥A'B',∵在△ABC中,∠ACB=90°,AB=10,cos∠BAC=35,∴AC=6,∵把△ABC绕着点C按照顺时针的方向旋转,∴AC=A'C=6,∠A'=∠BAC,∵cos∠A'=cos∠BAC==35,∴A'E=185,∵AC=A'C,CE⊥A'B',∴AA'=2A'E=36 5,故答案我:36 5.【点评】本题考查了旋转的性质,等腰三角形的性质,锐角三角函数的应用,求出A'E的长是本题的关键.18.(2019秋•徐汇区期末)如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕着点B顺时针旋转后得到矩形A'BC'D',点A的对应点A'在对角线AC上,点C、D分别与点C'、D'对应,A′D'与边BC交于点E,那么BE的长是25 8.【考点】旋转的性质;相似三角形的性质;矩形的性质.【专题】矩形菱形正方形;平移、旋转与对称;图形的相似;推理能力.【分析】如图,过点B 作BF ⊥AC ,过点E 作EH ⊥AC ,由勾股定理可求AC =5,由面积法可求BF =125,由勾股定理可求AF =95,由旋转的性质可得AB =BA ',∠BAD =∠BA 'D '=90°,可求CA '=75,由等腰三角形的性质可求HC 的长,通过证明△EHC ∽△ABC ,可得EC BC HC AC =,可求EC 的长,即可求解.【解答】解:如图,过点B 作BF ⊥AC ,过点E 作EH ⊥AC,∵AB =3,AD =4,∠ABC =90°,∴AC ===5,∵S △ABC =12AB ×BC =12AC ×BF ,∴3×4=5BF ,∴BF =125∴AF 22144925AB BF -=-95,∵将矩形ABCD 绕着点B 顺时针旋转后得到矩形A 'BC 'D ',∴AB =BA ',∠BAD =∠BA 'D '=90°,且BF ⊥AC ,∴∠BAC =∠BA 'A ,AF =A 'F =95,∠BA 'A +∠EA 'C =90°,∴A 'C =AC ﹣AA '=75,∵∠BA 'A +∠EA 'C =90°,∠BAA '+∠ACB =90°,∴∠ACB =∠EA 'C ,∴A 'E =EC ,且EH ⊥AC ,∴A 'H =HC =12A 'C =710,∵∠ACB =∠ECH ,∠ABC =∠EHC =90°,∴△EHC ∽△ABC ,∴BC HC AC EC =∴74105EC =∴EC =78,∴BE =BC ﹣EC =4﹣78=258,故答案为:258.【点评】本题考查了旋转的性质,矩形的性质,勾股定理,等腰三角形的性质,相似三角形的判定和性质,求出HC 的长是本题的关键.19.(2019秋•普陀区期末)如图,在RtΔABC 中,∠C=90°,AC=5,sinB=513,点P 为边BC 上一点,PC=3,将△ABC 绕点P 旋转得到△A'B'C'(点A ,B 、C 分别与点A'、B'、C'对应).使B'C'∥AB ,边A'C'与边AB 交于点G ,那么A'G 的长等于2013.【考点】旋转的性质;解直角三角形;平行线的判定,图形的旋转【专题】矩形菱形正方形;平移,旋转与对称;解直角一角形及其应用;应用意识。
2019-2021年上海各区数学中考一模压轴题分类汇编18题-定义新图形及其他题型含详解

专题定义新图形及其他题型【知识梳理】根据题目中给的知识点,结合所学函数及图形知识解答【历年真题】1.(2021秋•浦东新区期末)如图,a ∥b ∥c ,直线a 与直线b c与直线b 之间的距离为,等边△ABC 的三个顶点分别在直线a 、直线b 、直线c 上,则等边三角形的边长是.2.(2021秋•宝山区期末)如果一条抛物线y =ax 2+bx +c (a ≠0)与x 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“特征三角形”.已知y =x 2+bx (b >0)的“特征三角形”是等腰直角三角形,那么b 的值为.3.(2021秋•青浦区期末)如图,一次函数y =ax +b (a <0,b >0)的图象与x 轴,y 轴分别相交于点A ,点B ,将它绕点O 逆时针旋转90°后,与x 轴相交于点C ,我们将图象过点A ,B ,C 的二次函数叫做与这个一次函数关联的二次函数.如果一次函数y =﹣kx +k (k >0)的关联二次函数是y =mx 2+2mx +c (m ≠0),那么这个一次函数的解析式为.4.(2021秋•青浦区期末)若抛物线y 1=ax 2+b 1x+c 1的顶点为A ,抛物线y 2=ax 2+b 1x+c 1的顶点为B ,且满足顶点A 在抛物线y 2上,顶点B 在抛物线y 1上,则称抛物线y 1与抛物线y 2互为“关联抛物线”已知顶点为M 的抛物线y=(x-2)2+3与顶点为N 的抛物线互为“关联抛物线”,直线MN 与x 轴正半轴交于点D ,如果3tan MDO=4∠,那么顶点为N 的抛物线的表达式为5.(2020秋•长宁区期末)如果一条对角线把凸四边形分成两个相似的三角形,那么我们把这条对角线叫做这个凸四边形的相似对角线,在凸四边形ABCD中,AB=AC AD=CD=32,点E、点F分别是边AD,边BC上的中点.如果AC是凸四边形ABCD的相似对角线,那么EF的长等于.6.(2020秋•青浦区期末)如果四边形边上的点,它与对边两个端点的连线将这个四边形分成的三个三角形都相似,我们就把这个点叫做该四边形的“强相似点”.如图①,在四边形ABCD中,点Q在边AD上,如果△QAB、△QBC和△QDC都相似,那么点Q就是四边形ABCD的“强相似点”;如图②,在四边形ABCD中,AD∥BC,AB=DC=2,BC=8,∠B=60°,如果点Q是边AD上的“强相似点”,那么AQ=.7.(2020秋•浦东新区期末)如图,△ABC中,AB=10,BC=12,AC=8,点D是边BC上一点,且BD:CD=2:1,联结AD,过AD中点M的直线将△ABC分成周长相等的两部分,这条直线分别与边BC、AC相交于点E、F,那么线段BE的长为.8.(2020秋•徐汇区期末)如图,在△ABC中,∠ABC=120°,AB=12,点D在边AC上,点E在边BC上,sin∠ADE=45,ED=5,如果△ECD的面积是6,那么BC的长是.9.(2020秋•金山区期末)已知在Rt△ABC中,∠C=90°,BC=1,AC=2,以点C为直角顶点的Rt△DCE的顶点D在BA的延长线上,DE交CA的延长线于点G,若tan∠CED=12,CE=GE,那么BD的长等于.10.(2020秋•黄浦区期末)已知一个矩形的两邻边长之比为1:2.5,一条平行于边的直线将该矩形分为两个小矩形,如果所得两小矩形相似,那么这两个小矩形的相似比为.11.(2019秋•黄浦区期末)如图,在△ABC中,AB=AC,点D、E在边BC上,∠DAE=∠B=30°,且AD3=AE2,那么DEBC的值是.12.(2019秋•宝山区期末)如图,点A在直线34y x上,如果把抛物线y=x²沿OA方向平移5个单位,那么平移后的抛物线的表达式为__.专题定义新图形及其他题型【历年真题】1.(2021秋•浦东新区期末)如图,a ∥b ∥c ,直线a 与直线b c与直线b 之间的距离为,等边△ABC 的三个顶点分别在直线a 、直线b 、直线c 上,则等边三角形的边长是【考点】相似三角形的判定与性质;等边三角形的性质.【专题】图形的相似;模型思想.【分析】过点A 作AD ⊥直线b 于D ,将△ABD 绕点A 逆时针旋转60°得到△ACE ,作EG ⊥直线c 于G 交直线a 于F .想办法求出AE ,EC 即可解决问题.【解答】解:如图,过点A 作AD ⊥直线b 于D ,将△ABD 绕点A 逆时针旋转60°得到△ACE ,作EG ⊥直线c 于G 交直线a 于F .则有∠AEC =∠ADB =∠AFE =∠EGC =90°,AE =AD ,∠EAF =∠CEG =30°,∴EF =12AE =2,∴EG =2,CG =3EG =52,CE =2CG =5,∴AC =.∴等边△ABC 的边长为.故答案为:.【点评】本题考查了相似三角形的性质与判定,勾股定理的运用,直角三角形的性质的运用,相似三角形的性质的运用,解答时构造相似三角形是关键.2.(2021秋•宝山区期末)如果一条抛物线y =ax 2+bx +c (a ≠0)与x 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“特征三角形”.已知y =x 2+bx (b >0)的“特征三角形”是等腰直角三角形,那么b 的值为2.【考点】抛物线与x 轴的交点;等腰直角三角形;二次函数的性质;二次函数图象上点的坐标特征.【专题】二次函数图象及其性质;应用意识.【分析】根据抛物线的“特征三角形”是等腰直角三角形建立方程求解即可.【解答】解:设抛物线y =x 2+bx 与x 轴的交点坐标为A ,B ,顶点为D ,∴A (0,0),B (﹣b ,0),D (﹣2b ,﹣24b ),∵抛物线y =x 2+bx 对应的“特征三角形”是等腰直角三角形,∴AB 2=AD 2+BD 2=2AD 2,∴b 2=2(24b +416b ),解得:b =±2,∵b >0,∴b =2,故答案为:2.【点评】本题考查抛物线与x 轴的交点和抛物线的“特征三角形”的特点,关键是利用“特征三角形”是等腰直角三角形建立等量关系.3.(2021秋•青浦区期末)如图,一次函数y =ax +b (a <0,b >0)的图象与x 轴,y 轴分别相交于点A ,点B ,将它绕点O 逆时针旋转90°后,与x 轴相交于点C ,我们将图象过点A ,B ,C 的二次函数叫做与这个一次函数关联的二次函数.如果一次函数y =﹣kx +k (k >0)的关联二次函数是y =mx 2+2mx +c (m ≠0),那么这个一次函数的解析式为y =﹣3x +3.【考点】抛物线与x 轴的交点;坐标与图形变化﹣旋转;一次函数的性质;一次函数图象上点的坐标特征;待定系数法求一次函数解析式;待定系数法求二次函数解析式.【专题】一次函数及其应用;二次函数图象及其性质;平移、旋转与对称;推理能力.【分析】先由直线y =﹣kx +k 求得点A 和点B 的坐标,然后求得点C 的坐标,最后将点A 、B 、C 的坐标分别代入函数y =mx 2+2mx +c 中求得m 、k 、c 的值,即可得到一次函数的解析式.【解答】解:对y =﹣kx +k ,当x =0时,y =k ,当y =0时,x =1,∴A (1,0),B (0,k ),∴C (﹣k ,0),将A 、B 、C 的坐标代入y =mx 2+2mx +c 得,22020m m c c k mk mk c ⎧++=⎪=⎨⎪++=⎩,解得:000m k c =⎧⎪=⎨⎪=⎩或133m k c =-⎧⎪=⎨⎪=⎩或1311m k c ⎧=⎪⎪=-⎨⎪=-⎪⎩,∵m ≠0,k >0,∴m =﹣1,k =3,c =3,∴一次函数的解析式为y =﹣3x +3,故答案为:y =﹣3x +3.【点评】本题考查了一次函数图象上点的坐标特征、二次函数的解析式、旋转的特征,解题的关键是会求点B 经过逆时针旋转90°后的点的坐标.4.(2021秋•青浦区期末)若抛物线y 1=ax 2+b 1x+c 1的顶点为A ,抛物线y 2=ax 2+b 2x+c 2的顶点为B ,且满足顶点A 在抛物线y 2上,顶点B 在抛物线y 1上,则称抛物线y 1与抛物线y 2互为“关联抛物线”已知顶点为M 的抛物线y=(x-2)2+3与顶点为N 的抛物线互为“关联抛物线”,直线MN 与x 轴正半轴交于点D ,如果3tan MDO=4∠,那么顶点为N 的抛物线的表达式为2557(416y x =--+.【考点】待定系数法求二次函数解析式.【专题】二次函数图象及其性质;;推理能力.【分析】设顶点为N 的抛物线顶点坐标N 为(a ,b ),由题意可知34M M N y x x =-,即可求得D 点坐标为(6,0),则有直线MD 解析式为3(6)4y x =--,因为N 点过直线MD ,N 点也过抛物线y=(x-2)2+3,故有()23(6)423b a b a ⎧=--⎪⎨⎪=-+⎩,解得545716a b ⎧=⎪⎪⎨⎪=⎪⎩,故N 点坐标为(54,5716),可设顶点为N 的抛物线的表达式为2557(416y a x =-+,又因为M 点过2557()416y a x =-+,即可解得a=-1,故顶点为N 的抛物线的表达式为2557()416y x =--+.【解答】设顶点为N 的抛物线顶点坐标N 为(a ,b )已知抛物线y=(x-2)2+3的顶点坐标M 为(2,3)∵3tan 4MDO ∠=∴34M M N y x x =-即3324D x =-解得24D x =±∵直线MN 与x 轴正半轴交于点D ∴D 点坐标为(6,0)则直线MD 解析式为3(6)4y x =--N 点在直线MD 3(6)4y x =--上,N 点也在抛物线y=(x-2)2+3故有()23(6)423b a b a ⎧=--⎪⎨⎪=-+⎩化简得2394247b a b a a ⎧=-+⎪⎨⎪=-+⎩联立得2394742a a a --=-+化简得2135042a a -+=解得a=54或a=2(舍)将a=54代入3942b a =-有359157257442161616b =-⨯+=-+=解得545716a b ⎧=⎪⎪⎨⎪=⎪⎩故N 点坐标为(54,5716)则顶点为N 的抛物线的表达式为2557()416y a x =-+将(2,3)代入2557(416y a x =-+有25573(2)416a =-+化简得95731616a =+解得a=-1故顶点为N 的抛物线的表达式为2557(416y x =--+故答案为:2557(416y x =--+.【点评】本题考察了二次函数的图象及其性质,三角函数的应用.理解题意所述“关联抛物线”的特点,即若抛物线y 1=ax 2+b 1x+c 1的顶点为A ,抛物线y 2=ax 2+b 2x+c 2的顶点为B ,且满足顶点A 在抛物线y 2上,顶点B 在抛物线y 1上是解题的关键.5.(2020秋•长宁区期末)如果一条对角线把凸四边形分成两个相似的三角形,那么我们把这条对角线叫做这个凸四边形的相似对角线,在凸四边形ABCD 中,AB =ACAD=CD =32,点E 、点F 分别是边AD ,边BC 上的中点.如果AC 是凸四边形ABCD 的相似对角线,那么EF 的长等于414.【考点】相似图形;三角形中位线定理.【专题】图形的相似;推理能力.【分析】利用相似三角形的性质求出BC 长,再利用等腰三角形的性质和勾股定理计算出EF 的长即可.【解答】解:如图所示:∵AB=AC,AD=CD,△ABC∽△DAC,∴AC2=BC•AD,∵AC AD=32,∴CB=2,∵△ABC∽△DAC,∴∠ACB=∠CAD,∴CB∥AD,∵AB=AC,F为BC中点,∴AF⊥CB,BF=CF=1,∴∠AFC=90°,∵CB∥AD,∴∠FAE=∠AFC=90°,∵AC Rt△AFC中AF==,∵AD=32,E为AD中点,∴AE=34,∴EF414 =.故答案为:41 4.【点评】此题主要考查了相似三角形的性质,以及等腰三角形的性质和勾股定理,关键是掌握相似三角形对应边成比例、对应角相等.6.(2020秋•青浦区期末)如果四边形边上的点,它与对边两个端点的连线将这个四边形分成的三个三角形都相似,我们就把这个点叫做该四边形的“强相似点”.如图①,在四边形ABCD中,点Q在边AD上,如果△QAB、△QBC和△QDC都相似,那么点Q就是四边形ABCD的“强相似点”;如图②,在四边形ABCD中,AD∥BC,AB=DC=2,BC=8,∠B=60°,如果点Q是边AD上的“强相似点”,那么AQ=或.【考点】相似图形.【专题】图形的相似;推理能力.【分析】如图,当∠1=∠2=∠3时,△BAQ∽△QDC∽△CQB,设AQ=x.利用相似三角形的性质,构建方程求解即可.【解答】解:如图,当∠1=∠2=∠3时,△BAQ∽△QDC∽△CQB,设AQ=x.过点A作AE⊥BC于E,过点D作DF⊥BC于F,则四边形AEFD是矩形,∴AD=EF,∵AB=CD=2,AD∥BC,∴四边形ABCD是等腰梯形,∴∠ABE=∠DCF=60°,BE=AB•cos60°=1,CF=CD•cos60°=1,∴EF=BC﹣BE﹣CF=6,∴AD=EF=6,DQ=6﹣x,∵△BAQ∽△QDC,∴AB AQ=QD CD,∴x(6﹣x)=4,解得x=3±5,∴AQ=3±5故答案为:5或3-5【点评】本题考查相似三角形的判定和性质,等腰梯形的性质,解直角三角形等知识,解题的关键是理解题意,灵活运用所学知识解决问题.7.(2020秋•浦东新区期末)如图,△ABC中,AB=10,BC=12,AC=8,点D是边BC上一点,且BD:CD=2:1,联结AD,过AD中点M的直线将△ABC分成周长相等的两部分,这条直线分别与边BC、AC相交于点E、F,那么线段BE的长为2.【考点】相似三角形的判定与性质.【专题】图形的相似;推理能力.【分析】先求出BD=8,CD=4,再求出MH=4,DH=2,设BE=x,得出CE=12﹣x,CF=3+x,EH=10﹣x,再判断出△EHM∽△ECF,得出比例式,建立方程求解,即可得出结论.【解答】解:如图,∵点D是BC上一点,BC=12,∴BD:CD=2:1,∴BD=8,CD=4,过点M作MH∥AC交CD于H,∴△DHM∽△DCA,∴MH DH=ACDMCD AD=,∴点M是AD的中点,∴AD=2DM,∵AC=8,∴MH DH1=842=,∴MH=4,DH=2,过点M 作MG ∥AB 交BD 于G ,同理得,BG =DG =4,∵AB =10,BC =12,AC =8,∴△ABC 的周长为10+12+8=30,∵过AD 中点M 的直线将△ABC 分成周长相等的两部分,∴CE +CF =15,设BE =x ,则CE =12﹣x ,∴CF =15﹣(12﹣x )=3+x ,EH =CE ﹣CH =CE ﹣(CD ﹣DH )=12﹣x ﹣2=10﹣x ,∵MH ∥AC ,∴△EHM ∽△ECF ,∴MH EH =CF CE ,∴410-=3+12x x x,∴x =2或x =9,当x =9时,CF =12>AC ,点F 不在边AC 上,此种情况不符合题意,即BE =x =2,故答案为:2.【点评】此题主要考查了相似三角形的判定和性质,构造出相似三角形是解本题的关键.8.(2020秋•徐汇区期末)如图,在△ABC 中,∠ABC =120°,AB =12,点D 在边AC 上,点E 在边BC 上,sin ∠ADE =45,ED =5,如果△ECD 的面积是6,那么BC 的长是﹣6.【考点】解直角三角形;三角形的面积.【专题】解直角三角形及其应用;推理能力.【分析】如图,过点E 作EF ⊥BC 于F ,过点A 作AH ⊥CB 交CB 的延长线于H .解直角三角形求出BH ,CH 即可解决问题.【解答】解:如图,过点E 作EF ⊥BC 于F ,过点A 作AH ⊥CB 交CB 的延长线于H .∵∠ABC =120°,∴∠ABH =180°﹣∠ABC =60°,∵AB =12,∠H =90°,∴BH =AB •cos60°=6,AH =AB •sin60°=,∵EF ⊥DF ,DE =5,∴sin ∠ADE =EF DE =45,∴EF =4,∴DF 3==,∵S △CDE =6,∴12•CD •EF =6,∴CD =3,∴CF =CD +DF =6,∵tan C =EF AH CF CH =,∴4636CH=,∴CH =,∴BC =CH ﹣BH =6.故答案为:﹣6.【点评】本题考查解直角三角形,三角形的面积等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.9.(2020秋•金山区期末)已知在Rt △ABC 中,∠C =90°,BC =1,AC =2,以点C 为直角顶点的Rt △DCE 的顶点D 在BA 的延长线上,DE 交CA 的延长线于点G ,若tan ∠CED=12,CE =GE ,那么BD 的长等于2+【考点】解直角三角形;勾股定理.【专题】解直角三角形及其应用;推理能力.【分析】如图,过点A 作AH ⊥CE 于H .想办法证明AK =AC ,推出HK =CH ,推出AK =AD =2,即可解决问题.【解答】解:如图,过点A 作AH ⊥CE 于H .∵tan ∠CED =12=tan ∠BAC ,∴∠E =∠BAC ,∵CE =EG ,∴∠CGE =∠ECG ,∵∠BAC +∠GAK =180°,∴∠E +∠GAK =180°,∴∠AGE +∠AKE =180°,∵∠AKE +∠AKC =180°,∴∠AKC =∠CGE ,∴∠AKC =∠ACK ,∴AC =AK =2,∵AH ⊥CK ,∴KH =CH ,∵∠AHE =∠DCK =90°,∴AH ∥CD ,∴KA =AD ,∴DK =2AK =4,AD =AK =2,∵∠ACB =90°,BC =1,AC =2,∴AB =∴BD =AB +AD =,故答案为:【点评】本题考查解直角三角形,勾股定理,三角形的中位线定理等知识,解题的关键是学会添加常用辅助线,构造三角形的中位线解决问题.10.(2020秋·黄浦区期末)已知一个矩形的两邻边长之比为1:2.5.一条平行于边的直线将该矩形分为两个小矩形,如果所得两小矩形相似,那么这两个小矩形的相似比为2:1或1:2或1:1.【考点】相似多边形的性质;矩形的性质,四手拉手模型【专题】图形的相似;推理能力.【分析】如图,设AB=a,AD=2.5a,AE=x,则DE=2.5a-x,利用相似多边形的性质,构建方程求解,另外两个矩形全等也符合题意.【解答】解:如图,设AB=a,AD=2.5a,,AE=x,则DE=2.5a-x.∵矩形ABFE∽矩形EDCF∴AE EF=EF DE∴=2.5x aa a x整理得,x2-2.5xa+a2=0,解得x=2a或0.5a,∴矩形ABFE与矩形EDCF相似,相似比为2:1或1:2.当E,F分别是AD,BC的中点时,两个矩形全等,也符合题意,相似比为:1:1故答案为:2:1或1:2或1:1.【点评】本题考查相似多边形的性质,解题的关键是学会利用参数构建方程求解,属干电考常考题型11.(2019秋•黄浦区期末)如图,在△ABC中,AB=AC,点D、E在边BC上,∠DAE=∠B=30°,且AD3=AE2,那么DEBC的值是13318﹣1.【考点】等腰三角形的性质;相似三角形的判定与性质.【专题】等腰三角形与直角三角形;图形的相似;推理能力.【分析】证明△ADE∽△BAE,得出AE2=DE×BE,同理△ADE∽△CDA,得出AD2=DE×CD,得出2294AD CD AE BE ==,设CD =9x ,则BE =4x ,求出AB =AD AE×BE =6x ,作AM ⊥BC 于M ,由等腰三角形的性质得出BM =CM =12BC ,由直角三角形的性质得出AM =12AB =3x ,BM AM =x ,得出BC =2BM =,求出DE =BE +CD ﹣BC =13x ﹣x ,即可得出答案.【解答】解:∵AB =AC ,∴∠C =∠B =30°,∵∠DAE =∠B =30°,∴∠DAE =∠B =∠C ,∵∠AED =∠BEA ,∴△ADE ∽△BAE ,∴AD AE DE ==AB BE AE,∴AE 2=DE ×BE ,同理:△ADE ∽△CDA ,∴AD DE =CD AD ,∴AD 2=DE ×CD ,∴22239()24AD CD AE BE ===,设CD =9x ,则BE =4x ,∵AD AE AB BE =,∴AB =AD AE ×BE =32×4x =6x ,作AM ⊥BC 于M ,如图所示:∵AB =AC ,∴BM =CM =12BC ,∵∠B =30°,∴AM =12AB =3x ,BM AM =,∴BC =2BM =,∴DE =BE +CD ﹣BC =13x ﹣x ,∴13318DE EC ==﹣1;故答案为:13318﹣1.【点评】本题考查了等腰三角形的性质、相似三角形的判定与性质、直角三角形的性质等知识;证明三角形相似是解题的关键.12.(2019秋•宝山区期末)如图,点A 在直线34y x =上,如果把抛物线y=x ²沿OA 方向平移5个单位,那么平移后的抛物线的表达式为_y=(x-4)2+3_.【考点】二次函数图象与几何变换;一次函数图象上点的坐标特征,四二次函数的平移【专题】二次函数图象及其性质;运算能力;推理能力.【分析】过点A作AB丄x轴于B,求出OB、AB,然后写出点A的坐标,再利用顶点式解析式写出即可.【解答】解:如图,过点A作AB丄x轴于B,∵点A在直线34y x上,OA=5,∴OB=4,AB=3,∵点A的坐标为(4,3),∴平移后的抛物线解析式是y=(x-4)2+3故答案为y=(x-4)2+3.【点评】本题考查了二次函数图象与几何变换,平移的规律:左加右减,上加下减,此类题目,利用顶点的变化求解更简便.。
(绝密上海专用)2021上海市中考数学精品模拟试卷 (后附教师版答案详解)

2021上海市中考数学精品模拟试卷(后附教师版答案详解)(满分150分,答题时间120分钟)一、选择题〔共6小题,每题4分,共24分。
下列选项中有且只有一个选项是正确的,选择正确选项的代号并填涂在答题纸的相应位置上〕1.若x+y=2,z﹣y=﹣3,则x+z的值等于()A.5B.1C.﹣1D.﹣52.小红连续5天的体温数据如下(单位:℃):36.6,36.2,36.5,36.2,36.3.关于这组数据,下列说法正确的是()A.中位数是36.5℃B.众数是36.2°CC.平均数是36.2℃D.极差是0.3℃3.不等式组{2x−1≤3,x+1>2的解集在数轴上表示为()A.B.C.D.4.下列等式成立的是()A.3+4√2=7√2B.√3×√2=√5C.√36=2√3D.√(−3)2=35.下列图形中,既是轴对称图形又是中心对称图形的是()A B C D6.如图,在⊙O中,AB为直径,∠AOC=80°.点D为弦AC的中点,点E为BĈ上任意一点.则∠CED 的大小可能是()A.10°B.20°C.30°D.40°二、填空题〔共12小题,每题4分,共48分。
请将结果直接填入答题纸相应位置上〕7.计算:(π﹣1)0+|﹣2|=.8.分解因式:xy2﹣4x=.9.若一次函数y=2x+2的图象经过点(3,m),则m=.10.方程2x+10=0的解是.11.三角形的两边长分别为4和7,第三边的长是方程x2﹣8x+12=0的解,则这个三角形的周长是.12.二次函数y=﹣x2﹣2x+3的图象的顶点坐标为.13.如图所示的转盘,被分成面积相等的四个扇形,分别涂有红、黄、蓝、绿四种颜色.固定指针,自由转动转盘两次,每次停止后,记下指针所指区域(指针指向区域分界线时,忽略不计)的颜色,则两次颜色相同的概率是.14.某鸡腿生产公司的质检人员从两批鸡腿中各随机抽取了6个,记录相应的质量(g)如表,若甲、乙两个样本数据的方差分别为S甲2、S乙2,则S甲2S乙2(填“>“、“=”、“<”)15.如图,在▱ABCD中,∠B=60°,AB=10,BC=8,点E为边AB上的一个动点,连接ED并延长至点F,使得DF=14DE,以EC、EF为邻边构造▱EFGC,连接EG,则EG的最小值为.16.如图,在△ABC中,D、E为边AB的三等分点,EF∥DG∥AC,H为AF与DG的交点.若AC=6,则DH=.17.如图,等边三角形纸片ABC 的边长为6,E ,F 是边BC 上的三等分点.分别过点E ,F 沿着平行于BA ,CA 方向各剪一刀,则剪下的△DEF 的周长是 .18.如图,在矩形ABCD 中,AD =4,将∠A 向内翻折,点A 落在BC 上,记为A 1,折痕为DE .若将∠B 沿EA 1向内翻折,点B 恰好落在DE 上,记为B 1,则AB = .三、解答题〔共7小题,满分共78分〕19.计算:(12)﹣2﹣|√2−3|+2tan45°﹣(2021﹣π)020.解分式方程:2311xx x x +=--. 21.如图,在△ABC 中,∠C =90°,tan A =√33,∠ABC 的平分线BD 交AC 于点D ,CD =√3,求AB 的长?22.某商店代理销售一种水果,六月份的销售利润y (元)与销售量x (kg )之间函数关系的图象如图中折线所示.请你根据图象及这种水果的相关销售记录提供的信息,解答下列问题: (1)截止到6月9日,该商店销售这种水果一共获利多少元?(2)求图象中线段BC 所在直线对应的函数表达式.23.如图,在四边形ABCD 中,AD ∥BC ,对角线BD 的垂直平分线与边AD 、BC 分别相交于点M 、N .(1)求证:四边形BNDM 是菱形;(2)若BD =24,MN =10,求菱形BNDM 的周长.24. 如图,已知点()1,2A 、()()5,0B n n >,点P 为线段AB 上的一个动点,反比例函数()0ky x x=>的图像经过点P .小明说:“点P 从点A 运动至点B 的过程中,k 值逐渐增大,当点P 在点A 位置时k 值最小,在点B 位置时k 值最大.”(1)当1n =时.①求线段AB 所在直线的函数表达式.②你完全同意小明的说法吗?若完全同意,请说明理由;若不完全同意,也请说明理由,并求出正确的k 的最小值和最大值.(2)若小明的说法完全正确,求n 的取值范围.25.如图1,已知点O 在四边形ABCD 的边AB 上,且2OA OB OC OD ====,OC 平分BOD ∠,与BD 交于点G ,AC 分别与BD 、OD 交于点E 、F .(1)求证://OC AD ; (2)如图2,若DE DF =,求AE AF值;(3)当四边形ABCD 的周长取最大值时,求DEDF的值.2021上海市中考数学精品模拟试卷(满分150分,答题时间120分钟)一、选择题〔共6小题,每题4分,共24分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题19 计算题专项训练1.(2020·上海中考真题)解不等式组:1076713x xxx>+⎧⎪+⎨-<⎪⎩【答案】2<x<5.【分析】先求出不等式组中每一个不等式的解集,再求出它们的公共部分即可求解.【详解】解:由题意知:1076713①②>+⎧⎪⎨+-<⎪⎩x xxx,解不等式①,移项得:3x>6,系数化为1得:x>2,解不等式②,去分母得:3x-3<x+7.移项得:2x<10,系数化为1得:x<5,∴原不等式组的解集是2<x<5.故答案为:2<x<5.【点睛】本题考查解一元一次不等式组,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.2.(2020·上海中考真题)计算:1327(12)﹣2+|3.【答案】0.【分析】利用分数的指数幂的意义,分母有理化,负指数幂的意义,绝对值的性质计算后合并即可.【详解】原式=133(3)+2﹣4+32﹣4+3=0.【点睛】本题考查了分数指数幂的运算,负指数幂的运算,绝对值的意义以及分母有理化运算,熟练掌握实数的运算法则是解题的关键.3.(2020·上海九年级一模)计算:()2232cos 453tan 302sin 60cos60cot 30-︒+︒︒-︒-︒【答案】2-【分析】利用特殊锐角三角函数值计算求解即可.【详解】解:原式=223232122⎛-+ ⎝⎭=-⨯--⎝⎭ 【点睛】本题考查了特殊锐角三角函数值的计算,熟知特殊锐角三角函数值是解题的关键. 4.(2020·上海大学附属学校九年级三模)解方程组:222-620x y x xy y =⎧⎨--=⎩【答案】121242,22x x y y ==⎧⎧⎨⎨==-⎩⎩ 【分析】将第二个方程进行因式分解得到()(2)0+-=x y x y ,然后令因式2x y -和因式x y +分别为0即可求解.【详解】解:由题意可知: 222-620x y x xy y =⎧⎨--=⎩①② 对方程②进行因式分解得:()(2)0+-=x y x y即20x y -=或0x y +=∴原方程组化为2620x y x y -=⎧⎨-=⎩ 或 260x y x y -=⎧⎨+=⎩解得1142x y =⎧⎨=⎩或2222x y =⎧⎨=-⎩ 故原方程组的解为:1142x y =⎧⎨=⎩或2222x y =⎧⎨=-⎩. 【点睛】本题考查了因式分解的方法及二元方程组,熟练掌握常见的二元一次方程组的解法是解决此类题的关键.5.(2020·上海九年级二模)解不等式组:3(2)8(6)121123x x x x -≤-+⎧⎪+-⎨<+⎪⎩,并把解集在数轴上表示出来.【答案】﹣1<x ≤2,数轴见解析【分析】先求出每个不等式的解集,再求出不等式组的解集即可.【详解】解:()()3286121123x x x x ⎧--+⎪⎨+-<+⎪⎩①②,解不等式∴,得:2x ,解不等式∴,得:1x >-,将不等式解集表示在数轴上如下:所以不等式组的解集为12x -<.【点睛】本题考查了解一元一次不等式组和在数轴上表示不等式组的解集,能根据不等式的解集求出不等式组的解集是解此题的关键.6.(2020·上海九年级二模)先化简,再求值:2224112a a a a a -÷----,其中2a =. 【答案】12a -. 【分析】先根据分式的运算法则化简分式,再将a 的值代入计算即可.【详解】解:原式=2(1)(1)12(2)2a a a a a a +-⨯---- =122a a a a +--- =12a -,将2a =代入上式得,原式=. 【点睛】本题考查了分式的化简求值,掌握基本运算法则是解题的关键.1.(2020·上海九年级二模)解不等式组:26233122x x x x ⎧⎛⎫-<- ⎪⎪⎪⎝⎭⎨-⎪-⎪⎩并把解集在数轴上表示出来.【答案】﹣1≤x <3,见解析【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【详解】解不等式①,得:x <3,解不等式②,得:x≥﹣1,则不等式组的解集为﹣1≤x <3,将不等式组的解集表示在数轴上如下:【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.2.(2020·上海九年级二模)计算:12012()122tan 601)3π-+--+︒-(【答案】4【分析】原式利用零指数幂、负整数指数幂法则,分数指数幂法则,以及特殊角的三角函数值计算即可得到结果.【详解】原式)1=2121-+-3=-3=-=4.【点睛】此题考查了实数的运算,零指数幂、负整数指数幂,分数指数幂以及特殊角的三角函数值,熟练掌握运算法则是解本题的关键.3.(2020·上海九年级二模)计算:110311)183-⎛⎫-+++ ⎪⎝⎭. 【答案】【分析】先利用零次幂的运算法则,绝对值的意义,负整指数的运算法则以及分数指数幂的运算法则进行化简,再进行加减运算即可.【详解】解:原式.【点睛】本题是实数的混合运算,考查了零次幂的运算法则,绝对值的意义,负整指数的运算法则以及分数指数幂的运算法则,掌握基本运算法则是解题的关键.4.(2020·上海九年级二模)方程组22205x y x y -=⎧⎨+=⎩的解是_______. 【答案】12x y =⎧⎨=⎩或12x y =-⎧⎨=-⎩ 【分析】先将y 用含x 的式子表示,再代入解一元二次方程即可.【详解】22205x y x y -=⎧⎨+=⎩①②由①得:2y x =③将③代入②得:()2225x x +=解得:1x =± ,将1x =±代入③得: 2y =±∴12x y =⎧⎨=⎩或12x y =-⎧⎨=-⎩ 故答案为:12x y =⎧⎨=⎩或12x y =-⎧⎨=-⎩ 【点睛】本题考查二元二次方程组的解法,掌握代入消元是解题关键.5.(2020·上海九年级二模)解方程组:222;1.x y x xy y -=⎧⎨--=⎩【答案】121251,31x x y y ==⎧⎧⎨⎨==-⎩⎩ 【分析】用代入法解方程.【详解】,由①得x=2+y ③,将③代入②得22(2(2))1y y y y -+-=+, 解得13y =,21y =-,将13y =、21y =-分别代入③,得 15=x ,21x =,∴原方程组的解是 121251,31x x y y ==⎧⎧⎨⎨==-⎩⎩. 【点睛】此题考查解二元二次方程组,根据方程组的特点选择恰当的解法是解题的关键. 6.(2020·上海九年级二模)解方程组:222,{230.x y x xy y -=--=【答案】1111x y =⎧⎨=-⎩2231x y =⎧⎨=⎩【详解】x 2-2xy -3y 2="0"(x -y)2-4y 2=0又因:x -y=2代入上式4-4y 2=0y=1或y=-1再将y=1、y=-1分别代入x -y=2则 x=1、x=3∴1111x y =⎧⎨=-⎩2231x y =⎧⎨=⎩ 7.(2020·上海九年级一模)解方程组:2228560x y x xy y +=⎧⎨+-=⎩【答案】11122x y =⎧⎨=-⎩,228383x y ⎧=⎪⎪⎨⎪=⎪⎩【分析】先将第2个方程变形为x +6y =0,x ﹣y =0,从而得到两个二元一次方程组,再分别求解即可.【详解】解:2228560x y x xy y +=⎧⎨+-=⎩①②, 由∴得:x +6y =0,x ﹣y =0,原方程组可化为2860x y x y +=⎧⎨+=⎩或280x y x y +=⎧⎨-=⎩,故原方程组的解为11122x y =⎧⎨=-⎩,228383x y ⎧=⎪⎪⎨⎪=⎪⎩. 【点睛】本题考查的是高次方程,关键是通过分解,把高次方程降次,得到二元一次方程组,用到的知识点是因式分解、加减法.8.(2020·上海九年级一模)计算:24sin 30tan 60cot 30tan45--【分析】把特殊的锐角三角函数值代入计算即可.21432⨯-=;【点睛】本题主要考查了特殊的锐角三角函数值,掌握特殊的锐角三角函数值是解题的关键.9.(2020·上海)计算:22sin 30tan 60cot 45cos 60cos30sin 45︒︒︒︒︒︒⋅-+-+1.【分析】直接利用特殊角的三角函数值进而分别代入求出答案.【详解】解:原式=11122222⨯-+⎛- ⎝⎭22. 【点睛】本题主要考查特殊三角函数值的相关运算,牢记特殊三角函数值是解题的关键. 10.(2020·上海市民办协和双语学校九年级一模)计算:13tan 3045cos60︒︒︒-【答案】1.【分析】将特殊角的三角函数值代入,根据实数的运算法则求值即可.【详解】原式=131221=1.【点睛】本题考查了特殊角的三角函数值以及实数的混合运算,熟记特殊角的三角函数值、熟练掌握实数的运算法则是解题的关键. 11.(2020·上海)计算:22cot 602tan 30tan 60sin 452sin 30︒︒︒︒︒++-【答案】52【分析】根据特殊角的三角函数值即可代入求解.【详解】解:原式222331222+⎛=+- ⎝⎭⨯ 132=+52=【点睛】此题主要考查实数的运算,解题的关键是熟知特殊角的三角函数值. 12.(2020·上海九年级一模)计算:2tan 45cos60cot 602sin 30︒-︒+︒︒【答案】56【分析】先将特殊三角函数值分别算出原算式中的每一项,然后根据实数混合运算的法则进行计算即可. 【详解】解:2tan 45cos60cot 602sin 30︒-︒+︒︒2112122-=+⎝⎭⨯ 1123=+ 56=【点睛】本题考查的是特殊三角函数值,熟记特殊角度的三角函数值是解答此题的关键. 13.(2020·上海九年级一模)已知:::2:3:5a b c =.(1)求代数式323a b c a b c-++-的值; (2)如果324a b c -+=,求,,a b c 的值.【答案】(1)1;(2)6,9,15a b c ===【分析】(1)设a=2k ,b=3k ,c=5k (k 0)≠,代入代数式323a b c a b c-++-,即可求出答案; (2)把a 、b 、c 的值代入,求出即可.【详解】∵::2:3:5a b c =∴设a=2k ,b=3k ,c=5k (k 0)≠,(1)36358=1234958a b c k k k k a b c k k k k-+-+==+-+-;(2)∵324a b c -+=∴6k -3k+5k=24,∴k=3,∴a=2×3=6,b=3×3=9,c=5×3=15.【点睛】本题考查了比例的性质的应用,主要考查学生的计算能力.14.(2020·上海九年级一模)2sin60°•tan45°+4cos 230°﹣tan60°【答案】3【分析】直接利用特殊角的三角函数值分别代入求出答案.【详解】2sin60°•tan45°+4cos 230°﹣tan60°=×1+4×2=3.【点睛】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键. 15.(2020·上海九年级一模)计算:2cos30°+tan45°-2sin30°-cot30°【答案】0【分析】将特殊角的三角函数值代入即可【详解】2cos30°+tan45°-2sin30°-cot30°+1-2×12-1=0【点睛】本题主要考查特殊角的三角函数值,掌握特殊角的三角函数值是解题的关键. 16.(2020·上海九年级二模)解方程: 24211422xx x x .【答案】x =1.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解.【详解】去分母得:4x ﹣2x ﹣4=x 2﹣4﹣x +2,即x 2﹣3x +2=0,解得:x =1或x =2,经检验x =2是增根,所以,分式方程的解为x =1.【点睛】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.17.(2020·上海九年级一模)2318-【答案】-3.【分析】根据绝对值的性质,二次根式的混合运算,进行运算即可1243-+=-【点睛】此题考查二次根式的混合运算,解题关键在于掌握运算法则18.(2020·上海九年级二模)解方程组:226,320.x y x xy y +=⎧⎨-+=⎩【答案】114,2;x y =⎧⎨=⎩223,3.x y =⎧⎨=⎩【分析】先对x 2-3xy+2y 2=0分解因式转化为两个一元一次方程,然后联立①,组成两个二元一次方程组,解之即可.【详解】将方程22320x xy y -+= 的左边因式分解,得20x y -=或0x y -=. 原方程组可以化为6,20x y x y +=⎧⎨-=⎩或6,0.x y x y +=⎧⎨-=⎩ 解这两个方程组得114,2;x y =⎧⎨=⎩ 223,3.x y =⎧⎨=⎩ 所以原方程组的解是114,2;x y =⎧⎨=⎩ 223,3.x y =⎧⎨=⎩ 【点睛】本题考查了高次方程组,将高次方程化为一次方程是解题的关键.19.(2020·上海九年级三模)解方程:213221x x x x --=-∴ 【答案】11x =-∴213x = 分析:首先21x y x-=,然后将方程转化为y 的一元二次方程,从而求出y 的值,然后根据y 的值求出x 的值. 详解:设21x y x-=,则原方程化为2230y y --=∴ 解得123,1y y ==-∴ 当13y =时,得1x =- , 当11y =-时,得13x =∴ 经检验,11x =-∴213x =是原方程的解. 点睛:本题主要考查的是分式方程的解法以及换元思想的应用,属于中等难度的题型.学会换元思想是解题的关键.20.(2020·上海九年级二模)解不等式组31222236255134x x x x x --+⎧+<⎪⎪⎨-⎪+≤⎪⎩,并把解集在数轴上表示出来. 【答案】47x ≥,数轴见解析 【分析】本题可根据不等式组分别求出x 的取值,然后画出数轴,数轴上相交的点的集合就是该不等式的解集.若没有交点,则不等式无解 【详解】解:31222,2362551,34x x x x x --+⎧+<⎪⎪⎨-⎪+≤⎪⎩①② 解不等式①,得1x <. 解不等式②,得47x ≥. 所以不等式组的解集为47x ≥. 将解集表示在数轴上如下:【点睛】本题可分别解完不等式后可以利用数轴或口诀“比大的小,比小的大,中间找”得到最终结果,此题考查利用数形结合解不等式组,是对学生基本运算方法、运算法则、基本性质的运用能力的考查.21.(2020·上海九年级二模)先化简,再求值:22111121x x x x x x --÷+--+,其中x. 【答案】11x x -+,﹣3【分析】先根据分式的混合运算顺序和运算法则化简原式,再将x 的值代入计算可得.【详解】 解:原式21(1)1(1)(1)1x x x x x x -=-++-- 111x x x =-++ 11x x -=+,当1x =时,原式==3=.【点睛】本题主要考查分式的化简求值,解题的关键是熟练掌握分式的混合运算顺序和运算法则.。
