弱无穷小算子算法
【国家自然科学基金】_随机线性算子_基金支持热词逐年推荐_【万方软件创新助手】_20140802
2013年 序号 1 2 3 4 5 6 7 8 9 10
科研热词 推荐指数 非自治 1 隐式交替方向格式 1 美式期权 1 线性互补问题 1 概周期解 1 时滞 1 收敛性 1 投影算法 1 heston随机波动率模型 1 acquistapace-terreni条件 1
2014年 序号 1 2 3 4
2014年 科研热词 渐近行为 最小q-函数 对偶分支q-矩阵 对偶 推荐指数 1 1 1 1
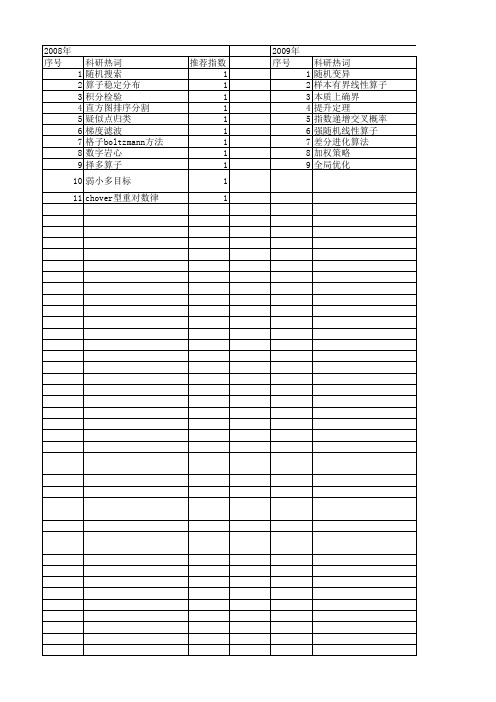
2008年 序号 1 2 3 4 5 6 7 8 9 10 11
科研热词 随机搜索 算子稳定分布 积分检验 直方图排序分割 疑似点归类 梯度滤波 格子boltzmann方法 数字岩心 择多算子 弱小多目标 hover型重对数律
推荐指数 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9
科研热词 随机变异 样本有界线性算子 本质上确界 提升定理 指数递增交叉概率 强随机线性算子 差分进化算法 加权策略 全局优化
推荐指数 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9
科研热词 随机微分方程 随机吸引子 遗传算法 缓增随机集 组换装时间 线性规划 强阻尼 单机调度 wiener过程
科研热词 推荐指数 随机赋范模 3 随机线性算子的c0-半群 2 随机线性算子 2 随机无穷小生成元 2 (ε ,λ )一拓扑 1 (ε , λ )-topology 1 随机自反 1 配流 1 调机运用 1 自适应测量 1 统计自相关函数 1 约束等距常数 1 粒子群优化算法 1 稀疏解 1 离散粒子群优化算法 1 矩阵向量乘算子 1 正交杂交 1 欠定线性方程组 1 有偏随机键遗传算法 1 最佳线性估计 1 最佳s项逼近 1 整数非线性规划 1 数值预报 1 收敛分析 1 快速图像重建 1 平均遍历定理 1 子集选择 1 奇异值分解 1 图像处理 1 可预报分量 1 参数均匀交叉 1 单向编组站 1 分块压缩感知 1 几乎处处幂有界的随机线性算子 1 random normed module 1 random linear operator 1 random infinitesimal generator1 lorenz系统 1 c0-semigroupsof random linear 1 operators (ε ,λ )-拓扑 1
数学专业术语

数学
量
假设
定理
逆否命题
猜想
验证
充要条件
论证
恒等式
公式
小于
不等方程
常数
复合
完全的
肯定的
离散的
周期
族
子集
并
直积集
差集
n元组
值域
逆映射
恒同映射
映入
同构
对称性
超穷基数
幺拟群
连通代数群
代数群的有理表示
左函数平移
代数群的李代数
典范态射
半单元
抽象根系
幂幺根
抛物子群
代数群的外尔群
布吕阿分解
谢瓦莱群
算术子群
拓扑群的直积
左一致结构
局部紧群
零化子的互反性
紧阿贝尔群
紧群的群环
局部单连通
泛覆叠群
可数无穷的
数理逻辑
形式语言
合式的
矢列式
论题
命题演算
联结词
逻辑加法
否定词
析取范式
真值
重言式
谓词变元
个体变元
非标准量词
前束词
闭公式
全域
一阶理论
相容性
可定义性
斯科伦壳
初等等价的
初等子模型
进退构造
原子理论
对象的余积
终对象
自由对象
对偶函子
忠实函子
常数函子
自然等价
泛性质
表示函子
推出
无穷小计算

无穷小计算
无穷小计算是现在互联网技术发展的重要趋势之一,它是指在互联网时代利用
低成本的云计算技术、以及智能化的物联网技术等,将大规模的计算任务分解为多个可独立执行的任务,然后由不同计算机并行执行,从而实现的计算性能扩展。
无穷小计算对传统的计算机技术和运算使用方式实现了革命性的改变,它将计算任务拆分成大量离散的小任务,再分发到不同计算机或网络节点上,通过节点之间的协作,从而实现更高性能的计算。
无穷小计算主要应用于大规模、高性能的计算,如实时数据分析、桌面虚拟化、视频编辑等,极大地提高了系统的吞吐量和处理数据量,可以有效缩短计算任务的完成时间。
此外,无穷小计算还可以实现在网络上的分布式计算,使得不同的计算机可以使用网络上的资源,从而节省计算机成本和服务器的影响,并能够更有效地共享用户资源。
无穷小计算带来了巨大的社会变革,它大大改变了我们处理海量数据的方式,
使我们更容易得到更准确、更及时的信息,成为依托快速发展的互联网行业的重要助力和载体,同时也为更多用户提供了个性化、有价值的信息服务。
总之,无穷小计算的出现使得计算能力得到近乎无限的扩展,为互联网时代的
发展带来了新的机遇,它将发挥更大的作用,推动现代社会智能化进程,促进社会发展和生活提升。
一类随机非线性系统自适应跟踪的模块化设计

引理 3 』假设 "和P是定义在 R “: 上的实值 函数 ,, 是 6c
正常数。 如果 P ∈ L 并且 t满 足 微分 不 等式 ≤一C , , O+
6() , ( )≥ 0 则 有 pt vO ,
: ,
0) 川 ㈣1 2+ V )
其 中 。T , , , , P是 类 函数 , 则称系统关于 ( ,)是输 人 ~状态稳定 的(S ) IS 。
其中 是状态变量 , : ( , , ) ∈R是系统 x 。 …, ;
的输入 , R是系统 的输 出; ( Y 互)∈R 是 已知 的光滑非线 p 性函数向量 , 满足 ;0 ( )=0 ; R 是未知参数向量 , p 的估
对于系统 不确定 噪声采用 随机扰动抑 制控制的机制 , 对 不确定参数采用 自适应 机制 , 用于跟 踪控制设 计 , 应 使跟 踪
误差在概率意义下 收敛到一个任意小范围 。
计值是 () 则误差定义为 () t, t :=0 () 田 ( 一 t , 互)eR 是
已知的光滑非线性 函数 向量 , W是定 义在概率 空间 ( F, 力, 尸) 上的 r 维相互独立 的方差不确定 Wi e 过程向量 , 中 为 e r n 其
识器结合 , 控制模块镇定 被控 对象 , 辨识 器能保 证独 立于控 制器 的特定有界特性 。用来 描述扰 动抑制 问题 的输入 一状 态稳定 (S ) 念 最初 由 Sna 出 l 。Focigr在文 IS 概 ot g提 4 lrh e J n
踪 问题 。通过设计强参数鲁棒稳定特 性的控制器 , 实现控 制 模块镇定 被控 对象 , 并能 和任 意 的标 准辨 识器 结 合。运用
无穷小阶的运算

无穷小阶的运算“无穷小阶”是当今数学领域最重要的概念之一,也是数学发展的重要组成部分。
它是一种技术,可以用来评估数学表达式中复杂问题的解决方案。
它被广泛应用于各种数学领域,包括统计,计算机科学,运算论等等,影响着社会科学,医学,工程等学科的研究。
无穷小阶的定义是:“一个变量的无限次近似值,使得其在给定问题中得到求解的解”。
无限次近似的解决方法通常是利用无穷级数,及其特殊的函数,形成的解的近似值。
这些解的近似值在运算上被认为是无限次近似值,因此被称为无穷小阶。
无穷小阶运算在许多数学领域中得到广泛应用,如统计,机器学习等等,因此对于研究者来说,无穷小阶的具体原理及应用是十分重要的。
无穷小阶的理论涉及到极限理论,级数,函数拟合,以及各种数值分析技术,同时也涉及到随机数据分析,概率论等等。
在非线性方面,无穷小阶经常被用于求解非线性解,尤其是非线性方程组,以及非线性最优化问题。
比如,在逼近非线性函数中,可以使用无穷小阶算法来比较非线性函数的结果。
此外,在解决无穷维极值问题时,可以利用无穷小阶的定理来求解不可避免的极值问题。
无穷小阶的几何概念也被广泛应用于微分几何,几何拟合,及计算几何技术中,用于研究复杂曲面的几何特征,解决不可避免的表面和几何拟合问题。
此外,无穷小阶还被用于各种数值计算技术,如有限差分,拉格朗日插值,样条插值,以及基于微分方程的数值计算等。
最后,无穷小阶运算也被应用于统计分析中,用于检验分布及性质,估计未知参数,以及其他分析工作。
总而言之,无穷小阶运算是一个技术,可以用来解决复杂的数学问题,并且广泛应用于统计,计算机科学,几何,微分几何,及其他数值计算技术中。
因此,学习无穷小阶运算的理论及其应用是非常有必要的。
事件驱动Markov型网络系统的输出反馈H∞控制

周学德,张艳 . 事件驱动 Markov 型网络系统的输出反馈 H∞ 控制 . 计算机工程与应用,2019,55(6):231-236. ZHOU Xuede, ZHANG Yan.Event-triggered output feedback H∞ control for networked Markov type systems. Computer Engineering and Applications, 2019, 55(6):231-236.
Abstract:In order to solve the H∞ output feedback control problem of event-triggered Markov type systems, Wirtinger’s inequality is used to estimate the upper bound of the weak infinitesimal operator of Lyapunov function by constructing Lyapunov function containing event- triggered and quantized output information. The stability criterion of event-triggered Markov network closed-loop system is obtained, and the output feedback controller design method is given. It satisfies the level of H∞ disturbance suppression, which can effectively overcome the impact of disturbance on the system. Key words:event-triggered; Markov type network control system; time delay; Wirtinger’s inequality; H∞ output feedback control
中立型灰色随机分布时滞系统的指数鲁棒稳定性

中立型灰色随机分布时滞系统的指数鲁棒稳定性苏春华;刘思峰【摘要】为了得到一类中立型灰色随机分布时滞系统的指数鲁棒稳定性,本文利用LyapunovKrasovskii泛函法、灰矩阵的连续矩阵覆盖的分解技术和It(o)公式,分别得到了以非线性矩阵不等式和线性矩阵不等式(LMI)表示的该系统指数鲁棒稳定的时滞依赖性判据.对非线性矩阵不等式判据,我们给出了一般性算法,解决了非线性矩阵不等式判据不便于实际应用的问题.数值例子表明,本文所给判据是有效的,且系统的指数稳定性和时滞,随着绝对灰度矩阵的谱范数的增大而减小.【期刊名称】《工程数学学报》【年(卷),期】2010(027)003【总页数】12页(P403-414)【关键词】中立随机系统;分布时滞;指数鲁棒稳定性;灰矩阵;线性矩阵不等式【作者】苏春华;刘思峰【作者单位】信阳师范学院数学与信息科学学院,信阳,464000;南京航空航天大学经济与管理学院,南京,210016【正文语种】中文【中图分类】N941.5;O231.31 引言由于随机微分系统在自然、社会和科技等领域具有广泛的应用,所以,近三十多年来,关于随机微分系统的稳定与控制问题,一直是很多学者关注的焦点问题,并取得了许多有价值的成果[1]。
其间,在二十世纪八十年代,Kolmanovaskii和Nosov基于化学工程和航空理论发展的需要,还建立了一类中立型随机泛函微分系统,并研究了该系统解的存在性、唯一性[2]、稳定性和渐近稳定性[3]的问题。
此后,一些学者又利用Lyaponuv泛函和Razumikhin技术,研究了中立型随机系统的指数稳定问题,得到了一些指数稳定的代数判据[4-6]。
2007年,Randjelovic和Jankovic则基于一个关于向量范数的p-阶矩不等式,给出了中立型随机系统的p-阶矩指数稳定的代数判据[7],且该判据还是文献[8]的结果的推广。
然而,关于中立型不确定随机系统的研究,目前仅有少量的报道。
高阶无穷小计算规则

高阶无穷小计算规则
嘿,朋友们!今天咱们来聊聊高阶无穷小的计算规则。
啥是高阶无穷小呢?简单说,就是在某个变化过程中,一个无穷小
量比另一个无穷小量趋向于零的速度更快。
在计算的时候,有这么几个重要的规则得记住哈。
允许这样做:如果有两个无穷小量α和β,当α/β的极限等于0 时,那α就是β的高阶无穷小。
比如说,当 x 趋向于 0 时,x²就是 x 的高
阶无穷小。
为啥呢?因为 x 趋向于 0 时,(x²)/x 的极限是 0 呀,这就说
明 x²趋向于 0 的速度比 x 快得多。
禁止这样做:可别随便把不同阶的无穷小量直接相加减就认为还是
无穷小量哦。
比如说 x 是一个无穷小量,x²是比 x 高阶的无穷小量,
要是直接把它们相加,x + x²,可不能简单地认为它还是个无穷小量。
还有哦,如果有一串无穷小量α₁,α₂,α₃……,按照阶数从高到
低排列。
那在计算的时候,低阶的那些无穷小量在高阶无穷小量面前,影响就很小啦,可以忽略不计。
为啥要搞清楚这些规则呢?这可太重要啦!比如说在研究函数的极限、泰勒展开这些地方,搞清楚高阶无穷小,就能让咱们更准确地把
握函数的变化趋势,不会出错。
就像走迷宫,知道了这些规则,就等
于有了一张清晰的地图,能更快更准地找到出口。
总之,高阶无穷小的计算规则虽然有点复杂,但只要咱们用心去理解,多做几道题练练手,就一定能掌握好,让数学变得不再那么可怕,反而有趣起来!
好啦,今天关于高阶无穷小计算规则就说到这儿,希望对大家有帮
助哟!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弱无穷小算子算法
简介
弱无穷小算子算法(Weak Infinitesimal Operator Algorithm)是一种用于解决
非线性优化问题的数值计算方法。
它通过将非线性问题转化为一系列线性问题的求解,从而有效地降低了计算的复杂度。
背景
在实际问题中,我们经常需要求解非线性优化问题,即最小化或最大化一个非线性目标函数的值。
这类问题通常无法直接应用传统的数值优化方法进行求解,因为非线性函数具有复杂的数学形式,难以找到全局最优解。
弱无穷小算子算法应运而生,为我们提供了一种有效且高效的求解非线性优化问题的方法。
基本思想
弱无穷小算子算法基于泰勒展开和牛顿迭代方法,并结合了弱收敛理论。
它将原始的非线性优化问题转化为一系列线性子问题来求解。
具体来说,该算法通过引入一个弱无穷小量(infinitesimal)来逐步逼近原始目标函数,并使用牛顿迭代方法
更新当前点的估计值,直到满足收敛准则为止。
算法步骤
1.初始化:选择初始点和收敛准则的阈值,设定迭代次数上限。
2.迭代更新:根据泰勒展开,将原始目标函数在当前点进行二阶近似,并引入
弱无穷小量。
3.线性子问题求解:将二阶近似后的目标函数转化为一个线性子问题,通过求
解线性子问题得到下一步的迭代点。
4.收敛判断:计算当前点与上一步迭代点之间的差异,并与收敛准则进行比较。
如果满足收敛准则,则停止迭代;否则返回第2步继续迭代。
5.输出结果:返回最终收敛的点作为最优解。
算法特点
•高效性:弱无穷小算子算法通过将非线性优化问题转化为一系列线性子问题来求解,大大降低了计算复杂度,提高了计算效率。
•全局收敛性:该算法基于牛顿迭代方法,具有全局收敛性。
在合理的初始点选择和适当的参数设定下,可以得到全局最优解。
•鲁棒性:弱无穷小算子算法对于非线性函数形式的要求相对较低,适用于各种类型的非线性优化问题。
•可扩展性:该算法可以与其他优化算法相结合,例如遗传算法、模拟退火等,形成一种混合优化方法,以解决更加复杂的问题。
应用领域
弱无穷小算子算法在许多领域都有广泛的应用,包括但不限于: - 机器学习:用
于求解非线性模型的参数优化问题。
- 金融工程:用于投资组合优化、风险管理
等问题。
- 工业工程:用于生产调度、物流规划等问题。
- 图像处理:用于图像分割、边缘检测等问题。
总结
弱无穷小算子算法是一种有效解决非线性优化问题的数值计算方法。
它通过将原始问题转化为一系列线性子问题来求解,在保证全局收敛性和高效性的同时,具有较好的鲁棒性和可扩展性。
该算法在实际应用中具有广泛的应用前景,可以帮助我们更好地解决各种复杂的非线性优化问题。
