单一参数交流电路的分析计算
合集下载
正弦交流电路的分析计算

2. 相位相同
3. 有效值关系:U IR
4. 相量关系:设 U U 0
则 I U 0 或 R
I U
U I R
(3-43)
电阻电路中的功率
1. 瞬时功率 p:瞬时电压与瞬时电流的乘积
i
u
R
i 2 I sin ( t) u 2U sin ( t)
p u i Ri 2 u 2 / R
则: I2 100 5 j5 10 2 45 A
I1 1090 j10 A I I1 I2 100 A A读数为 10安
R uR 若 i 2Isin t
u L uL 则 u 2IRsin t
C
uC
2I (L) sin(t 90 ) 2I ( 1 ) sin(t 90 )
C
(3-69)
相量模型
I
R U R
U
L U L
C U C
相量方程式:
U U R U L UC
设 I I0(参考相量)
则 U R IR
电感电路中复数形式的 欧姆定律
U I j X L
U U 领先!
其中含有幅度和相位信息
I
u、i 相位不一致 !
u iL ?
(3-51)
关于感抗的讨论
感抗(XL =ωL )是频率的函数, 表示电感电路中电
压、电流有效值之间的关系,且只对正弦波有效。
XL
+R
_e L
UL I XL
ω
ω=0时
XL = 0
P UI cos Q UI sin
S UI
S
Q
P
(有助记忆)
(3-82)
R、L、C 串联电路中的功率关系
单一参数正弦交流电路的分析计算小结剖析共56页文档

单一参数正弦交流电路的分析计算小 结剖析
11、用道德的示范
12、法律是无私的,对谁都一视同仁。在每件事上,她都不徇私情。—— 托马斯
13、公正的法律限制不了好的自由,因为好人不会去做法律不允许的事 情。——弗劳德
14、法律是为了保护无辜而制定的。——爱略特 15、像房子一样,法律和法律都是相互依存的。——伯克
END
16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
11、用道德的示范
12、法律是无私的,对谁都一视同仁。在每件事上,她都不徇私情。—— 托马斯
13、公正的法律限制不了好的自由,因为好人不会去做法律不允许的事 情。——弗劳德
14、法律是为了保护无辜而制定的。——爱略特 15、像房子一样,法律和法律都是相互依存的。——伯克
END
16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
单一参数正弦交流电路分析

? 平均功率或有功功率 P=0
iut+-p
,
? 无功功率 QC
iQ
C
用无功功率 QC衡量电容元件与外界交换能量的规模,即
无功功率计算式
QC
?
?UI
?
?I 2 XC
?
?
U2 XC
无功功率单位 乏尔(Var)
交换能量过程分析 p ? ui ? ?U Isin2? t
i
u
ωt
i
i
u
u
i
i
u
u
p 放电 P > 0 放电
教学内容 电阻R、电感 L、电容 C元件的电压电流关系,相 量形式的基尔霍夫定律( KVL、KCL)。
教学要求 1.掌握单一元件的电压电流关系。 2.熟练应用相量形式的 KVL、KCL进行电路分
析。 教学重点和难点
重点: 单一元件的电压电流关系和相量形式的 基尔霍夫定律应用。
难点: 电阻 R、电感 L、电容 C元件电压电流关 系的分析。
【讨论】 指出下列各式中哪些是对的,哪些是错的?
在电阻电路中: 在电感电路中:
在电容电路中:
I?U R
i? U R
i? u R
I? ? U? R
i? u XL
U ? jωL I
I? U ωL
U? I?
?
jX L
U? I?
?
XL u
?
L di dt
i? u ωL
U ? I ?ω C
u ? i ?X C
三、纯电容电路
1.电容元件
定义电容为 C ? q
u
根据电流 i ? dq dt
i ? C duc dt
第三章 单相交流电路的分析与计算
第二节
正弦量的相量表示法
若一个相量相对于另一个相量在相量图的逆时针位置上,则说明该 相量具有超前的相位;相对地,另一个相量就具有滞后的相位。 2)几个同频率正弦量的加减,可以借助于相量图用平行四边形法则 或三角形法则进行运算。
图3-9 相量图的几种表示形式
第二节
2.相量的运算 解:因为
正弦量的相量表示法
第五节
功率因数的提高
六、考核标准 单控照明电路的安装考核标准见表3⁃1。
表3-1 单控照明电路的安装考核标准
第五节
功率因数的提高
表3-1 单控照明电路的安装考核标准
一、实训目的 1)掌握照明电路中荧光灯电路的安装方法。 2)掌握双控开关的工作原理及连接方法。 3)掌握插座的连接方法 二、实训器材
第四节
交流电路分析
图3-21 电路性质分析
三、电路功率分析 在RLC串联电路中,电阻是耗能元件,电感与电容都是储能元件, 因此电路中既有有功功率,又有无功功率。
第四节
交流电路分析
第四节
交流电路分析
第四节
交流电路分析
图3-22 功率三角形
第四节
交流电路分析
解:借用例3-5的求解内容可得
第四节
口内中心弹簧片上的接线端子,中性线接入螺旋部分。 6)照明装置的接线必须牢固,接触良好。 一、实训目的
1)掌握照明电路中白炽灯以及单控开关的安装方法。 2)掌握单相电能表的连线。 二、实训器材
第五节
功率因数的提高
白炽灯、圆台、螺口平灯座、开关、熔断器、塑料铜芯导线、 塑料软线、木螺钉、螺钉、通用电工工具、接线端子(XT)及单相电 能表等。 三、实训内容 1)安装圆台、螺口平灯座、开关及熔断器等。 2)安装灯头,连接电路。
汽车电工电子技术课件 任务2单一参数正弦交流电路

1. 频率关系
由以上两个式子可知,电压 u 与i
是同频率的正弦量。
2. 大小关系 由以上两个式子可以得 到: U IX C ,即纯电容电路的电压和 电流在大小上符合欧姆定律。
3. 相位关系
以上两个式子可知,电压 u比 i 滞 后 i 90°或 比u 超 前 90°,它们的相量图如图
2.4(b)所示。若用相量分别表示纯电 容
它们的相量图如图2.2(b)所示。若用相
量分别表示纯电阻元件的电压与电流,则
它们的关系可写成: •
I
•
U
,即相量形式也
符合欧姆定律。
R
4. 纯电阻元件在交流电路中的功率 电阻元件是一种耗能元件,在交流电路 中,纯电阻元件的瞬时功率时刻在变化,在 工程上不太好衡量,将瞬时功率在一个周期 内的平均值计算出来称为平均功率,又叫有 功功率,用符号P表示,单位为瓦(W)。
一种储能元件,它与电源之间只存在能量的
交换。为了表达电感元件与电源之间电磁互
换的规模,定义无功功率用符号Q表示,单
位 为 乏 ( v a r ) 。Q
UI
I
2XL
U2 XL
2.2.3 纯电容正弦交流电路
如 图 2 . 4 ( a ) 所 示 , 若 u U m sin t
, 则 i UmCsin(t 90) 。定义 容
P UI I 2 R U 2 R
2.2.2 纯电感正弦交流电路
如 图 2 . 3 ( a ) 所 示 , 若 u U m sin t
, 则 i U m sin(t 90) L
Hale Waihona Puke 。定义感抗 X L L 2fL() ,该参数是一个代表电感元件对电流阻碍作用大小的物理量,可见,
3.3 单一参数的交流电路

P
ωt
注意:通常铭牌数据或测量的功率均指有功功率。
3.3.2 纯电感元件的交流电路
1. 电压与电流的关系 di 基本关系式: u e L L
i
+
设: i 2 I sin ω t
dt
u
d( I msinω t ) uL dt 2 Iω L sin(ω t 90) 2 U sin( ω t 90)
1 U m I m (1 cos 2 ω t ) 2结论:O Nhomakorabeaωt
p 0 (耗能元件),且随时间变化。
波形图说明: ① p在任何瞬间都为正值(R是耗能元件); ② p变化的频率是i的两倍。 瞬时功率不能表示电路中功率的大小,电路中通常所 指的功率是瞬时功率在一个周期内的平均值称为平均功率 或有功功率。
有效值
I U ω C 或 1 1 定义: XC 容抗(Ω) ωC 2 π f C
则:
1 U I ωC
U I XC
直流: XC
交流:f
1 XC 2π f C
,电容C视为开路
XC
所以电容C具有隔直通交的作用
1 XC 2π fC
容抗XC是频率的函数 由: u
I , XC
相量式:
I 0 I U 0 I R U
U R ZR I
2. 功率关系 (1) 瞬时功率 p:瞬时电压与瞬时电流的乘积
i 2 I sin ω t u 2 U sin ω t
小写
u i O p
i u
ωt p
p ui 2 Um I m sin ω t
u i
ωt
o
+
结论:
单一参数正弦交流电路的分析计算

S U
Q
I
R U R
L U L
C
U C
P
(二)一般正弦交流电路的解题步骤
1、据原电路图画出相量模型图(电路结构不变)
RR、LjXL、CjXC uU、iI、 eE
2、根据相量模型列出相量方程式或画相量图 3、用复数符号法或相量图求解 4、将结果变换成要求的形式
正弦交流电路的功率问题
RL
1 4
0.25S
t≥0 R C 0 .0S 3 R L 0 .2S 5
零输入响应
2 1 K
2
u 0
t
uC uC(0)e RC
4A
t
u
2
t>0
uC 0.01F 2
iL
1H
iL iL(0)e RL
零状态响应
完全响应
t≥0 R C 0 .0S 3 R L 0 .2S 5
R'C
5. t<0时电路处于稳态,t=0时开关K打开,试求 t≥0
时的uC 、iL、u的零输入响应、零状态响应和完全响
应。
2 1 K
2
t=0
4A u
iL
2 uC 0.01F 2
1H
初始状态值 t≥0
iL (0)iL (0)1 A uC(0+)=uC(0-) =2V
RC
三相交流电路的小结(1)--三相电源
e 三相四线制 A
e (Y形联接) C
A
三相电源
N 一般都是
eB
对称的,
B C
称三相对 称电源
三相三线制(Y形联接)
eA
A
eC
eB
B
C
3.3单一参数的交流电路
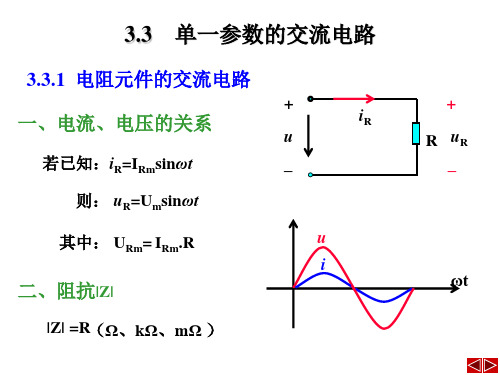
X = R + X arctan = Z φ R
2 2
-
-
分压公式:
+
I
Z
Z1 U U1 Z1 Z 2
U2
Z2 U Z1 Z 2
U -
例:
有两个阻抗 Z1 6.16 j9Ω、 Z 2 2.5 - j4Ω
它们串联接在 U 22030V 的电源上, 求 I 和 U1 、U 2 并作相量图。
解: Z Z1 Z 2 (6.16 2.5) j (9 - 4)
8.66 j 5 1030 ()
I
I
+
U
+ Z1 U 1
U 220 30 Z 1030
220
+ Z2 U 2
-
U1 Z1 I (6.16 j 9) 22V 239.855.6V
1 1 1
3.相量电路模型
例:若有-4j,则知XC=4Ω
例1. 一电感线圈,L=100mH,f=50HZ (1) i 7 2 sint A , 求 u=? (2) U=127∠-30°V, 求I并画相量图。 解(1) : XL=2πf L =31.4 (Ω) U=7×31.4 =220 (V) ∴ u= 220 2 sin( t 90º )V 解(2) : 已知U=127 V ∴ I=U/XL= 4 (A), -90° I= 4 -30° IL
不一定!
三、 阻抗的并联
Z1 Z 2 Z Z1 Z 2 Z1 Z 2
分流公式:
I
+
U
Z1
Z2
-
2 2
-
-
分压公式:
+
I
Z
Z1 U U1 Z1 Z 2
U2
Z2 U Z1 Z 2
U -
例:
有两个阻抗 Z1 6.16 j9Ω、 Z 2 2.5 - j4Ω
它们串联接在 U 22030V 的电源上, 求 I 和 U1 、U 2 并作相量图。
解: Z Z1 Z 2 (6.16 2.5) j (9 - 4)
8.66 j 5 1030 ()
I
I
+
U
+ Z1 U 1
U 220 30 Z 1030
220
+ Z2 U 2
-
U1 Z1 I (6.16 j 9) 22V 239.855.6V
1 1 1
3.相量电路模型
例:若有-4j,则知XC=4Ω
例1. 一电感线圈,L=100mH,f=50HZ (1) i 7 2 sint A , 求 u=? (2) U=127∠-30°V, 求I并画相量图。 解(1) : XL=2πf L =31.4 (Ω) U=7×31.4 =220 (V) ∴ u= 220 2 sin( t 90º )V 解(2) : 已知U=127 V ∴ I=U/XL= 4 (A), -90° I= 4 -30° IL
不一定!
三、 阻抗的并联
Z1 Z 2 Z Z1 Z 2 Z1 Z 2
分流公式:
I
+
U
Z1
Z2
-
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i u
R
1 T 1 T 2 P = ∫0 p dt = ∫0 2UI sin ωt dt T T
平均功率
=UI = I R =U
2
2
二.电感电路
1.电压与电流的响应 1.电压与电流的响应 i u L
R
(W, KW,mW)
i 设: =
2 I sin ωt
di 基本关系式 u = L dt
di u = L = 2 I ⋅ω L cosωt dt = 2 I ω L sin(ωt + 900 )
流过各元件的电流相同。 流过各元件的电流相同。 各部分电压瞬时值服从基尔 霍夫电压定律。 霍夫电压定律。
则:
+
2 IR sin ω t + 2 I (ω L ) sin( ω t + 90 0 ) 1 2I ( ) sin( ω t − 90 ° ) ωc
1. 相量方程式
i
R
ɺ ɺ ɺ ɺ U = U R + U L + UC
i
p = i ⋅ u = UI sin 2ωt
电感元件的瞬时功率 变化。 随时间以 2ω 变化。 能量转换过程可逆! 能量转换过程可逆!
u ωt
P >0 P <0 P >0 P <0 吸收 输出 吸收 输出 能量 能量 能量 能量
2)平均功率P(也称为有功功率) 平均功率P 也称为有功功率)
1 1 P = ∫ p dt = ∫ U I sin ( 2ω t ) dt = 0 T T
u=
2U sin ω t
U = IR
ɺ ɺ I U
u, i 同相
i=
2 I sin ω t
ɺ ɺ U = IR
单一参数正弦交流电路的分析计算汇总 单一参数正弦交流电路的分析计算汇总 正弦交流电路的分析计算
电路参数 L 基本关系
i
电路图 正方向) (正方向)
di u=L dt
功率 有功功率: 有功功率: 0 无功功率: 无功功率:
u
复阻抗
jX L = j ωL
UI I XL
2
电压、电流关系 电压、 瞬时值 设 则 有效值 相量图 相量式
i=
2 I sin ω t
sin(ωt + 90°)
U = IXL XL = ωL
Uɺ
u = 2 IωL
Iɺ
90° u领先 I 90°
ɺ ɺ U = I( jXL )
单一参数正弦交流电路的分析计算汇总 单一参数正弦交流电路的分析计算汇总
设: = i
2 I sin Biblioteka tuRuL C
uL
ɺ 或 I = I∠0°
uC
ɺ ɺ ɺ ɺ ɺ ɺ 则:UR = IR , UL = I ( jX L ) , UC = I (− jXC )
ɺ ɺ ɺ ɺ U = IR + I ( jX L ) + I (− jX C ) ɺ = I [R + j ( X − X )]
电压与电流的响应: 电压与电流的响应: 设:i =
0
2 I sin ω t
0
u = 2 I ω L sin(ωt + 90 ) = 2 U sin(ωt + 90 )
小结: 小结:u-i 之关系 u i
90 °
1)频率相同
ωt
XL
2)相位相差 0 相位相差90 领先i (u领先 900) 领先 3)有效值 U = IωL
Iɺ
UωC
ɺ U
U
复数形式的 欧姆定律
2.电容电路中的功率 2.电容电路中的功率
i= 2 I sin ω t u= 2U sin( ω t − 90 )
0
i u
瞬时功率p 1)瞬时功率
p = i ⋅ u = U I sin 2ω t
2)平均功率 平均功率P 电容性无 无功功率Q 3)无功功率 功取负值
二. 功率计算
1.瞬时功率 1.瞬时功率
p = i ⋅u
领先i( 设u领先 (电感性电路) 领先
p = I m sin ωt ⋅ U m sin(ωt + ϕ ) I mU m [cosϕ − cos(2ωt + ϕ )] = 2
2.2.1 单一参数交流电路的分析计算 一.电阻电路
1.电压与电流的响应 1.电压与电流的响应 由欧姆定律:u 由欧姆定律: 设: u = u i
R
= iR
2U sinω t
u U 则:i = = 2 sinω t = 2 I sinω t R R
u = 2U sinω t
u – i 响应
u U i = = 2 sinω t = 2 I sinω t R R
*复数阻抗的模也可由电压、电流有效值之比 复数阻抗的模也可由电压 也可由电压、
求得。 求得。
XL − XC Z = Z ∠ϕ= R +(XL − XC) ∠tg R
2 2 −1
i
R
uR uL
复阻抗的幅角
ɺ U U∠ϕu U Z= = = ∠ϕu −ϕi ɺ I I∠ϕi I
u
L C
uC
复阻抗的幅角等于电压与电流的初相位之差。 复阻抗的幅角等于电压与电流的初相位之差。 电压与电流的初相位之差 一定) *当(f一定)电路参数确定后,电压与电流间 一定 电路参数确定后, 的相位差也就确定了。 的相位差也就确定了。
U 2 1
2U sin ω t
U = IXC
Uɺ
u落后i90° 落后i90° i90
ɺ Iɺ U = ɺ I (− jX C )
2.2.2
i
R
R-L-C串联交流电路 串联交流电路
电压与电流的响应 一. 电压与电流的响应
uR uL
u
L C
uC
u=
di 1 u = uR + uL + uC = iR+ L + ∫ idt dt C 若: = 2 I sin ω t i
T T 0 0
结论:理想电感不消耗能量,只有能量的吞吐。 结论:理想电感不消耗能量,只有能量的吞吐。 3)无功功率 无功功率Q 定义:电感的瞬时功率所能达到的最大值。 定义:电感的瞬时功率所能达到的最大值。 (反映电感元件与电源进行能量交换的规模) 反映电感元件与电源进行能量交换的规模)
Q =U I = I XL =U
容抗XC
(单位:ω:rad/s C :f XL : ) 单位:
1 Xc = 是频率的函数 ωC
Xc
C为定值 为定值
f
XC表示电容上的电压、电流有 表示电容上的电压、 效值之间的关系, 效值之间的关系,且只对正弦 波有效。 波有效。 ɺ 4)相量关系式 设 U =U∠0O 则: Iɺ = I ∠ 90 0 = U ω C ∠ 90 0 ɺ = 1 I∠ − 90 0 = I (− j 1 ) ɺ ɺ U ωC ωC 复数容抗 复数容抗
ɺ ɺ U = I( j XL)
ɺ = I (− j 1 ) = I (− jX ) ɺ 电容电路: 电容电路: U ɺ C ωC 2.电阻为耗能元件 电阻为耗能元件, 2.电阻为耗能元件,L、C为储能元件 为储能元件
1 2 电感储能: 电感储能: WL = ∫ uL iLdt = L iL 2 1 2 电容储能: 电容储能 WC = ∫ u C i C dt = C u C 2
R
p = u ⋅ i = 2UI Sin ωt
1.p随时间变化 结论: 随时间变化 结论:1. 耗能元件) 2. p ≥ 0(耗能元件)
平均功率:一个周期内瞬时功率的平均值P 2)平均功率:一个周期内瞬时功率的平均值 大写
1 T 1 T 2 P = ∫0 p dt = ∫0 2UI sin ωt dt T T
注:Z 是一个复数,但不是一个正弦交流 是一个复数, 不是一个正弦交流 一个 相量( 上不加 );Z 相量( Z上不加 ); 在方程式中只是 一个运算符号。 一个运算符号。
ɺ ɺ U = I[R + jXL − jXC ]
Z = R+ j( XL − XC )
复数阻抗 2 2 −1 XL − XC Z = R+ j(XL − XC)= R +(XL − XC) ∠ tg = Z∠ ϕ R 阻抗的模 阻抗角 ɺ U U∠ϕu U U Z= = = ∠ϕu −ϕi Z= ɺ I∠ϕ I I I i
电路参数 C 基本关系
i
电路图 正方向) (正方向)
du i=C dt
C
功率 有功功率: 有功功率: 0 无功功率: 无功功率:
u
−j − jX = ωc
复阻抗 电压、电流关系 电压、 有效值
− UI − I XC
2
瞬时值 设 则
相量图
相量式
u=
i=
XC = 1 ωC ωC sin( ω t + 90 ° )
ɺ UC
U ≠UR +UL +UC
相量图 各部分电压之间的关系 ----- 电压三角形 复数阻抗的实部电阻, 复数阻抗的实部电阻,与虚部电抗间的关系 --- 阻抗三角形 U Z UL −UC i 阻抗三 ϕ UR uR 角形 R X=XL−XC R u
L C
uL
R = Z cos ϕ
X
L C
uC
− X = Z sinϕ
L为定值
f
X L = ωL 感抗
XL 是频率的函数 单位: (单位:ω:rad/s L:H XL : )
小结: 小结:u-i 之关系 感抗XL U = I ω L = I 2π fL = I X L XL表示电感上的电压、电流有效值之间的关 表示电感上的电压、 且只对正弦波有效。 系,且只对正弦波有效。 4)相量关系式 ɺ U ɺ 设:I = I∠00 Iω L 0 0
