相贯线在数控加工中的解析求法
机械制图相贯线

机械制图相贯线简介在机械制图中,相贯线是指两个或多个图形的交集,它通常用于确定零件之间的相对位置以及其运动轨迹。
相贯线在机械设计和制造过程中具有重要的作用,在设计阶段就能够精确地确定各个零件的相对位置关系,从而确保整个机械系统的正常运行。
相贯线的计算方法相贯线的计算方法主要依赖于图形的几何属性和运动规律。
下面介绍几种常见的相贯线计算方法。
1. 直线与直线的相贯线当两条直线相交时,它们的相贯线就是它们的交点。
如果两条直线不相交,则它们没有相贯线。
如上图所示,直线A和直线B相交于点O,因此它们的相贯线为点O。
2. 圆与直线的相贯线当一个圆与一条直线相交时,它们的相贯线可以是一个或两个交点。
相贯线的计算方法如下:•首先,确定圆心和半径。
•其次,确定直线的方程。
•然后,将直线方程代入圆的方程,求解相交点的坐标。
上图中,圆C与直线D相交于点E和点F,因此它们的相贯线为点E和点F。
3. 圆与圆的相贯线当两个圆相交时,它们的相贯线可以是一个或两个交点。
相贯线的计算方法如下:•首先,确定两个圆的圆心和半径。
•其次,根据两个圆的几何关系,列出它们的方程。
•然后,解方程得到相交点的坐标。
上图中,圆G与圆H相交于点I和点J,因此它们的相贯线为点I 和点J。
相贯线的应用相贯线在机械制图中具有广泛的应用,以下列举几个常见的应用场景。
1. 齿轮传动在齿轮传动中,相贯线用于确定齿轮之间的啮合关系。
通过计算齿轮的相贯线,可以确定齿轮的模数、齿数和啮合角等参数,从而确保齿轮传动的正常运转。
2. 运动机构相贯线在运动机构设计中起着重要的作用。
通过计算运动机构各个零件的相贯线,可以确定它们的相对运动轨迹,从而实现机构的运动控制。
3. 机械零件组装在机械零件组装过程中,相贯线被用于确定零件之间的相对位置关系。
正交相贯线坡口数控加工G代码的自动生成

度 范 围 内的投 影 圆周 运 动 ,见 图 1 b , z≤z z , ()即 。 ≤ 。 由图 1 b 可 知 : ()
z一
y I 2 p iw *i =S N( a/ )*r l
Z S R( 2 2 y 2 2 Y h- h 2 = Q r - — )
即可进行 ,该方法可有效降低生产成 本,具有 广泛 的推广意义 。
关键 词 : 管道 ; 相 贯 线 ;焊 接 坡 口;G 代 码 中 图分 类 号 :T 2 3: G4 7 6 P 7 T 5 . 文 献 标 识 码 :A
0 引言
较 大 ,管子 的直径 各不相 同,所 以即使 采用 C AM 软件 也需 要一个个 地建 立三维模 型 ,效率较低 。 本 文对 简化 编制这 些相 贯线 坡 口的加 工程 序 的方 法 进行 了研 究 , 以便 能够 满足生 产要 求 ,批量 化得 到
程零点。
( ) y平 面 a x"
【)y b ' 面 z平
图 1 正 交 相 贯 线 在 x 、y y z坐 标 系 的数 学 关 系
加工 过 程 中刀具 在 平 面 内作 以 r为半 径 的投 影匀速 圆周 运动 , 了方 便编程 , 以设定 平 面内 为 可
控制 刀具 路径 中任 一点 ( y z 的精度 , z, , ) 由图1 () a 可知 :
就 可 以实现 加工 G 代码 的批量 编程 ,同时可 以利用 刀
按 照 数控 程 序 的 格 式 输 出
NEXT CL0S E
具在 平 面 内的 投影 圆周 运动 的角速 度来 控制 G 代 码 与理论 曲线 的拟 合精度 。 以下 为 QB I ASC语 言 编程 的程序 实例 :
相贯线(机)
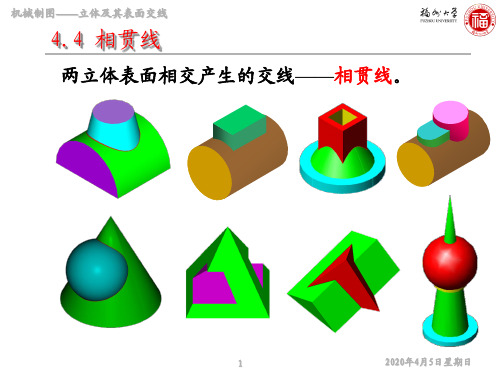
机械制图——立体及其表面交线
三、回转体与回转体相贯
★ 相贯线一般为封闭的马鞍形的空间四次曲线。
★ 相贯线的产生及影响其形状的因素: ★ 求相贯线的作图实质是找出相贯的两立
体表面的若干共有点的投影,光滑地连点成线。
★ 解题步骤: • 判断: • 求交:求点、连点成线 • 整形:进行可见性判断、 搞清轮廓线去留
机械制图——立体及其表面交线
表面交线小结
包括截交线和相贯线
一、表面交线的形状
1、平平相交是直线
表面性 封闭性 共有性
2、平曲相交五三一
★ 平面与锥柱球相交产生的交线为锥五柱三球一圆(平面图形)。 ★ 平面立体与锥柱球相交产生的交线为若干段平面曲线或直线组
成的空间折线。
41
2020年4月5日星期日
机械制图——立体及其表面交线
★ 求相贯线的步骤:
• 分析各棱面与回转体表面的相对位 置,从而确定交线的形状。
• 求出各棱面与回转体表面的截交线。 • 连接各段交线,并判断可见性。
6
2020年4月5日星期日
机械制图——立体及其表面交线
二.平面体与回转体相贯
例3 求作四棱柱与圆柱的相贯线。
7
2020年4月5日星期日
机械制图——立体及其表面交线
二.平面体与回转体相贯
例4 补全正面投影
8
四棱柱的四个 棱面分别与圆柱面 相交,前后两棱面 与圆柱轴线平行, 其交线为两段直线; 左右两棱面与圆柱 轴线垂直,其交线
为两段圆弧。
由于相贯线是 两立体表面的共有 线,所以相贯线的 侧面投影积聚在一 段圆弧上,水平投 影积聚在矩形上。
2020年4月5日星期日
例11 求水平投影
椭圆柱相贯线槽的数控加工

图1 柱形凸轮端面 曲线及工件坐标系 收 稿 日期 : 2 0 1 3 — 0 3 — 0 8
考虑编程取值的方便和曲线形状的因素 ,选择
作者简介 : 刘振超 ( 1 9 6 6 一) , 女, 广西岑溪人 , 副教授 , 主要从事机械加工工艺设 计、 数控技术应用的理论 研究 和教学工作。
3 宏 程序 的编写
3 . 1 变量 的确 定
图 6 步进角 的计算 图
以角度 t 为第一 自 变量 ,取 曲线槽上任意相邻两 点间的角度 z 3 t 相等, 定义为步进角度。然后 由参数方 程分别计算 出各点对应的 值 、 y值和 z 值 ,用 G 0 1 进行空间直线插补 , 以空间直线来逼近空间曲线。 同时以进刀切深值为第二 自变量 ,在 每次进刀 时z 坐标也跟着变化。 在编程 时要理顺两个 自变量之 间的关 系 ,利用 宏程序的循环嵌套方式进行编程。 3 . 2 最小角度步进值 / l t 的计算 ( 1 ) 求 曲线段 的最小 曲率半径 尺 如图 5 所示为椭圆曲线 , 其 曲线方程为 :
《 装备制造技术) ) 2 0 1 3 年第 6 期
椭 圆柱 相贯线槽 的数控J j n - r
刘振超
( 柳州铁道职业技术学院, 广西 柳州 5 4 5 0 0 7 )
摘 要: 通 过建立椭 圆柱相贯 线的数 学模型确 定刀具 的运动轨迹 , 利 用宏程 序的变量编程功能 实现 刀具轨迹 的控制 , 并 经过 插补误差计算 来确 定步进值 , 以确保复杂 曲线加工的精度。
该曲线槽在 X O Y平面上 的投影是 1 / 2 椭圆及一
条连接直线 。 考虑到取值计算的方便 , 以椭圆 1 的对
第四节相贯线

椭圆)(图5-14)。 四、 相贯线的简化画法
当圆柱与圆柱、圆柱与圆锥轴线相交,并公切于一圆球时,相贯线为椭圆,该椭圆的正面投影为一直线段,水平面投影为类似形(圆或 椭圆)(图5-14)。
三、 相贯性的特殊情况
• 两回转体相交时,其相贯线一般为空间曲线,但 在特殊情况下,也可能是平面曲线或直线。
• 当两个回转体具有公共轴线时,相贯线为圆,该 圆的正面投影为一直线段,水平面投影为圆的实 形(图5-13)。
图5-13 相贯线的特殊情况(一)
当圆柱与圆柱、圆柱与圆锥轴线相交,并公切于一圆球时,相贯线为椭圆,该椭圆的正面投影为一直线段,水平面投影为类似形(圆或
椭圆)(图5-14)。
例5-4求作圆柱与圆交时的相贯线。
当圆柱与圆柱、圆柱与圆锥轴线相交,并公切于一圆球时,相贯线为椭圆,该椭圆的正面投影为一直线段,水平面投影为类似形(圆或
四、 相贯线的简化画法
画相贯线常采用的方法是辅助平面法。
当两个回转体具有公共轴线时,相贯线为圆,该圆的正面投影为一直线段,水平面投影为圆的实形(图5-13)。
当两圆柱轴线平行或两圆锥共顶相交时,相贯线为直线(图5-15)。
四、 相贯线的简化画法
画相贯线常采用的方法是辅助平面法。
图5-14 相贯线的特殊情况(二)
• 当圆柱与圆柱、圆柱与圆锥轴线相交,并公切于 一圆球时,相贯线为椭圆,该椭圆的正面投影为 一直线段,水平面投影为类似形(圆或椭圆)(图514)。
• 当两圆柱轴线平行或两圆锥共顶相交时,相贯线 为直线(图5-15)。
图5-13 相贯线的特殊情况(一)
例5-4求作圆柱与圆锥台正交时的相贯线。
辅助平面法的原理是用一个截平面依次截切两个相贯的物体,所得的截交线必有几点处于三面共点的位置。
机械制图中相贯线的求解研究
机械制图中相贯线的求解研究作者:魏芳波来源:《高教学刊》2016年第05期(郧阳师范高等专科学校汽电系,湖北十堰 442000)摘要:通常求解相贯线的投影是利用投影的集聚性或运用辅助平面及球面几种方法进行,求解过程比较复杂。
运用编程技术来实现实体相贯线作图的过程,使用方便,但需要编程基础。
通过制作三维模型,利用自动生成工程投影,构建了相贯线投影图。
最后对几种求解的优势进行分析,为机械制图中相贯线教学提供参考。
关键词:相贯线;积聚性;制图模型;编程技术中图分类号:G642 文献标志码:A 文章编号:2096-000X(2016)05-0122-02Abstract: Solving the projection of intersection line is usually by use of Clustering of projection or the use of auxiliary plane and spherical several methods, so the process is more complicated. It is easy to realize the process of intersection line drawing by using programming techniques, but it requires programming. By making a 3D model, the projection of the intersecting line is constructed by using the projection of the project. Finally, this paper analyzes the advantages of several solutions, providing reference for the teaching of mechanical drawing.Keywords: intersecting line; clustering; drawing model; programming techniques相貫线形状一般比较复杂,是机械制图教学中的一个难点。
相贯线切割机编程的求解方法

相贯线切割机编程的求解⽅法
在多⾯正投影中求解相贯线属于初学者的难点之,⼀般多采⽤表⾯取点法求解。
表⾯取点法:当两个回转体中有⼀个表⾯的投影有积聚性时,可⽤在曲⾯⽴体表⾯上取点的⽅法作出两⽴体表⾯上的这些共有点;这种⽅法称为表⾯取点法。
辅助平⾯法:作⼀组辅助平⾯,分别求出这些辅助平⾯与这两个回转体表⾯的交点,这些点就是相贯线上的点。
这种⽅法称为辅助平⾯法。
为了作图⽅便,⼀般选特殊位置平⾯为辅助平⾯。
相贯线的形状取决于两⽴体的形状、⼤⼩和相对位置。
如两空间形体的表⾯都是曲⾯,相贯线是⼀条空间曲线;两空间形体的表⾯都是平⾯时,相贯线是⼀条空间折线;两空间形体的表⾯分别是平⾯和曲⾯时,相贯线是由⼏段平⾯曲线围成的线。
在给定两空间形体后,在多⾯正投影图中可以容易地画出两⽴体的投影,但它们的相贯线的投影并不能直接画出,通常采⽤辅助⾯法或其他⽅法先求出相贯线上若⼲点的投影,然后将它们连接成相贯线。
辅助⾯法是先作出⼀适当的⾯,再作出该⾯和两空间形体的交线,最后作出两交线的交点。
所得交点就是相贯线上的点。
按此⽅法改变辅助⾯的位置,重复作图,就能得到⾜够的点,将它们连结成相贯线。
图中为圆柱和圆锥台相交,为作出其相贯线上的点,选⽤⽔平⾯为辅助⾯,⽔平⾯与圆柱、圆锥台的交线分别是开⼝矩形和圆。
它们的两个交点是相贯线上的点。
运⽤辅助⾯法的关键在于选取合适的辅助⾯,辅助⾯和两空间形体表⾯的交线投影应是直线或者是圆。
作图中常选⽤平⾯或球⾯为辅助⾯。
数控管切割机床相贯线切割的研究

关键 词 :相 贯 线 坐 标 计 算 ;坡 口 处 理 ;数 控 系 统 中图 分 类 号 :T 4 @8 文 献标 识码 :A
Do : . 9 9 . s . 0 9 0 . 0 1 4 E) 2 i ( . 1 0 i 3
求 解 相 贯 线坐 标 ,不 能 直 接 提 供 给数 控 切 割机 床
加 工 ,本 文建 立 了一 种 在 同 坐 标 系下 求 解 相 贯 线
坐 标 的 数 学模 型 ,并 应 用 到 相 应 的数 控 系统 中 。
1 相贯 线 坐标 计 算
11 计 算切 管母 线方程 . 本 文 以2 管相 贯 为例 ,将 坐 标原 点设 在 切管 轴
l l 数 控 管 切 割 机 意 图 割
Z 轴 垂 直 与切 管轴 线 ,割 咀沿 其 做 上 下的 直 线 运动 2 0 轴 在 切割 轴 线 的切 平 面 内 ,割 咀 绕 回转 点 做 旋转 运 动
现 在 已 经 有 许多研 究 者 开 始研 究相 贯 线 切 割 和 坡 口处理 的数 学 模型 ” ,都 是 在不 同坐 标 系 中 。。
文 章 编 号 : 1 0—0 3 ( 0 14 上 ) 0 6 — 3 9 1 4 2 1 ) ( 一 0 5 0 0
0 引 言
桁架结构在现今的许多大跨度的场馆建筑,
如会 展 中心 、体 育 场 馆 或其 他 一 些大 型 公 共 建 筑
图 1 五轴 四联 动 相贯 线切 割数 控 机床 的示 意 图 , 为 它采 用P C + L 运动 控 制模 块+ 服 电机进 行 系统 控 伺 制 , 由上 位机 P 计 算 出相 贯线 点的 坐标 ,切 割坡 C 口的 实 际切 割 角 ,并将 这些 数 据 转 化 为 数 控 系统
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山 西 大 同大 学 学 报 ( 自然科 学 版 )
Junl f hn i tn nvr t N tr cec) o ra ax Da gU i s y a a Sine oS o e i ( ul
Vo _6 No 5 1 . . 2 Oc .0l t 2 O
相 贯 线 在 数 控 加 工 中 的解 析 求 法
王 晓 雪 ( 山西 大 同大学 工学 院 ,山西 大 同 0 70 ) 30 3
摘 要 : 贯 线是 画 法 几何 中的 重要 内容 , 画 法几 何 中我 们 一 般 用作 图 法 来 求 , 文 利 用 数 学 中 的 解析 法 相 在 本
中。 以根据 相贯 线 的曲线 方程 来控 制 切 割工 具 的 可 【 J
题. 而通 常我们 只用 作 图法来 求,作 图法 虽然形 象 、 直 观 、迅速 ,但却 由于受 到作 图操 作 和仪 器 工具 的 限制 , 再加 之作 图过程繁 顼 、图形绘 制不 准确, 往 往 给生 产制 作造 成许 多麻烦 ,且精 度更 不 能满 足现 代 技 术与计 算 机辅 助设 计 和数 控制 造技 术 的要 求 , 因 此这 我们采 用 图解 与计算 相结合 的方法 ,通 过投 影
程 为: 当0
一
" _ I T时有 : |
± s塑 ! e
c s tn3 R oa o 0a/+ c t
当 J ' B" I T <i T时有 :
一
堡
二 !
c s tn Rc t o Oa B+ oa
上式 即为相贯 线上任 一点 的极 坐标方 程, 在制
x
两圆柱轴线的交点为 0 它们之间的夹角为 6已知) , ( ,
以 0为 原点 , 别 建 立 各 自的 三 维 坐标 体 系 , 。 分 Y 轴 垂 直 于 】 面, 2 OJ Z平 y 轴垂 直 于 xo2 面, 0 和 2 平 z 而 j 2 xo: 好 在 同一 平 面 内, 以 Y 与 Y 为 同一 条轴 , 2 正 z 所 :
图上 的几 何关 系, 利 用解 析 方 法 , 再 建立 相 贯 线 上
( 这里 c s o仅
且 /-r ) . 2 <
在 制作 该 相 贯 线 时 , 将 圆柱 面 展 开成 板 , 可 横 坐 标 为 , 坐 标 为 , 数 控 机床 [ 用 数 控 线切 纵 在 5 1 上
割机 按坐 标便可加 工 出所需 曲线 .
作 者 简 介 : 晓雪 (9 8 )女 , 王 16 一 , 山西 五 台人 , 士 , 硕 副教 授 , 业 方 向 : 筑 与 土 木 工程 专 建
王晓雪 : 相贯线在数控加 工中的解析求法
( t f z ra 2+ ) xal ) 2 n 1 n_ = ( f l
() 2
设 xp o0 ypo0 =cs , =cs,这里 0 0 2 (< 代人 上 面 << 9,p R) ( 、( 两方 程并 联 立解 , 可 得 两立 体相 贯 线 的方 1 2 ) ) 便
之 间 的 截交 以及 曲面 立体 曲 面立 体之 间 的相 贯 问
一 — 一
=
OA + AB=
S nO 1
+ t o an
=
s nO l
+ t ano
V
.'io / n ̄ j s
。 tn a8
sn i3
二 : J ! 1 1 . !
sn i8 。 tn a6
线.
图 1 圆柱 体 与 圆 柱体 相贳
设 两 圆柱 的底 面半 径 分 别 为 r与 r 均 已知) ( ,
2 圆柱 体 与 圆锥 体 相 贯
如图 2 所示为轴线相交的圆柱体与圆锥体的相
贯rz 圆锥 顶角 为 2f  ̄ )圆 柱体 的中心 轴 线与 jj _, cc 7 , <1 "
平面
求得 平 面 与 立体 及 立 体 与 立 体 之 间 相 贯 线 的 函数 表 达 式 ,以便 于 利 用在 数 控 机 床 的 机 件 加 工 中
关 键 词 : 贯 圆柱 体 圆锥 体 相
中 图分 类 号 : 7 3 X 0. 5
文献标识码: A
在 我们 的生活 和生 产 中,常 常会遇 到 两个 或若 干 个立体 相交 的 问题 f 画法几 何 中, 在 我们 称之 为相 贯 )比如在 机 械生 产 、化工 设备 、 输 管 道 、 结 , 运 钢 构构 件 的连接 中, 常会 遇到 一些 平面 与 曲面立 体 通
点 的坐标方 程 或极 坐标方 程 . 根据 所 求 的坐标 方 并
程或 极 坐 标方 程 , 数 控 机床 上 利 用 切 割 工具 , 在 切
割出我们所需的各种相贯 曲线. 为此建立相贯线上 的点 的坐标方 程或极 坐标 方程 是非 常重要 的.
1 两 圆柱 体 相 贯
如图 1 所示 为轴 线相交 的两 圆柱体 相 贯『2( 】1 正 一 立 投 影 ) 现用 作 图与 解 析 相结 合 的方 法 来 求 相 贯 ,
图 2 圆柱 体 与圆 锥 体 相 贯 图
作 时将 圆锥 面展 开成 板, 数控线 切 割机按 该极坐 用
标方程 即可加工 成形 l 5 1 .
、 + 一Rct- / oc z  ̄
尺 Rc t oa
对 于任何平面与立体截交以及 立体与立体相
贯, 都可 求 出其 解析方程 , 使我们 在数控 机床 的生产
轴 的夹角 为 ( < )且其 中心轴 线 与 圆锥 中 0 ,
其 坐 标我 们 均计 为 由图 1的几 何关 系可 得 下 面 解析 式p】 。: 4 心轴线 相交 . 坐标如 图 2 示 , 圆柱 曲 面方 程 所 则 为:
收 稿 日期 : 0 1— 8 0 2000— 1
