光的衍射(二)
光的衍射2

棱镜光谱是零级光谱。只有 一个级次,没有重级现象。
定义恰能分辨的两条谱线的平均波长 与 R 它们的波长差 之比为光栅的分辨本领 R
由光栅方程
P
( a b) sin k ( k 0,1,2) 加强
kf x a b
( k 0,1,2)
明纹
播放动画
播放动画
例:分光计作光栅实验,用波长 = 632.8 nm的激光照射光栅常数 d = 1/300 mm的光栅上,问最多能看到几条谱线。
解:在分光计上观 察谱线,最大衍射 角为 90°,
d
( a b) sin k
kmax ( a b) sin 90
o x
f
P
kmax
( a b) sin 90
3 . 5
3 1 10 9 300 632.8 10
-8
单缝衍射 轮廓线
4 8
-4
0
a b k m a k'
(m 1,3) 2,
m为整数时,光栅谱线中m、2m、3m等 处缺级。
I单
当 m=4 时 谱线中的第 –8、 – 4、4、 8级条纹缺级。
-2 -1
0 I 光栅衍射 光强曲线 1 2
单缝衍射 轮廓线
4 8
-8
-4
0
第五节 光栅光谱
X 射线的应用不仅开创了研究晶体结构的新领域, 而且用它可以作光谱分析,在科学研究和工程技 术上有着广泛的应用。 在医学和分子生物学领域也不断有新的突破。 1953年英国的威尔金斯、沃森和克里克利用 X 射线的结构分析得到了遗传基因脱氧核糖 核酸(DNA) 的双螺旋结构,荣获了1962 年 度诺贝尔生物和医学奖。
衍射2

较大 符合
瑞利 判据
太小
小孔(直径D)对两个靠近的遥远的点光源的分辨 19
S1 *
D
0
I
* S2
最小分辨角 (angle of minimum resolution):
1
1 . 22
D
分辨本领(resolving power):
R 1
D 1 . 22
6
2、N=3
δ
-λ
3、N=4
0 0I
λ
δ
-λ
0
λ
I
N很大时,数目众多强度极弱 的次极大与极小混成一片, 淹没在杂散光的背景之中, 形成一片暗区,一般觉察不 δ 出它们的存在;各主极大成 为非常细的亮条纹。
三、光栅的衍射规律 1、可以证明:光栅衍射,是单缝衍射和多 光束干涉共同作用的结果。 各主极大受到单缝衍射的调制,衍射光强 大(小)的方向,主极大的光强也大(小)。
7
例:d 4a 情形
单缝衍射光强曲线 -2 -1
I
(参见书p181图4.12)
sin (/a)
多光束干涉光强曲线
0 I
1
2
-8
-4
0
I
4
sin 8 (/d)
光栅衍射光强曲线
单缝衍射 包络线
4 sin (/d)
8
-8
-4
0
8
19个明条纹
单缝衍射和多缝衍射干涉的对比 (d =10 a)
13
0
sin
五、光栅光谱
d sin k ( k 0 ,1 ,2 )
λ定, k |θ|
3级 2级 1级 0 1级
光的衍射2

例:以氦放电管发出的光垂直照射到某 以氦放电管发出的光垂直照射到某 光栅上,测得波长 光栅上 测得波长λ1=0.668µm 的谱线的衍 射角为 ϕ =20°.如果在同样 ϕ 角处出现波 如果在同样 λ2=0.447µm的更高级次的谱线 的更高级次的谱线, 长 那么光栅常数最小是多少? 那么光栅常数最小是多少 解:由光栅公式得 由光栅公式得 sin ϕ = k1λ1 (a + b) = k2λ2 (a + b) k1λ1 = k2λ2 k2 k1 = λ1 λ2 = 0.668 0.447
§4
光栅衍射
一. 衍射对双缝干涉的影响 不考虑衍射时, 双缝干涉的光强分布图: 不考虑衍射时, 双缝干涉的光强分布图:
I I0
− 3λ − λ − λ λ 0 2d d 2d 2d
λ
d
3λ 2d
sin θ
设双缝的每个缝宽均为 a,在夫琅禾费衍 射下,每个缝的衍射图样位置是相重叠的。 射下,每个缝的衍射图样位置是相重叠的。
准直缝 晶体 X射线 射线 劳厄斑
* 穿透力强 * 波长较短的电磁波, 波长较短的电磁波, 范围在 0.001nm~10nm之间。 之间。 之间
·· · ·
证实了X射线的波动性
二. X射线在晶体上的衍射
同一晶面上相邻原子 D C 散射的光波的光程差 ϕ 1 零 AD-BC= 0, 它们 , A B 相干加强。 相干加强。若要在该 P 2 N M 方向上不同晶面上原 d 3 子散射光相干加强, 子散射光相干加强, 则必须满足: 则必须满足: ∆ = NM + MP = kλ k = 1,2,3L 时各层面上的反射光相干加强, 即当 2d ⋅sin ϕ = kλ 时各层面上的反射光相干加强,形 成亮点, 级干涉主极大。该式称为布喇格公式 布喇格公式。 成亮点,称为 k 级干涉主极大。该式称为布喇格公式。 因为晶体有很多组平行晶面,晶面间的距离 d 各 因为晶体有很多组平行晶面, 不相同所以,劳厄斑是由空间分布的亮斑组成。 不相同所以,劳厄斑是由空间分布的亮斑组成。
光的衍射2

讨论
中央明纹集中大部分能量, 明条纹级次越高亮度越弱。
二级明纹中心:
1 部分光线干涉相长 5
I
1 部分光线干涉相长 3
讨论条纹随 、 a 的变化
2 f 中央明纹 x a
一定
讨论 其余明纹 x f a
a 衍射显著 a 光强太弱
a
衍射不明显 a 直线传播
sin
d 缺级: k k a
(k 1,2)
(3)单缝衍射中央明纹区主极大条数
d d 2( ) 1 2 2( ) 1 a进整 a 进整
sin
小结
光栅衍射是N缝干涉和N个单缝衍射的总效果
I I0( sin
光强分布 式中:
sin N 2 ) ( ) sin
sin N 2 ) ( ) sin
2
单缝衍射因子
多(N)缝干涉因子
a sin
d sin
a:
缝宽
d : 光栅常数 a+b
: 衍射角
I I0(
sin
sin N 2 ) ( ) sin
2
同一缝中的子波相干影响亮度分布
sin
k , I
同学们好!
§14.3 光的衍射
复习: 单缝夫琅和费衍射
*明暗纹条件:
0
中央明纹中心
a sin ( 2k 1) 2
各级明纹中心 暗纹
k
k 1、 2、 3
注意: 注意
k 0
*条纹角宽度
sin
0
k
中央明纹中心
08光的衍射二解答
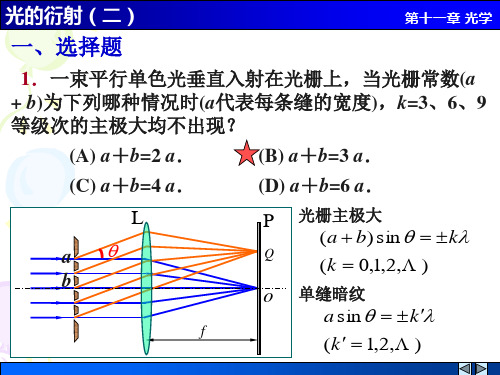
P
j
o
f
Q
3d d k 30 2 2
5.1 k 1.7
观察到k=0,±,-3, -5共5条明纹
光的衍射(二) 第十一章 光学 3.波长范围在450~650 nm之间的复色平行光垂直照 射在每厘米有5000条刻线的光栅上,屏幕放在透镜的 焦面处,屏上第二级光谱各色光在屏上所占范围的宽 度为35.1 cm.求透镜的焦距f. (1 nm=10-9 m) 解:光栅主极大 d sin k (k 0,1,2,) 1 k xk OQ f tan f tan[sin ( )] d 7
光栅主极大 d sin k
(k 0,1,2,) 1 k xk OQ f tan f tan[sin ( )] d
L
P
Q
a b
o
f
400107 x11 50 tan[sin ( )] 2.00cm 3 1.0 10 7 1 76010 x12 50 tan[sin ( )] 3.81cm 3 1.0 10
6
光的衍射(二)
第十一章 光学
5*.一平面透射多缝光栅,当用波长1=600nm的单 色平行光垂直入射时,在衍射角=30°的方向上可以看 到第2级主极大,并且在该处恰能分辨波长差=5×10-3 nm的两条谱线.当用波长2=400 nm的单色平行光垂直 入射时,在衍射角=30°的方向上却看不到本应出现的 第3级主极大.求光栅常数d和总缝数N,再求可能的缝 宽a。(不作要求) 解: 光栅主极大 d sin k (k 0,1,2,)
d sin j k (k 0,1,2,)
两光明纹重合处
d sin j k11 k22 440k1 660k2
第五章光的衍射(2)

~ i 2δ ~ ~ ik ( r1 + 2Δ ) E3 (θ ) = a0e sin cα = A0e sin cα
~ ~ i ( N -1) E N ( ) A0 e sin c
P点合振动的复振幅:
~ E (θ )
N 1
~ imδ A0 e s in cα
m 0
多缝衍射光强公式:
其中: ~ —衍射屏处复振幅及其它常量。 a0
e
ikrm
—第m个缝到P点的位相延迟。
sin c —单缝衍射因子,单缝在P 点引起的振动。
有:
~ ~ ~ ikr1 E1 (θ ) = a0 e sin cα = A0 sin cα
~ iδ ~ ~ ik ( r1 +Δ ) E2 (θ ) = a0 e sin cα = A0 e sin cα
sin
对多缝干涉因子
(
sin N sin
)
2
sin 0 sin N 2 当 时 ( ) 0 sin sin N 0
m' N
( m' 1, 2 N 1)
有干涉极小值。 两主极大间有N-1个极小值 。
对多缝干涉因子
(
sin N sin
)
r
r-OB
x
a
sin (P) I 0 I ( i
a (sin i sin i ) )
2
a (sin i sin i)
① sini - sini’ = 0 时, I(Pi’)有极大值 即i ’ =i 时, I(Pi’)=Imax (反射定律成立时) ② sini - sini’ ≠ 0, 即 i ’ ≠i 时 只要满足 a>>λ, I(Pi’)≈ 0
光的衍射(二)
光的衍射(二)1.一束单色平面电磁波垂直投射在每厘米刻有4000条刻痕的衍射光栅上,若在与光栅法线夹30°角处找到第二级极大,则该电磁波长应为( D )(A)2.50×10-2m (B) 2.50×10-4m(C)6.25×10-5m (D) 6.25×10-7md=1/4000=2.5×10-4cm=2.5×10-6md sinφ=kλ→λ= d sinφ/k=2.5×10-6×0.5/2=6.25×10-7m2.若用衍射光栅准确测定一单色可见光的波长,在下列各种光栅常数的光栅中选用哪一种最好?( D )(A)1.0×10-1mm (B) 5.0×10-1mm(C)1.0×10-2mm (D) 1.0×10-3mm3.波长4000Å~7600Å的自然光照射光栅,其衍射谱的第二级和第三级重迭,则第二级光谱重迭部分的波长范围是:( C )(A)5067Å~7600Å (B)4000Å~5067Å(C)6000Å~7600Å (D)5067Å~6000Å4.若光栅的光栅常数d,缝宽a和入射光波长λ都保持不变,而使其缝数N增加,则光栅光谱的同级光谱线将变得更细、更亮。
5.用一束自然光垂直照射在每毫米有200条刻痕的光栅,则屏上的中夹明纹的颜色为白色;在衍射角为30°处,在可见光范围内哪几种波长的光得到加强606250Å、5000 Å、4167 Å。
解: ∵d sinϕ=kλ, k=0,则对任何λ都有sinϕ=0,所有波长的中央明纹相重叠, ∴中央明纹的颜色为白色由d sinϕ=kλ得λ=d sinϕ/k=(1/400k)mm,∵4×10-4mm≤λ≤7.6×10-4mm ,即4×10-4≤1/400k≤7.6×10-4得3.3≤k≤6.25,k只能取整数,∴k = 4, 5, 6λ=6.25×10-4mm, 5×10-4mm, 4.16710-4mm6.若光栅常数为(a+b),缝宽为a,则满足a sinφ=±k'λd sinφ=±kλ条件时会出现缺级,要使3n(n=1,2,3……)级数缺级,则必须b=2a。
光的衍射(2)
(2) ∵
ab k , a k
k3
( a b)k 6 a 8.0 10 k( m) k
取 k 1 得
amin 8.0 106 ( m )
P.49.2.一单色光垂直照射宽为a的单缝,缝后放一 焦距为f的薄凸透镜,屏置于焦平面上,若屏上第 一级衍射明纹的宽度为△x,则入射光波长为( A ) (A)a△x/f (B)△x/af (C)f△x/a (D)a/f△x
例、波长为6000Å的单色光垂直入射在一光栅上,第 二级明纹出现在sin2=0.2处,第4级为第一个缺级。 求:(1)光栅常数。(2)狭缝可能的最小宽度是多少? (3)按上述选定的a、b值,实际上能观察到的全部明 纹数是多少? λ = 6000 Å k=2 解: (1)
kλ d sin k , d 6 μm sin φ sinφ2=0.2 d d ( 2 ) k k k 4, 则 a k 4 a d 得 amin 1.5 m 取k 1 4 b d amin 4.5m
sin
图2 单缝衍射
sin
图3
双缝衍射 (调制)
sin
d
b a
S
L1
光栅
P0
P
L2
x
f
幕
3. 光栅衍射(N为任意)
光栅每个缝形成各自的单缝衍射图样。
光栅缝与缝之间形成的多缝干涉图样。
光栅衍射条纹是单缝衍射与多缝干涉的总效果。
(1) 光栅方程
d
b a
a
P0
δ
S
L1
光栅
x
d
P
L2
∴ x2 f tan 2 f 2 0.5 0.01 0.005(m)
17、光的衍射-2
λ
θ 1= ± 140 28′
第三级明纹k=3 第三级明纹
3λ 3 × 500 × 10 9 sin θ 3 = ± =± = ±0.75 6 a+b 2 × 10
θ 3= ± 480 35′
2 × 10 6 = =4 9 500 × 10 即最多能看到第4级明条 即最多能看到第 级明条 纹,考虑缺级 (a+b)/a=(a+a)/a=2. . 级明纹不出现, 第2,4级明纹不出现, , 级明纹不出现 从而实际出现的只有级, 从而实际出现的只有级, 因而只能看到5条明纹 条明纹. 因而只能看到 条明纹.
2,光栅衍射的实验装置与衍射图样
反射光栅
屏幕上对应于光直线传播的成像位置上出现中央明纹; 屏幕上对应于光直线传播的成像位置上出现中央明纹; 屏幕上对应于光直线传播的成像位置上出现中央明纹 在中央明纹两侧出现一系列明暗相间的条纹,两明条纹分 在中央明纹两侧出现一系列明暗相间的条纹, 在中央明纹两侧出现一系列明暗相间的条纹 得很开,明条纹的亮度随着与中央的距离增大而减弱; 得很开,明条纹的亮度随着与中央的距离增大而减弱; 明条纹的宽度随狭缝的增多而变细. 明条纹的宽度随狭缝的增多而变细. 明条纹的宽度随狭缝的增多而变细
θ=
代入数据,得: 代入数据,
1.5 × 4 × 10 3 S= = 8.9 × 10 3 m 1.22 × 5500 × 10 10
rD S= 1.22λ
r θ = θ 0 = 1.22 = D S
λ
S
§17-4 衍射光栅 -
引言:对于单缝: 引言:对于单缝: 若缝宽大,条纹亮,但条纹间距小, 若缝宽大,条纹亮,但条纹间距小,不易分辨 若缝宽小,条纹间距大,但条纹暗, 若缝宽小,条纹间距大,但条纹暗,也不易分辨 因而利用单缝衍射不能精确地进行测量. 因而利用单缝衍射不能精确地进行测量. 问题:能否得到亮度大,分得开,宽度窄的明条纹? 问题:能否得到亮度大,分得开,宽度窄的明条纹? 结论:利用衍射光栅所形成的衍射图样——光栅光谱 结论:利用衍射光栅所形成的衍射图样 光栅光谱 应用: 应用: 精确地测量光的波长; 精确地测量光的波长; 是重要的光学元件,广泛应用于物理,化学,天文, 是重要的光学元件,广泛应用于物理,化学,天文, 地质等基础学科和近代生产技术的许多部门. 地质等基础学科和近代生产技术的许多部门.
第十二章光的衍射2
三、单缝衍射对多缝干涉图样的调制 单缝衍射对多缝干涉图样的调制
E
0
每条缝的单缝衍射图样相同且重 它对多缝干涉图样进行调制。 叠,它对多缝干涉图样进行调制。
I I0
单缝衍射
−2
多缝干涉
−1
0
1
2
− 6 − 5 − 4 − 3 − 2 −1 0 1 2 3 4 5 6
k = ±1,±2 ⋯
I
5λ 3λ − − 2a 2a
−λ a
I0
3λ 5λ 2 a 2a
λ
a
sin θ
§12-9 圆孔的夫琅和费衍射 12光学仪器的分辨率 一、圆孔的夫朗和费衍射
爱里斑 E
S
中央光斑称为爱里斑,光强占84% 中央光斑称为爱里斑,光强占84% .
θ1
d
f
E
第一级暗环半径对应的衍射角θ 第一级暗环半径对应的衍射角θ1满足
说明
A
P
x
θ C
θ
a
B
f
E
条纹在屏幕上的位置 x = f tgθ ≈ fθ
讨论: 讨论: (1)中央明纹:两个第 (1)中央明纹 中央明纹: 一级暗纹中心间的 明纹
θ1
E
半角宽
2 fλ 线宽度 ∆x0 = 2 f tg θ ≈ 2 fθ = a
∆θ 0 = θ1≈ sin θ1=
λ
a
(2)其它相邻明(暗)纹的间距是中央亮纹 (2)其它相邻明 其它相邻 纹的间距是中央亮纹 宽度的一半
解: (1)对双缝干涉第k级明纹有 (1)对双缝干涉第 对双缝干涉第k
d sin θ = ± kλ
第k级明纹在屏上的位置
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
光的衍射(二)
1.一束单色平面电磁波垂直投射在每厘米刻有4000条刻痕的衍射光栅上,若在与光栅法线夹30°角处找到第二级极大,则该电磁波长应为( D )
(A)2.50×10-2m (B) 2.50×10-4m
(C)6.25×10-5m (D) 6.25×10-7m
d=1/4000=2.5×10-4cm=2.5×10-6m
d sinφ=kλ→λ= d sinφ/k=2.5×10-6×0.5/2
=6.25×10-7m
2.若用衍射光栅准确测定一单色可见光的波长,在下列各种光栅常数的光栅中选用哪一种最好?( D )
(A)1.0×10-1mm (B) 5.0×10-1mm
(C)1.0×10-2mm (D) 1.0×10-3mm
3.波长4000Å~7600Å的自然光照射光栅,其衍射谱的第二级和第三级重迭,则第二级光谱重迭部分的波长范围是:( C )
(A)5067Å~7600Å (B)4000Å~5067Å
(C)6000Å~7600Å (D)5067Å~6000Å
4.若光栅的光栅常数d,缝宽a和入射光波长λ都保持不变,而使其缝数N增加,则光栅光谱的同级光谱线将变得更细、更亮。
5.用一束自然光垂直照射在每毫米有200条刻痕的光栅,则屏上的中夹明纹的颜色为白色;在衍射角为30°处,在可见光范围内哪几种波长的光得到加强
60
6250Å、5000 Å、4167 Å。
解: ∵d sinϕ=kλ, k=0,则对任何λ都有sinϕ=0,所有波长的中央明纹相重叠, ∴中央明纹的颜色为白色
由d sinϕ=kλ得λ=d sinϕ/k=(1/400k)mm,
∵4×10-4mm≤λ≤7.6×10-4mm ,
即4×10-4≤1/400k≤7.6×10-4
得3.3≤k≤6.25,k只能取整数,∴k = 4, 5, 6
λ=6.25×10-4mm, 5×10-4mm, 4.16710-4mm
6.若光栅常数为(a+b),缝宽为a,则满足a sinφ=±kλ条件时会出现缺级,要使3n(n=1,2,3……)级数缺级,则必须b=2a。
由缺级公式(a+b)/a=k/n=3n/n=3 得b=2a
7.平面透射光栅在1mm内刻有500条刻痕,现对波长λ=5893Å的钠光谱线进行观察,试求:
(1)当光线垂直入射光栅时,最多能看到第几级光谱线?
(2)当光线以30°角斜入射时,最多能看到第几级光谱线?
(参考教材P.129例12.11)
8.在垂直入射到光栅的平行光中,包含有波长分别为λ1和λ2=6000Å的两种光,已知λ1的第五级光谱级和6000Å的第四级光谱级恰好重合在离中央明条纹5cm处,并发现λ1的第三级缺级,已知:f=0.5m,
试求:
(1)波长λ1和光栅常数(a+b)
(2)光栅的缝宽a至少应为多少?
解: (1) ∵(a+b)sinφ=k1λ1=k2λ2 , k1=5 , k2=4 ∴λ1=k2λ2/k1=4×6000/5=4800Å
sinφ≈tanφ=x/f
a+b= k2λ2/sinφ= k2λ2f/x
=4×6000×10-10×0.5/5×10-2=2.4×10-5(m)
(2) ∵ (a+b)/a=k/k' , k=3
∴ a= (a+b)k'/k=8.0×10-6 k'(m)
取k'=1 得a min=8.0×10-6(m)。
