工程光学 5 习题课 1
工程光学 5 习题课 2
10
25
放大镜
tan 10 4 0.28 50
渐晕系数KD=0.5时
tan 15 04 tan 0.24 25
y (50 50) 0.1875 18.75mm 2 y 37.5mm
比较得知,棱镜第一面是视场 光阑,也是入窗。
A
F1
F2
从物点A向所有器件在物空间的共轭 像边缘作边缘光线,求孔径角
tan 1
30 0.25 120
tan 2
45 21.43 / 2 0.1935 tan P 0.048 120 112.5 120 102.86
1 2 P
l'
故圆光孔是孔径光阑,入瞳位于L1右102.86mm处,口径21.43mm。
线视场大小为37.5mm。
1 1 1 lP ' 48 90
lP ' 102.86mm DP ' DP 21.43mm
lP ' 102.86 2.143 lP 48
5-6
解
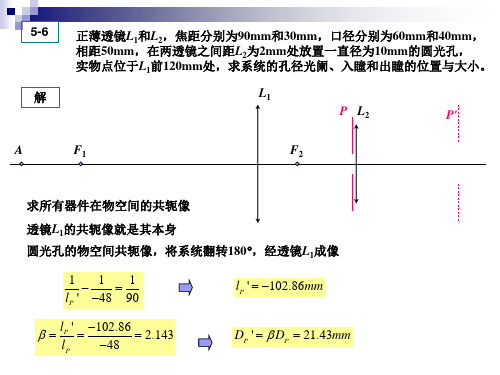
正薄透镜L1和L2,焦距分别为90mm和30mm,口径分别为60mm和40mm, 相距50mm,在两透镜之间距L2为2mm处放置一直径为10mm的圆光孔, 实物点位于L1前120mm处,求系统的孔径光阑、入瞳和出瞳的位置与大小。 L2' L1 P L2 P'
f2 ' l 2 30 2.143mm f 2 ' l 30 2
DP ''
l' D p 10.714mm l
出瞳位于L2左2.143mm处,口径10.714mm。
5-7
解
工程光学第五章习题及答案

第五章习题及答案
1、一个100W的钨丝灯,发出总光通量为,求发光效率为多少?
解:
2、有一聚光镜,(数值孔径),求进入系统的能量占全部能量的百分比。
解:
而一点周围全部空间的立体角为
3、一个的钨丝灯,已知:,该灯与一聚光镜联用,灯丝中
心对聚光镜所张的孔径角,若设灯丝是各向均匀发光,求1)灯泡总的光通量及进入聚光镜的能量;2)求平均发光强度
解:
4、一个的钨丝灯发出的总的光通量为,设各向发光强度相等,求以灯为中心,半径分别为:时的球面的光照度是多少?
解:
5、一房间,长、宽、高分别为:,一个发光强度为的灯挂在天花板中心,离地面,1)求灯正下方地板上的光照度;2)在房间角落处地板上的光照度。
解:。
工程光学第二版习题答案(李湘宁_贾志宏)

丝,问其通过球面的共轭像在何处?当入射高度
h=10mm,实际光线的像方截距为多少?与高斯像面的距离
为多少?
解:
8、一球面镜半径 r=-100mm, 求 = 0 , -0.1 , -0.2 , -1 ,1 , 5, 10,∝时的物距像距。
第 4 页 共 29 页
解:( 1)
东北石油大学测控 09 级工程光学期末复习资料
解:
100mm,则所得像与物
6.希望得到一个对无限远成像的长焦距物镜,焦距 系统最后一面到像平面的距离 (工作距) 为 并画出光路图。
解:
=1200mm,由物镜顶点到像面的距离 L=700 mm,由 ,按最简单结构的薄透镜系统考虑, 求系统结构,
7.一短焦距物镜,已知其焦距为 系统结构。
35 mm,筒长 L=65 mm,工作距 , 按最简单结构的薄透镜系统考虑,求
3.一光学系统由一透镜和平面镜组成,如图
3-29 所示,平面镜 MM与透镜光轴垂直交于 D 点,透镜前方
离平面镜 600 mm有一物体 AB,经透镜和平面镜后,所成虚像
至平面镜的距离为 150 mm,且像高为
物高的一半,试分析透镜焦距的正负,确定透镜的位置和焦距,并画出光路图。
解:平面镜成 β =1 的像,且分别在镜子两侧,物像虚实相反 级工程光学期末复习资料
第六章习题
1.如果一个光学系统的初级子午彗差等于焦宽(),则
应等于多少?
解:
2.如果一个光学系统的初级球差等于焦深
(),则
应为多少? 解:
3. 设计一双胶合消色差望远物镜,
和火石玻璃 F2(
,
面的曲率半径。
解:
,采用冕牌玻璃 K9 (
解:设一个气泡在中心处,另一个在第二面和中心之间。
工程光学练习答案(带样题).doc

工程光学练习答案(带样题)期末,东北石油大学审查了09级工程光学的测量和控制材料。
第一章练习1,假设真空中的光速为3米/秒,则计算水中(n=1.333)、皇冠玻璃(n=1.51)、燧石玻璃(n=1.65)、加拿大树胶(n=1.526)、钻石(n=2.417)和其他介质中的光速。
解决方案:当灯在水中时,n=1.333,v=2.25m米/秒,当灯在皇冠玻璃中时,n=1.51,v=1.99m米/秒,当灯在燧石玻璃中时,n=1.65,v=1.82m米/秒,当灯在加拿大树胶中时,n=1.526,v=1.97m米/秒,当灯在钻石中时,n=2.417,v=1.24米/秒。
2.一个物体穿过针孔照相机,在屏幕上形成一个60毫米大小的图像。
如果屏幕被拉开50毫米,图像的尺寸变成70毫米,计算出从屏幕到针孔的初始距离。
解决方案:在同一个均匀的介质空间中,光直线传播。
如果选择通过节点的光,方向不会改变,从屏幕到针孔的初始距离为x,则可以根据三角形的相似性得到:因此,x=300mm毫米意味着从屏幕到针孔的初始距离是300毫米。
3、一块厚度为200毫米的平行平板玻璃(n=1.5),下面放一块直径为1毫米的金属板。
如果玻璃板上覆盖有圆形纸片,则要求玻璃板上方的任何方向都不能看到纸片。
这张纸的最小直径是多少?解决方案:如果纸片的最小半径是x,那么根据全反射原理,当光束从玻璃发射到空气中的入射角大于或等于全反射临界角时,就会发生全反射,正是由于这个原因,在玻璃板上方看不到金属片。
全反射的临界角由下式确定:(1)其中N2=1,n1=1.5,根据几何关系,利用平板的厚度和纸张与金属片的半径计算全反射临界角的方法如下:(2)纸张的最小直径x=179.385mm毫米可以通过组合等式(1)和(2)来获得,因此纸张的最小直径为358.77毫米4.光纤芯的折射率是n1.包层的折射率为n2,光纤所在介质的折射率为n0。
计算光纤的数值孔径(即n0sinI1,其中I1是光在光纤中以全反射模式传播时,光在入射端面的最大入射角)。
现代工程光学第5章光学系统中光束的限制

(续1:)
或者
n1(u1 y1 u1 y1) n1(u1y1 u1y1) Ж (1)
等式左边的折射率和角度量对应于折射前(物空间)的相关参量,等式 右边表示折射后(像空间)的对应参量 。
n(uy uy) Ж 被定义为某折射面的拉格朗日不变量它对任意多次折
射过程均保持不变。
光线从一个面过渡到下一个面的过程中 Ж 的性质
根据光学系统拉格朗日不变量的性质,有
Ж n1u1h1 nkuk hk
—简称光学系统的 拉赫不变量。
21
(续:)
例:用拉赫不变量计算像的高度
m hk hk n1u1 1.0 0.025 h1 10 nkuk 1.0 (0.0999617)
与光线追迹得到的高度一致(见表2.3-2)。
2.共轴球面系统的拉赫不变量
5
(续:)
入瞳的大小是由光学系统对成像光能的要求或者对物体细节的分辨 能力(分辨率)的要求来确定。 对称于光阑的对称式系统,其入射光瞳面和出射光瞳面分别与光学 系统的物方主平面和像方主平面重合。
相对孔径以入瞳直径和焦距的比值表示: DEP f'
F数:相对孔径的倒数
f # f ' DEP 如:f 8 或 f :8
F数也被写成像方数值孔径NA的形式
NA nsinU
物在无限远时,F数和NA有如下关系:
F数= f # = 1
2NA
6
5.2 主光线与边光线 视场光阑
一、主光线与边光线
入瞳
A
边光线
物体
y
u
y
O
主光线
u z
通过入瞳中心的光线称为主光线,主光线是各个物点发出的成像光 束的光束轴线,它也同时通过孔经光阑和出射光瞳中心。 边光线是轴上物点发出的成像光束中通过入瞳边沿的光线。 边光线和主光线是两条特殊的子午光线,它们一起决定了物、像和 光瞳性质。
工程光学习题课

习题1:一个双薄透镜L 1、L 2构成的光学系统,L 1透镜的焦距为801='f mm ,通光口径401=D mm ,L 2透镜的焦距302='f mm ,通光口径402=D mm ,L 2在L 1的后面50mm 位置处,现有一束平行于光轴的光射入:(1)试判断系统的孔径光阑;(2)求系统出瞳的大小和位置。
1L 2L解:(1)试判断系统的孔径光阑将L 1的边框经过前面的光学系统成像到系统的物空间,由于前面没有成像元件,故L 1边框的像就是自身,即401='D mm 。
将L 2的边框经过前面的光学系统L 1成像到系统的物空间,设像为1l ',则由高斯公式有:3.133801501111111111='⇒-=-'⇒'=-'l l f l l mm 即1l '位于L 1右侧约133.3mm 处。
1072503.133202111111='='⇒='⇒'='=D y y l l y y βmm 即1l '的大小为107mm 。
由于401='D mm 小于1072='D mm ,故L 1自身对入射光束起到最大的限制作用,为系统入瞳,透镜L 1的边框即为系统的孔径光阑。
(2)求系统出瞳的大小和位置根据高斯公式及出瞳的定义有:75301501111122222='⇒=--'⇒'=-'l l f l l mm602507520222222='='⇒-='⇒'='=出D y y l l y y βmm 即系统的出瞳位于L 2右侧75mm 处,口径为60mm 。
习题2:已知两点光源S 1,S 2相距5.1=r m ,光源的发光强度分别为35I 1=cd ,95I 2=cd ,现将一白色的光屏置于S 1,S 2之间,且光屏的法线方向与S 1,S 2连线的夹角为i 。
工程光学第二版习题答案(李湘宁,贾志宏)

第一章习题1、已知真空中的光速c=3 m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s,当光在冕牌玻璃中,n=1.51时,v=1.99 m/s,当光在火石玻璃中,n=1.65时,v=1.82 m/s,当光在加拿大树胶中,n=1.526时,v=1.97 m/s,当光在金刚石中,n=2.417时,v=1.24 m/s。
2、一物体经针孔相机在屏上成一60mm大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm的平行平板玻璃(设n=1.5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
工程光学习题(1)

一、填空题1.用于制作光学零件的透射材料分为 、 、 。
2.一学生带500度近视眼镜,则该近视镜的焦距为 ,该学生裸眼所能看清的最远距离为 。
3.唯一能成完善像的最简单的光学元件是 。
4.一个右手坐标系的虚物,经一个屋脊棱镜的屋脊反射后,成 坐标系的 像。
5.光波的相干条件为 、 、 。
6.光的干涉现象是光的 的重要特征。
实验证明了光可以发生干涉。
7.影响干涉条纹可见度的主要因素是两相干光束的 、 、 。
8.摄影物镜的三个重要参数分别为 、 、 。
9.摄影物镜的类型主要分为普通摄影物镜、 、 、 和变焦距物镜等。
10.显微镜的照明方法有 、 、 、 。
11.摄影系统由 和 组成。
12.波的叠加原理可以表述为:几个波在相遇点产生的合振动是各个波单独在该点产生振动的 。
波的叠加原理表面了光波传播的 。
13.几何光学的四个基本定律分别为 、 、 、 。
14.反射棱镜的种类繁多,形状各异,大体上可分为 、 、 、 。
15.视场光阑经其前面的光学系统所成的像称为 ,视场光阑经其后面的光学系统所成的像称为 。
16.在理想光学系统中,除了垂轴放大率外,还有 和 两种放大率。
17.产生干涉的光波称为 ,其相应的光源称为 。
18.等厚干涉型的干涉系统称为斐索干涉仪,按测量对象分为 、 。
19.时间相干性好的同义语有 、 、 。
20.孔径光阑经其前面的光学系统所成的像称为 ,孔径光阑经其后面的光学系统所成的像称为 。
二、作图题1.求AB 的像B A ''。
图中C 为球面反射镜的曲率中心。
2.求AB 的像B A ''。
图中C 为球面反射镜的曲率中心。
3.求物AB经理想光学系统所成的像,并注明系统像方的基点位置和焦距。
5.求像方主平面和像方焦点。
1.简述几何光学的四个基本定律的含义。
答:(1)光的直线传播定律,几何光学认为,在各向同性的均匀介质中,光是沿着直线方向传播的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
已知放大镜的焦距f'=25mm,通光口径D1=25mm,人眼的瞳孔D2=2mm, 位于放大镜后10mm处,物体位于放大镜前23mm处,求(1)该系统的孔 径光阑、入瞳和出瞳;(2)人眼通过放大镜所看到的最大物面范围。 (2)求人眼通过放大镜所看到的 最大物面范围 y
解
放大镜是视场光阑,最大物面范围,可 以定义为渐晕为0的最大视场 连接入瞳的下边缘点和透镜的上边缘 点,并延长至物面,视场角为
(1)求系统的孔径光阑、入瞳和出瞳 放大镜的共轭像就是其本身, 求瞳孔的物空间共轭像,将系统翻转 180,经透镜成像
解
1 1 1 l ' 16.67mm l ' 10 25 l ' 16.67 D2 ' D2 3.334mm 1.667 l 10
由物体向所有物空间的器件像做边缘连线
D1
D2
D2'
tan
最大物高
25 / 2 3.334 / 2 0.85 16.67
y (23 16.67) 0.85 3.334 / 2 32.05mm 2 y 64.1mm
人眼通过放大镜所看到的最大物面范围为64.1mm。
5-2
解
一个焦距为100mm的透镜与一个在其后方相隔20mm的光孔组成的系统对 无限远物体成像。设透镜的口径为15mm,光孔的口径为10mm。 (1)分别计算系统的入瞳和出瞳的位置和大小? (2)分别计算光线从左到右与从右到左入射时的系统相对孔径? (2)光线从左到右入射时,
光孔的共轭像是入瞳,故有相对孔径
2 43.6
5-4
有两个薄透镜组成的双光组组合系统,透镜1的焦距为f1'=100mm,透镜2 的焦距为f2'=50mm,两透镜间距d=50mm,两透镜的通光口径均为20mm。 物体距前透镜50mm。请分别用作图法和解析法求出光学系统的孔径光阑、 入瞳和出瞳的位置与大小。
解
(1)作图法
L2' L1 L2 F2 F1' F2'
D1
D2
D2'
tan D1
12.5 0.54 23
tan D2 '
3.334 / 2 0.042 23 16.67
D ' D
2
1
可以判断,瞳孔的共轭像就是入瞳,位置在透镜后16.67mm处,大小为3.334mm。 瞳孔为孔径光阑,由于其后没有透镜,故瞳孔也就是出瞳。
5-5
F1
透镜L1的共轭像就是其本身;求透镜L2的物空间共轭像,将系统翻转180,经透 镜成像
1 1 1 l ' 50 100
l ' 100mm
l ' 100 2 l 50
D2 ' D2 40mm
从物点A作L1和L2'的边缘光线,
tan u1 10 0.2 50 tan u2 20 0.1333 150
182 122 tan 50
2 46.8
5-2
解
一个焦距为100mm的透镜与一个在其后方相隔20mm的光孔组成的系统对 无限远物体成像。设透镜的口径为15mm,光孔的口径为10mm。 (1)分别计算系统的入瞳和出瞳的位置和大小? (2)分别计算光线从左到右与从右到左入射时的系统相对孔径? (1)求所有器件在物空间的共轭像
5-1
已知照相物镜焦距f‘=50mm,相对孔径D/f’=1/2.8,底片面积为 24mm*36mm,求照相物镜的最大入瞳直径和最大视场角。
解
2
由图可以判断,照相物镜的边框即为孔径光阑,也就是入瞳
相对孔径
D 1 f ' 2.8
D
f ' 50 17.86mm 2.8 2.8
底片面积为24mm*36mm,其对角线对入射光瞳的张角即为最大视场角
D2 ' 12.5 1 f ' 100 8
光线从右到左入射时,
D1
D2
D2'
光孔是入瞳,故有相对孔径
D2 10 1 f ' 100 10
5-3
焦距f'=140mm的薄透镜,通光口径为40mm,在镜前50mm处有一直径为 30mm的圆孔,问物体处于什么范围光孔为孔径光阑,处于什么范围透镜 为孔径光阑?对于物体在无穷远时,系统无渐晕(K=1)及系统有一半渐 晕(K=0.5)时的视场角各为多少? (1)作经过透镜和圆孔边缘的光线,并延伸与 光轴相交 l 50 15 l 200mm l 20 D1 D2
透镜的共轭像就是其本身, 求光孔的物空间共轭像,将系统翻转180,经透镜成像
D1
D2
D2'
1 1 1 l ' 20 100
l ' 25mm
l ' 25 1.25 l 20
D2 ' D2 12.5mm
由无限远物体向所有物空间的器件像做边缘连线(此时为平行光束),可以判断, 光孔的共轭像就是入瞳,位置在透镜后25mm处,大小为12.5mm。光孔为孔径光 阑,由于其后没有透镜,故光孔也就是出瞳。
解
可得,当物体处于无穷远至-200mm范围内,光孔是孔径 光阑;当物体处于-200mm至0范围内,透镜是孔径光阑。 (2)物体在无穷远,系统无渐晕,对应光路如右 图,有
-l
tan
20 15 50
2 11.42
物体在无穷远,系统有一半渐晕,对应光路如右 图,有
20 tan 50
A
F1
确定孔径光阑和入瞳:透镜L1的共轭像就是其本身;作透镜L2的物空间共轭像, 得到L2'。从物点A作L1和L2'的边缘光线,比较入射孔径角,得知,L2'是入瞳, L2是孔径光阑。
L2是系统的孔径光阑,且后无透镜,故L2就是系统的出瞳。
5-4
解
有两个薄透镜组成的双光组组合系统,透镜1的焦距为f1'=100mm,透镜2 的焦距为f2'=50mm,两透镜间距d=50mm,两透镜的通光口径均为20mm。 物体距前透镜50mm。请分别用作图法和解析法求出光学系统的孔径光阑、 入瞳和出瞳的位置与大小。 L2' (2)解析法 L1 L2 A F2 F1' F2'
得知,L2'是入瞳,L2是孔径 光阑。
L2是系统的孔径光阑,且后无透镜,故L2就是系统的出瞳。
5-5
已知放大镜的焦距f'=25mm,通光口径D1=25mm,人眼的瞳孔D2=2mm, 位于放大镜后10mm处,物体位于放大镜前23mm处,求(1)该系统的孔 径光阑、入瞳和出瞳;(2)人眼通过放大镜所看到的最大物面范围。
