一种反常积分与正项级数收敛的判别法
正项级数敛散性的判断及其应用

正项级数敛散性的判断及其应用摘要级数是高等数学教学中的一个重要内容,而正项级数又是级数的重要组成部分,敛散性问题级数理论的一个基本问题,判别正项级数敛散性的方法很多.本文总结了正项级数的各种敛散性判别法,主要有比较判别法及其推广、积分判别法及其推广、导数判别法和一般项级数敛散性判别法;简单介绍了它们强弱性关系,给出了典型例题验证上述判别法的有效性.关键词正项级数;判别法;敛散性The Convergence Tests and Applicationfor Series of Positive Terms!AbstractHigher Mathematics series is an important part of teaching, The series of positive terms is an important series Part, Positive identification of Convergence and Divergence of many paper has summarized a variety of convergence judge methods for positive terms series, including comparison principle and its extension, integrated judge method and its extension, derivate judge method and judge methods of general series, some famous tests such as Cauchy Test, D’Alembert Test, Kummer Test and Gauss Test come from Comparison principle; given a brief introduction of their week and strong relationship of convergence, set examples for identifying the effectiveness of these judge methods.Key wordspositive terms series; judge methods; convergence1 前言历史上,人们曾把无穷个实数相加12n u u u +++看成无穷个数的和.恰如有限个数的和一样,这在直观上容易被人接受.在《庄子·天下篇》中提到“一尺之捶,日取半截,万世不竭”,把每天截下的那一部分的长度加起来:2311112222n ++++,从直观上看,它的和是1,但是下面“无限个实数相加”111111-+-+-的和是多少如果写成()(11)11(11)00-+-+-=++其结果是0.如果写成1(11)(11)(11)100------=---其结果是1.两个结果完全不同.因此提出这样的问题:“无限个数相加”是否存在“和”如果存在,“和”是多少十七八世纪的一些著名的数学家曾对此感到迷惑,并有许多争论,并给出了这个级数“和”的不同结果.例如莱布尼兹认为这个“和”是0到1之间的一个数.他论证说,这个级数前n 项和形成一个数列12341,0,1,0,S S S S ====,其中0和1出现的机会相同,因此取它的平均数01122+=为这个级数的和.这一说法得到了著名数学家伯努利(Bernouli)兄弟的首肯.有人做过如下论证:既然111111-+-+-是一个数,记为S ,由于11(1111)1111S S -=--+-+=-+-+=,即为1S S -=,得12S =.大数学家欧拉(Euler)也主张用等比公式:23111q q q q ++++=-,把1q =-代入得到111+112=--+,他用同样的讨论得到其他的一些结果.例如把2q =-代入得112483=-+-+,而这些结果现在看起来都是荒谬的.后来人们认识到“无穷多个数相加”,这是一个根本无法操作的过程,人们不知道怎样把无穷多个数相加.经过很长一段时间,数学家柯西(Cauchy)给出了无穷级数的严格定义,之后级数理论得到了充分地发展.无穷级数是表示函数、研究函数和数值计算的重要工具,我国古代数学家刘徵创立的“割圆术”对圆面积的近似计算已具有了初步的无穷级数的概念,无穷级数在自然科学与工程技术中具有广泛的应用.级数是否存在和,即为判断级数是否收敛的问题.级数的收敛性是级数首要的重要性质.因此对于一个给定的级数,首先应判断它是否收敛.若数项级数各项符号都相同称为同号级数.对于同号级数,只须研究各项是正数组成的级数---正项级数.定义在区间I 的函数项级数()1n n u x ∞=∑,当在I 内任意取定一点0x 时, 便得到一个数项级数.自然,对函数项级数的研究极大地依赖于对数项级数的研究,而正项级数是数项级数中最基础的级数,研究数项级数的性质如绝对收敛、条件收敛,需要用到正项级数敛散性判别法,在函数项级数如幂级数收敛半径求解,函数项级数一致收敛Weierstrass 判别法(M 判别法或优级数判别法)中也用到了正项级数敛散性. 1 正项级数的定义和收敛的充要条件正项级数的定义如果级数1n n u ∞=∑中各项均有0n u ≥,这种级数称为正项级数.正项级数收敛的充要条件如果级数1n n u ∞=∑中,部分和数列{}n S 有界,即存在某正数M ,对0,n ∀>有{}n S M <.2 比较判别法及其推广比较判别法【 1】设n u ∑和n v ∑是两个正项级数,如果存在某个正数N ,对一切n>N 都有n un v ≤,那么(1) 若级数n v ∑收敛,则级数n u ∑也收敛; (2) 若级数n u ∑发散,则级数n v ∑也发散.推论:比较判别法的极限形式:设n u ∑和n v ∑是两个正项级数.若limnn nu l v →∞=,则 (1)当0l <<+∞时,n u ∑和n v ∑同时收敛或同时发散; (2)当0l =时,若级数n v ∑收敛,则级数n u ∑也收敛; (3)当l =+∞,若级数n v ∑发散,则级数n u ∑也发散.定理[]1(达朗贝尔判别法或比值判别法)设为n u ∑正项级数,且存在某正整数0N 及常数(01)q q << (1) 若对一切0n N >,成立不等式1n nu q u +≤,则级数n u ∑收敛; (2)若对一切0n N >,成立不等式11n nu u +≥,则级数n u ∑发散.推论[]1(达朗贝尔判别法的极限形式) 设∑∞=1n n u 为正项级数,且1limn n nu q u +→∞=,则 (1)当1<q 时,级数∑∞=1n n u 收敛;(2)当1>q 或∞=q 时,级数∑∞=1n n u 发散.推论[4] 若为n u ∑正项级数,则(1)当1lim1n n n u u +→∞<时,级数n u ∑收敛;(2)当1lim1n n nu u +→∞≥时,级数n u ∑发散.例 讨论级数()()()()()()()1111110,0,0!11n n n n n αααβββαβγγγγ∞=++-++-+>>>++-∑的敛散性.解 令()()()()()()1111!11n n n u n n αααβββγγγ++-++-=++-,则()()()()111111lim lim lim 11n nn n n n n n n n n n n u e e n n e u n n e e n n γγαβαβγγαβαβ+--→∞→∞→∞+⎛⎫⎛⎫+⋅+ ⎪ ⎪⎡⎤++⎛⎫⋅⎝⎭⎝⎭====⎢⎥ ⎪++⋅⎛⎫⎛⎫⎝⎭⎣⎦+⋅+ ⎪ ⎪⎝⎭⎝⎭, 所以,当11γαβ+-->时,即0γαβ-->时,∑∞=1n n u 收敛,故原级数收敛;当11γαβ+--<时,即0γαβ--<时,∑∞=1n n u 发散,故原级数发散.例 讨论级数1!nn n n n e∞=∑的敛散性.解 令!nn n nu n e =,()()1111!!111nnnn n n n n n nn n e u n e H u n e n n ++⎡⎤⎢⎥⎡⎤+⎛⎫⎢⎥==⋅=⎢⎥ ⎪⎢⎥+⎢⎥⎛⎫⎝⎭⎣⎦+⎢⎥ ⎪⎝⎭⎣⎦,则 ()()()20001ln 1111lim ln lim 1ln 1lim1ln 11ln 1lim lim 11lim 212n n n n x x x n n H n n n nx x x x x x x →∞→∞→∞→→→⎛⎫+ ⎪⎝⎭-⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦+--+====+. 则12lim n n H e e →∞=<,由推论得级数1!nn n n n e∞=∑发散. 定理[]1(柯西判别法) 设∑∞=1n n u 为正项级数,且存在某正整数0N 及正常数l ,(1)若对一切0N n >,不等式1<≤l u nn 成立,则级数∑∞=1n n u 收敛;(2)若对一切0N n >,不等式1≥nn u 成立,则级数∑∞=1n n u 发散.推论[]1(柯西判别法的极限形式) 设∑∞=1n n u 为正项级数,且n l =.则(1)当1<l 时,级数∑∞=1n n u 收敛;(2)当1>l 时,级数∑∞=1n n u 发散.定理[]2 设∑∞=1n n u 为正项级数,若2211limlim n n n n n n u u u u ρ+→∞→∞+==,则当21<ρ时,∑∞=1n n u 收敛;当21>ρ时,∑∞=1n n u 发散.证明 当21<ρ时,取0>ε,使()121><=+s r sερ,则 212n s n u r u ρε<+=<,21112n s n u r u ρε++<+=<.取sn n b 1=,则21111lim lim 212sn s n n n b n b n +→∞→∞++⎛⎫== ⎪+⎝⎭,21lim lim 22sn s n n n b n b n →∞→∞⎛⎫== ⎪⎝⎭,由极限保号性得r b b n n >++112, 2nn b r b >,故112112++++>n n n n u u b b ,n n n n u u b b 22>,而∑∞=1n n b 收敛,由引理知∑∞=1n n u 收敛;当21>ρ时,由2211lim lim n n n n n n u uu u ρ+→∞→∞+==,对任意的0ε>当n 充分大时,有2n n u u ρερε-<<+与211n n u u ρερε++-<<+,取11-=n b n ,则2111limlim 22n n n n b n b n +→∞→∞+==,211lim lim 212n n n n b n b n →∞→∞-==-,对任意的0ε>当n 充分大时,有2111122n n b b εε++-<<+与21122n n b b εε-<<+,取1202ρε-<<,则当n 充分大时,有22n n n n b u b u <,212111n n n n b u b u ++++<,由引理知∑∞=1n n u 发散.例 判断正项级数21ln n nn∞=∑的敛散性. 解 ()()212ln 1lim lim 11ln n n n nn n a a n n +→∞→∞+==+,故由达朗贝尔判别法无法判断,而()()222ln 211lim lim 422ln nn n nn n a a n n →∞→∞==<,()()()()221211ln 2111lim lim 4221ln 1n n n n n n a a n n +→∞→∞+++==<++,由定理得21ln n nn∞=∑收敛. 推论[]3 设∑∞=1n n u 为正项级数,若()1lim0,1,21kn in nu i k u ρ-+→∞==-,当k 1<ρ时,∑∞=1n n u 收敛,当1k ρ>时,∑∞=1n n u 发散.推论[]3 设∑∞=1n n u 为正项级数,若1lim1n n n u u +→∞=且2lim n n nu u ρ→∞=,则当21<ρ时,∑∞=1n n u 收敛;当21>ρ时,∑∞=1n n u 发散.推论[]3 设∑∞=1n n u 为正项级数,且1limn n nu u ρ+→∞=,若1<ρ,则2211limlim 0n n n n n n u u u u +→∞→∞+==;若1>ρ,则2211lim lim n n n n n n u uu u +→∞→∞+==+∞. 3 积分判别法引理[]1 正项级数∑∞=1n n u 收敛的充要条件是:部分和数列{}n S 有界,即存在某正整数M ,对一切正整数n 有M S n <.定理[]1 设f 为[)+∞,1上非负递减函数,那么正项级数∑)(n f 与反常积分dx x f ⎰+∞1)(同时收敛或同时发散.例 讨论级数()21ln pn n n ∞=∑的敛散性.解 由定理知级数与反常积分()2ln pdx x x +∞⎰具有相同的敛散性,而()()()22ln =ln ln pppInn d x dx du u x x x +∞+∞+∞=⎰⎰⎰, 当1p >时收敛,当1p ≤时发散.故当1p >时级数收敛,当1p ≤级数时发散.定理[]5 设函数()x f 是单调递减的正值函数,如果存在充分大的N ,当N x >时,有()()x f e f e x x ρ<,则当01ρ<<时,级数∑)(n f 收敛;若()()x f e f e x x ≥,级数∑)(n f 发散.证明 当N x >时,有()()x f e f e x x ≥,对任意正数1n x x x -<,有()()dx x f dx e f e nn nn x x x x xx⎰⎰--<11ρ,变量替换后得()()dx x f dx x f nn nx n x x x e e ⎰⎰--≥11ρ.取如下序列{}n x , ,,,,,112321-====n x n x e x e x e x x ,故上述积分变为()()()111,2,3,n nnn x x xx f x dx f x dxn ρ+-≥=⎰⎰故有()()() ,3,2,111=≥⎰⎰+n dx x f dx x f e x x n nρ故有()()()()∞→∞→≥=⎰∑⎰⎰=+n dx x f n dx x f dx x f enk x x x k kn当1111ρ所以dx x f ⎰+∞1)(发散,由引理知∑)(n f 发散.若()()x f e f e x x ρ<,则()()()()1111221nkk ennx x ex k k f x dx f x dx f x dx f x dx ρ-===<<<+∞-⎰∑∑⎰⎰⎰,由比较判别法,dx x f ⎰+∞1)(收敛,由定理知∑)(n f 收敛.推论[]5 设函数()x f 是单调递减的正值函数,又设()()limx x x e f e f x λ→+∞=,则当1<λ时,级数∑)(n f 收敛;当 1>λ时,级数∑)(n f 发散.例 讨论级数()()11ln ln ln pqn n n n ∞=∑的敛散性.解 令()()()1ln ln ln pqf x x x x =,且()()()()1limlim ln ln ln x x p qqp x x e f e x x x f x --→+∞→+∞=,当10p ->,即1p <,或当1p =,0p q -<时,()()lim01x x x e f e f x →+∞=<,则级数()()11ln ln ln pqn n n n ∞=∑收敛;当1p q ==时,()()lim1x x x e f e f x →+∞=+∞>,则级数发散.4导数判别法定理[]6(导数极限判别法) 设∑)1(nf 为正项级数,)(x f 是一连续实函数,若级数∑)1(nf 收敛,则()00f =.定理[]6设∑)1(nf 为正项级数,)(x f 是一连续实函数且在0x =处二阶可导,则级数∑)1(nf 收敛的充分必要条件是0)0()0(='=f f .证明 必要性.由定理 得0)0(=f . 设(0)(0,)f a a '=≠∞,a xx f x f x f f x x ==-='→→)(lim )0()(lim)0(00,由归结原理得an n f n =⎪⎭⎫ ⎝⎛→11lim 0,取a <<ε0,当n N >时,ε<-⎪⎭⎫ ⎝⎛a nn f 11,即1a f n n ε-⎛⎫> ⎪⎝⎭,而11n n∞=∑发散,由比较判别法,得∑)1(nf 发散;当+∞=')0(f ,+∞==-='→→xx f x f x f f x x )(lim )0()(lim)0(00,由归结原理得+∞=⎪⎭⎫⎝⎛→n nf n 11lim 0.对任意正整数M ,存在正整数N ,当n N >时,Mnn f >⎪⎭⎫ ⎝⎛11,即n M n f >⎪⎭⎫ ⎝⎛1,由比较判别法,得∑)1(n f 发散,与条件矛盾,故0)0(='f .充分性 对于任意的01α<<有()()()()()111+00000()()1lim lim lim 0lim 0111+x x x x f x f f x f x x f x x x x ααααααα--→→→→''-'''====++, 于是由归结原理011lim01x f n n α→+⎛⎫⎪⎝⎭=,而()1110n nαα∞+=>∑收敛,故∑)1(n f 收敛. 例 判断级数11sin n n∞=∑的敛散性.解 级数11sin n n∞=∑为正项级数,()sin f x x =为连续二阶可导函数,且(0)10f '=≠,由定理知11sinn n∞=∑发散. 例 判断级数111cos n n ∞=⎛⎫- ⎪⎝⎭∑的敛散性.解 级数111cos n n ∞=⎛⎫- ⎪⎝⎭∑为正项级数,()1cos f x x =-为连续二阶可导函数,且0)0()0(='=f f ,由定理知111cos n n ∞=⎛⎫- ⎪⎝⎭∑收敛.5 两种一般项级数收敛性的方法 阿贝尔判别法定理[]1(阿贝尔判别法) 若{}n a 为单调有界数列,且n b ∑收敛,则n n a b ∑收敛.例 讨论级数()311ln 1ln n nn ∞=⎛⎫+ ⎪⎝⎭∑的敛散性.解 1ln 1n ⎧⎫⎛⎫+⎨⎬ ⎪⎝⎭⎩⎭为单调递减有界数列,且()311ln n n ∞=∑收敛,由阿贝尔判别法知级数()311ln 1ln n nn ∞=⎛⎫+ ⎪⎝⎭∑收敛.例 讨论级数211nnn⎛⎫+ ⎪⎝⎭∑的敛散性.解 数列11n n ⎧⎫⎪⎪⎛⎫+⎨⎬ ⎪⎝⎭⎪⎪⎩⎭单调有界,且211n n ∞=∑收敛,由阿贝尔判别法知211nn n ⎛⎫+ ⎪⎝⎭∑收敛. 狄利克雷判别法定理[]1 (狄利克雷判别法) 若数列{}n a 为单调递减,且lim 0n n a →∞=,又级数n b ∑的部分和有界,则n n a b ∑收敛.例 讨论2sin12ln n n nπ∞=∑的敛散性.解21cos cos sinsin 1661212ln ln 2ln 2ln 2ln n n n n n n n n nππππ-≥==-. 因为1ln n当n →∞时单调下降趋于零,又 121sin sin 31212cos 62sin 2sin1212k n k πππππ∞=+-=≤∑, ,由狄利克雷判别法知级数1cos6ln n n n π∞=∑收敛.而级数21ln n n ∞=∑发散,故级数2sin12ln n n nπ∞=∑发散. 判断一般项级数收敛性的方法,也适用于正项级数.若正项级数可以看成两级数通项乘积的形式,则可利用上述两种方法判断之. 6 结束语级数理论是数学分析的重要组成部分,无穷级数是表示函数、研究函数和数值计算的重要工具,无穷级数在自然科学与工程技术中具有广泛的应用.而正项级数又是级数理论中重要的组成部分,级数的收敛性是级数重要性质.判断正项级数的一般顺序是先检验通项的极限是否为0,若不为0,则发散,若为0,则判断级数的部分和是否有界,有界则收敛,否则发散.若级数的一般项可以进行适当的放缩则使用比较判别法,或可以找到其等价式用等价判别法.当通项具有一定的特点时,则根据其特点选择适用的方法,如达朗贝尔判别法、柯西判别法或拉贝判别法等.同时,根据条件选择积分判别法或导数判别法等.由此,我们可以得到正项级数的判别法是多种多样的,每当一种判别法无法判断时,就出现一种新的判别法来进行判断,因此对正项级数的判别法的探讨无穷无尽.正项级数收敛性判断的方法虽然较多,但使用起来仍有一定的技巧,根据不同的题目特点选择适宜的方法进行判断,能够节约时间,提高效率,特别是一些典型问题,运用典型方法,才能事半功倍.本文归纳正项级数收敛性判断的一些典型方法,收集了一些典型例题.正项级数收敛判别法也可用于判定负项级数及变号级数的绝对收敛性的判断,也可以推广到函数项级数的敛散性判别中.参考文献[1] 华东师范大学数学系.数学分析(第三版)[M].北京:高等教育出版社,2006:6-16.[2] 李铁烽.正项级数判敛的一种新的比值判别法[J].北京:数学通报,1990, (1) :46 - 47.[3] 龙艳.关于正项级数收敛性判断的一个推广[J].长春师范学院学报, 2009,28(6):1-3.[4] 冯江浪.关于一些特殊正项级数敛散性的判别法[J].中国科技信息,2009,(1):25.[5]裴礼文.数学分析中的典型问题与方法[M].北京:高等教育出版社,2006:448-452.[6] 刘玉璞.导数在正项级数敛散性判定中的应用[J]. 高等数学研究,1994,(2):13-14.致谢四年时光飞逝,大学即将毕业,在这里我要向数学系的老师同学们,尤其是我的指导老师王树泽老师表示诚挚的感谢!在写作过程中您对我进行了细心地指导,悉心地点拨,不仅使我接受了新的思想观念,激发了学习兴趣,而且提高了收集整理材料和自学能力,掌握了新的数学思想.另外,感谢校方提供了使我能够独立完成一个课题的机会,并在这个过程中给予我们各种方便,使我们在即将离校的最后一段时间里,能够更多学习一些实践应用知识,增强了我们实践能力和动手能力,提高了独立思考的能力.路漫漫其修远兮,吾将上下而求索.我愿在未来的学习和研究过程中,以更加丰厚的成果来答谢曾经关心、帮助和支持过我的所有领导、老师、同学、和朋友.学无止境.明天,将是我终身学习另一天的开始!%。
正项级数的判敛方法

n1
19
第九章 常数项级数
例8. 判别下列级数的敛散性:
1
(1) n1 np (p0)
(p 1 , 发 散 p 1 ,收 敛 )
解: an
1 np
,取
f (x)
1 xp
,
则 f ( x) 在[1, ) 上非负,连续,单减。
∵
1
1 x p dx
p p
∵ lim n
1 sin n
2
2 n 1 ,且 2 发散,∴原级数发散。
n1 n
n
1 n2 ln
(2)∵ lim 3 n 1 n lim
3n
ln(1 2 )
n 2,
n
1
n 3 n 1
1
4
n3
n
而
1 收敛,
∴原级数收敛。
4
n n1
3
11
第九章 常数项级数
ln n
1
0
,
n n 4
5
n4
而
1 收敛,故 ln n 收敛。
5
3
n n1 4
n n1 2
12
第九章 常数项级数
例6. 判别下列级数的敛散性:
(1)
n1
2n
tan3n
5 n
(2) n1 n 5
(3) 258(3n1) n1159(4n3)
n1
n1
(3)当 时,且 vn 发散,则 un 发散。
n1
n1
5
第九章 常数项级数
说明:极限形式的比较判别法其实是将两个正项级数的 通项作为无穷小量,来比较它们的阶。
反常积分收敛判别法

些 新 的判 别 方 法 .
二 、 常 积 分 基 本 判 别 方 法 反
反常积分与数值级数 ∑ n之间的 如下 类比
级 数 的通 项 : a 被 积 函数 )
级数的 部分和: n ∑N a
专 题 研 究
浆 § T 鼍 zH A I Y
’一
・
ห้องสมุดไป่ตู้
~ ●
Ju≮一 ——璃 r i 一…
…
一
●’-
≮≥ 9・
●
●
反常积分收敛判别法
◎高建平 刘 声 ( 州大学理学院 贵 ◎ 张 蕊 ( 南 信 阳 师 范 学 院 教 育 学 院 河
+… 的 和 问 题
单调有界, I _ ) ( d 则 厂 g ) x收敛; i h t ( Dr l 判别法: i e c 若 , A =f ()x n +。 上有界,( ) 。 +。) () 厂 d 存[ , 。) g 在[ , 。 上
因此要反常积分 f 厂 ) x存 在 , 须也 只需 对于任 ( d 必
知 , 些 反 常 积 分 能 化 为 级数 . 有
设 , xx … 有 d
g
一 () g 等= ÷
2 .级 数 判 别 法
函数的极限可以用两种方法来 表达 , “ 即 s一6说 法 ”与
(). ÷等
“ 整 序 变 量 说 法 ” 若 把 极 限 的 第 二 种 定 义 法 用 到 函 数 用 .
设 函数 _ 在 区 间 [ ,] 连 续 , 厂 ( ) 。 b上 b为瑕 点 . 有 则
£:
l _ _
《高等数学》第6章2 反常积分判敛法
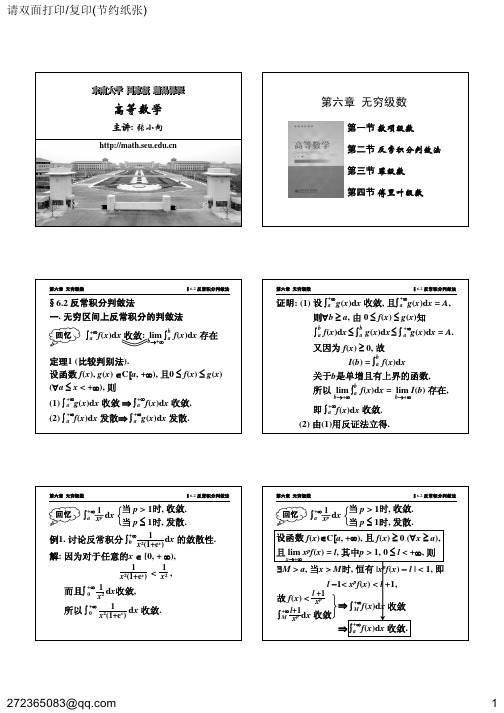
§6.2 反常积分判敛法
例3. 判别下列瑕积分的敛散性.
(1)
∫
1 0
lnx √x
dx.
分析: 令 f(x) = lnx , 则
lim (x − a)pf(x) = l
x→a+
p<1, 0≤l<+∞: 收敛
√x
p≥1, 0<l≤+∞: 发散
① f(x) ∈ C(0, 1],
k = p − 1/2
② f(x) ≤ 0 (∀0 < x ≤ 1),
第六章 无穷级数
§6.2 反常积分判敛法
证明:
(1)
设
∫
+∞ a
g(x)dx
收敛,
且∫
+a∞g(x)dx
=
A,
则∀b ≥ a, 由 0 ≤ f(x) ≤ g(x)知
∫
b a
f(x)dx
≤
∫
b a
g(x)dx ≤
∫
+a∞g(x)dx
=
A.
又因为 f(x) ≥ 0, 故
I(b)
=
∫
b a
f(x)dx
关于b是单增且有上界的函数,
∃M > a, 当x > M时, 恒有 |xpf(x) − l | < l/2, 即
l/2 < xpf(x) < 3l/2,
故 f(x) >
l/2 xp
∫
+∞ M
l/2 xp
dx
发散
⇒
∫
+∞ M
f(x)dx
发散
⇒
∫
+∞ a
f(x)dx
4.AD判别法

积的情况加以证明。
∫ 记 F( x) = x f (t)dt ,则 F (x) 在[a,b] 连续,且 F(a) = 0 。由于 f ( x) 在[a, b]上 a
连续,于是 F (x) 是 f ( x) 在[a, b]上的一个原函数,利用分部积分法,有
∫b a
f
( x) g ( x)dx
=
F ( x) g ( x)
收敛:
∫ (1)(Abel 判别法) +∞ f (x)dx 收敛, g( x) 在[a, + ∞) 上单调有界; a
(2)(Dirichlet
判别法) F (
A)
=
∫A a
f
( x )dx
在 [a,
+
∞)
上有界,g( x
)
在 [a,
+
∞)
上单调且 lim g(x) = 0 。 x→+∞
证 设ε 是任意给定的正数。
∫ A′ f (x)dx < 2M ; A
因为 lim x→+∞
g(x)
=
0 ,所以存在
A0
≥
a
,当 x
>
A0
时,有
|g(x) |< ε 。 4M
于是,对任意 A, A′ ≥ A0 ,
∫ ∫ ∫ A′
f (x)g(x)dx
≤ g( A) ⋅
ξ f (x)dx + g( A′) ⋅
A′
f (x)dx
A
ak +1Bk + ap BpB
k =1
k =1
p −1
∑ = ap - BpB
(ak+1 − ak )Bk 。
8.2正项级数

(1)当r 1时, 级数 un为收敛级数
n 1
(2)当r 1时, 级数 un为发散级数
n 1
(3)当r 1时, 级数 un可能收敛, 也可能发散
n 1
【微积分8-2-12】
2、证明: (1)当0 r
1时,
un1 un1 lim r , 对r r0 1, N , 使当n N时有 r0 ,即 n u un n
【微积分8-2-18】
n 1
3、应用举例:
an n 例8 判别级数 ( ) ( a 0)的敛散性 n 1 2n 1
na n a ) 解: lim un lim ( n n 2n 1 2
n n
a 当0 1即0 a 2时, 级数收敛 2
a 当 1即a 2时, 级数发散 2
n 1
un1 un1 1 1 当r 0时有, lim 0 , 故N , 使当n N时有 n u 2 un 2 n
同样可得级数 un为收敛级数
n 1
【微积分8-2-13】
un1 un1 (2)当r 1时, lim r 1,N , 使当n N时有 1 n u un n
n 1
1 n 1 1 n 解: 2 1 2 1 ln 2, 而级数 发散 n n 1 n
1 所以 (1 cos )收敛 n n 1
级数 ( n 2 1)为发散级数
n 1
【微积分8-2-11】
三、比值判别法
un1 r, 则有 1、定理: 设 un为正项级数, 且有 lim n u n 1 n
正项级数与负项级数统称为保号级数。
用比较判别法及其极限形式判别正项数列的收敛性

用比较判别法及其极限形式判别正项数列的收敛性∑n=1到无穷1/1+a的n次方当a>1时,级数和∑ 1/(1+a^n) 中b(n+1)/bn = (1+a^n)/(1+a^(n+1))=((1/a)^n+1+1/a)/((1/a)^(n+1)+1)趋于1/a<1,所以级数和收敛。
当0<=a<=1时,级数和∑ 1/(1+a^n)中每一项bn=1/(1+a^n) >= 1/(1+1) = 1/2,当然级数和是不收敛的。
当-1<a<0时,|a^n|=|a|^n < 1,所以-1< a^n < 1,级数和∑ 1/(1+a^n)中每一项bn=1/(1+a^n) >= 1/(1+1) = 1/2,当然级数和还是不收敛的。
当a=-1时,级数和∑ 1/(1+a^n)中的奇数项分母为零,没有意义。
当a<-1时,级数和∑ 1/(1+a^n) 中b(n+1)/bn = (1+a^n)/(1+a^(n+1))=((1/a)^n+1+1/a)/((1/a)^(n+1)+1)趋于1/a,绝对值<1,所以级数和也是收敛,并且是绝对收敛的。
阿贝尔(Abel)判别法是分析学中一条十分重要的判定法则,与狄利克雷(Dirichlet)判别法合称为A-D判别法。
主要用于判定任意项数项级数的收敛、函数项级数的一致收敛、反常积分的收敛以及含参变量反常积分的一致收敛等。
编辑本段级数应用数项级数若数列{an} 单调有界,级数Σ(n=1,∞) bn 收敛,则任意项数项级数Σ(n=1,∞) (an×bn) 收敛函数项级数若函数列 {an(x)} 对于每一个固定的x↔D关于n单调,且函数列{an(x)} 在D上一致有界,即存在M>0,使得│an(x)│≤M (x↔D,n↔N);同时,函数项级数Σ(n=1,∞) bn(x) 在D上一致收敛,则函数项级数Σ(n=1,∞) [an(x)×bn(x)] (x↔D) 在D上一致收敛编辑本段积分应用反常积分无穷限反常积分:若∫(a,+∞) f(x)dx收敛,g(x)在[a,+∞)上单调有界,则反常积分∫(a,+∞) f(x)g(x)dx收敛无界函数反常积分:若∫(a,b) f(x)dx收敛,g(x)在[a,b)上单调有界,则反常积分∫(a,b) f(x)g(x)dx收敛含参变量积分若(1)、∫(a,+∞) f(x,y)dx关于y在[c,d]上一致收敛;(2)、g(x,y)关于x单调,即对于每一个固定的y↔[c,d],g(x,y)是x的单调函数;(3)、g(x,y)一致有界,即存在M>0,使得│g(x,y)│≤M (a≤x<+∞,y↔[c,d])。
反常积分的审敛法

反常积分的可积性
定义:如果函数在区间上的积分存在,则称该函数在该区间上可积 性质:可积函数在其定义域内的积分等于其不定积分在区间上的增量 判断方法:通过定积分、不定积分、级数等方法判断函数是否可积 应用:在数学、物理等领域中有着广泛的应用,如计算面积、体积等
反常积分与连续函数的关系
反常积分收敛时,其极限值 可能为无穷小
反常积分与正常积分的区别
积分范围:反常积分在无穷区间或有限区间上积分,正常积分在有限区间上积分 积分性质:反常积分可能存在奇点或无界,正常积分无奇点或有界 积分收敛性:反常积分可能存在收敛或发散的情况,正常积分总是收敛的 积分结果:反常积分的积分结果可能存在极限或无穷大的情况,正常积分的结果总是有限的
物理学:反常积分在量子力学和热力学等领域有广泛应用,例如计算粒子在有限空间内的分布 情况
金融学:反常积分在金融领域用于计算风险价值和预期收益等指标
在概率论和统计学中的应用
反常积分可用 于计算概率分
布函数
反常积分可用 于计算随机变 量的期望和方
差
反常积分在统 计推断中的应 用,如参数估 计和假设检验
积分审敛法
定义:反常积分 审敛法是指通过 判断反常积分的 敛散性,来确定 函数在无穷区间 上的积分是否收 敛的方法。
分类:根据积分 的不同性质,反 常积分审敛法可 以分为比较审敛 法、Cauchy审 敛法和Dirichlet 审敛法等。
应用:反常积分 审敛法在数学、 物理和工程等领 域有着广泛的应 用,是研究函数 积分的重要工具 之一。
反常积分审敛法的改进方向
引入更精确的收敛 性判别方法
优化积分计算的数 值稳定性
拓展审敛法在复杂 积分中的应用
深入研究不同类型 反常积分的审敛特 性
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
$".G8
.G8
!则由对数判别法的极限形式可知
8
( ) .CS
G- HX
".G’8 .G8
+ .CS G- HX
.G8.G $".G88 .G8
+"!
因此!原级数发散"
通过以上的例子我们可以发现!当反常积分的被积函数与正项级数的通项是幂指函数时!我们
都可以采用对数判别法"
参考文献
/$0! 华东师大数学系$数学分析/;0$北京)高等教育出版社!%""$$ /%0! 裴礼文$数学分析的典型问题与方法/;0$北京)高等教育出版社!$’’!$
’ ’-(若存在
’ V"!使
".G.(G’GG(, $H’!则
HX
(’G(DG收敛&
’
’ ’.(若
".G.(G’GG(+ $!则
HX
(’G(DG发散"
’
’ 证’-(若
".G.(G’GG(, $H’!则
.G(’G(+ "’$H’(.GG!即
(’G(+
G$$H’!’ V"+
由
HX ’
G$$H’DG
HX
’ 收敛及比较判别法可知 (’G(DG收敛" ’
! 收稿日期)%""!-$%-%!!修改稿)%"")-"&-"%
%*
++ 高等数学研究 +++++++ + + +++++++%"")年 )月
因此!可以将反常积分的对数判别法推广到级数中去!从而得到正项级数敛散性的判别法"
X
命题 %+ 设正项级数*’8! 8+$
* ’-(若存在
’ V"!使当
8VA时!"..GG’88,
下载时间:2010年8月6日
’HX
’.(当 /V$时! (’G(DG发散" ’
’ 当
/+$时!反常积分是否收敛需要进一步审定"例如取
(’G( +
$!则 G
HX
(’G(DG发散&若取
’
’ (’G( +G$ !则 $H%.G.GG.GG
HX
(’G(DG收敛"
’
由于级数与反常积分在本质上是相同的!都是$求和%运算!只不过是对两种不同的变量求和"
!+ 例子
’HX
例 $+ 考察积分 O+ %
GCD.GGIG!’"X
YC!IYHX(的收敛性"
解 ! 令 (’G( +GC.$GIG!则由对数判别法的极限形式可知
.CS ".G(’G( + .CS .G’GC.GIG( + .CS C.G’G(HI.G’.G(G+ HX
.GG
$H’!则
X
’8收敛&
8+$
* ’.(若
8VA时!"..GG’88+
$!则
X
’8发散"
8+$
推论 ! 对数判别法的极限形式
*X
设正项级数 8+$’8!若G.-CSHX
".G’8 .G8
+/!
X
X
’-(当 /V$时!*’8收敛&!!’.(当 /Y$时!*’8发散"
8+$
8+$
同反常积分类似!当 /+$时!级数是否收敛需要进一步审定"
相似文献(1条)
1.期刊论文 张国铭 一道反常积分习题及其应用 -高等数学研究2010,13(2)
对一道反常积分习题提供了一个简洁的证明,所采用的方法是反常积分的定义,而后将这道习题作为定理,用其解答了五个例子,这五个例 子涉及到正项级数,二重积分,三重积分等.
本文链接:/Periodical_gdsxyj200503009.aspx 授权使用:中共汕尾市委党校(zgsw),授权号:e9a21a88-c0fd-488b-b837-9dca01122201
’ ’ ’.(若
".G.(G’GG(+ $!(’G(,
$!由 HX G’
$DG发散可知
HX
(’G(DG发散"
G
’
推论 ! 对数判别法的极限形式
设 (’G( V"!’G, ’V"(!(1 U’/’!)0(’任意的 )V’(!若
.CS
G-X
".G.(G’GG(
+/!
’HX
’-(当 /V$时! (’G(DG收敛& ’
G- HX
.GG
因此!当 CV$时!O收敛&当 CY$时 O发散"
当 C+$时!令 .GG+-!得
’ ’ O+
HX %
GCD.GGIG+
HX "X
D-I-!
易知 C+$时!有结论 IV$时!O收敛&当 I+ $时!O发散"
( ) *X
例 %+ 判别级数
$".G8
.G8
的敛散性"
8+%
8
( ) 解 ! 令 ’8 +
,-./(!0-/!++++++++++++++++ 高等数学研究
;>?/!%"")++++++++++++12345615078996:6;<2=6;<2571
%)
一种反常积分与正项级数收敛的判别法!
徐 ! 晶 !$黑龙江科技学院数力系 ! 黑龙江哈尔滨 !$)""%#%
摘!要 ! 介绍一种判别无穷限反常积分与正项级数敛散性的判别法" 关键词 ! 反常积分&正项级数&对数判别法 !!! 中图分类号 !8$#%K%!8$#!K$++ 文献标识码#<
作者: 作者单位: 刊名:
英文刊名: 年,卷(期): 被引用次数:
徐晶 黑龙江科技学院数力系,黑龙江,哈尔滨,150027
高等数学研究 STUDIES IN COLLEGE MATHEMATICS 2005,8(3) 0次
参考文献(2条) 1.华东师大数学系 数学分析 2001 2.裴礼文 数学分析的典型问题与方法 1993
"""""""""""""""""""""""""""""""""""""""""" ’上接 %&页(
本刊更名前的*数学学习’高等数学季刊(+继续单独列入!访问量统计为 &’!$" 又!在浏览网约 *""种左右$教育教学类%期刊$知名度排行榜%中!*高等数学研究+仍是唯一 进入前十位的数学类期刊"
一种反常积分与正项级数收敛的判别法
$+ 引言
’ 利用比较判别法来判别无穷限反常积分与正项级数的敛散性是很方便的"若取
HX ’
DGGC!’’ V
"(#* 8$C为比较的标准时!我们还可以得到下面的对数判别法!从中我们可以发现!对数判别法在
很多方面较比较判别法更方便"
%+ 对数判别法
命题 $+ 设 (’G( V"!’G, ’ V"!GV$(!(1 U’/’!)0(’任意的 )V’(
