中职数学基础模块下册《计数原理》ppt课件
合集下载
《计数原理》中职数学(基础模块)下册10.1【高教版】

LOGO
10.1 计数原理
运用知识 强化练习
邮政大厅有4个邮筒,现将三封信逐一投入邮筒, 共有多少种投法?
解 分成三个步骤,每个步骤投一封信,分别均有4种方法.
应用分步计数原理,投法共有
4 4 4 64(种).
思考:邮政大厅有3个邮筒,现将四封信逐一投入邮筒, 共有多少种投法?
第十章 概率与统计初步
10.1 计数原理
概率的起源
• 第一个系统地推算概率的人是16世纪的卡尔达诺。记载在他的著作《Liber de Ludo Aleae》中。书中关于概率的内容是由古尔德从拉丁文翻译出来的。
• 卡尔达诺的数学著作中有很多给赌徒的建议。这些建议都写成短文。例如: 《谁,在什么时候,应该赌博?》、
LOGO
10.1 计数原理
理论升华 整体建构
说出分类计数原理和分步计数原理的区别?
分类计数原理的特点:各类办法间相互独立,各类办法中 的每种办法都能独立完成这件事(一步到位).
分步计数原理的特点:一步不能完成,依次完成各步才能 完成这件事(一步不到位).
确定适用分类计数原理还是分步计数原理的关键是判断能 否一次完成 .
10.1 B组(选做)
作业
实践 用分类或者分步计数原理解释 调查 生活中的实例
LOGO
10.1 计数原理
编者语
• 要如何做到上课认真听讲?•我们都知道一个人的注意力集中时间是有限的,一节课45分钟如何保持时时刻刻都能认真听讲不走神呢?
•
1、往前坐
•
坐的位置越靠后,注意力就越难集中。老师不会注意到你的事实可以让你不再紧张,放心去做别的事情。坐在后面,视线分散,哪怕你是在看老师,如果有人移动,你的视线就会飘到那个同学的后脑勺上去,也就无法集中注意力。 而且,坐在后面很
中职数学10.1计数原理ppt课件

书 18 本,下层有不同的物理书 7 本.现从中任取一本书,
问有多少种不同的取法?
有三类取法
共有多少种不同的取法
第 1 类,从上层 15 本数学 书任取一本,有 15 种取法
任
取 一 本
第 2 类,从中层 18 本语文 书任取一本,有 18 种取法
书
第 3 类,从下层 7 本物理
书任取一本,有 7 种取法
解 : (1)从第1层任取一本,有4种取法,从第2层任取一本,有3
种取法,从第3层任取一本,有2种取法,共有
种取法。
4+3+2=9
分类时要做到不重不漏
答:从书架上任意取一本书,有9种不同的取法。
(2) 从书架的1 、 2 、 3层各取一本书,需要分三步完成, 第1 步,从第1层取1本书,有4种取法,第2步,从第2层取1本书,有3种 取法,第3步, 从第3层取1本书,有2种取法.由分步计数原理知, 共有
变式训练 1.诸城一中勤学楼楼共有3处楼梯口,问从1楼到5 楼共有多少种不同的走法?
答: 3×3×3×3=34=81(种)
2. 四名重本生各从A、B、 C三位教师中选一位作 自己的导师,共有___3_4__种选法;三名教师各从 四名重本生中选一位作自己的学生,共有__4_3__种 选法。
练习巩固
引入 问题 2.如图,该电路从A到B共有多少条不同 的线路可通电?
A B
引入 问题 2.如图,该电路从A到B共有多少条不同 的线路可通电? 路径 类1-1
A B
引入 问题 2.如图,该电路从A到B共有多少条不同 的线路可通电? 路径 类1-2
A B
引入 问题 2.如图,该电路从A到B共有多少条不同 的线路可通电? 路径 类1-3
计数的基本原理ppt课件
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
例2、如图,要给地图A、B、C、D四个区域 分别涂上3种不同颜色中的某一种,允许同一种 颜色使用多次,但相邻区域必须涂不同的颜色, 不同的涂色方案有多少种?
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
想一想?
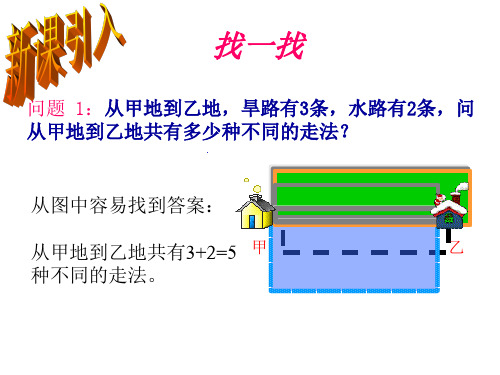
问题 2. 从甲地到乙地,可以乘火车,也可 以乘汽车,还可以乘轮船。一天中,火车 有2班, 汽车有3班,轮船有4班。那么一天 中乘坐这些交通工具从甲地到乙地共有多 少种不同的走法?
甲 为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能 地
乙 地
分析: 完成由甲地到乙地这件事有三类办法:
第一类办法乘火车,有2种不同走法,
第二类办法乘汽车,有3种不同走法 第三类办法乘轮船,有4种不同走法。
因此,在一天中,此人由甲地到乙地不同的走法共 有 2+3+4=9 种。
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
例3:体育福利彩票的中奖号码有7位数码,每位数若是 0~9这十个数字中任一个,则产生中奖号码所有可能的 种数是多少?
变2: 0~9这十个数字可组成多少数字不重复的七位数?
两个计数原理的联系和区别:
《计数原理》中职数学基础模块下册10.1ppt课件2【语文版】

每一步得到的只是中间结果,
每类办法都能独立完成
这件事情。
任何一步都不能能独立完成 这件事情,缺少任何一步也
不能完成这件事情,只有每
个步骤完成了,才能完成这
件事情。
各类办法是互斥的、 并列的、独立的
各步之间是相关联的
再见
编者语
• 要如何做到上课认真听讲?
•
我们都知道一个人的注意力集中时间是有限的,一节课45分钟如何保持时时刻刻都能认真听讲不走神呢?
•
与此相反,如果坐在前面,首先心情就很不同,自己比别人靠前的感觉让你听课时的态度变得更积极。与老师眼神交会的机会增多,感觉就好像是老师在做一对一个人辅导。
•
有的学生恰恰就是因为这一点,讨厌坐在前面。和老师眼神交会非常有负担,稍微做点儿小动作就会被老师发现,非常不方便。而且坐在前面说不定还会被问到一些难以回答的问题。
中有m1种不同的方法,在第2类方法中有m2种不同的方 法,……,在第n类方法中有mn种不同的方法,则完成这 件事共有
N= m1+m2+… + mn 种不同的方法
例题 解析
分类计数原理
例1 书架上层有不同的数学书 10本,中层有不同的语文 书 11 本,下层有不同的英语书 9 本.现从中任取一本书,问 有多少种不同的取法?
有 m1种不同的方法,做第2步有 m2种不同的方 法,…,做第n步有mn种不同的方法,那么完成这
件事共有:N m1 m2 mn 种不同的方法.
分类计数与分步计数原理的区别和联系:
联系
区别一
区别二
区别三
加法原理
乘法原理
分类计数原理和分步计数原理,回答的都是关于
完成一件事情的不同方法的种数的问题。 完成一件事情共有n类 完成一件事情,共分n个 办法,关键词是“分类” 步骤,关键词是“分步”
计数原理-完整版课件

解析: ∵C06+C16+C26+C36+C46+C56+C66=26=64, ∴C16+C26+C36+C46+C56=64-2=62. 答案: 62
• 7.某校高中部,高一有6个班,高二有7个班,高三有8个班,学 校利用星期六组织学生到某厂进行社会实践活动.
• 1.书架上有不同的语文书10本,不同的英语书7本,不同的数学 书5本,现从中任选一本阅读,不同的选法有( )
• A.22种 B.350种
• C.32种 D.20种
• 解析: 由分类加法计数原理得,不同的选法有10+7+5=22 种.
• 答案: A
• 2.一排9个座位坐了3个三口之家,若每家人坐在一起,则不同的 坐法种数为( )
两通项相乘得:C6r x3r Ck10x-4k=C6r C1k0x3r -4k,
令
r 3
-
k 4
=0,得4r=3k,这样一来,(r,k)只有三组:
(0,0),(3,4),(6,8)满足要求.
故常数项为:1+C36C410+C66C810=4 246.
答案: 4 246
6.C16+C26+C36+C46+C56的值为________.
• A.3×3! B.3×(3!)3
• C.(3!)4 D.9!
• 解析: 把一家三口看作一个排列,然后再排列这3家,所以有 (3!)4种.
• 答案: C
• 3.(2013·山东卷)用0,1,…,9十个数字,可以组成有重复数字的 三位数的个数为( )
• A.243 B.252
• C.261 D.279
• 解析: 能够组成三位数的个数是9×10×10=900,能够组成无 重复数字的三位数的个数是9×9×8=648,故能够组成有重复数字的三 位数的个数是900-648=252.
• 7.某校高中部,高一有6个班,高二有7个班,高三有8个班,学 校利用星期六组织学生到某厂进行社会实践活动.
• 1.书架上有不同的语文书10本,不同的英语书7本,不同的数学 书5本,现从中任选一本阅读,不同的选法有( )
• A.22种 B.350种
• C.32种 D.20种
• 解析: 由分类加法计数原理得,不同的选法有10+7+5=22 种.
• 答案: A
• 2.一排9个座位坐了3个三口之家,若每家人坐在一起,则不同的 坐法种数为( )
两通项相乘得:C6r x3r Ck10x-4k=C6r C1k0x3r -4k,
令
r 3
-
k 4
=0,得4r=3k,这样一来,(r,k)只有三组:
(0,0),(3,4),(6,8)满足要求.
故常数项为:1+C36C410+C66C810=4 246.
答案: 4 246
6.C16+C26+C36+C46+C56的值为________.
• A.3×3! B.3×(3!)3
• C.(3!)4 D.9!
• 解析: 把一家三口看作一个排列,然后再排列这3家,所以有 (3!)4种.
• 答案: C
• 3.(2013·山东卷)用0,1,…,9十个数字,可以组成有重复数字的 三位数的个数为( )
• A.243 B.252
• C.261 D.279
• 解析: 能够组成三位数的个数是9×10×10=900,能够组成无 重复数字的三位数的个数是9×9×8=648,故能够组成有重复数字的三 位数的个数是900-648=252.
《计数原理》中职数学基础模块下册10.1ppt课件1【语文版】

•
但是,那却是提升成绩最快的方法。学习要带有一定程度的紧张感,坐在前面,自然而然就会紧张起来。没有必要自己费心思集中精神,那种环境就能帮助你做到。虽然看上去好像不太方便,但其实那才是最便于学习的位置。
•
2、不要看书,要看老师的眼睛
•
只要老师不是在一味地读教材,那老师的“话”就不可能和你低头看着的教材上的“文字”一致。头脑聪明的学生,也许能做到既集中精神听老师的话,又集中精神看眼前书上的内容。可是实际上大部分的学生都做不到这一点。
特征:每类方式中每一种方法都能独立完成这件事
完成哪件事
是否一步到位
LOGO
巩固知识 典型例题
例1 三个袋子里分别装有9个红色球,8个蓝色球和10个
白色球.任取出一个球,共有多少种取法? (每个球都有编号,任意两个同色球都是不同的球) 解 取出一个球,可能是红色球、蓝色球或白色球.
完成什么事?
解 这件事可以分成两个步骤完成:
男、女生各一人
第一步:从26名男生中选出1人,有 k1 26 种选法;
第二步:从20名男生中选出1人,有 k2 20 种选法.
能否一步完成?
由分步计数原理有
N 26 20 520(种).
否
即共有520种选法.
LOGO
LOGO
练习
有不同颜色的上衣5件,裤子3条
1 从中选一样送给某人,共有
5+3=8 种不同的选法 --------------------
2 从中选一件上衣和一条裤子
5*3=15 送给某人,共有 --------------------
种
不同的选法
LOGO
10.1 计数原理
【高中课件】语文版中职数学基础模块下册10.1计数原理3课件.ppt

• 6、某电话局管辖范围内的电话号码由8位数字组 成,其中前4位的数字是不变的,后4位数字都是0 到9之间的一个数字,那么这个电话局最多有 个.
• 7、用1,5,9,13中的任意一个数作分子,4,8, 12,16中任意一个数作分母,可以构成
• 个不同的分数.
• 8、有4名同学分别报名参加学校的足球队,篮球 队,乒乓球队,每人限报其中的一个运动队,不 同的报名种数是 .
具体情况如下:
A大学
B大
学
生物学
数学
化学 学
会计
术学
果这名同学只能选一个专业,那么他共有多少种
• 一般归纳:分类计数原理
• 完成一件事情,有n类办法,在第1类办法中有种 不同的方法,在第2类办法中有种不同的方法…… 在第n类办法中有种不同的方法.那么完成这件事共 有
种不同的方法,N 它 m又1 称 m为2 加 法 原m理n 。
10.1计数原理
一、分类加法计数原理
• (1)提出问题 • 问题1.1:某职校14电子商务1班有65人,14电子商务
2班有64人,现在要从两个班当中选一名同学,把老 师手上唯一一张电影票送给他,一共有多少种选法?
• 问题1.2:从甲地到乙地,可以乘火车,也可以乘汽 车.如果一天中火车有3班,汽车有2班.那么一天中, 乘坐这些交通工具从甲地到乙地共有多少种不同的走 法?
A、4 B、7 C、11 D、28
43
34
• 2、4名同学报名参加数、理、化竞赛,每人限报 其中的1科,不同的报名方法种数( )
A.24
B.4
C.
D.
• 3、一只青蛙25在三角形5A2BC的三个顶点24之间跳动, 若此青蛙从A点起跳,跳4次后仍回到A点,则此 青蛙不同的跳法的种数是( )
• 7、用1,5,9,13中的任意一个数作分子,4,8, 12,16中任意一个数作分母,可以构成
• 个不同的分数.
• 8、有4名同学分别报名参加学校的足球队,篮球 队,乒乓球队,每人限报其中的一个运动队,不 同的报名种数是 .
具体情况如下:
A大学
B大
学
生物学
数学
化学 学
会计
术学
果这名同学只能选一个专业,那么他共有多少种
• 一般归纳:分类计数原理
• 完成一件事情,有n类办法,在第1类办法中有种 不同的方法,在第2类办法中有种不同的方法…… 在第n类办法中有种不同的方法.那么完成这件事共 有
种不同的方法,N 它 m又1 称 m为2 加 法 原m理n 。
10.1计数原理
一、分类加法计数原理
• (1)提出问题 • 问题1.1:某职校14电子商务1班有65人,14电子商务
2班有64人,现在要从两个班当中选一名同学,把老 师手上唯一一张电影票送给他,一共有多少种选法?
• 问题1.2:从甲地到乙地,可以乘火车,也可以乘汽 车.如果一天中火车有3班,汽车有2班.那么一天中, 乘坐这些交通工具从甲地到乙地共有多少种不同的走 法?
A、4 B、7 C、11 D、28
43
34
• 2、4名同学报名参加数、理、化竞赛,每人限报 其中的1科,不同的报名方法种数( )
A.24
B.4
C.
D.
• 3、一只青蛙25在三角形5A2BC的三个顶点24之间跳动, 若此青蛙从A点起跳,跳4次后仍回到A点,则此 青蛙不同的跳法的种数是( )
语文版中职数学基础模块下册10.1《计数原理》ppt课件1

N k1 k2
kn (种).
上面的计数原理叫做分步计数原理.
分步骤去做这件事,每个步骤都完成后,这件事才能完成
完成哪件事
是否一步到位
10.1 计数原理 LOGO
巩固知识
典型例题
例2 某校电子八班有男生26人,女生20人, 若要选男、女生各1人作为学生代表参加学校 伙食管理委员会,共有多少种选法? 完成什么事?
LOGO
第十章
概率与统计初步
10.1 计数原理
创设情境
兴趣导入
一天之内火车有30个班次
一天之内火车有20个班次
每天由长沙去北京有多少种不同的方法?
LOGO
创设情境
兴趣导入
解决这个问题需要分类进行研究. 由长沙去北京共有两类方式.第一类是乘火车,有30种 方法; 第二类是乘飞机,有20种方法, 并且,每类方式中的每一种方法都能够完成这件事(从 长沙到北京). 所以,每天从天津到北京的方法共有
N 9 8 10 27(种).
练习:教材P121第1、2题
完成什么事? 取一个球
能否一步完成?
是
LOGO
练习 2 2 练习
A 图1
B
如图1,该电路从A到B共有多 少种方法使一盏灯发光?
完成什么事? 能否一步到位?
10.1 计数原理 LOGO
典型例题
例3 邮政大厅有4个邮筒,现将三封信逐 一投入邮筒,共有多少种投法?
解 分成三个步骤,每个步骤投一封信,分别均有4种方法. 应用分步计数原理,投法共有
4 4 4 64 (种).
完成什么事? 三封信逐一投入 邮箱
能否一步完成?
练习:教材P121第1、2题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
练习
1题 书架的第1层放有4本不同的语文书,第2层放
有3本不同的数学书,第3层放有2本不同的英语 书;
(1)从书架上任取一本书,有多少种取法?
4+3+2=9
(2)从书架的第1、2、3层各取1本书,有多少种不 同的取法? 4×3×2=24 (3)从书架上取两本不同学科的书,有多少种不同的取 法 4×3+4×2+3×2=26
×
10 ×
10×
10×
10 ×
10
× 10
= 9×106
例2:体育福利彩票的中奖号码有7位数码,每位数若是 0~9这十个数字中任一个,则产生中奖号码所有可能的 种数是多少?
变2: 0~9这十个数字可组成多少数字不重复的 七位数?
百万 十万 万 千 百 十 个
9
×
9
× 8×
7× 6 × 5
×
4=544320
一般地,若完成一件事,需要分成 n 步, 做第1步有m1种不同的方法,做第2步有 m2 种不 同的方法,…,做第 n 步有 mn 种不同的方法, 那么完成这件事共有: N m1 m2 mn 种不同的方法.
注意:只有每步都完成,事情才能完成
分类计数原理(加法原理) 一般地,若完成一件事,有 n 类办 法,在第1类办法中有 m1 种不 同的方法,在第2类办法中有 m2 种不同的方法,…,在第 n 类办 法中有 mn 种不同的方法,那么 完成这件事共有: N m1 m2 mn 种不同的方法.
有条件的同学上网查阅更多关于四色问题 的介绍
课后作业
关于涂色问题的探究
如图,要给地图A、B、C、D四个区域分别涂上3种不 同颜色中的某一种,允许同一种颜色使用多次,但相邻区域 必须涂不同的颜色,不同的涂色方案有多少种? 探究: 如果有4种颜色呢?5种颜色呢?
又有多少种不同的涂色方法呢?
[ 延伸]:如果小李回家的时候需要转一次车后再
乘飞机(如图),则共有多少种不同的走法?
火车1 汽车1 A地 汽车2 飞机1
重庆
火车2 火车 3
B地
广州 飞机2
共有
:3×2×2=12种
[探究] :如果完成一件事情需要 n 步,每一步都有若
干种不同方法,那么应当如何计数呢?
分步计数原 (又叫:乘法原理) 理
种不同的方法.
注意:每类方法都能独立完成这件事,不重复,不遗漏
问题2: 在重庆工 作的小李欲回广州 老家过年,受雪灾 影响重庆到广州的 火车全部停运.于 是他决定先乘火车 到柳州,然后第二 天再乘汽车到广州 .一天中,火车有 3班,汽车有2班 ,问小李一共有多 少种走法?
问题2: 在重庆读书的小李欲回老家广州过年,受雪灾影
3. 某宾馆来了3个人投宿,此时宾馆还有4个单 间,请问有多少种安排方法? 4×3×2=24
分类计数原理与
分步计数原理 数学 源于生活
都是有关做一件事情的 不同方法的种数的问题。 分类计数原理:针 对的是“分类”问 题,其各种方法互 相独立,用其中任 何一种方法都可以 做完这件事。 分步计数原理:针对 的是“分步”问题, 各个步骤的方法相互 依存,只有各个步骤 都完成了才算做完这 件事。
例3
第29届奥运会在中国北京举行,在乒乓球比赛中,中国队 的马琳、王皓、王励勤包揽了男子单打的前三名。有4 位女粉丝前去献花,请问可能出现多少种献花情况。 3×3×3×3 =34 = 81
类似问题练习:
1. 有三封信需要寄出,现在有4个邮筒,请问有多 少种投递方法? 43 2. 学校创建语文、数学、英语3个兴趣小组,有4位同 学想要加入,但每人只能参加一科,请问有多少种报名 方法? 34
分步计数原理 (乘法原理) 一般地,若完成一件事,需要 分成 n 步,做第1步有 m1 种不 同的方法,做第2步有 m2 种不 同的方法,…,做第 n 步有 mn 种不同的方法,那么完成 这件事共有: N m1 m2 mn 种不同的方法.
区别
做一件事情可以分为几类办法,每一类都可以独立完成这 件事情 做一件事情要分为几步,每一步都完成了才能完成这件 事情
例2:体育福利彩票的中奖号码有7位数码,每
位数若是0~9这十个数字中任一个,则每次摇 奖产生的号码有多少种可能?
第一位 第二位 第三位 第四位 第五位 第六位 第七位
10
× 10
×10 ×
10 × 10
×
10
× 10
=107
变1:这十个数字一共可以组成多少个7位数?
百万 十万 万 千 百 十 个
9
响重庆到广州的火车全部停运.于是他决定先乘火车到柳 州,然后第二天再乘汽车到广州.一天中,火车有3班, 汽车有2班,问小李一共有多少种走法? 火车1 柳州 重庆 火车2 火车 3 汽车2 汽车1
广州
分析: 第一步, 由重庆去柳州有3种方法, 第二步, 由柳州去广州有2种方法;
所以 从重庆经柳州到广州共有3 ×2 = 6 种不同的方法。
分析: 从重庆到西昌有2类方法, Ⅰ.乘火车,3种方法; Ⅱ.乘汽车,2种方法;
重庆 火车1 火车2 火车 3 汽车1 汽车2 西昌
所以 从重庆到西昌共有 3 + 2 = 5 种不同方法。
[延伸]:
如果重庆到西昌,除了3班火车2班汽车外还有 2班飞机,
[探究]:
分类计数原理与分步计数原理
问题1: 重庆的
王先生想到西昌 现场观看嫦娥一 号卫星的发射, 从重庆到西昌可 以乘坐火车或者 汽车,一天中, 火车有3班,汽 车有2班,问从 重庆到西昌共有 多少种不同的走 法?
问题1: 重庆的王先生想到西昌现场观看嫦娥
一号卫星的发射,从重庆到西昌可以乘坐火 车或者汽车,一天中,火车有3班,汽车有 2班,问从重庆到西昌共有多少种不同的走 法.
小结
数学 用于生活
分 类 讨 论
归 纳 推 理
课后作业 关于涂色问题的探究
课后作业 问题背景:
关于涂色问题的探究
数学史上著名的“四色问题”.1852年,弗南西斯· 格思里来 到一家科研单位搞地图着色工作时,发现了一种有趣的现象 :“看来,每幅地图都可以用四种颜色着色,使得有共同边 界的国家着上不同的颜色。”这个结论能不能从数学上严格 证明呢? 这个猜想引起了 很多数学家的极大兴趣,但在这之后的100多 年期间,他们都没有能严格的证明其正确性,终于在1976年 ,美国数学家阿佩尔与哈肯在美国伊利诺斯大学的两台不同 的电子计算机上,用了1200个小时,作了100亿次判断,终于 完成了四色问题的证明。
3+2+2=7 种
如果完成一件事情有n类不同的办法,在每 一类中都有若干种不同方法,那么应当如何计 数呢?
分类计数原理
(又叫:加法原理)
一般地,若完成一件事,有 n 类办法,在第 1类办法中有 m1 种不同的方法,在第2类办法中 有m2 种不同的方法,…,在第 n 类办法中有 mn 种不同的方法,那么完成这件事共有: N m1 m2 mn
例题1. 某班级有男三好学生5人,女三好学生4人。 (1)从中任选一人去领奖, 有多少种不同的选法? (2) 从中任选男、女三好学生各一人去参加座谈 会,有多少种不同的选法?
分析:(1)完成从三好学生中任选一人去领奖,需分2类: 第一类,选一名男三好学生,有 5 种方法; 第二类,选一名女三好学生,有 4 种方法; 所以,根据分类计数原理,共有N =5 + 4 = 9种; (2) 完成从三好学生中任选男、女各一人去参加座谈 会, 需分2步完成, 第一步,选一名男三好学生,有 m1 = 5 种方法; 第二步, 选一名女三好学生,有 m2 = 4 种方法; 所以, 根据分步计数原理, 得到不同选法种数共 有 N = 5 × 4 = 20 种。
