信号与系统第1章习题
信号与系统第一章习题答案

t 0 > 0 函数式的信号的波形如图 1.2(b)所示. 。
3
cos ωt
1 … …
−
5π 2ω
−
3π 2ω
−
π 2ω
-1
π 2ω
(a)
3π 2ω
5π 2ω
t
cos ωtε (t )
1
ε (t )
1
…
π 2ω
3π 2ω
5π 2ω
t
t
(b)
-1 (c ) 图 1.1
cos ωtε (t − t 0 )
1
P = lim
E =∞
1 T → ∞ 2T
1 ∫ [ε (t )] dt = 2
T 2 −T
(2) ε (t ) − ε (t − 1) 是脉冲信号,其为能量信号,能量为:
E = lim
[ε (t ) − ε (t − 1)]2 dt = ∫0 [ε (t ) − ε (t − 1)]2 dt =1 T →∞ ∫−T
T
2
(4) 3 cos (ω 0t + θ ) 是功率信号,其平均功率为:
P = lim
1 T → ∞ 2T
2 ∫−T [3 cos (ω0 t + θ )] dt = Tlim →∞ T
1 2T
2
∫
T
−T
9
cos 2(ω0 t + θ ) + 1 1 9 9 dt = lim ⋅ ⋅ 2T = T → ∞ 2 2T 2 2
T 2
2ω t 1 − cos 0 1 cos ω0 t + 1 9ω 0t ω t 5 dt = lim + sin − sin 0 + ∫ − T T →∞ 2T 2 20 20 2
信号系统(第3版)习题解答

信号系统(第3版)习题解答《信号与系统》(第3版)习题解析高等教育出版社目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?(c) (d)题1-1图解 (a)、(c)、(d)为连续信号;(b)为离散信号;(d)为周期信号;其余为非周期信号;(a)、(b)、(c)为有始(因果)信号。
1-2 给定题1-2图示信号f ( t ),试画出下列信号的波形。
[提示:f ( 2t )表示将f ( t )波形压缩,f (2t )表示将f ( t )波形展宽。
] (a) 2 f ( t - 2 )(b) f ( 2t )(c) f ( 2t ) (d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示,R 、L 、C 元件可以看成以电流为输入,电压为响应的简单线性系统S R 、S L 、S C ,试写出各系统响应电压与激励电流函数关系的表达式。
题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i L t u L L d )(d )(= ⎰∞-=t C C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成,系统属于何种联接形式?试写出该系统的微分方程。
S R S L S C题1-4图解 系统为反馈联接形式。
设加法器的输出为x ( t ),由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有 )()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|,试判定该系统是否为线性时不变系统?解 设T 为系统的运算子,则可以表示为)()]([)(t f t f T t y ==不失一般性,设f ( t ) = f 1( t ) + f 2( t ),则)()()]([111t y t f t f T ==)()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性,故为非线性时不变系统。
信号与系统练习题

第一章绪论1、选择题1.1、f (5-2t )是如下运算的结果 CA 、 f (-2t )右移5B 、 f (-2t )左移5C 、 f (-2t )右移25D 、 f (-2t )左移25 1.2、f (t 0-a t )是如下运算的结果 C 。
A 、f (-a t )右移t 0;B 、f (-a t )左移t 0 ;C 、f (-a t )右移a t 0;D 、f (-a t )左移at 0 1.3、已知 系统的激励e(t)与响应r(t)的关系为:)()()(t u t e t r = 则该系统为 B 。
A 、线性时不变系统;B 、线性时变系统;C 、非线性时不变系统;D 、非线性时变系统 1.4、已知 系统的激励e(t)与响应r(t)的关系为:)()(2t e t r = 则该系统为 C 。
A 、线性时不变系统 B 、线性时变系统 C 、非线性时不变系统 D 、非线性时变系统 1.5、已知 系统的激励e(t)与响应r(t)的关系为:)1()(t e t r -= 则该系统为 B 。
A 、线性时不变系统B 、线性时变系统C 、非线性时不变系统D 、非线性时变系统1.6、已知 系统的激励e(t)与响应r(t)的关系为:)2()(t e t r = 则该系统为 B A 、线性时不变系统 B 、线性时变系统 C 、非线性时不变系统 D 、非线性时变系统 1.7.信号)34cos(3)(π+=t t x 的周期为 C 。
A 、π2 B 、π C 、2π D 、π21.8、信号)30cos()10cos(2)(t t t f -=的周期为: B 。
A 、15π B 、5π C 、π D 、10π1.9、dt t t )2(2cos 33+⎰-δπ等于 B 。
A.0 B.-1 C.2 D.-21.10、 若)(t x 是己录制声音的磁带,则下列表述错误的是: BA. )(t x -表示将此磁带倒转播放产生的信号B. )2(t x 表示将此磁带放音速度降低一半播放C. )(0t t x -表示将此磁带延迟0t 时间播放D. )(2t x 表示将磁带的音量放大一倍播放 1.11.=⋅)]([cos t u t dtdA A .)()(sin t t u t δ+⋅- B. t sin - C. )(t δ D.t cos1.12.信号t t t x o 2cos 4)304cos(3)(++=的周期为 B 。
信号与系统第一章习题及作业(1,2)

(2)(余弦序列是否为周期信号,取决于2л/Ω0是正整 (余弦序列是否为周期信号,取决于 Ω 有理数还是无理数。) 数、有理数还是无理数。) 因此, 因此, 2л/Ω0=2л·7/8л=7/4=N/m Ω =2л·7/8л 所以基波周期为N=7; 所以基波周期为N=7; N=7
因为2л/Ω =16л 为无理数, (4) 因为 Ω0=16л,为无理数,则此信号不是周期 信号. 信号. (5) 因为周期信号在[-∞,+∞]的区间上,而本题的重 因为周期信号在[ ∞,+∞]的区间上, 的区间上 复区间是[0, +∞],则此信号为非周期信号 则此信号为非周期信号, 复区间是[0, +∞],则此信号为非周期信号,
f(n) 1 0 3 6 … n
9、判断是否为线性系统?为什么? 、判断是否为线性系统?为什么?
( 3) ( 5) (7 )
y( t ) = ln y( t 0 ) + 3t 2 f ( t ) y( t ) = y( t 0 ) + f 2 ( t ) y( t ) = sin t ⋅ f ( t )
8、一个连续时间系统的输入-输出关系为 、一个连续时间系统的输入 输出关系为
1 t+T y ( t ) = T [ f ( t ) ] = ∫ T2 f (τ )d τ T t− 2 试确定系统是否为线性的?非时变的?因果的? 试确定系统是否为线性的?非时变的?因果的?
解:积分系统是线性的,因此系统是线性系统。 积分系统是线性的,因此系统是线性系统。
sin ω 0 tε ( t )
sin ω 0 ( t − t 0 )ε ( t )tt0 Nhomakorabeat
sin ω 0 tε ( t − t 0 )
信号与系统理论及应用 习题 - 第1章 -作业参考答案

1
t
1.5 写出如题图所示信号的解析表达式。
X1(t) E
0
(1)
2
t
X2(t) 1 0 -1
(2)
1
2
t
X3(t)
0
2T
4T
6T
8T
t
(3)
X4(n)
1
(4)
-2
-1
0
1
2
n
(1) x1 (t )
E (t 2)[u(t ) u(t 2)] 2
(2) x2 (t ) [u(t ) u(t 1)] [u(t 1) u(t 2)] (3) x3 (t ) e sin
t o
1 (t ) 2
(6) (9)
d t d [e (t )] (t ) '(t ) dt dt
0
et sin t (t 1)dt 0
(11)
1
1
(t 2 4)dt 0
1.7 已知 x(t)的波形如题图所示, 试画出 x(3-2t)、 x(3-t) 、 x(2t)、 x(t/2)的波形图。
1.14 请求出下面两个信号的 Nyquist 频率(即信号的最高频率)。
1. x1 (t ) cos(500 2 t ) sin(400 2 t ) 2. x2 (t ) cos(600 2 t ) sin(300 2 t ) 答:1. cos sin
答:
x(3-t) 1
0 -1
1
2
3
t
x(2t) 1
1
x(t/2)
0 -1
1
2
信号与系统课后习题答案

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD (15,6)=3 Hz 。
因此,公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD (5, 15)=5 Hz 。
因此,公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数,因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的,基频 =0f 1/π Hz 。
因此,公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号,显然有 1=P W1-3 解 周期T=7 ,一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+; (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
信号与系统(应自炉)习题答案第1章 习题解重点

(222222j t k j t j t j k f t k e
e
e
e
f t π
π
π
πππ+++++==⨯==
∴原函数是周期函数,令1k =,则基波周期为2π。
1-2.
求信号( 14sin( 110cos(2--+=t t t f的基波周期。
解:cos(101 t +的基波周期为15
π,s i n (4
1-8.
用阶跃函数写出题图1-8所示各波形的函数表达式。
t
t
t
(a (
bc
题图1-8
解:(a)((((((3[31]2[11]f t t u t u t u t u t =++-+++-- (((3[13]t u t u t +-+---
(((((
(3 3(1 1(1 1(3 3f
t t u t t u t t u t t u t =+++--++-+-+--(b)([( (1]2[(1 (2]4(2 f t u t u t u t u t u t =--+---+-
1 t -的基波周期为
1
2
π二者的最小公倍数为π,故( 14sin( 110cos(2--+=t t t f的基波周期为π。
1-3.
设(3, 0<=tt f ,对以下每个信号确定其值一定为零的t值区间。
(1)(t f -1(2)((t f t f -+-21(3)((t f t f --21(4)(t f 3(5)(f
(完整版)信号与系统第一章答案
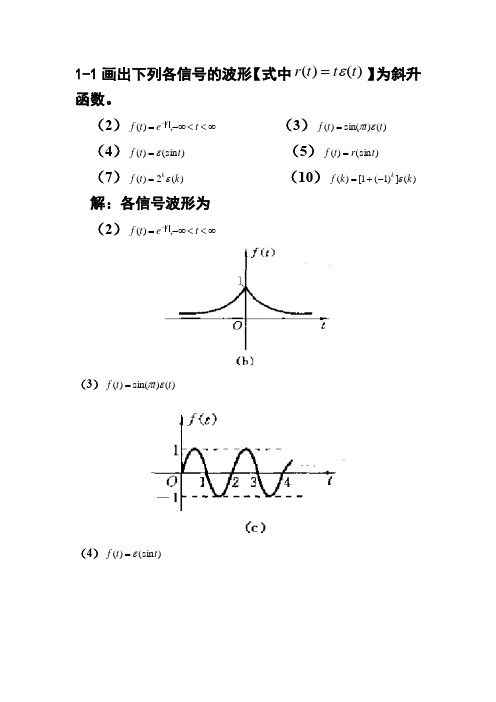
1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))f=rt)(sin(t(7))t=(kf kε(2)(10))f kεk=(k+-((])11[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f(5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(10) x(t+1) ·y(t-1)。
15
第1章 信号与系统的基本概念
题图 1.2
16
第1章 信号与系统的基本概念
解 (1) 将x(t)波形右移2个单位,得到题(1)波形如题解图 1.5-1所示。
题解图 1.5-1
17
第1章 信号与系统的基本概念
(2) 将x(t)波形右移1个单位,再结合单位阶跃信号的单边特 性,画出题(2)波形如题解图1.5-2所示。
题解图 1.5-8
27
第1章 信号与系统的基本概念
(9) 两个连续信号相加,任一时刻的和信号值等于两信号在 该时刻的信号值之和。题(9)信号波形如题解图1.5-9所示。
题解图 1.5-9
28
第1章 信号与系统的基本概念
(10) 两个连续信号相乘,任一时刻的积信号值等于两信 号在该时刻的信号值之积。题(10)信号波形如题解图1.5-10 所示。
解 为简化微、积分算符表示,本题采用第2章将要介绍 的微、积分算子概念求解。画出p算子电路模型如题解图1.13
所示,图中i1(t)和i2(t)为网孔电流。列出网孔方程:
59
第1章 信号与系统的基本概念
题解图 1.13
60
第1章 信号与系统的基本概念
因为
61
第1章 信号与系统的基本概念
所以
电路输入输出方程为
题解图 1.5-5
22
第1章 信号与系统的基本概念
(6) 将y(t)波形左移1个单位,再截取t<0部分,即为题(6)波 形(见题解图1.5-6)。
题解图 1.5-6
23
第1章 信号与系统的基本概念
24
第1章 信号与系统的基本概念
题解图 1.5-7
25
第1章 信号与系统的基本概念
26
第1章 信号与系统的基本概念
(2) 先画出x(k+2)图形, 并考虑到ε(1-k)=ε[-(k-1)], 仅在 k≤1时取值为1, 故在x(k+2)图形中, 截取k≤1部分就是题(2)序 列的图形(见题解图1.6-2)。
题解图 1.6-2
33
第1章 信号与系统的基本概念
(3) 因为
所以题(3)序列图形如题解图1.6-3所示。
号,其冲激强度取决于信号值跳变的方向和幅度。
39
第1章 信号与系统的基本概念
题解图 1.7
40
第1章 信号与系统的基本概念
1.8 已知信号f(t+1)的波形如题图1.4所示,试画出 的波形。
题图 1.4
41
第1章 信号与系统的基本概念
解 首先,应用信号平移、展缩操作,由f(t+1)波形画出 波形,然后求导并画出 的波形。具体过程参见题解图1.8。
后,
再左移1个单位;或者按照“平移-展缩”方式,先将x(t)波形 左移2个单位,再将波形“压缩” 形绘制过程如题解图1.5-4所示。 ,均可画出题(4)波形。波
20
第1章 信号与系统的基本概念
题解图 1.5-4
21
第1章 信号与系统的基本概念
(5) 将y(t)波形左移2个单位,即得题(5)波形(见题解图 1.5-5)。
37
第1章 信号与系统的基本概念
(6) 先画出x(k+2)、y(k-2)图形,再进行相乘运算,画出积 序列图形(见题解图1.6-6)。
题解图 1.6-6
38
第1章 信号与系统的基本概念
1.7 已知信号x(t)、y(t)的波形如题图1.2所示,分别画出 的波形。 解 通过观察x(t)和y(t)波形,直接画出 波形(见题解图1.7)。应特别注意,当x(t)、y(t)的信号值发生跳 变时, 会在相应时刻的 波形中呈现冲激信
10
第1章 信号与系统的基本概念
11
第1章 信号与系统的基本概念
1.4 判定下列信号是否为周期信号。若是周期信号,则确 定信号周期T。
12
第1章 信号与系统的基本概念
解
(1) 若有两个周期分别为T1和T2的连续信号相加,当
T1/T2为有理数时,其和信号亦是周期信号,相应周期为T1和T2的
最小公倍数;否则, 当T1/T2为无理数时,其和信号是非周期信
题解图 1.10-3
50
第1章 信号与系统的基本概念
(4) f4(t)=δ(2t-4)=
δ(t-2),波形如题解图1.10-4所示。
题解图 1.10-4
51
第1章 信号与系统的基本概念
1.11 计算下列各题。
52
第1章 信号与系统的基本概念
53
第1章 信号与系统的基本概念
1.12 如题图1.5所示电路,输入为is(t),分别写出以i(t)、 u(t)为输出时电路的输入输出方程。
34
第1章 信号与系统的基本概念
题解图 1.6-3
35
第1章 信号与系统的基本概念
(4) 先画出y(k)、y(-k)图形,然后进行相减运算,得到题 (4)序列图形如题解图1.6-4所示。
题解图 1.6-4
36
第1章 信号与系统的基本概念
(5) 和序列图形如题解图1.6-5所示。
题解图 1.6-5
解 此题练习离散信号的图形表示方法。要求熟悉常用指 数和正弦序列的图形表示、阶跃序列的定义和基本性质以及序
列平移和翻转操作对序列图形的影响。
7
第1章 信号与系统的基本概念
题解图 1.2
8
第1章 信号与系统的基本概念
1.3 试写出题图1.1各信号的解析表达式。
题图 1.1
9
第1章 信号与系统的基本概念
题图 1.5
54
第1章 信号与系统的基本概念
解 对题解图1.12, 写出节点a的KCL方程: i=is—iL 或写成 iL=is—i 写出节点b的KCL方程:
① ②
③
写出回路l的KVL方程: ④
55
第1章 信号与系统的基本概念
(1) 将式④代入式③得 ⑤ 再将式②代入式⑤, 整理得以i为输出时的输入输出方程:
(6) f6(t)=(1—
)[ε(t+2)—ε(t—2)];
2
第1章 信号与系统的基本概念
(7) f7(t)=3ε(t+1)—ε(t)—3ε(t—1)+ε(t—2); (8) f8(t)=e-t+1ε(t—1);
(9) f9(t)=cosπt[ε(3—t)—ε(—t)];
(10) f10(t)=r(t)—r(t—1)—r(t—2)+r(t—3),式中r(t)=tε(t)。
题解图 1.5-2
18
第1章 信号与系统的基本概念
(3) 由于x(2-t)=x[-(t-2)],故可将x(t)波形“翻转”后,再 右移2个单位,画出题(3)波形如题解图1.5-3中的f3(t)所示。
题解图 1.5-3
19
第1章 信号与系统的基本概念
(4) 按照“展缩-平移”方式,将x(t)波形“压缩”
(6) 因
均是周期为3的周期序列,故f6(k)也是以3为周期的周期序列。
14
第1章 信号与系统的基本概念
1.5 已知连续时间信号x(t)和y(t)分别如题图1.2(a)、(b)所示, 试画出下列各信号的波形图: (1) x(t-2); (3) x(2-t); (5) y(t+2); (7) y(-2-t); (9) x(t)+y(t); (2) x(t-1)ε(t); (4) x(2t+2); (6) y(t+1)ε(-t); (8) y( -1);
第1章 信号与系统的基本概念
解 (1) f1(t)=ε(t2-4),波形如题解图1.10-1所示。
题解图 1.10-1
48
第1章 信号与系统的基本概念
(2) f2(t)=δ(t+1)-δ(t-1),波形如题解图1.10-2所示。
题解图 1.10-2
49
第1章 信号与系统的基本概念
(3) f3(k)=ε(k2-4), 波形如题解图1.10-3所示。
此,k年后开发区拥有的总资金额可表示为
y(k)=(1+β)y(k-2)+(1+α)f(k-1)+f(k)
或写成
y(k)-(1+β)y(k-2)=f(k)+(1+α)f(k-1)
显然,这是一个二阶差分方程。
利润回报率稳定在β%。试建立预测若干年后该经济开发区拥
有的资金总额的数学模型。
64
第1章 信号与系统的基本概念
解 设k年后开发区拥有资金总额为y(k), 第k年投入资金 为f(k)。按题意,第(k-1)年投入资金f(k-1)在第k年度增长为
(1+α)f(k-1), 而资金y(k-2)在第k年度增长为(1+β)y(k-2)。因
42
第1章 信号与系统的基本概念
题解图 1.8
43
第1章 信号与系统的基本概念
1.9 分别计算题图1.3中信号x(k)、y(k)的一阶前向差分、一 阶后向差分和迭分。 解 x(k)的一阶前向差分:
x(k)的一阶后向差分:
44
第1章 信号与系统的基本概念
x(k)的迭分:
y(k)的一阶前向差分:
45
且T1/T2=
sin
的周期为T2=
为无理数,故f3(t)是非周期信号。
13
第1章 信号与系统的基本概念
(4) 在f4(t)中,
的周期分别为 其最小公倍数是1392π,故
f4(t)是周期信号,周期为1392π s。 (5) 信号A sint的周期为2π,自乘三次后,没有改变信号瞬时 值变化周期,故f5(t)是周期为2π s的周期信号。
