高考数学(理)总复习高考达标检测(五十)几何概型命题3角度——长度(角度)、面积、体积
高考数学总复习 高考达标检测(三十)平行问题3角度-线线、线面、面面 理-人教版高三全册数学试题

高考达标检测(三十)平行问题3角度——线线、线面、面面一、选择题1.(2017·某某模拟)设直线l,m,平面α,β,则下列条件能推出α∥β的是( ) A.l⊂α,m⊂α,且l∥β,m∥βB.l⊂α,m⊂β,且l∥mC.l⊥α,m⊥β,且l∥mD.l∥α,m∥β,且l∥m解析:选C 借助正方体模型进行判断.易排除选项A,B,D,故选C.2.如图,在长方体ABCDA′B′C′D′中,下列直线与平面AD′C平行的是( )A.B′C′B.A′BC.A′B′ D.BB′解析:选B 连接A′B,∵A′B∥CD′,∴A′B∥平面AD′C.3.(2017·某某模拟)设l为直线,α,β是两个不同的平面.下列命题中正确的是( ) A.若l∥α,l∥β,则α∥β B.若l⊥α,l⊥β,则α∥βC.若l⊥α,l∥β,则α∥β D.若α⊥β,l∥α,则l⊥β解析:选B 画出一个长方体ABCDA1B1C1D1.对于A,C1D1∥平面ABB1A1,C1D1∥平面ABCD,但平面ABB1A1与平面ABCD相交;对于C,BB1⊥平面ABCD,BB1∥平面ADD1A1,但平面ABCD 与平面ADD1A1相交;对于D,平面ABB1A1⊥平面ABCD,CD∥平面ABB1A1,但CD⊂平面ABCD;易知B正确.4.设α,β是两个不同的平面,m,n是平面α内的两条不同直线,l1,l2是平面β内的两条相交直线,则α∥β的一个充分不必要条件是( )A.m∥l1且n∥l2 B.m∥β且n∥l2C.m∥β且n∥β D.m∥β且l1∥α解析:选A 由m∥l1,m⊂α,l1⊂β,得l1∥α,同理l2∥α,又l1,l2相交,所以α∥β,反之不成立,所以m∥l1且n∥l2是α∥β的一个充分不必要条件.5.已知直线a,b,平面α,则以下三个命题:①若a∥b,b⊂α,则a∥α;②若a∥b,a∥α,则b∥α;③若a∥α,b∥α,则a∥b.其中真命题的个数是( )A.0 B.1C.2 D.3解析:选A 对于①,若a∥b,b⊂α,则应有a∥α或a⊂α,所以①是假命题;对于②,若a∥b,a∥α,则应有b∥α或b⊂α,因此②是假命题;对于③,若a∥α,b∥α,则应有a∥b或a与b相交或a与b异面,因此③是假命题.综上,在空间中,以上三个命题都是假命题.6.(2016·某某模拟)已知直线a,b异面,给出以下命题:①一定存在平行于a的平面α使b⊥α;②一定存在平行于a的平面α使b∥α;③一定存在平行于a的平面α使b⊂α;④一定存在无数个平行于a的平面α与b交于一定点.则其中论断正确的是( )A.①④ B.②③C.①②③ D.②③④解析:选D 对于①,若存在平面α使得b⊥α,则有b⊥a,而直线a,b未必垂直,因此①不正确;对于②,注意到过直线a,b外一点M分别引直线a,b的平行线a1,b1,显然由直线a1,b1可确定平面α,此时平面α与直线a,b均平行,因此②正确;对于③,注意到过直线b上的一点B作直线a2与直线a平行,显然由直线b与a2可确定平面α,此时平面α与直线a平行,且b⊂α,因此③正确;对于④,在直线b上取一定点N,过点N 作直线c与直线a平行,经过直线c的平面(除由直线a与c所确定的平面及直线c与b所确定的平面之外)均与直线a平行,且与直线b相交于一定点N,因此④正确.综上所述,②③④正确.二、填空题7.如图,在四面体ABCD中,若截面PQMN是正方形,则下列结论中正确的序号为________.①AC⊥BD;②AC∥截面PQMN;③AC=BD;④异面直线PM与BD所成的角为45°.解析:∵MN ∥PQ ,MN ⊂平面ACD ,PQ 平面ACD ,∴PQ ∥平面ACD .又平面ACD ∩平面ABC =AC ,∴PQ ∥AC ,从而AC ∥截面PQMN ,②正确;同理可得MQ ∥BD ,∵MQ ⊥PQ ,PQ ∥AC ,∴AC ⊥BD ,①正确;∵MQ ∥BD ,∠PMQ =45°,∴异面直线PM 与BD 所成的角为45°,故④正确;根据已知条件无法得到AC ,BD 长度之间的关系,故③不正确.故填①②④.答案:①②④8.在正四棱柱ABCD A 1B 1C 1D 1中,O 为底面ABCD 的中心,P 是DD 1的中点,设Q 是CC 1上的点,则点Q 满足条件________时,有平面D 1BQ ∥平面PAO .解析:如图所示,假设Q 为CC 1的中点,因为P 为DD 1的中点,所以QB ∥PA .连接DB ,因为P ,O 分别是DD 1,DB 的中点,所以D 1B ∥PO ,又D 1B ⊄平面PAO ,QB ⊄平面PAO ,所以D 1B ∥平面PAO ,QB ∥平面PAO ,又D 1B ∩QB =B ,所以平面D 1BQ∥平面PAO .故Q 满足条件Q 为CC 1的中点时,有平面D 1BQ ∥平面PAO .答案:Q 为CC 1的中点9.如图,在四棱锥V ABCD 中,底面ABCD 为正方形,E ,F 分别为侧棱VC ,VB 上的点,且满足VC =3EC ,AF ∥平面BDE ,则VBFB=________.解析:连接AC 交BD 于点O ,连接EO ,取VE 的中点M ,连接AM ,MF ,由VC =3EC ⇒VM =ME =EC ,又AO =CO ⇒AM ∥EO ⇒AM ∥平面BDE ,又由题意知AF ∥平面BDE ,∴平面AMF ∥平面BDE ⇒MF ∥平面BDE ⇒MF ∥BE⇒VF =FB ⇒VB FB=2. 答案:2三、解答题10.(2017·某某质检)如图所示,在三棱柱ABC A 1B 1C 1中,侧棱AA 1⊥底面ABC ,AB ⊥BC ,D 为AC 的中点,AA 1=AB =2.(1)求证:AB 1∥平面BC 1D ; (2)设BC =3,求四棱锥B DAA 1C 1的体积.解:(1)证明:连接B 1C ,设B 1C 与BC 1相交于点O ,连接OD ,如图所示.∵四边形BCC 1B 1是平行四边形,∴点O 为B 1C 的中点.∵D 为AC 的中点,∴OD 为△AB 1C 的中位线,∴OD ∥AB 1.∵OD ⊂平面BC 1D ,AB 1⊄平面BC 1D ,∴AB 1∥平面BC 1D .(2)∵AA 1⊥平面ABC ,AA 1⊂平面AA 1C 1C ,∴平面ABC ⊥平面AA 1C 1C .∵平面ABC ∩平面AA 1C 1C =AC ,作BE ⊥AC ,垂足为E ,则BE ⊥平面AA 1C 1C .∵AB =AA 1=2,BC =3,AB ⊥BC ,∴在Rt △ABC 中,AC =AB 2+BC 2=4+9=13,∴BE =AB ·BC AC =613, ∴四棱锥B AA 1C 1D 的体积V =13×12(A 1C 1+AD )·AA 1·BE =16×3213×2×613=3. 11.如图,四边形ABCD 中,AB ⊥AD ,AD ∥BC ,AD =6,BC =4,E ,F 分别在BC ,AD 上,EF ∥AB .现将四边形ABCD 沿EF 折起,使平面ABEF ⊥平面EFDC .若BE =1,在折叠后的线段AD 上是否存在一点P ,且AP ―→=λPD ―→,使得CP ∥平面ABEF ?若存在,求出λ的值,若不存在,说明理由.解:AD 上存在一点P ,使得CP ∥平面ABEF ,此时λ=32.理由如下:当λ=32时,AP ―→=32PD ―→,可知AP AD =35, 如图,过点P 作MP ∥FD 交AF 于点M ,连接EM ,PC ,则有MP FD =AP AD =35, 又BE =1,可得FD =5,故MP =3,又EC =3,MP ∥FD ∥EC ,故有MP 綊EC ,故四边形MPCE 为平行四边形, 所以CP ∥ME ,又CP ⊄平面ABEF ,ME ⊂平面ABEF ,故有CP ∥平面ABEF .12.(2016·某某高考)在如图所示的几何体中,D 是AC 的中点,EF ∥DB .(1)已知AB =BC ,AE =EC ,求证:AC ⊥FB ;(2)已知G ,H 分别是EC 和FB 的中点,求证:GH ∥平面ABC . 证明:(1)因为EF ∥DB ,所以EF 与DB 确定平面BDEF .如图,连接DE .因为AE =EC ,D 为AC 的中点,所以DE ⊥AC .同理可得BD ⊥AC .又BD ∩DE =D ,所以AC ⊥平面BDEF .因为FB ⊂平面BDEF ,所以AC ⊥FB .(2)如图,设FC 的中点为I ,连接GI ,HI .在△CEF 中,因为G 是CE 的中点,所以GI ∥EF .又EF ∥DB ,所以GI ∥DB .在△CFB 中,因为H 是FB 的中点,所以HI ∥BC .又HI ∩GI =I ,BC ∩DB =B ,所以平面GHI ∥平面ABC .因为GH ⊂平面GHI ,所以GH ∥平面ABC .。
高考数学总复习高考研究课(二)几何概型命题3角度_长度(角度)、面积、体积课件理
2.如图所示,在直角坐标系内,射线 OT 落在 30°角的 终边上,任作一条射线 OA,则射线 OA 落在∠yOT 内的概率为________.
解析:由题图,因为射线 OA 在坐标系内是等可能分布的,所 以 OA 落在∠yOT 内的概率为 1 答案: 6 60 1 = . 360 6
与体积有关的几何概型
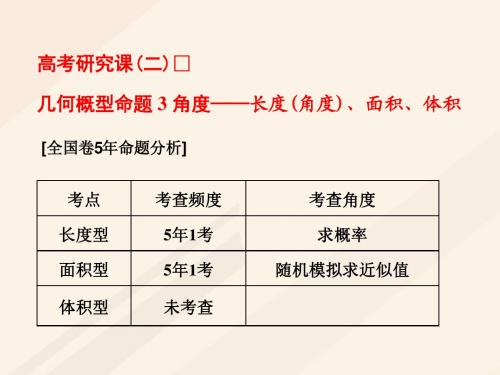
高考研究课(二) 几何概型命题 3 角度——长度(角度)、面积、体积
[全国卷5年命题分析]
考点 长度型 面积型 体积型
考查频度 5年1考 5年1考 未考查
考查ቤተ መጻሕፍቲ ባይዱ度 求概率 随机模拟求近似值
与长度(角度)有关的几何概型
[典例] (1)(2016· 山东高考)在[-1,1]上随机地取一个数 k,则
事件“直线 y=kx 与圆(x-5)2+y2=9 相交”发生的概率为_____.
几何概型,记“点 P 到点 O 的距离大于 1”为事件 A,则事件 A 发 生时,点 P 位于以 O 为球心,以 1 为半径的半球外. 14 3 2 又 V 正方体 ABCDA 1 B 1 C 1 D 1=2 =8,V 半球= ·π·1 = π, 23 3
3
2 8- π 3 π ∴所求事件概率 P(A)= =1- . 8 12
[典例] (2017· 烟台模拟)在棱长为 2 的正方体 ABCDA1B1C1D1
中,点 O 为底面 ABCD 的中心,在正方体 ABCDA1B1C1D1 内随机 取一点 P,则点 P 到点 O 的距离大于 1 的概率为________.
[解析] 由题意,在正方体 ABCDA1B1C1D1 内任取一点,满足
[答案]
1-
π 12
[方法技巧]
与体积有关的几何概型求法的关键点 对于与体积有关的几何概型问题, 关键是计算问题的总体积 (总空间)以及事件的体积(事件空间),对于某些较复杂的也可利 用其对立事件去求.
2023年高考数学总复习《立体几何》附答案解析

所以 z1=0,
,故可取
, ,,
于是 < , >
,
设所成锐二面角为θ,所以 sinθ
,
所以平面 PAD 和平面 PBE 所成锐二面角的正弦值为 .
第3页共3页
第1页共3页
∴CF CC1 AA1 , ∵∠BAC=90°,
∴CD
,
在 Rt△FCD 中,tan∠FDC 맨
,
故直线 DF 与平面 ABC 所成角的正切值为 .
2.如图所示,四棱锥 P﹣ABCD 的底面 ABCD 是边长为 1 的菱形,∠BCD=60°,E 是 CD 的中点,PA⊥底面 ABCD,PA=2. (1)证明:平面 PBE⊥平面 PAB; (2)求平面 PAD 和平面 PBE 所成二面角(锐角)的正弦值.
【解答】(1)证明:如图所示,连接 BD,由 ABCD 是菱形且∠BCD=60°, 知△ABC 是等边三角形. ∵E 是 CD 的中点, ∴BE⊥CD,又 AB∥CD, ∴AB⊥BE,∴BE⊥平面 PAB, 又 BE⊂平面 PBE, ∴平面 PBE⊥平面 PAB. (2)解:在平面 ABCD 内,过点 A 作 AB 的垂线,如图所示,以 A 为原点建立空间直角
【解答】(1)证明:连接 DG、FG, 由直三棱柱的性质知,BB1∥CC1,且 BB1=CC1, ∵B1E=2EB,C1F=2FC, ∴EB∥FC,且 EB=FC, ∴四边形 BCFE 为平行四边形, ∴EF∥BC,EF=BC, ∵BD=2DA,CG=2GA, ∴GD∥BC,且 GD BC, ∴EF∥GD,且 GD EF, ∴四边形 DEFG 为梯形,即 D、E、F、G 四点共面, ∴点 G 在平面 EFD 内. (2)解:由直三棱柱的性质知,CC1⊥平面 ABC, ∵F 为 CC1 上一点, ∴点 F 在平面 ABC 上的投影为点 C, 连接 CD,则∠FDC 即为直线 DF 与平面 ABC 所成角. ∵点 D 在棱 AB 上,且 BD=2DA, ∴AD AB , ∵C1F=2FC,
考点42 几何概型(长度、角度)-庖丁解题2019学年高一数学人教版(必修3)(原卷版)

原创精品资源学科网独家享有版权,侵权必究!
1
1.几何概型的定义
如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例
,则称这样的概率模型为几何概率模型,简称几何概型.
2.几何概型的特点
(1)试验中所有可能出现的结果(基本事件总数)有无限多个.
(2)每个基本事件出现的可能性相等.
3.几何概型的概率公式
()A P A =构成事件的区域长度试验的全部结果所构成的区域长度
. 【例】在面积为S 的ABC △的边AB 上任取一点P ,则PBC △的面积大于4
S 的概率是( ) A .14
B .12
C .34
D .23
【答案】C 【解析】如图.要使14PBC ABC S S >△△,只需14
PB AB >.故所求概率为3344AB P AB ==.
【易错易混】因为题目中涉及面积问题,表面看是面积,因为是同底的三角形,问题的本质是长度比问题.。
考点42 几何概型(长度、角度)-庖丁解题-学年高一数学人教版(必修3)

1.几何概型的定义如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称几何概型.2.几何概型的特点(1)试验中所有可能出现的结果(基本事件总数)有无限多个.(2)每个基本事件出现的可能性相等.3.几何概型的概率公式.【例】在面积为S的ABC△的边AB上任取一点P,则PBC△的面积大于4S的概率是()A.14B.12C.34D.23【易错易混】因为题目中涉及面积问题,表面看是面积,因为是同底的三角形,问题的本质是长度比问题.要点阐述典型例题1.下列概率模型中,是几何概型的有()①明天北京市区降水的概率;②从区间[]1010-,内任取出一个数,求取到绝对值不大于1的数的概率;③从区间[]1010-,内任取出一个整数,求取到大于1而小于2的数的概率;④向一个边长为4 cm的正方形ABCD内投一点P,求点P到正方形中心的距离不超过1 cm的概率.A.1个B.2个C.3个D.4个【答案】B2.在区间(15,25]内的所有实数中随机取一个实数a,则这个实数满足17<a<20的概率是() A.13B.12C.310D.510【答案】C【解析】a∈(15,25],∴P(17<a<20)=20-1725-15=310.【规律总结】在求解与长度有关的几何概型时,首先找到试验的全部结果构成的区域D,这时区域D可能是一条线段或几条线段或曲线段,然后找到事件A发生对应的区域d,在找d的过程中,确定边界点是问题的关键,但边界点是否取到却不影响事件A的概率.3.在长为12 cm的线段AB上任取一点C.现作一矩形,邻边长分别等于线段AC,CB的长,则该矩形面积小于32 cm2的概率为()A.16B.13C.23D.45小试牛刀【答案】C4.点A 为周长等于3的圆周上的一个定点,若在该圆周上随机取一点B ,则劣弧AB 的长度小于1的概率为 . 【答案】23【解析】如图,圆周上使AM 的长度等于1的点M 有两个,设为1M ,2M ,则过A 的圆弧12M AM 长为2,点B 落在优弧12M AM 上就能使劣弧AB 的长度小于1,所以劣弧AB 的长度小于1的概率为23. 5.如图所示,在直角坐标系内,射线OT 落在30°角的终边上,任作一条射线OA ,则射线OA 落在∠yOT内的概率为________.【答案】16【解析】根据题图,因为射线OA 在坐标系内是等可能分布的,所以OA 落在∠yOT 内的概率为60360=16.【易错易混】当涉及射线的转动、扇形中有关落点区域问题时,应以角的大小作为区域度量来计算概率,且不可用线段的长度代替,这是两种不同的度量手段.6.在圆心角为90°的扇形AOB 中,以圆心O 为起点作射线OC ,求使得∠AOC 和∠BOC 都不小于30°的概率. 【解析】如图所示,把圆弧AB 三等分,则∠AOF =∠BOE =30°,记A 为“在扇形AOB 内作一射线OC ,使∠AOC 和∠BOC 都不小于30°”,要使∠AOC 和∠BOC 都不小于30°,则OC 就落在∠EOF 内,∴P (A )=30°90°=13.1.在区间[0,1]上随机取一个数x ,则事件“log 0.5(4x -3)≥0”发生的概率为( )A .34B .23C .13D .14【答案】D【解析】由log 0.5(4x -3)≥0,得0<4x -3≤1,解得34<x ≤1,所以所求概率P =1-341-0=14.2.在区间[11]-,上随机地取一个数x ,2x 的值介于12到1之间的概率为( )A .14B .13C .12D .23【答案】C3.在[-1,1]上随机地取一个数k ,则事件“直线y =kx 与圆(x -5)2+y 2=9相交”发生的概率为________.【答案】34【解析】由直线y =kx 与圆(x -5)2+y 2=9相交,得 |5k |k 2+1<3,即16k2<9,解得-34<k <34. 由几何概型的概率计算公式可知P =34-⎝⎛⎭⎫-342=34.4.将一根长10 cm 的铁丝用剪刀剪成两段,然后再将每一段剪成等长的两段,并用这四段铁丝围成一个矩形,求围成的矩形面积大于62cm 的概率. 【解析】如图,AB 为长10 cm 的铁丝,剪断点为点M ,设AM x =cm (010)x <<,则矩形面积为1022x x-.考题速递投针试验1777年,法国科学家布丰做了一个投针试验,他在一张大纸上画了一些平行线,相邻两条平行线间的距离都相等,再把长度等于相邻两平行线间距离一半的针投到纸上,并记录投针的总次数及针落到纸上后与平行线中的某一条相交的次数,共计投针2212次,其中与平行线相交的有704次,发现它们的商2212 ,与π非常接近.这个试验被认为是本节所学几何概型的第一个试验.那么,投针试验为什么能算出π的近似值呢?数学文化。
高考数学一轮复习考点规范练55几何概型含解析新人教A版

考点规范练55 几何概型基础巩固1.(2021全国Ⅰ,文7)在区间(0,12)随机取1个数,则取到的数小于13的概率为( ) A.34 B.23 C.13 D.16答案:B解析:所求事件的概率P=13-012-0=23.2.若将一个质点随机地投入到如图所示的长方形ABCD 中,其中AB=2,BC=1,则质点落在以AB 为直径的半圆内的概率是( )A.π2 B.π4C.π6D.π8答案:B 解析:所求概率为S 半圆S 长方形=12π·122×1=π4,故选B .3.“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何?”其意思是:有一个正方形的池塘,池塘的边长为一丈,有一棵芦苇生长在池塘的正中央,露出水面一尺,若把它引向岸边,正好与岸边齐(如图所示),问水有多深?芦苇有多长?其中一丈为十尺.若从该芦苇上随机取一点,则该点取自水上的概率为( )A.1213 B.113C.314D.213答案:B解析:设水深为x 尺,根据勾股定理可得(x+1)2=x 2+52,解得x=12,则水深12尺,芦苇长13尺.根据几何概型概率公式可得,从该芦苇上随机取一点,该点取自水上的概率为P=113,故选B.4.某人从甲地去乙地共走了500 m,途经一条宽为x m的河流,该人不小心把一件物品丢在途中,若物品掉在河里就找不到,若物品未掉在河里,则能找到,已知该物品能被找到的概率为45,则河宽大约为()A.80 mB.50 mC.40 mD.100 m答案:D解析:由长度型的几何概型公式结合题意可知,河宽大约为500×(1-45)=100(m).5.已知在△ABC中,∠ABC=60°,AB=2,BC=6,在BC上任取一点D,则使△ABD为钝角三角形的概率为()A.16B.13C.12D.23答案:C解析:如图,当BE=1时,∠AEB为直角,则点D在线段BE(不包含B,E点)上时,△ABD为钝角三角形;当BF=4时,∠BAF为直角,则点D在线段CF(不包含C,F点)上时,△ABD为钝角三角形.故△ABD为钝角三角形的概率为1+26=12.6.有一个长、宽分别为50 m,30 m的游泳池,一名工作人员在池边巡视,某时刻出现在池边任一位置的可能性相同.一人在池中心(对角线的交点)处呼唤工作人员,其声音可传出15√2 m,则工作人员能及时听到呼唤(出现在声音可传到区域)的概率是()A.34B.38C.3π16D.12+3π32答案:B解析:如图,工作人员在池边巡视的长度为160,工作人员能及时听到呼唤的长度为30+30=60,故所求的概率为60160=38.7.若在区间[-1,1]上随机取一个数x ,则sin πS 4的值介于-12与√22之间的概率为( )A.14 B.13C.23D.56答案:D解析:∵-1≤x ≤1,∴-π4≤πS 4≤π4.由-12≤sinπS 4≤√22, 得-π6≤πS 4≤π4,则-23≤x ≤1.故所求事件的概率为1-(-23)1-(-1)=56.8.记函数f (x )=√6+S -S 2的定义域为D.在区间[-4,5]上随机取一个数x ,则x ∈D 的概率是 . 答案:59解析:由6+x-x 2≥0,即x 2-x-6≤0得-2≤x ≤3,所以D=[-2,3]⊆[-4,5].由几何概型的概率公式得x ∈D 的概率P=3-(-2)5-(-4)=59,答案为59.9.记集合A={(x ,y )|x 2+y 2≤4}和集合B={(x ,y )|x+y-2≤0,x ≥0,y ≥0}表示的平面区域分别为Ω1和Ω2,若在区域Ω1内任取一点M (x ,y ),则点M 落在区域Ω2的概率为 .答案:12π解析:作圆O :x 2+y 2=4,区域Ω1就是圆O 内部(含边界),其面积为4π,区域Ω2就是图中△AOB 内部(含边界),其面积为2,因此所求概率为24π=12π.10.在圆C :(x-3)2+y 2=3上任取一点P ,则锐角∠COP<π6(O 为坐标原点)的概率是 .答案:23解析:当∠COP=π6时,直线OP 的方程为x ±√3y=0,圆心C 到直线OP 的距离d=32.又圆C 的半径为√3,此时弦所对的圆心角为π3,所以所求概率P=1-π3×22π=23.能力提升11.在区间[-1,1]上随机取一个数k ,使直线y=kx+√52与圆x 2+y 2=1不相交的概率为( ) A.34 B.23C.12D.13答案:C 解析:要使直线y=kx+√52与圆x 2+y 2=1相交,应满足√52√≥1,解得-12≤k ≤12,所以在区间[-1,1]上随机取一个数k ,使直线y=kx+√52与圆x 2+y 2=1不相交的概率为P=12+121+1=12.故选C .12.如图,“赵爽弦图”是由四个全等的直角三角形(阴影部分)围成一个大正方形,中间空出一个小正方形组成的图形.若在大正方形内随机取一点,该点落在小正方形的概率为15,则图中直角三角形较大锐角的正弦值为( )A.√55B.2√55C.15D.√33答案:B解析:设小正方形的边长为1,直角三角形的直角边长分别为x ,1+x ,√S 2+(1+S )2. 由几何概型可得12S 2+(1+S )2=15,解得x=1(x=-2(舍)),所以直角三角形的边长分别为1,2,√5,直角三角形较大锐角的正弦值为√5=2√55,故选B .13.已知函数f (x )=x 2+bx+c ,其中0≤b ≤4,0≤c ≤4.记函数f (x )满足条件{S (2)≤12,S (-2)≤4为事件A ,则事件A 发生的概率为( ) A.14 B.58 C.12 D.38答案:C 解析:由题意, 得{4+2S +S ≤12,4-2S +S ≤4,0≤S ≤4,0≤S ≤4,即{2S +S -8≤0,2S -S ≥0,0≤S ≤4,0≤S ≤4,表示的区域(阴影部分)如图所示,可知阴影部分的面积为8, 所以所求概率为12,故选C .14.设点(a ,b )是区域{S +S -4≤0,S >0,S >0内的任意一点,则使函数f (x )=ax 2-2bx+3在区间[12,+∞)内是增函数的概率为 . 答案:13解析:作出不等式组{S +S -4≤0,S >0,S >0所对应的平面区域如图△AOB 区域,可知符合条件的点所构成的区域面积为S △AOB =12×4×4=8. 若f (x )=ax 2-2bx+3在区间[12,+∞)内是增函数,则{S >0,--2S 2S=S S ≤12,即{S >0,S -2S ≥0.则A (0,4),B (4,0), 由{S +S -4=0,S -2S =0得{S =83,S =43.即C (83,43). 则使函数f (x )=ax 2-2bx+3在区间[12,+∞)内为增函数的点(a ,b )所构成的区域为△OBC ,其面积为12×4×43=83.故所求的概率为838=13.15.如图,在Rt △ABC 中,∠BAC=90°,AB=1,BC=2.在边BC 上任取一点M ,则∠AMB ≥90°的概率为 .答案:14解析:如图,在Rt △ABC 中,作AD ⊥BC ,D 为垂足,由题意可得BD=12,且点M 在BD 上时,满足∠AMB ≥90°,故所求概率为SSSS=122=14.16.张先生订了一份报纸,送报人在早上6:30~7:30之间把报纸送到他家,张先生离开家去上班的时间在早上7:00~8:00之间,则张先生在离开家之前能得到报纸的概率是 . 答案:78解析:以横坐标x 表示报纸送到时间,纵坐标y 表示张先生离家时间,建立如图所示的平面直角坐标系.因为随机试验落在正方形区域内任何一点是等可能的,所以符合几何概型.根据题意只要点落到阴影部分,就表示张先生在离开家前能得到报纸,故所求的概率为1×1-12×12×121×1=78.高考预测17.若不等式x 2+y 2≤2所表示的平面区域为M ,不等式组{S -S ≥0,S +S ≥0,S ≥2S -6表示的平面区域为N ,现随机向区域N 内抛一粒豆子,则豆子落在区域M 内的概率为 . 答案:π24解析:分别作出平面区域M 和平面区域N 如图所示,可知平面区域M 与平面区域N 重叠部分的面积为14π(√2)2=π2,平面区域N 的面积为12×3×2+12×3×6=12,故所求的概率为12π12=π24.。
高考研究课(二) 几何概型命题3角度——长度(角度)、面积、体积
[解析]当 AM=AC 时,△ACM 为以 A 为顶点的等腰三角形, 180°-45° ∠ACM= =67.5°.当∠ACM<67.5°时,AM<AC, 2 ∠ACM的度数 67.5° 3 所以 AM 小于 AC 的概率 P= = = . ∠ACB的度数 90° 4 [答案] 3 4
几何概型命题3角度——长度(角度)、面积、体积
[解析] 由题意,在正方体 ABCDA1B1C1D1 内任取一点,满足
几何概型,记“点 P 到点 O 的距离大于 1”为事件 A,则事件 A 发 生时,点 P 位于以 O 为球心,以 1 为半径的半球外. 14 3 2 又 V 正方体 ABCDA 1 B 1 C 1 D 1=2 =8,V 半球= ·π·1 = π, 23 3
[典例]
结 束
(1)(2016· 山东高考)在[-1,1]上随机地取一个数 k,则
事件“直线 y=kx 与圆(x-5)2+y2=9 相交”发生的概率为_____.
[解析] 得 由直线 y=kx 与圆(x-5)2+y2=16k <9,解得- <k< . 4 4 k2+1
3
2 8- π 3 π ∴所求事件概率 P(A)= =1- . 8 12
[答案]
1-
π 12
几何概型命题3角度——长度(角度)、面积、体积
结 束
[方法技巧]
与体积有关的几何概型求法的关键点 关键是计算问题的总体积 对于与体积有关的几何概型问题, (总空间)以及事件的体积(事件空间),对于某些较复杂的也可利 用其对立事件去求.
3 3 -- 4 4 3 由几何概型的概率计算公式可知 P= = . 2 4 [答案] 3 4
几何概型命题3角度——长度(角度)、面积、体积
结 束
2020—2021年高考总复习数学《立体几何》高考考点专项复习及参考答案(精品试题).docx
届高三第二次模拟数学理试题分类汇编:立体几何一、填空、选择题1、(崇明县2016届高三二模)已知圆锥的母线长为5cm ,侧面积为15πcm2,则此圆锥的体积为cm 2.2、(奉贤区2016届高三二模)在棱长为1的正方体ABCD A B C D ''''-中,若点P 是棱上一点,则满足2PA PC '+=的点P 的个数_______.3、(虹口区2016届高三二模)已知A 、B 是球O 的球面上两点,90AOB ∠=o ,C 为该球面上的动点,若三棱锥ABC O -体积的最大值为323,则球O 的表面积为__________4、(黄浦区2016届高三二模)已知一个凸多边形的平面展开图由两个正六边形和六个正方形构成,如右上图所示,若该凸多面体所有棱长均为1,则其体积V =5、(静安区2016届高三二模)如图,正四棱锥P ABCD -的底面边长为23cm ,侧面积为 283cm ,则它的体积为.6、(闵行区2016届高三二模)若一个圆锥的母线长是底面半径的3倍,则该圆锥的侧面积是底面积的 倍.7、(浦东新区2016届高三二模)已知四面体ABCD 中,2==CD AB ,E ,F分别为BC ,AD 的中点,且异面直线AB 与CD 所成的角为3π,则EF =________.8、(普陀区2016届高三二模)若a 、b 表示两条直线,α表示平面,下列命题中的真命题为( )(A )若α⊥a ,b a ⊥,则α//b (B )若α//a ,b a ⊥,则α⊥b (C )若α⊥a ,α⊆b ,则b a ⊥ (D )若α//a ,α//b ,则b a // 9、(徐汇、金山、松江区2016届高三二模).如图,圆锥形容器的高为,h 圆锥内水面的高为1,h 且11,3h h =若将圆锥倒置,水面高为2,h 则2h 等于------------------------------------------------( )(A )23h (B )1927h (C )363h (D )3193h10、(杨浦区2016届高三二模)已知命题:“若a,b 为异面直线,平面α过直线a 且与直线b 平行,则直线b 与平面α的距离等于异面直线a,b 之间的距离”为真命题.根据上述命题,若a,b 为异面直线,且它们之间的距离为d ,则空间中与a,b 均异面且距离也均为d 的直线c 的条数为( )A0条 B.1条 C.多于1条,但为有限条 D.无数多条11、(闸北区2016届高三二模)已知,,,S A B C 是球O 表面上的点,SA ⊥平面ABC ,AB BC ⊥,1SA AB == 2BC =,则球O 的表面积等于( )A .π4 B .π3 C .π2 D .π12、(长宁、青浦、宝山、嘉定四区2016届高三二模)下列命题正确的是( ).(A )若直线1l ∥平面α,直线2l ∥平面α,则1l ∥2l ; (B )若直线l 上有两个点到平面α的距离相等,则l ∥α;(C )直线l 与平面α所成角的取值范围是⎪⎭⎫⎝⎛2,0π;(D )若直线1l ⊥平面α,直线2l ⊥平面α,则1l ∥2l .13、(闵行区2016届高三二模)如图,在正方体1111ABCD A B C D -中,E 是1AA 的中点,P 为底面ABCD 内一动点,设1PD PE 、与底面ABCD 所成的角分别为12θθ、(12θθ、均不为0).若12θθ=,则动点P 的轨迹为哪种曲线的一部分( ).(A)直线 (B)圆 (C) 椭圆 (D) 抛物线14、(浦东新区2016届高三二模)给出下列命题,其中正确的命题为( )(A )若直线a 和b 共面,直线b 和c 共面,则a 和c 共面;(B )直线a 与平面α不垂直,则a 与平面α内的所有直线都不垂直; (C )直线a 与平面α不平行,则a 与平面α内的所有直线都不平行; (D )异面直线a 、b 不垂直,则过a 的任何平面与b 都不垂直. 二、解答题1、(崇明县2016届高三二模)如图,在棱长为1的正方体1111ABCD A B C D -中,点E 是棱BC 的中点,点F 是棱CD 的中点. (1)求证:11EF B D ∥; (2)求二面角1C EF A --的大小(结果用反三角函数值表示).AC BC 1A 1B 1(第19题图)D 1D FE2、(奉贤区2016届高三二模)面ABC 外的一点P ,,,AP AB AC 两两互相垂直,过AC 的中点D 作ED ⊥面ABC ,且1ED =,2PA =,2AC =,连,BP BE ,多面体B PADE -的体积是33. (1)画出面PBE 与面ABC 的交线,说明理由; (2)求面PBE 与面ABC 所成的锐二面角的大小.ADBCPEQ A DCBP (第20题图)3、(虹口区2016届高三二模)如图,在四棱锥ABCD P -中,已知⊥PA 平面ABCD ,且四边形ABCD 为直角梯形,90ABC BAD ∠=∠=︒,2AB AD AP ===,1BC =.(1) 求点A 到平面PCD 的距离; (2) 若点Q 为线段BP 的中点,求直线CQ 与平面ADQ 所成角的大小.4、(黄浦区2016届高三二模)如图,小凳的凳面为圆形,凳脚为三根细钢管,考虑到钢管的受力等因素,设计的小凳应满足:三根细钢管相交处的节点P 与凳面圆形的圆心O 的连线垂直于凳面和地面,且P 分两钢管上下两段的比值为0.618,三只凳脚与地面所成的角均为60°,若A 、B 、C 是凳面圆周的三等分点,18AB =厘米,求凳面的高度h 及三根细钢管的总长度(精确到0.01);5、(静安区2016届高三二模)设点,E F 分别是棱长为2的正方体1111ABCD A B C D -的棱1,AB AA 的中点.如图,以C 为坐标原点,射线CD 、CB 、1CC 分别是x 轴、y 轴、z 轴的正半轴,建立空间直角坐标系.(1)求向量1D E u u u u r与1C F u u u u r 的数量积;(2)若点,M N 分别是线段1D E 与线段1C F 上的点,问是否存在直线MN ,MN ⊥平面ABCD ?若存在,求点,M N 的坐标;若不存在,请说明理由E FB 1A 1C 1D 1BC DA6、(闵行区2016届高三二模)如图,在直角梯形PBCD中,//PB DC,DC BC⊥,22PB BC CD===,点A是PB的中点,现沿AD将平面PAD折起,设PABθ∠=.(1)当θ为直角时,求异面直线PC与BD所成角的大小;(2)当θ为多少时,三棱锥P ABD-的体积为26.7、(浦东新区2016届高三二模)如图,在圆锥SO中,AB为底面圆O 的直径,点C为»AB的中点,SO AB=.(1)证明:AB⊥平面SOC;(2)若点D为母线SC的中点,求AD与平面SOC所成的角.(结果用反三角函数表示)8、(普陀区2016届高三二模)在正四棱柱1111D C B A ABCD -中,底面边长为1,B C 1与底面ABCD 所成的角的大小为2arctan ,如果平面11C BD 与底面ABCD 所成的二面角是锐角,求出此二面角的大小(结果用反三角函数值)9、(徐汇、金山、松江区2016届高三二模)在直三棱柱111C B A ABC -中,1==AC AB ,90=∠BAC ,且异面直线BA 1与11CB 所成的角等于060,设a AA =1. (1)求a 的值;(2)求三棱锥BC A B 11-的体积.1A 1B 1CA BCD.A 1CEA BCDB 110、(杨浦区2016届高三二模)如图,底面是直角三角形的直三棱柱111ABC A B C -中,1112AC BC AA ===,D 是棱1AA 上的动点.(1)证明:1DC BC ⊥; (2)求三棱锥1C BDC -的体积.11、(闸北区2016届高三二模)在长方体1111ABCD A B C D -中,2AB =,1AD =,11AA =,点E 在棱AB 上移动.(1)探求AE 多长时,直线1D E 与平面11AA D D成45o 角;(2)点E 移动为棱AB 中点时,求点E 到平面11A DC 的距离.12、(长宁、青浦、宝山、嘉定四区2016届高三二模)如图,在直三棱柱111C B A ABC -中,底面△ABC 是等腰直角三角形,21===AA BC AC ,D 为侧棱1AA 的中点.(1)求证:⊥BC 平面11A ACC ;(2)求二面角11C CD B --的大小(结果用反三角函数值表示). 参考答案一、填空、选择题ABCA 1B 1C 1D1、12π2、23、64π4、3325、4106、37、1 或3 8、C 9、D 10、D 11、A 12、D13、B 14、D二、解答题1、可得有关点的坐标为11111(0,0,1),(1,1,1),(,1,0),(0,,0),(0,1,1)22D BEF C 11(,,0)22EF =--u u u r ,11(1,1,0)B D =--u u u u r (4)分所以112B D EF =u u u u r u u u r...............................5分所以11EF B D ∥...............................6分(2)设1(,,)n u v w =u r是平面1C EF 的一个法向量.因为111,n EF n FC ⊥⊥u r u u u u r u r u u u u r所以1111110,0222n EF u v n FC v w ⋅=--=⋅=+=u r u u u ru r u u u u r解得,2u v v w =-=- .取1w = ,得1(2,2,1)n =-u r.............................9分因为1DD ABCD ⊥平面,所以平面ABCD 的一个法向量是2(0,0,1)n =u u r (10)分设1n u r 与2n u u r 的夹角为α ,则12121cos 3||||n n n n α⋅==⋅u r u u ru r uu r .......................11分结合图形,可判别得二面角1C EF A --是钝角,其大小为1arccos 3π- (12)分2、(1)根据条件知:PE 与AD 交点恰好是C 1分ACBC 1A 1B 1(第19题图)D 1 D FE x yz,C PE C ∈∴∈面PBE ,,C AC C ∈∴∈面ABC 2分B ∈面PBE ,B ∈面ABC3分 面PBE与面ABC的交线BC5分 (2)(理) ,,AP AB AC 两两互相垂直,BA ⊥面EDAP 7分多面体B PADE -的体积是()113323PA DE AD BA ⨯+⨯⨯=9分233BA ∴=10分建立空间直角坐标系,设平面的法向量是()1,,n x y z u r23,0,03B ⎛⎫ ⎪ ⎪⎝⎭,()0,2,0C ()0,1,0D ()0,1,1E ()0,0,2P23,0,23BP ⎛⎫=- ⎪ ⎪⎝⎭u u u r ,23,1,13BE ⎛⎫=- ⎪ ⎪⎝⎭u u u r123203n BP x z ⋅=-+=u r u u u r12303n BE x y z ⋅=-++=u r u u u r()13,1,1n ∴=u r11分面ABC 的法向量()20,0,1n =u u rADBC PE zxyQA D CBP(第20题解答图)z yx 1212cos n nn n θ⋅==⋅u r u u ru r u u r 1555= 12分所以面PBE 与面ABC 所成的锐二面角大小5arccos 513分注:若作出二面角得2分,计算再3分 (2)(文),,AP AB AC 两两互相垂直,BA ⊥面EDAP7分多面体B PADE -的体积是()113323PA DE AD BA ⨯+⨯⨯=9分233BA ∴=10分 连接AEAE 是BE 在面EDAP 的射影BEA ∠是BE 与面PADE 所成的线面角. 11分 计算2AE =,2363tan 32BAE ∠==12分BEA ∠是BE 与面PADE 所成的线面角6arctan 3. 13分3、 (理)解:(1)以},,{AP AD AB 为正交基底建立空间直角坐标系xyz A -,则相关点的坐标为B (2,0,0),(2,1,0),(0,2,0),(0,0,2).C D P ……2分设平面PCD 的法向量为(,,),n x y z =r由(2,1,0),DC =-uuu r (0,2,2),DP =-u u u r (0,2,0).DA =-u u u r则ADBCPE202,2.220n DC x y y x z x n DPy z r u u u r r u u u r ìïì?-==ïïïÞ眄镲=?-+=ïîïî 令1x =,则(1,2,2)n =r.……5分所以点A 到平面PCD 的距离为:(0,2,0)(1,2,2)4.(1,2,2)3DA n d nu u u r r r×-?=== ……7分(2) 由条件,得(1,0,1),Q =(0,2,0),(1,0,1),AD AQ ==u u u r u u u r 且(1,1,1).CQ u u u r=--设平面ADQ 的法向量为0000(,,),n x y z =r 则00000000200,.0n AD y y z x n AQx z r u u u r r u u u r ìïì?==ïï镲Þ眄镲=-?+=ïïîî令01x =,则0(1,0,1)n =-r.……10分设直线CQ 与平面ADQ 所成角为,θ则00026sin cos ,.332CQ n CQ n CQ n θ⋅=<>===⋅u u u r u u r u u u r u u ru u u r u u r故直线CQ 与平面ADQ 所成角的大小为6sin.3arc ……14分注:第(1)小题也可用等积法来做.4、[解] 联结PO ,AO ,由题意,PO ⊥平面ABC ,因为凳面与地面平行, 所以PAO ∠就是PA 与平面ABC 所成的角,即60PAO ∠=︒.(2分) 在等边三角形ABC 中,18AB =,得63AO =,(4分)在直角三角形PAO 中,318OP AO ==,(6分)由0.618OPh OP=-,解得47.13h ≈厘米.(9分)三根细钢管的总长度3163.25sin 60h≈︒厘米.(12分)5、(1)在给定空间直角坐标系中,相关点及向量坐标为11(2,0,2),(1,2,0),(1,2,2)D E D E =--u u u u r (2)分PA BCD xy z PA BCD 11(0,0,2),(2,2,1),(2,2,1)C F C F =-u u u u r (4)分所以111222(2)(1)4D E C F ⋅=-⨯+⨯+-⨯-=u u u u r u u u u r。
专题05 立体几何(选择题、填空题)——三年(2018-2020)高考真题理科数学分项汇编(含解析)
点).记直线 PB 与直线 AC 所成的角为α,直线 PB 与平面 ABC 所成的角为β,二面角 P–AC–B 的平面角
为γ,则
A.β<γ,α<γ
B.β<α,β<γ
C.β<α,γ<α
D.α<β,γ<β
16.【2018 年高考全国Ⅰ卷理数】某圆柱的高为 2,底面周长为 16,其三视图如图.圆柱表面上的点 M 在
9.
的
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
10.
【2020 年新高考全国Ⅰ卷】日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的
影子来测定时间.把地球看成一个球(球心记为 O),地球上一点 A 的纬度是指 OA 与地球赤道所在平面
所成角,点 A 处的水平面是指过点 A 且与 OA 垂直的平面.在点 A 处放置一个日晷,若晷面与赤道所在平
专题 05
立体几何(选择题、填空题)
1.【2020年高考全国Ⅰ卷理数】埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.
以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高
与底面正方形的边长的比值为
A.
5 1
4
B.
5 1
2
C.
5 1
4
D.
5 1
19.【2018 年高考浙江卷】某几何体的三视图如图所示(单位:cm)
A.2
B.4
C.6
D.8
20.【2018 年高考全国Ⅲ卷理数】设 A ,B ,C ,D 是同一个半径为 4 的球的球面上四点, △ ABC 为等边三
高考数学总复习《立体几何》部分试题及答案
高考数学总复习试卷立体几何综合训练第I卷(选择题共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列命题正确的是()A.直线a,b与直线l所成角相等,则a//bB.直线a,b与平面α成相等角,则a//bC.平面α,β与平面γ所成角均为直二面角,则α//βD.直线a,b在平面α外,且a⊥α,a⊥b,则b//α2.空间四边形ABCD,M,N分别是AB、CD的中点,且AC=4,BD=6,则()A.1<MN<5 B.2<MN<10C.1≤MN≤5 D.2〈MN<53.已知AO为平面α的一条斜线,O为斜足,OB为OA在α内的射影,直线OC在平面α内,且∠AOB=∠BOC=45°,则∠AOC等于()A.30°B.45°C.60°D.不确定4.甲烷分子结构是:中心一个碳原子,外围四个氢原子构成四面体,中心碳原子与四个氢原子等距离,且连成四线段,两两所成角为θ,则cosθ值为()A.B.C.D.5.对已知直线a,有直线b同时满足下面三个条件:①与a异面;②与a成定角;③与a距离为定值d,则这样的直线b有()A.1条B.2条C.4条D.无数条6.α,β是不重合两平面,l,m是两条不重合直线,α//β的一个充分不必要条件是()A.,且l//β,m//βB.,且l//mC.l⊥α,m⊥β,且l//m D.l//α,m//β,且l//m7.如图正方体中,E,F分别为AB,的中点,则异面直线与EF所成角的余弦值为( )A.B.C.D.8.对于任一个长方体,都一定存在一点:①这点到长方体的各顶点距离相等;②这点到长方体的各条棱距离相等;③这点到长方体的各面距离相等,以上三个结论中正确的是()A.①②B.①C.②D.①③9.在斜棱柱的侧面中,矩形最多有几个?A.2 B.3 C.4 D.610.正六棱柱的底面边长为2,最长的一条对角线长为,则它的侧面积为()A.24 B.12 C.D.11.异面直线a,b成80°角,P为a,b外的一个定点,若过P有且仅有2条直线与a,b所成的角相等且等于α,则角α属于集合()A.{α|0°〈α〈40°} B.{α|40°<α〈50°}C.{α|40°〈α<90°}D.{α|50°<α〈90°}12.从水平放置的球体容器的顶部的一个孔向球内以相同的速度注水,容器中水面的高度与注水时间t之间的关系用图象表示应为()第II卷(非选择题共90分)二、填空题(本大题共4个小题,每小题4分,共16分,把答案填在题中横线上)13.正四棱锥S—ABCD侧棱长与底面边长相等,E为SC中点,BE与SA所成角的余弦值为_____________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考达标检测(五十)几何概型命题3角度——长度(角度)、面积、体积 一、选择题
1.如图所示,A 是圆上一定点,在圆上其他位置任取一点A ′,连接
AA ′,得到一条弦,则此弦的长度小于或等于半径长度的概率为( )
A.1
2 B.32
C.13
D.14
解析:选C 当AA ′的长度等于半径长度时,∠AOA ′=π
3,A ′点在A 点左右都可取
得,故由几何概型的概率计算公式得P =2π32π=1
3
.
2.在区间[0,1]上随意选择两个实数x ,y ,则使x 2
+y 2
≤1成立的概率为( ) A.π2 B.π4 C.
π3 D.π5
解析:选B 如图所示,试验的全部结果构成正方形区域,使得x 2
+y 2
≤1成立的平面区域为以坐标原点O 为圆心,1为半径的圆的1
4与x 轴正半轴,y 轴
正半轴围成的区域,由几何概型的概率计算公式得,所求概率P =π41=π
4.故选
B.
3.(2017·湖南师大附中检测)利用计算机产生0~1之间的均匀随机数a ,b ,则事件
“⎩⎪⎨⎪⎧
3a -1>03b -1>0
”发生的概率为( )
A.49
B.1
9 C.23
D.13
解析:选A 由题意可知⎩
⎪⎨
⎪⎧
0≤a ≤1,
0≤b ≤1,该不等式组表示的区域为一个边长为1的正方
形,其面积是1.⎩⎪⎨⎪⎧
3a -1>0,3b -1>0,
0≤a ≤1,
0≤b ≤1表示的区域为一个边长为23的正方形,面积是4
9
,所以
所求概率为4
9
.
4.(2017·辽宁五校联考)若实数k ∈[-3,3],则k 的值使得过点A (1,1)可以作两条直线与圆x 2+y 2
+kx -2y -54
k =0相切的概率等于( )
A.12
B.13
C.14
D.16
解析:选D 由点A 在圆外可得k <0,由题中方程表示圆可得k >-1或k <-4,所以-1<k <0,故所求概率为1
6
,故选D.
5.(2016·长沙三模)如图,矩形OABC 内的阴影部分由曲线f (x )=sin x (x ∈(0,π))及直线x =a ()a ∈
,π
与x 轴围成,向矩形OABC
内随机投掷一点,若该点落在阴影部分的概率为3
16
,则a 的值为( )
A.7π12
B.2π3
C.3π4
D.5π6
解析:选B 由题意知,阴影部分的面积为⎠⎛0a
sin x d x =(-cos x ) ⎪
⎪⎪
a 0
=-cos a +
cos 0=1-cos a ,根据几何概型的概率计算公式知1-cos a a ·
8a
=316,即cos a =-1
2,而a
∈(0,π),故a =2π
3
,故选B.
6.(2017·伊春模拟)在区间⎣⎢⎡⎦
⎥⎤-π6,π2上随机取一个数x ,则sin x +cos x ∈[1, 2 ]的概率是( )
A.12
B.34
C.38
D.58
解析:选 B 因为x ∈⎣⎢⎡⎦⎥⎤-
π6,π2,所以x +π
4∈⎣⎢⎡⎦
⎥⎤π12,3π4,由sin x +cos x =2
sin ⎝ ⎛⎭⎪⎫x +π4∈[1, 2 ],得22≤sin ⎝ ⎛⎭⎪⎫x +π4≤1,所以x ∈⎣⎢⎡⎦⎥⎤0,π2,故要求的概率为
π2-0π2-⎝ ⎛⎭
⎪⎫-π6=3
4.
7.(2017·商丘模拟)已知P 是△ABC 所在平面内一点,PB ―→+PC ―→+2PA ―→
=0,现将一粒豆随机撒在△ABC 内,则黄豆落在△PBC 内的概率是( )
A.14
B.13
C.12
D.23
解析:选C 如图所示,设点M 是BC 边的中点,因为PB ―→+PC ―→
+2PA ―→
=0,所以点P 是中线AM 的中点,所以黄豆落在△PBC 内的概率P =
S △PBC S △ABC =1
2
,故选C. 8.(2016·烟台模拟)在区间[0,1]上任取两个数a ,b ,则函数f (x )=x 2
+ax +b 2
无零点的概率为( )
A.12
B.23
C.34
D.14
解析:选C 要使该函数无零点,只需a 2
-4b 2
<0, 即(a +2b )(a -2b )<0.∵a ,b ∈[0,1],a +2b >0, ∴a -2b <0. 作出⎩⎪⎨⎪
⎧
0≤a ≤1,0≤b ≤1,
a -2
b <0
的可行域(如阴影部分所示),
易得该函数无零点的概率P =1-12×1×1
21×1=3
4.
二、填空题
9.已知线段AC =16 cm ,先截取AB =4 cm 作为长方体的高,再将线段BC 任意分成两
段作为长方体的长和宽,则长方体的体积超过128 cm 3
的概率为________.
解析:依题意,设长方体的长为x cm ,则相应的宽为(12-x )cm ,由4x (12-x )>128得x 2
-12x +32<0,4<x <8,因此所求的概率等于8-412=13
.
答案:1
3
10.(2017·湖北七市联考)AB 是半径为1的圆的直径,M 为直径AB 上任意一点,过点
M 作垂直于直径AB 的弦,则弦长大于3的概率是________.
解析:依题意知,当相应的弦长大于3时,圆心到弦的距离小于
12
-⎝
⎛⎭⎪⎫322=1
2
,因此相应的点M 应位于线段AB 上与圆心的距离小于12的地方,所求的概率等于1
2
.
答案:1
2
11.(2017·重庆检测)在不等式组⎩⎪⎨⎪
⎧
x -y +1≥0,x +y -2≤0,
y ≥0
所表示的平面区域内随机地取
一点P ,则点P 恰好落在第二象限的概率为________.
解析:画出不等式组⎩⎪⎨⎪
⎧
x -y +1≥0,x +y -2≤0,
y ≥2
表示的平面区域(如图中阴影部分所示),
因为S △ABC =12×3×32=9
4,S △AOD =12×1×1=1
2,
所以点P 恰好落在第二象限的概率为S △AOD S △ABC =1
294
=2
9
.
答案:29
12.在底和高等长度的锐角三角形中有一个内接矩形ABCD ,矩形 的一边BC 在三角形的底边上,如图,在三角形内任取一点,则该点取自矩形内的最大概率为________.
解析:设AD =x ,AB =y ,则由三角形相似可得x a =
a -y
a
,解得y =a -x ,所以矩形的面
积S =xy =x (a -x )≤⎝ ⎛⎭⎪⎫x +a -x 22=a 24
,当且仅当x =a -x ,即x =a 2时,S 取得最大值a 2
4,所
以该点取自矩形内的最大概率为
a 2
41
2
×a ×a =12
. 答案:1
2
三、解答题
13.设关于x 的一元二次方程x 2
+2ax +b 2
=0.若a 是从区间[0,3]任取的一个数,b 是从区间[0,2]任取的一个数,求方程有实根的概率.
解:设事件A 为“方程x 2
+2ax +b 2
=0有实根”.当a ≥0,b ≥0时,方程x 2
+2ax +
b 2=0有实根的充要条件为a ≥b .试验的全部结果所构成的区域为{(a ,b )|0≤a ≤3,0≤b ≤2},构成事件A 的区域为{(a ,b )|0≤a ≤3,0≤b ≤2,a ≥b },
根据条件画出构成的区域,可得所求的概率为 P (A )=3×2-12×2
2
3×2=2
3
.
14.已知向量a =(-2,1),b =(x ,y ).
(1)若x ,y 分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足a ·b =-1的概率;
(2)若x ,y 在连续区间[1,6]上取值,求满足a ·b <0的概率.
解:(1)将一枚质地均匀的正方体骰子先后抛掷两次,所包含的基本事件总数为6×6=36(个).
由a ·b =-1有-2x +y =-1,所以满足a ·b =-1的基本事件为(1,1),(2,3),(3,5),共3个.
故满足a ·b =-1的概率为336=1
12
.
(2)若x ,y 在连续区间[1,6]上取值,则全部基本事件的结果为Ω={(x ,y )|1≤x ≤6,1≤y ≤6};满足a ·b <0的基本事件的结果为A ={(x ,
y )|1≤x ≤6,1≤y ≤6且-2x +y <0};画出图形如图,矩形的面积为S 矩形
=25,阴影部分的面积为S 阴影=25-1
2
×2×4=21,
故满足a ·b <0的概率为21
25.。
