Mathcad - 杆件计算
用Mathcad进行有限元法的理论验证与计算

第24卷 第1期2003年3月内蒙古农业大学学报Journal of Inner Mongolia Agricultural UniversityVol.24 No.1Mar.2003文章编号:1009-3575(2003)01-0090-04用Mathcad进行有限元法的理论验证与计算Ξ韩克平, 申向东(内蒙古农业大学水利与土木建筑工程学院,呼和浩特 010018)摘要: 本文分析了目前有限元法的理论验证与计算中存在的一些矛盾和问题,提出了用Mathcad来进行有限元法的理论验证与计算,并以实例具体说明。
关键词: 有限元法; Mathcad中图分类号: O342 文献标识码: ACON D UCTING THE THEORETICAL TEST AN D CALCU LATION OF FINITE E LEMENT METH OD B Y USING MATH CADHAN K e-ping, SHEN Xiang-dong(College of Water Conservancy and Civil Architecture Engineering,Inner Morgolia Agricultural University,Huhhot 010019) Abstract: This paper analyzes some contradictions and problems existing in the theoretical test and calculation of Finite Element Method.It also suggests conducting the theoretical test and calculation of finite Element Method by using Mathcad and to illustrate with examples.K ey w ords: Finite Element method; Mathcad有限元法(Finite Element Method,FEM)是现代工程科学的重要工具,其重要性仅次于数学,尤其在水利、机械、建筑等领域应用很广。
钢与混凝土组合梁mathcad计算书.
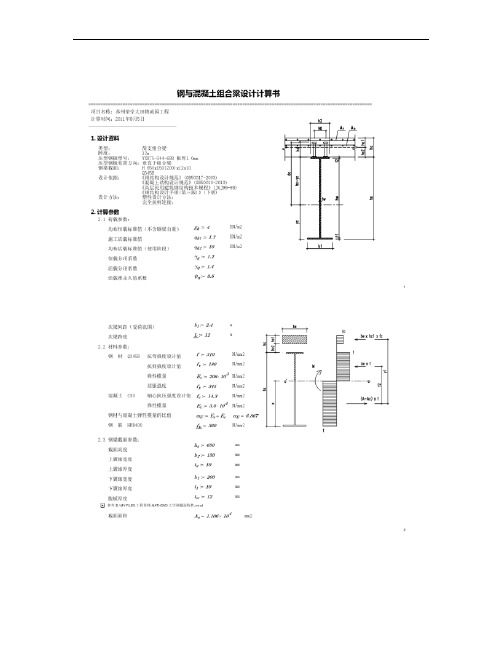
荷载标准组合下的挠度挠度最终计算值Δscl := 5( g1k + g2k + ψq ⋅ qk L ⋅ 10 384Bs ( 3 4 mm Δscl = 18.151 Δ L 10 3 mm mm Δ := Δc + max ( Δsc , Δscl = 56.605 = 1 211 结论:变形不满足验算要求 4.7 栓钉数量验算一个剪跨内的剪力计算需要的栓钉数量实际布置的栓钉数量 Vs := min ( As ⋅ f , be ⋅ hc1 ⋅ fc ⋅ 10 nf := Vs ÷ Nvc n := L ⋅ ns ÷ 0.344 −3 Vs = 2.119 × 10 nf = 43.095 n = 69.767 3 KN 个个结论:栓钉数量满足完全抗剪要求 4.8 局部稳定性验算(按《钢规范》11.1.6)钢梁的轴力按《钢规范》表9.1.4 允许宽厚比(翼缘)N := 0 Χb := 9 KN 235 fy 235 fy Χb = 7.272 Χh = 58.172 χb = 6.9 χh = 52.5 允许高厚比(腹板) 3 ⎛ N ⋅ 10 ⎞ Χh := ⎜72 − 100 ⎟⋅ As ⋅ f ⎠⎝设计实际的宽厚比(翼缘)χb := χh := b2 − tw 2t2 hw tw 设计实际的高厚比(腹板)结论:局部稳定满足要求 114.9 混凝土翼板内横向钢筋验算 b-b 界面的剪力设计值 Vlb := ns ⋅ Nvc ⋅ 10 ai 3 Vlb = 285.907 3 N/mm a-a 界面的剪力设计值 ns ⋅ Nvc ⋅ 10 ⋅ b11 Vla := ai ⋅ b e k1 := 0.9 k2 := 0.19 s := 1 Vla = 131.957 N/mm 抗剪承载力折减系数应力单位纵向受剪界面的周边长度 N/mm2 lsb := 120 × 2 + 109 lsa := hc1 lsb = 349 lsa = 76 Asvb = 0.67 Asva = 0.67 VBb = 482.94 VBa = 206.492 mm mm mm2/mm mm2/mm N/mmN/mm 与界面相交的横向钢筋面积 Asvb := Asva := 2Ab 1000 At + Ab 1000 纵向受剪截面的抗剪承载力 VBb := min ( k1 ⋅ s ⋅ lsb + 0.7Asvb ⋅ fy , k2 ⋅ lsb ⋅ fc VBa := min ( k1 ⋅ s ⋅ lsa + 0.7Asva ⋅ fy , k2 ⋅ lsa ⋅ fc 结论:验算满足要求 12。
MathCAD工程计算

工程计算的行业标准PTC Mathcad 是用于求解、分析和共享您最重要的工程计算的行业标准软件MathCAD综合概述Mathcad作为行业中功能最强大的工程计算资源,它可让工程师轻松执行、记录和共享计算与设计结果。
Mathcad 提供可识别单位的真实数学符号,并且具有强大的计算功能和开放的体系结构,可简化重要的设计流程,使公司能够加快产品上市速度和击败竞争对手。
Mathcad 之所以引人注目,是因为它不仅功能强大,而且还易于使用。
实际上,它是首个可让用户在一个工作表中同时对工程计算进行求解和记录的解决方案,能减少代价高昂和耗费时间解决的错误和重新设计问题,同时促进真正的工程协作。
Mathcad 并不要求用户具备专业的编程技能,因为它的界面直观易用,并以一种便于呈现的格式将真实的标准数学符号、文字和图形组合在一起。
利用该格式,可以捕捉知识、重复使用和验证设计方案,从而改善产品质量。
功能和优势∙易学易用- 基于任务的界面提高了可用性,并可让您快速轻松地学习不熟悉的功能或特征。
∙以文档为中心- 功能强大并以文档为中心的计算环境可让您快速轻松地以便于呈现和易于理解的格式创建复杂、专业的工程设计文档。
∙高级数学研究- 显示、处理、分析以及用图形表示数据,而且在整个应用程序中全面支持单位,这可让您创建计算以进行测试,然后再将计算加入到设计方案中。
∙在所有计算中均提供动态单位支持- 这可以减少错误和提高结果的准确性,并可在工程师和团队之间进行更明确的沟通,从而改善产品开发过程的效率。
关于PTC Mathcad Prime 3.0PTC Mathcad Prime 3.0 已经极大地提高了其计算功能,让您可以更快的解决复杂的问题。
PTC Mathcad内置了几百个数学函数,并使您能够不受限制地定义您自己的函数,提供以数字和符号形式求解方程的功能以及求解复杂方程组的功能,进而支持您的高级工程设计探索的要求。
最终,一个功能全面的工具应运而生,它让每个工程师都能将更多时间真正花在工程上- 无论此人是只需要记录设计参数的来源的普通用户,还是需要进行复杂的设计研究和权衡分析的高级用户。
钢结构计算书—杆件计算

四、杆件设计(1) 上弦杆整个上弦采用等截面,按FG,GH 杆件之最大设计内力设计。
862.77N KN = 上弦杆计算长度:在屋架平面内,为节间轴线长度:150.7ox l cm =在屋架平面外,根据支撑布置和内力变化情况,取:2150.7301.4oy l cm =⨯=由于l 0y =2 l 0x ,故截面宜选用两个不等肢角钢,短肢相并(图4)。
腹杆最大内力N=511.67KN ,查表9.6.4,节点板厚度选用12 mm ,支座节点板厚度用14 mm 。
截面在x 和y 平面皆属于b 类,则设λ=60,查附录4得ϕ=0.807。
需要截面积为: A s =3862.77100.807215N f ϕ⨯=⨯=4973 mm 2 需要的回转半径为:0150.7 2.51260xx l i λ=== cm 0301.45.02360y y l i λ=== cm 根据需要查角钢规格表,选用2∟140×90×12短肢相并,A=52.80 cm 2,i x =2.536 cm ,i y =6.89 cm ,按所选角钢进行验算:截面验算:0150.759.422.536x x x l cm i cmλ=== ∵b 1/t=140/12=11.67>0.56y l 0/ b 1=0.56×3014/140=12.06yz y λλ==43.74<[λ]=150截面在x 和y 平面皆属于b 类,由于λyz>λx 只需求y ϕ,。
查附表4-2,y ϕ=0.810,故3862.7710201.70.8105280y y N A σϕ⨯===⨯ N/mm 2<f =215 N/mm 2。
满足要求,所选截面合适。
图4 上弦杆截面(2) 下弦杆整个下弦采用同一截面,按最大内力所在的杆de 计算:852.57de N KN = cm l ox 300=1035oy l cm =(跨中有通长系杆)需要截面积为: A n =3852.5710215N f ⨯==3965 mm 2选用2∟140×90×10,因为l 0y >>l 0x ,故用不等肢角钢,短肢相并(图5)。
挂篮横向结构计算(用Mathcad 15计算)

1
2015-01-31
三、拉、压杆计算
挂篮横向桁架受力图
挂篮横向桁架轴力图
1、拉杆计算 8至19,31至32共计14个单元均使用普通槽钢10,经计算可知拉杆单元31,32受
力最大。31、32拉杆应力如下:
σ拉(F , A) := F A
F := 281226.59N
σ拉(F , A) = 224.742 MPa
挂篮横向桁架弯矩图
最弯矩出现在4,6号杆末端,应力计算如下:
σ(M , W) := M W
M := 66785.95N⋅m
σ(M , W) = 93.215⋅MPa 五、剪切应力计算
(满足)
W := 716471.01mm3
挂篮横向桁架剪力图 最大剪切出现在5,7号杆末端,应力计算如下:
I := 100305942mm4 S := 630757mm3 t := 14⋅2mm = 28⋅mm
三角挂篮结构计算
挂篮横断面结构计算
一、挂篮横断面设计图及断面参数
6500 1083 1083 1083 1083 1083 1083
3450
3450
挂篮横向桁架结构尺寸图
1000
3027
挂篮横向桁架杆件断面图、参数表 二、挂篮横断面受力简化
后上横梁外侧吊杆拉力为:20tonne 挂篮立柱在受压 1034352.44N ,将结构受 力简化如下:
2单元的压杆计算如下:
绕X轴计算长度为 6.5 m, 绕X轴长细比为 46.961, 绕X轴截面为c类截面 绕Y轴计算长度为 6.5 m, 绕Y轴长细比为 85.983, 绕Y轴截面为c类截面 按 GB 50017--2003 第132页注1 计算, 算得绕X轴受压稳定系数 φx = 0.794, 算得绕 Y轴受压稳定系数 φy = 0.541 强度验算:
简支钢梁稳定设计计算书(Mathcad)

平均弯矩 Mab := Ma + Mb Mab = 1.822 × 103
2 σab = 80.069 N/mm2
KN⋅m
τab := Vab⋅103 h01⋅tw1
τab = 50.558 N/mm2
因双轴对称截面梁的受压翼缘扭转受到约束 λb1 := h01 ⋅ fy λb1 = 0.643
tw1⋅177 235
1.1⋅ fv if λs1 > 1.2 λs12
集中力均为次梁传来, 且次梁处设加劲肋。
σcab := 0
⎛⎜ σab ⎞⎟2 + ⎛⎜ τab ⎞⎟2 + (0)2 = 0.205 ⎝ σcrab ⎠ ⎝ τcrab ⎠
≤ 1.0
满足要求
2)中间II区格bc段
剪力 Vbc := 945 KN
弯矩 Mb := 3645 Mc := 6480 平均弯矩
2⋅tf2
fy
端部截面 翼缘外伸肢
(b1 − tw1) = 9.042 < 11⋅ 235 = 9.079
2⋅tf1
fy
2加劲肋设计校核
80⋅ 235 = 66.026 fy
< h04 = 107.778 < tw4
170⋅ 235 = 140.305 受压翼缘扭转受约束
fy
150⋅ 235 = 123.799 受压翼缘扭转无约束
σbc := Mbc⋅106 ⋅ h02 I2 2
Mbc := Mb + Mc 2
Mbc = 5.063 × 103
σbc = 192.98 N/mm2
KN⋅m
τbc := Vbc⋅103 h02⋅tw2
τbc = 35.114 N/mm2
基于MathCAD的G-M法桥梁横向分布影响线计算
基于MathCAD的G-M法桥梁横向分布影响线计算
张玥
【期刊名称】《天津城市建设学院学报》
【年(卷),期】2008(014)001
【摘要】对于宽度与跨度之比(B/L)>0.5的宽桥,用G-M法进行横向分布计算,可得到较为精确的结果,但利用计算图表手工计算则较为繁琐.笔者尝试利用MathCAD软件,计算其横向分布影响线,并给出算例,可供桥梁工程技术人员及高校师生参考.
【总页数】3页(P31-33)
【作者】张玥
【作者单位】内蒙古科技大学,建筑与土木工程学院,内蒙古,包头,014010
【正文语种】中文
【中图分类】U441
【相关文献】
1.桥梁横向分布影响线的平面杆系有限元计算方法 [J], 王家林;彭凯;孙全胜
2.用铰接板法计算桥梁荷载横向分布影响线的程序算法 [J], 王中伟
3.利用MATHCAD计算公路桥梁荷载的横向分布系数 [J], 徐光铭;王磊;张婷
4.基于影响线法的铁路桥梁载荷计算 [J], 张保福;张学超;李烽;孟宪玖
5.用G-M法计算非均匀布置肋梁桥横向分布 [J], 蒋志刚;胡正怡
因版权原因,仅展示原文概要,查看原文内容请购买。
mathcad、结构力学求解器、SAP2000、Ansys等软件计算入门
按理说,荷载应按双向板分配在主梁和次梁上,但为了方便,此处只加在主梁上 所以计算结果对主梁是准确的 ,对于次梁是不准确的。
建模: 打开SAP2000 → 新建一个文件 单位选择 N,mm,C 点击轴网
建好所需要的轴网,确定 很多时候轴距都是不一样的,需要调整
→
坐标系统/轴网(D)
也可以选择空白的模板,然后在CAD 里将模型画好,另存为DXF文件导入。
结构力学求解器的介绍:
幕墙龙骨出现多跨、悬挑、弯折钢架等平面内的结构形式时候,公式无法解决, 可以用结构力学求解器求解: 如:
均布线荷载:
q := 3.5KN ⋅ m
−1
1
2 ( 0 , 3000)
3 ( 0 , 4000)
4 ( 0 , 6000)
点击
输入节点坐标
( 0 , 0)
生成四个点
点击
连接点为杆件
了解了每一个数字表达的意思 ,可直接在代码里修改。如单元荷载中第一个表示 杆件的标号,第二个表示荷载的类型,第三个表示荷载的大小。 求解内力:
→
可以得到弯矩图:
可得弯矩的最大值出现在节点 3 处。 若该杆件的抵抗矩为: 该杆件的应力为:
M := 7000000N ⋅ mm
3
Wxa := 80000mm σ := M Wxa
Mathcad的介绍:
Mathcad 其实是一个计算书写软件:
如要计算一个边长为a的正方形的面积: 首先要定义边长,定义的等号是通过“shift+ :”实现的,后面的单位“mm”手动输入 这种定义的等号通长是有一个 “:=”形式。(必须在英文注入法状太下)
a := 5mm a := 6mm
编辑面积的公式,相当于把A重新定义。注意公式中出现的字母都必须事先定义。 上面定义了两个a 公式选择离他最近的一个,即6mm。若并排,则选择最右
Mathcad - 四肢格构柱计算
四肢格构柱计算1 、计算依据《钢结构设计规范》GB50017---20032 、设计承载力轴心受压500kN3 、设计支柱柱高20m四肢缀条式格构柱材料:Q235分肢:圆管直径:351mm壁厚:10mm缀条:普槽10断面图及局部立面图如下:单位:毫米断面立面单个圆管截面特性:四个圆管截面特性:普槽10截面特性:4 、格构柱检算Q235钢材设计强度(厚度小于16mm ):f 215MPa :=f v 125MPa :=f y 235MPa :=4.1抗压强度检算轴心压力:净截面积:A n 42851mm 2:=σN A n , ()11.668MPa⋅=σN A n , ()f <抗压强度满足使用要求。
4.2稳定性检算(1)整个构件对对称轴的长细比:构件对主轴x 的计算长度:l 0x 20m :=构件截面对主轴x 的回转半径:i x 514.3419mm :=因截面为正方形:(2)对虚轴的换算长细比:构件截面中垂直于x 轴的各斜缀条毛截面积之和:A 1x 21251.3324⋅mm 2 2.503103×mm 2⋅=:=因截面为正方形:(3)分肢长细比计算分肢计算长度:l 分1m :=分肢钢管的回转半径:i 分120.6135mm:=分肢长细比:λ分0.7λ0x ⋅<满足规范5.1.4要求(4)稳定性校核构件换算长细比约为47,钢材屈服强度235MPa ,查表5.1.2-1得截面类型为b 类。
查附录C 轴心受压构件的稳定系数为:φ0.87:=13.412MPa f<四肢格构柱稳定性满足使用要求。
4.3 缀条验算轴心受压构件的计算剪力:剪力V 沿构件全长不变剪力由斜缀条分担,则斜缀条轴心受力为:斜缀条的水平夹角α45°:=缀条计算长度:缀条最小回转半径:i 14.2mm :=缀条长细比约为99.718,钢材屈服强度235MPa ,查表5.1.2-1得截面类型为b 类。
Mathcad在钢筋混凝土T形截面梁正截面配筋计算中应用
一类 T 形截面或第二类 T 形截面);
(2)针对不同条
件,
采用相应计算公式。
在以下 Mathcad 编程设计中,各符号含义及单
位如下:
M—— 弯 矩 设 计 值(N·mm);b—— 截 面 宽 度
(mm);h——截面高度(mm);b'f ——翼缘计算宽度
(mm);
h'f ——翼缘高度(mm);
面)
判断条件:
收稿日期:2020-12-28
基金项目:福建省中青年教师教育科研项目(科技类)
“Mathcad 在混凝土结构计算中应用研究”
(JAT191231)
作者简介:
郑元锋(1964—),
男,
福建莆田人,福建水利电力职业技术学院建筑工程系副教授,
硕士,研究方向:
建筑结构。
郑元锋:Mathcad 在钢筋混凝土 T 形截面梁正截面配筋计算中应用
3 使用编程程序注意事项
采用以上 Mathcad 编程程序,
计算钢筋混凝土 T
0.94,其间按线性内插法确定);ξ b ——相对界限受
形截面梁的纵向受力钢筋面积时,
应注意以下几点:
钢筋计算面积。
型、
混凝土等级及钢筋直径有关,
主要与钢筋布置排
压区高度;As ——受拉钢筋计算面积;A's ——受压
钢筋混凝土 T 形截面梁配筋计算的 Mathcad 编
[2] 中 华 人 民 共 和 国 国 家 标 准. 混 凝 土 结 构 设 计 规 范 :
[3]
类 T 形截面,
单筋截面梁,
求 As =?
)
度等级为 C30(f c =14.3 N/mm ,f t =1.43 N/mm ),钢
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
+
1
Lpf = 15.537
cm
Lpl := 50
cm
(一)、面板采用花纹钢板:
δm := 4.5
mm
(二)、纵梁选用[10,布置见下图:
(三)、中间横梁选用I22a
1、荷载计算
a、自重: 钢材重度: γg := 7.85
t
γz := 1.2
m3
面板
qmb := δm⋅10− 3⋅Lj⋅γg
qmb = 0.106
δ := 12 mm
焊缝高度:
hf := 0.8 cm
焊缝的强度设计值:
1、上弦杆端节点: N1 := −58
ft := 16000
t
m2
N1 = −58
t
焊缝面积: 焊缝长度: 2、下弦杆端节点:
Af1 :=
N1 ⋅104 ft
Lf1 :=
Af1 2 ⋅ hf ⋅ 0.7
+1
N3 := 31.3
Af1 = 36.25
M :=
R 4
⋅⎛⎜ ⎝
aL
−
LB ⎞⎟ 2⎠
M = 3.02
t⋅m
Q := R 2
Q = 28.76
t
M
8
σlz :=
M
π 32
⋅dB3
t
σr := 1.45⋅104
m2
σlz = 9.114 × 103
t m2
3、轴承板 容许应力
采用 容许剪应力
σlz < σr 满足要求
τ := 4 ⋅ Q
3
Nmax1 := Pe1
Nmax1 = 6.53
t
σ51 :=
Nmax1 A2⋅10− 4
t σ51 = 1.298 × 103 m2
Nmax2 := Pe2
Nmax2 = 20.8
t
由长细比λ查(JTJ283-99)规范附录B得稳定系数:
σ42 :=
Nmax2 Ψ⋅A2⋅10− 4
t σ42 = 5.506 × 103 m2
Lk := 0.3 m σ := R
dk⋅Lk
σ ≤ σψ 满足要求
σΦ := 2000 t m2
LB := Lk
dB :=
R LB⋅ σ Φ
dB := 0.15 m
Lk = 0.177
m
σ = 383.46
t
m2
LB = 0.3
m
dB = 0.096
m
轮轴承受的弯矩及剪力:
aL := 0.36 m
Iy2 := 2⋅934.5
rx2 :=
Ix2 A2
ry2 :=
Iy2 A2
Ll := 3.0⋅ 2
Lx2 := 0.8⋅Ll
Ly2 := Ll
λx2 :=
Lx2⋅102 rx2
λy2 :=
Ly2⋅102 ry2
四、杆件验算
材料:Q235B,其抗拉、抗压和抗弯强度设计值:
2
ry1 = 6.787
cm
λx1 = 28.289 λy1 = 44.202
A2 = 50.3
cm2
Ix2 = 1.302 × 103 cm4
Iy2 = 1.869 × 103 cm4
rx2 = 5.087
cm
ry2 = 6.096
cm
Ll = 4.243
m
Lx2 = 3.394
m
Ly2 = 4.243
m
λx2 = 66.72 λy2 = 69.601
Ψ := 0.878 σ1 < f 满足要求
σ2 < f 满足要求
Ψ := 0.791 σ3 < f 满足要求
σ41 < f 满足要求 Ψ := 0.751
σ42 < f 满足要求
σ51 < f 满足要求 Ψ := 0.751
σ42 < f 满足要求
3
五、节点连接焊缝计算
(一)、节点板厚度选用:
根据最大腹杆内力,按(JTJ283-99)规范9.5.8条采用: (二)、节点焊缝计算:
Lf5 :=
Af5 2 ⋅ hf ⋅ 0.7
+1
N5 = −45.3
t
Af5 = 28.313
cm2
Lf5 = 26.279
cm
4、斜杆节点:
N6 := Pd1
N6 = 37.58
t
焊缝面积: 焊缝长度: 5、竖杆节点:
Af6 :=
N6 ⋅104 ft
Lf6 :=
Af6 2 ⋅ hf ⋅ 0.7
+1
t/m
γg := 1.4
2、强度验算
Mg = 3.189
t⋅m
Mmax := Mz + Mg
Mmax = 3.713
t⋅m
5
3、挠度计算 (四)、端横梁选用2I22a
Wx := 309
cm3
σh :=
Mmax Wx⋅10− 6
σh < f 满足要求
q := qmb + qzl + qhl + 1.0⋅qgy
t/m
纵梁 横梁
qzl :=
10⋅5⋅Lj⋅10− 3 B
qhl := 33⋅10− 3
qzl = 0.033
t/m
qhl = 0.033
t/m
( ) Mz :=
γz⋅
qmb
+
qzl
+
qhl
⋅
B2 8
b、人群荷载 弯矩
Mz = 0.523
t⋅m
qgy := qr⋅Lj
Mg
:=
γg⋅qgy⋅
B2 8
qgy = 0.9
t
σd = 8.051 × 103
m2
t
1.05f = 2.257 × 104 m2 (镇定钢)
σd < 1.05f 满足要求
八、挠度计算 SP×Si×L/F数值详见附表。 由自重引起的挠度:
由人行荷载引起的挠度:
t
t
L = 36 qz := 0.3
m2
qr := 0.27 m2
f.z :=
5 ⋅ qz⋅L3 384 E⋅2⋅Ix1⋅10− 8
cm
ry1 :=
Iy1 A1
Lx1 := 3.0
m
Ly1 := 3.0
m
λx1 :=
Lx1⋅102 rx1
λy1 :=
Ly1⋅102 ry1
2、斜杆、竖杆(采用2[16)。
E := 2.06⋅107
t
m2
A2 := 2⋅25.15
Ix2 := 2⋅83.4 + 2⋅25.15⋅(6.5 − 1.75)2
f.z = 0.043
m
f.r :=
5 ⋅ qr⋅L3 384 E⋅2⋅Ix1⋅10− 8
f.r = 0.039
m
fmax := f.z + f.r
fmax = 0.082 m
6
frx :=
L 400
fmax < frx
满足要求
frx = 0.09 m
九、支座计算 (一)、支座最大反力 不均匀系数
Ld := 0.35 m Lq := 36 m
G := qz⋅B⋅Lq
G = 43.74
每个千斤顶承受的荷载:
不均匀系数
γ := 1.3
Pd := γ⋅G 4
Pd = 14.216
t
Md := Pd⋅Ld
Md = 4.975
t⋅m
Wx := 2Wx
Wx = 618
cm3
σd :=
Md Wx⋅10− 6
t
m2
A1 := 2⋅45.62
Ix1 := 2⋅5130.45 Iy1 := 2⋅242.144 + 2⋅45.62⋅(8.4 − 2.016)2
rx1 :=
Ix1 A1
1
t t t t
A1 = 91.24
cm2
Ix1 = 1.026 × 104
cm4
Iy1 = 4.203 × 103
cm4
rx1 = 10.605
Nmax1 = 37.58
t
σ41 :=
Nmax1 A2⋅10− 4
t σ41 = 7.471 × 103 m2
Nmax2 := Pd2
Nmax2 = 2.8
t
由长细比λ查(JTJ283-99)规范附录B得稳定系数:
σ42 :=
Nmax2 Ψ⋅A2⋅10− 4
5、竖杆
σ42 = 741.225
t
m2
3⋅τ
2 l
τl = 2.671 × 103
σl = 7.509 × 103
σlj = 8.82 × 103
t
2
9
lj
l
l
lj
m2
σr > σlj 满足要求
10
4
11
一、荷载计算 1、自重 2、活荷载
人群荷载
36×4.5×3米钢引桥计算
t
qz := 0.27
m2
t
qr := 0.3
m2
钢引桥结构尺度: 二、杆件内力计算
长 宽 高 节间距 节间数
L := 36 m B := 4.5 m H := 3 m Lj := 3 m nj := 12
a、上弦杆:
组合内力
Pa := −104.2
t f := 21500 m2
1、上弦杆
Nmax := Pa
Nmax = 104.2 t
