2016年秋季新版浙教版七年级数学上学期6.7、角的和差同步练习2

合集下载

6.7 角的和差同步测试(浙教版)-七年级数学上册同步测试(浙教版)

6.7角的和差同步测试【浙教版】参考答案与试题解析一．选择题1．（2020春•新泰市期末）如图，∠AOC和∠BOD都是直角，∠BOC＝60°，则∠AOD＝（）A．30°B．60°C．90°D．120°【思路点拨】根据同角的余角相等解答．【答案】解：∵∠AOC是直角，∴∠AOD+∠DOC＝90°，∵∠BOD是直角，∴∠BOC+∠DOC＝90°，∴∠AOD＝∠BOC＝60°，故选：B．【点睛】本题考查的是角的计算、余角的概念，掌握交的和差计算、余角的概念是解题的关键．2．（2020春•普陀区期末）如图，已知∠AOB：∠BOC＝2：3，∠AOC＝75°，那么∠AOB＝（）A．20°B．30°C．35°D．45°【思路点拨】由∠AOB：∠BOC＝2：3，可得∠AOB＝∠AOC进而求出答案，做出选择．【答案】解：∵∠AOB：∠BOC＝2：3，∠AOC＝75°，∴∠AOB＝∠AOC＝×75°＝30°，故选：B．【点睛】本题考查角的有关计算，按比例分配转化为∠AOB＝∠AOC是解答的关键．3．（2019秋•芜湖期末）若∠AOB＝60°，∠AOC＝40°，则∠BOC等于（）A．100°B．20°C．20°或100°D．40°【思路点拨】此题要分两种情况，一种是OC落在∠AOB内，OC落在∠AOB外，分别进行计算．【答案】解：∠BOC＝∠AOB+∠AOC＝60°+40°＝100°，∠BOC＝∠AOB﹣∠AOC＝60°﹣40°＝20°，故选：C．【点睛】此题考查了角的计算．解题的关键是在进行角的计算时，要能够考虑全面，不要漏解．4．（2019秋•朝阳区期末）α，β都是钝角，有四名同学分别计算（α+β），却得到了四个不同的结果，分别为26°，50°，72°，90°，老师判作业时发现其中有正确的结果，那么计算正确的结果是（）A．26°B．50°C．72°D．90°【思路点拨】根据钝角的取值范围，得到两个钝角和的取值范围，除以6后看所给的哪个角在这个范围内即可．【答案】解：∵α、β都是钝角，∴90°＜α＜180°，90°＜β＜180°，∴180°＜α+β＜360°，∴30°＜（α+β）＜60°，∴计算正确的结果是50°．故选：B．【点睛】本题考查了角的有关计算问题．解题的关键是求（α+β）的范围．5．（2019秋•武侯区期末）已知∠AOB＝60°，∠AOC＝∠AOB，射线OD平分∠BOC，则∠COD的度数为（）A．20°B．40°C．20°或30°D．20°或40°【思路点拨】分两种情况（OC在∠AOB内或外），分别首先求得∠BOC的度数，然后根据角平分线的定义求得∠COD的度数．【答案】解：当OC在∠AOB内时，如图1，则∠BOC＝∠AOB﹣∠AOC＝60°﹣，∴∠COD＝∠BOC＝20°；当OC在∠AOB外时，如图2，则∠BOC＝∠AOB+∠AOC＝60°+，∴∠COD＝∠BOC＝40°．综上，∠COD＝20°或40°．故选：D．【点睛】本题考查了角平分线的定义，角的和差，正确求得∠BOC的度数是关键，因考虑不周，容易漏掉一种情况的解．6．（2019秋•娄底期末）一个钝角减去一个锐角所得的差是（）A．直角B．锐角C．钝角D．以上三种都有可能【思路点拨】根据直角、锐角、钝角的定义解答即可．【答案】解：一个钝角减去一个锐角所得的差可能是直角、也可能是锐角或钝角．故选：D．【点睛】本题考查了直角、锐角、钝角．解题的关键是明确等于90°的角是直角，大于0°小于直角的角是锐角，大于直角小于平角的角是钝角．7．（2019秋•温岭市校级期末）如图，OA的方向是北偏东15°，OC的方向是北偏西40°，若∠AOC＝∠AOB，则OB的方向是（）A．北偏东70°B．东偏北25°C．北偏东50°D．东偏北15°【思路点拨】先根据角的和差得到∠AOC的度数，根据∠AOC＝∠AOB得到∠AOB的度数，再根据角的和差得到OB的方向．【答案】解：∵OA的方向是北偏东15°，OC的方向是北偏西40°，∴∠AOC＝15°+40°＝55°，∵∠AOC＝∠AOB，∴∠AOB＝55°，15°+55°＝70°，故OB的方向是北偏东70°．故选：A．【点睛】考查了方位角，方位角是表示方向的角；以正北，正南方向为基准，来描述物体所处的方向．利用角的和差得出OB与正北方的夹角是解题关键．8．（2019秋•安庆期末）在所给的：①15°、②65°、③75°、④135°、⑤145°的角中，可以用一副三角板画出来的是（）A．②④⑤B．①②④C．①③⑤D．①③④【思路点拨】用一副三角板能画出来的角有：15°，30°，45°，75°，90°，105°，135°，150°，180°．【答案】解：①45°﹣30°＝15°，可以用一副三角板画出来；②65°不可以用一副三角板画出来；③45°+30°＝75°，可以用一副三角板画出来；④90°+45°＝135°，可以用一副三角板画出来；⑤145°不可以用一副三角板画出来；故选：D．【点睛】本题考查了角的计算，熟记三角尺的角度，利用和、差关系求解是解答此题的关键．二．填空题9．如图，（1）∠AOC＝∠AOB+∠BOC＝∠AOD﹣∠COD；（2）∠AOD﹣∠AOB＝∠BOD＝∠BOC+∠COD；（3）∠BOC＝∠AOD﹣∠AOB﹣∠COD＝∠AOC﹣∠AOB＝∠BOD﹣∠COD．【思路点拨】根据角的定义和图示可求得角与角之间的关系．【答案】解：（1）∠AOC＝∠AOB+∠BOC＝∠AOD﹣∠COD（2）∠AOD﹣∠AOB＝∠BOD＝∠BOC+∠COD（3）∠BOC＝∠AOD﹣∠AOB﹣∠COD＝∠AOC﹣∠AOB＝∠BOD﹣∠COD【点睛】本题主要考查了角的和差关系．解题的关键是要读懂图，并找准角与角之间的位置和数量关系，用和差的形式表示出来．10．已知∠α＝12°18′，∠β＝22°42′，∠α+∠β＝45°；∠β﹣∠α＝10°24′．【思路点拨】根据角的单位的转换，直接运算可得答案．【答案】解：根据题意，∠α+∠β＝12°18′+22°42′＝35°，∠β﹣∠α＝22°42′﹣12°18′＝10°24′．故答案为35°、10°24″．【点睛】本题考查角的运算，注意度分秒的转换即可．11．（2020春•浦东新区期末）已知∠AOB＝40°，∠BOC＝3∠AOC，则∠AOC的度数是10°或20°．【思路点拨】求出∠AOC的度数，分为两种情况：①OC在∠AOB内部时，②OC在∠AOB外部时，求出即可．【答案】解：当OC在∠AOB内部时，如图1，∵∠AOB＝40°，∠BOC＝3∠AOC，∴∠AOC＝；当OC在∠AOB外部时，如图2，∵∠BOC﹣∠AOC＝∠AOB，∠AOB＝40°，∠BOC＝3∠AOC，∴3∠AOC﹣∠AOC＝40°，∴∠AOC＝20°．综上，∠AOC＝10°或20°．故答案为：10°或20°．【点睛】此题主要考查了角的计算，关键是注意此题分两种情况．12．（2019秋•抚州期末）射线OA，OB，OC，OD是同一平面内互不重合的四条射线，∠AOB＝60°，∠AOD＝40°，∠AOB＝3∠BOC，则∠COD的度数为40°或80°或120°．【思路点拨】分四种情况画图分别进行解答，即①OD在∠AOB的内部，OC在∠AOB的外部，②OD 在∠AOB的外部，OC在∠AOB的外部，③OD在∠AOB的外部，OC在∠AOB的内部，④OD在∠AOB 的内部，OC在∠AOB的内部．【答案】解：①当OD在∠AOB的内部，OC在∠AOB的外部，如图1所示；∵∠AOB＝60°，∠AOD＝40°，∠AOB＝3∠BOC，∴∠BOD＝∠AOB﹣∠AOD＝60°﹣40°＝20°，∠BOC＝∠AOB＝×60°＝20°，∴∠COD＝∠BOC+∠BOD＝20°+20°＝40°；②当OD在∠AOB的外部，OC在∠AOB的外部，如图2所示；∠COD＝∠DOA+∠AOB+∠BOC＝40°+60°+20°＝120°；③当OD在∠AOB的外部，OC在∠AOB的内部，如图3所示；∠COD＝∠AOD+∠AOC＝∠AOD+（∠AOB﹣∠BOC）＝40°+（60°﹣20°）＝80°；④当OD在∠AOB的内部，OC在∠AOB的内部时，OC与OD重合，不符合题意；所以，∠COD的度数为40°或80°或120°，故答案为：40°或80°或120°，【点睛】考查角的有关计算，通过题意分别画出不同情况的图形，利用各个角的和或差进行计算即可．13．（2019秋•天心区期末）如图，以O点为观测点，OA的方向是北偏东15°，OB的方向是北偏西40°，若∠AOC＝∠AOB，则OC的方向是北偏东70°．【思路点拨】先求出∠AOB＝55°，再求得OC的方位角，从而确定方位．【答案】解：∵OA的方向是北偏东15°，OB的方向是北偏西40°，∴∠AOB＝40°+15°＝55°，∵∠AOC＝∠AOB，∴∠AOC＝55°，∵15°+55°＝70°，∴OC的方向是北偏东70°．故答案为：北偏东70°．【点睛】主要考查了方位角．能够根据方位角的描述准确的找到所对应的角度是解题的关键．14．（2019秋•自贡期末）如图，长方形纸片ABCD，点E，F分别在边AB，CD上，连接EF，将∠BEF对折B落在直线EF上的点B′处，得折痕EM；将∠AEF对折，点A落在直线EF上的点A′得折痕EN，若∠BEM＝62°15′，则∠AEN＝27°45′．【思路点拨】根据折叠的性质即可求解．【答案】解：根据折叠可知：EM平分∠BEB′，∴∠B′EM＝∠BEM＝62°15′，∴∠AEA′＝180°﹣2×62°15′＝55°30′，EN平分∠AEA′，∴∠AEN＝∠A′EN＝AEA′＝55°15′＝27°45′，故答案为：27°45′．【点睛】本题考查了角的计算、度分秒的换算，解决本题的关键是准确进行度分秒的换算．三．解答题15．（2019秋•高台县期末）如图，直线AB，CD相交于点O，OA平分∠EOC．（1）若∠EOC＝70°，求∠BOD的度数；（2）若∠EOC：∠EOD＝2：3，求∠BOD的度数．【思路点拨】（1）根据角平分线定义得到∠AOC＝∠EOC＝×70°＝35°，然后根据对顶角相等得到∠BOD＝∠AOC＝35°；（2）先设∠EOC＝2x，∠EOD＝3x，根据平角的定义得2x+3x＝180°，解得x＝36°，则∠EOC＝2x＝72°，然后与（1）的计算方法一样．【答案】解：（1）∵OA平分∠EOC，∴∠AOC＝∠EOC＝×70°＝35°，∴∠BOD＝∠AOC＝35°；（2）设∠EOC＝2x，∠EOD＝3x，根据题意得2x+3x＝180°，解得x＝36°，∴∠EOC＝2x＝72°，∴∠AOC＝∠EOC＝×72°＝36°，∴∠BOD＝∠AOC＝36°．【点睛】考查了角的计算：1直角＝90°；1平角＝180°．也考查了角平分线的定义和对顶角的性质．16．（2019秋•铁锋区期末）如图，OA的方向是北偏东15°，OB的方向时被北偏西40°．（1）若∠AOC＝∠AOB，则OC的方向是北偏东70°；（2）OD是OB的反方向延长线，OD的方向是南偏东40°；（3）若∠BOE＝90°，请用方位角表示OE的方向是南偏西50°或北偏东50°；（4）在（1）（2）（3）的条件下，则∠COE＝160°或20°．【思路点拨】（1）先根据OB的方向是西偏北50°求出∠1的度数，进而求出∠FOC的度数即可；（2）根据OB的方向是西偏北50°求出∠DOH的度数，即可求出OD的方向；（3）分两种情况作答；（4）根据∠AOF＝15°，∠AOC＝55°，求出∠COG的度数，再根据∠COE＝∠EOH+∠HOG+∠COG 即可解答．【答案】解：（1）∵OB的方向是北偏西40°，OA的方向是北偏东15°，∴∠1＝40°，∴∠AOB＝∠1+15°＝55°，∵∠AOB＝∠AOC，∴∠AOC＝55°，∴OC的方向是北偏东70°；（2）∵OD是OB的反向延长线，∴∠1＝∠2＝40°，∴OD的方向是南偏东40°；（3）当OE在OB的逆时针方向时，OE的方向是南偏西50°；当OE在OB的顺时针方向时，OE的方向是北偏东50°．∴OE的方向是南偏西50°或北偏东50°；（4）∠COE＝90°+50°+20°＝160°．故答案为（1）北偏东70°；（2）南偏东40°；（3）南偏西50°或北偏东50°；（4）160°或20°．【点睛】本题主要考查了方向角的表达即方向角一般是指以观测者的位置为中心，将正北或正南方向作为起始方向旋转到目标的方向线所成的角（一般指锐角），通常表达成北（南）偏东（西）多少度，同时考查了互补互余的概念，难度适中．17．（2019秋•柯桥区期末）已知∠AOB是一个直角，作射线OC，再分别作∠AOC和∠BOC的平分线OD，OE．（1）如图①，当∠BOC＝40°时，求∠DOE的度数；（2）如图②，当射线OC在∠AOB内绕O点旋转时，∠DOE的大小是否发生变化，说明理由；（3）当射线OC在∠AOB外绕O点旋转且∠AOC为钝角时，画出图形，直接写出∠DOE的度数（不必写过程）．【思路点拨】（1）如图①，当∠BOC＝40°时，求∠DOE的度数；（2）如图②，当射线OC在∠AOB内绕O点旋转时，∠DOE的大小是否发生变化，说明理由；（3）当射线OC在∠AOB外绕O点旋转且∠AOC为钝角时，画出图形，直接写出相应的∠DOE的度数（不必写出过程）．【答案】解：（1）如图，∠AOC＝90°﹣∠BOC＝50°，∵OD、OE分别平分∠AOC和∠BOC，∴∠COD＝∠AOC＝25°，∠COE＝∠BOC＝20°，∴∠DOE＝∠COD+∠COE＝45°；（2）∠DOE的大小不变，理由是：∠DOE＝∠COD+∠COE＝∠AOC+∠COB＝（∠AOC+∠COB）＝∠AOB＝45°；（3）∠DOE的大小发生变化情况为，如图3，则∠DOE为45°；如图4，则∠DOE为135°，分两种情况：如图3所示，∵OD、OE分别平分∠AOC和∠BOC，∴∠COD＝∠AOC，∠COE＝∠BOC，∴∠DOE＝∠COD﹣∠COE＝（∠AOC﹣∠BOC）＝45°；如图4所示，∵OD、OE分别平分∠AOC和∠BOC，∴∠COD＝∠AOC，∠COE＝∠BOC，∴∠DOE＝∠COD+∠COE＝（∠AOC+∠BOC）＝×270°＝135°．【点睛】本题考查了角的计算，熟练掌握角平分线定义是解本题的关键．18．（2019秋•南宁期末）将一张长方形纸片按如图所示的方式折叠，EF为折痕，点A落在点G处，EH平分∠FEB（1）如图1，若EG与EH重合，求∠FEH的度数；（2）如图2，若∠FEG＝34°，求∠GEH的度数；（3）如图3，若∠FEG＝α（60°＜α＜90°），求∠GEH的度数（用α的式子表示）【思路点拨】（1）根据折叠的性质可得∠AEF＝∠FEH，再根据角平分线的性质以及平角的定义解答即可；（2）根据折叠的性质可得∠FEG＝34°，再根据角平分线的性质以及角的和差解答即可；（3）根据折叠的性质可得∠AEF＝∠FEG，用α的代数式分别表示出∠AEF和∠FEB，再根据角平分线的性质以及角的和差解答即可．【答案】解：（1）由折叠可知∠AEF＝∠FEH，∵EH平分∠FEB，∴∠FEH＝∠BEH，∴∠AEF＝∠FEH＝∠BEH，∵∠AEF+∠FEH+∠BEH＝180°，∴∠FEH＝60°；（2）由折叠可知∠AEF＝∠FEG，∵∠FEG＝34°，∴∠AEF＝34°，∠FEB＝180°﹣34°＝146°，∵EH平分∠FEB，∴，∴∠GEH＝∠FEH﹣∠FEG＝73°﹣34°＝39°；（3）由折叠可知∠AEF＝∠FEG，∵∠FEG＝α，∴∠AEF＝α，∠FEB＝180°﹣α，∵EH平分∠FEB，∴∴．【点睛】该题主要考查了翻折变换及其应用问题，灵活运用翻折变换的性质是解题的关键．19．（2019秋•兴国县期末）（1）如图（a），将一副三角尺（∠A＝60°，∠B＝45°）的直角顶点C叠放在一起，边CD与BE相交．①若∠DCE＝25°，则∠ACB＝155°；若∠ACB＝130°，则∠DCE＝50°；②猜想∠ACB与∠DCE的数量关系．直接写出答案，无需证明．（2）如图（b），若两个相同的三角尺60°锐角的顶点A重合在一起，边CD与AE相交，则∠DAB与∠CAE有何数量关系？请说明理由．【思路点拨】（1）①若∠DCE＝25°，根据90°计算∠ACE的度数，再利用和计算∠ACB的度数；若∠ACB＝130°，同理，反之计算可得结果；②先计算：∠ACB＝90°+∠BCD，再加上∠DCE可得结果；（2）先计算∠DAB＝60°+∠CAB，再加上∠CAE可得结果．【答案】解：（1）①若∠DCE＝25°，∵∠ACD＝90°，∠DCE＝25°，∴∠ACE＝90°﹣25°＝65°，∵∠BCE＝90°，∴∠ACB＝∠ACE+∠BCE＝65°+90°＝155°；若∠ACB＝130°，∵∠BCE＝90°，∴∠ACE＝130°﹣90°＝40°，∵∠ACD＝90°，∴∠DCE＝90°﹣40°＝50°，故答案为：155°；50°；②∠ACB+∠DCE＝180°，理由如下：∵∠ACB＝∠ACD+∠BCD，＝90°+∠BCD，∴∠ACB+∠DCE，＝90°+∠BCD+∠DCE，＝90°+∠BCE，＝180°；（2）∠DAB+∠CAE＝120°，理由如下：∵∠DAB＝∠DAC+∠CAB，＝60°+∠CAB，∴∠DAB+∠CAE，＝60°+∠CAB+∠CAE，＝60°+∠EAB，＝120°．【点睛】本题考查了余角和补角的定义，熟知如果两个角的和等于90°（直角），就说这两个角互为余角，注意角的和与差．20．（2019秋•崂山区期末）已知长方形纸片ABCD，点E在边AB上，点F、G在边CD上，连接EF、EG．将∠BEG对折，点B落在直线EG上的点B′处，得折痕EM；将∠AEF对折，点A落在直线EF上的点A′处，得折痕EN．（1）如图1，若点F与点G重合，求∠MEN的度数；（2）如图2，若点G在点F的右侧，且∠FEG＝30°，求∠MEN的度数；（3）若∠MEN＝α，请直接用含α的式子表示∠FEG的大小．【思路点拨】（1）根据角平分线的定义，平角的定义，角的和差定义计算即可．（2）根据∠MEN＝∠NEF+∠FEG+∠MEG，求出∠NEF+∠MEG即可解决问题．（3）分两种情形分别求解即可．【答案】解：（1）∵EN平分∠AEF，EM平分∠BEF∴∠NEF＝∠AEF，∠MEF＝∠BEF∴∠MEN＝∠NEF+∠MEF＝∠AEF+∠BEF＝（∠AEF+∠BEF）＝∠AEB∵∠AEB＝180°∴∠MEN＝×180°＝90°（2）∵EN平分∠AEF，EM平分∠BEG∴∠NEF＝∠AEF，∠MEG＝∠BEG∴∠NEF+∠MEG＝∠AEF+∠BEG＝（∠AEF+∠BEG）＝（∠AEB﹣∠FEG）∵∠AEB＝180°，∠FEG＝30°∴∠NEF+∠MEG＝（180°﹣30°）＝75°∴∠MEN＝∠NEF+∠FEG+∠MEG＝75°+30°＝105°（3）若点G在点F的右侧，∠FEG＝2α﹣180°，若点G在点F的左侧侧，∠FEG＝180°﹣2α．【点睛】本题考查角的计算，翻折变换，角平分线的定义，角的和差定义等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．21．（2020秋•南岗区校级月考）已知：∠AOB和∠COD是直角．（1）如图1，当射线OB在∠COD内部时，请探究∠AOD和∠BOC之间的关系；（2）如图2，当射线OA，射线OB都在∠COD外部时，过点O作射线OE，射线OF，满足∠BOE＝∠BOC，∠DOF＝∠AOD，求∠EOF的度数；（3）如图3，在（2）的条件下，在平面内是否存在射线OG，使得∠GOF：∠GOE＝2：3，若不存在，请说明理由，若存在，求出∠GOF的度数．【思路点拨】（1）根据已知条件，∠AOB和∠COD是直角，可得出∠BOD和∠AOC与∠BOC的关系式，再根据∠AOC与∠AOB和∠BOD列出等量关系，即可得出答案；（2）根据已知条件∠BOE＝∠BOC，可设∠BOE＝a，则∠BOC＝3a，再根据周角的关系可得到∠AOD 的等量关系，再根据∠DOF＝∠AOD，可得到∠AOF的等量关系式，由∠BOE、∠AOB和∠∠AOF可列出等量关系，即可得到答案；（3）分两种情况，①当射线OG在∠EOF内部时，由∠GOF：∠GOE＝2：3，可得出结果，当射线OG在∠EOF外部时，由∠GOF：∠GOE＝2：3，可得出结果．【答案】（1）∠AOD+∠BOC＝180°．证明：∵∠AOB和∠COD是直角，∴∠AOB＝∠COD＝90°，∵∠BOD+∠BOC＝∠COD，∴∠BOD＝90°﹣∠BOC，同理：∠AOC＝90°﹣∠BOC，∴∠AOD＝∠AOB+∠BOD＝90°+90°﹣∠BOC＝180°﹣∠BOC，∴∠AOD+∠BOC＝180°；（2）解：设∠BOE＝a，则∠BOC＝3a，∵∠BOE+∠EOC＝∠BOC，∴∠EOC＝∠BOC﹣∠BOE＝2a，∵∠AOD+∠COD+∠BOC+∠AOB＝360°，∴∠AOD＝360°﹣∠COD﹣∠BOC﹣∠AOB＝360°﹣90°﹣3a﹣90°＝180°﹣3a，∵∠DOF＝∠AOD，∴∠DOF＝（180°﹣3a）＝120°﹣2a，∴∠AOF＝∠AOD＝（180°﹣3a）＝60°﹣a，∴∠EOF＝∠BOE+∠AOB+∠AOF＝a+90°+60°﹣a＝150°，∠EOF的度数为150°；（3）①当射线OG在∠EOF内部时，∴∠GOF：∠GOE＝2：3，∴∠GOF＝（∠GOF+∠GOE）＝∠EOF＝150°＝60°；②当射线OG在∠EOF外部时，∵∠GOF：∠GOE＝2：3，∴∠GOF＝（∠GOF+∠GOE）＝∠EOF＝（∠DOF+∠COD+∠EOC）＝（120°﹣2a+90°+2a）＝84°．综上所述，∠GOF的度数是60°或84°．【点睛】本题主要考查角的计算，根据题意列出相应的等量关系是解决本题的关键．。

浙教版-数学-七年级上册-6.7 角的和差作业

角的和差一、基础过关1.下列关于角的说法正确的个数是( )①角是由两条射线组成的图形；②角的边越长,角越大；③在角一边延长线上取一点D；④角可以看作由一条射线绕着它的端点旋转而形成的图形。

A.1个B.2个C.3个D.4个2.下列4个图形中,能用∠1,∠AOB,∠O三种方法表示同一角的图形是( )3.已知∠1=36°45′,则∠1的余角是（）A.53°55′B.53°15′C.143°55D.63°15′4.如果一个角的补角是150°，则这个角的度数是（）A.30°B.60°C.90°D.120°5.任意一个锐角的补角比它的余角（）A.大90°B.大180°C.小90°D.小180°6.已知∠1和∠2互为余角，且∠2与∠3互补，∠1=65°，则∠3=（）A.65°B.25°C.115°D.1557.下列哪个角不能由一副三角板作出( )A.105ºB.15ºC.175ºD.135º二、综合训练1.23°45ˊ+24°15ˊ=_______；100°2ˊ33"-14°14ˊ53"=_______．2.若∠1 =50°，则它的余角是，它的补角是。

3.若∠α =110°，则它的补角是，它的补角的余角是。

4.如图，AOB是一条直线，∠AOD∶∠DOB＝3∶1，OD平分∠COB。

则∠DOC的度数为_____。

参考答案一、基础过关1.C2.B3.A4.A5.A6.D7.C二、综合训练1.47°60ˊ 85°47ˊ40"2.40°130°3.70°20°4.67.5°。

七年级数学上册 6.7 角的和差同步训练 (新版)浙教版

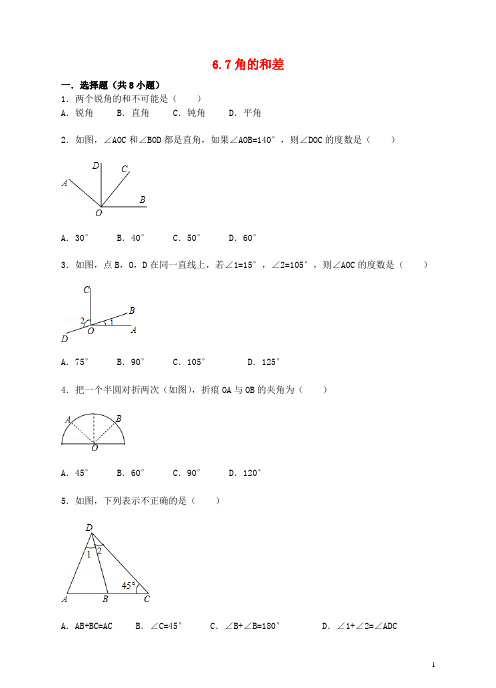
6.7角的和差一．选择题（共8小题）1．两个锐角的和不可能是（）A．锐角 B．直角 C．钝角 D．平角2．如图，∠AOC和∠BOD都是直角，如果∠AOB=140°，则∠DOC的度数是（）A．30° B．40° C．50° D．60°3．如图，点B，O，D在同一直线上，若∠1=15°，∠2=105°，则∠AOC的度数是（）A．75° B．90° C．105° D．125°4．把一个半圆对折两次（如图），折痕OA与OB的夹角为（）A．45° B．60° C．90° D．120°5．如图，下列表示不正确的是（）A．AB+BC=AC B．∠C=45° C．∠B+∠B=180°D．∠1+∠2=∠ADC6．如图，小明将自己用的一副三角板摆成如图形状，如果∠AOB=155°，那么∠COD等于（）A．15° B．25° C．35° D．45°7．已知∠AOB=70°，以O为端点作射线OC，使∠AOC=42°，则∠BOC的度数为（）A．28° B．112° C．28°或112° D．68°8．用一副三角板不可以拼出的角是（）A．105° B．75° C．85° D．15°二．填空题（共6小题）9．∠α+∠β=90°，且∠α=2∠β，则∠α=，∠β=．10．已知∠AOB=50°，∠BOC=30°，则∠AOC= ．11．如图，∠AOC和∠DOB都是直角，如果∠DOC=28°，那么∠AOB= ．12．如图，已知∠COB=2∠AOC，OD平分∠AOB，且∠COD=20°，则∠AOB的度数为．13．如图，将一副直角三角板叠在一起，使直角顶点重合于点O，则∠AOB+∠DOC= 度．14．如图，点O是直线AD上的点，∠AOB，∠BOC，∠COD三个角从小到大依次相差25°，则这三个角的度数是．三．解答题（共3小题）15．如图，已知OD平分∠AOB，射线OC在∠AOD内，∠BOC=2∠AOC，∠AOB=114°．求∠COD 的度数．16．已知在平面内，∠AOB=70°，∠BOC=40°，求∠AOC的度数．17．如图，OM是∠AOC的平分线，ON是∠BOC的平分线．（1）如图1，当∠AOB=90°，∠BOC=60°时，∠MON的度数是多少？为什么？（2）如图2，当∠AOB=70°，∠BOC=60°时，∠MON= （直接写出结果）．（3）如图3，当∠AOB=α，∠BOC=β时，猜想：∠MON= （直接写出结果）．6.7角的和差参考答案与试题解析一．选择题（共8小题）1．解：∵锐角一定大于0°，且小于90°，∴两个角的和不可能是平角．故选D．2．解：如右图所示，∵∠AOC=∠BOD=90°，∠AOB=140°，∴∠AOD=∠AOB﹣∠BOD=140°﹣90°=50°，∴∠DOC=∠AOC﹣∠AOD=90°﹣50°=40°．故选B．3．解：∵∠2=105°，∴∠BOC=180°﹣∠2=75°，∴∠AOC=∠1+∠BOC=15°+75°=90°．故选：B．4．解：把一个半圆对折两次后展开（如图），∠AOD=∠DOC=∠COE=∠EOB=45°；∠AOC=∠DOE=∠COB=90°；故选：C．5．解：A、看图可知AB+BC=AC；B、∠1+∠2=∠ADC，∠C可能等于45°；C、不正确，写法不规范，应该是∠ABD+∠CBD=180°D、看图可知，∠1+∠2=∠ADC．故选C．6．解：∵三角板的两个直角都等于90°，所以∠BOD+∠AOC=180°，∵∠BOD+∠AOC=∠AOB+∠COD，∵∠AOB=155°，∴∠COD等于25°．故选B．8．解：已知一副三角板各角的度数是30度，60度，45度，90度，可以拼出的度数就是用30度，60度，45度，90度相加减，45°+60°=105°，30°+45°=75°，45°﹣30°=15°，显然得不到85°．故选：C．二．填空题（共6小题）9．解：∵∠α+∠β=90°，且∠α=2∠β，∴，解得∠α=60°，∠β=30°，故答案为60°、30°．10．解：当OC在∠AOB内部，因为∠AOB=50°，∠BOC=30°，所以∠AOC为20°；当OC在∠AOB外部，因为∠AOB=50°，∠BOC=30°，所以∠AOC为80°；故∠AOC为20°或80°．11．解：∵∠AOC=∠DOB=90°，∠DOC=28°，∴∠AOB=∠AOC+∠DOB﹣∠DOC，=90°+90°﹣28°，=152°．故答案为：152°12．解：∵∠COB=2∠AOC，OD平分∠AOB，且∠COD=20°，∴设∠COB=2∠AOC=2x，∠AOD=∠BOD=1.5x，∴∠COD=0.5x=20°，∴x=40°，∴∠AOB的度数为：3×40°=120°．故答案为：120°．13．解：如右图所示，∵∠AOD+∠COD=90°，∠COD+∠BOC=90°，∠BOD=∠COD+∠BOC，∠AOD+∠BOD=∠AOB，∴∠AOD+∠COD+∠COD+∠BOC=180°，∴∠AOD+2∠COD+∠BOC=180°，∴∠AOB+∠COD=180°．故答案是180．14．解：设∠AOB=x，∠BOC=x+25°，∠COD=x+50°，∵∠AOB+∠BOC+∠COD=180°，∴3x+75°=180°，x=35°，∴这三个角的度数是35°，60°，85°，故答案为35°，60°，85°．三．解答题（共3小题）15．解：∵OD平分∠AOB，∠AOB=114°，∴∠AOD=∠BOD==57°．∵∠BOC=2∠AOC，∠AOB=114°，∴∠AOC=．∴∠COD=∠AOD﹣∠AOC=57°﹣38°=19°．16．解：分两种情况考虑：（1）当∠BOC在∠AOB外部时，∠AOC=∠AOB+∠BOC═70°+40°=110°；（2）当∠BOC在∠AOB内部时，∠AOC=∠AOB﹣∠BOC═70°﹣40°=30°，则∠AOC的度数为110°或30°．17．解：（1）如图1，∵∠AOB=90°，∠BOC=60°，∴∠AOC=90°+60°=150°，∵OM平分∠AOC，ON平分∠BOC，∴∠MOC=∠AOC=75°，∠NOC=∠BO C=30°∴∠MON=∠MOC﹣∠NOC=45°．（2）如图2，∵∠AOB=70°，∠BOC=60°，∴∠AOC=70°+60°=130°，∵OM平分∠AOC，ON平分∠BOC，∴∠MOC=∠AOC=65°，∠NOC=∠BOC=30°∴∠MON=∠MOC﹣∠NOC=65°﹣30°=35°．故答案为：35°．。

浙教版七年级数学上册同步练习(PDF版)-6.5-6.7 角与角的度量、角的大小比较及角的和差

6.5-6.7 角与角的度量、角的大小比较及角的和差一、选择题（共15小题；共75分）1. 下列四个角中，最有可能与70∘角互补的是 ( )A. B.C. D.2. 已知∠α=35∘，则∠α的补角的度数是 ( )A. 55∘B. 65∘C. 145∘D. 165∘3. 如图，OA是北偏东30∘方向的一条射线，若射线OB与射线OA垂直，则OB的方位角是 ( )A. 北偏西30∘B. 北偏西60∘C. 东偏北30∘D. 东偏北60∘4. 已知∠α=35∘，则∠α的余角的度数是 ( )A. 55∘B. 45∘C. 145∘D. 135∘5. 已知：如图所示，直线AB、CD相交于O，OD平分∠BOE，∠AOC=42∘，则∠AOE的度数为 ( )A. 126∘B. 96∘C. 102∘D. 138∘6. 在直线AB上任取一点O，过点O作射线OC,OD，使OC⊥OD，当∠AOC=30∘时，∠BOD的度数是 ( )A. 60∘B. 120∘C. 60∘或90∘D. 60∘或120∘7. 如图，某轮船在O处，测得灯塔A在它北偏东40∘的方向上，渔船B在它的东南方向上，则∠AOB的度数是 ( )A. 85∘B. 90∘C. 95∘D. 100∘8. 在∠AOB的内部任取一点C，作射线OC，则一定存在 ( )A. ∠AOB>∠AOCB. ∠AOB<∠BOCC. ∠BOC>∠AOCD. ∠AOC>∠BOC9. ∠α=39∘22ʹ，则∠α的补角为 ( )A. 39∘22ʹB. 139∘22ʹC. 140∘38ʹD. 50∘38ʹ10. 钟表 1 点 20 分时，时针与分针所成的角是 ( )A. 150度B. 80度C. 120度D. 90度11. 如果∠α和∠β互补，且∠α>∠β，则下列表示∠β的余角的式子中：① 90∘−∠β；② ∠α−90∘；③ 12(∠α+∠β)；④ 12(∠α−∠β)．正确的有 ( )A. 4个B. 3个C. 2个D. 1个12. 一个角的补角是它的余角的3倍，则这个角的度数是 ( )A. 30∘B. 45∘C. 60∘D. 75∘13. 如图，已知∠AOB=40∘，∠AOC=90∘，OD平分∠BOC，则∠AOD的度数是 ( )A. 20∘B. 25∘C. 30∘D. 35∘14. 足球射门，不考虑其他因素，仅考虑射点到球门AB的张角大小时，张角越大，射门越好．如图的正方形网格中，点A，B，C，D，E均在格点上，球员带球沿CD方向进攻，最好的射点在( )A. 点CB. 点D或点EC. 线段DE（异于端点）上一点D. 线段CD（异于端点）上一点15. 若∠1，∠2互为补角，且∠1>∠2，则∠2的余角是 ( )A. 12(∠1+∠2) B. ∠1−90∘ C. 12∠1−∠2 D. 12(∠2−∠1)二、填空题（共15小题；共75分）16. 若∠α=39∘21ʹ，则∠α的补角为．17. 如图，A，O，B在一直线上，∠AOC=∠BOC，若∠1=∠2，则图中互余的角共有对．18. 40.5∘=40∘ʹ19. 计算：50∘−15∘30ʹ=．，则这个角为．20. 一个角的补角与它的余角的4倍的和等于周角的171821. 画一个∠AOB，使∠AOB=30∘，再作OC⊥OA，OD⊥OB，则∠COD的度数是．22. 如图所示，在锐角∠AOB内部，画1条射线，可得3个锐角；画2条不同射线，可得6个锐角；画3条不同射线，可得10个锐角；⋯．照此规律，画6条不同射线，可得锐角个．23. 一副三角板按如图所示方式重叠，若图中∠DCE=35∘25ʹ，则∠ACB=．24. 如图所示，OM，ON分别是∠BOC和∠AOC的平分线，∠AOB=84∘．① ∠MON=度；② 当OC在∠AOB内绕点O转动时，∠MON的值改变．（填“会”或“不会”）25. 一个角的补角比它的余角的2倍大40度，则这个角的度数为度．26. 如图，已知∠EOC是平角，OD平分∠BOC，在平面上画射线OA，使∠AOC和∠COD互余，若∠BOC=50∘，则∠AOB是．27. 如图，在∠AOB内以点O为端点的射线有n条，则图中共有个角．28. 计算：0.3∘=ʹ，900ʹ=∘，75∘15ʹ36ʹ=∘．29. 在平角∠AOB的内部引n条射线．（1）当n=1时，图中共有个小于平角的角．（2）当n=2时，图中共有个小于平角的角．（3）当n=3时，图中共有个小于平角的角．（4）当n=k时，图中共有个小于平角的角．30. 已知∠AOB=α，∠BOC=β，（α>β），且OD，OE分别为∠AOB，∠BOC的角平分线，则∠DOE的度数为或（结果用α，β的代数式表示）．三、解答题（共5小题；共65分）31. 已知一个角的补角等于这个角的余角的4倍，求这个角的度数．32. 如图，O在直线AC上，OD是∠AOB的平分线，OE在∠BOC内．Ⅰ若OE是∠BOC的平分线，则有OD⊥OE，试说明理由；∠EOC，∠DOE=72∘，求∠EOC的度数．Ⅱ若∠BOE=1233. 如图，有A、B、C、P四个点，根据以下要求画图（保留画图痕迹）Ⅰ（1）画直线AB；（2）画线段BC；（3）画射线AP；Ⅱ若点B在点A正东方向，那么点P在点A的方向；Ⅲ在射线AP上取线段AD，使AD=AB+BC（尺规作图）；Ⅳ在平面上确定一点O，使AO+BO+CO+DO长度最短，这是根据原理．34. 如图，直线AB与CD相交于点O，OP是∠BOC的平分线，OE⊥AB，OF⊥CD．Ⅰ如果∠AOD=40∘，那么根据，可得∠BOC=度．Ⅱ图中除直角外，还有相等的角吗?请写出三对：（i）；（ii）；（iii）．Ⅲ求∠POF的度数．35. 如图1，已知∠AOB=150∘，∠AOC=40∘，OE是∠AOB内部的一条射线，且OF平分∠AOE．Ⅰ若∠EOB=10∘，则∠COF=；Ⅱ若∠COF=20∘，则∠EOB=；Ⅲ若∠COF=n∘，则∠EOB= ---（用含n的式子表示）．Ⅳ当射线OE绕点O逆时针旋转到如图2的位置时，请把图补充完整；此时，∠COF与∠EOB 有怎样的数量关系?请说明理由．答案第一部分1. D2. C3. B4. A5. B6. D7. C8. A9. C 10. B11. B 12. B 13. B 14. C 15. B第二部分16. 140∘39ʹ．17. 418. 3019. 34∘30ʹ20. 40∘21. 30∘或150∘22. 2823. 144∘35ʹ24. 42；不会25. 4026. 115∘或15∘27. (n+1)(n+2)228. 18；0.25；75.2629. （1）2；（2）5；（3）9；（4）k(k+3)230. 12α−12β或12α+12β第三部分31. 设这个角为x，则它的补角为(180∘−x)，余角为(90∘−x)．由题意得180∘−x=4(90∘−x)．解得x=60∘．答：这个角的度数为60∘．32. （1）∵OD、OE分别是∠AOB和∠BOC的平分线，∴∠DOB=12∠AOB，∠BOE=12∠BOC，∴∠DOB+∠BOE=12(∠AOB+∠BOC)=90∘，∴OD⊥OE．（2）设∠BOE=x．∵∠BOE=12∠EOC，∴∠EOC=2x．∵∠DOE=72∘，∴∠DOB=12∠AOB=72−x，∴2(72−x)+x+2x=180，解得x=36∘．∴∠EOC=72∘．33. （1）（2）南偏东30∘（3）AD即为所求．（4）连接AC，BD交点即为O．是根据两点之间线段最短原理．34. （1）对顶角相等；40（2）（i）∠AOD=∠BOC；（ii）∠COP=∠BOP；（iii）∠EOC=∠BOF （3）因为OP是∠BOC的平分线，∠BOC=20∘．所以∠COP=12因为∠DOF+∠BOF+∠COP+∠BOP=180∘，∠DOF=90∘，∠COP=20∘，所以∠BOF+∠BOP=180∘−90∘−20∘=70∘．故∠POF=∠BOF+∠BOP=70∘．35. （1）30∘（2）30∘（3）70∘−2n∘（4）画图∠EOB=70∘+2∠COF（仅写出结论，没写理由得1分）设∠COF=n∘，则∠AOF=∠AOC−∠COF=40∘−n∘．又OF平分∠AOE，所以∠AOE=2∠AOF=80∘−2n∘．所以∠EOB=∠AOB−∠AOE=150∘−(80∘−2n∘)=(70+2n)∘即∠EOB=70∘+2∠COF．。

七年级数学上册第六章图形的初步知识 6.7 角的和差同步练习 (新版)浙教版

6．7 角的和差知识点一角的和差的意义一般地，如果一个角的度数是另两个角的度数的和，那么这个角就叫做另两个角的和；如果一个角的度数是另两个角的度数的差，那么这个角就叫做另两个角的差．1．根据图6－7－1填空：图6－7－1(1)∠AOB ＝∠AOC ＋________；(2)∠COB ＝∠COD －________＝________－________；(3)∠AOB ＋∠COD －∠AOD ＝________.知识点二角平分线的定义从一个角的顶点引出的一条______，把这个角分成__________的角，这条射线叫做这个角的________．如图6－7－2，OC 是∠AOB 的平分线，则∠AOC ＝∠BOC ＝12∠AOB ，∠AOB ＝∠AOC ＋∠BOC ＝2∠AOC ＝2∠BOC .图6－7－2图6－7－32．如图6－7－3，下列式子中不能表示“OC 是∠AOB 的平分线”的是( )A ．∠AOC ＝∠BOCB ．∠AOC ＝12∠AOB C ．∠AOB ＝2∠BOC D ．∠AOC ＋∠BOC ＝∠AOB类型一与角平分线有关的计算例1 教材例2针对训练已知：如图6－7－4所示，OC是∠AOD的平分线，OE是∠BOD 的平分线．(1)若∠AOB＝140°，求∠COE的度数；(2)在(1)的条件下，如果∠COD＝20°，求∠BOE的度数．图6－7－4【归纳总结】与角平分线有关的计算的“三点注意”：(1)要灵活应用角平分线的三种表达方式，不要一味地想到“等”，还要想到“倍”或“分”；(2)注意转化，即用已知代替未知，将未知转化为已知；(3)灵活运用整体方法，不要着眼于局部．类型二角度计算中的分类讨论例2 教材补充例题已知∠AOB＝40°，过点O作射线OC(不同于OA，OB)，满足∠AOC＝35∠BOC，求∠AOC的度数．【归纳总结】本题结合了分类讨论思想和方程思想，当角与角之间的数量关系较多时，可以通过设未知数，理清数量之间的关系，然后建立方程求解．, 小结◆◆◆)反思◆◆◆)你能说出用同一副三角尺能画出多少个小于平角的角吗？你能将画出的这些角进行分类吗？详解详析【学知识】知识点一1．[答案] (1)∠BOC(2)∠BOD ∠AOB ∠AOC(3)∠BOC知识点二射线两个相等平分线2．[解析]D A 项，∵∠AOC ＝∠BOC，∴OC 平分∠AOB，即OC 是∠AOB 的平分线，正确，故不符合题意．B 项，∵∠AOC ＝12∠AOB ，∴∠AOB ＝2∠AOC＝∠AOC＋∠BOC，∴∠AOC ＝∠BOC，∴OC 平分∠AOB，即OC 是∠AOB 的平分线，正确，故不符合题意． C 项，∵∠AOB ＝2∠BOC＝∠AOC＋∠BOC，∴∠AOC ＝∠BOC，∴OC 平分∠AOB，即OC 是∠AOB 的平分线，正确，故不符合题意．D 项，∵∠AOC ＋∠BOC＝∠AOB，∴假如∠AOC＝30°，∠BOC ＝40°，∠AOB ＝70°，符合上式，但OC 不是∠AOB 的平分线，故符合题意．故选D .【筑方法】例1 解：(1)∠COE＝∠COD＋∠DOE＝12∠AOD ＋12∠BOD ＝12(∠AOD＋∠BOD)＝12∠AOB ＝70°.(2)由(1)知∠COE＝70°，因为∠COD＝20°，所以∠DOE＝50°.又因为OE 是∠BOD 的平分线，所以∠BOE＝∠DOE＝50°.例2 [解析] 由于原题没有图，故射线OC 既可以在∠AOB 的内部也可以在∠AOB 的外部．解：如图①，当射线OC 在∠AOB 的内部时，设∠BOC＝x °，则∠AOC ＝⎝ ⎛⎭⎪⎫35x °，x ＋35x ＝40，解得x ＝25，35x ＝15，所以∠AOC＝15°.如图②，当OC 在∠AOB 的外部时，设∠BOC＝x °，则∠AOC＝⎝ ⎛⎭⎪⎫35x °，x －35x ＝40, 解得x ＝100，35x ＝60，所以∠AOC ＝60°. 综上所述，∠AOC 的度数为15°或60°.【勤反思】[反思] 由一副三角尺能画出11个角，分别是15°，30°，45°，60°，75°，90°，105°，120°，135°，150°，165°.这11个角中，锐角有5个：15°，30°，45°，60°，75°；直角有1个：90°；钝角有5个：105°，120°，135°，150°，165°. 欢迎您的下载，资料仅供参考！。

浙教版初中数学七年级上册《6.7 角的和差》同步练习卷

浙教新版七年级上学期《6.7 角的和差》同步练习卷一．选择题（共27小题）1．如图，OB是∠AOC内部的一条射线，把三角尺的角的顶点放在点O处，转动三角尺，当三角尺的边OD平分∠AOB时，三角尺的另一边OE也正好平分∠BOC，则∠AOC的度数为（）A．100°B．110°C．120°D．130°2．如图，点O在直线AB上，OC平分∠AOD，若∠COD＝∠BOD，则∠COB 的度数为（）A．115°B．105°C．95°D．85°3．借助常用的直角三角尺，能画出一些度数的角，下列选项中不能画出的角是（）A．15°B．100°C．165°D．135°4．用一副三角板可以画出的最大锐角的度数是（）A．85°B．75°C．60°D．45°5．已知∠AOB＝70°，以O端点作射线OC，使∠AOC＝28°，则∠BOC的度数为（）A．42°B．98°C．42°或98°D．82°6．如图，点O在直线AB上，OD是∠AOC的平分线，OE是∠COB的平分线．若∠DOC＝70°，则∠BOE的度数是（）A．30°B．40°C．25°D．20°7．如图，O是直线AB上一点，OD平分∠BOC，∠COE＝90°，若∠AOC＝40°，则∠DOE为（）A．15°B．20°C．30°D．45°8．在同一平面内，若∠BOA＝50.3°，∠BOC＝10°30′，则∠AOC的度数是（）A．60.6°B．40°C．60.8°或39.8D．60.6°或40°9．如图，∠AOC＝∠BOD＝80°，如果∠AOD＝140°，那么∠BOC等于（）A．20°B．30°C．50°D．40°10．如图，已知点M是直线AB上一点，∠AMC＝52°48′，∠BMD＝72°19′，则∠CMD等于（）A．49°07′B．54°53′C．55°53′D．53°7′11．如图，已知∠BOC＝2∠AOB，OD平分∠AOC，∠BOD＝14°，则∠AOB 的度数为（）A．14°B．28°C．32°D．40°12．用一副三角板可以画出一些指定的角，下列各角中，不能用一副三角板画出的是（）A．15°B．75°C．85°D．105°13．把两块三角板按如图所示那样拼在一起，则∠ABC等于（）A．70°B．90°C．105°D．120°14．把一副三角板按照如图所示的位置摆放，则形成两个角，设分别为∠α、∠β，若已知∠α＝65°，则∠β＝（）A．15°B．25°C．35°D．45°15．如图，点C、O、B在同一条直线上，∠AOB＝90°，∠AOE＝∠DOB，则下列结论：①∠EOD＝90°；②∠COE＝∠AOD；③∠COE＝∠DOB；④∠COE+∠BOD＝90°．其中正确的个数是（）A．1B．2C．3D．416．如图，∠AOC和∠DOB都是直角，如果∠AOB＝150°，那么∠DOC＝（）A．30°B．40°C．50°D．60°17．已知两角之比为2：1，且这两角之和为直角，则这两个角的大小分别为（）A．70°，22°B．60°，30°C．50°，40°D．55°，35°18．如图，点B，O，D在同一直线上，若∠DOC＝105°，则∠BOC的度数是（）A．75°B．90°C．105°D．125°19．在同一平面内，∠AOB＝70°，∠BOC＝40°，则∠AOC的度数为（）A．110°B．30°C．110°或150°D．30°或110°20．如图，点O在直线AB上，射线OC、OD在直线AB的同侧，∠AOD＝40°，∠BOC＝50°，OM、ON分别平分∠BOC和∠AOD，则∠MON的度数为（）A．135°B．140°C．152°D．45°21．如图，∠AOB＝30°，OB平分∠AOC，OC平分∠BOD，OD平分∠COE，则∠COE＝（）A．30°B．45°C．60°D．90°22．把一副三角板按如图所示那样拼在一起，那么∠ABC的度数是（）A．150°B．135°C．120°D．105°23．如图，是一副特制的三角板，用它们可以画出一些特殊角．在54°、60°、63°、72°、99°、120°、144°、150°、153°、171°的角中，能画出的角有（）A．7个B．8个C．9个D．10个24．如图，将一副三角板叠放在一起，使直角的顶点重合于O，则∠AOC+∠DOB ＝（）A．90°B．120°C．160°D．180°25．如图，OC是∠AOB的平分线，OD是∠AOC的平分线，且∠COD＝25°，则∠AOB等于（）A．50°B．75°C．100°D．120°26．如图，将长方形纸片ABCD的角C沿着GF折叠（点F在BC上，不与B，C重合），使点C落在长方形内部点E处，若FH平分∠BFE，则∠GFH的度数α是（）A．90°＜α＜180°B．0°＜α＜90°C．α＝90°D．α随折痕GF位置的变化而变化27．α，β都是钝角，甲、乙、丙、丁计算，（α+β）的结果依次为50°，26°，72°，90°，其中有正确的结果，则计算正确的是（）A．甲B．乙C．丙D．丁二．填空题（共6小题）28．如图，若∠3：∠2＝2：5，且∠2﹣∠1＝12°，∠3等于．29．将一张长方形纸片按如图所示的方式折叠，BD、BE为折痕，若∠ABE＝34°，则∠DBC为度．30．已知∠AOB＝80°，∠BOC＝50°，OD是∠AOB的角平分线，OE是∠BOC 的角平分线，则∠DOE＝．31．将一副三角板如图摆放，若∠BAE＝135°17′，则∠CAD的度数是．32．如图所示，点C，O，D在同一条直线上，∠AOC＝40°，∠BOD＝50°，OM，ON分别是∠AOC，∠BOD的平分线，则∠MON＝．33．如图，直线AB、CD相交于点O，∠DOE＝∠BOE，OF平分∠AOD，若∠BOE＝28°，则∠EOF的度数为．三．解答题（共17小题）34．如图，∠AOB＝120°，点C为∠AOB内部一点，OD平分∠BOC，OE平分∠AOD（1）如果∠AOC＝30°，依题意补全图形；（2）在（1）的条件下，求∠EOC的度数；（3）如果∠AOC＝α（0°＜α＜120°），直接用含α的代数式表示∠EOC的度数．35．如图OC是∠AOB内部的一条射线，∠BOC＝2∠AOC，OD平分∠AOC．（1）若∠AOB＝120°，求∠BOC和∠BOD的度数；（2）画出∠BOC的平分线OE，说明∠DOE＝∠AOB．36．如图1所示：已知，∠AOB＝90°，∠BOC＝30°，OM平分∠AOC，ON 平分∠BOC．（1）∠MON═；（2）如图2，∠AOB＝90°，∠BOC＝x°，仍然分别作∠AOC、∠BOC的平分线OM、ON，能否求出∠MON的度数若能，求出其值；若不能，说明理由．（3）如图3，若∠AOB＝α，∠BOC＝β（α、β均为锐角，且α＞β），仍然分别作∠AOC、∠BOC的平分线OM、ON，能否求出∠MON的度数．若能，求∠MON的度数．（4）从（1）、（2）、（3）的结果中，你发现了什么规律？37．如图1，O为直线AB上一点，过点O作射线OC，∠AOC＝30°，将一直角三角板的直角顶点放在点O处，一边ON在射线OA上，另一边OM与OC 都在直线AB的上方．现将图25﹣1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周．（1）如图2，若经过t秒后，线段OM恰好平分∠BOC，此时∠COM＝°；∠AON＝°；t＝秒；（2）在（1）的条件下，线段ON是否平分∠AOC？请说明理由；（3）如图3，若三角板在转动的同时，射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周，那么经过多长时间OC平分∠MON？38．如图，已知∠AOB＝90°，∠EOF＝60°，OE平分∠AOB，OF平分∠BOC，求∠COB和∠AOC的度数．39．如图，已知∠AOB＝90°，射线OC绕点O从OA位置开始，以每秒4°的速度顺时针方向旋转；同时，射线OD绕点O从OB位置开始，以每秒1°的速度逆时针方向旋转．当OC与OA成180°时，OC与OD同时停止旋转．（1）当OC旋转10秒时，∠COD＝°．（2）当OC与OD的夹角是30°时，求旋转的时间．（3）当OB平分∠COD时，求旋转的时间．40．如图所示，已知∠AOB＝90°，∠BOC＝30°，OM平分∠AOC，ON平分∠BOC；（1）求∠MON；（2）∠AOB＝α，∠BOC＝β，求∠MON的度数．41．如图，已知∠AOC＝60°，∠BOD＝90°，∠AOB是∠DOC的3倍，求∠AOB的度数．42．如图，直线AB，CD相交于点O，OA平分∠EOC．（1）若∠EOC＝70°，求∠BOD的度数；（2）若∠EOC：∠EOD＝2：3，求∠BOD的度数．43．如图，已知∠BOC＝2∠AOC，OD平分∠AOB，且∠AOC＝40°，求∠COD 的度数．44．已知∠AOB＝54°，从O点引出一条射线OC，∠BOC＝14°．求∠AOC的度数．45．已知O为直线AB上的一点，∠COE是直角，OF平分∠AOE．（1）如图1，若∠COF＝34°，则∠BOE＝；若∠COF＝m°，则∠BOE＝；∠BOE与∠COF的数量关系为．（2）当射线OE绕点O逆时针旋转到如图2的位置时，（1）中∠BOE与∠COF 的数量关系是否仍然成立？请说明理由．46．已知：如图，∠AOB是直角，∠AOC＝40°，ON是∠AOC的平分线，OM 是∠BOC的平分线．（1）求∠MON的大小；（2）当锐角∠AOC的大小发生改变时，∠MON的大小是否发生改变？为什么？47．如图，O为直线DA上的一个点，∠AOB＝130°，OE是∠AOB的平分线，∠COB＝90°，求∠AOC和∠COE的度数．48．下列各小题中，都有OE平分∠AOC，OF平分∠BOC．（1）如图①，若点A、O、B在一条直线上，∠EOF＝；（2）如图②，若点A、O、B不在一条直线上，∠AOB＝140°，则∠EOF＝；（3）由以上两个问题发现：当∠AOC在∠BOC的外部时，∠EOF与∠AOB的数量关系是∠EOF＝；（4）如图③，若OA在∠BOC的内部，∠AOB和∠EOF还存在上述的数量关系吗；请简单说明理由；49．已知点O在直线AB上，OD平分∠AOC，OE平分∠BOC．（1）若OC⊥AB于点O，如图1，直接写出∠DOE的度数为；OD与OE 的位置关系是；（2）若OC与AB不垂直，如图2，其它条件不变，（1）中的结论还成立吗？若成立，请说明你的猜想是正确的；若不成立，请说明理由；（3）如图2，若∠AOD＝40°，请你利用（2）中得到的结论，求∠BOE的度数．50．如图，已知OE平分∠AOC，OF平分∠BOC（1）若∠AOB是直角，∠BOC＝60°，求∠EOF的度数．（2）若∠AOC＝x°，∠EOF＝y°，∠BOC＝60°，请用x的代数式来表示y．（直接写出结果就行）．浙教新版七年级上学期《6.7 角的和差》同步练习卷参考答案与试题解析一．选择题（共27小题）1．如图，OB是∠AOC内部的一条射线，把三角尺的角的顶点放在点O处，转动三角尺，当三角尺的边OD平分∠AOB时，三角尺的另一边OE也正好平分∠BOC，则∠AOC的度数为（）A．100°B．110°C．120°D．130°【分析】根据角平分线的定义得到∠BOD＝∠AOB，∠BOE＝∠BOC，则∠EOD＝∠AOB+∠BOC＝∠AOC，然后把∠EOD＝60°代入计算即可．【解答】解：∵OD边平分∠AOB，OE平分∠BOC，∴∠BOD＝∠AOB，∠BOE＝∠BOC，∴∠EOD＝∠AOB+∠BOC＝∠AOC，∵∠EOD＝60°，∴∠AOC＝2×60°＝120°．故选：C．【点评】本题考查了角的计算：1°＝60′，1′＝60″．关键是根据角平分线的定义解答．2．如图，点O在直线AB上，OC平分∠AOD，若∠COD＝∠BOD，则∠COB 的度数为（）【分析】根据角平分线的定义得到∠AOC＝∠COD，根据平角的定义列方程即可得到结论．【解答】解：∵OC平分∠AOD，∴∠AOC＝∠COD，∵∠COD＝∠BOD，∴∠AOC＝∠COD＝∠BOD，∵∠AOC+∠COD+∠BOD＝180°，∴∠BOD+∠BOD+∠BOD＝180°，∴∠BOD＝30°，∠COD＝75°，∴∠COB＝∠COD+∠BOD＝105°，故选：B．【点评】本题考查了角的计算，角平分线的定义，平角的定义，求得∠BOD＝30°是解题的关键．3．借助常用的直角三角尺，能画出一些度数的角，下列选项中不能画出的角是（）A．15°B．100°C．165°D．135°【分析】先分清一副三角尺，各个角的度数分别为多少，然后将各个角相加或相减即可得出答案．【解答】解：A、利用45°和30°的角可以画出15°的角，故本选项错误；B、＝，不合题意，即借助常用的直角三角尺，能画出一些度数的角，不能画出100度的角，故本选项正确；C、利用90°、45°和30°组合即可画出165°的角，故本选项错误；D、利用90°和45°组合即可画出165°的角，故本选项错误；故选：B．【点评】此题主要考查了用三角板直接画特殊角，关键掌握用三角板画出的角的规律：都是15°的倍数．4．用一副三角板可以画出的最大锐角的度数是（）【分析】根据三角板原有的30°、45°、60°、90°四种角，依据可以直接画出的角和利用和或差画出的角，即可得到结论．【解答】解：用一副三角板可以画出：30°、45°、60°、75°、15°，五个锐角，其中最大的锐角为75°．故选：B．【点评】本题主要考查了角的计算，按照直接画出和通过角的求和或求差作出的角即可得出所有情况．5．已知∠AOB＝70°，以O端点作射线OC，使∠AOC＝28°，则∠BOC的度数为（）A．42°B．98°C．42°或98°D．82°【分析】根据题意画出图形，利用分类讨论思想求解即可．【解答】解：如图，当点C与点C1重合时，∠BOC＝∠AOB﹣∠AOC＝70°﹣28°＝42°；当点C与点C2重合时，∠BOC＝∠AOB+∠AOC＝70°+28°＝98°．故选：C．【点评】本题考查的是角的计算，在解答此题时要注意进行分类讨论，不要漏解．6．如图，点O在直线AB上，OD是∠AOC的平分线，OE是∠COB的平分线．若∠DOC＝70°，则∠BOE的度数是（）A．30°B．40°C．25°D．20°【分析】根据角平分线的定义求出∠AOC，根据邻补角的定义求出∠BOC，根据角平分线的定义计算即可．【解答】解：∵OD是∠AOC的平分线，∴∠AOC＝2∠COD＝140°，∴∠BOC＝180°﹣∠AOC＝40°，∵OE是∠COB的平分线，∴∠BOE＝∠BOC＝20°，故选：D．【点评】本题考查的是角平分线的定义、角的计算，掌握角平分线的定义、结合图形正确进行角的计算是解题的关键．7．如图，O是直线AB上一点，OD平分∠BOC，∠COE＝90°，若∠AOC＝40°，则∠DOE为（）A．15°B．20°C．30°D．45°【分析】先根据平角的定义求出∠BOC＝140°，再由OD平分∠BOC，根据角平分线的定义求出∠COD＝∠BOC＝70°，即可求出∠DOE＝20°．【解答】解：∵∠AOC＝40°，∴∠BOC＝180°﹣∠AOC＝140°，∵OD平分∠BOC，∴∠COD＝∠BOC＝70°，∵∠COE＝90°，∴∠DOE＝90°﹣70°＝20°．故选：B．【点评】本题考查了角平分线的定义；弄清各个角之间的数量关系是解决问题的关键．8．在同一平面内，若∠BOA＝50.3°，∠BOC＝10°30′，则∠AOC的度数是（）A．60.6°B．40°C．60.8°或39.8D．60.6°或40°【分析】分OC在∠AOB内部和∠AOB外部两种情况分别求解可得．【解答】解：∠AOC＝∠BOA+∠BOC＝50.3°+10°30′＝50.3°+10.5°＝60.8°或∠AOC＝∠BOA﹣∠BOC＝50.3°﹣10°30′＝50.3°﹣10.5°＝39.8°，故选：C．【点评】本题主要考查角的计算，解题的关键是掌握分类讨论思想的运用和角度的转换．9．如图，∠AOC＝∠BOD＝80°，如果∠AOD＝140°，那么∠BOC等于（）A．20°B．30°C．50°D．40°【分析】先求出∠COD的度数，然后根据∠BOC＝∠BOD﹣∠COD，即可得出答案．【解答】解：∵∠AOC＝80°，∠AOD＝140°，∴∠COD＝∠AOD﹣∠AOC＝60°，∵∠BOD＝80°，∴∠BOC＝∠BOD﹣∠COD＝80°﹣60°＝20°．故选：A．【点评】本题主要考查了角的计算能力，熟练掌握角相互间的和差关系是基础．10．如图，已知点M是直线AB上一点，∠AMC＝52°48′，∠BMD＝72°19′，则∠CMD等于（）A．49°07′B．54°53′C．55°53′D．53°7′【分析】根据∠AMC＝52°48′，∠BMD＝72°19′和∠CMD＝180°﹣∠AMC ﹣∠BMD，代入计算即可．【解答】解：∵∠AMC＝52°48′，∠BMD＝72°19′，∴∠CMD＝180°﹣∠AMC﹣∠BMD＝180°﹣52°48′﹣72°19′＝54°53′；故选：B．【点评】此题考查了角的计算，掌握平角的定义是本题的关键，是一道基础题．11．如图，已知∠BOC＝2∠AOB，OD平分∠AOC，∠BOD＝14°，则∠AOB 的度数为（）A．14°B．28°C．32°D．40°【分析】根据∠BOC＝2∠AOB，OD平分∠AOC，∠BOD＝14°，可以得到∠AOB与∠AOD的关系，从而与∠BOD建立关系，得到∠AOB的度数．【解答】解：∵已知∠BOC＝2∠AOB，OD平分∠AOC，∴∠AOC＝3∠AOB＝2∠AOD，∴∠AOD＝1.5∠AOB，∴∠AOD﹣∠AOB＝0.5∠AOB＝∠BOD＝14°，∴∠AOB＝28°，故选：B．【点评】本题考查角的计算、角平分线的定义，解题的关键是找出各个角之间的关系，与已知条件建立关系．12．用一副三角板可以画出一些指定的角，下列各角中，不能用一副三角板画出的是（）A．15°B．75°C．85°D．105°【分析】一副三角板中的度数有：90°、60°、45°、30°；用三角板画出角，无非是用角度加减法，根据选项一一分析，排除错误答案．【解答】解：A、15°的角，45°﹣30°＝15°；B、75°的角，45°+30°＝75°；C、85°的角，不能直接利用三角板画出；D、105°的角，45°+60°＝105°．故选：C．【点评】此题考查的知识点是角的计算，关键是用三角板直接画特殊角的步骤：先画一条射线，再把三角板所画角的一边与射线重合，顶点与射线端点重合，最后沿另一边画一条射线，标出角的度数．13．把两块三角板按如图所示那样拼在一起，则∠ABC等于（）A．70°B．90°C．105°D．120°【分析】∠ABC等于30度角与直角的和，据此即可计算得到．【解答】解：∠ABC＝30°+90°＝120°．故选：D．【点评】本题考查了角度的计算，理解三角板的角的度数是关键．14．把一副三角板按照如图所示的位置摆放，则形成两个角，设分别为∠α、∠β，若已知∠α＝65°，则∠β＝（）A．15°B．25°C．35°D．45°【分析】按照如图所示的位置摆放，利用∠α、∠β和直角正好在一条直线上，用平角减去直角再减去65°即可得出答案．【解答】解：如图所示，一副三角板按照如图所示的位置摆放，则∠α+∠β+90°＝180°，即∠β＝180°﹣90°﹣65°＝25°．故选：B．【点评】此题主要考查学生对角的计算的理解和掌握，解答此题的关键是利用∠α、∠β和直角正好在一条直线上，难度不大，是一道基础题．15．如图，点C、O、B在同一条直线上，∠AOB＝90°，∠AOE＝∠DOB，则下列结论：①∠EOD＝90°；②∠COE＝∠AOD；③∠COE＝∠DOB；④∠COE+∠BOD＝90°．其中正确的个数是（）A．1B．2C．3D．4【分析】结合图形，根据平角的定义、余角的性质和等量代换可以进行判断，注意运用角的和差的运算．【解答】解：∵∠AOB＝90°∴∠AOD+∠BOD＝90°∵∠AOE＝∠DOB∴∠AOE+∠AOD＝90°，即∠EOD＝90°∴∠COE＝∠AOD，∠COE+∠BOD＝90°∴①②④正确．故选：C．【点评】解题时注意运用余角的性质：同角的余角相等．16．如图，∠AOC和∠DOB都是直角，如果∠AOB＝150°，那么∠DOC＝（）A．30°B．40°C．50°D．60°【分析】根据图象∠AOB等于两个直角的和减去∠COD计算．【解答】解：∠DOC＝90°+90°﹣∠AOB＝180°﹣150°＝30°．故选A．【点评】本题注意，∠COD是两个直角重叠的部分．17．已知两角之比为2：1，且这两角之和为直角，则这两个角的大小分别为（）A．70°，22°B．60°，30°C．50°，40°D．55°，35°【分析】由两角之比是2：1，即可设这两个角分别为：2x°，x°，又由两角之和为直角，即可得方程：2x+x＝90，解此方程即可求得答案．【解答】解：设这两个角分别为：2x°，x°，根据题意得：2x+x＝90，解得：x＝30．则这两个角分别为：60°，30°．故选：B．【点评】此题考查了角的计算．解题时注意掌握方程思想的应用．18．如图，点B，O，D在同一直线上，若∠DOC＝105°，则∠BOC的度数是（）A．75°B．90°C．105°D．125°【分析】根据邻补角的定义解答即可．【解答】解：∵点B，O，D在同一直线上，∠DOC＝105°，∴∠BOC＝180°﹣105°＝75°，故选：A．【点评】本题考查的角的计算，解题的关键是邻补角的定义．19．在同一平面内，∠AOB＝70°，∠BOC＝40°，则∠AOC的度数为（）A．110°B．30°C．110°或150°D．30°或110°【分析】分OC在∠AOB内和OC在∠AOB外两种情况考虑，依此画出图形，根据角与角之间结合∠AOB、∠BOC的度数，即可求出∠AOC的度数．【解答】解：当OC在∠AOB内时，如图1所示．∵∠AOB＝70°，∠BOC＝40°，∴∠AOC＝∠AOB﹣∠BOC＝30°；当OC在∠AOB外时，如图2所示．∵∠AOB＝70°，∠BOC＝40°，∴∠AOC＝∠AOB+∠BOC＝110°．故选：D．【点评】本题考查了角的计算，分OC在∠AOB内和OC在∠AOB外两种情况考虑是解题的关键．20．如图，点O在直线AB上，射线OC、OD在直线AB的同侧，∠AOD＝40°，∠BOC＝50°，OM、ON分别平分∠BOC和∠AOD，则∠MON的度数为（）A．135°B．140°C．152°D．45°【分析】根据题意可求出∠COD＝90°，再根据角平分线的性质即可求出∠MON 的度数．【解答】解：易知：∠COD＝180°﹣∠AOD﹣∠BOC＝90°，∵OM、ON分别平分∠BOC和∠AOD，∴∠NOD＝∠AOD＝20°，∠COM＝∠BOC＝25°，∴∠MON＝20°+25°+90°＝135°故选：A．【点评】本题考查角度计算，涉及角平分线的性质，解题的关键是求出∠COD的度数，本题属于基础题型．21．如图，∠AOB＝30°，OB平分∠AOC，OC平分∠BOD，OD平分∠COE，则∠COE＝（）A．30°B．45°C．60°D．90°【分析】直接利用角平分线的性质分别得出∠BOC，∠COD，∠EOD的度数，进而得出答案．【解答】解：∵∠AOB＝30°，OB平分∠AOC，∴∠AOB＝∠BOC＝30°，∵OC平分∠BOD，∴∠DOC＝∠BOC＝30°，∵OD平分∠COE，∴∠DOE＝∠COD＝30°，∴∠COE＝2∠COD＝60°．故选：C．【点评】此题主要考查了角的计算以及角平分线的性质，正确得出∠COD的度数是解题关键．22．把一副三角板按如图所示那样拼在一起，那么∠ABC的度数是（）A．150°B．135°C．120°D．105°【分析】∠ABC等于30度角与直角的和，据此即可计算得到．【解答】解：∠ABC＝30°+90°＝120°，故选：C．【点评】本题考查了角度的计算，理解三角板的角的度数是关键．23．如图，是一副特制的三角板，用它们可以画出一些特殊角．在54°、60°、63°、72°、99°、120°、144°、150°、153°、171°的角中，能画出的角有（）A．7个B．8个C．9个D．10个【分析】一副三角板中的度数，用三角板画出角，无非是用角度加减法，逐一分析即可．【解答】解：54°＝90°﹣36°，则54°角能画出；60°不能写成36°、72°和45°、90°的和或差的形式，不能画出；63°＝90°﹣72°+45°，则63°可以画出；72°可以利用三角板的72°角直接画出；99°＝90°+45°﹣36°，则99°角能画出；120°不能写成36°、72°和45°、90°的和或差的形式，不能画出；144°＝72°+72°，则144°角能画出；150°不能写成36°、72°和45°、90°的和或差的形式，不能画出；153°＝72°+72°+45°﹣36°，则153°可以画出；171°＝90°+36°+45°，则171°可以画出．总之，能画出的角有7个．故选：A．【点评】此题考查的知识点是角的计算，关键是用三角板直接画特殊角的步骤：先画一条射线，再把三角板所画角的一边与射线重合，顶点与射线端点重合，最后沿另一边画一条射线，标出角的度数．24．如图，将一副三角板叠放在一起，使直角的顶点重合于O，则∠AOC+∠DOB ＝（）A．90°B．120°C．160°D．180°【分析】因为本题中∠AOC始终在变化，因此可以采用“设而不求”的解题技巧进行求解．【解答】解：设∠AOD＝a，∠AOC＝90°+a，∠BOD＝90°﹣a，所以∠AOC+∠BOD＝90°+a+90°﹣a＝180°．故选：D．【点评】本题考查了角度的计算问题，在本题中要注意∠AOC始终在变化，因此可以采用“设而不求”的解题技巧进行求解．25．如图，OC是∠AOB的平分线，OD是∠AOC的平分线，且∠COD＝25°，则∠AOB等于（）A．50°B．75°C．100°D．120°【分析】根据角的平分线定义得出∠AOD＝∠COD，∠AOB＝2∠AOC＝2∠BOC，求出∠AOD、∠AOC的度数，即可求出答案．【解答】解：∵OC是∠AOB的平分线，OD是∠AOC的平分线，∠COD＝25°，∴∠AOD＝∠COD＝25°，∠AOB＝2∠AOC，∴∠AOB＝2∠AOC＝2（∠AOD+∠COD）＝2×（25°+25°）＝100°，故选：C．【点评】本题考查了对角平分线定义和角的计算等知识点的应用，主要考查学生运用角平分线定义进行推理的能力和计算能力，题目较好，难度不大．26．如图，将长方形纸片ABCD的角C沿着GF折叠（点F在BC上，不与B，C重合），使点C落在长方形内部点E处，若FH平分∠BFE，则∠GFH的度数α是（）A．90°＜α＜180°B．0°＜α＜90°C．α＝90°D．α随折痕GF位置的变化而变化【分析】根据折叠的性质可以得到△GCF≌△GEF，即∠CFG＝∠EFG，再根据FH平分∠BFE即可求解．【解答】解：∵∠CFG＝∠EFG且FH平分∠BFE．∠GFH＝∠EFG+∠EFH∴∠GFH＝∠EFG+∠EFH＝∠EFC+∠EFB＝（∠EFC+∠EFB）＝×180°＝90°．故选：C．【点评】本题主要考查了折叠的性质，注意在折叠的过程中存在的相等关系．27．α，β都是钝角，甲、乙、丙、丁计算，（α+β）的结果依次为50°，26°，72°，90°，其中有正确的结果，则计算正确的是（）A．甲B．乙C．丙D．丁【分析】本题是对钝角定义的考查，求解时可根据定义求得结果．【解答】解：∵α，β都是钝角，所以大于90°，小于180°，∴180°＜（α+β）＜360°，∴30°＜（α+β）＜60°，则只有50°符合要求．故选：A．【点评】本题是钝角的定义的考查，利用不等式的性质求解．二．填空题（共6小题）28．如图，若∠3：∠2＝2：5，且∠2﹣∠1＝12°，∠3等于32°．【分析】根据比例可设∠3＝2x，∠2＝5x，利用方程和平角解答即可．【解答】解：∵∠3：∠2＝2：5，设∠3＝2x，∠2＝5x，∵∠1+∠2+∠3＝180°，∠2﹣∠1＝12°，可得：5x﹣12°+5x+2x＝180°，解得：x＝16，所以∠3＝2×16°＝32°，故答案为：32°【点评】本题考查角度计算，解题的关键是熟练利用平角的定义和方程解答．29．将一张长方形纸片按如图所示的方式折叠，BD、BE为折痕，若∠ABE＝34°，则∠DBC为56度．【分析】根据翻折的性质可知，∠ABE＝∠A′BE，∠DBC＝∠DBC′，再根据平角的度数是180°，∠ABE＝34°，继而即可求出答案．【解答】解：根据翻折的性质可知，∠ABE＝∠A′BE，∠DBC＝∠DBC′，又∵∠ABE+∠A′BE+∠DBC+∠DBC′＝180°，∴∠ABE+∠DBC＝90°，又∵∠ABE＝34°，∴∠DBC＝56°．故答案为：56【点评】此题考查了角的计算，根据翻折变换的性质，得出三角形折叠以后的图形和原图形全等，对应的角相等，得出∠ABE＝∠A′BE，∠DBC＝∠DBC′是解题的关键．30．已知∠AOB＝80°，∠BOC＝50°，OD是∠AOB的角平分线，OE是∠BOC 的角平分线，则∠DOE＝65°或15°．【分析】需要分类讨论：射线OC在∠AOB的内部和射线OC在∠AOB的外部两种情况．由题意可得∠BOD＝×80°＝40°，∠EOB＝×50°＝25°，则由∠DOE、∠BOD与∠EOB的关系可求得∠DOE的度数．【解答】解：∵∠AOB＝80°，∠BOC＝50°，且OD，OE分别为∠AOB，∠BOC的角平分线，∴∠BOD＝∠AOB＝40°，∠EOB＝∠BOC＝25°，①当OC在∠AOB内时，如图1，∴∠DOE＝∠DOB﹣∠EOB＝40°﹣25°＝15°．②当OC在∠AOB外时，如图2，∠DOE＝∠DOB+∠EOB＝40°+25°＝65°．综上所述，∠DOE的度数为65°或15°．故答案是：65°或15°．【点评】本题考查了角的计算以及角平分线线的定义的运用．解题时注意结合图形求得角与角间的和差关系：∠DOE＝∠BOD﹣∠EOB或∠DOE＝∠BOD+∠EOB．31．将一副三角板如图摆放，若∠BAE＝135°17′，则∠CAD的度数是44°43′．【分析】利用三角形的各角度数和图中角与角的关系计算．【解答】解：∠BAE＝∠BAD+∠CAE﹣∠CAD则∠CAD＝∠BAD+∠CAE﹣∠BAE＝90+90﹣∠BAE＝44°43′．故填44°43′．【点评】对∠BAE＝∠BAD+∠CAE﹣∠CAD这一关系的认识是解题的关键．32．如图所示，点C，O，D在同一条直线上，∠AOC＝40°，∠BOD＝50°，OM，ON分别是∠AOC，∠BOD的平分线，则∠MON＝135°．【分析】根据角平分线的定义得到∠MOA＝∠AOC＝20°，∠NOB＝∠BOD ＝25°，结合图形计算即可．【解答】解：∵∠AOC＝40°，∠BOD＝50°，∴∠AOB＝90°，∵OM，ON分别是∠AOC，∠BOD的平分线，∴∠MOA＝∠AOC＝20°，∠NOB＝∠BOD＝25°，∴∠MON＝∠MOA+∠AOB+∠NOB＝135°，故答案为：135°．【点评】本题考查的是角的计算，掌握角的和差计算、正确认识图形是解题的关键．33．如图，直线AB、CD相交于点O，∠DOE＝∠BOE，OF平分∠AOD，若∠BOE＝28°，则∠EOF的度数为90°．【分析】根据已知条件“∠DOE＝∠BOE，OF平分∠AOD，若∠BOE＝28°”和平角的定义可以求得∠AOF＝∠DOF＝∠AOD＝62°，∠DOE＝∠BOE ＝28°；然后根据图形求得∠EOF＝∠DOF+∠DOE＝62°+28°＝90°．【解答】解：∵∠DOE＝∠BOE，∠BOE＝28°，∴∠DOB＝2∠BOE＝56°；又∵∠AOD+∠BOD＝180°，∴∠AOD＝124°；∵OF平分∠AOD，∴∠AOF＝∠DOF＝∠AOD＝62°，∴∠EOF＝∠DOF+∠DOE＝62°+28°＝90°．故答案是：90°．【点评】本题考查了角的计算．解题时，注意利用隐含在题干中的已知条件“∠AOB＝180°”．三．解答题（共17小题）34．如图，∠AOB＝120°，点C为∠AOB内部一点，OD平分∠BOC，OE平分∠AOD（1）如果∠AOC＝30°，依题意补全图形；（2）在（1）的条件下，求∠EOC的度数；（3）如果∠AOC＝α（0°＜α＜120°），直接用含α的代数式表示∠EOC的度数．【分析】（1）根据题意画出图形即可；（2）首先求出∠COB的度数，然后根据角平分线的定义求得∠DOB＝∠DOC＝45°，那么∠DOA＝75°，再根据角平分线的定义求得∠DOE，然后根据∠EOC＝∠DOC﹣∠DOE求解；（3）与（2）解法相同．【解答】解：（1）如图1所示：（2）∵∠AOB＝120°，∠AOC＝30°，∴∠COB＝90°；∵OD平分∠BOC，∴∠DOB＝∠DOC＝45°；∵∠AOB＝120°，∠DOB＝45°，∴∠DOA＝75°；∵OE平分∠AOD，∴∠DOE＝∠AOE＝37.5°；∴∠EOC＝∠DOC﹣∠DOE＝45°﹣37.5°＝7.5°；（3）∵∠AOB＝120°，∠AOC＝α，∴∠COB＝120°﹣α；∵OD平分∠BOC，∴∠DOB＝∠DOC＝60°﹣α；∵∠AOB＝120°，∠DOB＝60°﹣α，∴∠DOA＝60°+α；∵OE平分∠AOD，∴∠DOE＝∠AOE＝30°+α；∴∠EOC＝|∠DOE﹣∠DOC|＝|30°+α﹣（60°﹣α）|＝|α﹣30°|．【点评】本题考查了角度的计算，理解角平分线的定义是关键．35．如图OC是∠AOB内部的一条射线，∠BOC＝2∠AOC，OD平分∠AOC．（1）若∠AOB＝120°，求∠BOC和∠BOD的度数；（2）画出∠BOC的平分线OE，说明∠DOE＝∠AOB．【分析】（1）设∠AOC＝x，根据题意列出方程，解方程求出x，计算即可；（2）根据角平分线的定义证明．【解答】解：（1）设∠AOC＝x，则∠BOC＝2x，所以x+2x＝120°，则x＝40°，即∠AOC＝40°，∠BOC＝80°，因为OD平分∠AOC，∴∠DOC＝20°，所以∠DOB＝∠DOC+∠BOC＝20°+80°＝100°；（2）∠BOC的平分线OE如图所示：因为OD平分∠AOC，∴∠DOC＝∠AOC，因为OE平分∠BOC，∴∠EOC＝∠BOC，∠DOE＝∠DOC+∠EOC＝∠AOC+∠BOC＝∠AOB．【点评】本题考查的是角的计算、角平分线的定义，掌握角平分线的定义以及角平分线的画法是解题的关键．36．如图1所示：已知，∠AOB＝90°，∠BOC＝30°，OM平分∠AOC，ON 平分∠BOC．（1）∠MON═45°；（2）如图2，∠AOB＝90°，∠BOC＝x°，仍然分别作∠AOC、∠BOC的平分线OM、ON，能否求出∠MON的度数若能，求出其值；若不能，说明理由．（3）如图3，若∠AOB＝α，∠BOC＝β（α、β均为锐角，且α＞β），仍然分别作∠AOC、∠BOC的平分线OM、ON，能否求出∠MON的度数．若能，求∠MON的度数．（4）从（1）、（2）、（3）的结果中，你发现了什么规律？【分析】（1）根据题意可知，∠AOC＝120°，由OM平分∠AOC，ON平分∠BOC；推出∠MOC＝∠AOC＝60°，∠CON＝∠BOC＝15°，由图形可知，∠MON＝∠MOC﹣∠CON，即∠MON＝45°；（2）根据（1）的求解思路，先利用角平分线的定义表示出∠MOC与∠NOC的度数，然后相减即可得到∠MON的度数；（3）用α、β表示∠MOC，∠NOC，根据∠MON＝∠MOC﹣∠NOC得到．（4）由（1）、（2）、（3）的结果中，∠MON的度数与∠BCO无关，∠MON＝．【解答】解：（1）∵∠AOB＝90°，∠BOC＝30°，∴∠AOC＝∠AOB+∠BOC＝90°+30°＝120°，∵OM平分∠AOC，ON平分∠BOC，∴∠MOC＝∠AOC＝60°，∠CON＝∠BOC＝15°，∴∠MON＝∠MOC﹣∠CON＝60°﹣15°＝45°；故答案为：45；（2）能．∵∠AOB＝90°，∠BOC＝x°，∴∠AOC＝90°+x°∵OM、ON分别平分∠AOC，∠BOC，∴∠MOC＝∠AOC＝（90°+x°）＝45°+x，∴∠CON＝∠BOC＝x，∴∠MON＝∠MOC﹣∠CON＝45°+x﹣x＝45°．（3）∵∠AOB＝α，∠BOC＝β，∴∠AOC＝∠AOB+∠BOC＝α+β，∵OM平分∠AOC，∴∠MOC＝∠AOC＝（α+β），∵ON平分∠BOC，∴∠NOC＝∠BOC＝，∴∠MON＝∠MOC﹣∠NOC＝（α+β）﹣＝．（4）规律：∠MON的度数与∠BCO无关，∠MON＝．理由：∵∠AOB＝α，∠BOC＝β，∴∠AOC＝∠AOB+∠BOC＝α+β，∵OM平分∠AOC，∴∠MOC＝∠AOC＝（α+β），∵ON平分∠BOC，∴∠NOC＝∠BOC＝，∴∠MON＝∠MOC﹣∠NOC＝（α+β）﹣＝．【点评】本题考查角的和差定义、角平分线的定义，利用∠MON＝∠MOC﹣∠NOC是解决问题的关键．37．如图1，O为直线AB上一点，过点O作射线OC，∠AOC＝30°，将一直角三角板的直角顶点放在点O处，一边ON在射线OA上，另一边OM与OC 都在直线AB的上方．现将图25﹣1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周．（1）如图2，若经过t秒后，线段OM恰好平分∠BOC，此时∠COM＝75°；∠AON＝15°；t＝5秒；（2）在（1）的条件下，线段ON是否平分∠AOC？请说明理由；（3）如图3，若三角板在转动的同时，射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周，那么经过多长时间OC平分∠MON？【分析】（1）根据角平分线的定义计算即可；（2）求出∠AON，∠CON的值即可判断；（3）设∠AON＝3t，∠AOC＝30+6t，根据∠AOC﹣∠AON＝∠CON，构建方程即可解决问题；【解答】解：（1）如图2中，∵∠AOC＝30°，∴∠BOC＝180°﹣∠AOC＝150°，∵OM平分∠BOC，∴∠COM＝∠BOM＝∠BOC＝75°，∠AON＝180°﹣90°﹣75°＝15°，∴t＝＝5s，故答案为75，15，5；（2）结论：ON平分∠AOC．理由：∵∠AOC＝30°，∠AON＝15°，∴∠CON＝∠AOC﹣∠AON＝15°，∴∠AON＝∠CON．∴ON平分∠AOC．（3）∵OC平分∠MON，∠MON＝90°，∴∠CON＝∠COM＝45°，∵三角板绕点O以每秒3°的速度，射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周，∴设∠AON＝3t，∠AOC＝30+6t，∵∠AOC﹣∠AON＝∠CON，∴30+6t﹣3t＝45，解得t＝5，∴经过5秒OC平分∠MON．【点评】本题考查角的计算、角平分线的定义、旋转变换等知识，解题的关键是理解题意，学会利用参数解决问题，属于中考常考题型．38．如图，已知∠AOB＝90°，∠EOF＝60°，OE平分∠AOB，OF平分∠BOC，求∠COB和∠AOC的度数．【分析】直接利用角平分线的定义结合已知角度得出∠BOF的度数，进而分析得出答案．【解答】解：∵∠AOB＝90°，OE平分∠AOB，∴∠BOE＝∠AOB＝45°，∵∠EOF＝60°，∴∠BOF＝∠EOF﹣∠BOE＝15°，∵OF平分∠BOC，∴∠BOC＝2∠BOF＝30°，∴∠AOC＝∠AOB+∠BOC＝120°．【点评】此题主要考查了角的计算以及角平分线的定义，正确应用角平分线的定义是解题关键．39．如图，已知∠AOB＝90°，射线OC绕点O从OA位置开始，以每秒4°的速度顺时针方向旋转；同时，射线OD绕点O从OB位置开始，以每秒1°的速度逆时针方向旋转．当OC与OA成180°时，OC与OD同时停止旋转．（1）当OC旋转10秒时，∠COD＝40°．（2）当OC与OD的夹角是30°时，求旋转的时间．（3）当OB平分∠COD时，求旋转的时间．【分析】（1）根据已通知以及即可得到结论；（2）设转动t秒，OC与OD的夹角是30度，①如图1，列方程即可得到结论；②如图2，列方程即可得到结论；（3）如图3，设转动m秒时，根据角平分线的定义列方程即可得到结论．【解答】解：（1）∵射线OC绕点O从OA位置开始，以每秒4°的速度顺时针方向旋转，∴当OC旋转10秒时，∠COD＝×10＝40°，故答案为：40；（2）设转动t秒，OC与OD的夹角是30度，①如图1，4t+t＝90﹣30，t＝12，②如图2，4t+t＝90+30，t＝24，∴旋转的时间是12秒或24秒；（3）如图3，设转动m秒时，OB平分∠COD，则4m﹣90＝m，解得，m＝30，∴旋转的时间是30秒．【点评】本题考查了角的有关计算和角平分线定义的应用，熟记角平分线的定义是解题的关键．40．如图所示，已知∠AOB＝90°，∠BOC＝30°，OM平分∠AOC，ON平分∠BOC；（1）求∠MON；（2）∠AOB＝α，∠BOC＝β，求∠MON的度数．【分析】（1）根据角平分线的定义得到∠MOC＝∠AOC，∠NOC＝∠BOC，则∠MON＝∠MOC﹣∠NOC＝（∠AOC﹣∠BOC）＝∠AOB，然后把∠AOB的度数代入计算即可；（2）同理可得，∠MOC＝，∠CON＝，所以∠MON＝∠MOC ﹣∠CON＝＝．【解答】解：（1）∵OM平分∠AOC，ON平分∠BOC，∴∠MOC＝∠AOC，∠NOC＝∠BOC，∵∠AOC＝∠AOB+∠BOC，∴∠MON＝∠MOC﹣∠NOC＝（∠AOB+∠BOC﹣∠BOC）＝∠AOB，∵∠AOB＝90°，∴∠MON＝×90°＝45°．（2）同理可得，∠MOC＝，∠CON＝，∴∠MON＝∠MOC﹣∠CON＝＝．【点评】本题考查了角平分线的定义，属于基础题，解决本题的关键是熟记平分线的定义．41．如图，已知∠AOC＝60°，∠BOD＝90°，∠AOB是∠DOC的3倍，求∠AOB的度数．【分析】设∠COD＝x，则∠AOD可表示为60°﹣x，于是∠AOB＝90°+60°﹣x＝150°﹣x，再根据∠AOB是∠DOC的3倍得到150°﹣x＝3x，解得x＝37.5°，然后计算3x即可．【解答】解：设∠COD＝x，∵∠AOC＝60°，∠BOD＝90°，∴∠AOD＝60°﹣x，∴∠AOB＝90°+60°﹣x＝150°﹣x，。

初中数学浙教版七年级上册6.7角的和差同步练习

初中数学浙教版七年级上册6.7角的和差同步练习一、单选题（共10题；共20分）1.如图，OC为内一条直线，下列条件中不能确定OC平分的是A. B.C. D.2.如图，OC在∠AOB的内部，∠BOC：∠AOC＝1：2．∠AOB＝63°，则∠AOC＝（）A. 52°B. 42°C. 39°D. 21°3.如图，∠AOC＝∠BOD＝90°，∠AOD＝140°，则∠BOC的度数为（）A. 30°B. 45°C. 50°D. 40°4.∠AOB的大小可由量角器测得(如右图所示)，则180°-∠AOB的大小为( )A. 0°B. 70°C. 110°D. 180°5.如图，是直角顶点重合的一副三角尺，若∠BCD=30°，下列结论错误的是（）A. ∠ACD=120°B. ∠ACD=∠BCEC. ∠ACE=120°D. ∠ACE-∠BCD=120°6.如图，射线OA的端点O在直线CD上，若∠COA＝40°，则∠AOD的度数是（）A. 170°B. 160°C. 150°D. 140°7.借助常用的直角三角尺，能画出一些度数的角，下列选项中不能画出的角是（）A. 15°B. 100°C. 165°D. 135°8.在同一平面内，若∠BOA＝50.3°，∠BOC＝10°30′，则∠AOC的度数是( )A. 60.6°B. 40°C. 60.8°或39.8D. 60.6°或40°9.如图，∠AOB是直角，∠AOC=38°，OD平分∠BOC，则∠AOD的度数为（）A. 52°B. 38°C. 64°D. 26°10.如图，∠AOB=130°，射线OC是∠AOB内部任意一条射线，OD、OE分别是∠AOC、∠BOC的平分线，下列叙述正确的是（）A. ∠DOE的度数不能确定B. ∠AOD+∠BOE=∠EOC+∠COD=∠DOE=65°C. ∠BOE=2∠CODD. ∠AOD=二、填空题（共4题；共7分）11.如图，OB是________的平分线；OC是________的平分线，∠AOD＝________，∠BOD＝________．12.，，________13.将两个三角尺的直角顶点重合为如图所示的位置，若，则________．14.如图，∠AOC=90°，∠BOC=60°，OM平分∠AOB，ON平分∠BOC．∠MON的度数为________．三、解答题（共3题；共25分）15.用三角尺或量角器，画出三角形AC 边上的高，BC 边上的中线，∠ACB 的角平分线．不写作法，写好结论．16.已知一条射线OA，若从点O再引两条射线OB和OC，使∠AOB=60°，∠BOC=20°，求∠AOC的度数．17.将一副三角板放在同一平面内，使直角顶点重合于点O（1）如图①，若∠AOB=155°，求∠AOD、∠BOC、∠DOC的度数.（2）如图①，你发现∠AOD与∠BOC的大小有何关系？∠AOB与∠DOC有何关系？直接写出你发现的结论.（3）如图②，当△AOC与△BOD没有重合部分时，（2）中你发现的结论是否还仍然成立，请说明理由.答案解析部分一、单选题1.【答案】C【解析】【解答】解：A、能确定OC平分∠AOB，故不符合题意；B、能确定OC平分∠AOB，故不符合题意；C、∠AOC+∠COB=∠AOB，不能确定OC平分∠AOB，故符合题意；D、能确定OC平分∠AOB，故不符合题意。

七年级数学上册6.5_6.7角与角的度量、角的大小比较及角的和差同步练习(新版)浙教版【含解析】

x ∠M ON =
度；
y 当 OC 在 ∠AOB 内绕点 O 转动时，∠M ON 的值
改变．（填“会”或“不会”）
度．
第 1 页，共 2 页
三、解答题 15. 计算： (1) 153◦29′42′′ + 26◦40′32′′； (2) 110◦36′ − 90◦37′28′′．
16. 如图，∠A + ∠B = 90◦，点 D 在线段 AB 上，点 E 在线段 AC 上，DF 平分 ∠BDE，DF 与
18 解得 x = 40．
∴ 这个角是 40◦．
10. 计算：50◦ − 15◦30′ =
．
11. 把角度化为度、分的形式，则 20.5◦ = 20◦
′．
12. 把 15◦30′ 化成度的形式，则 15◦30′ =
度．
13. 一个角的补角与它的余角的 4 倍的和等ห้องสมุดไป่ตู้周角的 17 ，则这个角为
．
18
14. 如图所示，OM ，ON 分别是 ∠BOC 和 ∠AOC 的平分线，∠AOB = 84◦．
又因为 ∠1 > ∠2，所以 ∠2 为锐角，
所以 ∠2 的余角就等于 90◦ − ∠2 = 90◦ − (180◦ − ∠1) = ∠1 − 90◦．
二、填空题
9. 40 解析：
10. 34◦30′
11. 30
12. 15.5◦
13. 40◦ 解析：设这个角为 x 度，根据题意可得 (180 − x) + 4 (90 − x) = 360 × 17
A. ∠1 > ∠2 > ∠3
B. ∠2 > ∠1 > ∠3
C. ∠1 > ∠3 > ∠2

6.7角的和差同步练习卷 2024—2025学年浙教版数学七年级上册

浙教版七年级上册《6.7 角的和差》同步练习卷一、选择题1．在同一平面上，若∠BOA=60°，∠BOC=20°，则∠AOC的度数是（）A．80°B．40°C．20°或 40°D．80°或 40°（α+β），却得到了四个2．α，β都是钝角，有四名同学分别计算16不同的结果，分别为26°，50°，72°，90°，老师判作业时发现其中有正确的结果，那么计算正确的结果是（）A．26°B．50°C．72°D．90°3．如图，两块直角三角板的直角顶点O重合在一起，若∠BOC= 17∠AOD，则∠BOC的度数为（）A．22.5°B．30°C．45°D．60°4．将一张长方形纸片ABCD按如图所示的方式折叠，AE、AF为折痕，点B、D折叠后的对应点分别为B′、D′，若∠B′AD′=10°，则∠EAF的度数为（）A．40°B．45°C．50°D．55°二、填空题5．角的和差：一般地，如果一个角的度数是另两个角的度数的和，那么这个角就叫作另 ______ ；如果一个角的度数是另两个角的差，那么这个角就叫作______ ，两个角的和差仍是一个角．例如：如图所示，∠AOB是∠1与∠2的和，记作：∠AOB=∠1+∠2；∠1是∠AOB与∠2的差，记作：∠1=∠AOB-∠2．6．如图，点A、O、B在一条直线上，且∠AOC=48°32′，OD平分∠AOC，则图中∠BOD= ______ ．7．如图，∠AOB为平角，OC是∠AOD的平分线，∠DOE：∠BOE=3：5，∠COE=75°，则∠AOD的度数为______ ．8．如图，小明同学在参加“几何小能手”社团活动时，制作了一副与众不同的三角板，用它们可以画出一些特殊的角度．在①9°；②18°；③55°；④117°中，能用这副三角板画出的角度是 ______ ．（填写序号）9．如图，点O在直线AB上，如果∠COB=∠DOE=90°，∠BOE=15°，那么∠AOD= ______ ．10．如图，点E，F分别在长方形ABCD的边AD，CD上，连接BE．将长方形ABCD沿BE对折，点A落在A′处；将∠DEA′对折，点D落在EA′的延长线上的D′处，得到折痕EF，若∠BEA′=70°，∠FED′= ______ ．三、解答题11．如图1，A，O，B三点在同一直线上，∠BOD与∠BOC互补．（1）请判断∠AOC与∠BOD的大小关系，并验证你的结论；（2）如图2，若OM平分∠AOC，ON平分∠AOD，∠BOD=a,求∠MON的度数．（用含a的式子表示）12．点O为直线AB上一点，过点O作射线OC，使∠BOC=65°．将一直角三角板的直角顶点放在点O处．（1）如图1，将三角板MON的一边ON与射线OB重合时，则∠MOC= ______ ；（2）如图2，将三角板MON绕点O逆时针旋转一定角度，此时OC是∠MOB的角平分线，求旋转角∠BON和∠CON的度数．13．将一副三角板如图摆放，已知∠BAE=136°，求∠CAD的度数．14．如图，直线AB，CD相交于点O，OE平分∠BOC，∠COF=90°，（1）若∠BOD：∠BOE=1：2，求∠AOC的度数；（2）若∠BOE=70°，求∠AOF的度数．15．如图，两直线AB，CD相交于点O，已知OE平分∠BOD，且∠AOC：∠AOD=3：7，（1）求∠DOE的度数；（2）若OF⊥OE，求∠COF的度数．16．如图，点O在直线AB上，∠COD=60°，∠AOE=2∠DOE．（1）若∠BOD=60°，求∠COE的度数；（2）试猜想∠BOD和∠COE的数量关系，并说明理由．17．如图，直角三角板的直角边OM在直线AB上，作射线OC，使∠BOC=125°．（1）三角板绕直角顶点O逆时针旋转，当直角边OM在∠BOC的内部，直角边ON在直线AB的下方时：①若∠BON=15°，则∠COM的度数为 ______ ；②若∠BON=α，则∠COM的度数为 ______ （用含α的代数式表示）；（2）若三角板绕点O按每秒7°的速度逆时针旋转一周，在旋转的过程中，经过多少秒时，射线OC恰好是∠AOM的平分线？。

七年级数学上册6.7角的和差课堂练习(无答案)(新版)浙教版.doc

6.7角的和差目标一：角的和差概念及计算想一想，已知Zl = 30°,Z2 = 90°,,3 = 12@)三个角的度数Z间有怎样的关系?归纳概念如果一个角的度数是另两个角的度数的和，那么这个角就叫做 ____________________ ,记做Z3二Z1+ Z2;如果一个角的度数是另两个角的度数的差，那么这个角就叫做 __________________ .记做Zl = Z3 — Z2.两个角的和或差仍是一个角.找一找1.根据图形填空：同一端点的三条射线如图，问：ZAOC = Z ____________ + Z _______________ZBOC = Z ____________ - Z _______________ZAOB = Z ____________ - Z _______________先找后算2.已知：如图，ZAOC = 120° , ZBOC =ZBOD = 90° .(1)ZCOD= _____ - ZAOD= _____________ 度(2)ZBOD = ____________ - ZCOD = _________________ 度3.________________________________________________ 如图，点0 在直线AC±, ZA0B二55°,则ZB0C=Z __________________________________________________________________ -Z _____________ = _________ 度.归纳方法◊冃标二：利用角的和差画角例1 •已知Z1和Z2,用量介器作Z1与Z2的和・归纳作法◊目标三：角的平分线概念及画法归纳概念：角平分线概念：从-•个角的顶点引出的一条射线，把这个角分成__________________________ 这条射线叫做这个角的平分线.几何语言画一画任意画一个JT JZAOB,你冇什么方法画出它的平分线?归纳◊目标四：角的和差倍分简单计算用一用例2：如图若ZCBD=30°, ZABC=90°, BP平分ZABD,求ZABP度数?归纳方法试一试3.已知0为直线AB上一点，0E平分ZAOC, OF平分ZC0B,求ZEOF的度数.4.已知:如图，ZA0B是直角,ZA0C=40o , ON是ZA0C的平分线,0M是ZB0C的平分线.(1)求ZM0N的人小.(2)当锐角ZA0C的人小发牛改变时，ZM0N的人小是否发牛改变？为什么？C【学习检测】1.同一端点的三条射线如图所示.若ZA0B=75° , ZAOC二48。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

6．7 角的和差
1．点P 在∠MAN 内，现有如下等式：①∠PAM ＝12∠MAN ；②∠PAN ＝1
2∠MAN ；③∠PAM ＝∠PAN ；
④∠MAN ＝2∠PAN .其中能表示AP 是角平分线的等式有(D )
A ．1个
B ．2个
C ．3个
D ．4个
2．如图，一副三角尺(直角顶点重合)摆放在桌面上，若∠AOD ＝150°，则∠BOC 等于(A ) A ．30° B．45° C ．50° D．60°
,(第2题)) ,(第3题))
3．如图，∠AOC ＝∠BOD ＝90°，下列结论中正确的个数是(C ) ①∠AOB ＝∠COD ②∠AOD ＝3∠BOC ③∠AOD ＋∠BOC ＝∠AOC ＋∠BOD A ．0 B ．1 C ．2 D ．3
4．如图，OD 是∠AOC 的平分线，OC 是∠BOD 的平分线，且∠COD ＝40°，则∠AOB ＝(C ) A ．80° B．100° C ．120° D．160°
(第4题)
(第5题)
5．如图，将长方形ABCD 沿AE 折叠，使点D 落在BC 边上的点F 处，若∠BAF ＝60°，则∠DAE ＝(A )
A ．15° B．30° C ．45° D．60°
(第6题)
6．如图，已知∠BOD ＝2∠AOB ，OC 是∠AOD 的平分线，则下列四个结论：①∠BOC ＝1
3∠AOB ；
②∠DOC ＝2∠BOC ；③∠BOC ＝1
2∠AOB ；④∠DOC ＝3∠BOC .其中正确的是(B )
A ．①② B．③④ C ．②③ D．①④
7．如图，∠AOB 和∠COD 都是直角，则∠AOD ＋∠BOC ＝180°．
,(第7题)) ,(第8题))
8．如图，点O 是直线AB 上一点，已知∠BOD ＝30°，OE 平分∠AOD ，那么∠AOE 的度数是
__75°__．
9．如图，OC 平分∠AOB ，OD 平分∠AOC ，OE 平分∠BOC ，则图中与∠AOD 相等的角有__3__个，与∠AOC 相等的角有__2__个．
,(第9题))
,(第10题))
10．如图，OB 是∠AOC 的平分线，OD 是∠COE 的平分线． (1)如果∠AOC ＝80°，那么∠BOC ＝40°；
(2)如果∠AOC ＝80°，∠COE ＝50°，那么∠BOD ＝__65°__．
(第11题)
11．如图，直线AB ，CD 交于点O ，OB 平分∠DOE .如果∠COE ＝80°，求∠EOB 与∠AOC 的度数．
【解】 ∵∠COE ＝80°，AB ，CD 交于点O ， ∴∠EOD ＝180°－∠COE ＝100°. ∵OB 平分∠EOD ，
∴∠EOB ＝∠BOD ＝1
2∠EOD ＝50°，
∴∠AOC ＝∠BOD ＝50°.
12．如图，已知∠AOC ＝90°，∠COB ＝α，OD 平分∠AOB ，则∠COD 等于(B ) A.α2 B ．45°－α2 C ．45°－α D ．90°－α
(第12题)
【解】 ∵∠AOB ＝∠AOC ＋∠COB ＝90°＋α，又∵OD 平分∠AOB ，
∴∠BOD ＝12∠AOB ＝45°＋α
2
，
∴∠COD ＝∠BOD －∠COB ＝45°＋α
2－α＝
45°－α2
.
13．如图，在2×2的方格中，连结AB ，AC ，AD ，则∠2＝45°，∠1＋∠2＋∠3＝135°．【解】 ∵∠1＋∠3＝90°，∠2＝45°， ∴∠1＋∠2＋∠3＝90°＋45°＝135°.
,(第13题)) ,(第14题))
14．如图，将书页斜折过去，使顶角A 落在A ′处，BC 为折痕，然后把BE 边折过去，使BE 与A ′B 边重合，折痕为BD ，那么两折痕BC ，BD 间的夹角度数为__90°__．【解】由题意，可得BC ，BD 分别为∠ABA ′，∠EBE ′的平分线， ∴∠CBA ′＝12∠ABA ′，∠E ′BD ＝1
2∠EBE ′，
∴∠CBA ′＋∠E ′BD ＝12∠ABA ′＋1
2∠EBE ′
＝1
2(∠ABA ′＋∠EBE ′) ＝1
2×180°＝90°，即∠CBD ＝90°.
(第15题)
15．如图，∠COD 是平角，∠AOC ＝40°，∠BOD ＝50°，OM ，ON 分别是∠AOC ，∠BOD 的平分线，求∠MON 的度数．
【解】 ∵OM ，ON 分别是∠AOC ，∠BOD 的平分线， ∴∠MOC ＝12∠AOC ＝1
2×40°＝20°，
∠NOD ＝12∠BOD ＝1
2×50°＝25°.
又∵∠COD 是平角，
∴∠MOC ＋∠MON ＋∠NOD ＝180°， ∴20°＋∠MON ＋25°＝180°， ∴∠MON ＝135°.
16．如图，已知∠AOB 是直角，∠BOC ＝30°，OM 平分∠AOC ，ON 平分∠BOC . (1)求∠MON 的度数；
(2)若∠AOB ＝α，其他条件不变，求∠MON 的度数．
(第16题)
【解】 (1)∵∠AOB ＝90°，∠BOC ＝30°， ∴∠AOC ＝∠AOB ＋∠BOC ＝120°. ∵OM 平分∠AOC ，ON 平分∠BOC ， ∴∠MOC ＝12∠AOC ＝1
2×120°＝60°，
∠NOC ＝12∠BOC ＝1
2
×30°＝15°.
∴ ∠MON ＝∠ MOC －∠NOC ＝ 60°－15°＝45°.
(2)∵∠AOB ＝α ，∠BOC ＝30°， ∴∠AOC ＝∠AOB ＋∠BOC ＝α＋30°. ∵OM 平分∠AOC ，ON 平分∠BOC ， ∴∠MOC ＝12∠AOC ＝α＋30°
2，
∠NOC ＝1
2∠BOC ＝15°.
∴∠MON ＝∠ MOC －∠NOC ＝α＋30°2－15°＝α
2
.。