高等土力学(李广信)26-土的剑桥模型PPT课件
合集下载
高等土力学第一章 课件
土的动应力-应 变关系
土的动力性质分 类
地震工程中的土动力学问题
土的动力性质：土的动剪切强度、动压缩强度和阻尼比等 地震工程中的土动力学问题：地震引起的土体液化、震陷、滑坡等 土的动力学模型：土的动力学本构模型、数值模拟方法等 抗震设计方法：基于土动力学原理的抗震设计方法、土体加固技术等
抗震设计方法与措施
土的应力-应变关系
土的应变：土体变形的程度
土的应力：土体受到的压力 或拉力
土的应力-应变关系曲线： 描述土的应力与应变之间的
关系
土的应力-应变关系的影响 因素：如土的种类、含水率、
温度等
04
土的强度与稳定性
土的强度
土的强度定义：土体抵抗剪切破坏的极限能力
土的强度分类：天然强度、有效强度、瞬时强度
地下水渗流 对工程的影 响
排水设计的 基本原则和 方法
排水设施的 种类和特点
排水设施的 布置和设计 要点
排水设施的 施工和维护
渗流对土体稳定性的影响
渗流现象及其产生原因 渗流对土体稳定性的影响 土体排水与加固措施 实际工程中的应用与案例分析
06
土的动力性质与地 震工程
土的动力性质
土的动强度
土的动变形
土力学的基本原理和概念 土力学在土木工程中的应用范围 土力学在土木工程中的具体应用案例 高等土力学在土木工程中的重要性
高等土力学在水利工程中的应用
水利工程中的土压力问题：介绍土压力的 产生、分类和计算方法，以及在水利工程 中的应用。
水利工程中的渗流问题：介绍渗流的基本 原理、计算方法和在水利工程中的应用， 包括堤坝、水库等。
土的物理性质
土的分类：根据土的颗粒大小、矿物成分、结构等特点进行分类 土的物理性质指标：包括密度、含水量、孔隙率、塑性指数等，用于描述土的物理性质 土的力学性质：包括抗剪强度、压缩性、渗透性等，用于描述土在力作用下的行为 土的工程分类：根据土的工程性质和特点，将土分为不同的类型，以便于工程设计和施工
岩土塑性力学剑桥模型
(6.3.15)
图 6 - 1 6 表 示 土 样 在 单 剪 时 的 变 形 情 况 。 土 样 高 为 H ， 水 平 截 面 积 为 A . 剪 切 变 形 后 ， 水 平 位 移 为 d u ， 竖 向 位 移 为 d v， 如 图 6 - 1 6
中 所 示 。 在 剪 切 变 形 过 程 中 ， 正 应 力 ’ 和 剪 应 力 所 做 的 功 等 于 - ’ 。假 设 由 于 摩 擦 所 产 生 的 能 量 消 耗 与 摩 擦 系
间中。正常固结土应力路径都在Roscoe面上，超固结状态用位于该面下面的点表示，在该面以上是不可能有点来表示
应力状态的。Roscoe面成为一个边界，在该面的面上或以下是可能的状态，在该面以上是不可能的状态， Roscoe面
称为状态边界面。超固结上样的应力路径在土样破坏时到达Hvorslev面，在土样破坏后应变增大时趋向临界状态。
有关，为了适用更一般的情况，采用等效的符号改写式6.3.17，得
(6.3.18)
式中负号是由于一 代表膨胀引起，这也是剑桥模型的假设之一 。
将 式 6 . 3 . 1 8 代 入 式 6 . 3 . 1 2 ， 并 考 虑 = 0 ， 得
(6.3.19)
结 合 式 6 . 3 . 9 ， 式 6 . 3 .1 0 ， 式 6 . 3 . 1 5 和 式 6 . 3 . 1 9 ， 得 到 能 量 方 程
6.3剑桥模型
正常固结粘土的排水与不排水应力路径
超固结土样排水和不排水三轴实验破坏状态
各向等压加 载 与卸 载 试 验
超固结比对不 排 水 应 力路 径 的 影 响
6.3.3 完全的状态边界面
在p'，q，v空间中，正常固结和超固结土样的应力路径不能超过 Roscoe面和Hvorslev面，处在这两个面包围的空
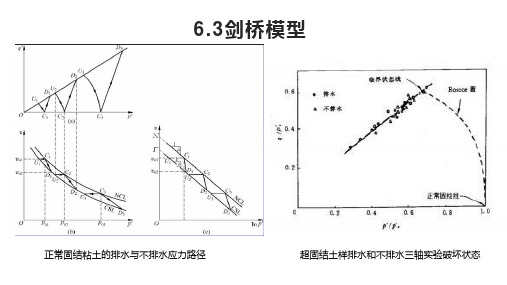
图 6 - 1 6 表 示 土 样 在 单 剪 时 的 变 形 情 况 。 土 样 高 为 H ， 水 平 截 面 积 为 A . 剪 切 变 形 后 ， 水 平 位 移 为 d u ， 竖 向 位 移 为 d v， 如 图 6 - 1 6
中 所 示 。 在 剪 切 变 形 过 程 中 ， 正 应 力 ’ 和 剪 应 力 所 做 的 功 等 于 - ’ 。假 设 由 于 摩 擦 所 产 生 的 能 量 消 耗 与 摩 擦 系
间中。正常固结土应力路径都在Roscoe面上，超固结状态用位于该面下面的点表示，在该面以上是不可能有点来表示
应力状态的。Roscoe面成为一个边界，在该面的面上或以下是可能的状态，在该面以上是不可能的状态， Roscoe面
称为状态边界面。超固结上样的应力路径在土样破坏时到达Hvorslev面，在土样破坏后应变增大时趋向临界状态。
有关，为了适用更一般的情况，采用等效的符号改写式6.3.17，得
(6.3.18)
式中负号是由于一 代表膨胀引起，这也是剑桥模型的假设之一 。
将 式 6 . 3 . 1 8 代 入 式 6 . 3 . 1 2 ， 并 考 虑 = 0 ， 得
(6.3.19)
结 合 式 6 . 3 . 9 ， 式 6 . 3 .1 0 ， 式 6 . 3 . 1 5 和 式 6 . 3 . 1 9 ， 得 到 能 量 方 程
6.3剑桥模型
正常固结粘土的排水与不排水应力路径
超固结土样排水和不排水三轴实验破坏状态
各向等压加 载 与卸 载 试 验
超固结比对不 排 水 应 力路 径 的 影 响
6.3.3 完全的状态边界面
在p'，q，v空间中，正常固结和超固结土样的应力路径不能超过 Roscoe面和Hvorslev面，处在这两个面包围的空
剑桥模型不排水及土结效应PPT教案
第1页/共11页
剑桥模型
f
(
ij
)
k 1 e0
ln
p p0
k 1 e0
1 M
q p
（vp1） 0
应变增量： dij dij e dij p
A、弹性应变：
由广义Hooke定律得出：
d
e ij
1 E
d ij
E
d kkij
d
e v
d1e1
d
e 22
d
e 33
3(1 2 ) E
dp
其中： E 3(1 2) 1 e0 p 例如（不排水条件下）：
第5页/共11页
D、孔隙水压力：
不排水条件下: d v 0
即：d
e v
d
p v
0
d
p v
1 e0
1 [(M Mp'
q' )][dp' p'
dq' M q'
]
A(dp du) Bdq
p'
d
e v
3(1 2 ) E
dp'
C(dp
du)
A 1 [(M q' )], B 1
剑桥模型不排水及土结效应
会计学
1
剑桥模型不排水下应力应变关系
已知条件：M
0.95，
0.3， 1 e0
0.00403 ，1e，0 采0.用002剑51桥
模型，做常规三轴压缩下等p=200kPa固结不排水下的土的应力
应变曲线。
f
ln 1 e0
p k p0 1 e0
1 M
qp剑 桥vp模 型0
3%
1%
u /100
高等土力学第一章 课件
添加副标题
高等土力学第一章课件
汇报人：
目录
CONTENTS
01 添加目录标题 03 土的应力与应变
02 土力学基本概念 04 土的强度与稳定性
05 土压力与挡土墙设 计
06 地基承载力与沉降 计算
07 特殊土工程性质与 处理方法
添加章节标题
土力学基本概念
土的气组成的自然体
黄土的工程分类：根据黄土的工程性质，可 以将黄土分为不同的类型，不同类型的黄土 在工程中的处理方法也有所不同。
黄土的处理方法：包括排水固结法、强夯 法、换填法等，这些方法可以有效地改善 黄土的工程性质，提高工程的稳定性和安 全性。
膨胀土工程性质与处理方法
膨胀土的定义与分类
膨胀土的工程性质
膨胀土的膨胀机理
土的应变：土体变形的大小 和方向
土的应力-应变关系曲线：描述 土的应力与应变之间关系的曲 线
土的应力：土体受到的力，包 括压应力、剪应力和弯应力等
土的应力-应变关系特点：非 线性和弹塑性等
土的强度与稳定性
土的强度
土的强度定义：土体抵抗剪切破坏的极限能力 土的强度分类：天然强度、残余强度、有效强度等 影响土强度的因素：土的成分、结构、应力历史、环境条件等 土的强度试验方法：直接剪切试验、三轴压缩试验、无侧限抗压试验等
稳定的能力。
地基承载力的影响 因素：包括土的物 理性质、力学性质、 地质条件、地下水 位、荷载大小和分
布等。
添加标题
添加标题
地基承载力与沉降 计算的关系：地基 承载力是影响建筑 物沉降的重要因素 之一，通过合理的 地基设计和沉降计 算，可以确保建筑 物的稳定性和安全
性。
添加标题
地基承载力与建筑 物安全性的关系： 地基承载力不足可 能导致建筑物沉降、 倾斜甚至倒塌，因 此在进行建筑设计 时，必须充分考虑 地基承载力的要求。
高等土力学第一章课件
汇报人：
目录
CONTENTS
01 添加目录标题 03 土的应力与应变
02 土力学基本概念 04 土的强度与稳定性
05 土压力与挡土墙设 计
06 地基承载力与沉降 计算
07 特殊土工程性质与 处理方法
添加章节标题
土力学基本概念
土的气组成的自然体
黄土的工程分类：根据黄土的工程性质，可 以将黄土分为不同的类型，不同类型的黄土 在工程中的处理方法也有所不同。
黄土的处理方法：包括排水固结法、强夯 法、换填法等，这些方法可以有效地改善 黄土的工程性质，提高工程的稳定性和安 全性。
膨胀土工程性质与处理方法
膨胀土的定义与分类
膨胀土的工程性质
膨胀土的膨胀机理
土的应变：土体变形的大小 和方向
土的应力-应变关系曲线：描述 土的应力与应变之间关系的曲 线
土的应力：土体受到的力，包 括压应力、剪应力和弯应力等
土的应力-应变关系特点：非 线性和弹塑性等
土的强度与稳定性
土的强度
土的强度定义：土体抵抗剪切破坏的极限能力 土的强度分类：天然强度、残余强度、有效强度等 影响土强度的因素：土的成分、结构、应力历史、环境条件等 土的强度试验方法：直接剪切试验、三轴压缩试验、无侧限抗压试验等
稳定的能力。
地基承载力的影响 因素：包括土的物 理性质、力学性质、 地质条件、地下水 位、荷载大小和分
布等。
添加标题
添加标题
地基承载力与沉降 计算的关系：地基 承载力是影响建筑 物沉降的重要因素 之一，通过合理的 地基设计和沉降计 算，可以确保建筑 物的稳定性和安全
性。
添加标题
地基承载力与建筑 物安全性的关系： 地基承载力不足可 能导致建筑物沉降、 倾斜甚至倒塌，因 此在进行建筑设计 时，必须充分考虑 地基承载力的要求。
高等土力学第1.2.3章课件
δ ij = 1 i = j
s1
= σ1
−
1 3
σ
kk
= σ1 −σm
s2 = σ 2 −σ m
主应力偏量
s3 = σ 3 − σ m
15
i= j
2.2 应力和应变 2.2.1 应力 偏应力张量的不变量
第一偏应力 不变量
J1 = Skk = S1 + S2 + S3 ≡ 0
第二偏应力
不变量
J2
=
1 2
三轴压缩： b=0；θ=-30o
应力洛德角与上述参数的关系 三轴拉伸：
tanθ = μσ = 2b −1
33
b=1.0；θ=+30o
应力洛德角和洛德参数都反映中主应 力和其他两个应力间的相对比例
25
2.2 应力和应变 2.2.1 应力
土力学中常用的三个应力（不）变量
p
=
1 3
(σ1
+σ2
+σ3)
[ ] q =
τ oct
=
1 3
⎡⎣(σ
1
−
σ
2
)2
+ (σ 2
− σ 3 )2
+ (σ 3
1
− σ1)2 ⎤⎦ 2
=
21
3
J
2
2
广义剪应力（等效剪应力）
q=
1 2
⎡⎣(σ1
− σ 2 )2
+ (σ2
−σ3)2
+ (σ3
1
−σ1)2 ⎤⎦ 2
=
3 2
τ
oct
=
3J2
20
2.2 应力和应变 2.2.1 应力
高等土力学第二章课件
A＋
f
T
D
g
＝
D
D
g
A
＋
f
f
T
D
T
D
g
d
＝ D ep d
Dep＝D
Dg
f
T
ห้องสมุดไป่ตู้
D
A＋f
T
Dg
不相适应： fg
Dep＝D
Df
f
T
D
A＋f
T
Df
相适应： f=g
2.6 土的剑桥模型（Cam-clay)
2.6 土的剑桥模型
2.6.1 正常固结粘土的物态边界面（state boundary surface) 2.6.2 超固结土及完全的物态边界面 2.6.3 弹性墙与剑桥模型的屈服函数 2.6.4 修正的剑桥模型
弹性－理想塑性 Elasto-Plastic
刚塑性 Perfectly plastic
增量弹塑性-
Incremental Elastoplastic
不同塑性模型的应用：
刚塑性理论-极限平衡法：刚体滑动法、各 种条分法、滑移线法（不计变形，不计过程）
弹－塑性理论：在一定范围为弹性，超过 某一屈服条件为塑性变形。数值计算中出现
CS：v=常数的Roscoe 面 TS：超固结土的强度线-Hvorslev面 0T：零应力线 包括了正常固结土、重超固结土的 可能的（极限）应力状态
包括超固 结土的完 全的物态 边界面
vi-Ti-Si-Ni
HS
超固结
CS
正常 固结
2.6.3 弹性墙与屈服轨迹
1. 弹性墙 正常固结粘土与轻超固结粘土 （wet clay) 各向等压固结: 加载：NCL
土力学_李广信_土的抗剪强度
第五章 土的抗剪强度
作业 5-1、5-2（CD试验） 5-3、5-5、3-9 5-8、5-4、5-9
1
§5 土的抗剪强度
本章特点
• 有较严格的理论体系 • 各种关系较复杂 • 前面各章知识的综合运用
学习要点
• 理清应力、应变、体变、孔压、强度间的关系 • 砂性土与粘性土强度的区别与联系 • 试验条件与实际工程情况的对应关系
主要难点
• 正常固结粘性土的强度 • 不固结不排水剪的应力应变关系及强度 • 强度指标的运用
2
§5 土的抗剪强度
土工结构物或地基
土
渗透问题 变形问题 强度问题
渗透特性 变形特性 强度特性
3
§5 土的抗剪强度
§5.1 土体破坏与强度理论 §5.2 抗剪强度测定试验 §5.3 应力路径与破坏主应力线 §5.4 抗剪强度指标 §5.5 砂土的振动液化
4
§5 土的抗剪强度 §5.1 土体破坏与强度理论
一、土的强度特点 二、工程中土体的破坏类型 三、土的强度机理 四、莫尔-库仑强度理论
5
§5 土的抗剪强度 §5.1 土体破坏与强度理论
一、土的强度特点
1. 碎散性：强度不是颗粒矿物本身的强度，而是颗粒间 相互作用—主要是抗剪强度（剪切破坏），颗粒间粘 聚力与摩擦力；
2. 三相体系：三相承受与传递荷载—有效应力原理； 3. 自然变异性：土的强度的结构性与复杂性。
6
§5 土的抗剪强度 §5.1 土体破坏与强度理论
二、工程中土体的破坏类型 1. 挡土结构物的破坏
美国某桥头挡土墙破坏（2003年9月10日）
7
§5 土的抗剪强度 §5.1 土体破坏与强度理论
二、工程中土体的破坏类型 1. 挡土结构物的破 坏
作业 5-1、5-2（CD试验） 5-3、5-5、3-9 5-8、5-4、5-9
1
§5 土的抗剪强度
本章特点
• 有较严格的理论体系 • 各种关系较复杂 • 前面各章知识的综合运用
学习要点
• 理清应力、应变、体变、孔压、强度间的关系 • 砂性土与粘性土强度的区别与联系 • 试验条件与实际工程情况的对应关系
主要难点
• 正常固结粘性土的强度 • 不固结不排水剪的应力应变关系及强度 • 强度指标的运用
2
§5 土的抗剪强度
土工结构物或地基
土
渗透问题 变形问题 强度问题
渗透特性 变形特性 强度特性
3
§5 土的抗剪强度
§5.1 土体破坏与强度理论 §5.2 抗剪强度测定试验 §5.3 应力路径与破坏主应力线 §5.4 抗剪强度指标 §5.5 砂土的振动液化
4
§5 土的抗剪强度 §5.1 土体破坏与强度理论
一、土的强度特点 二、工程中土体的破坏类型 三、土的强度机理 四、莫尔-库仑强度理论
5
§5 土的抗剪强度 §5.1 土体破坏与强度理论
一、土的强度特点
1. 碎散性：强度不是颗粒矿物本身的强度，而是颗粒间 相互作用—主要是抗剪强度（剪切破坏），颗粒间粘 聚力与摩擦力；
2. 三相体系：三相承受与传递荷载—有效应力原理； 3. 自然变异性：土的强度的结构性与复杂性。
6
§5 土的抗剪强度 §5.1 土体破坏与强度理论
二、工程中土体的破坏类型 1. 挡土结构物的破坏
美国某桥头挡土墙破坏（2003年9月10日）
7
§5 土的抗剪强度 §5.1 土体破坏与强度理论
二、工程中土体的破坏类型 1. 挡土结构物的破 坏
高等土力学l课件剑桥模型
高等土力学课件剑桥模型1.本文档介绍了高等土力学课程中的剑桥模型，该模型被广泛应用于土壤力学的研究和工程实践中。
剑桥模型以其简洁的理论基础和良好的实用性而闻名，并成为土壤的力学性质分析和设计的重要工具之一。
2. 剑桥模型的基本原理剑桥模型是一种多相介质力学理论，将土壤看作是由固相颗粒和孔隙水组成的两相介质。
通过假设土壤中颗粒和孔隙水之间的相互作用可以简化为线性弹性关系，剑桥模型建立了土壤力学的基本方程。
剑桥模型中的基本假设包括：•颗粒之间的相互作用力满足胡克定律；•孔隙水的流动满足达西定律；•土壤是各向同性的。
基于这些假设，剑桥模型可以通过求解弹性力学方程和流体力学方程来分析土壤的力学性质。
具体而言，剑桥模型可以用来计算土壤的应力、应变和孔隙水压力等参数。
3. 剑桥模型的应用剑桥模型在土力学领域具有广泛的应用，以下列举了其中几个常见的应用领域：3.1 地基基础工程剑桥模型可以用来分析地基基础的稳定性和承载力。
通过计算土壤的应力分布和变形情况，可以评估地基基础的安全性，并指导设计和加固工程。
3.2 土壤侧压问题在土木工程中，土体对结构的侧向施压是一个重要的问题。
剑桥模型可以用来分析土体的侧向力学特性，解决土体侧压引起的结构变形和破坏问题。
3.3 地下水位变化分析地下水位变化对土体力学性质有着重要影响。
剑桥模型可以用来模拟地下水位变化引起的孔隙水压力变化，从而评估土壤的稳定性和水力特性。
3.4 土石坡稳定性分析土石坡的稳定性分析是土力学工程中的重要问题。
剑桥模型可以用来计算土石坡的应力分布和变形情况，评估土石坡的稳定性，并指导加固和防护措施的设计。
4.高等土力学课件剑桥模型是一种基于多相介质力学理论的土壤力学分析模型。
该模型以其简洁的理论基础和广泛的应用领域而受到广泛关注和应用。
通过剑桥模型，我们可以更准确地分析土壤的力学性质，提高土力学工程设计的准确性和可靠性。
高等土力学l课件剑桥模型课件
总结与展望
1 应用前景
剑桥模型ppt课件将会在教育、企业培训等领 域得到广泛应用。
2 发展趋势
剑桥模型ppt课件将更加注重移动端适配、用 户体验和数据可视化等方面的发展。
感谢致辞
感谢各位参与本次剑桥模型ppt课件的学习，希望能够为您提t课件的使用技巧
引人入胜
使用生动的图像和动画，吸 引受众的注意力。
简短扼要
文字内容要简洁明了，结合 图像进行信息展示。
互动体验
增加互动元素，引导受众积 极参与，并提供反馈机制。
案例展示
1
成功案例分享
展示使用剑桥模型ppt课件取得成功的案例，分析其设计要点和效果。
2
错误案例分析
分析使用剑桥模型ppt课件出现的错误和不当设计，并提出改进建议。
2 舒适阅读
剑桥模型ppt课件应选择适合的字体和颜色，提供良好的阅读体验。
3 重点突出
剑桥模型ppt课件应通过排版、颜色等手段，突出重点和关键信息。
剑桥模型ppt课件的制作步骤
准备
明确目标和受众，收集素材和 数据。
设计
选择合适的模板，排版内容， 添加图像和动画。
编辑
优化内容表达，精细调整动画 效果。
剑桥模型ppt课件的特点
生动性
剑桥模型ppt课件能够利用图像和动画等元素，提高课件内容的生动性。
互动性
剑桥模型ppt课件可以增加互动元素，使受众积极参与和互动。
可视化
剑桥模型ppt课件以图像和动画等可视化元素为主要表现形式，增强了信息的传达效果。
剑桥模型ppt课件的设计原则
1 简洁明了
剑桥模型ppt课件应简洁明了，突出主题，避免信息过载。
高等土力学课件剑桥模型ppt 课件
高等土力学(李广信)2.4 土的弹性模型
ε →0
1
图2－34 泊松比中参数的确定 －
ν →f
i
νi=f=G-F lg(σ3 /pa)
ε1趋近于0，νt→νi
νi与围压σ3成对数关系
d(−ε 3 ) (1 − Dε1 ) f + Dε1 f νt = = 2 dε1 (1 + Dε1 )
ε1 =
νt =
1− b(σ 1 − σ 3 )
a(σ 1 − σ 3 )
(2)非线性强度包线
σ 3 ϕ = ϕ0 − ∆ϕ lg P a
Ss = S 4
σ3
(3)加卸载判断（考虑围压 与应力水平）
pa
σ1 −σ 3 S= (σ1 − σ 3 )f
(4)中主应力的影响
（σ2＋σ3)/2代替σ3或者考虑 平面应变试验的φp
σ
3
3
σ3
σ2
代替σ3
2. 各种非线性K,G 模型
B = K bP ( a
σ3
P a
)
m
试验参数Kb, m
4）E-ν模型：假设ε1与-ε3成双曲线关系
ε
1=
f + D(−ε 3 )
−ε 3
−ε3
ε1
= f − Dε 3
d(−ε 3 ) (1 − Dε1 ) f + Dε1 f νt = = 2 dε1 (1 + Dε1 )
d(−ε 3 ) (1 − Dε1 ) f + Dε1 f νt = = 2 dε1 (1 + Dε1 )
(σ1 − σ 3 )f Rf = (σ1 − σ 3 )ult
(σ1-σ3)ult
破坏比Rf
σ1-σ3
(σ1-σ3)f
高等土力学-课件
E 1
ε
1、沉降计算问题
σ
τf
ε
2、土压力问题 3、边坡稳定问题 4、地基承载力问题
强度问题加变形问题
极限平衡分析 条分法 k=1.4
强度问题加变形问题
上海倒楼问题 成寿寺邮电出版社基坑(上抬)
相互作用问题
有限土体土压力问题
深、大基础承载力问题 Pu=cNC + rdNq + rbNr/2
内蒙鄂尔多斯某砼搅拌站
（1930年，美国哈佛大学工硬化 加工软化
εa
不同应力路径下来做三轴试验:
1、常规 σr不变 σa增加
三轴压缩
σr不变 σa减小
三轴挤压（三轴拉伸）
其他
σa不变 σr增加 三轴挤压 σa不变 σr减小 三轴压缩 σa增大 σr减小 但平均应力不变
三轴压缩
σr增大 σa减小 但平均应力不变 三轴挤压
J.H.Atkinson, P.L.Bransby
主要内容
1、引言 2、土工试验 3、应力分析、应变分析 4、屈服准则 5、几个模型
Duncan— Chang Model Lade—Duncan Model Cambridge Model 6、渗流问题 7、简单的测试与讨论
李广信 70万字
龚晓南 24万字
高等土力学
（Advanced Soil Mechanics）
张钦喜
北京工业大学
2014.09
高等土力学（32h） （Advanced Soil Mechanics）
主要参考文献：
1、土的本构关系 蒋彭年 科学出版社 1982 2、土的塑性力学 屈智炯 成都科技大学出版社
1987 3、土的塑性力学 龚晓南 浙江大学出版社
ε
1、沉降计算问题
σ
τf
ε
2、土压力问题 3、边坡稳定问题 4、地基承载力问题
强度问题加变形问题
极限平衡分析 条分法 k=1.4
强度问题加变形问题
上海倒楼问题 成寿寺邮电出版社基坑(上抬)
相互作用问题
有限土体土压力问题
深、大基础承载力问题 Pu=cNC + rdNq + rbNr/2
内蒙鄂尔多斯某砼搅拌站
（1930年，美国哈佛大学工硬化 加工软化
εa
不同应力路径下来做三轴试验:
1、常规 σr不变 σa增加
三轴压缩
σr不变 σa减小
三轴挤压（三轴拉伸）
其他
σa不变 σr增加 三轴挤压 σa不变 σr减小 三轴压缩 σa增大 σr减小 但平均应力不变
三轴压缩
σr增大 σa减小 但平均应力不变 三轴挤压
J.H.Atkinson, P.L.Bransby
主要内容
1、引言 2、土工试验 3、应力分析、应变分析 4、屈服准则 5、几个模型
Duncan— Chang Model Lade—Duncan Model Cambridge Model 6、渗流问题 7、简单的测试与讨论
李广信 70万字
龚晓南 24万字
高等土力学
（Advanced Soil Mechanics）
张钦喜
北京工业大学
2014.09
高等土力学（32h） （Advanced Soil Mechanics）
主要参考文献：
1、土的本构关系 蒋彭年 科学出版社 1982 2、土的塑性力学 屈智炯 成都科技大学出版社
1987 3、土的塑性力学 龚晓南 浙江大学出版社
高等土力学-李广信-清华版
6
第一章 土工试验及测试
(6) 减载的三轴伸长（RTE：Reduced triaxial extension）试验 试样首先在σ c 下等向压缩固结，然后保持室压σ c 不变，轴向σ a 减小，即 ∆σ 3 = ∆σ a < 0 ，
∆σ 1 = ∆σ 2 = ∆σ c = 0 ，试样被轴向伸长，可达到破坏。由于室压不变，试样伸长，所以这种试验 也被称为三轴伸长试验。这时θ = 30o 或 b = 1.0 。当σ 3 < 0 时，试样中实际上存在拉应力，可引起
三轴试验。对于所有的三轴试验，试样受到的三个主应力总有两个是相等的。所以常用平均主应力 p
和广义剪应力σc) q=（σa‐σc） 在一般应力状态下，为了表示中主应力的大小，常用另外两个参数表示：
（1.1.1） （1.1.2）
b = (σ 2 − σ 3 ) /(σ 1 − σ 3 )
第一章 土工试验及测试
由于土的力学性质的复杂多变，土工试验是土力学中的基本内容，试验土力学成为土力学的一 个重要分支。另一方面，由于现场原状土的结构性，土工问题的诸多影响因素使现场原位测试和工 程原型监测成为工程实践中不可缺少的一部分。
广义的土工试验包括室内试验、原位测试、模型试验和原位监测等；从内容上又可分为物理性 质试验、力学性质试验和水力学性质试验；也可以从宏观和微观不同尺度进行试验和测试。本章侧 重于土的力学性质试验。
土工试验的不可替代的作用表现在： 1. 只有通过试验才能揭示土作为一种碎散多相的地质材料的一般的和特有的力学性质。 2. 只有对具体土样的试验，才能揭示不同类型、不同产地、不同状态土的不同力学性质，如：
非饱和土、区域性土、人工复合土等。 3. 试验是确定各种理论参数的基本手段。 4. 试验是验证各种理论的正确性及实用性的主要手段。 5. 足尺试验、模型试验可以验证土力学理论与数值计算结果的合理性；也是认识和解决实际
第一章 土工试验及测试
(6) 减载的三轴伸长（RTE：Reduced triaxial extension）试验 试样首先在σ c 下等向压缩固结，然后保持室压σ c 不变，轴向σ a 减小，即 ∆σ 3 = ∆σ a < 0 ，
∆σ 1 = ∆σ 2 = ∆σ c = 0 ，试样被轴向伸长，可达到破坏。由于室压不变，试样伸长，所以这种试验 也被称为三轴伸长试验。这时θ = 30o 或 b = 1.0 。当σ 3 < 0 时，试样中实际上存在拉应力，可引起
三轴试验。对于所有的三轴试验，试样受到的三个主应力总有两个是相等的。所以常用平均主应力 p
和广义剪应力σc) q=（σa‐σc） 在一般应力状态下，为了表示中主应力的大小，常用另外两个参数表示：
（1.1.1） （1.1.2）
b = (σ 2 − σ 3 ) /(σ 1 − σ 3 )
第一章 土工试验及测试
由于土的力学性质的复杂多变，土工试验是土力学中的基本内容，试验土力学成为土力学的一 个重要分支。另一方面，由于现场原状土的结构性，土工问题的诸多影响因素使现场原位测试和工 程原型监测成为工程实践中不可缺少的一部分。
广义的土工试验包括室内试验、原位测试、模型试验和原位监测等；从内容上又可分为物理性 质试验、力学性质试验和水力学性质试验；也可以从宏观和微观不同尺度进行试验和测试。本章侧 重于土的力学性质试验。
土工试验的不可替代的作用表现在： 1. 只有通过试验才能揭示土作为一种碎散多相的地质材料的一般的和特有的力学性质。 2. 只有对具体土样的试验，才能揭示不同类型、不同产地、不同状态土的不同力学性质，如：
非饱和土、区域性土、人工复合土等。 3. 试验是确定各种理论参数的基本手段。 4. 试验是验证各种理论的正确性及实用性的主要手段。 5. 足尺试验、模型试验可以验证土力学理论与数值计算结果的合理性；也是认识和解决实际
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（6）
dW epdv e
dp' （7）
1e
2) 假定塑性变性能可表示为：
dW pM pdpM pd
（8）：这是一个重 要假设
dWppdV pqdp
（4）
d E d W e d W p 1 ed p ' M p d（（（987）））＝＋
p'dv1edpp'' Mp' q' d
（10）＝（1） ＋（9)
比体积：v1+e v=e
e
1
v－e/(1+e0)
图2－44 的几何意义
固结不排水试验的有效应力路径相似性
q
D3
U3
D2
U2
U1
D1
临界状态线
CSL: Critical State Line
p
C1
C2
C3
C-D：固结排水试验有效应力路径 图2－45 固结不排水试验
C-U：固结不排水试验有效应力路径
的有效应力路径
NCL: normal consolidation line
CSL: critical state line
q=M p
v=N- lnp（NCL)
v=- lnp (CSL)
N
p＝exp(-v)/
图2－46
正常固结粘土的排水与不排水应力路径
物态边界面与临界状态线
v=- lnp
p＝exp((-v)/ ) q=Mp=M exp((-v)/ )
卸载－弹性墙
弹性墙
图2－56 弹性墙
2. 能量方程
dEp'dvq'd （1）
变性能＝弹性变性能＋塑性变性能
dEdW edW p （2）
其中
dWepdveqde
（3）
dWppdvpqdp
（4）
塑性变性能的基本假设： 1）假设一切剪应变是不可恢复的，亦即：
d e 0 （5）
dV e 1dvee1edpp''
dV p
dv
1 1e
p'
dp'
(11)
p'dv pM p' q' d
(12)=(11) +(10)
d d p
dVp dp
Mqp''
M
(13)
3. 屈服轨迹与屈服方程
弹性墙上塑性体应变pv为 常数，如果以pv为硬化参数
则AF(A´F´)为屈服轨迹
图2－57 屈服轨迹
dVp dp
Mqp''
（1）
5. “湿粘土”的应力应变关系表达式
q' p'
M Nvlnp'
（1） 微分此式
d v
dv 1 e
dv1 1eM ddpp'' （2） 代入下式
d E 1 ed p 'M 'd p p 'd v q 'd
d
1 eMp'
dq'
M
dp'
1 e
p'd Mdp'
Mp'M
（3） （4）
应力应变关系
dv 1 1eM ddpp''
（2）
d
1 eMp'
dq'
M
dp'
1 e
p'd Mdp'
Mp'M
（4）
2.6.4 修正的剑桥模型
1.屈服函数
塑性能能量方程： 假设：
dWppdV pqdp
dWpp dV p 2Mdp 2 （1）
代入流动规则： dp'dvpdq'dp0
（15）
边界条件：p=p0, q=0: v=v0
f
q'
M ln
p' 0
p'
p
(16): 屈服函数
弹性墙在q-p平面上的 投影AF －
子弹头屈服轨迹
弹性墙上－v0p及pv唯一
图2－59 子弹头屈服轨迹
4. 物态边界面的方程
屈服轨迹沿NCL移动，得到三维变量表示的物态 边界面方程：
q' p'
M Nvlnp'
图2－52 完全的物态边界面
完全的物态边界面
包括超固结土的 完全的物态边界 面－(状态只能在 面内和面上）
Vi-Ti-Si-Ni
图2－53 完全的物态边界面
HS
超固结
CS
正常固结
图2－54 排水试验的应力体变曲线
图2－55 正常固结土与超固结土的应力路径
2.6.3 弹性墙与屈服轨迹
1. 弹性墙 正常固结粘土与轻超固结粘土（wet clay) 各向等压固结: 加载：NCL
临界状态线，物态面
图2－47 正常固结粘 土的物态边界面
三维空间的物态边 界面
（1）p,q,e三者一一对应 （2）有效应力路径的唯一性
图2－48正常固结粘土的物态边界面
图2－49 各向等 压的加载与卸载
v=N- lnp：初始加载 v=v- lnp：回弹曲线
2.6.2 超固结土及完全的物态边界面
M
（13）
图2－58 正交性示意图
上式表示了流动规则：
M时，dpv=0 0时， dvp/dp =M
流
动
屈服函数：
规
d
p v
d p
d 则q dp
与曲线正交
dVp dp
q' M
p'
M
(13)
dq' dp'
q' p'
M
0
（14）
dq' dp'
q' p'
M
0
（14）
积分：
q' ln p' ln c Mp'
重超固结粘土： 0－pm －H－DH(UH) H-DH-RH: 排水试验－剪胀与 软化 H-UH: 不排水试验,负孔压， 强度超过临界状态线
pm
峰值强度（TS)与残余强度 （临界线上）
排水试验的应 力应变曲线
图2－51重超固结粘土的路径
完全的物态边界面： 0T：零应力线（无拉应力） TS：超固结土的强度线-Hvorslev面 CS：v=常数的Roscoe 面 包括了正常固结土、重超固结土的 可能的（极限）应力状态
M
图2－60 修正剑桥模型的椭圆帽子屈服面
2.应力应变关系
dv1 1eM 2 2d 2dp p''（4）
d1 e M 2 2 2M 2 2d 2dp p'' （5）
dq' dp'
M2 2 2
0
（2）
对式（2)积分，带入边界条件，得到方程：
dq' M2 2
0
dp' 2
p
p
0
M2 M 2 2 （3）
p'
p 0 2
2M q' 2
p' 0 2
2
（3）
修正剑桥模型的屈服面方程
p'
p 0 2
2M q' 2
p' 0 2
2
（3）
屈服轨迹的形状：
(2)
椭圆（帽子）屈服面
1.正常固结粘土 2.轻超固结粘土：OCR比较小，卸载范围不大 3.强超固结粘土：OCR很大, 卸载后的应力比先期
固结应力小很多
轻超固结粘土：
0－ pm －L－D(U)
SL－回弹曲线，L位于
pm
NCL与CSL之间
LD:排水试验－体缩
LU:不排水－体积变， 正孔压
强度线唯一，剪缩
图2－50 轻超固结粘土的路径
2.6 土的剑桥模型
2.6.1 正常固结粘土的物态边界面 （state boundary surface)
2.6.2 超固结土及完全的物态边界面 2.6.3 弹性墙与剑桥模型的屈服函数 2.6.4 修正的剑桥模型
2.6.1 正常固结粘土的物态边界面
三轴应力状态：
偏应力： q= 平均主应力：p=(+2)/3