培优专题(加法原理)
六年级竞赛培优举一反三第26周-加法、乘法原理PPT课件

-
5
从上面的三道例题可以看出如下的规律:
第26周 加法、 乘法原理
-
1
在做一件事情时,如果有几类不同的方法,而每一类方法中又 有几种可能的情况,要求一共有多少种不同的方法,就用加 法原理来解决;而做一件事情时,如果要分几步完成,完成 每一步时又有几种不同的方法,要知道完成这件事一共有多 少种方法,就用乘法原理来解决。
-
2
【例题1】小红、小丽和小敏三个人到世纪公园游玩拍照留念 (不考虑站的顺序),共有多少种不同的拍照方法?
【思路导航】我们不妨按照相的人数来分类。一个人照相:小 红、小丽和小敏共3种拍照方法;两人合影:小红和小丽合 影、小红和小敏合影、小丽和小敏合影共3种拍照方法;三 个人合影只有1种拍照方法。
3+3+1=7(种)
答:共有7种不同的拍照方法.
-
3
【例题2】从北京到天津的列车中途要经过4个站,这列列车从 北京到天津共要准备多少种不同的车票?
【思路导航】从北京到天津的列车中途要经过4个站,那么以 北京为起点,共要准备5种不同的车票(分别为到途中第一 站、第二站、第三站、第四站和终点天津站);以途中第一 站为起点共要准备4种不同的车票(分别为到途中第二站、 第三站、第四站和终点天津站);照此类推,以途中第二站 为起点共要准备3种不同的车票;以途中第三站为起点共要 准备2种不同的车票;以途中第四站为起点共要准备1种不同 的车票;
【思路导航】方法一:首先根据题意画出树状图,然后由树状图求得所有 等可能的结果以及有多少个真分数.画树状图得:
六年级数学培优之加乘原理

第六讲加乘原理例1:一个盒子内装有5个小球,另一个盒子内装有9个小球,所有这些小球颜色各不相同。
问:①从两个盒子内任取一个小球,有多少种不同的取法?②从两个盒子内各取一个小球,有多少种不同的取法?例2:从1到399的所有自然数中,不含有数字3的自然数有多少个?例3:用5种颜色给图1的五个区域染色,相邻的区域染不同的颜色,每个区域染一种颜色。
问:共有多少种不同的染色方法?例4:学校羽毛球队有12名男队员,10名女队员。
(l)要挑选一名男队员和一名女队员组成一对男、女混合双打选手,有多少种不同的搭配方法?(2)该羽毛球队在比赛中获团体总分第一名,学校选一名运动员去领奖,有多少种选法?例5:找出图2中从A点出发,经过C点和D点到B点的最短路线,共有多少条?例6:现有壹元的人民币4张,贰元的人民币2张,伍元的人民币5张,如果从中至少取一张,至多取11张,那么共可以配成多少种不同的钱数?例7:由数字1、2、3、4、5、6、7、8、9可组成多少个①三位数?②三位偶数?③没有重复数字的三位偶数?④百位为9的没有重复数字的三位数?⑤百位为9的没有重复数字的三位偶数?A1.从0、1、2、3、4这五个数字中任取3个,可以组成______个无重复数字的三位数。
2.在m×n的方格纸上,取两个相邻的小方格共有______种取法。
3.书架上有不同的数学书20本,不同的语文书10本,现从书架上取书,试问:(1)取出一本书,有______种不同的取法。
(2)取出数学书和语文书各一本,有______种不同的取法。
4.将1、2、3、4这4个数字从小到大排成一行,在4个数中间任意插入乘号,可以得到______个不同的乘积(要求最少有一个乘号)。
5.将一个长方形用对角线分成四份,如图所示,现用五种颜色染色,要求每小块染一种颜色,相邻的两小块(有公共边的)必须染不同的颜色。
那么,总共有______种不同的染色方法。
B6.用红、绿、黄、蓝四种颜色分别去涂图中的A、B、C、D四个区域,要求相邻区域不可同色,共有______种不同涂法。
六年级数学培优资料

六年级数学培优资料一、数学基础知识1.四则运算:加、减、乘、除。
2.数学符号的含义:加号、减号、乘号、除号、等号、大于号、小于号等。
3.数字间的大小比较:正数、负数、零及其大小顺序。
4.小数的概念和大小比较:小数点的位置代表了小数的大小。
5.分数的概念和大小比较:分子和分母的大小决定了分数的大小。
二、数字的认识与进位1.数位的认识:个位、十位、百位、千位等。
2.0~9999的数字识别、认读和写法。
3.进位原理的理解:十进位、百进位、千进位等。
4.进位运算的实现方法:列式计算法和口诀计算法。
三、数字的加减法1.加法原理的掌握:加数、被加数、和的概念。
2.加法的背诵要点:进位原则、竖式加法口诀(竖式加法、横式加法)。
3.减法的概念和掌握:被减数、减数、差等。
4.竖式减法和口诀计算法:不退位减法和退位减法。
四、数字的乘除法1.乘法的概念:乘数、被乘数、积等。
2.乘法口诀的记忆和应用:2~9口诀、竖式乘法口诀、小数乘法口诀。
3.长除法的掌握:被除数、除数、商等。
4.除法口诀的记忆和应用:整除法、小数除法口诀。
五、应用题训练1.问题解决的方法:分解问题、构造模型、试错、逻辑推理等。
2.应用题的类型:魔术数字、等价数字、变幻数字、逻辑推理等。
3.综合应用题的训练:小学数学综合应用题训练册。
六、数学思维和学习方法1.数学思维方法:逻辑思维、空间思维、想象力、分析思考等。
2.学习方法的总结与归纳:记忆技巧、复习方法、总复习等。
3.思维能力训练的方法:游戏、解决问题、比赛等。
四则运算相关例题:例1:计算70 ÷ 5解:因为70 ÷ 5 =14,所以70 ÷ 5 =14.例2:计算8 × 17解:因为8 × 17 = 136,所以8 × 17 = 136.例3:计算59 - 18解:因为59 - 18 = 41 ,所以59 - 18 = 41.例4:计算86 + 14解:因为86 + 14 = 100 ,所以86 + 14 = 100.例5:计算6.5 - 3.25解:因为6.5 - 3.25 = 3.25 ,所以6.5 - 3.25 = 3.25.例6:如果一份工只有60元,那么6小时工作的总工资是多少?解:因为6 × 60 =360,所以6小时工作的总工资是360元。
六年级上册数学讲义-小升初培优:第06讲 加乘原理 (解析版)全国通用
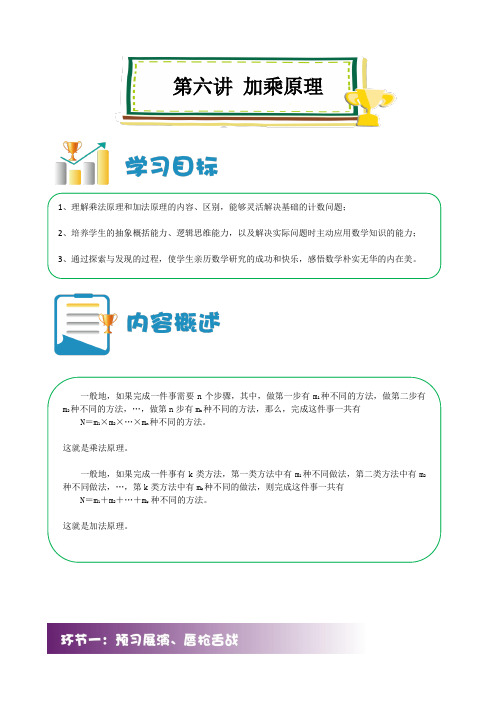
第六讲加乘原理一般地,如果完成一件事需要n个步骤,其中,做第一步有m1种不同的方法,做第二步有m2种不同的方法,…,做第n步有m n种不同的方法,那么,完成这件事一共有N=m1×m2×…×m n种不同的方法。
这就是乘法原理。
一般地,如果完成一件事有k类方法,第一类方法中有m1种不同做法,第二类方法中有m2种不同做法,…,第k类方法中有m k种不同的做法,则完成这件事一共有N=m1+m2+…+m k 种不同的方法。
这就是加法原理。
1、理解乘法原理和加法原理的内容、区别,能够灵活解决基础的计数问题;2、培养学生的抽象概括能力、逻辑思维能力,以及解决实际问题时主动应用数学知识的能力;3、通过探索与发现的过程,使学生亲历数学研究的成功和快乐,感悟数学朴实无华的内在美。
乐羊羊到食堂去买饭,主食有三种,副食有五种,甜点一种,喜羊羊主食和副食各买一种,甜点可买可不买,共有多少种不同的买法?【解析】喜羊羊买饭要分三步完成,即先买一种主食,再买一种副食(或先买副食后买主食),然后甜点。
其中,买主食有3种不同的方法,买副食有5种不同的方法,买甜点有2种不同的方法(买或者不买)。
故可以由乘法原理解决。
解答:共有3×5×2=30种不同的方法。
学校组织读书活动,要求每个同学读一本书。
小明到图书馆借书时,图书馆有不同的外语书150本,不同的科技书200本,不同的小说书100本。
那么,小明借一本书可以有多少种不同的选法?【解析】在这个问题中,小明选一本书有三类方法。
即要么选外语书,要么选科技书,要么选小说。
所以,是应用加法原理的问题。
解答:小明借一本书共有:150+200+100=450种不同的选法。
由数字0、1、2、3组成三位数,问:(1)可组成多少个不相等的三位数?(2)可组成多少个没有重复数字的三位数? 讲演者:得分:讲演者:得分:【解析】在确定由0、1、2、3组成的三位数的过程中,应该一位一位地去确定。
高二培优特训:两个计数原理
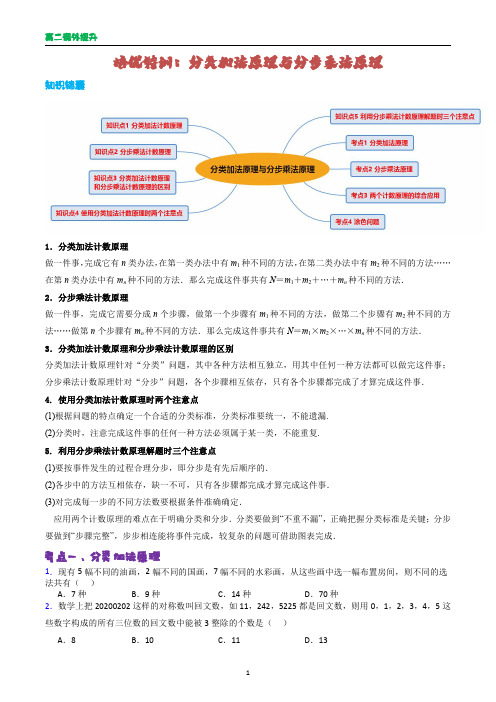
培优特训:分类加法原理与分步乘法原理知识锦囊1.分类加法计数原理做一件事,完成它有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法……在第n类办法中有m n种不同的方法.那么完成这件事共有N=m1+m2+…+m n种不同的方法.2.分步乘法计数原理做一件事,完成它需要分成n个步骤,做第一个步骤有m1种不同的方法,做第二个步骤有m2种不同的方法……做第n个步骤有m n种不同的方法.那么完成这件事共有N=m1×m2×…×m n种不同的方法.3.分类加法计数原理和分步乘法计数原理的区别分类加法计数原理针对“分类”问题,其中各种方法相互独立,用其中任何一种方法都可以做完这件事;分步乘法计数原理针对“分步”问题,各个步骤相互依存,只有各个步骤都完成了才算完成这件事.4.使用分类加法计数原理时两个注意点(1)根据问题的特点确定一个合适的分类标准,分类标准要统一,不能遗漏.(2)分类时,注意完成这件事的任何一种方法必须属于某一类,不能重复.5.利用分步乘法计数原理解题时三个注意点(1)要按事件发生的过程合理分步,即分步是有先后顺序的.(2)各步中的方法互相依存,缺一不可,只有各步骤都完成才算完成这件事.(3)对完成每一步的不同方法数要根据条件准确确定.应用两个计数原理的难点在于明确分类和分步.分类要做到“不重不漏”,正确把握分类标准是关键;分步要做到“步骤完整”,步步相连能将事件完成,较复杂的问题可借助图表完成.考点一、分类加法原理1.现有5幅不同的油画,2幅不同的国画,7幅不同的水彩画,从这些画中选一幅布置房间,则不同的选法共有()A.7种B.9种C.14种D.70种2.数学上把20200202这样的对称数叫回文数,如11,242,5225都是回文数,则用0,1,2,3,4,5这些数字构成的所有三位数的回文数中能被3整除的个数是()A.8B.10C.11D.13A.5B.8CB=,在6.已知集合{2,4,6,8,10}A=,{1,3,5,7,9}则其中m n>的数对有多少个考点二、分步乘法原理1.甲、乙分别从4门不同课程中选修1门,且2考点三、两个计数原理的综合应用.12号线开通运营,甲、乙、丙、丁四位同学决定乘坐地铁去观洲、人民公园、6.重庆九宫格火锅,是重庆火锅独特的烹饪方式.九宫格下面是相通的,实现了通”它把火锅分为三个层次,一类格子形状相同):“中间格“火力旺盛,不宜久煮,适合放一些质地嫩脆、顷刻即熟的食物;A.108B.考点四、涂色问题A.72B.962.用红、黄、蓝、绿、橙五种不同颜色给如图所示的同一种颜色,有公共边的区域使用不同颜色,则共有涂色方法3.学习涂色能锻炼手眼协调能力,更能提高审美能力荷绿,欲给小房子中的四个区域涂色,要求相邻区域不涂同一颜色,且橄榄绿与薄荷绿也不涂在相邻的区域内,则共有4.西部五省,有五种颜色供选择涂色,要求每省涂一色,相邻省不同色,有4.中国是世界上最早发明雨伞的国家,伞是中国劳动人民一个重要的创造.如图所示的雨伞,其伞面被伞骨分成8个区域,每个区域分别印有数字1,2,3,..,8,现准备给该伞面的每个区域涂色,要求每个区域涂一种颜色,相邻两个区域所涂颜色不能相同,对称的两个区域(如区域1与区域5)所涂颜色相同.若有7种不同颜色的颜料可供选择,则不同的涂色方案有()A.1050种B.1260种C.1302种D.1512种。
小学四年级培优数学第六章第三课:计数问题之加法原理和乘法原理

典型问题
2、小又和爸爸进入一家中餐厅后,发现 主食有3种,热菜有20种.他们打算主食和 热菜各买一种,一共有多少种不同的买 法?
典型问题
3、传说地球上有7颗不同的龙珠,如果 找齐这7颗龙珠,并且按照特定的顺序排 成一行,就会有神龙出现.勇敢的小又找 到了这7颗龙珠,但是她不知道排列的特 定顺序.请问:运气不好的小又最多要试 几次才能遇见神龙?
培优数学
第六部分
计数问题
“一分耕耘一分收获。”
第3讲
加法原理与乘法原理
理解加法原理和乘法原理,体会分类 计数与分步计数的区别;能够根据题 目条件,对问题进行合理的分类与分 步;学习用标数法解决各类路径问题.
典型问题
1、小又和爸爸出去吃午饭,发现附近的 中餐厅有9个,火锅店有3个,羊肉汤馆 有2个.他们准备随便在一家吃饭,一共有 多少种不同的选择?
典型问题
4、电影院里有10个空座位,小又和哥哥 去看电影,每个人坐一个座位,共有多 少种不同的坐法?
典型问题 5、用红、黄、蓝三种颜色给图中的三个 圆圈染色,一个圆圈只能染一种颜色, 并且相连的两个圆圈不能同色.一共有多 少种不同的染色方法?
A
B
C
四年级下册数学奥数试题-培优拓展训练--第1讲:加乘原理(教师版)
第一讲加乘原理加法原理:完成一件工作共有N类方法。
在第一类方法中有m1种不同的方法,在第二类方法中有m2种不同的方法,……,在第N类方法中有m n种不同的方法,那么完成这件工作共有N=m1+m2+m3+…+m n种不同方法。
运用加法原理计数,关键在于合理分类,不重不漏。
要求每一类中的每一种方法都可以独立地完成此任务;两类不同办法中的具体方法,互不相同(即分类不重);完成此任务的任何一种方法,都属于某一类(即分类不漏)。
合理分类也是运用加法原理解决问题的难点,不同的问题,分类的标准往往不同,需要积累一定的解题经验。
乘法原理:完成一件工作共需N个步骤:完成第一个步骤有m1种方法,完成第二个步骤有m2种方法,…,完成第N个步骤有m n种方法,那么,完成这件工作共有m1×m2×…×m n种方法。
运用乘法原理计数,关键在于合理分步。
完成这件工作的N个步骤,各个步骤之间是相互联系的,任何一步的一种方法都不能完成此工作,必须连续完成这N步才能完成此工作;各步计数相互独立;只要有一步中所采取的方法不同,则对应的完成此工作的方法也不同。
这两个基本原理是排列和组合的基础,教学时要先通过生活中浅显的实例,如购物问题、行程问题、搭配问题等,帮助孩子理解两个原理,再让孩子学习运用原理解决问题。
运用两个原理解决的都是比较复杂的计数问题,在解题时要细心、耐心、有条理地分析问题。
计数时要注意区分是分类问题还是分步问题,正确运用两个原理。
灵活机动地分层重复使用或综合运用两个原理,可以巧妙解决很多复杂的计数问题。
小学阶段只学习两个原理的简单应用。
一:两种原理的基础内容的记忆和计算的方法。
二:两种计数原理的区分和综合应用。
【题目】:1用1角、2角和5角的三种人民币(每种的张数没有限制)组成1元钱,有多少种方法?【解析】:运用加法原理,把组成方法分成三大类:①只取一种人民币组成1元,有3种方法:10张1角;5张2角;2张5角。
人教版高中数学选择性必修第三册培优系列讲义第1讲分类加法计数原理与分步乘法计数原理(无答案)
第1讲分类加法计数原理与分步乘法计数原理【考点梳理】知识点一分类加法计数原理完成一件事有两类不同方案,在第1类方案中有m 种不同的方法,在第2类方案中有n 种不同的方法,那么完成这件事共有N =m +n 种不同的方法.知识点二分步乘法计数原理完成一件事需要两个步骤,做第1步有m 种不同的方法,做第2步有n 种不同的方法,那么完成这件事共有N =m ×n 种不同的方法.知识点三两个计数原理的区别与联系分类加法计数原理分步乘法计数原理相同点回答的都是有关做一件事的不同方法种数的问题不同点针对的是“分类”问题不同点各种方法相互独立,用其中任何一种方法都可以做完这件事各个步骤中的方法互相依存,只有每一个步骤都完成才算做完这件事知识点四两个计数原理的应用用两个计数原理解决计数问题时,最重要的是在开始计算之前要仔细分析两点:一、要完成的“一件事”是什么;二、需要分类还是需要分步.(1)分类要做到“不重不漏”,分类后再分别对每一类进行计数,最后用分类加法计数原理求和,得到总数.(2)分步要做到“步骤完整”,即完成了所有步骤,恰好完成任务.分类后再计算每一步的方法数,最后根据分步乘法计数原理,把完成每一步的方法数相乘,得到总数.【题型归纳】考点一分类计算原理【例1-1】(2021·全国·高二单元测试)如图所示,从甲地到乙地有3条公路可走,从乙地到丙地有2条公路可走,从甲地不经过乙地到丙地有2条水路可走.则从甲地经过乙地到丙地和从甲地到丙地的走法种数分别为()A.6,8B.6,6C.5,7D.6,2【例1-2】(2021·江西·横峰中学)由数字1,2,3组成的无重复数字的整数中,偶数的个数为()A.15B.12C.10D.5【考点精练】1.(2021·甘肃·静宁县第一中学)如图所示,在A,B间有四个焊接点1,2,3,4,若焊接点脱落导致断路,则电路不通,则焊接点脱落的不通情况有()种.A.9B.11C.13D.152.(2021·全国·高二课时练习)从1,2,3,4,5,6,7,8,9这9个数字中任取两个,其中一个作为底数,另一个作为真数,则可以得到不同对数值的个数为()A.64B.56C.53D.513.(2021·全国·高二课时练习)设椭圆22xa+22yb=1的焦点在y轴上,其中a∈{1,2,3,4,5},b={1,2,3,4,5,6,7},则满足上述条件的椭圆个数为()A.20B.24C.12D.114(2021·全国·高二课时练习)算盘是中国古代的一项重要发明.现有一种算盘(如图1),共两档,自右向左分别表示个位和十位,档中横以梁,梁上一珠拨下,记作数字5,梁下五珠,上拨一珠记作数字1(如图2中算盘表示整数51).如果拨动图1算盘中的三枚算珠,可以表示不同整数的个数为()A.16B.15C.12D.10考点二分步计算原理【例2-1】(2021·全国·高二课时练习)一植物园的参观路径如图所示,若要全部参观并且路线不重复,则不同的参观路线共有()A.6种B.8种C.36种D.48种【例2-2】(2021·福建·泉州科技中学)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,如图,将一个四棱锥的每一个顶点染上一种颜色,并使同一条棱上的两端异色,如果只有5种颜色可供使用,则不同的染色方法总数为()A.180B.240C.420D.480【考点精练】1.(2021·全国·高二课时练习)沪宁高铁线上有六个大站:上海、苏州、无锡、常州、镇江、南京,铁路部门应为沪宁线上的六个大站(这六个大站之间)准备不同的火车票的种数为()A.15B.30C.12D.362.(2021·全国·高二课时练习)现有四件不同款式的上衣与三条不同颜色的长裤,如果选一条长裤与一件上衣配成一套,那么不同的选法种数为()A.7B.64C.12D.813.(2021·全国·高二课时练习)(多选题)有4位同学报名参加三个不同的社团,则下列说法正确的是()A.每位同学限报其中一个社团,则不同的报名方法共有43种B.每位同学限报其中一个社团,则不同的报名方法共有34种C.每个社团限报一个人,则不同的报名方法共有24种D.每个社团限报一个人,则不同的报名方法共有33种4.(2021·全国·高二课时练习)将3个不同的小球放入4个盒子中,不同放法种数为()A.81B.64C.14D.12考点三两个计数原理的综合运用【例3-1】(2021·全国·高二课时练习)用0、1、2、3、4、5可以组成多少个无重复数字的(1)密码箱的四位密码;(2)比2000大的四位偶数.【例3-2】(2021·全国·高二课时练习)用()*3,n n n ≥∈N 种不同的颜色给如图所示的A ,B ,C ,D 四个区域涂色,要求相邻区域不能用同一种颜色.(1)当6n =时,图①、图②各有多少种不同的涂色方案?(2)若图③有180种不同的涂色方案,求n 的值.【考点精练】1.(2021·全国·高二课时练习)已知甲的车牌尾数为9,他的四位同事的车牌尾数分别为0,2,1,5,为遵守当地某月5日至9日5天的限行规定(奇数日车牌尾数为奇数的车通行,偶数日车牌尾数为偶数的车通行),五人商议拼车出行,每天任选一辆符合规定的车,但甲的车最多只能用一天,则不同的用车方案种数为()A.64B.80C.96D.1202.(2021·全国·高二课时练习)王华同学有课外参考书若干本,其中有5本不同的外语书,4本不同的数学书,3本不同的物理书,他欲带参考书到图书馆阅读.(1)若他从这些参考书中带1本去图书馆,则有________种不同的带法;(2)若带外语、数学、物理参考书各1本,则有________种不同的带法;(3)若从这些参考书中选2本不同学科的参考书带到图书馆,则有________种不同的带法.3.(2021·全国·高二课时练习)将红、黄、蓝、白、黑五种颜色涂在如图所示“田”字形的4个小方格内,每格涂一种颜色,相邻两格涂不同的颜色,如果颜色可以反复使用,共有多少种不同的涂色方法?4.(2021·全国·高二课时练习)用0,1,2,3,4五个数字.(1)可以排成多少个三位数字的电话号码?(2)可以排成多少个三位数?(3)可以排成多少个能被2整除的无重复数字的三位数?5.(2021·全国·高二课时练习)如图,将一个四棱锥的每一个顶点染一种颜色,并使同一条棱上的两端点异色,如果只有4种颜色可供使用,则不同的染色方法有________种.。
加法原理(讲师版)
学科培优数学“加法原理”学生姓名授课日期教师姓名授课时长知识定位无论自然界还是学习生活中,事物的组成往往是分门别类的,例如解决一件问题的往往不只一类途径,每一类途径往往又包含多种方法,如果要想知道一共有多少种解决方法,就需要用到加法原理知识梳理一、加法原理一般地,如果完成一件事有k类方法,第一类方法中有m1种不同做法,第二类方法中有m2种不同做法,…,第k类方法中有mk种不同的做法,则完成这件事共有N=m1+m2+…+mk种不同的方法.加法原理运用的范围:完成一件事的方法分成几类,每一类中的任何一种方法都能完成任务,这样的问题可以使用加法原理解决.我们可以简记为:“加法分类,类类独立”.二、加法原理解题三部曲:1、完成一件事分N类;2、每类找种数(每类的一种情况必须是能完成该件事);3、类类相加例题精讲【试题来源】【题目】小明、小华、小红三人去公园玩,想排成一行拍照留念,他们只拍了一张照片(人相同,位置不同为一张),请问他们共有多少种不同的照法?【答案】7【解析】1、要仔细审题,特别注意一道题小括号的内容,往往括号能提供解题的关键信息。
2、审题发现题目问的实质是有几种人员组合,这个组合不需要考虑组合里的人位置的变化。
3、知道题问的是什么后,就开始用我们今天所学的加法原理解题了。
第一步:分类,一共三个人,那么人员的组合可分三类了。
第一类:一个人第二类:二个人第三类:三个人把每类有几种人员组合找出来,然后类类相加即可。
最后答案是7.【知识点】加法原理【适用场合】当堂例题【难度系数】1【试题来源】【题目】有数字1、2、3可以组成多少个数?(每个数字最多只能用一次)【答案】15【解析】三个数字每个数字最多只能用一次,那么就是说每个数字也可以不用。
那么1、2、3三个数字组成一个数该怎么分类呢?一共三个数,那么顶多可组成一个三位数;想到这个地方就豁然开朗了。
原来是可以分成三类的。
第一类:组成一位数第二类:组成两位数第三类:组成三位数每类里找种数,就是我们在乘法原理中学过的数码问题了。
加法原理及乘法原理课件
在保险业务中,可能会面临多种风险,如火灾、盗窃、车祸等。根据加法原理,可以分别计算每种风险发生的概 率,然后将这些概率相加以获得多种风险同时发生的总概率。这有助于保险公司制定合理的保险费率,以应对可 能出现的多种风险。
02
乘法原理
定义
乘法原理
做一件事,完成它需要分成几步 ,每一步又可以独立地完成,那 么完成这件事的方法数就是每一 步方法数的乘积。
适用范围
适用于分步骤完成的任何事情, 每一步的方法数是固定的。
适用范围
01
02
03
组合问题
乘法原理可以用于计算组 合数,即从n个不同元素 中取出m个元素的不同取 法数。
排列问题
乘法原理也可以用于计算 排列数,即从n个不同元 素中取出m个元素进行排 列的不同排法数。
概率问题
在概率论中,乘法原理可 以用于计算多步骤事件的 概率,即多个独立事件的 概率乘积。
应用实例
组合问题
从5个不同元素中取出3个元素的 组合数为C(5,3)=10,这是通过 将第一个元素的选择方法数(5 种)与第二个元素的选择方法数
(4种)相乘得到的。
排列问题
对于3个不同元素的全排列数为 A(3,3)=6,这是通过将第一个元 素的选择方法数(3种)与第二 个元素的选择方法数(2种)相
05
加法原理与乘法原理的实践 意义
提高数学思维能力
掌握加法原理与乘法原理,能够 更好地理解和运用数学概念,提
高数学思维能力。
通过运用加法原理与乘法原理, 可以解决各种数学问题,提高数
学解题能力。
掌握加法原理与乘法原理,有助 于发现数学中的规律和模式,培
养数学直觉和创造性思维。
培养逻辑推理能力
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、下图中共有多少个角?
做一做:
3、下图中一共有多少个正方形?
做一做:
4、用1元、2元、5元和10元的纸币各1张, 一共可以组成几种不同的币值? 5、10把钥匙开10把锁,但钥匙已经混乱了, 问最多试多少次即可以将钥匙和锁配起来?
做一做:
6、有三种不同长度的小木棒如下图所示 (若干根),能搭出几种不同的长方体 和正方体?(2013年东华小升初招生试题)
例题3:
在4×4的方格图中(如图),共有多少 个正方形?
例题4:
爸爸、妈妈和小明三人在公园照相,共 有多少种不同的照法?
例题5:
□ - ○ = ◎的减法算式,要求所用的 数为1、2、3、…、9。你能列出多少种 不同的算式?
Hale Waihona Puke 一做:1、一列火车从上海开往杭州,中途要经过4 个站,应为这列火车准备多少种不同的车票?
在做一件事时,如果有几类不同的方法, 而且每一类方法中,又有几种可能的做法, 那么完成这件事有多少种做法,应当将各类 中可能的种数加起来,这就是我们将要讨论 的加法原理。
例题1:
书架上有10本故事书、3本历史书、12 本科普读物。小明任意从书架上取一本书, 有多少种不同的取法?
例题2:
一列火车从上海到南京,中途要经过6个 站,这列火车要准备多少种不同的车票?
12cm 8cm 4cm
