平移练习题大全
平移练习题

平移练习题(一)一、连一连。
升旗时国旗的运动钟摆的运动在算盘上拨珠平移电梯的运动风扇叶片的运动火车的运动光盘在电脑里的运动旋转把握汽车的方向盘二、操作。
1、向( )平移了( )格。
2、把上面的小船图向上平移5格3、画出的另一半,使它成为轴对称图形。
三、选择。
汽车在公路上运动时,轮子的运动是( )。
A、平移B、旋转C、既平移又旋转平移练习题(二)一、看图填一填。
1、长方形向()平移了()格。
2、六边形向()平移了()格。
3、五角星向()平移了()格。
二、从镜子中看到的左边图形的样子是什么?画“√”三、按要求操作。
1、把图中长方形向上平移2格;2、把图中三角形向右平移3格;3、把图中平行四边形向左平移5格。
四、按要求填图五、分别画出下面图形向下平移2格后再向右平移8格后得到的图形六、画出拖拉机先向左平移4格,再向下平移3格后的图形。
平移练习题(三)一、看图填一填。
1、长方形向()平移了()格。
2、六边形向()平移了()格。
3、五角星向()平移了()格。
二、按要求操作。
1、把图中下边的长方形向上平移2格;2、把图中左边的三角形向右平移3格;3、把图中上边的长方形向下平移4格;4、把图中右边的平行四边形向左平移5格。
5、平移后的图像什么?三、接着往下画。
四、在各图形中填上合适的数。
五、下图是按照一定规律排列起来的,请按这一规律在空格处画出适当的图形。
六、画一画。
七、在下图空格内画出合适的图形。
小学数学圆的平移练习题

小学数学圆的平移练习题一、选择题1. 一个圆向右平移3个单位,再向下平移2个单位,下列哪个选项表示平移后的圆?A. (x3, y2)B. (x+3, y+2)C. (x3, y+2)D. (x+3, y2)2. 一个圆的圆心坐标为(2, 3),将其平移后,圆心坐标变为(5,7),则该圆平移的方向是?A. 向右平移3个单位,向上平移4个单位B. 向左平移3个单位,向下平移4个单位C. 向右平移4个单位,向上平移3个单位D. 向左平移4个单位,向下平移3个单位3. 下列哪个图形是圆平移后得到的?A. 正方形B. 长方形C. 椭圆形D. 同样大小的圆二、填空题4. 一个圆的半径为5,将这个圆向左平移6个单位,再向上平移4个单位,平移后圆的圆心坐标是______。
5. 一个圆的圆心坐标为(3, 2),将其向右平移5个单位,再向下平移3个单位,平移后圆的圆心坐标是______。
6. 一个圆的圆心在原点(0, 0),将其沿x轴正方向平移8个单位,沿y轴负方向平移6个单位,平移后圆的圆心坐标是______。
三、判断题7. 圆平移后,圆的大小和形状都不会改变。
()8. 将一个圆向左平移3个单位,再向上平移2个单位,圆的位置会发生改变。
()9. 圆的平移是沿直线运动。
()四、作图题10. 在方格纸上画一个圆,圆心坐标为(4, 2),半径为3。
然后将这个圆向右平移2个单位,再向下平移3个单位,画出平移后的圆。
11. 在方格纸上画一个圆,圆心坐标为(1, 3),半径为2。
然后将这个圆向左平移4个单位,再向上平移5个单位,画出平移后的圆。
12. 在方格纸上画一个圆,圆心在原点(0, 0),半径为5。
然后将这个圆沿x轴正方向平移7个单位,沿y轴负方向平移6个单位,画出平移后的圆。
五、简答题13. 描述一个圆向左平移5个单位,再向下平移3个单位后,圆心坐标的变化。
14. 如果一个圆的圆心坐标为(10, 5),将其沿x轴负方向平移4个单位,圆心坐标会发生怎样的变化?15. 解释为什么圆在平移过程中,圆的半径不会发生改变。
二年级下册平移练习题

二年级下册平移练习题一、选择题(每题2分,共10分)1. 平移是指图形在平面上沿某个方向移动一定的距离,以下哪个图形是平移后的图形?A. 旋转后的图形B. 翻转后的图形C. 平移后的图形D. 缩放后的图形2. 下列哪个选项描述了平移的特点?A. 形状不变,大小不变B. 形状改变,大小不变C. 形状不变,大小改变D. 形状改变,大小改变3. 平移后,图形的哪些属性会发生变化?A. 形状B. 大小C. 位置D. 颜色4. 如果一个图形向右平移3个单位长度,那么它的哪个属性不会改变?A. 形状B. 大小C. 位置D. 方向5. 平移操作不适用于以下哪个几何图形?A. 直线B. 圆C. 三角形D. 点二、填空题(每题2分,共10分)6. 平移后的图形,其________保持不变。
7. 如果一个图形向下平移2个单位长度,那么它的________会发生变化。
8. 平移不改变图形的________和________。
9. 平移后的图形,其________属性会发生变化。
10. 平移操作可以应用于所有的________图形。
三、判断题(每题1分,共10分)11. 平移是一种保持图形大小和形状不变的变换。
()12. 平移后的图形,其方向可能会发生变化。
()13. 平移操作只适用于直线和三角形,不适用于圆形。
()14. 平移后的图形,其面积不会发生变化。
()15. 平移后的图形,其周长也不会发生变化。
()四、简答题(每题5分,共20分)16. 请简述平移操作的定义。
17. 请说明平移操作与旋转操作的区别。
18. 描述一个图形向右平移5个单位长度后,其位置如何变化。
19. 如果一个图形平移后,其形状和大小都发生了变化,那么这种变换是平移吗?为什么?五、操作题(每题10分,共30分)20. 根据题目所给的图形,完成以下平移操作:- 将图形A向上平移3个单位长度。
- 将图形B向左平移4个单位长度。
- 将图形C向下平移2个单位长度。
小学数学平移练习题

小学数学平移练习题练习题一:图形平移1. 小明用方格纸做了一个图形,如图所示。
请你将这个图形向右平移两个单位,并用方格纸绘制平移后的图形。
2. 用已知线段作为边,分别绘制一个正方形、一个长方形和一个菱形。
然后将这些图形分别向下平移三个单位,并用方格纸绘制平移后的图形。
3. 小红用三角尺绘制了一个直角三角形ABC,其中∠ABC为直角。
请你将这个三角形向左平移四个单位,并用三角尺绘制平移后的三角形。
练习题二:图形的翻转1. 小明用方格纸做了一个图形,如图所示。
请你将这个图形以原点为对称中心进行翻转,并用方格纸绘制翻转后的图形。
2. 用已知线段作为边,分别绘制一个正方形、一个长方形和一个菱形。
然后将这些图形以原点为对称中心进行翻转,并用方格纸绘制翻转后的图形。
3. 小红用三角尺绘制了一个等腰直角三角形,其中∠ABC为直角,AB=BC。
请你将这个三角形以AB为对称轴进行翻转,并用三角尺绘制翻转后的三角形。
练习题三:图形的旋转1. 小明用方格纸做了一个图形,如图所示。
请你将这个图形以原点为中心逆时针旋转90°,并用方格纸绘制旋转后的图形。
2. 用已知线段作为边,分别绘制一个正方形、一个长方形和一个菱形。
然后将这些图形以原点为中心逆时针旋转180°,并用方格纸绘制旋转后的图形。
3. 小红用三角尺绘制了一个等边三角形ABC。
请你将这个三角形以顶点B为中心逆时针旋转60°,并用三角尺绘制旋转后的三角形。
练习题四:坐标系中的平移1. 在坐标系中,点A(-3, 2)、B(-1, 5)、C(0, -1)、D(-4, -3)分别表示平面上的四个点。
请你将这些点向右平移5个单位,并写出平移后的坐标。
2. 在坐标系中,点E(2, 1)、F(4, -3)、G(5, 0)、H(1, -2)分别表示平面上的四个点。
请你将这些点向左平移3个单位,并写出平移后的坐标。
3. 在坐标系中,点I(0, 3)、J(2, 0)、K(3, 1)、L(-1, -2)分别表示平面上的四个点。
五年级上册平移 练习题

五年级上册平移练习题题1:平移-正数1. 在坐标平面上,给定一个点A(2, 3),将点A向右平移4个单位,得到点B,求点B的坐标。
解:根据平移的性质,将点A向右平移4个单位,相当于将A的横坐标增加4个单位,纵坐标保持不变。
所以点B的横坐标为2 + 4 = 6,纵坐标为3。
因此,点B的坐标为(6, 3)。
2. 在平面直角坐标系上,给定点C(5, 7),将点C向上平移3个单位,得到点D,求点D的坐标。
解:根据平移的性质,将点C向上平移3个单位,相当于将C的纵坐标增加3个单位,横坐标保持不变。
所以点D的横坐标为5,纵坐标为7 + 3 = 10。
因此,点D的坐标为(5, 10)。
3. 在坐标平面上,给定点E(-2, -4),将点E向右平移7个单位,得到点F,求点F的坐标。
解:根据平移的性质,将点E向右平移7个单位,相当于将E的横坐标增加7个单位,纵坐标保持不变。
所以点F的横坐标为-2 + 7 = 5,纵坐标为-4。
因此,点F的坐标为(5, -4)。
题2:平移-负数1. 在平面直角坐标系上,给定点G(3, 5),将点G向左平移2个单位,得到点H,求点H的坐标。
解:根据平移的性质,将点G向左平移2个单位,相当于将G的横坐标减少2个单位,纵坐标保持不变。
所以点H的横坐标为3 - 2 = 1,纵坐标为5。
因此,点H的坐标为(1, 5)。
2. 在坐标平面上,给定点I(-4, -6),将点I向下平移5个单位,得到点J,求点J的坐标。
解:根据平移的性质,将点I向下平移5个单位,相当于将I的纵坐标减少5个单位,横坐标保持不变。
所以点J的横坐标为-4,纵坐标为-6 - 5 = -11。
因此,点J的坐标为(-4, -11)。
3. 在平面直角坐标系上,给定点K(0, 0),将点K向左平移3个单位,得到点L,求点L的坐标。
解:根据平移的性质,将点K向左平移3个单位,相当于将K的横坐标减少3个单位,纵坐标保持不变。
所以点L的横坐标为0 - 3 = -3,纵坐标为0。
二年级平移练习题

二年级平移练习题一、选择题:1. 平移是指图形在平面内沿着某个方向移动一定的距离,下列哪个图形发生了平移?A. 一个正方形旋转90度B. 一个三角形沿着直线移动了5厘米C. 一个长方形缩小了一半2. 如果一个图形向右平移了3个单位,那么它的哪个坐标会发生变化?A. 横坐标B. 纵坐标C. 两个坐标都会变3. 下列哪个操作不是平移?A. 一个圆沿着直线移动了一段距离B. 一个长方形沿着对角线移动了一段距离C. 一个正方形沿着边旋转二、填空题:1. 平移图形时,图形的______不变。
2. 如果一个图形沿着直线向右平移了5个单位,那么它的横坐标会增加______。
3. 平移图形时,图形的______和______不会发生变化。
三、判断题:1. 平移图形时,图形的形状和大小会发生变化。
(对/错)2. 平移图形时,图形的位置会发生变化,但方向不变。
(对/错)3. 旋转图形不是平移。
(对/错)四、计算题:1. 一个长方形的左上角坐标是(2,3),如果它向右平移了4个单位,那么新的左上角坐标是多少?2. 一个三角形的顶点坐标分别是(0,0),(3,0)和(1,4),如果它向上平移了2个单位,那么新的顶点坐标分别是多少?五、应用题:1. 一个长方形的长是5厘米,宽是3厘米,它的左下角坐标是(1,1)。
如果这个长方形沿着x轴正方向平移了6厘米,那么它新的左下角坐标是多少?2. 一个正方形的边长是4厘米,它的一个顶点坐标是(0,0)。
如果这个正方形沿着y轴正方向平移了3厘米,那么它新的顶点坐标分别是多少?六、图形题:1. 画出一个正方形,然后画出它向右平移了3厘米后的图形。
2. 画出一个等边三角形,然后画出它向上平移了2厘米后的图形。
七、思考题:1. 如果一个图形沿着对角线平移,那么它的坐标会如何变化?2. 请解释为什么旋转不是平移,并给出一个例子来说明。
八、综合题:1. 一个图形在平面直角坐标系中,它的一个顶点坐标是(3,4)。
平移练习题(含答案)
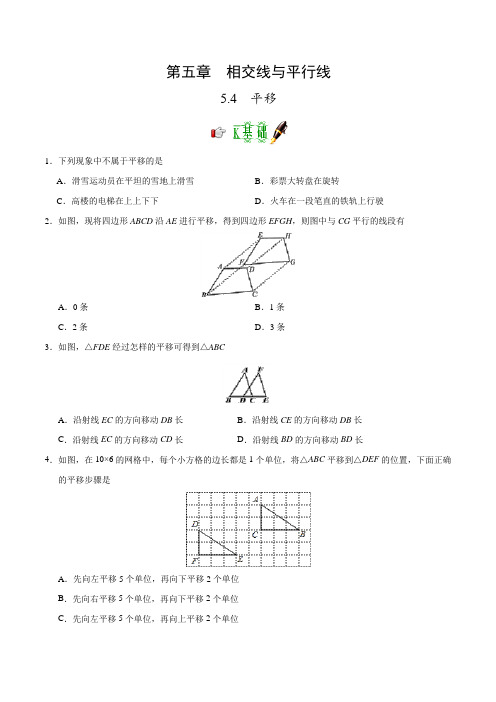
第五章相交线与平行线5.4 平移1.下列现象中不属于平移的是A.滑雪运动员在平坦的雪地上滑雪B.彩票大转盘在旋转C.高楼的电梯在上上下下D.火车在一段笔直的铁轨上行驶2.如图,现将四边形ABCD沿AE进行平移,得到四边形EFGH,则图中与CG平行的线段有A.0条B.1条C.2条D.3条3.如图,△FDE经过怎样的平移可得到△ABCA.沿射线EC的方向移动DB长B.沿射线CE的方向移动DB长C.沿射线EC的方向移动CD长D.沿射线BD的方向移动BD长4.如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是A.先向左平移5个单位,再向下平移2个单位B.先向右平移5个单位,再向下平移2个单位C.先向左平移5个单位,再向上平移2个单位D .先向右平移5个单位,再向下平移2个单位5.如图,将△ABE 向右平移得到△DCF ,AE 与CD 交于点G ,其中45B ∠=︒,60F ∠=︒,则AGC ∠=A .75︒B .105︒C .125︒D .85︒6.如图,将△ABE 向右平移2 cm 得到△DCF ,如果△ABE 的周长是16 cm ,那么四边形ABFD 的周长是A .16 cmB .18 cmC .20 cmD .21 cm7.如图,把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C 平移的距离CC '=____.8.如图,三角形ADE 是由三角形DBF 沿BD 所在的直线平移得到的,AE ,BF 的延长线交于点C.若∠BFD =45°,则∠C 的度数是 ________9.如图,A B C '''△ 是△ABC 向右平移4 cm 得到的,已知∠ACB =30°,B ′C =3 cm ,则∠C ′=_________,B ′C ′=________cm.10.要在台阶上铺设某种红地毯,已知这种红地毯每平方米的售价是40元,台阶宽为3米,侧面如图所示.购买这种红地毯至少需要__________元.11.如图,△ABC沿直线BC向右移了3 cm,得△FDE,且BC=6 cm,∠B=40°.(1)求BE;(2)求∠FDB的度数;(3)找出图中相等的线段(不另添加线段);(4)找出图中互相平行的线段(不另添加线段).12.如图,将△ABC平移,可以得到△DEF,点B的对应点为点E,请画出点A的对应点D、点C的对应点F的位置,并作出△DEF.13.如图,在三角形ABC中,已知AB=3cm,AC=4cm,BC=5cm.现将三角形ABC沿着垂直于BC的方向平移6cm,到三角形DEF的位置,求三角形ABC所扫过的面积.14.如图,在6个边长为1的小正方形及其部分对角线构成的图形中,如图从A点到B点只能沿图中已有的线段走,那么从A点到B点的最短距离的走法共有A.1种B.2种C.3种D.4种15.多边形的相邻两边互相垂直,则这个多边形的周长为A.a+b B.2a+bC.2a+2b D.2b+a16.如图,平移△ABC可得到△DEF,如果∠C=60°,AE=7cm,AB=4cm,那么∠F= ______ 度,DB= ______ cm.17.如图,某宾馆在重新装修后,准备在大厅的主楼梯上铺上红色地毯,已知这种红色地毯的售价为每平方米32元,主楼梯宽为2 m,其侧面与正面如图所示,则购买地毯至少需要多少元?18.如图,在四边形ABCD中,AD∥BC,且AD<BC,△ABC平移到△DEF的位置.(1)指出平移的方向和平移的距离;(2)试说明AD+BC=BF.19.(2017•铜仁)如图,△ABC沿着BC方向平移得到△A′B′C′,点P是直线AA′上任意一点,若△ABC,△PB′C′的面积分别为S1,S2,则下列关系正确的是A.S1>S2B.S1<S2C.S1=S2D.S1=2S21.【答案】B【解析】A.滑雪运动员在平坦的雪地上滑雪,属于平移,故本选项错误;B.彩票大转盘在旋转,不属于平移,故本选项正确;C. 高楼的电梯在上上下下,属于平移,故本选项错误;D. 火车在一段笔直的铁轨上行驶,属于平移,故本选项错误.故选:B.4.【答案】A【解析】根据网格结构,观察对应点A,D,点A向左平移5个单位,再向下平移2个单位即可到达点D 的位置,所以平移步骤是:先把△ABC 向左平移5个单位,再向下平移2个单位,故选A . 5.【答案】B【解析】∵△ABE 向右平移得到△DCF ,∴AB ∥CD ,AE ∥DF ,∴∠DCF =∠B =45°,∴∠CDF =180°- 45°-60°=75°,∴∠AGC =∠DGE =180°-75°=105°,故选B . 6.【答案】C【解析】已知,△ABE 向右平移2 cm 得到△DCF ,根据平移的性质得到EF =AD =2 cm ,AE =DF ,又因△ABE 的周长为16 cm ,所以AB +BE +AE =16 cm ,则四边形ABFD 的周长=AB +BC +CF +DF +AD =16+2+ 2=20(cm ),故选C . 7.【答案】5【解析】∵把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,∴三角板向右平移了5个单位,∴顶点C 平移的距离CC ′=5.故答案为:5. 8.【答案】45°【解析】∵△ADE 是由△DBF 沿BD 所在的直线平移得到的, ∴DE ∥BC ,∠BFD =∠AED , ∴∠AED =∠C ∴∠C =∠BFD =45°. 故答案是:45°. 9.【答案】30°,7【解析】∵A B C '''△ 是△ABC 向右平移4 cm 得到的, ∴BB ′=CC ′=4 cm ,∠C ′=∠ACB =30°, ∵B ′C =3 cm , ∴B ′C ′=4+3=7 cm . 故答案为:30°,7.12.【解析】如图:13.【解析】由题意可知,长方形BEFC的面积为5×6=30cm2,直角三角形ABC的面积为3×4÷2=6cm2,30+6=36cm2.∴三角形ABC所扫过的面积为36cm2.14.【答案】C【解析】如图,由题意和“两点之间线段最短”及“平行四边形的对边相等”可知,由A到B的最短距离的走法有下面三种:(1)由A→C→D→B;(2)由A→F→E→B;(3)由A→F→D→B,故选C.17.【解析】利用平移线段,把楼梯的横竖向上向左平移,构成一个长方形,长、宽分别为5米,3米,∴地毯的长度为5+3=8(米),∴地毯的面积为8×2=16(平方米),∴买地毯至少需要16×32=512(元).18.【解析】(1)平移的方向是点A到点D的方向,平移的距离是线段AD的长度;(2)∵△ABC平移到△DEF的位置,∴CF=AD,∵CF+BC=BF,∴AD+BC=BF.19.【答案】C【解析】∵△ABC沿着BC方向平移得到△A′B′C′,∴AA′∥BC′,∵点P是直线AA′上任意一点,∴△ABC,△PB′C′的高相等,∴S1=S2,故选C.。
平移与旋转练习题

平移与旋转练习题一、平移题1. 平面上有一个点P(2, 5),要将点P向右平移4个单位和向上平移3个单位,请求出平移后点的坐标。
解析:根据平移的性质,点向右平移4个单位等价于在横坐标上加4,点向上平移3个单位等价于在纵坐标上加3。
所以,平移后点的坐标为(2 + 4, 5 + 3),即(6, 8)。
2. 平面上有一个点Q(-3, 1),要将点Q向左平移2个单位和向下平移6个单位,请求出平移后点的坐标。
解析:根据平移的性质,点向左平移2个单位等价于在横坐标上减2,点向下平移6个单位等价于在纵坐标上减6。
所以,平移后点的坐标为(-3 - 2, 1 - 6),即(-5, -5)。
二、旋转题1. 平面上有一条线段AB,其中A的坐标为(-1, 3),B的坐标为(2, 6)。
以原点为中心,逆时针旋转30度,请求出旋转后线段AB的新坐标。
解析:以原点为中心逆时针旋转30度,相当于对每个点进行坐标变换。
设点A'和点B'是旋转后的点,根据旋转公式可以得到:A'的横坐标 = A的横坐标 * cos(30度) - A的纵坐标 * sin(30度)A'的纵坐标 = A的横坐标 * sin(30度) + A的纵坐标 * cos(30度)B'的横坐标 = B的横坐标 * cos(30度) - B的纵坐标 * sin(30度)B'的纵坐标 = B的横坐标 * sin(30度) + B的纵坐标 * cos(30度)代入A(-1, 3)和B(2, 6)的坐标,计算得到:A'的横坐标 = (-1) * cos(30度) - 3 * sin(30度) ≈ -0.134A'的纵坐标 = (-1) * sin(30度) + 3 * cos(30度) ≈ 2.732B'的横坐标 = 2 * cos(30度) - 6 * sin(30度) ≈ 2.598B'的纵坐标 = 2 * sin(30度) + 6 * cos(30度) ≈ 6.732所以,旋转后线段AB的新坐标为A'(-0.134, 2.732)和B'(2.598, 6.732)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平移练习题大全
平移是几何学中的一项重要概念,涉及到二维平面中物体在空间中
的移动。
通过平移,我们可以将一个图形沿着特定的方向和距离移动,而保持其形状和大小不变。
平移练习题是帮助学生巩固理解平移操作
以及应用平移进行图形变换的重要工具。
在本文中,我们将为您提供
一些常见的平移练习题,旨在帮助您更好地掌握平移的概念和应用。
一、基础练习题
1. 将矩形ABCD向右平移3个单位,写出平移后的矩形坐标。
2. 以点O为中心,将三角形ABC向左平移5个单位,写出平移后
的三角形坐标。
3. 将正方形EFGH向上平移2个单位,写出平移后的正方形坐标。
4. 在坐标系上,点A(2, 3)进行平移,平移向量为(4, -1),写出平移
后的点坐标。
5. 将线段MN按照向量(6, -2)进行平移,写出平移后的线段坐标。
二、综合练习题
1. 图形ABCD经过平移,得到图形A'B'C'D',已知A(3, 4)经过平移
变成A'(7, -1),求平移向量。
2. 将图形PQRST按照平移向量(2, 5)平移,得到图形P'Q'R'S'T',已
知点P(2, 3)平移后变成P'(4, 8),求图形PQRST的坐标。
3. 在坐标系上,绘制图形ABC,并将其按照向量(3, -2)进行平移,
得到图形A'B'C',求点C的坐标。
4. 图形MNPQ经过平移变换得到图形M'N'P'Q',已知平移向量为(-5, 3),求图形MNPQ的顶点坐标。
5. 已知三角形XYZ经过平移变换得到三角形X'Y'Z',平移向量为(-2, -6),求三角形XYZ的顶点坐标。
三、应用练习题
1. 在平面坐标系上,有一个矩形ABCD,其中A(-3, 2),B(4, 2),
C(4, -1),D(-3, -1),按照向量(-5, 3)将矩形进行平移得到矩形A'B'C'D',求A'B'C'D'的顶点坐标。
2. 图形WXYZ按照向量(2, -4)进行平移得到图形W'X'Y'Z',已知图
形WXYZ的坐标为W(-1, 3),X(2, 5),Y(1, 2),Z(-2, 0),求图形
W'X'Y'Z'的坐标。
3. 有一个平移向量为(3, 1),使得一点A(2, 4)经过平移到了点B,求点B的坐标。
4. 在平面坐标系上,有一个正方形EFGH,其中E(-2, -2),F(-2, 2),G(2, 2),H(2, -2),按照向量(1, -3)将正方形进行平移得到正方形
E'F'G'H',求E'F'G'H'的顶点坐标。
5. 图形PQRST按照向量(-3, 2)进行平移得到图形P'Q'R'S'T',已知点P(1, 5)平移后变成P'(x, y),求点P'的坐标。
通过以上的练习题,您可以更好地理解平移的操作和应用。
平移作为几何学中最基本的变换之一,对于理解和应用其他几何变换具有重要的作用。
通过多做练习题,您可以提高自己的几何学能力,并加深对平移的理解。
希望本文提供的平移练习题能对您的学习有所帮助。
祝您在几何学的学习中取得好成绩!。
